1.4.1正弦函数、余弦函数的图象导学案 2
专题1.4.1-2 正弦函数与余弦函数的图象与性质重难点题型(举一反三)(解析版)

1.4.1-2正、余弦函数的图象与性质重难点题型【举一反三系列】【知识点1 正弦函数、余弦函数图象的画法】1.描点法:按照列表、描点、连线三步法作出正弦函数、余弦函数图象的方法。
2.几何法:利用三角函数线作出正弦函数和余弦函数在]2,0[π内的图象,再通过平移得到x y sin =和cos y x =的图象。
3.五点法:先描出正弦曲线和余弦曲线的波峰、波谷和三个平衡位置这五个点,再利用光滑曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象。
要点诠释:(1)熟记正弦函数、余弦函数图象起关键作用的五点。
(2)若x R ∈,可先作出正弦函数、余弦函数在]2,0[π上的图象,然后通过左、右平移可得到x y sin =和cos y x =的图象。
(3)由诱导公式cos sin()2y x x π==+,故cos y x =的图象也可以将x y sin =的图象上所有点向左平移2π个单位长度得到。
【知识点2 正弦曲线、余弦曲线】1.定义:正弦函数sin ()y x x R =∈和余弦函数cos ()y x x R =∈的图象分别叫做正弦曲线和余弦曲线。
2.图象要点诠释:(1)由正弦曲线和余弦曲线可以研究正弦函数、余弦函数的性质。
(2)运用数形结合的思想研究与正弦函数、余弦函数有关的问题,如[]0,2x π∈,方程lg sin x x =根的个数。
【知识点3 函数图象的变换】图象变换就是以正弦函数、余弦函数的图象为基础通过对称、平移而得到。
sin sin()sin()y x y x y A x ϕωϕ=→=+→=+【知识点4 周期函数的定义】函数)(x f y =,定义域为I ,当I x ∈时,都有)()(x f T x f =+,其中T 是一个非零的常数,则)(x f y =是周期函数,T 是它的一个周期.1.定义是对I 中的每一个x 值来说的,只有个别的x 值满足)()(x f T x f =+或只差个别的x 值不满足)()(x f T x f =+都不能说T 是)(x f y =的一个周期.2.对于周期函数来说,如果所有的周期中存在一个最小的正数,就称它为最小正周期,三角函数中的周期一般都指最小正周期.【知识点5 正弦函数、余弦函数的图象和性质】【知识点6 正弦型函数和余弦型函数的性质】函数sin()y A x ωϕ=+与函数cos()y A x ωϕ=+可看作是由正弦函数sin y x =,余弦函数cos y x =复合而成的复合函数,因此它们的性质可由正弦函数sin y x =,余弦函数cos y x =类似地得到: (1)定义域:R ; (2)值域:[],A A -;(3)单调区间:求形如sin()y A x ωϕ=+与函数cos()(,0)y A x A ωϕω=+>的函数的单调区间可以通过解不等式的方法去解答,即把x ωϕ+视为一个“整体”,分别与正弦函数sin y x =,余弦函数cos y x =的单调递增(减)区间对应解出x ,即为所求的单调递增(减)区间.比如:由)(2222Z k k x k ∈+≤+≤-ππϕωππ解出x 的范围所得区间即为增区间,由)(23222Z k k x k ∈+≤+≤+ππϕωππ解出x 的范围,所得区间即为减区间.(4)奇偶性:正弦型函数sin()y A x ωϕ=+和余弦型函数cos()(,0)y A x A ωϕω=+>不一定具备奇偶性.对于函数sin()y A x ωϕ=+,当()k k z ϕπ=∈时为奇函数,当()2k k z πϕπ=±∈时为偶函数;对于函数cos()y A x ωϕ=+,当()k k z ϕπ=∈时为偶函数,当()2k k z πϕπ=±∈时为奇函数.要点诠释:判断函数sin()y A x ωϕ=+,cos()y A x ωϕ=+的奇偶性除利用定义和有关结论外,也可以通过图象直观判断,但不能忽视“定义域关于原点对称”这一前提条件.(5)周期:函数sin()y A x ωϕ=+及函数cos()y A x ωϕ=+的周期与解析式中自变量x 的系数有关,其周期为2T πω=.(6)对称轴和对称中心与正弦函数sin y x =比较可知,当()2x k k z πωϕπ+=±∈时,函数sin()y A x ωϕ=+取得最大值(或最小值),因此函数sin()y A x ωϕ=+的对称轴由()2x k k z πωϕπ+=±∈解出,其对称中心的横坐标()x k k z ωϕπ+=∈,即对称中心为,0()k k z πϕω-⎛⎫∈⎪⎝⎭.同理,cos()y A x ωϕ=+的对称轴由()x k k z ωϕπ+=∈解出,对称中心的横坐标由()2x k k z πωϕπ+=±∈解出.【考点1 正、余弦函数的定义域】【例1】(2019春•南湖区校级月考)已知函数()f x 的定义域为 .【分析】根据根式满足的条件,解三角不等式即可. 【答案】解:∵2sin (2x ﹣)﹣1≥0⇒sin (2x ﹣)≥,∴2k π+≤2x ﹣≤2k π+,k ∈Z ,∴k π+≤x ≤k π+,k ∈Z .故答案是{x|kπ+≤x≤kπ+,k∈Z}【点睛】本题考查函数的定义域及其求法,解三角不等式.【变式1-1】(2019秋•黄冈期末)函数y的定义域是.【分析】由题意可得sin x≥0,cos x≥0,故2kπ+0≤x≤2kπ+,k∈z,解出x的范围,即得所求.【答案】解:由题意可得sin x≥0,cos x≥0,∴2kπ+0≤x≤2kπ+,k∈z,故函数的定义域为(2kπ,2kπ+),k∈z,故答案为:(2kπ,2kπ+),k∈z.【点睛】本题考查求函数的定义域,以及三角函数在各个象限中的符号,得到2kπ+0≤x≤2kπ+,k∈z,是解题的关键,属于基础题.【变式1-2】函数1sin21sin2xyx+=-的定义域为.【分析】此为一分式函数,令分母不为0即可解出函数的定义域来.【答案】解:令﹣sin x≠0,即sin x≠,如图x≠2kπ+,x≠2kπ+=(2k﹣1)π﹣,k∈z,故其形式可以统一为x≠kπ+(﹣1)k,k∈z.所以函数的定义域为{x|x≠kπ+(﹣1)k,k∈z.}应填{x|x≠kπ+(﹣1)k,k∈z.}【点睛】考查定义域的求法与解三角方程,本题中把两种情况的答案合二为一是一个技巧,答题者应细心体会其中的规律.【变式1-3】(2019秋•安福县校级期中)函数(2cos 21)y lg x =+的定义域为 .【分析】由题意可得 ,化简可得 ,由此求出x 的范围,即得函数的定义域. 【答案】解:∵函数,∴,即 .化简可得 ,解得﹣<x <.故函数的定义域为(﹣,),故答案为(﹣,).【点睛】本题主要考查求余弦函数的定义域和值域,求对数函数的定义域,属于基础题. 【考点2 正、余弦函数的值域】【例2】(2018秋•启东市校级月考)函数()sin(2)4f x x π=-在区间[0,]2π上的值域为 .【分析】由题意利用正弦函数的定义域和值域,求得函数f (x )=sin 在区间上的值域.【答案】解:在区间上,2x ﹣∈[﹣,],sin (2x ﹣)∈[﹣,1],故函数f (x )=sin 在区间上的值域为[﹣,1],故答案为:[﹣,1].【点睛】本题主要考查正弦函数的定义域和值域,属于基础题.【变式2-1】(2019秋•射阳县校级期中)函数2()2cos 3sin 2f x x x =++,[6x π∈,2]3π的值域 . 【分析】根据同角公式化简函数解析式,得到关于sin x 的二次函数,根据二次函数的图象和性质,可得函数的值域.【答案】解:y =2cos 2x +3sin x +2=2(1﹣sin 2x )+3sin x +2=﹣2(sin x ﹣)2+,x ∈[,],∴sin x ∈[,1],∴当sin x =时,函数f (x )取最大值,当sin x =或sin x =1时,函数f (x )取最小值5, 故函数f (x )=2cos 2x +3sin x +2,x ∈[,]的值域为[5,],故答案为:[5,]【点睛】此题考查学生灵活运用同角公式化简求值,会利用二次函数的图象及增减性求出函数的值域.做题时注意余弦函数的值域.【变式2-2】(2019春•淄博校级月考)函数3sin 3sin xy x-=+的值域为 .【分析】先换元t =sin x ,t ∈[﹣1,1],,利用凑分母分离常数,然后逐一求式子的范围,即可求函数的值域.【答案】解:令t =sin x ,t ∈[﹣1,1], 所以:,∵﹣1≤t ≤1, ∴2≤t +3≤4, ∴, ∴, ∴, 函数的值域为. 故答案为:.【点睛】本题重点考查分式函数求值域问题,用到换元,利用凑分母分离常数.【变式2-3】(2019秋•西城区期末)已知函数()sin()6f x x π=+,其中[3x π∈-,]a .当2a π=时,()f x 的值域是 ;若()f x 的值域是1[2-,1],则a 的取值范围是 .【分析】当a =时,由x ∈[﹣,]利用正弦函数的定义域和值域可得f (x )的值域.若f (x )的值域是[﹣,1],则由正弦函数的图象可得≤a +≤,由此解得a 的取值范围. 【答案】解:当a =时,由x ∈[﹣,]可得﹣≤x +≤,∴﹣≤sin (x +)≤1,∴f (x )的值域是[﹣,1]. 若f (x )的值域是[﹣,1],则≤a +≤,解得≤a +≤π,即a 的取值范围是[,π],故答案为[﹣,1]、[,π].【点睛】本题主要考查正弦函数的定义域和值域,属于基础题. 【考点3 正、余弦函数作图】【例3】(2019春•郑州期末)已知函数()sin()(04f x x πωω=->,)x R ∈的最小正周期为π.(Ⅰ)求3()4f π; (Ⅱ)在给定的平面直角坐标系中,画出函数()y f x =在区间[2π-,]2π上的图象.【分析】(1)根据T =,求出周期,得到函数的解析式,代入值计算即可;(2)利用五点作图法作图即可. 【答案】解:(1)依题意得,T ==π,解得ω=2,所以f (x )=sin (2x ﹣),所以 f (π)=sin (2×﹣)=sin (π+)=﹣sin=﹣,(2)画出函数在区间上的图象如图所示:【点睛】本题考查了三角函数的周期性质,以及三角函数值的求法和函数图象的做法,属于基础题.【变式3-1】画出下列函数的简图:π;(1)1sinx∈,2]=-,[0y xπ.(2)3cos1x∈,2]y x=+,[0【分析】根据五点做出函数的简图,即可得到结论.【答案】解:(1)列表如下:画出图形,如图:(2)列表为函数图象如下:【点睛】本题主要考查三角函数的图象和性质,要求熟练掌握五点法作图以及图象之间的关系,属于基本知识的考查.【变式3-2】画出下列函数的图象.π(1)13cosy x=+,[0x∈,2]π.(2)2sin1x∈,2]=-,[0y x【分析】(1)用五点法作出函数y=1+3cos x在一个周期上的简图.(2)用五点法作出函数y=2sin x﹣1在一个周期上的简图.【答案】解:(1)列表:如图:(2)列表:如图:【点睛】本题主要考查用五点法作函数 y =A sin (ωx +φ)的图象、y =A cos (ωx +φ)的图象,属于基础题.【变式3-3】用多种方法在同一坐标系中画出下列函数. (1)sin y x =,[0x ∈,2]π (2)sin 1y x =+,[0x ∈,2]π (3)cos y x =,[2x π∈-,]2π (4)cos y x =-,[2x π∈-,3]2π. 【分析】利用五点作图法和图象的平移即可得到各个函数的图象. 【答案】解:同一坐标系中各个函数的图象如下:【点睛】本题主要考查三角函数的图象和性质,考察作图能力,属于基础题. 【考点4 正、余弦函数的最小正周期】 【例4】求下列函数的最小正周期. (1)sin(3)2y x π=+;(2)|cos |y x =【分析】(1)由条件根据函数y =A sin (ωx +φ)的周期为,可得结论. (2)由条件根据函数y =|A cos (ωx +φ)|的周期为•,可得结论. 【答案】解:(1)y =sin (x +3)的最小正周期为=4,(2)y =|cos x |的最小正周期为•=π.【点睛】本题主要考查三角函数的周期性,利用了函数y =A sin (ωx +φ)的周期为,函数y =|A cos(ωx +φ)|的周期为•,属于基础题.【变式4-1】求下列函数的最小正周期 (1)cos2y x =; (2)sin 2xy =;(3)1sin y x =+.【分析】利用三角函数的周期性及其求法即可得解. 【答案】解:(1)∵y =cos2x ,∴最小正周期T ==π;(2)∵y =sin ,∴最小正周期T ==4π;(3)∵y =1+sin x ,∴最小正周期T ==2π;【点睛】本题主要考查了三角函数的周期性及其求法,属于基础题. 【变式4-2】求下列函数的最小正周期(1)2sin()32xy π=-(2)1cos(2)36y x π=-(3)|sin |y x =【分析】分析:(1)利用了y =A sin (ωx +φ )的周期等于,即可求值;(2)利用了y =A cos (ωx +φ )的周期等于,即可求值;(3)根据y =|A sin (ωx +φ )|、y =|A sin (ωx +φ )|的周期等于,得出结论.【答案】解:(1)∵y =2sin (﹣)=﹣2sin (),∴T ==4π;(2)∵y =cos (2x ﹣),∴T ==π;(3)根据y =|sin x |的周期等于y =sin x 的周期的一半,故y =|sin x |的周期为×2π=π.【点睛】本题主要考查三角函数的周期性及其求法,利用了y =A sin (ωx +φ )、y =A cos (ωx +φ )的周期等于,y =|A sin (ωx +φ )|、y =|A sin (ωx +φ )|的周期等于,属于基础题.【变式4-3】求下列函数的最小正周期. (1)1cos(2)33y x π=-;(2)cos ||y x =.【分析】(1)由条件利用y =A cos (ωx +φ)的周期等于 T =,可得结论.(2)根据y =cos|x |=cos x ,而且y =A cos (ωx +φ)的周期等于 T =,可得结论.【答案】解:(1)y =cos (2x ﹣)的最小正周期为=π,(2)y =cos|x |=cos x 的最小正周期为=2π.【点睛】本题主要考查余弦函数的周期性,利用了y =A cos (ωx +φ)的周期等于 T =,属于基础题.【考点5 正、余弦函数的奇偶性】 【例5】判断下列函数的奇偶性: (1)cos2y x =,x R ∈; (2)cos(2)2y x π=-;(3)2sin()3y x π=+;(4)cos()4y x π=-.【分析】分别化简函数后根据正弦函数、余弦函数的图象和性质逐一判断即可. 【答案】解:(1)由余弦函数的图象和性质可知y =cos2x ,x ∈R 为偶函数; (2)∵y =cos (2x ﹣)=sin2x ,∴由正弦函数的图象和性质可知y =sin2x ,为奇函数;(3)∵y =sin (x +π)=﹣sin x ,∴由正弦函数的图象和性质可知y =﹣sin x ,为奇函数; (4)∵y =cos (x ﹣),且f (﹣x )=cos (﹣x ﹣)=cos (x +),∴由余弦函数的图象和性质可知y =cos (x ﹣),为非奇函数,非偶函数.【点睛】本题主要考察了正弦函数、余弦函数的图象和性质,属于基本知识的考查. 【变式5-1】判断下列函数的奇偶性 (1)()sin()f x x x π=+; (2)1cos ()sin xf x x-=. 【分析】(1)利用诱导公式化简函数的解析式,再根据函数的奇偶性的定义,得出结论. (2)利用半角公式化简函数的解析式,再根据函数的奇偶性的定义,得出结论. 【答案】解:(1)∵f (x )=x sin (π+x )=﹣x sin x ,它的定义域为R , 且满足f (﹣x )=﹣x •sin (﹣x )=x sin x =f (x ),故该函数为偶函数. (2)对于函数 f (x )==tan ,它的定义域为{x |x ≠k π,k ∈Z },关于原点对称,且满足f (﹣x )=tan (﹣)=﹣tan =﹣f (x ), 故该函数为奇函数.【点睛】本题主要考查三角公式,三角函数的奇偶性的判断方法,属于基础题.【变式5-2】判断下列函数的奇偶性:(1)()2f x x ; (2)33()sin()42x f x π=+;(3)()f x =.【分析】求出定义域,判断是否关于原点对称,注意运用诱导公式,定义域化简函数式,再计算f (﹣x ),与f (x )比较即可判断其偶性.【答案】解:(1)定义域为R ,f (﹣x )=sin (﹣2x )=﹣sin2x =﹣f (x ),则f (x )为奇函数; (2)f (x )=sin (+)=﹣cos,定义域为R ,f (﹣x )=﹣cos (﹣)=﹣cos=f (x ), 则f (x )为偶函数;(3)由1﹣cos x ≥0且cos x ﹣1≥0,则cos x =1, 解得,x =2k π,k ∈Z ,则定义域关于原点对称,由于f (x )=0,则f (﹣x )=f (x ),且f (﹣x )=﹣f (x ), 则f (x )既是奇函数,也是偶函数.【点睛】本题考查函数的奇偶性的判断,注意运用定义,考查运算能力,属于基础题. 【变式5-3】判断下列函数的奇偶性. (1)1sin cos ()1sin cos x xf x x x--=++;(2)44()sin cos cos 2f x x x x =-+.【分析】(1)容易判断f (x )的定义域包含x =,不包含,即定义域不关于原点对称,从而得出f (x )为非奇非偶函数;(2)容易得出f (﹣x )=f (x ),从而得出f (x )为偶函数. 【答案】解:(1)∵;∴时,f (x )有意义,时,f (x )没意义;∴f (x )的定义域关于原点不对称; ∴f (x )为非奇非偶函数;(2)f (﹣x )=sin 4(﹣x )﹣cos 4(﹣x )+cos (﹣2x )=sin 4x ﹣cos 4x +cos2x =f (x ); 即f (﹣x )=f (x ); ∴f (x )为偶函数.【点睛】考查奇函数、偶函数的定义,奇函数、偶函数定义域的特点. 【考点6 正、余弦函数的对称轴及对称中心】【例6】(2019春•资阳区校级月考)求函数12sin()26y x π=-的对称轴和对称中心.【分析】由条件根据正弦函数的对称性,求得函数y =2sin (x ﹣)的对称轴和对称中心. 【答案】解:对于函数y =2sin (x ﹣),令x ﹣=k π+,k ∈z ,求得x =2k π+,故函数的对称轴方程为 x =2k π+,k ∈z .令x ﹣=k π,k ∈z ,求得x =2k π+,故函数的对称中心为 (2k π+,0)k ∈z .【点睛】本题主要考查正弦函数的对称性,属于基础题. 【变式6-1】求2cos(2)6y x π=-单调性对称轴对称中心.【分析】对于函数y =2cos (2x ﹣),令2k π﹣π≤2x ﹣≤2k π,求得x 的范围,可得函数的增区间;令2k π≤2x ﹣≤2k π+π,求得x 的范围,可得函数的减区间.令2x ﹣=k π,求得x 的值,可得函数的图象的对称中心. 【答案】解:对于y =2cos (﹣2x )=2cos (2x ﹣), 令2k π﹣π≤2x ﹣≤2k π,求得k π﹣≤x ≤k π+,可得函数的增区间为[k π﹣,k π+],k ∈z . 令2k π≤2x ﹣≤2k π+π,求得k π+≤x ≤k π+, 可得函数的减区间为[k π+,k π+],k ∈z . 令2x ﹣=k π,求得x =+, 可得函数的图象的对称中心为(+,0).【点睛】本题主要考查余弦函数的单调性、余弦函数的图象的对称中心,属于基础题.【变式6-2】变式训练1:求函数的对称轴,对称中心(1)1())4f x x π=+;(2)1()2cos()123f x x π=-+.【分析】直接根据正余弦函数的图象及性质求解即可. 【答案】解:(1)f (x )=sin (2x +π);令2x +π=,k ∈Z 可得:x =,∴对称轴方程为:x =,k ∈Z 令2x +π=k π,k ∈Z 可得:x =,∴对称中心(,0).k ∈Z(2)f (x )=2cos (x ﹣)+1.令x ﹣=,k ∈Z可得:x =2k π ∴对称中心(2k π,1).k ∈Z令x =k π,k ∈Z可得:x =,∴对称轴方程为:x =,k ∈Z【点睛】本题考查了正余弦函数的图象及性质的应用.属于基础题. 【变式6-3】求下列函数图象的对称轴、对称中心. (1)sin()24x y π=-;(2)2sin(2)3y x π=++.【分析】由条件利用正弦函数的图象的对称性,得出结论.【答案】解:对于(1)y =sin (﹣),令﹣=k π+,求得x =2k π+,可得函数的图象的对称轴为x =2k π+,k ∈Z .令﹣=k π,求得x =2k π+,可得函数的图象的对称中心为(2k π+,0),k ∈Z .(2)对于y =2+sin (+2x ),令2x +=k π+,求得x =k π+,可得函数的图象的对称轴为x =k π+,k ∈Z .令2x +=k π,求得x =k π﹣,可得函数的图象的对称中心为(k π﹣,0),k ∈Z .【点睛】本题主要考查正弦函数的图象的对称性,属于基础题. 【考点7 正、余弦函数的单调性】【例7】(2019•上城区校级模拟)设函数()3sin()(0)4f x x πωω=+>,且以23π为最小正周期.(1)求()f x 的解析式;(2)求()f x 的对称轴方程及单调递增区间.【分析】(1)由题意利用正弦函数的周期性,求得ω的值,可得函数的解析式.(2)由题意利用正弦函数的图象的对称性,求得它的对称轴方程;再利用正弦函数单调性求得它的单调递增区间.【答案】解:(1)由于函数,且以为最小正周期,∴=,∴ω=3, f (x )=3sin (3x +).(2)令3x +=k π+,求得x =+,故函数的图象的对称轴方程为 x =+,k ∈Z .令 2k π﹣≤3x +≤2k π+,求得﹣≤x ≤+,可得函数的增区间为[﹣,+],k ∈Z .【点睛】本题主要考查正弦函数的周期性,正弦函数单调性以及它的图象的对称性,属于基础题. 【变式7-1】(2018秋•嘉兴期末)已知函数()2sin(2)()6f x x m m R π=-+∈的最小值为1. (Ⅰ)求m 的值及取此最小值时的x 值;(Ⅱ)求函数()f x 的最小正周期和单调递增区间.【分析】(Ⅰ)由题意利用正弦函数的最值,求出m 的值及取此最小值时的x 值.(Ⅱ)利用正弦函数的周期性以及单调性,求得函数f (x )的最小正周期和单调递增区间. 【答案】解:(Ⅰ)函数 f (x )=2sin (2x ﹣)+m (m ∈R )的最小值为﹣2+m =1,∴m =3. 取取此最小值时,2sin (2x ﹣)=﹣1,2x ﹣=2k π﹣,求得x =k π﹣,k ∈Z .(Ⅱ)由(Ⅰ)可得 f (x )=2sin (2x ﹣)+3,它的最小正周期为=π,令2k π﹣≤2x ﹣≤2k π+,求得k π﹣≤x ≤k π+,可得函数的增区间为[k π﹣,k π+],k ∈Z .【点睛】本题主要考查正弦函数的最值,周期性以及单调性,属于中档档题. 【变式7-2】(2019春•靖远县期末)已知函数1()2cos()212f x x π=+.(1)求()f x 的单调递增区间; (2)求不等式()1f x >的解集.【分析】(1)根据余弦函数的单调增区间可得,然后解出x 的范围即可;(2)由f (x )>1可得,则,k ∈Z ,解出x 的范围即可. 【答案】解:(1), 由, ∴,∴f (x )的单调递增区间为;(2)∵f (x )>1,∴,∴,∴,k ∈Z , ∴,k ∈Z ,∴不等式的解集为,k ∈Z .【点睛】本题考查了余弦函数的单调性和解三角不等式,考查了运算能力,属基础题.【变式7-3】(2019秋•福建月考)已知函数())4f x x π=-,[,]82x ππ∈-(1)求函数()f x 的单调区间.(2)求函数()f x 在区间[,]82ππ-上的最小值和最大值,并求出取得最值时x 的值.【分析】(1)x ∈[﹣,]⇒2x ﹣∈[﹣,],利用余弦函数的单调性即可求得f (x )=cos (2x ﹣)的单调区间;(2)利用(1)f (x )=cos (2x ﹣)在区间[﹣,]上为增函数,在区间[,]上为减函数,即可求得其最小值和最大值及取得最值时x 的值. 【答案】解:(1)∵f (x )=cos (2x ﹣),x ∈[﹣,],∴2x ﹣∈[﹣,],由﹣≤2x ﹣≤0得:﹣≤x ≤,∴当x ∈[﹣,]时,函数f (x )的单调递增区间为[﹣,];由0≤2x ﹣≤得,≤x ≤,∴当x ∈[﹣,]时,函数f (x )的单调减区间为[,];(2)∵f (x )=cos (2x ﹣)在区间[﹣,]上为增函数,在区间[,]上为减函数,又f =0, f =, f=cos=﹣cos =﹣1,∴函数f (x )在区间[﹣,]上的最大值为,此时x =,最小值为﹣1,此时x =.【点睛】本题考查余弦函数的单调性,考查余弦函数的定义域和值域,考查运算能力,属于中档题. 【考点8 正、余弦函数的综合应用】【例8】(2019春•延吉市校级期中)已知函数()12sin(2)3f x x π=+-.(1)求对称轴,对称中心(2)求()f x 在[,]42x ππ∈的最大值和最小值;(3)若不等式|()|2f x m -<在[,]42x ππ∈上恒成立,求实数m 的取值范围【分析】(1)令2x ﹣=可得对称轴,令2x ﹣=k π可得对称中心;(2)由x ∈[],可求,结合正弦函数的图象及性质可求;(3)由|f (x )﹣m |<2可得m ﹣2<f (x )<m +2恒成立,从而有m >f (x )max ﹣2且m <f (x )min +2可求.【答案】解:(1)令2x ﹣=可得对称轴x =,k ∈z , 令2x ﹣=k π可得,x =,k ∈z 可得对称中心为(,1),k ∈z ,(2)∵f (x )=1+2sin (2x ﹣),∵x ∈[],∴,∴,∴f (x )在x ∈[]的最大值3,最小值2,(3)∵|f (x )﹣m |<2在x ∈[]上恒成立,∴m ﹣2<f (x )<m +2,∴m >f (x )max ﹣2且m <f (x )min +2, ∴1<m <4,即m 的取值范围是(1,4).【点睛】本题主要考查了正弦函数的图象与性质的综合应用,解题 的关键是性质的熟练掌握并能灵活应用.【变式8-1】已知函数()2sin(2)26f x a x a b π=-+++的定义域为[0,]2π,值域为[5-,1].(1)求实数a ,b 的值;(2)求函数()4sin()3g x a bx π=--的最小值并求出对应x 的集合.【分析】(1)由x 的取值范围,求出2x +的取值范围,从而求出2sin (2x +)的取值范围;讨论a>0、a <0时,函数f (x )的最值问题,从而求出a 和b 的值.(2)根据(1)的结论,分两种情况讨论,根据正弦函数的性质即可求出. 【答案】解:(1)∵0≤x ≤,∴≤2x +≤, ∴≤sin (2x +)≤1, ∴﹣1≤2sin (2x +)≤2,当a >0时,解得a =2,b =﹣7, 当a <0时,,解得a =﹣2,b =1,(2)当a =2,b =﹣7时,g (x )=﹣8sin (﹣7x ﹣)=8sin (7x +),其最小值为﹣8,7x +=﹣+2k π,k ∈Z ,即x =﹣+,k ∈Z ,对应x 的集合为{x |x =﹣+,k ∈Z },当a =﹣2,b =1时,g (x )=﹣8sin (x ﹣)=﹣8sin (x ﹣),其最小值为﹣8,x ﹣=+2k π,k ∈Z ,即x =π+2k π,k ∈Z ,对应x 的集合为{x |x =π+2k π,k ∈Z }.【点睛】本题考查了三角函数的图象与应用问题,解题时应根据三角函数的最值与值域的关系,利用分类讨论的方法,求出a 和b 的值. 【变式8-2】已知函数23()sin cos 2f x x a x =+-,a R ∈. (1)当1a =时,求函数()f x 的最大值;(2)对于区间[0,)2π上的任意x ,都有1)(≤x f 成立,求实数a 的取值范围.【分析】(1)把a =1代入函数解析式,利用平方关系化正弦为余弦,平方后求最值; (2)f (x )=sin 2x +a cos x ﹣=,令t =cos x 换元,则原函数化为y =.由f (x )≤1,得≤1在t ∈(0,1]上成立,分离参数a ,由对勾函数的单调性求得g (t )=t +在t ∈(0,1]上的最小值,则答案可求.【答案】解:(1)当a =1时,f (x )=sin 2x +cos x ﹣ ==.当cos x =时,f (x )取最大值为;(2)f (x )=sin 2x +a cos x ﹣=,令t =cos x ,∵x ∈[0,),∴t =cos x ∈(0,1].则原函数化为y =.由f (x )≤1,得≤1在t ∈(0,1]上成立,即,也就是a ≤t +在t ∈(0,1]上成立,令g (t )=t +,由对勾函数的单调性可得在t ∈(0,1]上g (t )的最小值为g (1)=.∴a.即实数a 的取值范围是(﹣∞,].【点睛】本题考查三角函数中的恒等变换应用,训练了利用分离参数法求解恒成立问题,考查利用对勾函数的单调性求最值,是中档题.【变式8-3】(2019春•鹤壁期末)已知函数()sin(2)3f x x π=-.(Ⅰ)当1(2x π∈-,)3π-,2(0,)6x π∈时12()()0f x f x +=,求12x x -的值; (Ⅱ)令()()3F x f x =-,若对任意x 都有2()(2)()20F x m F x m -+++…0≤m 恒成立,求m 的最大值. 【分析】(Ⅰ)运用正弦函数的诱导公式,解方程即可得到所求值;(Ⅱ)令t =F (x ),可得t ∈[﹣4,﹣2],转化为二次不等式恒成立问题解法,结合图象可得m 的最大值. 【答案】解:(Ⅰ)f (x 1)+f (x 2)=0, 即为sin (2x 1﹣)+sin (2x 2﹣)=0, 即有sin (2x 1﹣)=﹣sin (2x 2﹣)=sin (﹣2x 2),可得2x 1﹣=2k π+﹣2x 2,或2x 1﹣=2k π+π﹣+2x 2,k ∈Z ,即有x 1+x 2=k π+或x 1﹣x 2=k π﹣,k ∈Z , 由x 1∈(﹣,﹣),x 2∈(0,),可得x 1﹣x 2∈(﹣,﹣),可得x 1﹣x 2=﹣; (Ⅱ)F (x )=f (x )﹣3即F (x )=sin (2x ﹣)﹣3,令t =F (x ),可得t ∈[﹣4,﹣2],对任意x都有F2(x)﹣(2+m)F(x)+2+m≤0恒成立,即为t2﹣(2+m)t+2+m≤0,则16+4(2+m)+2+m≤0,4+2(2+m)+2+m≤0,即m≤﹣.且m≤﹣,.解得m≤﹣,即m的最大值为﹣.【点睛】本题考查正弦函数的图象和性质,考查换元法和二次函数的性质,以及化简运算能力,属于中档题.。
高中数学导高中数学学案2:1.4.1 正弦函数、余弦函数的图象

必修四 第一章 三角函数1.4.1 正弦函数、余弦函数的图象使用说明:“自主学习”15分钟,发现问题,小组讨论,展示个人成果,教师对重点概念点评. “合作探究”10分钟,小组讨论,互督互评,展示个人成果,教师对重点讲评. “巩固练习”5分钟,组长负责,组内点评.“个人总结”5分钟,根据组内讨论情况,指出对规律,方法理解不到位的问题. “能力展示”5分钟,教师作出总结性点评. 通过本节学习应达到如下目标:1.认识并理解五点法作正弦函数、余弦函数图象2.发展运用数学语言的能力,感受集合语言的意义和作用,学习从数学的角度认识世界. 3.通过合作学习培养合作精神. 学习重点:五点法作正弦函数、余弦函数图象 学习难点:五点法作正弦函数、余弦函数图象 学习过程 一. 自主学习 ①“五点法”作简图:观察y=Sinx ,x ∈[0,2π]的图象,在作图连线过程中起关键作用的是哪几个点? 能否利用这些点作出正弦函数的简图?关键五点:(0,0)、(2π,1)、(π,0)、(32π ,-1)、(2π,0)。
事实上,只要指出这五个点,y=Sinx ,x ∈[0,2π]的图象形状就基本定位了。
因此在精确度要求不高时,我们就常先找出这五个关键点,然后用光滑的曲线将它们连结起来,就得到函数的简图,这种作图的方法称为“五点法”作图。
注: 五个关键点中,重点应突出点的横坐标,纵坐标即相应函数值;画简图时应掌握曲线的形状及弯曲的“方向”。
二.合作探讨如何准确简便的做出正弦函数与余弦函数图象二. 巩固练习1.已知函数在一个周期内的图象如图所示,要得到函数的图象,则需将函数的图象( )A .向右平移B .向左平移C .向右平移D .向左平移 2.为了得到的图象,只需将的图象( )A .向左平移个单位B .向右平移个单位C .向左平移个单位 D .向右平移个单位)0(sin >=ωωx y )1221sin(π+=x y x y ωsin=12π12π6π6π)32sin(π+=x y x y 2sin =3π3π6π6π3.设ω>0,函数y=sin(ωx+3π)的图像向右平移34π个单位后与原图像重合,则ω的最小值是( ) (A )32 (B)34 (C)23(D)3 4.将函数x y 4sin =的图像向左平移12π个单位,得到)4sin(ϕ+=x y 的图像,则ϕ等于( ) A 、12π-B 、3π-C 、3π D 、12π 5.若函数的图象相邻两条对称轴间距离为,则等于( ) A .B .C .2D .46.已知函数2sin()(0)y x ωϕω=+>)在区间[]02π,的图像如右:那么ω=( ) A .1B .2C .21D .317.函数的图像的两个相邻零点为和(,0)2π,且该函数的最大值为2,最小值为-2,则该函数的解析式为( ) A 、 B 、)42sin(2π+=x y C 、)623sin(2π+=x y D 、)62sin(2π+=x y 8.若函数()sin()f x x ωϕ=+的图像(部分)如下图所示,则ω和ϕ的取值是( ) A 、1,3πωϕ==B 、1,3πωϕ==-C 、1,26πωϕ== D 、1,6πωϕ==- cos()3y x πω=+(0)ω>2πω1212)0,0)(sin(πϕϕω<<>+=A x A y )0,6(π-)423sin(2π+=x yx四.个人收获与问题 知识:方法:我的问题五.拓展能力:已知()sin()(0,0,)22f x A x A ππωϕωϕ=+>>-≤≤的图象如右图(Ⅰ)求()y f x =的解析式;(Ⅱ)说明()y f x =的图象是由sin y x =的图象经过怎样的变换得到?答案:三. 巩固练习四. 1—8、DCCCC, BAC 五.拓展能力: 解: ( 1) 由图知A= 4由35466T πππ=-=,得109T π= 所以95ω=由 9562ππϕ⨯+=,得5πϕ= 所以,9()4sin()55f x x π=+(2) ①由sin y x =得图象向左平移5π单位得sin()5y x π=+的图象② 再由sin()5y x π=+图象的横坐标缩短为原来59得9sin()55y x π=+的图象③由9sin()55y x π=+的图象纵坐标伸长为原来的4倍得9()4sin()55f x x π=+的图象。
人教a版必修4学案:1.4.1正弦函数、余弦函数的图象(含答案)
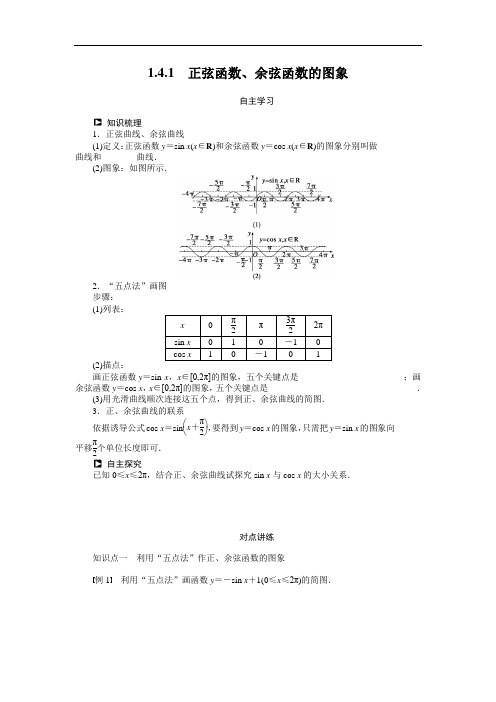
1.4.1 正弦函数、余弦函数的图象自主学习知识梳理1.正弦曲线、余弦曲线 (1)定义:正弦函数y =sin x (x ∈R )和余弦函数y =cos x (x ∈R )的图象分别叫做__________曲线和________曲线.(2)图象:如图所示.2.“五点法”画图 步骤: (1)列表:x 0 π2 π 3π2 2π sin x 0 1 0 -1 0 cos x1-11(2)描点:画正弦函数y =sin x ,x ∈[0,2π]的图象,五个关键点是________________________;画余弦函数y =cos x ,x ∈[0,2π]的图象,五个关键点是__________________________________.(3)用光滑曲线顺次连接这五个点,得到正、余弦曲线的简图. 3.正、余弦曲线的联系依据诱导公式cos x =sin ⎝⎛⎭⎫x +π2,要得到y =cos x 的图象,只需把y =sin x 的图象向______平移π2个单位长度即可.自主探究已知0≤x ≤2π,结合正、余弦曲线试探究sin x 与cos x 的大小关系.对点讲练知识点一 利用“五点法”作正、余弦函数的图象例1 利用“五点法”画函数y =-sin x +1(0≤x ≤2π)的简图.回顾归纳作正弦、余弦曲线要理解几何法作图,掌握五点法作图.“五点”即y=sin x或y=cos x的图象在一个最小正周期内的最高点、最低点和与x轴的交点.“五点法”是作简图的常用方法.变式训练1利用“五点法”画函数y=-1-cos x,x∈[0,2π]的简图.知识点二利用三角函数图象求定义域例2求函数f(x)=lg sin x+16-x2的定义域.回顾归纳一些三角函数的定义域可以借助函数图象直观地观察得到,同时要注意区间端点的取舍.变式训练2求函数f(x)=cos x+lg(8x-x2)的定义域.知识点三利用三角函数的图象判断方程解的个数例3在同一坐标系中,作函数y=sin x和y=lg x的图象,根据图象判断出方程sin x =lg x的解的个数.回顾归纳三角函数的图象是研究函数的重要工具,通过图象可较简便的解决问题,这正是数形结合思想方法的应用.变式训练3求方程x2=cos x的实数解的个数.1.正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础.2.五点法是画三角函数图象的基本方法,要熟练掌握,与五点法作图有关的问题是高考常考知识点之一.课时作业一、选择题1.函数y =sin x (x ∈R )图象的一条对称轴是( ) A .x 轴 B .y 轴C .直线y =xD .直线x =π22.函数y =-cos x 的图象与余弦函数y =cos x 的图象( ) A .只关于x 轴对称 B .关于原点对称 C .关于原点、x 轴对称 D .关于原点、坐标轴对称 3.如果x ∈[0,2π],则函数y =sin x +-cos x 的定义域为( )A .[0,π] B.⎣⎡⎦⎤π2,3π2C.⎣⎡⎦⎤π2,πD.⎣⎡⎦⎤3π2,2π 4.在(0,2π)内使sin x >|cos x |的x 的取值范围是( ) A.⎝⎛⎭⎫π4,3π4 B.⎝⎛⎦⎤π4,π2∪⎝⎛⎦⎤5π4,3π2 C.⎝⎛⎭⎫π4,π2 D.⎝⎛⎭⎫5π4,7π4 5.已知函数y =2sin x ⎝⎛⎭⎫π2≤x ≤5π2的图象与直线y =2围成一个封闭的平面图形,那么此封闭图形的面积( )A .4B .8C .4πD .2π二、填空题6.函数y =cos x1+sin x的定义域为____________.7.函数y =2cos x +1的定义域是______________.8.设0≤x ≤2π,且|cos x -sin x |=sin x -cos x ,则x 的取值范围为________.三、解答题9.利用“五点法”作出下列函数的简图:(1)y =-sin x (0≤x ≤2π);(2)y =1+cos x (0≤x ≤2π).10.分别作出下列函数的图象.(1)y =|sin x |,x ∈R ;(2)y =sin|x |,x ∈R .§1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象答案知识梳理1.(1)正弦 余弦2.(2)(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0) (0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫3π2,0,(2π,1) 3.左 自主探究解 正、余弦曲线如图所示.由图象可知①当x =π4或x =5π4时,sin x =cos x ,②当π4<x <5π4时,sin x >cos x .③当0≤x <π4或5π4<x ≤2π时,sin x <cos x .对点讲练例1 解 利用“五点法”作图 取值列表:x 0 π2π3π2 2π sin x 0 1 0 -1 0 1-sin x 1 0 121变式训练1 x0 π2 π 3π2 2π cos x 1 0 -1 0 1 -1-cos x-2-1-1-2例2 解 由题意,x 满足不等式组⎩⎨⎧sin x >016-x 2≥0, 即⎩⎨⎧-4≤x ≤4sin x >0,作出y =sin x 的图象,如图所示.结合图象可得:x ∈[-4,-π)∪(0,π).变式训练2 解 由⎩⎪⎨⎪⎧8x -x 2>0cos x ≥0,得⎩⎨⎧0<x <8cos x ≥0.画出y =cos x ,x ∈[0,3π]的图象,如图所示.结合图象可得:x ∈⎝⎛⎦⎤0,π2∪⎣⎡3π2,5π2.例3 解 建立坐标系xOy ,先用五点法画出函数y =sin x ,x ∈[0,2π]的图象,再依次向左、右连续平移2π个单位,得到y =sin x 的图象.描出点⎝⎛⎭⎫1101,(1,0),(10,1)并用光滑曲线连接得到y =lg x 的图象,如图所示.由图象可知方程sin x =lg x 的解有3个.变式训练3 解 作函数y =cos x 与y =x 2的图象,如图所示, 由图象,可知原方程有两个实数解.课时作业 1.D2.C [结合图象易知.]3.C [∵sin x ≥0且-cos x ≥0,∴x ∈⎣⎡⎦⎤π2π.] 4.A[∵sin x >|cos x |,∴sin x >0,∴x ∈(0,π),在同一坐标系中画出y =sin x ,x ∈(0,π)与y =|cos x |,x ∈(0,π)的图象,观察图象易得x ∈⎝⎛⎭⎫π4,3π4.]5.C [数形结合,如图所示.y =2sin x ,x ∈⎣⎡⎦⎤π2,5π2的图象与直线y =2围成的封闭平面图形面积相当于由x =π2,x =5π2, y =0,y =2围成的矩形面积,即S =⎝⎛⎭⎫5π2-π2×2=4π.]6.⎝⎛⎦⎤-π22k π,π2+2k π (k ∈Z ) 解析 x 应满足:⎩⎪⎨⎪⎧1+sin x ≠0⇒sin x ≠-1,cos x ≥0,综合正、余弦函数图象可知:-π2+2k π<x ≤π2+2k π. 7.⎣⎡⎦⎤2k π-2π3,2k π+2π3 ,(k ∈Z ) 解析 由2cos x +1≥0,得cos x ≥-12,∴2k π-2π3x ≤2k π+2π3,k ∈Z .8.⎣⎡⎦⎤π4,5π4 解析 由题意知sin x -cos x ≥0,即cos x ≤sin x ,在同一坐标系画出y =sin x ,x ∈[0,2π] 与y =cos x ,x ∈[0,2π]的图象,如图所示:观察图象得:π4≤x ≤5π4.9.解 利用“五点法”作图. (1)列表:(2)列表:10.解 (1)y =|sin x |=⎩⎪⎨⎪⎧sin x (2k π≤x ≤2k π+π)-sin x (2k π+π<x ≤2k π+2π)(k ∈Z ).其图象如图所示,(2)y =sin|x |=⎩⎪⎨⎪⎧sin x (x ≥0)-sin x (x <0),其图象如图所示,。
1.4.1正弦函数、余弦函数的图象知识点归纳与练习(含详细答案)(可编辑修改word版)

2第一章 三角函数 §1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象课时目标 1.了解正弦函数、余弦函数的图象.2.会用“五点法”画出正弦函数、余弦函数的图象.1. 正弦曲线、余弦曲线2. “五点法”画图画正弦函数 y =sin x ,x ∈[0,2π]的图象,五个关键点是 ; 画余弦函数 y =cos x ,x ∈[0,2π]的图象,五个关键点是.3.正、余弦曲线的联系依据诱导公式 cos x =sin (x +π),要得到 y =cos x 的图象,只需把 y =sin x 的图象向π平移 个单位长度即可.2知识点归纳:1. 正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础.2. 五点法是画三角函数图象的基本方法,要熟练掌握,与五点法作图有关的问题是高考常考知识点之一.一、选择题 1. 函数 y =sin x (x ∈R )图象的一条对称轴是( ) A .x 轴 B .y 轴πC .直线 y =xD .直线 x =2π2. 函数 y =cos x (x ∈R )的图象向右平移2个单位后,得到函数 y =g (x )的图象,则 g (x )的解析式为( ) A .-sin x B .sin x C .-cos x D .cos x2 4 4 2 4 4π 3π3. 函数 y =-sin x ,x ∈[-2, 2]的简图是()4. 在(0,2π)内使 sin x >|cos x |的 x 的取值范围是()A.(π,3π)B.(π π] (5π 3π], ∪ , C.(π,π)D.(5π,7π)5. 若函数 y =2cos x (0≤x ≤2π)的图象和直线 y =2 围成一个封闭的平面图形,则这个封闭图 形的面积是( ) A .4 B .8 C .2π D .4π 6.方程 sin x =lg x 的解的个数是( )π7. 函数 y =sin x ,x ∈R 的图象向右平移2个单位后所得图象对应的函数解析式是 .8. 函数 y = 2cos x +1的定义域是 . 9. 方程 x 2-cos x =0 的实数解的个数是 . 10. 设 0≤x ≤2π,且|cos x -sin x |=sin x -cos x ,则 x 的取值范围为 . 三、解答题1.利用“五点法”作出下列函数的简图: (1)y =1-sin x (0≤x ≤2π);(2)y =-1-cos x (0≤x ≤2π).4 4 4 212.分别作出下列函数的图象.(1)y=|sin x|,x∈R;(2)y=sin|x|,x∈R.能力提升13.求函数f(x)=lg sin x+16-x2的定义域.14.函数f(x)=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k 有且仅有两个不同的交点,求k 的取值范围.( )解析 y =sin x −−−−−−→ y =sin x - 2 2 23 3知识梳理§1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象答案2.(0,0),( ,1),(π,0),( π,-1),(2π,0) (0,1),( ,0),(π,-1),( π,0),(2π,1)π 3 π 3 22223.左 作业设计1.D 2.B 3.D 4.A [∵sin x >|cos x |,∴sin x >0,∴x ∈(0,π),在同一坐标系中画出 y =sin x ,x ∈(0,π)与 y =|cos x |,x ∈(0,π)的图象,观察图象易得 x ∈(π,3π).]4 45.D [作出函数 y =2cos x ,x ∈[0,2π]的图象,函数 y =2cos x ,x ∈[0,2π]的图象与直线 y =2 围成的 平面图形,如图所示的阴影部分.利用图象的对称性可知该平面图形的面积等于矩形 OABC 的面积,又∵|OA |=2,|OC |=2π, ∴S 平面图形=S 矩形OABC =2×2π=4π.]6.C [用五点法画出函数 y =sin x ,x ∈[0,2π]的图象,再依次向左、右连续平移 2π 个单位, 得到 y =sin x 的图象.描出点 1,-1 ,(1,0),(10,1)并用光滑曲线连接得到 y =lg x 的图象,如图所示.10由图象可知方程 sin x =lg x 的解有 3 个.] 7.y =-cos x向右平移 2个单位 ( π)∵sin (x -π)=-sin (π-x )=-cos x ,∴y =-cos x . 8.[2k π-2π,2k π+2π],k ∈Z解析 2cos x +1≥0,cos x ≥-1,结合图象知 x ∈[2k π-2π,2k π+2π],k ∈Z . 2 3 39.2解析 作函数 y =cos x 与 y =x 2 的图象,如图所示,4 4由图象,可知原方程有两个实数解.10.[π,5π]解析由题意知sin x-cos x≥0,即cos x≤sin x,在同一坐标系画出y=sin x,x∈[0,2π]与y=cos x,x∈[0,2π]的图象,如图所示:π 5观察图象知x∈[ ,π].4 411.解利用“五点法”作图(1)列表:X 0π2π3π22πsin x 0 1 0 -1 01-sin x 1 0 1 2 1(2)列表:X 0π2π3π22πcos x 1 0 -1 0 1-1-cos x -2 -1 0 -1 -212.解(1)y=|sin x|=Error! (k∈Z).其图象如图所示,(2)y=sin|x|=Error!,其图象如图所示,13.解由题意,x 满足不等式组Error!,即Error!,作出y=sin x 的图象,如图所示.结合图象可得:x∈[-4,-π)∪(0,π).14.解f(x)=sin x+2|sin x|=Error!图象如图,若使f(x)的图象与直线y=k 有且仅有两个不同的交点,根据上图可得k 的取值范围是(1,3).。
《正弦函数、余弦函数的图像》教案与导学案

《第五章三角函数》《5.4.1正弦函数、余弦函数的图像》教案【教材分析】由于三角函数是刻画周期变化现象的数学模型,这也是三角函数不同于其他类型函数的最重要的地方,而且对于周期函数,我们只要认识清楚它在一个周期的区间上的性质,那么它的性质也就完全清楚了,因此本节课利用单位圆中的三角函数的定义、三角函数值之间的内在联系性等来作图,从画出的图形中观察得出五个关键点,得到“五点法”画正弦函数、余弦函数的简图.【教学目标与核心素养】课程目标1.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.2.理解正弦曲线与余弦曲线之间的联系.数学学科素养1.数学抽象:正弦曲线与余弦曲线的概念;2.逻辑推理:正弦曲线与余弦曲线的联系;3.直观想象:正弦函数余弦函数的图像;4.数学运算:五点作图;5.数学建模:通过正弦、余弦图象图像,解决不等式问题及零点问题,这正是数形结合思想方法的应用.【教学重难点】重点:正弦函数、余弦函数的图象.难点:正弦函数与余弦函数图象间的关系.【教学方法】:以学生为主体,小组为单位,采用诱思探究式教学,精讲多练。
【教学过程】一、情景导入遇到一个新的函数,非常自然地是画出它的图象,观察图象的形状,看看有什么特殊点,并借助图象研究它的性质,如:值域、单调性、奇偶性、最大值与最小值等.我们也很自然地想知道y=sinx与y=cosx的图象是怎样的呢?回忆我们在必修1中学过的指数函数、对数函数的图象是什么?是如何画出它们图象的(列表描点法:列表、描点、连线)?请学生尝试画出当x∈[0,2π]时,y=sinx 的图象.要求:让学生自由发言,教师不做判断。
而是引导学生进一步观察.研探.二、预习课本,引入新课阅读课本196-199页,思考并完成以下问题1.任意角的正弦函数在单位圆中是怎样定义的?2.怎样作出正弦函数y=sinx的图像?3.怎样作出余弦函数y=cosx的图像?4.正弦曲线与余弦曲线的区别与联系.要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
1.4.1正弦函数、余弦函数的图象知识点归纳与练习(含详细答案)

第一章 三角函数 §1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象课时目标 1.了解正弦函数、余弦函数的图象.2.会用“五点法”画出正弦函数、余弦函数的图象.1.正弦曲线、余弦曲线2.“五点法”画图画正弦函数y =sin x ,x ∈[0,2π]的图象,五个关键点是_________________________; 画余弦函数y =cos x ,x ∈[0,2π]的图象,五个关键点是__________________________. 3.正、余弦曲线的联系依据诱导公式cos x =sin ⎝⎛⎭⎫x +π2,要得到y =cos x 的图象,只需把y =sin x 的图象向________平移π2个单位长度即可.知识点归纳:1.正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础.2.五点法是画三角函数图象的基本方法,要熟练掌握,与五点法作图有关的问题是高考常考知识点之一.一、选择题1.函数y =sin x (x ∈R )图象的一条对称轴是( ) A .x 轴 B .y 轴C .直线y =xD .直线x =π22.函数y =cos x (x ∈R )的图象向右平移π2个单位后,得到函数y =g (x )的图象,则g (x )的解析式为( )A .-sin xB .sin xC .-cos xD .cos x3.函数y =-sin x ,x ∈[-π2,3π2]的简图是( )4.在(0,2π)内使sin x >|cos x |的x 的取值范围是( ) A.⎝⎛⎭⎫π4,3π4 B.⎝⎛⎦⎤π4,π2∪⎝⎛⎦⎤5π4,3π2 C.⎝⎛⎭⎫π4,π2 D.⎝⎛⎭⎫5π4,7π4 5.若函数y =2cos x (0≤x ≤2π)的图象和直线y =2围成一个封闭的平面图形,则这个封闭图形的面积是( )A .4B .8C .2πD .4π 6.方程sin x =lg x 的解的个数是( )A .1B .2C .3D .4 题 号 1 2 3 4 5 6 答 案 7.函数y =sin x ,x ∈R 的图象向右平移π2个单位后所得图象对应的函数解析式是__________.8.函数y =2cos x +1的定义域是________________. 9.方程x 2-cos x =0的实数解的个数是________.10.设0≤x ≤2π,且|cos x -sin x |=sin x -cos x ,则x 的取值范围为________. 三、解答题11.利用“五点法”作出下列函数的简图: (1)y =1-sin x (0≤x ≤2π); (2)y =-1-cos x (0≤x ≤2π).12.分别作出下列函数的图象.(1)y=|sin x|,x∈R;(2)y=sin|x|,x∈R.能力提升13.求函数f(x)=lg sin x+16-x2的定义域.14.函数f(x)=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,求k 的取值范围.§1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象答案知识梳理2.(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫32π,-1,(2π,0) (0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫32π,0,(2π,1) 3.左 作业设计1.D 2.B 3.D 4.A [∵sin x >|cos x |,∴sin x >0,∴x ∈(0,π),在同一坐标系中画出y =sin x ,x ∈(0,π)与y =|cos x |,x ∈(0,π)的图象,观察图象易得x ∈⎝⎛⎭⎫π4,34π.] 5.D [作出函数y =2cos x ,x ∈[0,2π]的图象,函数y =2cos x ,x ∈[0,2π]的图象与直线y =2围成的平面图形,如图所示的阴影部分.利用图象的对称性可知该平面图形的面积等于矩形OABC 的面积,又∵|OA |=2,|OC |=2π, ∴S 平面图形=S 矩形OABC =2×2π=4π.]6.C [用五点法画出函数y =sin x ,x ∈[0,2π]的图象,再依次向左、右连续平移2π个单位,得到y =sin x 的图象.描出点⎝⎛⎭⎫110,-1,(1,0),(10,1)并用光滑曲线连接得到y =lg x 的图象,如图所示.由图象可知方程sin x =lg x 的解有3个.]7.y =-cos x解析 y =sin x 2π−−−−−−→向右平移个单位y =sin ⎝⎛⎭⎫x -π2 ∵sin ⎝⎛⎭⎫x -π2=-sin ⎝⎛⎭⎫π2-x =-cos x ,∴y =-cos x . 8.⎣⎡⎦⎤2k π-23π,2k π+23π,k ∈Z 解析 2cos x +1≥0,cos x ≥-12,结合图象知x ∈⎣⎡⎦⎤2k π-23π,2k π+2π3,k ∈Z . 9.2解析 作函数y =cos x 与y =x 2的图象,如图所示, 由图象,可知原方程有两个实数解.10.⎣⎡⎦⎤π4,5π4解析 由题意知sin x -cos x ≥0,即cos x ≤sin x ,在同一坐标系画出y =sin x ,x ∈[0,2π]与 y =cos x ,x ∈[0,2π]的图象,如图所示:观察图象知x ∈[π4,54π].11.解 利用“五点法”作图 (1)列表:X 0 π2 π 3π2 2π sin x 0 1 0 -1 0 1-sin x1121描点作图,如图所示.(2)列表:X0 π2 π 3π2 2π cos x 1 0 -1 0 1 -1-cos x-2-1-1-2描点作图,如图所示.12.解 (1)y =|sin x |=⎩⎪⎨⎪⎧sin x (2k π≤x ≤2k π+π)-sin x (2k π+π<x ≤2k π+2π) (k ∈Z ).其图象如图所示,(2)y =sin|x |=⎩⎪⎨⎪⎧sin x (x ≥0)-sin x (x <0),其图象如图所示,13.解 由题意,x 满足不等式组⎩⎪⎨⎪⎧ sin x >016-x 2≥0,即⎩⎪⎨⎪⎧-4≤x ≤4sin x >0,作出y =sin x 的图象,如图所示.结合图象可得:x ∈[-4,-π)∪(0,π).14.解 f (x )=sin x +2|sin x |=⎩⎪⎨⎪⎧3sin x x ∈[0,π],-sin x x ∈(π,2π].图象如图,若使f (x )的图象与直线y =k 有且仅有两个不同的交点,根据上图可得k 的取值范围是(1,3).。
1.4.1正弦函数、余弦函数的图象(解析版)

§1.4三角函数的图象与性质1.4.1正弦函数、余弦函数的图象学习目标1.了解利用单位圆中的正弦线画正弦曲线的方法.2.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.3.理解正弦曲线与余弦曲线之间的联系.知识点一 正弦函数、余弦函数的概念实数集与角的集合之间可以建立一一对应关系,而一个确定的角又对应着唯一确定的正弦(或余弦)值.这样,任意给定一个实数x ,有唯一确定的值sin x (或cos x )与之对应.由这个对应法则所确定的函数y =sin x (或y =cos x )叫做正弦函数(或余弦函数),其定义域是R . 知识点二 几何法作正弦函数、余弦函数的图象利用正弦线,这种作图方法称为“几何法”,其基本步骤如下:①作出单位圆:作平面直角坐标系,并在直角坐标系中y 轴左侧的x 轴上取一点O 1,作出以O 1为圆心的单位圆;②等分单位圆,作正弦线:从⊙O 1与x 轴的交点A 起,把⊙O 1分成12等份.过⊙O 1上各分点作x 轴的垂线,得到对应于0,π6,π3,π2,…,2π等角的正弦线;③找横坐标:把x 轴上从0到2π这一段分成12等份;④找纵坐标:把角x 的正弦线向右平移,使它的起点与x 轴上对应的点x 重合,从而得到12条正弦线的12个终点;⑤连线:用光滑的曲线将12个终点依次从左至右连接起来,即得到函数y =sin x ,x ∈[0,2π]的图象,如图.因为终边相同的角有相同的三角函数值,所以函数y =sin x ,x ∈[2k π,2(k +1)π),k ∈Z 且k ≠0的图象与函数y =sin x ,x ∈[0,2π)的图象的形状完全一致.于是只要将函数y =sin x ,x ∈[0,2π)的图象向左、向右平行移动(每次2π个单位长度),就可以得到正弦函数y =sin x ,x ∈R 的图象,如图.把y =sin x ,x ∈R 的图象向左平移π2个单位长度,即可得到y =cos x ,x ∈R 的图象.正弦函数的图象和余弦函数的图象分别叫做正弦曲线和余弦曲线. 知识点三 “五点法”作正弦函数、余弦函数的图象“五点法”作正弦函数y =sin x (x ∈[0,2π])、余弦函数y =cos x ,x ∈[0,2π]图象的步骤 1.列表2.描点画正弦函数y =sin x ,x ∈[0,2π]的图象,五个关键点是 (0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0); 画余弦函数y =cos x ,x ∈[0,2π]的图象,五个关键点是 (0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫3π2,0,(2π,1). 3.用光滑曲线顺次连接这五个点,得到正弦函数y =sin x (x ∈[0,2π])、余弦函数y =cos x (x ∈[0,2π])的简图.1.正弦函数y =sin x 的图象向左、右和上、下无限伸展.( × )提示 正弦函数y =sin x 的图象向左、右无限伸展,但上、下限定在直线y =1和y =-1之间.2.函数y =sin x 与y =sin(-x )的图象完全相同.( × ) 提示 二者图象不同,而是关于x 轴对称.3.余弦函数y =cos x 的图象与x 轴有无数个交点.( √ )4.余弦函数y =cos x 的图象与y =sin x 的图象形状和位置都不一样.( × ) 提示 函数y =cos x 的图象与y =sin x 的图象形状一样,只是位置不同.题型一“五点法”作图的应用例1利用“五点法”作出函数y=1-sin x(0≤x≤2π)的简图.考点正弦函数图象题点正弦函数图象解(1)取值列表:(2)描点连线,如图所示.反思感悟作正弦曲线要理解几何法作图,掌握五点法作图.“五点”即y=sin x或y=cos x 的图象在[0,2π]内的最高点、最低点和与x轴的交点.“五点法”是作简图的常用方法.跟踪训练1 利用“五点法”作出函数y =-1-cos x (0≤x ≤2π)的简图. 解 (1)取值列表如下:(2)描点连线,如图所示.题型二 利用正弦、余弦函数图象求定义域 例2 求函数f (x )=lg sin x +16-x 2的定义域. 考点 正弦函数图象 题点 正弦函数图象的应用解 由题意,得x 满足不等式组⎩⎪⎨⎪⎧sin x >0,16-x 2≥0,即⎩⎪⎨⎪⎧sin x >0,-4≤x ≤4,作出y =sin x 的图象,如图所示.结合图象可得x ∈[-4,-π)∪(0,π).反思感悟 一些三角函数的定义域可以借助函数图象直观地观察得到,同时要注意区间端点的取舍.跟踪训练2 求函数y = log 21sin x-1的定义域. 考点 正弦函数图象 题点 正弦函数图象的应用解 为使函数有意义,需满足⎩⎪⎨⎪⎧log 21sin x -1≥0,sin x >0,即0<sin x ≤12.由正弦函数的图象或单位圆(如图所示),可得函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪2k π<x ≤2k π+π6或2k π+5π6≤x <2k π+π,k ∈Z .正弦、余弦函数图象的应用典例 利用正弦曲线,求满足12<sin x ≤32的x 的集合.考点 正弦函数的图象 题点 正弦函数图象的应用解 首先作出y =sin x 在[0,2π]上的图象,如图所示,作直线y =12,根据特殊角的正弦值,可知该直线与y =sin x ,x ∈[0,2π]的交点横坐标为π6和5π6.作直线y =32,该直线与y =sin x ,x ∈[0,2π]的交点横坐标为π3和2π3. 观察图象可知,在[0,2π]上,当π6<x ≤π3或2π3≤x <5π6时,不等式12<sin x ≤32成立.所以12<sin x ≤32的解集为⎩⎨⎧ x ⎪⎪ π6+2k π<x ≤π3+2k π,⎭⎬⎫或2π3+2k π≤x <5π6+2k π,k ∈Z . [素养评析] 作出相应正弦、余弦函数的图象,借助三角函数图象使问题得解,这正是数学核心素养直观想象的具体体现.1.用“五点法”作y =2sin 2x 的图象时,首先描出的五个点的横坐标是( ) A .0,π2,π,3π2,2πB .0,π4,π2,3π4,πC .0,π,2π,3π,4πD .0,π6,π3,π2,2π3考点 正弦函数图象 题点 正弦函数图象 答案 B解析 “五点法”作图是当2x =0,π2,π,3π2,2π时的x 的值,此时x =0,π4,π2,3π4,π,故选B.2.函数y =-sin x ,x ∈⎣⎡⎦⎤-π2,3π2的简图是( )考点 正弦函数图象 题点 正弦函数图象 答案 D解析 方法一 由y =sin x ,x ∈⎣⎡⎦⎤-π2,3π2的图象,作关于x 轴的对称图象,就可以得到函数y =-sin x ,x ∈⎣⎡⎦⎤-π2,3π2的简图. 方法二 可以用特殊点来验证. x =0时,y =-sin 0=0,排除A ,C. 当x =3π2时,y =-sin 3π2=1,排除B.3.在[0,2π]内,不等式sin x <-32的解集是( ) A .(0,π) B.⎝⎛⎭⎫π3,4π3 C.⎝⎛⎭⎫4π3,5π3 D.⎝⎛⎭⎫5π3,2π考点 正弦函数图象 题点 正弦函数图象的应用 答案 C解析 画出y =sin x ,x ∈[0,2π]的草图如下:因为sin π3=32,所以sin ⎝⎛⎭⎫π+π3=-32,sin ⎝⎛⎭⎫2π-π3=-32. 即在[0,2π]内,满足sin x =-32的是x =4π3或x =5π3. 可知不等式sin x <-32的解集是⎝⎛⎭⎫4π3,5π3. 4.点M ⎝⎛⎭⎫π2,-m 在函数y =sin x 的图象上,则m =________. 考点 正弦函数图象 题点 正弦函数图象的应用 答案 -1解析 点M 在y =sin x 的图象上, 代入坐标得-m =sin π2=1,所以m =-1.5.函数y =cos x ,x ∈[0,2π]的图象与直线y =-12的交点有________个.答案 2解析 画图可知(图略).1.对“五点法”画正弦函数图象的理解(1)与前面学习函数图象的画法类似,在用描点法探究函数图象特征的前提下,若要求精度不高,只要描出函数图象的“关键点”,就可以根据函数图象的变化趋势画出函数图象的草图.(2)正弦型函数图象的关键点是函数图象中最高点、最低点以及与x轴的交点.2.作函数y=a sin x+b的图象的步骤3.用“五点法”画的正弦型函数在一个周期[0,2π]内的图象,如果要画出在其他区间上的图象,可依据图象的变化趋势和周期性画出.一、选择题1.以下对正弦函数y =sin x 的图象描述不正确的是( ) A .在x ∈[2k π,2(k +1)π](k ∈Z )上的图象形状相同,只是位置不同 B .介于直线y =1与直线y =-1之间 C .关于x 轴对称 D .与y 轴仅有一个交点 考点 正弦函数的图象 题点 正弦函数图象的应用 答案 C解析 画出y =sin x 的图象(图略),根据图象可知A ,B ,D 三项都正确.2.用“五点法”作函数y =2sin x -1的图象时,首先应描出的五点的横坐标可以是( ) A .0,π2,π,3π2,2πB .0,π4,π2,3π4,πC .0,π,2π,3π,4πD .0,π6,π3,π2,2π3考点 正弦函数图象 题点 正弦函数图象 答案 A解析 由“五点法”可知选A.3.(2018·山西孝义高二期末)对于余弦函数y =cos x 的图象,有以下描述: ①将[0,2π]内的图象向左、向右平移2k π(k ∈Z )个单位长度;②与y=sin x图象形状完全一样,只是位置不同;③与x轴有无数个交点;④关于y轴对称.其中正确的描述有()A.1个B.2个C.3个D.4个考点余弦函数的图象题点余弦函数图象的应用答案 D解析根据余弦函数的图象可以判断都正确.4.(2018·安徽滁州高二期末)函数y=1-sin x,x∈[0,2π]的大致图象是()考点正弦函数的图象题点正弦函数图象答案 B解析 当x =π2时,y =0;当x =0时,y =1; 当x =2π时,y =1;结合正弦函数的图象可知B 正确. 5.下列各组函数中图象相同的是( ) ①y =cos x 与y =cos(π+x ); ②y =sin ⎝⎛⎭⎫x -π2与y =sin ⎝⎛⎭⎫x +π2; ③y =sin x 与y =sin(-x ); ④y =sin(2π+x )与y =sin x .A .①③B .①②C .③④D .④ 考点 正弦、余弦函数图象的综合应用 题点 正弦、余弦函数图象的综合应用 答案 D解析 由诱导公式知,只有④中,y =sin(2π+x )=sin x . 6.方程|x |=cos x 在(-∞,+∞)内( ) A .没有根 B .有且仅有一个根 C .有且仅有两个根 D .有无穷多个根考点 余弦函数的图象 题点 余弦函数图象的应用 答案 C解析 在同一坐标系中作出函数y =|x |及函数y =cos x 的图象,如图所示.由图知两函数的图象有两个交点,所以方程|x |=cos x 有两个根. 7.(2018·广西贺州高二期末)在[0,2π]上,满足sin x ≥22的x 的取值范围是( ) A.⎣⎡⎦⎤0,π6 B.⎣⎡⎦⎤π4,5π4 C.⎣⎡⎦⎤π4,3π4 D.⎣⎡⎦⎤3π4,π考点 正弦函数图象 题点 正弦函数图象的应用 答案 C解析 如图所示,在同一坐标系内作出y =sin x 在[0,2π]上的图象和y =22的图象.由图可知,满足sin x ≥22的x 的取值范围是⎣⎡⎦⎤π4,3π4. 8.函数y =cos x +|cos x |,x ∈[0,2π]的大致图象为( )答案 D解析 y =cos x +|cos x |=⎩⎨⎧2cos x ,x ∈⎣⎡⎦⎤0,π2∪⎣⎡⎦⎤3π2,2π,0,x ∈⎝⎛⎭⎫π2,3π2,故选D.二、填空题9.若sin x =2m +1且x ∈R ,则m 的取值范围是________. 答案 [-1,0]解析 ∵2m +1=sin x ∈[-1,1], 即-1≤2m +1≤1, ∴-1≤m ≤0.10.不等式sin x <-12,x ∈[0,2π]的解集为________.答案 ⎝⎛⎭⎫7π6,11π611.已知函数f (x )=⎩⎪⎨⎪⎧sin x ,x ≥0,x +2,x <0,则不等式f (x )>12的解集是____________.考点 正弦函数图象 题点 正弦函数图象的应用答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪-32<x <0或π6+2k π<x <5π6+2k π,k ∈N 解析 在同一平面直角坐标系中画出函数f (x )和函数y =12的图象,如图所示.当f (x )>12时,函数f (x )的图象位于函数y =12的图象的上方,此时-32<x <0或π6+2k π<x <5π6+2k π(k ∈N ).三、解答题12.求函数y =1-2cos x +lg(2sin x -1)的定义域. 考点 正弦、余弦函数图象的综合应用 题点 正弦、余弦函数图象的综合应用 解 要使函数有意义,只要⎩⎪⎨⎪⎧1-2cos x ≥0,2sin x -1>0,即⎩⎨⎧cos x ≤12,sin x >12.如图所示.cos x ≤12的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π3+2k π≤x ≤53π+2k π,k ∈Z .sin x >12的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π6+2k π<x <5π6+2k π,k ∈Z ,它们的交集为⎩⎨⎧⎭⎬⎫x ⎪⎪π3+2k π≤x <5π6+2k π,k ∈Z ,即为函数的定义域.13.用“五点法”作出函数y =1-2sin x ,x ∈[-π,π]的简图,并回答下列问题: (1)观察函数图象,写出满足下列条件的x 的区间.①y>1;②y<1.(2)若直线y=a与y=1-2sin x,x∈[-π,π]的图象有两个交点,求a的取值范围.考点正弦函数图象题点正弦函数图象的应用解列表如下:描点并将它们用光滑的曲线连接起来,如图:(1)由图象可知,图象在直线y=1上方部分时y>1,在直线y=1下方部分时y<1,所以①当x∈(-π,0)时,y>1;②当x∈(0,π)时,y<1.(2)由图可知,当直线y=a与y=1-2sin x,x∈[-π,π]的图象有两个交点时,1<a<3或-1<a<1,所以a的取值范围是(-1,1)∪(1,3).14.(2018·广西钦州高二期末)已知函数y =sin x ,x ∈⎣⎡⎦⎤π2,5π2的图象与直线y =1围成一个平面图形,则这个封闭图形的面积是( ) A .2 B .4 C .2π D .4π 考点 正弦函数图象 题点 正弦函图图象的应用 答案 C解析 如图,由正弦函数图象的对称性知,所围成平面图形的面积是长为5π2-π2=2π,宽为1的矩形的面积, ∴S =2π.15.函数f (x )=sin x +2|sin x |,x ∈[0,2π]的图象与直线y =k 有且仅有两个不同的交点,求k 的取值范围.考点 正弦函数图象 题点 正弦函数图象的应用解 f (x )=sin x +2|sin x |=⎩⎪⎨⎪⎧3sin x ,x ∈[0,π],-sin x ,x ∈(π,2π].图象如图所示,若使f (x )的图象与直线y =k 有且仅有两个不同的交点,根据图象可得k 的取值范围是(1,3).。
正弦函数、余弦函数的图象 导学案 高一数学人教A版第一册(全国)

第五章 三角函数5.4.1 正弦函数、余弦函数的图象【学习要求】1.了解正弦函数图象的正弦线画法,掌握正弦函数图象的几何特征;2.掌握五点法,并能熟练画一些简单函数的图象. 【教学过程】 一、情境引入1.终边相同角的诱导公式:sin(2)k απ+= ()k Z ∈.2.周期函数:当函数对于自变量的一切值每增加或减少一个定值(定值可以有很多个),函数值就重复出现时,这个函数就叫做周期函数.一般地,对于函数f (x ),如果存在非零常数T ,使得定义域内的“每一个x 值”,都有f (x+T )=f (x ),那么函数f (x )就叫做周期函数,非零常数T 叫做f (x )的周期.3.正弦函数的周期是: ;最小正周期是: .二、知识整理用描点法作出正弦函数在最小正周期上的图象sin ,[0,2]y x x π=∈,(2)描点连线(3)因为终边相同的角的三角函数值相同,所以sin y x =在……,[4,2]ππ--, [2,0]π-,[0,2]π,[2,4]ππ,……的图象与sin y x =,[0,2]x π∈的图象相同.方法小结:(1)用“五点法”作正弦函数的图象; (2)“五点法”作图的关键点.x 0 2π π32π 2πy1-1三、典例选讲例1.作下列函数的简图(1)1sin ,[0,2]y x x π=+∈; (2)sin 2,[0,]y x x π=∈;(3)5sin(),[,]333y x x πππ=+∈-; (4)53sin(2),[,]366y x x πππ=+∈- .思考:几何法(利用三角函数线画正弦函数图象)四、小结提升通过这节课的学习①你经历了什么样的过程?②你获得了什么样的知识、技能、方法?③你感受最深的是什么?五、练习巩固1.1sin y x =+,x ∈[0,2π]的图象与直线y =1.5的交点个数为 .2.在[0,2π]内4sin y x =的单调增区间为 ;单调减区间为 .3.用五点法分别作下列函数在[2,2]ππ-上的图象:(1) sin y x =-; (2) sin 2y x =-.4.把第3题所作的图象和sin y x =,[2,2]x ππ∈-的图象进行比较,说明这些图象与sin y x =,[2,2]x ππ∈-的图象的位置关系.5.画出下列函数的图象(1) sin()y x =-,[0,2];x π∈ (2) sin()4y x π=-,9[,]44x ππ∈(3)12sin()26y x π=-, 13[,]33x ππ∈ (4)sin(2)14y x π=+-, 7[,]88x ππ∈-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1.4.1正弦函数、余弦函数的图象
出题人: 尹书燕 审核人: 一、 学习目标:
1、能借助正弦线画出正弦函数的图象,并在此基础上由诱导公式画出余弦函数的图象。
2、能熟练运用“五点法”作图。
二、知识回顾:
1、弧度定义:长度等于半径长的弧所对的圆心角称为1弧度的角。
2、正、余弦函数定义:设α是一个任意角,在α的终边上任取(异
于原点的)一点P (x,y ),则:r= =αsin =αcos
3、正弦线、余弦线:设任意角α的终边与单位圆相交于点P(x ,
OM 叫做角α的余弦线。
三、 知识梳理:
1、 正弦函数图象的画法: (1)、几何法—借助三角函数线 (2)、描点法—五点法
用“五点法”画正弦函数y=sinx ,x ∈[0,2π]的图象中,五个关键点是:
、 、 、 、 。
2、 余弦函数图象的画法: (1)、要得到y=cosx 的图象,只需要把y=sinx 的图象 单位长度便可,这
是由于cosx=
(2)、用“五点法”画余弦函数y=cosx ,x ∈[0,2π]的五个点关键是 、 、 、 、 。
四、
小试牛刀:
例1:用“五点法”画下列函数的简图
(1)y=-1+sinx ,x ∈[0,2π] (2)y=-cosx
例2:如何利用y=sinx ,x ∈[0,2π]的图象,通过图形变换(平移、翻转
等)来得到(1)y =-1+sinx ,x ∈[0,2π〕的图象;(2)y=sin(x-π/3),x
∈[0,2π]的图象;
小结:函数值加减,图像 移动;自变量加减,图像 移动。
例3:用“五点法”画
的简图
五、
能力创新:
1、函数1sin ,[0,2]y
x x π=-∈的大致图象是 ( )
A B. C. D.
2、不等式cos 0,[0,2]x x π<∈的解集为( ) A .
3、将sin 1y x =-的图象向左平移再向上平移1个单位,得到()f x 的图象,则()f x =____________________. 4
y 的取值范围是( )
A.[1,1]-
B.
六、
选做题:
1、函数1sin ,[0,2]y x x π=+∈的图象与直线
)
2、作出下列函数的简图:
(1)2cos ,[0,2];y x x π=+∈ (2)2sin ,[0,2].y x x π=-∈
3、函数f(x)=2|sinx|,x ∈[0,2π]的图象与直线y k =有且仅有两个不同交点,求k 得取值范围.。
