初中几何 一线三等角模型
初中几何 一线三等角模型
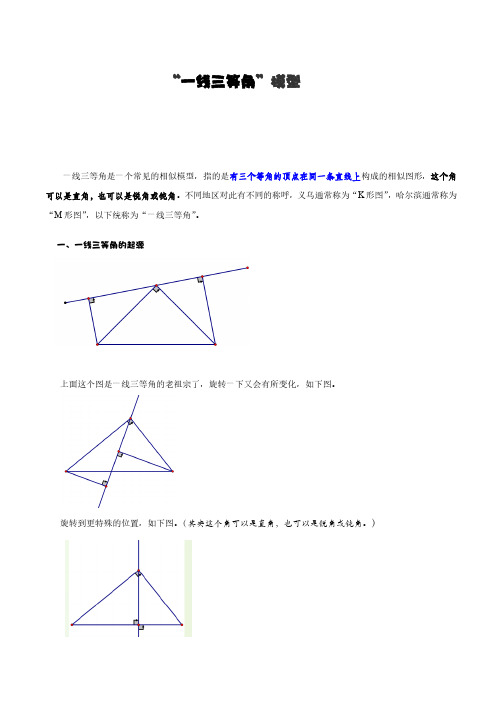
一、一线三等角的起源上面这个图是一线三等角的老祖宗了,旋转一下又会有所变化,如下图。
旋转到更特殊的位置,如下图。
(其实这个角可以是直角,也可以是锐角或钝角。
)“一线三等角”模型一线三等角是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,义乌通常称为“K 形图”,哈尔滨通常称为“M 形图”,以下统称为“一线三等角”。
二、一线三等角的两种基本类型1.三等角都在直线的同侧2.三等角分居直线的两侧l三、一线三等角的性质1.一般情况下,由∠1=∠2=∠3,易得△AEC∽△BDE. 2.当等角所对的边相等时,两个三角形全等。
如图,当CE=ED时,易得△AEC≌△BDE.3.“中点型一线三等角”的特殊性质如图,当∠1=∠2=∠3且D 是BC 的中点时,△BDE ∽△CFD ∽△DFE .如图,加画两条垂线......,“一线三等角”就与“四边形中的半角模型”联系在一起了。
半角模型:EF =EM +FN . 4.“中点型一线三等角”的变式 如图,当∠1=∠2且∠AOC =90°+21∠BAC 时,点O 是△ABC 的内心.易证∠4=∠5=∠6,以下就省略了。
四、一线三等角的常用构图下面以等腰三角形为例说明一线三等角的常见构图。
由于角顶点位置的改变,或角绕顶点旋转会产生各种各样的变式,但万变不离其宗:构造相似三角形列比例式解决问题。
当然,特殊情况下也可能是全等。
五、一线三等角的应用1.一线三等角应用的三个层次⑴初级阶段:图形中已经存在“一线三等角”,直接应用模型解题;⑵中级阶段:图形中存在“一线二等角”,补上“一等角”构造此模型;⑶高级阶段:图形中只有直线上的一个角,补上“二等角”构造此模型。
2.在张角问题中,构造“一线三等角”是基本手段之一。
对坐标系中的张角问题,在x轴或y轴(也可以是平行于x轴或y轴的直线)上构造“一线三等角”是解决问题的关键。
初中数学58种模型之一线三等角模型

初中数学58种模型之一线三等角模型“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形。
这个角可以是直角,也可以是锐角或者钝角。
对于“一线三等角”,有的地区叫“K型图”,也有的地区叫“M型图”。
“一线三等角”的起源DE 绕A 点旋转,从外到内,从一般位置到特殊位置.下面分几种类型讨论:一、直角形“一线三等角”——“一线三直角”结论:△ADB ∽△CEA二、锐角形“一线三等角结论:△ADB∽△CEA∽△CAB三、钝角形“一线三等角结论:△ADB∽△CEA∽△CAB下面总结几种常考类型:类型一三角齐见,模型自现类型一概述以上两例都是典型的“一线三等角”试题,由于模型的框架已搭建,因此降低了试题的起点.两道题虽涉及不同的图形变换,但解法本质一致,均为利用模型构建比例式解决问题.两道题都着重考查学生在图形变换过程中的观察理解、直观感知、推理转化等数学能力和思想.类型二隐藏局部,小修小补类型二概述上述两道题虽分别以四边形和一次函数为命题背景,但图形的共性较明显: 均将原有“一线三等角”模型中的一角进行了隐藏,而这就要求学生理性地从图形的角度进行思考与联想,发现其中最本质的特征,挖掘蕴含在图中的几何模型.两道题均较好地体现了对“四基”的综合考查,提升了学生思维的层次性和灵活性.类型三一角独处,两侧添补类型三概述上述几道题虽呈现的背景不同,但都蕴知识技能、思想方法、数学模型于图形之中.题中的“特殊角”是解题的关键,也是搭建模型框架的基础,更是学生解题思路的来源与“脚手架”.这几道题实质上都是考查学生利用模型进行数学思考的能力,同时也有效地检测了学生对数学本质属性的把握情况.类型四线角齐藏,经验来帮类型四概述本题实质上以图形的旋转为问题的切入点,较好地激发学生探索的意愿,促使学生在模拟图形运动的同时,自发地利用题中所蕴含的特殊角,展开适当的联想,寻找图形间的联系,利用数学解题经验,搭建模型框架。
中考数学相似三角形重要模型一线三等角模型
相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
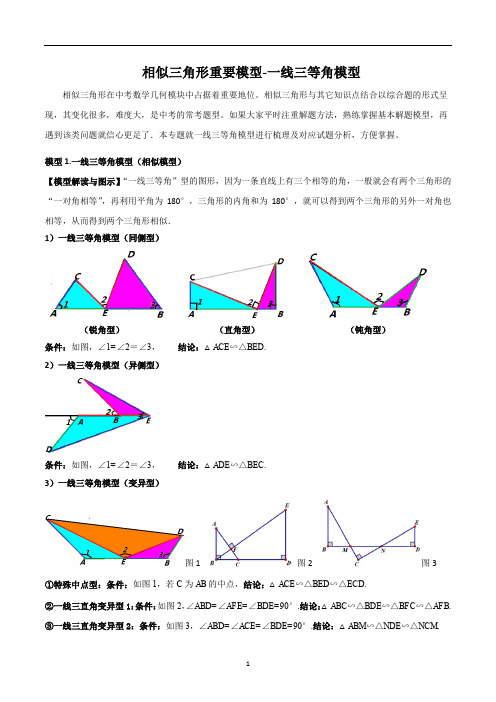
模型1.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1 图2 图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.例1.(2023·山东东营·统考中考真题)如图,A B C为等边三角形,点D,E分别在边B C,A B上,60A D E∠=︒,若4B D D C=, 2.4D E=,则A D的长为()A.1.8B.2.4C.3D.3.2例2.(2023·湖南·统考中考真题)如图,,C A ADE D A D⊥⊥,点B是线段A D上的一点,且C B B E⊥.已知8,6,4A B A C D E===.(1)证明:A B C D E B∽△△.(2)求线段B D的长.例3.(2022·河南新乡·九年级期中)某学习小组在探究三角形相似时,发现了下面这种典型的基本图形.(1)如图1,在ABC中,∠BAC=90°,A BA C=k,直线l经过点A,BD⊥直线I,CE上直线l,垂足分别为D、E.求证:B DA E=k.(2)组员小刘想,如果三个角都不是直角,那么结论是否仍然成立呢?如图2,将(1)中的条件做以下修改:在ABC中,A BA C=k,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问(1)中的结论还成立吗?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,在ABC中,沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG,A BA E =A CA G=12,AH是BC边上的高,延长HA交EG于点I.①求证:I是EG的中点.②直接写出线段BC与AI之间的数量关系:.例4.(2022·四川·一模)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形:(1)如图1,已知:在△ABC 中,A B A C=,D 、A 、E 三点都在直线m 上,并且有B D AA E CB AC α∠=∠=∠=.试猜想DE 、BD 、CE 有怎样的数量关系,请证明你的结论;(2)老师鼓励学习小组继续探索相似的情形.于是,学习小组又研究以下问题:如图2,△ABC 中,(060)B C αα∠=∠=<<︒.将一把三角尺中30°角顶点P 放在BC 边上,当P 在BC 边上移动时,三角尺中30°角的一条边始终过点A ,另一条边交AC 边于点Q ,P 、Q 不与三角形顶点重合.设C P Qβ∠=.当β在许可范围内变化时,α取何值总有△ABP ∽△PCQ ?当α在许可范围内变化时,β取何值总有△ABP ∽△QCP ?(3)试探索有无可能使△ABP 、△QPC 、△ABC 两两相似?若可能,写出所有α、β的值(不写过程);若不可能,请说明理由.例5.(2022·山西晋中·一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在A B C中,90A C B ∠=︒,A C B C=,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:A D C C E B△≌△.(1)探究问题:如果A CB C≠,其他条件不变,如图②,可得到结论;A D CC E B△∽△.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线12y x=与直线C D 交于点()2,1M ,且两直线夹角为α,且3ta n 2α=,请你求出直线C D 的解析式.(3)拓展应用:如图④,在矩形A B C D 中,3A B=,5B C=,点E为B C 边上—个动点,连接A E ,将线段A E 绕点E 顺时针旋转90︒,点A 落在点P 处,当点P 在矩形A B C D外部时,连接P C ,P D .若D P C △为直角三角形时,请你探究并直接写出B E 的长.Rt ABD中,上一动点,连接折叠得H E F,延长②B E M H E M≅;③当M2B,则正确的有(九年级校考阶段练习)已知A B C是等边三角形,E F和B D F∠,将B C E沿B则A F=P C D△;九年级校考阶段练习)如图,在A B C中,12.(2022·山东济宁·二模)情境观察:将含45°角的三角板的直角顶点R放在直线l上,分别过两锐角的顶点M,N作l的垂线,垂足分别为P,Q,(1)如图1.观察图1可知:与NQ相等的线段是______________,与N R Q∠相等的角是_____(2)问题探究直角A B C中,90B∠=︒,在AB边上任取一点D,连接CD,分别以AC,DC为边作正方形ACEF 和正方形CDGH,如图2,过E,H分别作BC所在直线的垂线,垂足分别为K,L.试探究EK与HL之间的数量关系,并证明你的结论.(3)拓展延伸:直角A B C中,90B∠=︒,在AB边上任取一点D,连接CD,分别以AC,DC为边作矩形ACEF和矩形CDGH,连接EH交BC所在的直线于点T,如图3.如果A C kC E=,试探究TE与TH=,C D kC H之间的数量关系,并证明你的结论.将.A B P沿着这样的点P,使得点问题解决(3)15.(2023春·四川广安·九年级校考阶段练习)如图1和图2,在平面直角坐标系中,点C的坐标为(0,4),A是x轴上的一个动点,M是线段AC的中点.把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB.过B作x轴的垂线、过点C作y轴的垂线,两直线交于点D,直线DB交x轴于点E.设A点的横坐标为m.(1)求证:△AOC∽△BEA;(2)若m=3,则点B的坐标为;若m=﹣3,则点B的坐标为;(3)若m>0,△BCD的面积为S,则m为何值时,S=6?(4)是否存在m,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时m的值;若不存在,请说明理由.16.(2020·四川雅安·中考真题)如图,已知边长为10的正方形A B C D E、不重,是B C边上一动点(与B C 合),连结A E G,是B C延长线上的点,过点E作A E的垂线交D C G∠的角平分线于点F,若F G B G⊥.(1)求证:A B E E G FE C=,求C E F△△;(2)若2∽△的△的面积;(3)请直接写出E C为何值时,C E F面积最大.的何位置时有B E H B A E∽?B C。
几何模型:一线三等角模型
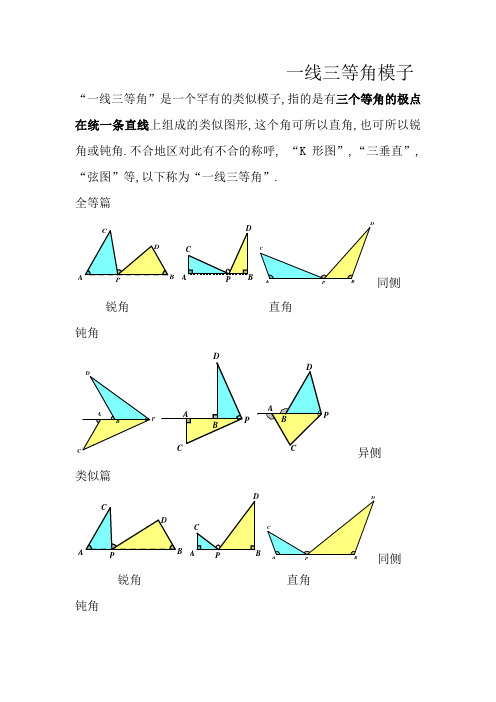
一线三等角模子“一线三等角”是一个罕有的类似模子,指的是有三个等角的极点在统一条直线上组成的类似图形,这个角可所以直角,也可所以锐角或钝角.不合地区对此有不合的称呼, “K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”.全等篇同侧锐角直角钝角异侧类似篇A同侧锐角直角钝角DCPBACDPB ADPCAB异侧三.“一线三等角”的性质1.一般情形下,如图 3-1,由∠1=∠2=∠3,易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如图 3-1,若 CE=ED,则△AEC≌△BDE.3.中点型“一线三等角”如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE.4.“中点型一线三等角“的变式(懂得)如图 3-3,当∠1=∠2 且1902BOC BAC∠=︒+∠时,点 O 是△ABC 的心坎.可以斟酌结构“一线三等角”.如图 3-4“中点型一线三等角”平日与三角形的心坎或旁心相干,1902BOC BAC∠=︒+∠这是心坎的性质,反之未必是心坎.在图 3-4(右图)中,假如延伸 BE 与 CF,交于点 P,则点 D 是△PEF 的旁心.5.“一线三等角”的各类变式(图 3-5,以等腰三角形为例进行解释 )图 3-5其实这个第 4 图,延伸 DC 反而好懂得.相当于两侧型的,不延伸懂得,认为是一种新型的,同侧穿越型?不管怎么变,都是由三等角肯定类似三角形来进行解题四.“一线三等角”的运用1.“一线三等角”运用的三种情形.a.图形中已经消失“一线三等角”,直策运用模子解题;b.图形中消失“一线二等角”,不上“一等角”结构模子解题;c.图形中只有直线上一个角,不上“二等角”结构模子解题.领会:感到最后一种情形消失比较多,尤其是压轴题中,经常会有一个特别角或指点该角的三角函数值时,我经常结构“一线三等角”来解题.2.在定边对定角问题中,结构一线三等角是根本手腕,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可所以平行于 x 轴或y 轴的直线)上结构一线三等角解决问题更是主要的手腕.3.结构一线三等角的步调:找角.定线.构类似坐标系中,要讲求“线”的特别性如图 3-6,线上有一特别角,就斟酌结构同侧型一线三等角当然只加这两条线平日是不敷的,为了运用这个特别角导线段的关系,过 C.D 两点作直线 l 的垂线是必不成少的.两条垂线平日情形下是为了“量化”的须要.上面就是作帮助线的一般程序,看起来线条比较多,许多先生都认为一会儿不轻易控制.解题示范例 1 如图所示,一次函数4y x =-+与坐标轴分离交于 A.B 两点,点 P 是线段 AB 上一个动点(不包含 A.B 两头点),C 是线段 OB 上一点,∠OPC=45°,若△OPC 是等腰三角形,求点 P 的坐标. 例 2 如图所示,四边形 ABCD 中,∠C=90°,∠ABD=∠DBC=22.5°,AE⊥BC 于 E,∠ADE=67.5°,AB=6,则 CE= . 例 3 如图,四边形 ABCD 中,∠ABC=∠BAD=90°,∠ACD=45°,AB=3,AD=5.求 BC 的长.例 4 如图,△ABC 中,∠BAC=45°,AD ⊥BC,BD=2,CD=3,求 AD 的长.一线三等角,补形最主要,内构勤思虑,外构更精妙.找出类似形, 比例不克不及少.巧设未知数,妙解方程好照样可以纵横斜三个偏向结构,坐标系中一般斟酌纵横两个偏向结构例 5 如图,在△ABC 中,∠BAC=135°, AC = 2AB, AD ⊥AC 交 BC 于点 D,若2, 求△ABC 的面积当然有45°或 135°等特别角,据此也可以结构不合的一线三等角一线三等角所有的结构都是把分家定角两侧的数据分散在一路,是类似分散前提的一种 . 大练身手:例7:在平面直角坐标系中,已知点A (1,0),B (0,3),C (-3,0),D 是线段AB 上一点,CD 交y 轴于E ,且S △BCE =2S △AOB . (1)求直线AB 的解析式;(2)求点D 的坐标,猜测线段CE 与线段AB 的数目关系和地位关系,并解释来由;(3)若F 为射线CD 上一点,且∠DBF =45°,例8:如图,直线y =x +2与y 轴交于点C ,A .B 两点(A 在B 的左侧),BC =2AC ,点P (1)求抛物线的函数表达式;(2)若点P 在直线AB 的下方,求点P 到直线AB 的距离的最大值; (3)若点P 在直线AB 的上方,且∠BPC =45°,求所有知足前提的点P 的坐标.练1:.如图,抛物线的极点为C B 和坐标原点O ,点B 的横坐标为-3(1)求抛物线的解析式;(2)若点D 为抛物线上的一点,的面积,请直接写出点D 的坐标;(3)若点E 的坐标为(0,2),点,是否消失点P ,使得∠OPE =45°?若消失,求出点P 的坐标;若不消失,请解释来由.课后功课:如图,点A(0,-1),B(3,0),P 为直线y= -x+5上一点,若∠APB=45°,求点P 的坐标在四边形ABCD 中,∠ABC=∠BAD=90°,∠ACD=45°,AB=3,AD=4,求AC 的长.如图,正方形ABCD 中,点E,F,G 分离在AB,BC,CD 上,△EFG 为等边三角形,求证:如图,△ABC △DBA,且求证:CD=2AB.如图,在四边形ABCD 中,∠ABC =90°,AB =3,BC =4,CD =10,DA =55,求BD 的长如图,点A 是反比例(X >0)图形上一点,点B 是X 轴正半轴上一点,点C 的坐标为(0,2),点△ABC 是等边三角形时,求点A 的坐标.如图,抛物线y =ax 2+bx +4与x 轴交于A .B 两点(点A 在点B 的左侧),与y 轴交于点C ,直线l :y =-12x +m 经由点A ,与抛物线交于另一点D (5,-72),点P 是直线l 上方的抛物线上的动点,衔接PC .PD .(1)求抛物线的解析式;(2)当△PCD 为直角三角形时,求点P 的坐标;(3)设△PCD 的面积为S ,请你探讨:使S 的值为整数的点P 共有几个,解释来由.,已知直线y =kx与抛物线.2742-=x y(1)求直线y=kx的解析式和线段OA的长度;(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x 轴于点M(点M.O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探讨:线段QM与线段QN的长度之比是否为定值?假如是,求出这个定值,假如不是,解释来由;(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O.A不重合),点D(m,0)是x轴正半轴上的动点,且知足∠BAE=∠BED=∠AOD.持续探究:m在什么规模时,相符前提的E点的个数分离是1个.2个?如图,线y=在A(1(2)点D为抛物线上一点,∠DCA=45°,求点D的坐标;备用图。
初二《全等三角形》数学模型之“一线三等角”模型

初二《全等三角形》数学模型之“一线三等角”模型.doc在初中数学中,全等三角形是一个重要的知识点,其中有许多模型。
掌握好这些模型,对于研究几何和提高成绩都有帮助。
今天我要介绍的是“一线三等角”模型。
这个模型贯穿初中几何的始终,也是相似三角形一个非常重要的知识点。
一线三等角”是指三个相等的角的顶点在同一条直线上。
例如,如果在直线AB上,有∠1=∠2=∠3,那么这就是一个“一线三等角”模型。
对于这个模型,我们可以得到以下性质:1.只要题目中满足“一线三等角”的条件,三角形必相似。
2.如果题目中还有对应边相等的条件,那么三角形就必全等。
一线三等角”模型常见的背景图形包括正方形、等边三角形、等腰三角形等等。
例如,正方形ABCD中,有一个直角的顶点在边AB上。
又如,等腰直角三角形ABC中,有一个45°角的顶点在边AB上。
下面以一个例题来说明如何运用“一线三等角”模型:已知在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE。
解析:因为BD⊥直线m,CE⊥直线m,所以有∠BDA=∠CEA=90°。
又因为∠BAC=90°,所以∠BAD+∠CAE=90°。
又∠BAD+∠ABD=90°,所以∠CAE=∠ABD。
因为AB=AC,所以△ADB≌△CEA,从而AE=BD,AD=CE。
因此,XXX。
如果将条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角。
请问结论DE=BD+CE是否成立?如果成立,请给出证明;如果不成立,请说明理由。
一线三等角模型结论及证明

一线三等角模型结论及证明
摘要
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,它们的夹角均为120度。
本文将详细阐述一线三等角模型的结论及证明,以及如何使用它来解决实际问题。
一、定义
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,它们的夹角均为120度。
二、结论
一线三等角模型的结论如下:
1、如果在一条直线上有三个等角,则它们的夹角均为120度。
2、如果三条直线的夹角均为120度,则它们共线。
三、证明
1、证明一:假设在一条直线上有三个等角,设它们的夹角为α,β,γ,则有
α+β+γ=360°,由等角性质可知α=β=γ=120°,得证。
2、证明二:假设三条直线的夹角均为120°,设它们的夹角分别为α,β,γ,则有α+β+γ=360°,此时α=β=γ=120°,由此可知,三条直线共线,得证。
四、实际应用
一线三等角模型可以用来解决实际问题,比如,在建筑设计中,可以根据一线三等角模型设计出美观的建筑结构,如三角形的屋顶,具有特殊的视觉效果。
结论
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,
它们的夹角均为120度。
本文详细阐述了一线三等角模型的结论及证明,并且给出了如何使用它来解决实际问题的实例。
几何模型:一线三等角模型 (最终版)

初中几何模型之“一线三等角模型”一.【一线三等角概念】“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.【一线三等角的分类】2.1 全等篇_同侧A PA P锐角直角钝角2.2 全等篇_异侧PDPP锐角直角钝角2.3 相似篇_同侧DCA BPP锐角直角钝角2.4 相似篇_异侧PDPP锐角直角钝角三、【性质】1.相似,如图 3-1,由∠1=∠2=∠3,或者α=α2=α3易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如下图,若 CE=ED,则△AEC≌△BDE.异侧结果同样。
3.中点型“一线三等角”——相似中多了一位兄弟如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE. 4.“中点型一线三等角“的变式(了解)如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明)图 3-5四、【“一线三等角”的应用】1.应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,构造“一等角”模型解题;c.图形中只有直线上一个角,构造“二等角”模型解题.注意:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.适应场景:在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造步骤:找角、定线、构相似【引例】例 1如图,l1、l2、l3是同一平面内的三条平行线,l1、l2之间的距离是21/5,l2、l3之间的距离是21/10,等边△ABC 的三个顶点分别在l1、l2、l3上,求△ABC 的边长.思路引导:【脑洞大开-三角构造】例 1 如图,四边形 ABCD 中,∠ABC=∠BAD=90°,∠ACD=45°,AB=3,AD=5.求 BC 的长.横向构造纵向构造斜向构造斜A相似构造:例 2 如图,△ABC 中,∠BAC=45°,AD⊥BC,BD=2,CD=3,求 AD 的长.纵向横向斜向一线三垂直的补形:角含半角补形练一练:1.如图,在△ABC 中,∠BAC=135°, AC= 2AB, AD⊥AC 交 BC 于点 D,若 AD = 2,求△ABC的面积思路提示:【中点型一线三等角】例1、如图,在Rt⊿ABC 中,AB = AC =2,∠A = 90°,现取一块等腰直角三角板,将45° 角的顶点放在BC 中点O 处,三角板的直角边与线段AB、AC 分别交于点E、F,设BE =x,CF = y,∠BOE = α( 45° ≤ α ≤ 90°) .( 1) 试求y 与x 的函数关系式,并写出x 的取值范围;( 2) 试判断∠BEO 与∠OEF 的大小关系?并说明理由;( 3) 在三角板绕O 点旋转的过程中,⊿OEF 能否成为等腰三角形? 若能,求出对应x 的值; 若不能,请说明理由.例2.如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90∘,△DEF的顶点E与△ABC的斜边BC的中点重合。
(完整版)几何模型:一线三等角模型

一线三等角模型一.一线三等角概念“一线三等角”是一个常见的相似模型, 上构成的相似图形,这个角可以是直角, 不同的称呼,“K 形图”, 二•一线三等角的分类 全等篇指的是有三个等角的顶点在同一条直线 也可以是锐角或钝角。
不同地区对此有 “弦图”三、“一线三等角” 1. 一般情况下,如图2•当等角所对的边相等时,则两个三角形全等 易得△ AE3A BDE..如图 3-1,若 CE=ED 则厶 AE3A BDE.锐角同侧异侧相似篇 锐角同侧异侧“三垂直”,等,以下称为“一线三等角”。
的性质3-1,由/1 = / 2=7 3,AVABOCff构造模型解题在图3-4造“一线三等角如图3- 4 如图3-3,当/仁/ 2且 BOC 90 4•“中点型一线三等角“的变式(了中点时,△ BD 0A CFS A DFE.阳3-13.中点型“一线三等角”如图3-2,当/仁/ 2=7 3,且 D 是BC^3-3图 3^“中点型一线三等角”通常与三角形的内心或旁心相关,1 90BAC 这是内心的性质,反之未必是内心 .2(右图)中,如果延长 BE 与CF ,交于点P ,则点D 是厶PEF 的旁心-BAC 时,点0是厶ABC 的内心.可以考虑构 25.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明图3-5其实这个第4图,延长DC 反而好理解.相当于两侧型的,不延长理解,以为 是一种新型的,同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进 行解题 四、“一线三等角”的应用 1.“一线三等角”应用的三种情况.a. 图形中已经存在“一线三等角”,直接应用模型解题;b. 图形中存在“一线二等角”,不上“一等c.图形中只有直线上一个角,不上“二等角”构造模型解题•体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题•2.在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在x 轴或y轴(也可以是平行于x轴或y轴的直线)上构造线三等角解决问题更是重要的手段•3.构造一线三等角的步骤:找角、定线、构相似在DC的延长銭上截取CE= —, CD的延怅:規上藪取DF= —>贝I」mZAEP= t3nZPFB= t3M J»JZAEP= ZPFH= a= ZAPR ,所1^APAlw ABPF .在CP上蔵取CE= —, 1£ DP蒙取DF=—,则tmZAEC= tanZBFD=taDGiWlZAEC= ZBFD= a= ZA?B^^iPAE«iBPF ・坐标系中,要讲究“线”的特殊性如图3-6,线上有一特殊角,就考虑构造同侧型一线三等角当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过C、D两点作直线I的垂线是必不可少的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、一线三等角的起源
上面这个图是一线三等角的老祖宗了,旋转一下又会有所变化,如下图。
旋转到更特殊的位置,如下图。
(其实这个角可以是直角,也可以是锐角或钝角。
)
“一线三等角”模型一线三等角是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,义乌通常称为“K 形图”,哈尔滨通常称为“M 形图”,以下统称为“一线三等角”。
二、一线三等角的两种基本类型
1.三等角都在直线的同侧
2.三等角分居直线的两侧
l
三、一线三等角的性质
1.一般情况下,由∠1=∠2=∠3,易得△AEC∽△BDE. 2.当等角所对的边相等时,两个三角形全等。
如图,当CE=ED时,易得△AEC≌△BDE.
3.“中点型一线三等角”的特殊性质
如图,当∠1=∠2=∠3且D 是BC 的中点时,△BDE ∽△CFD ∽△DFE .
如图,加画两条垂线......
,“一线三等角”就与“四边形中的半角模型”联系在一起了。
半角模型:EF =EM +FN .
4.“中点型一线三等角”的变式
如图,当∠1=∠2且∠AOC =90°+2
1∠BAC 时,点O 是△ABC 的内心.
易证∠4=∠5=∠6,以下就省略了。
四、一线三等角的常用构图
下面以等腰三角形为例说明一线三等角的常见构图。
由于角顶点位置的改变,或角绕顶点旋转会产生各种各样的变式,但万变不离其宗:构造相似三角形列比例式解决问题。
当然,特殊情况下也可能是全等。
五、一线三等角的应用
1.一线三等角应用的三个层次
⑴初级阶段:图形中已经存在“一线三等角”,直接应用模型解题;
⑵中级阶段:图形中存在“一线二等角”,补上“一等角”构造此模型;
⑶高级阶段:图形中只有直线上的一个角,补上“二等角”构造此模型。
2.在张角问题中,构造“一线三等角”是基本手段之一。
对坐标系中的张角问题,在x轴或y轴(也可以是平行于x轴或y轴的直线)上构造“一线三等角”是解决问题的关键。
3.构造一线三等角的步骤:找角、定线、构相似。
