圆柱体体积练习题
(完整版)圆柱的体积练习题(最新整理)
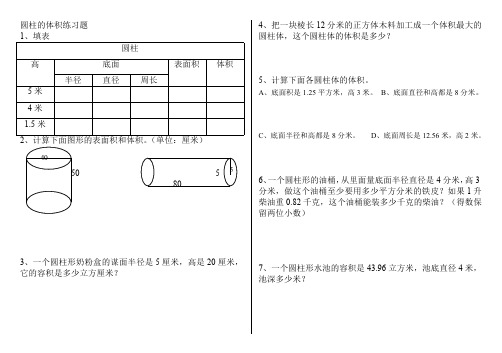
圆柱的体积练习题1、填表圆柱底面高半径直径周长表面积体积5米4米1.5米2(单位:厘米)3、一个圆柱形奶粉盒的谋面半径是5厘米,高是20厘米,它的容积是多少立方厘米?4、把一块棱长12分米的正方体木料加工成一个体积最大的圆柱体,这个圆柱体的体积是多少?5、计算下面各圆柱体的体积。
A、底面积是1.25平方米,高3米。
B、底面直径和高都是8分米。
C、底面半径和高都是8分米。
D、底面周长是12.56米,高2米。
6、一个圆柱形的油桶,从里面量底面半径直径是4分米,高3分米,做这个油桶至少要用多少平方分米的铁皮?如果1升柴油重0.82千克,这个油桶能装多少千克的柴油?(得数保留两位小数)7、一个圆柱形水池的容积是43.96立方米,池底直径4米,池深多少米?8、一口周长是6.28米的圆柱形水井,它的深是10米,平时蓄水深度是井深的0.8倍,这口井平时的水量是多少立方米?9、一个长8分米,宽6分米,高4分米的长方体与一个圆柱体的体积相等,高相等,这个圆柱的底面积是多少?10、一段圆柱形钢材,长50厘米,横截面半径是4厘米,如果每立方厘米钢是7.9克,这段钢材的重量是多少千克?(得数保留一位小数)12、有一段底面是环形的钢管,外圆直径是40厘米,内圆直径是20厘米,这根钢管长250厘米,求这根钢管的体积是多少立方厘米?圆柱的体积练习二1、一个圆柱的底面半径是6厘米,高是2分米,求这个圆柱的体积。
2、小刚有一个圆柱形的水杯,水杯的底面半径是5厘米,高是10厘米,有资料显示:每人每天的正常饮水量大约是1升,小刚一天要喝几杯水?3、一个圆柱形水桶,底面直径和高都是40厘米,用这个水桶容积的85%装水,每升水重1千克,桶中的水大约有多少千克?4、一个底面半径是10米的圆柱形蓄水池,能蓄水2512立方米,若再挖深2米,可蓄水多少立方米?5、一个圆柱形油桶,内底面直径是40厘米,高是50厘米,它的容积是多少升?如果1升柴油重0.85千克,这具油桶可装柴油多少千克?(得数保留整千克)6、一个圆柱形玻璃杯底面半径是10厘米,里面装不水,水的高度是12厘米,把一小块铁块放进杯中,水上升到15厘米,这块铁块重多少克?(每立方厘米铁重7.8克)7、下图是一个长15厘米,宽6厘米、高15厘米的长方体钢制机器零件,中间有一个底面半径为5求这个零件的体积。
圆柱的体积 非常详细

圆柱的体积巩固与加深圆柱的体积:体积=底面积×高 V=r2πh1、正方体的体积,长方体的体积都可以表示为:底面积×高2、圆柱体体积公式: V=r2πh,体积公式推导过程如下:长方体的长等于圆柱的(底面周长的一半,即πr)长方体的宽等于圆柱的(底面半径,即r)长方体的高等于圆柱的(高,即h)长方体的体积=长×宽×高圆柱的体积=(πr)×(r)×(h)=r 2πh=底面积×高V = S h【针对性练习】一、填空题1、做一节底面直径是10厘米、长85厘米的圆柱体通风管,至少用一张长()厘米,宽()厘米的长方形铁皮。
2、一个圆柱的底面面积是25平方厘米,高是10分米,它的体积是()立方厘米。
3、一个圆柱的体积是314立方分米,它的底面面积是6.28平方分米,它的高是()。
4、一个圆柱的底面半径为2厘米,侧面展开后正好是一个正方形,这个圆柱的体积是()。
5、一个长为6厘米,宽为4厘米的长方形,以长为轴旋转一周,将会得到一个底面半径是(),高为()的()体,它的体积是()。
6、一个底面半径为2厘米,高为4厘米的圆柱,侧面积是(),表面积是(),体积是()。
7、底面周长和高分别相等的圆柱和长方体,体积相比较,()的体积较大。
8、把4段底面周长相等的圆柱钢材焊接成一个圆柱,减少的底面有()个。
9、一个圆柱形油桶,从桶内量得底面直径是20分米,高是20分米,这个油桶的容积是()。
10、把一个底面直径和高都是4分米的圆柱体切开拼成一个近似的(),这个长方体底面的长约是(),宽约(),高是(),底面面积约是(),体积约是()11、一个圆柱的底面半径扩大2倍,高不变,它的底面积扩大()倍,侧面积扩大()倍,体积扩大()倍;12、一个圆柱的底面半径扩大2倍,高也扩大2倍,它的底面积扩大()倍,侧面积扩大()倍,体积扩大()倍;13、一个圆柱的底面半径扩大2倍,高扩大3倍,它的底面积扩大()倍,侧面积扩大()倍,体积扩大()倍。
圆柱的表面积和体积的练习题作业32道

8、边长是2.4分米的正方形铁板,四个角分别去掉 一个小正方形,剩下的恰好焊成一个无盖的正方 体容器,这个容器的占地面积是多少? 9 、长方体,宽增加 5 厘米就成了正方体,表面积 增加了160平方厘米,这个长方体的体积是多少? 10、压路机的前轮是圆柱,底面直径是1米,长是 1.5米,共滚动了450周,这条公路有多长?压过的 路面有多少平方米?
11、把一个棱长是20厘米的正方体削成一个最大的 圆柱,这个圆柱的表面积是多少?
12、把一个底面直径是6厘米,高是5厘米的 圆柱形木料沿着与底面平行的面锯成3段,它 的表面积增加了多少?
13、一个圆柱高 8厘米,截下2厘米的一段后, 圆柱的表面积减少了12.56平方厘米,求原来 圆柱体的表面积。
14、一根圆柱形木料,长2米,底面半径是 5 厘米,把它锯成4段,表面积增加了多少? 15、有一个长15米的钢管,外直径是6厘米, 管壁厚2厘米,这根钢管的体积是多少?
1.把一个圆柱的底面分成许 多相等的扇形,沿高切开 后,拼成一个近似的长方 体,表面积增加了180平方 厘米,如果这个圆柱的高 是10厘米,体积是多少立 方厘米?
11.一台压路机,前轮直径 1米,轮宽1.2米。工作时
每分钟滚动15周。这台压 路机工作1分钟前进了多少 米?工作1分钟前轮压过的
路面是多少平方米?
28、把一个圆柱切成两个半圆柱,切面是边 长2厘米的正方形,原来圆柱的表面积是多少 平方厘米?
29、一个长方形长8厘米,宽4厘米,以长方 形的长为轴旋转一周得到一个立体图形,这 个立体图形的底面积、侧面积、体积各是多 少?
30、一个圆柱的侧面展开图是一个正方形, 如果圆柱的高缩短2厘米,表面积就减少 12.56平方厘米,求原来这个圆柱的体积。
圆柱圆锥练习题以及答案

圆柱圆锥练习题以及答案一、选择题1. 一个圆柱的底面半径为3厘米,高为5厘米,其体积为:A. 141.3立方厘米B. 282.6立方厘米C. 94.2立方厘米D. 47.1立方厘米2. 一个圆锥的底面半径为4厘米,高为9厘米,其体积为:A. 75.36立方厘米B. 100.48立方厘米C. 50.24立方厘米D. 37.68立方厘米3. 圆柱的侧面积公式是:A. 2πr²B. πr²C. 2πrhD. πrh4. 圆锥的侧面积公式是:A. πr²B. πrlC. πr²+πrlD. 2πrh二、填空题1. 一个圆柱的底面直径为6厘米,高为10厘米,其侧面积为______平方厘米。
2. 一个圆锥的底面半径为5厘米,高为12厘米,其体积为______立方厘米。
三、解答题1. 一个圆柱形水桶的底面直径为40厘米,高为60厘米,求这个水桶的容积。
2. 一个圆锥形沙堆,底面半径为3米,高为4米,如果每立方米沙重1.5吨,求这堆沙的重量。
四、计算题1. 一个圆柱形油桶,底面直径为50厘米,高为80厘米,求油桶的表面积。
2. 一个圆锥形粮仓,底面直径为20米,高为15米,如果每立方米粮食重750千克,求粮仓的容积以及能装多少千克的粮食。
答案:一、选择题1. B2. B3. C4. C二、填空题1. 376.82. 188.4三、解答题1. 水桶的容积为:V=πr²h=π×(20)²×60=37680立方厘米。
2. 圆锥形沙堆的体积为:V=1/3πr²h=1/3×π×(3)²×4=12.56立方米。
沙堆的重量为:12.56×1.5=18.84吨。
四、计算题1. 油桶的表面积为:A=2πr(h+r)=2π×25(80+25)=4712.5平方厘米。
2. 圆锥形粮仓的体积为:V=1/3πr²h=1/3×π×(10)²×15=1570立方米。
圆柱体体积表的练习题

圆柱体体积表的练习题一、填空题1. 圆柱体的体积公式是 V = ________。
2. 若圆柱体的底面半径为 r,高为 h,则体积 V = ________。
3. 一个圆柱体的底面直径为 10cm,高为 20cm,其体积为________ cm³。
4. 当圆柱体的底面半径和高都增加一倍时,体积变为原来的________ 倍。
5. 已知圆柱体的体积为500π cm³,底面半径为 5cm,则高为________ cm。
二、选择题A. V = πr²hB. V = πr² + hC. V = 2πrhD. V = 2πr²2. 一个圆柱体的底面半径为 3cm,高为 4cm,其体积为多少?A. 36π cm³B. 12π cm³C. 24π cm³D. 48π cm³3. 若圆柱体的底面半径和高相等,下列哪个选项是正确的?A. 体积为πr²hB. 体积为2πr²C. 体积为4πr²D. 体积为8πr²4. 圆柱体的底面积为25π cm²,高为 10cm,其体积为多少?A. 250π cm³B. 50π cm³C. 125π cm³D. 75π cm³5. 下列哪个条件不能确定圆柱体的体积?A. 底面半径和高B. 底面直径和高C. 底面周长和高D. 底面面积和底面直径三、计算题1. 已知圆柱体的底面半径为 7cm,高为 10cm,求其体积。
2. 一个圆柱体的底面直径为 14cm,高为 30cm,求其体积。
3. 若圆柱体的体积为900π cm³,底面半径为 15cm,求其高。
4. 计算底面半径为 5cm,高为 12cm 的圆柱体体积。
5. 已知圆柱体的底面周长为 31.4cm,高为 20cm,求其体积。
圆柱体体积表的练习题(续)四、应用题1. 一个圆柱形水桶,底面直径为1米,桶内水深0.8米,求桶内水的体积。
圆柱练习题含答案

圆柱练习题含答案1. 计算圆柱的体积和表面积已知圆柱的底面半径为r,高为h,请计算该圆柱的体积和表面积。
解答:- 圆柱的体积计算公式为:V = π * r^2 * h- 圆柱的表面积计算公式为:A = 2 * π * r^2 + 2 * π * r * h其中,π(pi)取3.14。
根据给定的底面半径和高,代入公式进行计算即可得到圆柱的体积和表面积。
2. 计算圆柱的侧面积和母线长度已知圆柱的底面半径为r,高为h,请计算该圆柱的侧面积和母线长度。
解答:- 圆柱的侧面积计算公式为:S = 2 * π * r * h- 圆柱的母线长度计算公式为:L = √(r^2 + h^2)根据给定的底面半径和高,代入公式进行计算即可得到圆柱的侧面积和母线长度。
3. 圆柱的应用场景圆柱是一种常见的几何体,在生活和工程中有着广泛的应用。
下面列举几个圆柱的应用场景:- 水桶:水桶的形状就是一个圆柱,圆柱的设计使得水桶能够存储大量的液体,并且容易倒出。
- 柱形雕塑:许多雕塑作品采用圆柱形状,例如公园中的柱形雕塑。
圆柱形状使得雕塑具有更好的稳定性。
- 管道:在建筑工程中,许多管道采用圆柱形状。
圆柱的设计使得管道具有较大的容纳空间,并且易于连接和安装。
这些场景都体现了圆柱的特点和优势,圆柱在不同领域中发挥着重要的作用。
总结:通过以上练习题,我们学习了如何计算圆柱的体积、表面积、侧面积和母线长度。
圆柱在生活和工程中有着广泛的应用,了解和掌握圆柱的相关知识对我们理解和应用几何学具有重要意义。
希望以上内容能够帮助到您,并且满足您的需求。
如有其他问题或需要进一步解答,请随时告知。
2022-2023学年人教版数学六年级下册圆柱的体积练习题(含答案)
【分析】等底等高圆锥体积是圆柱体积的 ;也就是圆柱体积是圆锥体积的3倍;再用圆柱的体积减去圆锥的体积,剩下的就是削去部分的体积,再用削去部分的体积除以圆锥的体积,把圆柱的体积看作是3,则圆锥体积是1;即可解答。
【详解】(3-1)÷1
=2÷1
=2
把一个圆柱形木料削成一个最大的圆锥,圆锥的体积是圆柱的 ,消去部分是圆锥体积的2倍。
=50.868(平方米)
50.868×128=6511.104(元)
答:贴瓷砖的面积是50.868平方米,需要购买6511.104元的瓷砖。
【点睛】本题考查了圆柱相关的应用题,这个水池相当于没有上面底面的圆柱。
17.不相同,一个体积是50.24立方厘米,另一个体积是100.48立方厘米。
【分析】以这个长方形的长为轴旋转得到的圆柱底面半径是2厘米、高是4厘米,以这个长方形的宽为轴旋转得到的圆柱底面半径是4厘米、高是2厘米,根据圆柱体积=底面积×高,分别计算出两个圆柱的体积,再比较即可。
【点睛】利用圆柱的认识及特征以及圆柱的体积公式进行解答。
9.30
【分析】把长方体钢材截成两段,表面积会增加2个截面的面积,先用增加的表面积除以2,求出一个截面的面积,再根据公式V=Sh,代入数据计算即可求出这个钢材原来的体积。
【详解】2÷2=1(平方分米)
1×30=30(立方分米)
【点睛】掌握长方体切割的特点,明确增加的表面积是哪些面的面积,以此为突破口,利用公式列式计算。
9.把一根长30分米的长方体钢材截成两段,表面积比原来增加了2平方分米,这个钢材原来的体积是( )立方分米。
10.把一个圆柱形木料削成一个最大的圆锥,圆锥的体积是圆柱的( ),削去部分是圆锥体积的( )。
10道圆柱体积的计算和答案
10道圆柱体积的计算和答案例题1:一个圆柱,底面周长9.42分米,高20厘米。
求它的体积?20厘米= 2分米底面半径:9.42 ÷ 3.14 ÷ 2 = 1.5(分米)体积:3.14 × 1.5²× 2 = 14.13(立方分米)答:它的体积是14.13立方分米。
例题2:一个圆柱形蓄水池,水池底面积是3.14平方米,深2米,这个蓄水池可以蓄水多少升?V=3.14x2=6.28立方米6.28立方米=6280立方分米=6280升答:这个蓄水池可以蓄水6280升。
例题3:万大叔家定制了一个圆柱形粮仓,底面半径是2米,高是5米。
如果每立方米稻谷重750千克,这个粮仓可以放稻谷多少吨?V=3.14x2x2x5=62.8立方米62.8x750=47100kg=47.1t答:这个粮仓可以放稻谷47.1吨。
例题4:一种圆柱形固体胶,底面直接是2cm,高是7cm,这种固体胶的体积是多少?V=3.14x(2÷2)x(2÷2)x7=21.98立方厘米答:这种固体胶的体积是21.98立方厘米。
例题5:天然气供气站立着一个大型圆柱存气桶。
量的底面圆的周长是25.12米,高是8米,这个气桶存气多少升?25.12÷3.14÷2=4米V=3.14x4x4x8=401.92立方米401.92立方米=401920立方分米=401920升答:这个气桶可以存气401920升。
例题6:一个圆柱形的粮囤,从里面量得底面周长是9.42米,高是2米,每立方米稻谷约重545千克,这个粮囤约装稻谷多少千克?(得数保留整千克数)。
3.14 ×(9.42÷3.14÷2)² × 2 × 545 = 7700.85 ≈ 7701(千克)答:这个粮囤约装稻谷7701千克。
例题7:有一个高为6.28分米的圆柱形机件,它的侧面展开正好是一个正方形,求这个机件的体积?3.14 ×(6.28÷3.14÷2)² × 6.28 =19.7192(立方分米)答:这个机件的体积是19.7192立方分米。
苏教版小学六年级数学下册第二单元《圆柱体体积》同步练试题共四套
3、砌一个圆柱形水池,底面周长 25.12 米,深 2 米,要在底面和四周抹上水泥,如果每平方 米用水泥 10 千克,共需水泥多少千克?
4、把一段长 20 分米的圆柱形木头沿着底面直径劈开,表面积增加 柱形木头的表面积是多少?
80 平方分米,原来这段圆
5、一个圆柱形的粮囤,从里面量得底面周长是 9.42 米,高 2 米,每立方米稻谷约重 545 千 克,这个粮囤约装稻谷多少千克?(得数保留整千克数)
(16) 一个无盖的圆柱形铁皮油桶, 底面直径是 1.2 米,高是 2 米,要在水桶里、 外两面都漆防锈漆,
油漆的面积大约是多少平方米?(得数保留一位小数)如果每立方米的油重
0.82 吨,这个油桶可以
盛放多少吨油?
小学六年级数学下册圆柱体练习题 4
7
姓名
成绩
1、 填空。
( 1)一个圆柱体,底面周长是 125.6 厘米,高是 12 厘米,它的侧面积是(
)平方厘
米。
( 2)一个圆柱体,底面半径是 3 厘米,高是 5 厘米,它的侧面积是(
)平方厘米,表
பைடு நூலகம்
面积是(
)平方厘米。
( 3)把一张长 8 分米,宽 5 分米的白纸, 围成一个圆柱形纸筒, 这个纸筒的侧面积是 (
)
平方分米。
( 4)一个圆柱体,底面半径是 3 厘米,高是 15 厘米,它的表面积是(
)平方厘米。
( 2)底面周长 12.56dm,高是 1.5dm.
1
小学六年级数学下册同步练习 13
( 3)底面直径是 4cm,高是 2.5cm
思维拓展题 5.一个圆柱形粮囤,从里面量,底面周长是 克,那么这个粮囤大约能装稻谷多少吨?
62.8 米,高是 3 米,每立方米稻谷重 545 千
(完整版)圆柱体的体积练习题
圆柱体的体积练习题〔一〕1 .把一个棱长是6分米的正方体木块,削成一个最大的圆柱体,这个圆柱体的体积是多少立方分米?2.有一个高为6.28分米的圆柱体的机件,它的侧面积展开正好是一个正方形, 求这个机件的体积.3 .要制作容量是62.8升的圆柱形铁桶,如果底面半径是2分米,高应是多少分米?4.一个圆柱形油桶,装满了油,把桶里的油倒出3/4,还剩20升,油桶高8分米,油桶的底面积是多少平方分米?5 .把一种空心混凝土管道,内直径是40厘米,外直径是80厘米,长300厘米, 求浇制100节这种管道需要多少混凝土?6.一个圆柱体的底面半径是4厘米,高8厘米,求它的体积和外表积.7 .做一个无盖的圆柱形铁皮水桶,高30厘米,底面直径20厘米,做这个水桶至少要用多少平方分米的铁皮?这个水桶能装多少千克的水?〔1立方分米水重1千克〕圆柱体的体积练习题〔二〕1、一个圆柱形油桶,从里面量的底面半径是20厘米,高是2分米.这个油桶的容积是多少?2、把一个棱长是6分米的正方形木块,削成一个最大的圆柱,需要削去多少立方分米的木块?3、一个圆柱体的体积是10立方分米,底面积是2.5平方分米,它的高是多少分米?4、一个圆柱的底面周长是12.56分米,高是3米,它的体积是多少立方分米?5、一根长2米的圆木,截成两段后,外表积增加了24平方厘米,这根圆木原来的体积是多少?6、一个底面直径是6厘米的茶杯里,装有7厘米高的水,放入一块小石头,水面上升到10厘米,这个石头的体积是多少立方厘米?7、把一张长62.8厘米,宽31.4厘米的长方形硬纸片,卷成一个圆柱形纸筒, 它的体积是多少?8、一个圆柱体的侧面积是31.4平方厘米,底面周长是6.28厘米,这个圆柱体的体积是多少立方厘米圆柱体的体积练习题〔三〕1、一个圆柱体汽油桶,从里面量底面半径20厘米、高1米.如果每立方米汽油重0.73千克,这个油桶最多能装汽油多少千克?2、把一个棱长6分米的正方体木块切削成一个体积最大的圆柱体,这个圆柱的体积是多少立方分米?3、将一个棱长为6分米的正方体钢材熔铸成底面半径为3分米的圆柱体,这个圆柱有多长?4、一个底面半径为3分米,高为8分米圆柱形水槽,把一块石块完全浸入这个水槽,水面上升了2分米,这块石块的体积是多少?5、一个无盖的圆柱形水桶,侧面积是188.4平方分米,底面周长是62.8分米做这个水桶至少要多少平方分米?这个水桶的容积是多少立方分米?6、把一个长、宽、高分别是9cm 7cm 3cm的长方体铁块和一个棱长是5cm的正方体铁块,熔铸成一个圆柱体.这个圆柱体的底面直径是20cm,高是多少厘米?7、将一个圆柱体沿着底面直径切成两个半圆柱,外表积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米?8、用一块长50厘米,宽30厘米的长方形铁皮做圆柱形容器的侧面,再另用一块铁皮做底,怎样做才能使此容器的容积最大?9、用一块长60厘米、宽40厘米的铁皮做圆柱形水桶的侧面,另找一块铁皮做底.这样做成的铁桶的容积最大是多少?圆柱体的体积练习题〔四〕1、一个长方体长7厘米,宽4厘米,高6厘米,把它削成一个体积最大的圆柱体,圆柱体的体积是多少?2、在一只底面半径为20厘米的圆柱形小桶里,有一半径为10厘米的圆柱形钢材浸没在水中.当钢材从桶里取出后,桶里的水下降了3厘米.求这段钢材的长.3、在半径为20厘米的圆柱形储水桶里,有一段截面为正方形的方钢浸没在水中, 正方形的边长是4厘米.当这段方钢从水中取出时,桶里的水面下降了0.5厘米这段方钢长多少厘米?4、一个圆柱形的玻璃杯中盛有水,水面高 2.5cm,玻璃杯内侧的底面积是72平方厘米,在这个杯中放进棱长6cm的正方体铁块后,水面没有淹没铁块,这时水面高多少厘米?5、有一种饮料瓶的瓶身呈圆柱形〔不包括瓶颈〕,容积是30分米3.现在瓶中装有一些饮料,正放时饮料高度为20厘米,倒放时空余局部的高度为5厘米. 瓶内现有饮料多少立方分米?6、把一个底面半径是1厘米的圆柱体侧面展开,得到一个正方形,这个圆柱体的体积是多少立方厘米?7、在一底面半径为30厘米的圆柱形容器内,有一半径为20 H米的圆柱形钢材浸没在水中.当取出钢材之后,水面下降了4厘米.求圆钢的长度.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱体积练习题
班级姓名
一、填空:
1.把一个底面直径和高都是2分米的圆柱体切开拼成一个近似的(),这个长方体底面的长约是(),宽约(),高是(),底面面积约是(),体积约是()。
2.一个圆柱的底面面积是25平方厘米,高是10分米,它的体积是()。
3.一个圆柱的体积是314立方分米,它的底面面积是6.28平方分米,它的高是()。
4.一个圆柱的底面半径扩大2倍,高不变,它的底面积(),侧面积(),体积();一个圆柱的底面半径扩大2倍,高也扩大2倍,它的底面积(),侧面积(),体积();一个圆柱的底面半径扩大2倍,高扩大3倍,它的底面积(),侧面积(),体积()。
5.一个圆柱的底面半径为4厘米,侧面展开后正好是一个正方形,这个圆柱的体积是()。
6.一个长为6厘米,宽为4厘米的长方形,以长为轴旋转一周,将会得到一个底面半径是(),高为()的()体,它的体积是()。
7.把一根长2米的圆木,截成两段后表面积增加了48平方厘米,这根圆木原来的体积是()。
8.一个底面半径为2厘米,高为4厘米的圆柱,侧面积是(),表面积是(),体积是()。
9.底面周长和高分别相等的圆柱和长方体,体积相比较,()的体积较大。
10.把4段底面周长相等的圆柱钢材焊接成一个圆柱,减少的底面有()个。
11.一个圆柱形油桶,从桶内量得底面直径是20分米,高是20分米,这个油桶的体积是(),容积是()。
12. 2.54立方米=()立方分米=()升
85000毫升=()升=()立方分米
1500立方厘米=()毫升=()升
13.两个圆柱的高相等,底面周长的比是2:5,则体积之比是()。
14.两个圆柱的高相等,底面半径的比是2:3,则体积之比是()。
15.一个油桶的体积()它自身的容积。
16.一个圆柱的底面周长是314米,高是10分米,它的底面积是(),侧面积是(),表面积是(),体积是()。
二、判断题:
1.圆柱的底面积越大,体积越大。
()
2.把正方体木块削成一个最大的圆柱,则此圆柱的直径与高相等。
()
3.圆柱体的高不变,底面积扩大2倍,体积扩大4倍。
()
4.一个圆柱体的高扩大2倍,底面积缩小2倍,它的体积不变。
()5.两相圆柱的侧面积相等,它们的体积也一定相等。
()
6.长方体、正方体和圆柱体的体积,都可以用底面积乘高来求。
()7.圆柱体的体积公式是由长方体的体积计算公式推导而来的。
()
8.把一个圆柱切成两半,表面积和体积都增加了。
()
三、解决问题:
1、按要求计算:(写小标题)
(1)(求体积):底面积14平方厘米,高5厘米
(2)(求表面积、体积):底面直径6分米,高10分米
(3)(求表面积、体积):底面周长37.68米,高10分米
2.一个圆柱水杯,底面直径10厘米,高40厘米,现在有9.42升的水倒入这个水杯中,可以倒几杯?
3.右图是一个圆柱的展开图,求这
个圆柱的体积。
(单位:厘米)
4.求下面钢管的体积:
内径:8厘米外径:10厘米长:80厘米
5.一个圆柱形的粮囤,从里面量得底面半径是2.5米,高是2米,这个粮囤能装玉米多少立方米?如果每立方米玉米重545千克,这个粮囤大约能装多少千克玉米?
6.如图,一个圆柱体沿着直径垂直切开,表面积增加了64平方厘米,已知这个圆柱体的高是8厘米,求圆柱的体积。
7.一个圆柱的底面半径是5分米,侧面积是188.4平方分米,体积是多少立方分米?。
