二年级奥数讲义7
奥数-二年级-教案--第07讲-枚举法-教师版

第七讲 枚举法初步新年到了,爸爸要给小昊买一个四阶魔方作为圣诞礼物,这个魔方的价格是28元8角。
小昊发现,可以有多种付钱方法:(1)2张10元,1张5元,3张1元,1张5角,3张1角;(2)1张10元,3张5元,3张1元,1张5角,1张2角,1张1角;(3)1张20元,4张2元,8张1角;(4)3张10元,收30元找回1元2角;等等。
一般的,根据问题要求,一一列举问题的解答,或者为了解决问题的方便把问题分成不遗漏不重复的优先种情况,并加以解决,最终达到解决整个问题的目的。
这种分析问题解决问题的方法,称之为枚举法。
注意:运用枚举法解决问题时,必须注意无重复,无遗漏。
为此必须要求有次序有规律的进行枚举。
把一个整数表示成若干个小于它的自然数值和,叫做整数的拆分。
整数4有多少种不同的拆分方法?分拆时,将自然数按从达到小的顺序出现,一共有4种不同的分拆方法:4=3+1,4=2+2,4=2+1+1,4=1+1+1+1。
用一台天平和重1克、3克、9克的砝码各一个(不再用其他物品当砝码),当砝码只能放在同一个盘内时,可以称出的重量有多少种?共有三个重量不同的砝码,可以取出其中的一个,两个,三个来称量。
一一来列举这三种情况。
取一个砝码可称:1克、3克、9克。
有3种。
取两个砝码可称:1+3=4(克)、1+9=10(克)、3+9=12(克),3种。
取三个砝码可称:1+3+9=13(克),有1种。
注意到1、3、9、4、10、12、13各不相同,所以可以称出: 3+3+1=7(种)课外小组组织30人做游戏,按1~30号排队报数。
第一次报数后,单号全部站出来,然后每次余下的人中第一个开始站出来,隔一人站出来一个人,到第几次这些人全部站出来?最后站出的人应该是第几号?根据题目的特点,先用排列法把题中的条件问题列出来,再用枚举法完成题目要求。
排好队的人依次是1,2,3,4,5,......28,29,30从上面的列表中我们毫无遗漏的排列,得出到第五次这些人全部站出来,最后在个人是16号。
二年级奥数 第七讲:重叠问题

第七讲 重叠问题 哪吒智闯水晶宫---哪吒被骗了哪吒继续往前去寻宝,只见一位白胡子老爷爷拿着哪吒地乾坤圈站在大厅中间。
“那是我的乾坤圈!”哪吒激动的叫起来。
哪吒赶紧跑过去一看,“怎么有两个乾坤圈?” 白胡子老爷爷微笑的说:“哪吒不认识我了?”哪吒仔细打量了这位老爷爷后说:“我记起来了,你是太白金星。
”太白金星:“哪吒,我听说了你的事后,特意来帮助你的,你看,我帮你把乾坤圈要回来了。
”哪吒:“那怎么有两个乾坤圈?”太白金星:“这其中一个是我的金钢圈,另一个是你的乾坤圈,刚才我拿一个圈称连我共重67千克,拿另一个圈称连我共重68千克,我的金刚圈比你的乾坤圈重,你猜得出来你的乾坤圈和我的金刚圈多重,我就把你的宝贝还给你”哪吒:“太白金星,你说话可得算数!”太白金星:“那当然了,我胡子都白了,还会骗你?你就在这里想吧,我有事先走,一会儿就回来”哪吒在原地想了一天一夜,也没有想出答案,他明白了,他并不知道太白金星的体重是不可能算出乾坤圈和金刚圈的重量的,他被骗了,那个老人根本不是太白金星!他不过是中了龙王的圈套而已,哪吒气冲冲的继续前进,心想,要再被我碰到这假冒的太白金星,我一定把他的胡子拔了!例题精讲例1 小朋友们排队练体操,小红的左边有6个人,右边有2个人,这一排共有几个人?6 小红 2分析:由图知道,小红所在一队的小朋友,可以分成三部分:第一部分是小红的左边的6个人,第二部分是小红这1个人,第三部分是小红右边的2个人。
要求一共有多少人,就是把这三部分加起来。
即6+1+2=9(人)。
小朋友排队去春游,小云的前面有5个同学,小云的后面有几个同学?小云分析:这一队的小朋友,可以分成三部分:要求小云后面有几个同学,就要从总人数12里面去掉小云前面的5个同学,再去掉小云1个人,才能求出问题。
即12―5―1=6(人)。
例3 幼儿园小朋友排队参观盆景,从前面数,小林是第10个,从后面数,小林是第17个,这一排共有几个小朋友?分析:“从前面数,小林是第10个”说明小林和他前面同学一共是10人,这个“10”里面包括小林,也包括他前面的同学;“从后面数,小林是第17个”,说明小林和他后面同学一共是17人,这个“17”里面包括小林,也包括他后面的同学。
二年级数学奥数讲义练习第7讲火柴棒游戏(全国通用版,含答案)

二年级数学奥数讲义练习第7讲火柴棒游戏(全国通用版,含答案)【专题简析】用火柴棒做游戏,小朋友们感兴趣吗?火柴棒游戏中有很多窍门,让我们共同了解火柴棒中的数学,了解数学的其妙,使小朋友们在有趣的数学游戏中变得更加聪明。
用火柴棒摆成的算式,可以根据算式中给的数的特点,移动火柴棒使它变成另一个数,或改变一个运算符号,使等式成立,如果是图形,可以直接拿掉或移动多余的几根火柴棒,还要考虑让火柴棒重复使用,这样可增加图形的个数【例题1】下面是用火柴棒摆成的两道算式,但都不能成立,请你只移动一根火柴棒,使算式成立。
(1)(2)思路导航:移动火柴棒时,要保证火柴棒的根数没有变化。
如“”与“”、“”与“”、“”与“”之间都可以相互转化。
第(1)题中,等号左边的计算结果是21,而右边只是1,所以应通过移动火柴棒,使左边减小右边增大。
把左边的“+”变成“-”,左边移动一根火柴棒到右边,使“1”变成“7”,等式成立。
第(2)题中,观察算式两边。
等号左边的计算结果是641,右边的计算结果是141,所以应从等号左边移一根火柴棒到右边,把等号左边的减数121变成21,则左边的计算结果是741。
等号右边141中,添上移过来的一根火柴棒,恰好变成741,于是等式成立。
解;(1)17-7=7或4+7=11(2)741+21-21=741或141+121-121=141练习11,下面的算式是用火柴棒摆成的,等号两边不相等,请移动其中一根使等式成立。
(1)(2)2,移动一根火柴棒使等式成立。
(1)(2)3,只许移动一根火柴棒,使等式成立。
(1)(2)【例题2】有一把椅子如图(1)所示,椅子翻倒还掉了一条腿。
请移动2根火柴,使椅子翻过来,且看上去也不缺少腿。
(1)(2)思路导航:要把椅子翻过来,就要使下面有四条腿,上面有靠背。
移动后的结果如图(2)所示,虚线表示移走的火柴。
解;见图(2)练习21,下面是用火柴棒摆成头朝上的龙虾,移动3根,使它头朝下。
二年级奥数第七讲-------找规律(二)
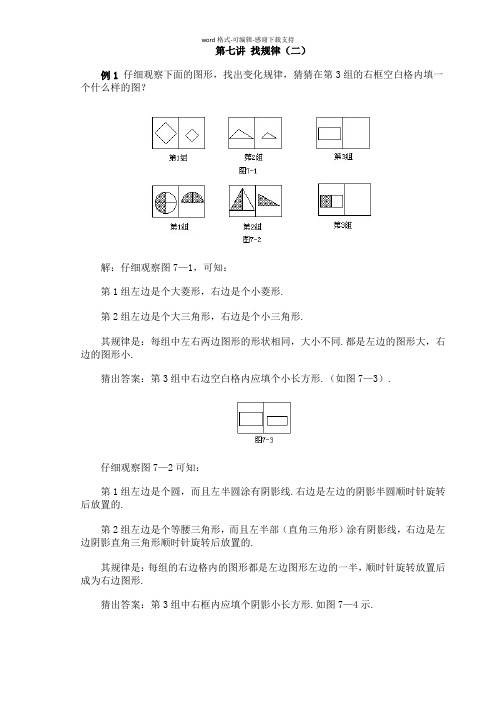
第七讲找规律(二)例1仔细观察下面的图形,找出变化规律,猜猜在第3组的右框空白格内填一个什么样的图?解:仔细观察图7—1,可知:第1组左边是个大菱形,右边是个小菱形.第2组左边是个大三角形,右边是个小三角形.其规律是:每组中左右两边图形的形状相同,大小不同.都是左边的图形大,右边的图形小.猜出答案:第3组中右边空白格内应填个小长方形.(如图7—3).仔细观察图7—2可知:第1组左边是个圆,而且左半圆涂有阴影线.右边是左边的阴影半圆顺时针旋转后放置的.第2组左边是个等腰三角形,而且左半部(直角三角形)涂有阴影线,右边是左边阴影直角三角形顺时针旋转后放置的.其规律是:每组的右边格内的图形都是左边图形左边的一半,顺时针旋转放置后成为右边图形.猜出答案:第3组中右框内应填个阴影小长方形.如图7—4示.例2按顺序仔细观察图7—5、7—6的形状,猜一猜第3组的“?”处应填什么图?解:图7—5的?处应填○▲.注意观察第1组和第2组,每组都是由三对小图形组成;而每对小图形都是由一个“空白”的和一个“黑色”的小图形组成;而且它俩的排列顺序都是“空白”的在左边,“黑色”的在右边.再按着第1、第2、第3组的顺序观察下去,可发现每对小图形在各组中的位置的变化规律:它们都在向左移动,当一对小图形移动到最左边后,下一步它就回到了最右边.按这个移动规律,可知图7—5中第3组“?”处应填:○▲.图7—6的?处应填□△0.仔细观察可发现第1组和第2组中间的部分都是由三个小图形构成的.构成的规律是:当你按照第1、第2、第3组的顺序观察时,6个小图形都在向左移动,而且移动的同时又在重新分组和组合,但排列顺序保持不变,当某一个小图形移动到了最左边时,下一步它就回到了最右边.按这个规律可知图7—6中第3组中间“?”处是:□△0.例3观察图7—7的变化,请先回答:在方框(4)中应画出怎样的图形?再答按(1)、(2)、(3)、……的顺序数下去,第(10)个方框中是怎样的图形?解:先按(1)、(2)、(3)、……的顺序仔细观察,可发现:方框中的箭头是按逆时针方向旋转的;方框中的其他小图形,如△、□和○也都是按逆时针方向旋转的.也就是说,方框连同内部的所有小图形作为一个整体在按逆时针方向旋转.因此,方框(4)中的小图形应画成图7—8状.再按已找到的规律,进一步可发现图形的变化是有“周期性”的,也就是说,每过4个方框后,同样的图形又重新出现一次.如,你可看到第(1)和第(5)是完全一样的;因此,你可以想像得到,第(2)和第(6)及第(10)个图形应当是完全一样的.即第(10)个方框中的图形应是图7—9所示的样子.例4观察图7—10的变化,请先回答:第(4)、(8)个图中,黑点在什么地方?第(10)、(18)个图中,黑点在什么地方?解:(1)按图7—10中(1)、(2)、(3)、……的顺序仔细观察,可发现黑点位置的变化规律:在(1)中,黑点在最上面第一条横线上;在(2)中,黑点下降了一格,在上面第二条横线上;在(3)中,黑点又下降了一格,在中间一条线上了.按黑点位置的这种变化可推测出:在(4)中,黑点又下降一格,它的位置应如图7—11所示.继续观察下去:在(5)中,黑点下降到最下面的一条横线上;在(6)中,黑点开始往上升一格;在(7)中,黑点再上升一格,按着黑点位置的这种变化可推测出:在(8)中,黑点又上升一格,它的位置应如图7—12所示.(2)进一步仔细观察图7—10(1)~(9),可发现黑点位置变化的“周期性”规律:也就是说,每隔8个小图,黑点又回到原来的位置.因为2+8=10,2+8+8=18.所以第(10)、(18)个小图中,黑点的位置应与第(2)个小图相同,见图7—13所示.习题七1.仔细观察图7—14,找找变化规律,猜猜在第3组的空白格内填一个什么样的图?2.仔细观察图7—15,找找变化规律,猜猜在第3组的空白格内填一个什么样的图?3.仔细观察图7—16,找找变化规律,猜猜在第3组的空白格内填一个什么样的图?4.按顺序仔细观察下列图形,猜一猜第3组的“?”处应填什么图?5.按顺序仔细观察下列图形,猜一猜第3组的“?”处应填什么图?6.按顺序仔细观察下列图形,猜一猜第3组的“?”应填什么图?7.按顺序仔细观察下列图形,猜一猜第3组的“?”应填什么图?8.仔细观察下列图形的变化,请先回答:①在方框(4)中应画出怎样的图形?②再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?9.仔细观察下列图形的变化,请先回答:①在方框(4)中应画出怎样的图形?②再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?习题七解答①先按(1)、(2)、(3)、……的顺序仔细观察,可以发现:在(1)中,*在左上角,在(2)中它在右上角,在(3)中它在右下角,……可见它在沿顺时针方向转动.其他三个小图形,即□、△、○,也和*一样都在沿着顺时针方向转动.发现规律:因方框中的每个小图形的位置的变化都是按顺时针方向旋转,可以说,方框连同内部的小图形及整体在按顺时针方向旋转.②进一步猜想,根据所发现的规律进一步推测可知,第(4)个方框中的图形的样子.③按(1)、(2)、(3)、……的顺序仔细观察,进一步还可发现,图形的变化是有“周期性”的,也就是说,每过4个方框后,完全同样的图形又重新出现,如第(1)、(5)、(9)个图形是完全一样的.因为2+4+4=10,所以第(10)个方框内的图形与第(2)完全相同.9.答:(见图7—31)。
二年级奥数第七讲和倍问题

第七讲和倍问题智慧屋我们把已知几个数的和以及它们之间的倍数关系,求这几个数各是多少的题目称为和倍问题。
解答和倍问题时,我们要确定一个数为标准,一般是比较小的那个数,假定它为一倍(一份),再根据其他几个数与较小数的倍数关系,确定这几个数是较小数的几倍,然后用除法求出较小数,再算出其他各数。
例1、二(1)班和二(2)班共为“希望工程”捐书120本。
(1)班捐的本数是(2)班的2倍,两个班各捐书多少本?画图:同步演练1五、六年级的同学们共植树180棵,已知六年级植树的棵数是五年级2倍。
每个年级各植树多少棵?例2、王老师和李老师共有100元钱,如果再给王老师20元钱,那么李老师的钱数就正好是王老师的2倍。
王老师原来有多少元钱?同步演练2 两个仓库共存粮83吨,第二个仓库如果再存入7吨,就正好是第一个仓库的2倍。
两个仓库原来各存粮多少吨?例3 有两堆棋子,每一堆有67个,第二堆有53个。
从第二堆拿出多少个给第一堆,就能使第一堆的棋子是第二堆的5倍?同步演练3甲、乙两仓库原来各存粮40吨、50吨。
要使乙仓库的粮食是甲仓库的2倍,必须从甲仓库运出多少吨给乙仓库?例4、将被除数个位的0去掉后,被除数与除数相等。
已知被除数与除数的和是66,被除数和除数各是多少?同步演练4被除数除以除数等于9,且被除数和除数的和是90.被除数和除数各是多少?形成平台:1、光明小学买来足球和篮球共30个,已知买来的足球的个数比篮球的2倍还多3个,学校买来足球和篮球各多少个?2、甲、乙、丙三个数的和是270,甲数是乙数的2倍,乙数是丙数的3倍。
甲、乙、丙三个数各是多少?家庭作业:1、王明和张华共有42本练习本,王明比张华的3倍少2本。
两人各有练习本多少本?哈佛思维训练:哈林捡球哈林是一名乒乓球爱好者。
一天,她在打乒乓球的时候,不小心把球掉进球场的一个小洞里。
这是一个老鼠洞,这个洞太深了,她够不到,而且由于洞到了中间就拐弯了,所以即便用木棍也无法把球拿出来。
二年级上册奥数(课件)第7讲:乘法应用题

20+36=56(元) 答:买门来自一共要56元钱。例题四
同学们看演出。一排座位坐4人还多2个座位,如果把6排 座位全坐满,可以坐多少人?
一排可以坐:4+2=6(人)
6×6=36(人)
答:可以坐36人。
一排可以坐多 少人?
练习四
找一找!
乘法应用题
例题一
操场上有5组小朋友在做游戏,每组8个小朋友,一共 有多少个小朋友?
8×5=40(个)
答:一共有40个小朋友。
练习一
为庆祝“国庆”,同学们做纸花。9位同学每人做4朵花, 他们一共做了多少朵花?
9×4=36(朵)
答:他们一共做了36朵花。
例题二
15名游客去参观“世界之窗”,每辆车限乘4人, 4辆这样的小车能一次把他们送去吗?
答:这三个班一共有21人参加了舞蹈表演。
总结
解应用题,要从已知条件入手,分析时, 要注意题中的问题是什么。遇到这类应用题 时,已知份数和每份的个数,求总数就用乘 法计算。
例题三
一家饭店荤菜9元一份,素菜4元一份,博士点了 3份荤菜,5份素菜,一共要付多少钱?
3份荤菜的价钱: 9×3=27(元)
5份素菜的价钱: 4×5=20(元)
27+20=47(元)
份数×每份的钱数=总数
答:一共要付47元。
练习三
2位老师带6个小朋友去公园玩,公园门票成人10元, 儿童6元。买门票一共要多少元钱?
一共:8+20=28(架)
答:他们一共折了28架纸飞机。
练习五(选做)
学校的晚会,二(1)班有9个人参加了舞蹈表演, 二(2)班和二(3)班参加舞蹈表演的都比二(1)班少 3人,这三个班一共有多少人参加了舞蹈表演?
二年级奥数第七讲:重叠问题

第七讲 重叠问题
哪吒智闯水晶宫 --- 哪吒被骗了 哪吒继续往前去寻宝,只见一位白胡
人? 分析:队伍还剩的人就是报单数的人。这 10名队员报数结果是: 1、 2、3、1、2、3、1、2、3、1,这里面双数只有 2,出现了 3次,其他 都是单数,所以报单数的人有 7人。即10-3=7(人)。 例5 洗好的8块手帕夹在绳子上晾干,同一个夹子夹住相邻的两块手帕 的两边,这样一共要多少个夹子?
子老爷爷拿着哪吒地乾坤圈站在大厅中间。“那是我的乾坤圈!”哪吒激动的叫起来。哪吒赶 紧跑过去一看,“怎么有两个乾坤圈?”
白胡子老爷爷微笑的说:“哪吒不认识我了?”哪吒仔细打量了这位老爷爷后说:“我 记起来了,你是太白金星。”太白金星:“哪吒,我听说了你的事后,特意来帮助你的,你 看,我帮你把乾坤圈要回来了。”哪吒:“那怎么有两个乾坤圈?”太白金星:“这其中一个 是我的金钢圈,另一个是你的乾坤圈,刚才我拿一个圈称连我共重 67千克,拿另一个圈称连我
共重68千克,我的金刚圈比你的乾坤圈重,你猜得出来你的乾坤圈和我的金刚圈多重,我就把 你的宝贝还给你”哪吒:“太白金星,你说话可得算数!”太白金星:“那当然了,我胡子都 白了,还会骗你?你就在这里想吧,我有事先走,一会儿就回来”哪吒在原地想了一天一夜, 也没有想出答案,他明白了,他并不知道太白金星的体重是不可能算出乾坤圈和金刚圈的重量 的,他被骗了,那个老人根本不是太白金星!他不过是中了龙王的圈套而已,哪吒气冲冲的继 续前进,心想,要再被我碰到这假冒的太白金星,我一定把他的胡子拔了!
二年级奥数第七讲方阵问题

• 3、一个三层的中空方阵,最内层共有 80 人,这个方阵共有多 少人?
• 例 4:某班抽出一些学生参加节日活动表演,如果排成一个正 方形实心方阵多 7
• 人,如果每行每列增加 1 人,就少 4 人,共抽出学生多少人?
• 18、某班同学在军训队列表演中恰站成一个双层空心方阵,外层每边站了 9 个 • 同学。若让这个班同学在一条 250 米长的笔直马路上站岗,从一端开始每隔 5 • 米站一人,则站满之后还剩下几人? • 19、正方形广场的边界上共插有 48 面黄旗和红旗。每条边上的棋子数目相同, • 且每两面红旗间的黄旗数目也相同。如果四个角上都插有红旗,每条边上的 • 红旗比黄旗少 5 面,那么每 2 面红旗间有多少面黄旗? • 20ቤተ መጻሕፍቲ ባይዱ一个六边形广场的边界上插有 336 面红旗和黄旗。六边形的每个顶点处都 • 插有红旗,每条边上的红旗数目一样多,并且每两面红旗间插有相同数目的 • 黄旗。已知每条边上黄旗的数目比红旗的 2 倍还多 12 面,那么每两面红旗 • 间插有几面黄旗?
21、一个方阵花坛,共 5 层,最内层有 20 株花草,这个花坛共有多少株 花草?
• 14、一队战士排成三层空心方阵多出 16 人,如果在空心部分再增加一层又差 28 • 人。这队战士共有多少人? • 15、某小学四年级的同学排成一个四层空心方阵还多 15 人,如果在方阵的空心 • 部分再增加一层又少 21 人。这个小学四年级的学生一共有多少人? • 16、一个方阵花坛,共 20 层,最内层有 20 株花草,这个方阵花坛一共有多少 • 株花草? • 17、红红用棋子摆空心方阵,最外层每边摆 20 颗棋子,一共摆了 5 层,一共用 • 了多少颗棋子?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7×8= 4×6= 2×8= 6×3= 5×9= 6×9= 3×7= 9×4= 6×7= 3×5= 2×4= 4×9= 8×8= 9×9= 3×1=
① 如果想把一个正方形分成大小相等,形状相同的4个小正方形,都能怎样分呢?
②丽丽家有三块连在一起的地板砖,如右图所示,她想把它分成大小、形状
都相同的四块来垫桌腿,你有没有好办法?
③请把下面图形,分成形状、大小完全相同的两部分,不能破坏图形中方格。
(数学花园探秘)
第六讲
图形的剪拼
答案及详解------------------------------------------------------------ ①常规分割方法共6种,更多方式可以鼓励孩子自己尝试。
②题中没给我们小格子,那么我们可以自己先把小格子画上。
画完发现一共有12个小
格,平分成四块,12÷4=3(个),每个形状里应该有3个格。
确定大小后用尝试法确
定形状。
③通过计算可知,每个部分应该有40÷2=20(个)小方格,可包含一个4×4
正方形和一个2×2的正方形。
所以具体分法如右图。
核心思想——数格子:先定大小、再定形状
复习:图形的剪拼
等分的概念:正方形二等分——对折;正方形四等分——对折再对折
图形的割补:先画大框再尝试
1、图形的剪拼
①找图形特点:正方形:直角;等腰三角形:“腰”相等……
②画大框到数格子:
⑴定大小:没格画框,有格数格
⑵确定最长边
③认识常见图形的变换(三角←→正方)2、不规则图形的等分
①定大小:数格子——做除法找每份数
②定形状:尝试画小图形 第六讲 图形的剪拼和等分。
