广义表c语言实现
广义表的链式存储结构

广义表是一种扩展了线性表的数据结构,它可以包含其他广义表作为其元素,形成树状结构。
广义表的链式存储结构通常采用链表来表示,这样便于处理不同长度的子表。
下面是关于广义表链式存储结构的详细介绍:**广义表的定义:**广义表是线性表的推广,可以包含元素和子表。
一个广义表可以为空表,也可以是一个单一元素或由若干元素和子表组成的序列。
**链式存储结构:**在链式存储结构中,广义表的每个元素都由一个节点表示,节点中包含两个域:数据域和指针域。
数据域用来存储元素的值,而指针域则指向下一个节点,形成链表。
对于广义表的节点,数据域可以是一个基本元素,也可以是另一个广义表。
**节点定义示例:**```pythonclass Node:def __init__(self, data):self.data = dataself.next = None```**广义表链式存储的构建:**广义表的链式存储结构可以通过递归方式进行构建。
每个节点的数据域可以是基本元素,也可以是一个新的广义表。
```python# 示例:构建广义表(a, b, (c, d), e)a_node = Node('a')b_node = Node('b')c_node = Node('c')d_node = Node('d')e_node = Node('e')# 构建子表(c, d)sublist_node = Node(c_node)c_node.next = Node(d_node)# 构建主表(a, b, (c, d), e)a_node.next = Node(b_node)b_node.next = Node(sublist_node)sublist_node.next = Node(e_node)```**广义表链式存储的优点:**1. **灵活性:** 链式存储结构允许广义表的元素包含不同长度的子表,使得数据结构更加灵活。
数据结构-c语言描述(第二版)答案耿国华编著

第1章绪论2.(1)×(2)×(3)√3.(1)A(2)C(3)C5.计算下列程序中x=x+1的语句频度for(i=1;i<=n;i++)for(j=1;j<=i;j++)for(k=1;k<=j;k++)x=x+1;【解答】x=x+1的语句频度为:T(n)=1+(1+2)+(1+2+3)+……+(1+2+……+n)=n(n+1)(n+2)/66.编写算法,求一元多项式p n(x)=a0+a1x+a2x2+…….+a n x n的值p n(x0),并确定算法中每一语句的执行次数和整个算法的时间复杂度,要求时间复杂度尽可能小,规定算法中不能使用求幂函数。
注意:本题中的输入为a i(i=0,1,…n)、x和n,输出为P n(x0)。
算法的输入和输出采用下列方法(1)通过参数表中的参数显式传递(2)通过全局变量隐式传递。
讨论两种方法的优缺点,并在算法中以你认为较好的一种实现输入输出。
【解答】(1)通过参数表中的参数显式传递优点:当没有调用函数时,不占用内存,调用结束后形参被释放,实参维持,函数通用性强,移置性强。
缺点:形参须与实参对应,且返回值数量有限。
(2)通过全局变量隐式传递优点:减少实参与形参的个数,从而减少内存空间以及传递数据时的时间消耗缺点:函数通用性降低,移植性差算法如下:通过全局变量隐式传递参数PolyValue(){int i,n;float x,a[],p;printf(“\nn=”);scanf(“%f”,&n);printf(“\nx=”);scanf(“%f”,&x);for(i=0;i<n;i++)scanf(“%f”,&a[i]);/*执行次数:n次*/p=a[0];for(i=1;i<=n;i++){p=p+a[i]*x;/*执行次数:n次*/x=x*x;}printf(“%f”,p);}算法的时间复杂度:T(n)=O(n)通过参数表中的参数显式传递float PolyValue(float a[],float x,int n){float p,s;int i;p=x;s=a[0];for(i=1;i<=n;i++){s=s+a[i]*p;/*执行次数:n次*/p=p*x;}return(p);}算法的时间复杂度:T(n)=O(n)第2章线性表习题1.填空:(1)在顺序表中插入或删除一个元素,需要平均移动一半元素,具体移动的元素个数与插入或删除的位置有关。
数据结构(C语言版)_第3章 串与数组

char data; struct lnode *next;
}lstring;
3.3.3 串的存储结构——链式存储结构
当结点大小>1时,可以采用块链结构。
#define CHUNKSIZE 100
/*可由用户定义块的大小*/
typedef struct Chunk
第三章 串与数组
本章要点
➢字符串的基本概念与基本运算 ➢字符串的存储和基本运算的实现 ➢数组的概念和基本运算 ➢数组的存储结构 ➢特殊矩阵的压缩存储及运算 ➢广义表的概念及相关术语 ➢广义表的存储形式
3.1 “文学研究助手”案例导入
“文学研究助手”引例:请从下面的英文文章里,统计其中 good出现的次数和位置,并查找单词the所在的行号,该行中出 现的次数以及在该行中的相应位置。
3.4.1 数组的定义
数组是n个具有相同类型的数据元素构成的有限序列,数组 中的数据是按顺序存储在一块地址连续的存储单元中。
数组中的每一个数据通常称为数组元素,数组元素用下标 区分,其中下标的个数由数组的维数决定。
若线性表中的数据元素为非结构的简单元素,则称为一维 数组,又称为向量;若一维数组中的数据元素又是一维数组结 构,则称为二维数组;依次类推,若二维数组中的元素又是一 个一维数组结构,则称作三维数组。
3.3.4 串的基本操作的实现算法
第二种顺序存储方式下几种基本操作的算法
算法1:串连接操作 算法2:串比较操作 算法3:取子串操作 算法4:串插入操作 算法5:串删除操作 算法6:串置换函数 算法7:子串定位操作
3.3.5 串的应用
【例3-1】设计一个算法求串s中出现的第1个最长重复子串 及其位置。
数据结构C语言版第2版课后习题答案

数据结构(C语言版)(第2版)课后习题答案李冬梅目录第1章绪论............................................. 错误!未定义书签。
第2章线性表........................................... 错误!未定义书签。
第3章栈和队列......................................... 错误!未定义书签。
第4章串、数组和广义表................................. 错误!未定义书签。
第5章树和二叉树....................................... 错误!未定义书签。
第6章图................................................ 错误!未定义书签。
第7章查找............................................. 错误!未定义书签。
第8章排序............................................. 错误!未定义书签。
第1章绪论1.简述下列概念:数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。
答案:数据:是客观事物的符号表示,指所有能输入到计算机中并被计算机程序处理的符号的总称。
如数学计算中用到的整数和实数,文本编辑所用到的字符串,多媒体程序处理的图形、图像、声音、动画等通过特殊编码定义后的数据。
数据元素:是数据的基本单位,在计算机中通常作为一个整体进行考虑和处理。
在有些情况下,数据元素也称为元素、结点、记录等。
数据元素用于完整地描述一个对象,如一个学生记录,树中棋盘的一个格局(状态)、图中的一个顶点等。
数据项:是组成数据元素的、有独立含义的、不可分割的最小单位。
例如,学生基本信息表中的学号、姓名、性别等都是数据项。
第5章 广义表
12
例:求下列广义表操作的结果(严题集5.10②) (k, p, h) ; 1. GetTail【(b, k, p, h)】=
2. GetHead【( (a,b), (c,d) )】= 3. GetTail【( (a,b), (c,d) )】=
(c,d)
((c,d)) ;
;
4. GetTail【 GetHead【((a,b),(c,d))】】=(b) ; 5. GetTail【(e)】= 6. GetHead 【 ( ( ) )】= 7. GetTail【 ( ( ) ) 】= () ; . .
讨论:广义表与线性表的区别和联系? 广义表中元素既可以是原子类型,也可以是列表; 当每个元素都为原子且类型相同时,就是线性表。
3
广义表是递归定义的线性结构,
LS = ( 1, 2, , n ) 其中:i 或为原子 或为广义表
例如: A = ( ) F = (d, (e)) D = ((a,(b,c)), F) C = (A, D, F) B = (a, B) = (a, (a, (a, , ) ) )
13
(a,b)
()
()
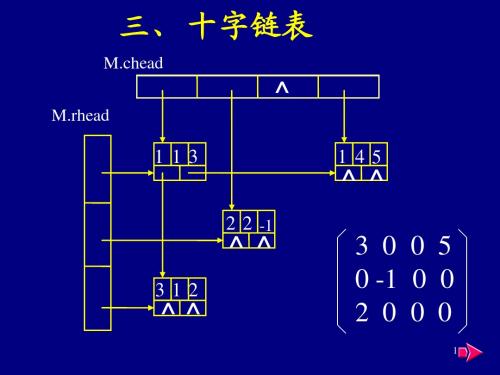
5.5 广义表的存储结构
由于广义表的元素可以是不同结构(原子或列表),难以用 顺序存储结构表示 ,通常用链式结构,每个元素用一个结 点表示。 注意:列表的“元素”还可以是列表,所以结点可能有两种形 式 1.原子结点:表示原子,可设2个域或3个域,依习惯而选。 法1:标志域,数值域 tag=0 标志域 value 数值域 法2:标志域、值域、表尾指针 tag=0 atom
} ADT Glist
10
基 结构的创建和销毁 InitGList(&L); DestroyGList(&L); 本 CreateGList(&L, S); CopyGList(&T, L); 操 作 状态函数
广义表存储结构与算法设计分析

第 2期
、
延安大学学报 ( 自然科学 版)
Ju l fYa a ies y( trlS in eE io o ma n nUnv ri Nau a ce c dt n o t i
Vol2 No 2 _9 .
21 0 0年 6月
Jn 2 l u .00
广 义 表 存 储 结 构 与 算 法 设计 分 析
1 广义表 的定 义
广 义表是 线性 表 的推 广 , 称列 表 , 泛应 用 于 也 广
为某个 数 据对象 } 和数 据 关 系 R(={ , ) <e e>I
e , ∈D, ≤i } ’ 同 时定 义 了若 干 广义 表 e 2 ≤凡 ) ,
人工智能等领域的表处理 LS 语言中 IP 引。广义表
层 次性是 广 义表 的主要 特 点之 一 。单 元 素结点
收 稿 日期 :0 0—0 1 21 3— 2 基 金 项 目 : 南 师 范 学 院 研 究 生 专 项 基 金 (0 K 0 7 渭 1Y Z 5 )
以是 单 个元 素 , 可 以是广 义表 。 也 卜
作者简介 : 王
敏 (9 2 ) 女 , 17 一 , 陕西临潼人 , 渭南师范学院讲师 。
构 , 出具体 的操 作 算 法 及 其 C语 言描 述 , 对 各 给 并
个算 法 进行 时 间复杂度 分 析 。
=
记 A T 描 述 中包括 广义 表 的数 据 对 象 D(={ i D) eI
12 … , ; , , n 凡≥0 e ∈ tm e 或 e ∈Gi ,tm e ; Ao St ltAo St s
的长 度 、 深度 、 头 及 表 尾 等 操 作 应 基 于 的 存 储 结 表
(完整word版)数据结构C语言版期末考试试题(有答案)

“数据结构”期末考试试题一、单选题(每小题2分,共12分)1.在一个单链表HL中,若要向表头插入一个由指针p指向的结点,则执行( )。
A. HL=ps p一>next=HLB. p一>next=HL;HL=p3C. p一>next=Hl;p=HL;D. p一>next=HL一>next;HL一>next=p;2.n个顶点的强连通图中至少含有( )。
A.n—l条有向边B.n条有向边C.n(n—1)/2条有向边D.n(n一1)条有向边3.从一棵二叉搜索树中查找一个元素时,其时间复杂度大致为( )。
A.O(1)B.O(n)C.O(1Ogzn)D.O(n2)4.由权值分别为3,8,6,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为( )。
A.24 B.48C. 72 D. 535.当一个作为实际传递的对象占用的存储空间较大并可能需要修改时,应最好把它说明为( )参数,以节省参数值的传输时间和存储参数的空间。
A.整形B.引用型C.指针型D.常值引用型·6.向一个长度为n的顺序表中插人一个新元素的平均时间复杂度为( )。
A.O(n) B.O(1)C.O(n2) D.O(10g2n)二、填空题(每空1分,共28分)1.数据的存储结构被分为——、——、——和——四种。
2.在广义表的存储结构中,单元素结点与表元素结点有一个域对应不同,各自分别为——域和——域。
3.——中缀表达式 3十x*(2.4/5—6)所对应的后缀表达式为————。
4.在一棵高度为h的3叉树中,最多含有——结点。
5.假定一棵二叉树的结点数为18,则它的最小深度为——,最大深度为——· 6.在一棵二叉搜索树中,每个分支结点的左子树上所有结点的值一定——该结点的值,右子树上所有结点的值一定——该结点的值。
7.当向一个小根堆插入一个具有最小值的元素时,该元素需要逐层——调整,直到被调整到——位置为止。
《数据结构与算法》第五章-数组和广义表学习指导材料

《数据结构与算法》第五章数组和广义表本章介绍的数组与广义表可视为线性表的推广,其特点是数据元素仍然是一个表。
本章讨论多维数组的逻辑结构和存储结构、特殊矩阵、矩阵的压缩存储、广义表的逻辑结构和存储结构等。
5.1 多维数组5.1.1 数组的逻辑结构数组是我们很熟悉的一种数据结构,它可以看作线性表的推广。
数组作为一种数据结构其特点是结构中的元素本身可以是具有某种结构的数据,但属于同一数据类型,比如:一维数组可以看作一个线性表,二维数组可以看作“数据元素是一维数组”的一维数组,三维数组可以看作“数据元素是二维数组”的一维数组,依此类推。
图5.1是一个m行n列的二维数组。
5.1.2 数组的内存映象现在来讨论数组在计算机中的存储表示。
通常,数组在内存被映象为向量,即用向量作为数组的一种存储结构,这是因为内存的地址空间是一维的,数组的行列固定后,通过一个映象函数,则可根据数组元素的下标得到它的存储地址。
对于一维数组按下标顺序分配即可。
对多维数组分配时,要把它的元素映象存储在一维存储器中,一般有两种存储方式:一是以行为主序(或先行后列)的顺序存放,如BASIC、PASCAL、COBOL、C等程序设计语言中用的是以行为主的顺序分配,即一行分配完了接着分配下一行。
另一种是以列为主序(先列后行)的顺序存放,如FORTRAN语言中,用的是以列为主序的分配顺序,即一列一列地分配。
以行为主序的分配规律是:最右边的下标先变化,即最右下标从小到大,循环一遍后,右边第二个下标再变,…,从右向左,最后是左下标。
以列为主序分配的规律恰好相反:最左边的下标先变化,即最左下标从小到大,循环一遍后,左边第二个下标再变,…,从左向右,最后是右下标。
例如一个2×3二维数组,逻辑结构可以用图5.2表示。
以行为主序的内存映象如图5.3(a)所示。
分配顺序为:a11 ,a12 ,a13 ,a21 ,a22,a23 ; 以列为主序的分配顺序为:a11 ,a21 ,a12 ,a22,a13 ,a23 ; 它的内存映象如图5.3(b)所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
int CmpC(char *str)
{
int i=0;
char k;
LLS *q;
LLS head1,head2,head3;
head1.next=head2.next=head3.next=NULL;
while((k=str[i]) !='\n')
{
if(k=='(')
{
q=(LLS *)malloc(sizeof(LLS));
Point_0-=1;
}
return 0;
}
int main(void)
{
int *tws;
int S=0;
int *data=(int *)malloc(sizeof(int));
inistak(tws);
while(1)
{
printf("Select:\n1.PUSH head\n2.POP head\n3.PUSH tail\n4.POP tail");
Ons=(int *)malloc((N+1)*sizeof(int));
for(i=0;i<=N;i++) *(Ons+i)=0;
for(i=0;i<N;i++)
{
push(train[i]);
printf("Train %d push\n",i+1);
if(Ons[Point]) {pop(temp+j);j++;printf("Train %d out\n",i+1);}
}
system("pause");
return 0;
}
#include<stdio.h>
typedef struct LLS{
int C;
struct LLS *next;
}LLS;
int Count(char *str)
{
int i=0;
LLS head;
LLS *q;
char k;
head.next=(LLS*)malloc(sizeof(LLS));
#include<stdio.h>
int Point_0=0;
int Point_1=11;
void inistak(int *tws)
{
int i=0;
while(!(tws=(int *)malloc((2*5+1)*sizeof(int))));
for(i=1;i<=10;i++) *(tws+i)=0;
printf("\n");
S=push(tws,1,data);
if(S) printf("Stack is full");
else printf("%d is Pushed",*data);
}
else if(S==4)
{
if(pop(tws,1,data)) printf("Stack is empty");
}
else if(S==2)
{
if(pop(tws,0,data)) printf("Stack is empty");
else printf("pop is %d",*data);
}
else if(S==3)
{
printf("Input data(int): ");
scanf("%d",data);
head.next=q;
}
while(1)
{
k=getchar();
if(k=='@' && !head.next) break;
else if(!head.next) return 0;
else if(k!=head.next->C) return 0;
head.next=head.next->next;
{
while(1)
{
if(CmpC()) printf("Not Matched!!\n");
else printf("Matched!!\n");
}
system("pause");
return 0;
}
#include<stdio.h>
typedef struct LLS{
char C;
struct LLS *next;
q->next=head2.next;
head2.next=q;
}
else if(k==']')
{
if(!head2.next) return 1;
else head2.next=head2.next->next;
}
else if(k=='{')
{
q=(LLS *)malloc(sizeof(LLS));
*(Ons+Point)=x;
return 0;
}
int pop(int *x)
{
if(Point)
{
*x=*(Ons+Point);
Point--;
return 0;
}
return 1;
}
void Arrange(int *ons,int *train,int *temp)
{
int i=0,j=0;
}
int push(int *tws,int i,int *x)/*i=0时正向,i=1时反向*/
{
int j;
if(i)
{
Point_1--;
j=Point_1;
if(j<=5) {++Point_1;return 1;}
}
else
{
Point_0++;
j=Point_0;
if(j>5) {--Point_0;return 1;}
printf("\n");
scanf("%d",&S);
if(S==1)
{
printf("Input data(int): ");
scanf("%d",data);
printf("\n");
S=push(tws,0,data);
if(S) printf("Stack is full");
else printf("%d is Pushed",*data);
q->next=head3.next;
head3.next=q;
}
else if(k=='}')
{
if(!head3.next) return 1;
else head3.next=head3.next->next;
}
i++;
}
if(head1.next || head2.next || head3.next) return 1;
case '/' : head.next->next->C=head.next->next->C /head.next->C;head.next->C=head.next->next->C;i++;break;
default : q=(LLS*)malloc(sizeof(LLS));
q->C=0;
while(k<'9' && k>'0')
{
q->C=q->C*10+(k-'0');
i++;
k=str[i];
}
i++;
q->next=head.next;
head.next=q;
}
k=str[i];
}
return head.next->C;
}
int main(void)
{
char str[100];
char C;
struct LLS *next;
}LLS;
int CmpS(void)
{
LLS head;
LLS *q;
char k;
head.next=NULL;
while((k=getchar())!= '&')
{
q=(LLS *)malloc(sizeof(LLS));
q->C=k;
q->next=head.next;
q->next=head1.next;
head1.next=q;
}
else if(k==')')
{
if(!head1.next) return 1;
else head1.next=head1.next->next;
}
else if(k=='[')
{
q=(LLS *)malloc(sizeof(LLS));
else if(m>0 && n>=0) return g(m-1,2*n)+n;
}
int main(void)
{
