圆周角定理及其推论随堂练习试卷
圆周角定理练习题

圆周角定理练习题在数学中,圆周角定理是一个非常重要的定理,它关于圆周角和圆心角的关系进行了阐述。
理解和掌握这个定理对于解决与圆相关的问题非常有帮助。
那么,现在我们来进行一些圆周角定理的练习题,以便加深对该定理的理解和运用能力。
练习题一:已知半径为r的圆上的弧AB所对的圆周角为θ,求弧AB的长度。
解答:根据圆周角定理可知,圆周角θ所对的弧的长度等于半径r乘以圆周角的弧度。
即弧AB的长度为rθ。
练习题二:已知弧CD的长度为s,求弧CD所对的圆周角。
解答:根据圆周角定理可知,弧CD所对的圆周角的弧度等于弧长s除以半径r。
即圆周角θ等于s/r。
练习题三:已知圆O的半径为r,圆弧AB所对的圆周角为θ,求圆O的周长。
解答:根据圆周角定理可知,圆周角θ所对的弧AB的长度为rθ。
因为圆O的周长等于圆周率π乘以直径d,而直径d等于半径r的两倍,所以圆O的周长为2πr。
练习题四:已知半径为r的圆上的弧AB的长度为s,求弧AB所对的圆周角。
解答:根据圆周角定理可知,弧AB所对的圆周角的弧度等于弧长s除以半径r。
即圆周角θ等于s/r。
练习题五:已知圆O的半径为r,圆上的弧AB所对的圆周角为θ,求弧AB所对的圆心角。
解答:根据圆周角定理可知,圆周角θ所对的圆心角的度数为360°乘以θ/2π。
通过以上练习题,我们可以更好地理解和应用圆周角定理。
掌握这个定理对于解决与圆有关的各种问题非常重要。
希望通过练习能够加深你对圆周角定理的理解,并培养你的数学思维和解题能力。
圆周角+同步练习++2024—2025学年人教版数学九年级上册

24.1.4 圆周角学习目标1. 理解圆周角的概念.2. 掌握圆周角定理及其推论.3. 理解圆内接四边形的性质,探究四点共圆时的性质.课堂学习检测一、填空题1. 在圆上,并且角的两边都的角叫做圆周角.2. 一条弧所对的圆周角等于圆心角的 .3. 所对的圆周角 .4. 所对的圆周角是直角;90°的圆周角所对的弦是 .5. 圆内接四边形的对角 .̂的中点,则图中与∠BAC相等的角有6. 如图, 在⊙O中, 若点 C 是BD.二、选择题7. 如图, OA是⊙O的半径, 弦BC⊥OA, D 是⊙O上一点, 且点 D 在优弧BC 上. 若∠ADB =28°, 则∠AOC的度数为 ( ).(A) 14° (B) 28° (C) 56° (D) 84°综合·运用·诊断一、填空题8. 如图, AB是⊙O的直径, CD是弦. 若∠ACD =65°, 则∠BAD的度数为9. 如图, 点 B, C, D 在⊙O 上. 若∠BCD =130°, 则∠BOD 的度数为 .10. 如图, A, B, C是⊙O上的三点, 且四边形OABC是菱形. 若点 D 是圆上异于A, B, C 的另一点, 则∠ADC的度数是 .二、选择题11. 如图, 点A, B, C, D, E均在⊙O上, 且AC为⊙O的直径, 则∠A+∠B+∠C的度数为( ).(A) 30° (B) 45° (C) 60° (D) 90°̂分成相等的三段弧,点P 在AĈ上. 若点Q在12. 如图, AB是⊙O的直径, 点C, D将ABAB̂上且∠APQ=115°,则点 Q所在的弧是 ( ).̂(B)PĈ(C)CD̂(D)DB̂(A)AP三、解答题.13. 如图, A, B, C, D四个点都在⊙O上, AD是⊙O的直径且AD=6cm,∠ABC=∠CAD.(1) 求弦AC的长;(2) 求∠CAD的度数.14. 如图, ⊙O为△ABC的外接圆,CE是⊙O的直径,CD⊥AB于点 D.求证:∠ACD=∠BCE.拓展·探究·思考15. 如图,四边形ABCD 是圆的内接四边形,∠A=60°,∠B=90°,AB=2,CD=1,求AD的长.16. 如图, AB是⊙O的直径, 弦(CD⊥AB,E是⌢AC上一点, AE, DC的延长线交于点 F.求证:∠AED=∠CEF.。
圆周角定理 专题练习

圆周角定理专题练习1.在圆周角定理中,已知∠CBO=45°,∠CAO=15°,求∠AOB的度数。
答案:B.60°。
2.在平面直角坐标系中,已知⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,),C(,6),求⊙A的半径。
答案:C.5.3.在圆周角定理中,已知点A,B,C在⊙O上,且∠A=50°,求∠BOC的度数。
答案:A.130°。
4.已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,求∠BCD的度数。
答案:A.116°。
5.已知圆心角∠BOC=78°,求圆周角∠BAC的度数。
答案:A.156°。
6.在圆周角定理中,已知OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,求∠XXX的度数。
答案:D.20°。
7.在圆周角定理中,已知AB是半圆的直径,点D是AC 的中点,∠ABC=50°,求∠DAB的度数。
答案:XXX°。
8.在圆周角定理中,已知A、B、C三点在⊙O上,且∠AOB=80°,求∠XXX的度数。
答案:D.40°。
9.已知AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=12∠BOD,求⊙O的半径。
答案:B.5.10.在圆周角定理中,已知DC是⊙O直径,XXX⊥CD于F,连接BC,DB,判断下列结论错误的是:答案:B.AF=XXX。
11.在圆周角定理中,已知点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,求AE的长。
答案:B.5.12.在圆周角定理中,已知点A、B、C在⊙O上,且∠C=30°,求∠AOB的度数。
答案:XXX°。
13.在圆周角定理中,已知⊙O中∠BAC=∠CDA=20°,求∠ABO的度数。
答案:B.70°。
人教版九年级上册数学圆周角定理及推论测试题

人教版九年级数学考试题测试题人教版初中数学24.1.4 圆周角第1课时圆周角定理及推论一、选择题1.如图1,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于().A.140° B.110° C.120° D.130°(1) (2) (3)2.如图2,∠1、∠2、∠3、∠4的大小关系是()A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠23.如图3,AD是⊙O的直径,AC是弦,OB⊥AD,若OB=5,且∠CAD=30°,则BC等于().A.3 B. C.5-12D.5二、填空题1.半径为2a的⊙O中,弦AB的长为,则弦AB所对的圆周角的度数是________.2.如图4,A、B是⊙O的直径,C、D、E都是圆上的点,则∠1+∠2=_______.•B(4) (5)3.如图5,已知△ABC为⊙O内接三角形,BC=•1,•∠A=•60•°,•则⊙O•半径为_______.三、综合提高题1.如图,弦AB 把圆周分成1:2的两部分,已知⊙O 半径为1,求弦长AB .2.如图,已知AB=AC ,∠APC=60° (1)求证:△ABC 是等边三角形.(2)若BC=4cm ,求⊙O 的面积.3.如图,⊙C 经过坐标原点,且与两坐标轴分别交于点A 与点B ,点A 的坐 标为(0,4),M 是圆上一点,∠BMO=120°. (1)求证:AB 为⊙C 直径. (2)求⊙C 的半径及圆心C 的坐标.A参考答案一、1.D 2.B 3.D二、1.120°或60° 2.90° 3.3三、1.(1)证明:∵∠ABC=∠APC=60°,又AB AC=,∴∠ACB=∠ABC=60°,∴△ABC为等边三角形.(2)解:连结OC,过点O作OD⊥BC,垂足为D,在Rt△ODC中,DC=2,∠OCD=30°,设OD=x,则OC=2x,∴4x2-x2=4,∴OC=433.(1)略(2)4,(,2)初三第一学期期末学业水平调研数学本试卷共8页,共三道大题,28道小题,满分100分。
圆周角定理经典训练卷(含答案)

圆周角定理经典训练卷一.选择题1.如图,AB、CD都是⊙O的弦,且AB⊥CD.若∠CDB=62°,则∠ACD的大小为()(1)(2)(3)A.28°B.31°C.38°D.62°2.如图,⊙O是△ABC的外接圆,已知∠ABO=40°,则∠ACB的大小为()A.40°B.30°C.45°D.50°3.如图,AB是⊙O的弦,点C在圆上,已知∠OBA=40°,则∠C=()A.40°B.50°C.60°D.80°4.如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是()(4)(5)(6)(7)A.30°B.40°C.50°D.60°5.如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是()A.50°B.55°C.60°D.65°6.如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为()A.2B.4C.D.27.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为()A.80°B.75°C.70°D.65°8.如图,在⊙O中,AB平分∠CAO,∠BAO=25°,则∠BOC的大小为()A.25°B.50°C.65°D.80°(8)(9)(10)9.如图,⊙O中,劣弧AB所对的圆心角∠AOB=120°,点C在劣弧AB上,则圆周角∠ACB=()A.60°B.120°C.135°D.150°10.如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是()A.60°B.120°C.60°或120°D.30°或150°11.如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知和所对的圆心角分别为90°和50°,则∠P=()A.45°B.40°C.25°D.20°12.已知△ABC中,AB=AC,∠A=50°,⊙O是△ABC的外接圆,D是优弧BC上任一点(不与A、B、C重合),则∠ADB的度数是()A.50°B.65°C.65°或50°D.115°或65°13.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是()(13)(14)(15)A.75°B.60°C.45°D.30°14.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为()A.30°B.45°C.60°D.75°15.如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是()A.25°B.30°C.40°D.50°16.如图,AB是⊙O的直径,CD是⊙O的弦.若∠BAC=23°,则∠ADC的大小为()A.23°B.57°C.67°D.77°17.如图,AB为⊙O的直径,CD为⊙O的弦,∠ABD=53°,则∠BCD为()(16)A.37°B.47°C.45°D.53°(17)(18)(19)18.如图,若AB为⊙O的直径,CD是⊙O的弦,∠ABD=65°,则∠BCD的度数为()A.25°B.45°C.55°D.75°19.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=()A.20°B.30°C.40°D.70°20.在⊙O中,点A、B在⊙O上,且∠AOB=84°,则弦AB所对的圆周角是()A.42°B.84°C.42°或138°D.84°或96°二.填空题21.如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=.(21)(22)(23)22.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=.23.如图,⊙O的直径CD经过弦EF的中点G,∠DCF=20°,则∠EOD等于.24.如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是°.25.如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠B=20°,则∠ADC的度数为.26.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为.27.如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为.(25)(26)(27)28.如图,在⊙O中,AB为直径,C、D为⊙O上两点,若∠C=25°,则∠ABD=.29.如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC=.(28)(29)(30)30.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于D,若AC:BC=4:3,AB=10cm,则OD的长为cm.三.解答题31.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.32、如图,△ABC的高AD、BE相交于点H,延长AD交ABC的外接圆于点G,连接BG.求证:HD=GD.33.已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.∠BAC=40°(1)求∠EBC的度数;(2)求证:BD=CD.34.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.35.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;.36.如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC 于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.37.如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.8.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE的延长线与AB交于F.试分析AC、AF、AB的关系,并说明理由.39.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,(1)判断△DBC的形状,并说明理由.(2)若∠BAC=60°,判断AD、AB、AC有怎样的关系?并说明理由.40.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC 的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?一.选择题(共20小题)1.D;2.C;3.A;4.C;5.A;6.D;7.A;8.B;9.C;10.A;11.D;12.C;13.C;14.B;15.B;16.A;17.C;18.D;19.A;20.D;二.填空题(共10小题)21.;22.80°;23.70°;24.60°;25.5;26.40°;27.60;28.65°;29.;30.4;三解答题28.如图,AB是⊙O的直径,C是⊙O上的点,AC=6cm,BC=8cm,∠ACB的平分线交⊙O于点D,求AB和BD的长.【解答】解:如图,∵AB是⊙O的直径,∴∠ACB=90°,∠ADB=90°.∴AB===10(cm).∵AC=6cm,BC=8cm,∵CD是∠ACB的平分线,∴∠ACD=∠BCD,则=,∴AD=BD,∴BD=AB=5cm.综上所述,AB和BD的长分别是10cm,5cm.29.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=3cm.求⊙O的半径.【解答】解:作直径CD,连结BD,如图,∵CD为直径,∴∠CBD=90°,∵∠D=∠A=30°,∴CD=2BC=2×3=6,∴⊙O的半径为3cm.30.如图,AB是⊙O的直径,过圆上一点C作CD⊥AB于点D,点C是弧AF的中点,连接AF交CD于点E,连接BC交AF于点G.(1)求证:AE=CE;(2)已知AG=10,ED:AD=3:4,求AC的长.【解答】(1)证明:∵点C是弧AF的中点,∴∠B=∠CAE,∵AB是⊙O的直径,∴∠ACB=90°,即∠ACE+∠BCD=90°,∵CD⊥AB,∴∠B+∠BCD=90°,∴∠B=∠CAE=∠ACE,∴AE=CE …(6分)(2)解:∵∠ACB=90°,∴∠CAE+∠CGA=90°,又∵∠ACE+∠BCD=90°,∴∠CGA=∠BCD,∵AG=10,∴CE=EG=AE=5,∵ED:AD=3:4,∴AD=4,DE=3,∴AC=…(10分).31.(2015秋•扬中市期中)如图,△ABC中,AB>AC,∠BAC的平分线交外接圆于D,DE⊥AB于E,DM⊥AC于M.(1)求证:BE=CM.(2)求证:AB﹣AC=2BE.【解答】证明:(1)连接BD,DC,∵AD平分∠BAC,∴∠BAD=∠CAD,∴弧BD=弧CD,∴BD=CD,∵∠BAD=∠CAD,DE⊥AB,DM⊥AC,∵∠M=∠DEB=90°,DE=DM,在Rt△DEB和Rt△DMC中,,∴Rt△DEB≌Rt△DMC(HL),∴BE=CM.(2)∵DE⊥AB,DM⊥AC,∵∠M=∠DEA=90°,在Rt△DEA和Rt△DMA中∴Rt△DEA≌Rt△DMA(HL),∴AE=AM,∴AB﹣AC,=AE+BE﹣AC,=AM+BE﹣AC,=AC+CM+BE﹣AC,=BE+CM,=2BE.34.(2009秋•哈尔滨校级期中)如图,△ABC的三个顶点都在⊙O上,CD是高,D是垂足,CE是直径,求证:∠ACD=∠BCE.【解答】解:连接AE,∵CE为直径,∴∠EAC=90°,∴∠ACE=90°﹣∠AEC,∵CD是高,D是垂足,∴∠BCD=90°﹣∠B,∵∠B=∠AEC(同弧所对的圆周角相等),∴∠ACE=∠BCD,∴∠ACE+∠ECD=∠BCD+∠ECD,∴∠ACD=∠BCE.39.如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,作CE⊥AD,垂足为E,CE 的延长线与AB交于F.试分析∠ACF与∠ABC是否相等,并说明理由.【解答】解:延长CE交⊙O于M,∵AD是⊙O的直径,作CE⊥AD,∴弧AC=弧AM,∴∠ACF=∠ABC(在同圆中,等弧所对的圆周角相等).40.如图,△ABC内接于⊙O,AD为△ABC的外角平分线,交⊙O于点D,连接BD,CD,判断△DBC的形状,并说明理由.【解答】解:△DBC为等腰三角形.理由如下:∵AD为△ABC的外角平分线,∴∠EAD=∠DAC,∵∠EAD=∠DCB,∠DBC=∠DAC,∴∠DBC=∠DCB,∴△DBC为等腰三角形.1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是上的任意一点,AG、DC 的延长线相交于点F,∠FGC与∠AGD的大小有什么关系?为什么?【解答】解:∠FGC与∠AGD相等.理由如下:连接AD,如图,∵CD⊥AB,∴=,∴∠AGD=∠ADC,∵∠FGC=∠ADC,∴∠FGC=∠AGD11。
圆周角定理及推论知识点与练习

圆周角定理及推论知识点与练习(总3页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--圆周角定理及推论知识点与练习1、圆周角定理:在同圆或等圆中,一条弧所对的圆周角等于它所对的圆心角的一半。
特别提示:证明圆周角定理时,可以分以下三种情况进行分类讨论: ①圆心在圆周角外 ②圆心在圆周角上 ③圆心在圆周角内特别提示:圆周角定理的证明分三种情况,利用三角形外角和定理证明。
2、推论:①圆周角的度数等于它所对的弧度数的一半;②在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等。
③半圆(直径)所对的圆周角是直角。
90°的圆周角所对的弦是直径。
注意:在圆中,同一条弦所对的圆周角有无数个,同一条弦所对的圆周角的度数有两个,一个是所对的劣弧度数,另一个是所对的优弧度数。
3、应用(1)运用圆周角定理及推论时,注意在同圆或等圆中;(2)运用此定理要善于从弧到角或从角到弧的转化,常用弧相等来证角相等;(3)在圆中常添加直角所对的弦或构造直径所对的圆周角为直角有关的辅助线,利用直角三角形解决有关的计算问题。
例:⊙O 半径OA ⊥OB ,弦AC ⊥BD 于E 。
求证:AD ∥BC证明:∵OA ⊥OB ,∴∠AOB =90º∵AB ⋂=AB ⋂,∴∠C=∠D=21∠AOB=45º∵AC ⊥BD ,∴∠AED=90º, ∴∠EAD=∠AED -∠D=45º ∴∠C=∠EAD, ∴AD ∥BC练习一、选择题1、在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是( ) ° °或150° ° °或120°2、如图1,BD 是⊙C 的直径,弦AC 与BD 相交于点,则下列结论一定成立的是() A.ABD ACD ∠=∠ B.ABD AOD ∠=∠C.AOD AED ∠=∠ D.ABD BDC ∠=∠图5A P CB O 3. 如图2,四边形ABCD 内接于⊙O ,若它的一个外角70DCE ∠=,则BOD ∠=() A.35B.70C.110D.140 º4. 如图3,A C B 、、是⊙O 上三点,若40AOC ∠=,则ABC ∠的度数是 ( ) A.10B.20C.40D.805. 如图4,⊙O 中弧AB 的度数为60,AC 是O 圆的直径,那么BOC ∠等于( )A .150B .130C .120D .606. 如图5,圆心角∠AOB=120︒,P 是AB ⋂上任一点(不与A ,B 重合),点C 在AP 的延长线上,则∠BPC 等于( )A.45︒B.60︒C.75︒D.85︒1、如图1,AB 为⊙O 的直径,点C 、D 、E 均在⊙O 上,则∠1+∠2= 。
圆周角定理及其推论随堂练习试卷

圆周角定理及其推论随堂练习试卷一、选择题(共20小题;共100分)1. 如图,AB是⊙O的直径,∠AOC=130∘,则∠D等于 ( )A. 25∘B. 35∘C. 50∘D. 65∘2. 如图,四边形ABCD是⊙O的内接四边形,∠B=135∘,则∠AOC的度数为( )A. 45∘B. 90∘C. 100∘D. 135∘3. 如图,正三角形ABC内接于⊙O,动点P在圆周的劣弧上,且不与A,B重合,则∠BPC等于( )A. 30∘B. 60∘C. 90∘D. 45∘4. 如图,四边形ABCD内接于⊙O,∠BCD=120∘,则∠BAD的度数是( )A. 30∘B. 60∘C. 80∘D. 120∘5. 如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50º,则∠BCE的度数为( )A. 40ºB. 50ºC. 60ºD. 130º6. 小宏用直角三角板检查某些工件的弧形凹面是否是半圆,下列工件的弧形凹面一定是半圆的是( )A. B.C. D.7. 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,如果∠DAB=65∘,那么∠AOC等于( )A. 25∘B. 30∘C. 50∘D. 65∘8. 如图.四边形ABCD内接于⊙O,E为CD延长线上一点,如果∠ADE=120∘,那么∠B等于 ( )A. 130∘B. 120∘C. 80∘D. 60∘9. 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,cosD=23,则AB的长为( )A. 8√133B. 163C. 24√55D. 1210. 在数学实践活动课中,小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径.如图,直角角尺中,∠AOB=90∘,将点O放在圆周上,分别确定OA,OB与圆的交点C,D,读得数据OC=8,OD=9,则此圆的直径约为( )A. 17B. 14C. 12D. 1011. 如图,△ABC内接于⊙O,若∠AOB=100∘,则∠ACB的度数是( )A. 40∘B. 50∘C. 60∘D. 80∘12. 如图1,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图 2所示,那么点P的运动路线可能为( )A. O→B→A→OB. O→A→C→OC. O→C→D→OD. O→B→D→O13. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20∘,那么∠AOD等于( )A. 160∘B. 150∘C. 140∘D. 120∘14. 如图,A,B,C三点在已知的圆上,在△ABC中,∠ABC=70∘,∠ACB=30∘,D是BAC的中点,连接DB,DC,则∠DBC的度数为( )A. 30∘B. 45∘C. 50∘D. 70∘15. 如图,四边形ABCD内接于⊙O,∠A=110∘,则∠BOD的度数是( )A. 70∘B. 110∘C. 120∘D. 140∘16. 如图,△ABC为等边三角形,点O在过点A且平行于BC的直线上运动,以△ABC的高为半径的⊙O分别交线段AB,AC于点E,F,则EF所对的圆周角的度数( )A. 从0∘到30∘变化B. 从30∘到60∘变化C. 总等于30∘D. 总等于60∘17. 如图,四边形ABCD内接于⊙O,F是CD上一点,且DF=BC,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105∘,∠BAC=25∘,则∠E的度数为( )A. 45∘B. 50∘C. 55∘D. 60∘18. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58∘,则∠BCD的度数为( )A. 32∘B. 58∘C. 64∘D. 116∘19. 如图所示,△ABC为⊙O的内接三角形,AB=1,∠C=30∘,则⊙O的内接正方形的面积为( )A. 2B. 4C. 8D. 1620. 如图,AB是⊙O的直径,C,D两点在⊙O上,如果∠C=40∘,那么∠ABD的度数为( )A. 40∘B. 90∘C. 80∘D. 50∘二、填空题(共10小题;共50分)21. 已知⊙O,如图所示.(1)求作⊙O的内接正方形(要求尺规作图,保留作图痕迹,不写作法);(2)若⊙O的半径为4,则它的内接正方形的边长为.22. 如图,在⊙O中,∠BOC=100º,则∠A的度数是.23. 如右图,四边形ABCD内接于⊙O,E是BC延长线上一点,若BAD=105∘,则∠DCE的度数是.24. 阅读下面材料:在数学课上,老师提出如下问题:小芸的作法如下:①取AB=c,作AB的垂直平分线交AB于点O;②以点O为圆心,OB长为半径画圆;③以点B为圆心,a长为半径画弧,与⊙O交于点C;④连接BC,AC.则Rt△ABC即为所求.老师说:"小芸的作法正确."请回答:小芸的作法中判断∠ACB是直角的依据是.25. 数学课上,老师让学生用尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的做法如图所示,你认为小明这种做法中判断∠ACB是直角的依据是.26. 阅读下面材料:在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:小敏的作法如下:老师认为小敏的作法正确.请回答:连接OA,OB后,可证∠OAP=∠OBP=90∘,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是.27. 如图,⊙O是△ABC的外接圆,点A在优弧BC上,∠BOC=100∘,则∠A的度数为.28. 如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是.29. 如图,已知四边形ABCD内接于⊙O,点O在∠D的内部,∠OAD+∠OCD=50∘,则∠B=.30. 如图是由两个长方形组成的工件平面图(单位,mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是( )mm.三、解答题(共5小题;共65分)31. 如图,AB是直径,弦CD⊥AB,E是AC上一点,AE,DC的延长线交于点F.求证:∠AED=∠CEF.32. 已知:如图,A、B、C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45∘,求AB的长.33. 如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D.点E在BD上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.Ⅰ求证:CF⊥AB;Ⅱ若CD=4,CB=4√5,cos∠ACF=4,求EF的长.534. 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.Ⅰ求证:AB=AC;Ⅱ若AB=4,BC=2√3,求CD的长.35. 已知:⊙O是△ABC的外接圆,点M为⊙O上一点.Ⅰ如图,若△ABC为等边三角形,BM=1,CM=2,求AM的长;小明在解决这个问题时采用的方法是:延长MC到E,使ME=AM,从而可证△AME为等边三角形,并且△ABM≌△ACE,进而就可求出线段AM的长.请你借鉴小明的方法写出AM的长,并写出推理过程.Ⅱ若△ABC为等腰直角三角形,∠BAC=90∘,BM=a,CM=b(其中b>a),直接写出AM的长(用含有a,b的代数式表示).圆周角定理及其推论随堂练习试卷答案第一部分1. A2. B3. B4. B5. B6. A7. C8. B9. D 10. C11. B 12. C 13. C 14. C 15. D16. C 17. B 18. A 19. A 20. D第二部分21. (1)如图:(2)4√222. 50∘23. 105∘24. 直径所对的圆周角是直角.25. 直径所对的圆周角是直角26. 直径所对的圆周角是直角;经过半径外端并且垂直于这条半径的直线是圆的切线27. 50∘28. 30∘或150∘29. 130∘30. 50第三部分31. 连接AD.因为AD=AC,所以∠AED=∠ADC,因为∠CEF+∠AEC=∠ADC+∠AEC=180∘,所以∠ADC=∠CEF.所以∠AED=∠CEF.32. 连接OA、OB.∵∠ACB=45∘,∴∠AOB=2∠ACB=90∘ .又OA=OB .∴△AOB是等腰直角三角形.∴AB2=OA2+OB2=22+22=8 .∴AB=2√2 .答:AB的长为2√2cm.33. (1)连接BD,如图 1.∵AB是⊙O的直径,∴∠ADB=90∘.∴∠DAB+∠1=90∘.∵∠1=∠2,∠2=∠3,∴∠1=∠3.∴∠DAB+∠3=90∘.∴∠CFA=180∘−(∠DAB+∠3)=90∘.∴CF⊥AB.(2)连接OE,如图 2.∵∠ADB=90∘,∴∠CDB=180∘−∠ADB=90∘.∵在Rt△CDB中,CD=4,CB=4√5,∴DB=√CB2−CD2=8.∵∠1=∠3,∴cos∠1=cos∠3=45.∵在Rt△ABD中,cos∠1=DBAB =45,∴AB=10.∴OA=OE=5,AD=√AB2−DB2=6.∵CD=4,∴AC=AD+CD=10.∴在Rt△ACF中,CF=AC⋅cos∠3=8.∴AF=√AC2−CF2=6.∴OF=AF−OA=1.∴在Rt△OEF中,EF=√OE2−OF2=2√6.34. (1)因为ED=EC,所以∠EDC=∠C,因为∠EDC=∠B,所以∠B=∠C,所以AB=AC.(2)连接AE,因为AB为直径,所以AE⊥BC,由(1)知AB=AC,BC=√3,所以BE=CE=12因为CE⋅CB=CD⋅CA,AC=AB=4,所以√3⋅2√3=4CD,所以CD=3.235. (1)AM=3.延长MC到E,使ME=AM.∵△ABC为等边三角形,∴∠ABC=60∘.∴∠AME=60∘.∴△AME为等边三角形.∴AM=AE,∠BAM=∠CAE.又AB=AC,∴△ABM≌△ACE.∴AM=ME=3.(2)AM=√22(a+b)或√22(b−a).。
圆周角定理及其推论随堂练习考试卷
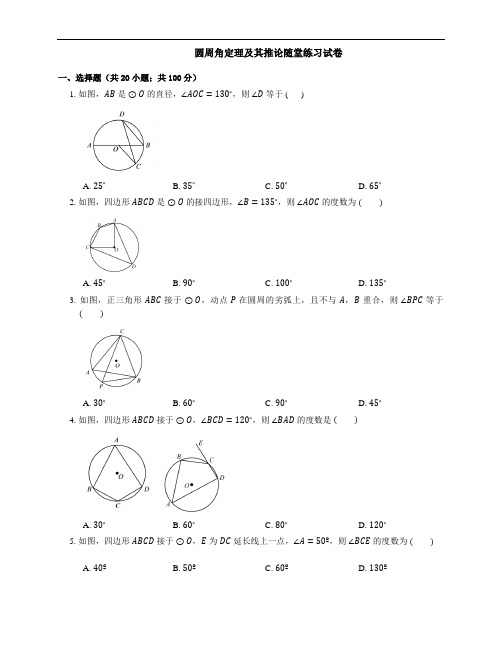
圆周角定理及其推论随堂练习试卷一、选择题(共20小题;共100分)1. 如图,AB是⊙O的直径,∠AOC=130∘,则∠D等于 ( )A. 25∘B. 35∘C. 50∘D. 65∘2. 如图,四边形ABCD是⊙O的接四边形,∠B=135∘,则∠AOC的度数为( )A. 45∘B. 90∘C. 100∘D. 135∘3. 如图,正三角形ABC接于⊙O,动点P在圆周的劣弧上,且不与A,B重合,则∠BPC等于( )A. 30∘B. 60∘C. 90∘D. 45∘4. 如图,四边形ABCD接于⊙O,∠BCD=120∘,则∠BAD的度数是( )A. 30∘B. 60∘C. 80∘D. 120∘5. 如图,四边形ABCD接于⊙O,E为DC延长线上一点,∠A=50º,则∠BCE的度数为( )A. 40ºB. 50ºC. 60ºD. 130º6. 小宏用直角三角板检查某些工件的弧形凹面是否是半圆,下列工件的弧形凹面一定是半圆的是( )A. B.C. D.7. 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,如果∠DAB=65∘,那么∠AOC等于( )A. 25∘B. 30∘C. 50∘D. 65∘8. 如图.四边形ABCD接于⊙O,E为CD延长线上一点,如果∠ADE=120∘,那么∠B等于 ( )A. 130∘B. 120∘C. 80∘D. 60∘9. 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,cosD=23,则AB的长为( )A. 8√133B. 163C. 24√55D. 1210. 在数学实践活动课中,小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径.如图,直角角尺中,∠AOB=90∘,将点O放在圆周上,分别确定OA,OB与圆的交点C,D,读得数据OC=8,OD=9,则此圆的直径约为( )A. 17B. 14C. 12D. 1011. 如图,△ABC接于⊙O,若∠AOB=100∘,则∠ACB的度数是( )A. 40∘B. 50∘C. 60∘D. 80∘12. 如图1,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图 2所示,那么点P的运动路线可能为( )A. O→B→A→OB. O→A→C→OC. O→C→D→OD. O→B→D→O13. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20∘,那么∠AOD等于( )A. 160∘B. 150∘C. 140∘D. 120∘14. 如图,A,B,C三点在已知的圆上,在△ABC中,∠ABC=70∘,∠ACB=30∘,D是BAC的中点,连接DB,DC,则∠DBC的度数为( )A. 30∘B. 45∘C. 50∘D. 70∘15. 如图,四边形ABCD接于⊙O,∠A=110∘,则∠BOD的度数是( )A. 70∘B. 110∘C. 120∘D. 140∘16. 如图,△ABC为等边三角形,点O在过点A且平行于BC的直线上运动,以△ABC的高为半径的⊙O分别交线段AB,AC于点E,F,则EF所对的圆周角的度数( )A. 从0∘到30∘变化B. 从30∘到60∘变化C. 总等于30∘D. 总等于60∘17. 如图,四边形ABCD接于⊙O,F是CD上一点,且DF=BC,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105∘,∠BAC=25∘,则∠E的度数为( )A. 45∘B. 50∘C. 55∘D. 60∘18. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58∘,则∠BCD的度数为( )A. 32∘B. 58∘C. 64∘D. 116∘19. 如图所示,△ABC为⊙O的接三角形,AB=1,∠C=30∘,则⊙O的接正方形的面积为( )A. 2B. 4C. 8D. 1620. 如图,AB是⊙O的直径,C,D两点在⊙O上,如果∠C=40∘,那么∠ABD的度数为( )A. 40∘B. 90∘C. 80∘D. 50∘二、填空题(共10小题;共50分)21. 已知⊙O,如图所示.(1)求作⊙O的接正方形(要求尺规作图,保留作图痕迹,不写作法);(2)若⊙O的半径为4,则它的接正方形的边长为.22. 如图,在⊙O中,∠BOC=100º,则∠A的度数是.23. 如右图,四边形ABCD接于⊙O,E是BC延长线上一点,若BAD=105∘,则∠DCE的度数是.24. 阅读下面材料:在数学课上,老师提出如下问题:小芸的作法如下:①取AB=c,作AB的垂直平分线交AB于点O;②以点O为圆心,OB长为半径画圆;③以点B为圆心,a长为半径画弧,与⊙O交于点C;④连接BC,AC.则Rt△ABC即为所求.老师说:"小芸的作确."请回答:小芸的作法中判断∠ACB是直角的依据是.25. 数学课上,老师让学生用尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的做法如图所示,你认为小明这种做法中判断∠ACB是直角的依据是.26. 阅读下面材料:在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:小敏的作法如下:老师认为小敏的作确.请回答:连接OA,OB后,可证∠OAP=∠OBP=90∘,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是.27. 如图,⊙O是△ABC的外接圆,点A在优弧BC上,∠BOC=100∘,则∠A的度数为.28. 如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是.29. 如图,已知四边形ABCD接于⊙O,点O在∠D的部,∠OAD+∠OCD=50∘,则∠B=.30. 如图是由两个长方形组成的工件平面图(单位,mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是( )mm.三、解答题(共5小题;共65分)31. 如图,AB是直径,弦CD⊥AB,E是AC上一点,AE,DC的延长线交于点F.求证:∠AED=∠CEF.32. 已知:如图,A、B、C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45∘,求AB的长.33. 如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D.点E在BD上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.Ⅰ求证:CF⊥AB;Ⅱ若CD=4,CB=4√5,cos∠ACF=4,求EF的长.534. 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.Ⅰ求证:AB=AC;Ⅱ若AB=4,BC=2√3,求CD的长.35. 已知:⊙O是△ABC的外接圆,点M为⊙O上一点.Ⅰ如图,若△ABC为等边三角形,BM=1,CM=2,求AM的长;小明在解决这个问题时采用的方法是:延长MC到E,使ME=AM,从而可证△AME为等边三角形,并且△ABM≌△ACE,进而就可求出线段AM的长.请你借鉴小明的方法写出AM的长,并写出推理过程.Ⅱ若△ABC为等腰直角三角形,∠BAC=90∘,BM=a,CM=b(其中b>a),直接写出AM的长(用含有a,b的代数式表示).圆周角定理及其推论随堂练习试卷答案第一部分1. A2. B3. B4. B5. B6. A7. C8. B9. D 10. C11. B 12. C 13. C 14. C 15. D16. C 17. B 18. A 19. A 20. D第二部分21. (1)如图:(2)4√223. 105∘24. 直径所对的圆周角是直角.25. 直径所对的圆周角是直角26. 直径所对的圆周角是直角;经过半径外端并且垂直于这条半径的直线是圆的切线27. 50∘28. 30∘或150∘29. 130∘30. 50第三部分31. 连接AD.因为AD=AC,所以∠AED=∠ADC,因为∠CEF+∠AEC=∠ADC+∠AEC=180∘,所以∠ADC=∠CEF.所以∠AED=∠CEF.32. 连接OA、OB.∵∠ACB=45∘,∴∠AOB=2∠ACB=90∘ .又OA=OB .∴△AOB是等腰直角三角形.∴AB2=OA2+OB2=22+22=8 .∴AB=2√2 .答:AB的长为2√2cm.33. (1)连接BD,如图 1.∵AB是⊙O的直径,∴∠ADB=90∘.∴∠DAB+∠1=90∘.∵∠1=∠2,∠2=∠3,∴∠1=∠3.∴∠DAB+∠3=90∘.∴∠CFA=180∘−(∠DAB+∠3)=90∘.∴CF⊥AB.(2)连接OE,如图 2.∵∠ADB=90∘,∴∠CDB=180∘−∠ADB=90∘.∵在Rt△CDB中,CD=4,CB=4√5,∴DB=√CB2−CD2=8.∵∠1=∠3,∴cos∠1=cos∠3=45.∵在Rt△ABD中,cos∠1=DBAB =45,∴AB=10.∴OA=OE=5,AD=√AB2−DB2=6.∵CD=4,∴AC=AD+CD=10.∴在Rt△ACF中,CF=AC⋅cos∠3=8.∴AF=√AC2−CF2=6.∴OF=AF−OA=1.∴在Rt△OEF中,EF=√OE2−OF2=2√6.34. (1)因为ED=EC,所以∠EDC=∠C,因为∠EDC=∠B,所以∠B=∠C,所以AB=AC.(2)连接AE,因为AB为直径,所以AE⊥BC,由(1)知AB=AC,BC=√3,所以BE=CE=12因为CE⋅CB=CD⋅CA,AC=AB=4,所以√3⋅2√3=4CD,所以CD=3.235. (1)AM=3.延长MC到E,使ME=AM.∵△ABC为等边三角形,∴∠ABC=60∘.∴∠AME=60∘.∴△AME为等边三角形.∴AM=AE,∠BAM=∠CAE.又AB=AC,∴△ABM≌△ACE.∴AM=ME=3.(2)AM=√22(a+b)或√22(b−a).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆周角定理及其推论随堂练习试卷、选择题(共20小题;共100 分)1. 如图,•是矗:讨的直径,只駅::二加「,贝y 等于()A. 2胪B.站”C. 50^D. 65^2. 如图,四边形風总罰是丨用璃的内接四边形,」:」,则出也谢的度数为A. 45 "B.勺C. 100D. 135°3. 如图,正三角形'内接于⑥巨,动点因在圆周的劣弧上,且不与', 重合,则I空決匸等于()A.30 B. 60°4.如图,四边形風沁岀内接于,C. 90,则■'''的度数是C.805.如图,四边形’内接于,•‘为.延长线上一点, ,则D.D.⑵■的度数为A. 'B. 1C.'6.小宏用直角三角板检查某些工件的弧形凹面是否是半圆,下列工件的弧形凹面7.如图,问I是⑧/的直径,、网是上两点,f^|,如果于8.如图•四边形’■内接于,•-为延长线上一点,如果于()A.130° B. 120 C. 80 D.BC = 85的长为9.如图,是 '的直径,、网是圆上的两点•若A. B. C. D.D.定是半圆的是B.—■,那么应罔等B. C. D.^1D£= 12O ,那么10.在数学实践活动课中,小辉利用自己制作的一把 直角角尺”测量、计算一些圆的直径•如图,直角角尺中,^\0B = 90',将点U 放在圆周上,分别确定 朗,OR 与圆的交点 G D ,读得数据 :儿二琴,: ,则此圆的直径约为A. B.网 C. D.'ii. 如图,△皿G 内接于oo ,若山。
* =丄00",则山聊的度数是(:)A. 40"B. 50 亠C. 60°D.曲12.如图1,、:是.的两条互相垂直的直径,点 岡从点口出发沿图中某一个扇形顺时针匀速运动,设 A/'-:-':'(单位:度),如果 与点同运动的时间•(单位:秒)的函数关系的图象大致如图2所示,那么点 忸的运动路线可能为A. 0-4心0B. O T UOC. SDfOD. O T E T D T O、13.如图,线段屹罰是;的直径,弦|二:一宀;|,"代-'二,那么|二煎纠等于,A.财B. I 亦C.丄D.曲14. 如图,儿也4三点在已知的圆上,在AMG 中,=,"CE = p 是励匚的中点,连接■,-,则|"0彳的度数为A.汨B.估亠C. 5创D .15. 如图,四边形川比"内接于©°,山=11° ,则皿>1)的度数是(>a--a o pA. 70B.订°C. 120D.丄4°16. 如图,色心汀为等边三角形,点■在过点制且平行于:的直线上运动,以I色描用的高为半径的分别交线段-注;L 于点,■‘,则| '所对的圆周角的度数C.总等于O CZJ ②17. 如图,四边形’ 内接于危:二,「是」上一点,且’,连接并延长交!的延长18.如图,若力B是© °的直径,3是◎ a的弦,= 则丄卩CD的度数为()D.总等于B.从石"I到A.从0 "到30变化变化45°线于点,连接;•若•U 耳的度数为119.如图所示,1为的内接三角形,D.,则的内接正方形的面积为20.如图,|总|是烽二|的直径,-, 两点在•上,如果am,那么卜总綁I的度数为A. 40"B. 9旷C. 00°D. 50、填空题(共10小题;共50分)21.已知,如图所示.(1)求作kml的内接正方形(要求尺规作图,保留作图痕迹,不写作法);23. 如右图,四边形磁°内接于© °,日是丿血延长线上一点,若= 105°,则ME的度数24. 阅读下面材料:在数学课上,老师提出如下问题:小芸的作法如下:k!;:取' =匚,作月甘的垂直平分线交AM于点。
;以点为圆心,■■-长为半径画圆;以点眉I为圆心,长为半径画弧,与交于点忖•连接I, ■.则匕厶门用即为所求.IXII老师说:”小芸的作法正确.”请回答:小芸的作法中判断■是直角的依据是 __________ .25. 数学课上,老师让学生用尺规作图画■';,使其斜边苗二呵,一条直角边护门剧•小明的做法如图所示,你认为小明这种做法中判断|才臥」|是直角的依据是__________ .26.阅读下面材料:如图,(1)连接。
乩作线段。
卩的乖氏平分线交(7尸于点C;⑵ 以点t?为闘也<70的长为半径作関, 交OO于/K忘两点:⑶作WKM, PB.所以力細M皿就是所求的切红.老师认为小敏的作法正确.切|L OAP=^OBP= 90请回答:连接“,■■后,可证,■'都是 -的切线,其依据是 ________________ .27•如图,是|匕如也的外接圆,点在优弧上,"J;- 心,贝y 的度数,其依据是;由此可证明直线loo 的半径,那么弦'所对的圆周角的度数是' 内接于,点■在以的内部,'■■-M30. 如图是由两个长方形组成的工件平面图(单位,加冏),直线平面图形的圆面的最小半径是65分)31.如图,卜疋I是直径,弦肚;丄肚;是」求证:上一点,匸咗I 的延长线交于点■-.L AED= MEF32.已知:如图, ;、;、为I -:5' ■■■■■ 上的三个点,心/的直径为嗣,:’,求’的'中,’是「的直径,与交于点•.点•在' '33.如图,在:,连接并延长交于点,;:.上,连接DE\5是它的对称轴,能完全覆盖这个34.已知「,以’为直径的•分别交’于•,于,连接,若.35.已知:「是•■'的外接圆,点罔为 '上一点.I如图,若—为等边三角形,工汴二〔,二二'■,求的长;小明在解决这个问题时采用的方法是:延长’ 到,使占忑三挥二.|,从而可证卜“也応为等边三角形,并且△心匸三乙严:二,进而就可求出线段'的长•请你借鉴小明的方法写出•的长,并写出推理过程.n 若CD = ^ C8二=4昉COSZ.ACF=号求,的长.n若八亦为等腰直角三角形,♦八 --11,吕駕二込•1(其中),直接写出艮刃的长(用含有,:的代数式表示)圆周角定理及其推论随堂练习试卷答案第一部分1.A2.B3.B4.B5.B6.A7.C8.B9.D10.C11 .B12.C13.C14.C15.D16 .C17.B18.A19.A20.D第二部分21. (1)如图:(2)22. 5023. 105°24. 直径所对的圆周角是直角.25. 直径所对的圆周角是直角26. 直径所对的圆周角是直角;经过半径外端并且垂直于这条半径的直线是圆的切线27. 5028. 或15°29. 130°30. ''第三部分31. 连接■'.IZ1 ②因为沖D = AC,所以一• - - :' ■'」';因为二L :「’. ;■I : 1所以辽疋三「汎炉所以•.32. 连接 . .JL AOB=2£ACB= 90 . 又干闕.—f 是等腰直角三角形•:.AB2= OA Z + 052= 23 + 22=8答:;.的长为■■':'■■33. (1) 连接卜二,如图1.1是’的直径,:、JL ADB = 90 .■■ JL DAB + ^1 = 90'\|v rl =疋2|,匕2 =山,-"=G:、JL DAB + ^.3 = 90^CFA = 180 ° - (^L DAB + 213) = 90 A CF L /ID.(2) 连接'",如图2.till■a a ■■ = 180 -rZDF = 90 . T 在 Rl A CDH 中,ED=4|,:* DB = ^CB 2 - CD 2 = 8';□二-■,4:' cusr I = cus^.3 =亍 _DS _4|T 在 RIA/IHD 中,二丽=丐,| A X/i = 1(1|.卜tM = OE = 5,加=加'-血 “v CD = 4-■■ AC -AD + CD = 10•••在 Rt A ACF\ 中,徉二 734 = 8 :* AF = jj?匸看=6■■■ 01' = AI- - OA = 1.•:在 Rt A OEF 中,EF = ^OE 2 - OF 2 = 2<6 34. (1)因为所以 i' "- - LC因为上誇匕二汐所以• ‘二-■'所以’出二八-(2)连接凹,因为CE*CR = CD ■ CA, 二川円二化所以旷.'',_3所以CD = 2.'化丄浜;为等边三角形,-JL ABC= 60 °:、AAME= 60°亠卅J为等边三角形.■■■ AM = AE, = 1.CAE又= . I、::沁AEMW ICE.-■AM = ME = 3^a E因为卜园为直径,所以L迪:,由(1)知’二<■■■所以35. (1)';= :延长•至U ,使卜丁呂二汽M(2)。
