【大学物理 东南大学】平面简谐波函数
大学物理平面简谐波的波函数

x
A cost
2πx
ห้องสมุดไป่ตู้
第十章 波动
4
物理学
第五版
6-2 平面简谐波的波函数
波函数 y Acos[(t x) ]
u
质点的振动速度,加速度
v y Asin[(t x) ]
t
u
a
2 y t 2
2
A cos[ (t
具有一般意义,即为沿 x 轴正方向传播的平
面简谐波的波函数,又称波动方程.
第十章 波动
3
物理学
第五版
6-2 平面简谐波的波函数
利用 2π 2πν 和 uT
T
可得波动方程的几种不同形式:
y
A cos t
x u
A
cos
2π
t T
物理学
第五版
6-2 平面简谐波的波函数
一 平面简谐波的波函数
设有一平面简谐波沿x 轴正方向传播,
波速为u,坐标原点 O处质点的振动方程为
yO Acost
y A
u
P
x
O
x
A
第十章 波动
1
物理学
第五版
6-2 平面简谐波的波函数
yO Acost
yO表示质点O 在 t 时刻离开平衡位置的距离. 振动落考后察波t线 上x ,PP点点(在坐标t 时x 刻),的P 点位比移O是点O的点
第十章 波动
13
物理学
第五版
大学物理10-2平面简谐波函数

解: ① 波源振动方程 y
y A cos(t ) 0.04 m
0.4m
o
T /u
0.2m
u P
2 / T 2u / 2 0.08 / 0.4 2 / 5
§2.平面简谐波的波函数 / 四.举例
t
t
=
0
时,o点处的
y 0.04 m
a
b
质点向 y 轴负向
o
运动
/2
y0.2m
u P
波源的振动方程为
y
0.04
cos
2
5
t
2
o
u =0.08 m/s
② 波函数
y
0.04
cos
2
5
t
x 0.08
2
§2.平面简谐波的波函数 / 四.举例
【例题3】如图所示,平面简谐波在 t =0时刻与 t =2s
时刻的波形曲线。求:
(1)坐标原点处介质质点的振动方程;
(2)该波的波动方程。 解:由图的已知量有
o
t
y
A
cos t
x u
y f (x,t)
波函数是波程 x 和时 y
间 t 的函数
o
x
§2.平面简谐波的波函数 / 三.波函数的物理意义
1. 当x一定时,y=y(t)
x=x0,
yxo
(t)
A c os t
x0 u
即 x=x0 处质点的振动方程。 2. 当t一定时,y=y(x)
t=t0
第二节
平面简谐波的 波函数
基本要求
1、掌握简谐波的波函数及其物理意义; 2、能熟练写出简谐波的波动方程; 3、能画波动曲线,并与振动图线相比较。
10-02 平面简谐波的波函数(26)
t x y = A cos[ 2π ( − ) + ϕ ] T λ
(1)
10 – 2 平面简谐波的波函数 确定初相角: 确定初相角:∵t
第十章 波动
=0 x=0
O
∂y y = 0, v = >0 ∂t
π ∴ϕ = − 2
A
(2)
y ω
于是有: 于是有: (3)
10 – 2 平面简谐波的波函数 2.求 t = 1 . 0 s 波形图; 求 波形图; 由(3)式令 t = 1 . 0 s 式令
x = 0 .5 m 处质点的振动规律并做图 ; t x π y = (1.0m)cos[2 π( − )− ] 2.0s 2.0m 2 x = 0 .5 m 处质点的振动方程: 处质点的振动方程:
于是有: 于是有:
3 4
O
y = (1.0m) cos[(π s )t − π ]
y
1.0 2 0 -1.0*1 2 *
x x ∆ ϕ = −ω = − 2 π u λ
10 – 2 平面简谐波的波函数
第十章 波动
波线上各点的简谐运动图
10 – 2 平面简谐波的波函数
第十章 波动
2.令 t 一定:波函数 令 一定:波函数y=y(x),描述 t 时刻距原点 , 不同处x 轴上所有质点谐振动的位移分布情况。 不同处 轴上所有质点谐振动的位移分布情况。 时刻波线上各质点相对其平衡位置的位移, 表示 t 时刻波线上各质点相对其平衡位置的位移, 即此刻的波形图: 即此刻的波形图:
10 – 2 平面简谐波的波函数
第十章 波动
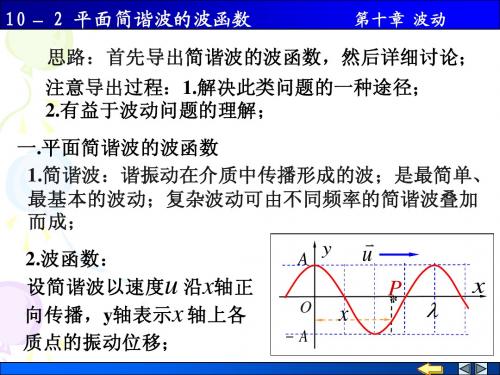
思路:首先导出简谐波的波函数,然后详细讨论; 思路:首先导出简谐波的波函数,然后详细讨论; 简谐波的波函数 注意导出过程: 解决此类问题的一种途径 解决此类问题的一种途径; 注意导出过程:1.解决此类问题的一种途径; 导出过程 2.有益于波动问题的理解; 有益于波动问题的理解; 有益于波动问题的理解 一.平面简谐波的波函数 平面简谐波的波函数 1.简谐波:谐振动在介质中传播形成的波;是最简单、 简谐波: 简谐波 谐振动在介质中传播形成的波;是最简单、 最基本的波动; 最基本的波动;复杂波动可由不同频率的简谐波叠加 而成; 而成; 2.波函数: 波函数: 波函数 设简谐波以速度u 沿x轴正 向传播, 轴表示 向传播,y轴表示x 轴上各 质点的振动位移; 质点的振动位移;
大学物理 东南大学3-1-1 谐波函数

(1)平面波
波线
波线
波面
波面
(2)球面波 波线 波 面 波面
波线
四、描述波动的三个物理量
振动状态(即位相)在单位时间内传播的距 1、波速 u 离称为波速 ,也称之相速 2、周期和频率 波的周期:一个完整波形通过介质中某固定点所需 的时间,用T 表示。 波的频率:单位时间内通过介质中某固定点完整波 的数目,用 表示。
机械振动在弹性介质中的传播称为机械波:声波、水波
波具有特殊性和共性 波动是一切微观粒子的本身属性,物质波(量子波)
§1 谐波函数
一、波动的概念
1 波动:振动的传播 2 机械波:机械振动的传播
3 简谐波:简谐振动的传播
二、机械波产生的条件
1 波源:初始机械振动的物体 2 波场:有连续的弹性介质
三、简谐波的分类
(3)波的本质是波源(及各质点)的状态或能量的传播
2、根据波面的形状
波线(波射线)--代表波的传播方向的射线。 波面--波场中同一时刻振动位相相同的点的轨迹。 波前(波阵面)--某时刻波源最初的振动状态 传到的波面。 结论 各向同性均匀介质中,波线恒与波面垂直 沿波线方向各质点的振动相位依次落后
T
2
1
T
3、波长
同一波线上相邻的位相差为2 的两质点的距离
T u
u
介质决定
波源决定
T
பைடு நூலகம்
1 根据振动方向与传播方向的关系 (1)横波——振动方向与传播方向垂直
t0
t T / 4
t T / 2
t 3T / 4
t T
t 5T / 4
平面简谐波的波函数标准形式

平面简谐波的波函数表达式
平面简谐波的波函数表达式是y=Asin(ωx+φ),其中A为振幅,2π/ω为周期,φ为初相
平面简谐波是最基本的波动形式。
平面传播时,若介质中体元均按余弦(或正弦)规律运动,就叫平面简谐波。
如果所传播的是谐振动,且波所到之处,媒质中各质点均做同频率、同振幅的谐振动,这样的波称为简谐波,也叫余弦波或正弦波。
如果简谐波的波面是平面,这样的简谐波称为平面简谐波。
平面简谐波传播时,介质中各质点都作同一频率的简谐振动,但在任一时刻,各点的振动相位一般不同,它们的位移也不相同,但根据波阵面的定义知道,
在任一时刻处在同一波阵面上的各点有相同的相位,它们离开各自的平衡位置有相同的位移。
简谐平面波都往往被简称为简谐波或者平面波,后者频繁在量子力学中使用。
本书的量子力学部分也会大量使用平面波这个简称,无论波动是几维的。
广义来说,平面波未必是简谐的,只需要等相位面都是平面即可:例如波长随空间变化,频率随时间变化也仍然是平面波。
而简谐波也未必是平面的,球面波也可以在径向也是简谐函数。
大学物理(下册) 10.3平面简谐波的波函数

例题 10.3.1
设平面简谐波的波函数为:
y 0.05cos(50 t 0.1x)
试求波的振幅、波长、周期及波速。
解:分析 将波函数写成标准形式对比可得结果:
t x y A cos[2 ( )] T
t x y 0.05 cos( 50t 0.1x) 0.05 cos[ 2 ( )] 0.04 20 A 0.05m; 20m; T 0.04s; u 500m s -1 T
x y A cos[(t ) ] u
2 u -1 A 4 m , 4 m , 2 200 s 由图示可得: T
坐标原点处置点振动的初相由旋转矢量法可求:
由 t 0 y 2 4cos ,即原点处质点的位移为2,代入 波函数得: 2 4 o 3 由旋转矢量法知,原点处质点沿轴 3 正向运动,故得到: A
y
故平面简谐波的波函数为:
3
y 4 cos[200 (t x ) ] 400 3
例题 10.3.4 设平面简谐波沿轴正方向传播,波 长 4m ,已知坐标原点处质点的振动曲线如图 10.7所示,试求: (1) 原点处质点的振动方程; (2) 波函数的表达式; (3) 画出t =1s时刻的波形曲线。 解: (1)设坐标原点处质点的振动方程为:
A y
O
u
x
P *
A
x
沿x轴正向传播简谐波的表达式可写为:
y y ( x, t )
各质点相对平衡 位置位移
(1)
波线上各质点 平衡位置
波函数:介质中坐标为 x 的质点相对其平衡位置的位 移 y 随 t 的变化关系 y ( x, t ) 称为波函数;
大学物理 平面简谐波的波函数
y Acos[2 π x (2π t )] T
y(x,t) y(x ,t)(波具有空间的周期性)
波程差
x21 x2 x1
12
1 2
2π
x2 x1
2π
x21
2π
x
回目录
3若
x, t 均变化,波函数表示波形沿传播方向的运动情况(行波).
yu
t 时刻
x
O
x
t t 时刻
xx
x 0.5处m质点的振动方程
y 1.0cos(π t π)m
y
y/m
3
1.0
3*
2
4
4O
2
0
* 1.0
* 2.0
*
t /s
1 -1.0* 1
*
x 0.5 m 处质点的振动曲线
回目录
例2 一平面简谐波以速度
沿u直线传20播m,波线/ s上点 A 的简谐运动方
程
. yA 310 2 cos(4 π t)m
y Acos式(中Bt Cx)
A, B, C 为正常数,求波长、波速、波传播方向上相距为 的两点间的相位差.
d
y Acos(Bt Cx)
y Acos2 π ( t x )
T
2π
C
T 2π B
u B
TC
2π d dC回目录
二 波函数的物理意义
y Acos[(t x) ] Acos[2 π( t x ) ]
u
8m 5m 9m
C
B oA
Dx
1)以 A 为坐标原点,写出波函数
两种方法:时间推迟法和相位落后法
y 3102 cos[4 π(t x )]m 20
大学物理 东南大学3-1-2 谐波函数
简谐波的波面是平面 波线
波面
y0 A cos( t 0 )
O
y
v
yP ?
x
P
六、平面简谐波的波动方程
1、右行波
x y A cos[ (t ) 0 ] v x t (O点状态传到P点的时间) v
y0 A cos( t 0 )
O
y
v
x
yP ?
x
P
2、左行波
x y A cos[ (t ) 0 ] v
y0 A cos( t 0 )
O
y
v
x
yP ?
x
P
结论:沿传播方向相位减小
3、行波
x y A cos[ (t ) 0 ] v
t x y A cos[ 2 ( ) 0 ] T y A cos[ 2ft kx 0 ]
y
v
t
t t
O
x x
x
O
2xP
y
v
0 )
yP ?
x
P
y P (t ) A cos(t
讨论 (1)xP处质点的振动初相为
2xP
2xP
2x P
0 )
0
(2)xP处质点落后原点的位相
(3)若xP=
则 xP处质点落后于原点的位相为2
结论:是波在空间上的周期性的标志
(4)同一波线上任意两点的振动位相差
x y A cos[ (t0 ) 0 ] v
Y
u
O
x1
x2
X
3.如x,t 均变化y=y(x,t)包含了不同时刻的波形
大学物理(II)下册教学课件:平面简谐波函数
A cos t
x u
沿 x 轴正方向传播的平面简谐波的波函数.
沿 x轴方向传播的波函数
y
u
A
P
x
O
x
A
P点振动比O点超前了 Δt x u
故P点的振动方程(波函数)为:
y
yo
t
t
Acos
t
x u
利用 2π 2πν
T
uT 和
k 2
可得波函数的几种不同形式:
y
A cos t
C
B oA
Dx
(4)分别求出 BC ,CD 两点间的相位差 yA (3102 m) cos(4 π s1)t
B C
2 π xB xC
2 π 8 10
1.6 π
C
D
2 π
xC
xD
2 π 22 10
4.4 π
u
10m 8m 5m 9m
C
B oA
10m
Dx
例3 、已知平面简谐波的某一图形,写出 波函数
2.0 2.0 2
y (1.0) cos[π π x]
2
t 1.0s
sin πx (m)
波形方程
y/m
1.0
O
-1.0
t 1.0 s
2.0
x/m
时刻波形图
(3) x 0.5m 处质点的振动规律并作图
y (1.0) cos[2 π( t x ) π] 2.0 2.0 2
x 0.5m 处质点的振动方程
设图示为平面简谐波在 波形图,求该波的波动方程。
播,且 u 4.0m s1
解:由图上直接读出
t 0
时刻的
已知波沿 ox 轴正方向传
大学物理平面简谐波波动方程
§4-2平面简谐波的波动方程振动与波动最简单而又最基本的波动是简谐波! 简谐波:波源以及介质中各质点的振动都是简谐振动。
任何复杂的波都可看成是若干个简谐波的叠加。
对平面简谐波,各质点都在各自的平衡位置附近作简谐振动,但同一时刻各质点的振动状态不同。
需要定量地描述出每个质点的振动状态。
波线是一组垂直于波面的平行射线,可选用其中一根波线为代表来研究平面简谐波的传播规律。
一、平面简谐波的波动方程设平面简谐波在介质中沿 x 轴正向传播,在此波线上任取一参考点为坐标原点参考点原点的振动方程为()00cos y A t ωϕ=+任取一点 P ,其坐标为 x ,P 点如何振动? A 和 ω 与原点的振动相同,相位呢?沿着波的传播方向,各质点的相位依次落后,波每向前传播 λ 的距离,相位落后 2π现在,O 点的振动要传到 P 点,需要向前传播的距离为 x ,因而 P 点的相位比 O 点落后 22x x ππλλ=P 点的振动方程为区别联系振动研究一个质点的运动。
波动研究大量有联系的质点振动的集体表现。
振动是波动的根源。
波动是振动的传播。
x02c o s P y A t x πωϕλ⎛⎫=+- ⎪⎝⎭ 由于 P 点的任意性,上式给出了任意时刻任意位置的质点的振动情况,将下标去掉02c o s y A t x πωϕλ⎛⎫=+- ⎪⎝⎭就是沿 x 轴正向传播的平面简谐波的波动方程。
如果波沿 x 轴的负向传播,P 点的相位将比 O 点的振动相位超前2x πλ沿 x 轴负向传播的波动方程为02c o s y A t x πωϕλ⎛⎫=++⎪⎝⎭利用 2ωπν=, u λν=沿 x 轴正向传播的平面简谐波的波动方程又可写为02c o s y A t x πωϕλ⎛⎫=-+⎪⎝⎭02c o s A t x u πνωϕ⎛⎫=-+⎪⎝⎭0c o s x A t u ωϕ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦即 0c o s x y A t u ωϕ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦原点的振动状态传到 P 点所需要的时间 xt u∆=P 点在 t 时刻重复原点在 x t u ⎛⎫- ⎪⎝⎭时刻的振动状态波动方程也常写为x02c o s y A t x πωϕλ⎛⎫=-+⎪⎝⎭()0c o s A t k x ωϕ=-+ 其中 2k πλ=波数,物理意义为 2π 长度内所具有完整波的数目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y Acos[2π ( t x ) ]
T
y (3102 m) cos2π (
t
x)
0.5s 10m
u
8m 5m
9m
C
B oA
Dx
(2) 以 B 为坐标原点,写出波动方程
yA (3102 m) cos(4 π s1)t
B A
B π
2π
xB xA
2π
5 10
π
yB (3102 m) cos[(4π s1)t π ]
2.0 2.0 2
y (1.0) cos[π π x]
2
t 1.0s
sin πx (m)
波形方程
y/m
1.0
O
-1.0
2.0
x/m
t 1.0 s 时刻波形图
(3) x 0.5m 处质点的振动规律并作图
y (1.0) cos[2 π( t x ) π] 2.0 2.0 2
x 0.5m处质点的振动方程
Dx
(4)分别求出 BC ,CD 两点间的相位差 yA (3102 m) cos(4 π s1)t
B C
2 π xB xC
2 π 8 10
1.6 π
C
D
2 π
xC
xD
2 π 22 10
4.4 π
u
10m
C
8m 5m
9m
B oA
10m
Dx
例3 、已知平面简谐波的某一图形,写出 波函数
y cos[(π s1)t π] (m)
y
y/m
3
3
1.0
*
4O
2
O 2* 1.0 *4 2.0 * t / s
1 -1.0 * 1
*
x 0.5 m 处质点的振动曲线
例2 一平面简谐波以速度 u 20m s沿-1
直线传播,波线上点 A 的简谐运动方 程
yA 3102 cos(4 π t) ; ( y, t单位分别为m,s).
x u
A
cos2π
t T
x
A cos(t kx )
从实质上看:波动是振动(相位)的传播.
(t, x) t kx (x) (0, x) kx (x 0) (t 0, x 0)
y Acos(t kx )
y A cos[(t t0 ) k (x x0 ) (t0 , x0 )]
问题:若已知 (1)任一时刻的波形图 (2)任一点振动图 (3)波形传播图
求波动方程(波函数)
例1 一平面简谐波沿 Ox轴正方向传播,
已知振幅A 1.0m,T 2.0,s 2.0.m在 t 0时
坐标原点处的质点在平衡位置沿 O轴y正向 运 动. 求: (1)波动方程;(2) t 1.0s波形图; (3) x 0.5m 处质点的振动规律并作图.
设图示为平面简谐波在 波形图,求该波的波动方程。
播,且 u 4.0m s1
解:由图上直接读出
t0
时刻的
已知波沿 ox 轴正方向传
y(102 m)
A 0.10m
10
0.04m 所以 T 0.01s
u
0.5 o 5
y
A
8m
(3102 m)
5m
9m
cos(41π0sm1
)t
C
B oA
Dx
点 D 的相位落后于点 A
yD
(3102 m) cos[(4 π s1)t
2π
AD ]
(3102 m) cos[(4 π s1)t 9 π]
5
u
y
A
8m
(3102 m)
5m
9m
cos(41π0sm1
)t
10m
C
B oA
2 t一定 x变化 y Acost kx
令 t C(定值)
则 y Acos kx
该方程表示 t时刻波传播方向上各质点 的位移, 即t时刻的波形(y x的关系)
y
o
x
3 x、 t都变
方程表示在不同时刻各质点的位移,即 不同时刻的波形,体现了波的传播.
yu
O
x
从形式上看:波动是波形的传播.
平面简谐波的波函数
设有一平面简谐波沿 x轴正方向传播,
波速为u,坐标原点 O处质点的振动方程为
yO Acost
yO表示质点O在 t时刻离开平衡位置的距离.
y A
u
P
x
O
x
A
位P点移比是OO点点的在振t 动t落时后刻t的 u位x ,移P,点由在此t 得时刻的
yP yO (t Δt) Acosωt Δt φ
若已知的振动点不位于坐标原点o,是距o为x0
的Q,且
y Acos[t ] 那么任一点p的振动
即
yp
A cos [(t
r) u
]
y Acos[(t x x0 ) ]
u
O
Q
P
x0 r x x0
x
波函数 y Acos[(t x) ]
u
质点的振动速度,加速度
v y Asin[(t x) ]
求:(1)以 A 为坐标原点,写出波动方程;
(2)以 B 为坐标原点,写出波动方程;
(3)求传播方向上点C、D 的简谐运动方程;
(4)分别求出 BC ,CD 两点间的相位差.
u
8m 5m
9m
C
B oA
Dx
(1) 以 A 为坐标原点,写出波动方程
A 3102 m T 0.5s 0
uT 10m
y (3102 m) cos[2π ( t x ) π ]
0.5s 10m
u
8m 5m
9m
C
oB A
Dx
(3) 写出传播方向上点C、D的运动方程
点102 m) cos[(4 π s1)t
2π
AC ]
(3102 m) cos[(4 π s1)t 13 π] 5
u
解 (1) 写出波动方程的标准式
y Acos[2π ( t x ) ] T
y Acos[2π ( t x ) ] T
t0 x0
y 0, v y 0 π
t
2
y cos[2π( t x ) π ] (m) 2.0 2.0 2
O
y
A
(2)求 t 1.0s波形图
y 1.0 cos[2π( t x ) π ]
t
u
a
2 t
y
2
2
A cos[ (t
x) u
]
四、 波函数的物理含义
1 x一定,t变化 y Acost kx
令 (x) kx
y
则 y Acost (x) O
t
表示x点处质点的振动方程( y t的关系)
y(x,t) y(x,t T ) (波具有时间的周期性)
波线上各点的简谐运动图
A cos t
x u
沿 x 轴正方向传播的平面简谐波的波函数.
沿 x轴方向传播的波函数
y
u
A
P
x
O
x
A
P点振动比O点超前了 Δt x u
故P点的振动方程(波函数)为:
y
yo
t
t
Acos
t
x u
利用 2π 2πν
T
uT 和
k 2
可得波函数的几种不同形式:
y
A cos t
