工程力学(静力学与材料力学)单辉祖工力-8轴向拉伸与要点
单辉祖工力-8.2轴向拉压变形详解

解:1. 计算 FN与 l
FN
2F1 F2 sin 30
6F
l
6F
l sin 60
4
3Fl
EA
EA
刚体 EA
2. 画变形图
3. 位移计算
Ay
AA' 2CC'
2l cos 60
16 3Fl EA
( )
单辉祖:材料力学Ⅰ
13
§9 简单拉压静不定问题
静不定问题与静不定度 静不定问题分析 例题
1. 轴力与变形分析
FN1 2F (拉伸) FN2 F (压缩)
l1
FN1l1 E1 A1
2F 2l 2Fl
EA
EA
( 伸长)
l2
FN2l2 E2 A2
Fl EA
(缩短)
单辉祖:材料力学Ⅰ
10
2. 作图法求节点位移 圆弧法 切线代圆弧法
用切线或垂 线代替圆弧
3. 节点位移计算
Ax AA2 Δl2 ()
(b) 螺栓的横向变形 d
单辉祖:材料力学Ⅰ
8
解:1. 横截面正应力 l 7.4110-4
l
E 148.2 MPa 2. 螺栓横向变形
' 2.22 104 d ' di 0.0034 mm 螺栓直径缩小 0.0034 mm
单辉祖:材料力学Ⅰ
9
节点位移分析
图示桁架,试求节点 A 的水平与铅 垂位移。已知 E1A1= E2A2=EA, l2=l
l1 l3cos 保证结构连续性所应
满足的变形几何关系
胡克定律
l1
FN1l1 E1 A1
补充方程
l3
FN3l1cos
E3 A3
工程力学课后习题答案单辉祖著

工程力学课后习题答案单辉祖著工程力学课后习题答案(单辉祖著)在学习工程力学这门课程时,课后习题的练习与答案的参考对于巩固知识、加深理解起着至关重要的作用。
单辉祖所著的《工程力学》一书,以其严谨的逻辑和丰富的内容,成为众多学子学习工程力学的重要教材。
下面,我们将为您详细呈现这本教材的课后习题答案。
首先,让我们来谈谈第一章的习题。
在这部分中,主要涉及到静力学的基本概念和受力分析。
例如,有一道题是关于一个简单的支架结构,要求画出其受力图。
对于这道题,我们需要明确各个构件之间的连接方式,判断是固定铰支座、活动铰支座还是其他约束类型,然后根据力的平衡条件,准确地画出每个构件所受到的力。
答案中,我们清晰地标注了各个力的大小、方向和作用点,并且通过合理的布局,使受力图易于理解。
第二章的习题重点围绕平面汇交力系和平面力偶系展开。
其中,有一道计算题要求计算多个力在某一点的合力。
在解答这道题时,我们首先将每个力分解为水平和垂直方向的分力,然后分别计算水平和垂直方向上的合力,最后通过勾股定理求出总的合力大小和方向。
答案的给出过程中,每一步的计算都有详细的说明,让学习者能够清晰地看到解题的思路和方法。
第三章的内容是平面任意力系。
这一章的习题难度有所增加,涉及到力系的简化、平衡方程的应用等。
比如,有一道题是求解一个复杂结构在给定载荷下的支座反力。
解题时,我们先对力系进行简化,找到主矢和主矩,然后根据平衡方程列出方程组,通过求解方程组得到支座反力的大小和方向。
答案中不仅给出了最终的结果,还展示了求解方程组的具体步骤和计算过程,方便学习者对照检查自己的解题过程。
第四章是空间力系。
这部分的习题对于空间想象力和数学运算能力有一定的要求。
例如,有一道题要求计算空间力在坐标轴上的投影以及对某点的矩。
在解答时,我们需要运用空间直角坐标系的知识,通过三角函数等方法求出投影的大小,再根据矩的定义计算出对某点的矩。
答案中会详细说明投影和矩的计算过程,并且配以适当的图示,帮助学习者更好地理解空间力系的概念。
工程力学静力学与材料力学课后习题答案单辉祖

1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
BAOW (a) B AO W F(b)OW (c)AAOW(d)BAOW (e)F BF ABO W(a) B AO W F(b) F AF B AO W(c)AF O A O W(d)F B F AAOW (e)F B F A AWC B(c)D (a)A WC E B(b)AW CD B解:1-3 试画出以下各题中AB 梁的受力图。
AB F(d) CABW(e)C ABW (e)CF B F AAB F(d)CBF A(a) F D BF ED A WCE (b)AWC D B F D F BF A(c)AWCBF BAAW C(a) ABC D(c)AF q D(b)CCA BF WD(d)ABF(e)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:A W C(a) F BF AAF qD(b)F CF DWBC (c)F CF BCA B F WD(d)F F AF DAB F(e)F BxF ByF AABF(a) DCWAF (b)DB(c) FABDD ’ABF(d)CDWA BD(e)WAC (f)ABF(a)DCWF AxF AyF DAF (b)BF BF A(c)FABDF BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
解:(a)AB F(d) CF B F CW AB (e)F BF AWB (f)F F BCA B W (c) B CW 1W 2 FA F D A BC E F (d)A F ABF AT F ABF BAF BTWAB P P (b) W AB C C ’ O G (e)(b)(c)(d)(e)F CAPCF BB PCF ’CF AAB PPF B F NBCW 1W 2 F AF CxF CyF AxF AyB W 1F A F Ax F AyF Bx F ByB C W 2 F Cx F CyF ’Bx F ’By FA BC F C F BDC E F F E F ’C F F FDAB C E F F EF FF BB C D G F B F C W ABCC ’ DO GF Oy F OxF A B O W F BF OyF Ox2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
工程力学第8章轴向拉伸与压缩
( FN A
)max
·截面设计
A
FN
·许用载荷确定 FN A
例:图示变截面由两种材料制成,AE 段为铜质,EC 段为钢质。 钢的许用应力[σ]1 = 160MPa,铜的许用应力[σ]2 = 120MPa , AB 段 横截面面积1000mm2,AB 段横截面面积是BC 段的两倍,。外力 F = 60kN ,作用线沿杆方向,试对此杆进行强度校核。
解:⑴ 求杆的轴力,作轴力图
AD 段:
Fx 0 :
解得:
FN1 2F 0
FN1 2F 120kN
DB段:
Fx 0 : FN2 2F F 0
解得:
FN2 F 60kN
BC 段:
Fx 0 : FN3 F 0
解得: FN3 F 60kN
解得: FN1 2F (拉)
FN2 F (压)
FN1 2F (拉) FN2 F (压)
确定载荷的最大许用值
1杆强度条件
FN1 2F At
F At 100106 200106 14.14kN
2
2
2杆强度条件
FN2 F Ac
一、材料的力学性能概述
1. 材料的力学性能
材料从受力开始到破坏过程中所表现出的在变形和 破坏等方面的特性。
2. 试验试件
拉伸试件 压缩试件
拉伸试件 压缩试件
圆形截面试件 l 10d l 5d 矩形截面试件 l 11.3 A l 5.65 A
圆形截面试件 h (1 3)d 方形截面试件
解得: FN2 50kN
CD 段:
《工程力学》课程教学大纲

《工程力学》课程教学大纲课程名称:工程力学课程类别:专业基础课教学学时: 72课程学分: 4学分开课专业: 工程管理开课学期: 第2学期参考教材:1. 《工程力学》,高等教育出版社,2004年1月(主编:单辉祖,谢传锋)2. 《工程力学》,黄河水利出版社,2009年7月(主编:孟凡深)一、课程性质《工程力学》课程是工程管理专业的一门专业基础必修课。
本课程是一门理论性、系统性较强的专业基础课必修课,是后续其它各门力学课程和相关专业课程的基础,同时在许多工程技术领域中有着广泛的直接应用。
二、课程目标(一)知识目标使学生具备工程力学的基础知识,掌握正确的受力分析和力系的破坏平衡条件。
对工程结构中杆件的强度问题具有明确的概念和一定的计算能力。
初步掌握杆件体系的分析方法,初步了解常用结构形式的受力性能。
掌握各种结构在荷载作用下维持平衡的条件以及承载能力的计算方法。
(二)职业技能目标掌握本专业必备的基础理论知识,具有本专业相关领域工作的岗位能力和专业技能,适应建筑工程生产一线的技术、管理等职业岗位群要求的技术及管理人才。
(三)素质养成目标培养适应社会主义现代化建设需要的德、智、体、美全面发展的高端应用型人才。
三、教学内容及学时分配四、教学内容要点第一章绪论教学学时数:1一、教学目的及要求通过本章的学习,要求学生了解工程力学的研究对象和任务,了解国内外力学发展史及概况,并对其发展与展望作简单介绍,激发学生学习兴趣。
二、教学重点与难点(一)教学重点:1、工程力学课程的性质、任务和要求。
2、力学在科技发展与工程应用中的作用与地位(二)教学难点:力学在科技发展与工程应用中的作用与地位三、主要教学内容1、工程力学课程的性质、任务和要求2、力学在科技发展与工程应用中的作用与地位3、国内外力学发展与展望简介四、考核点工程力学的研究对象和任务。
第二章静力学基本知识第一节基本概念和公理教学学时数:2一、教学目的及要求理解静力学的基本概念和基本公理。
工程力学(静力学与材料力学)课后习题答案(单辉祖) 2
D
D
2
A C F
F
A D
F
F B
B F ( d C ( e
W
B F F ( f
W
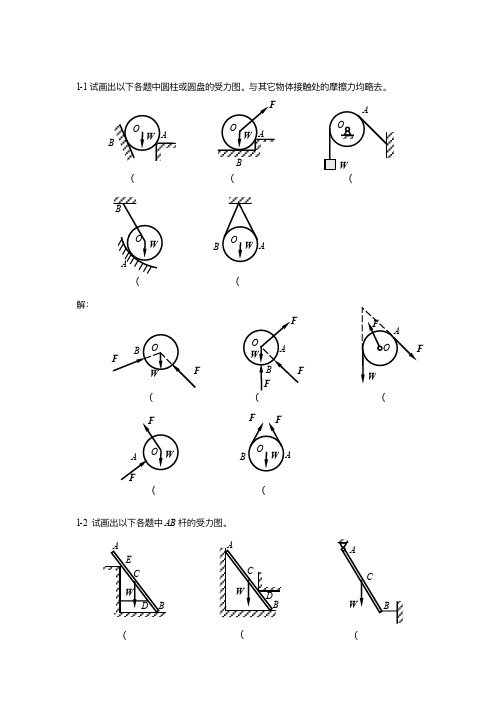
1-5 试画出以下各题中指定物体的受力力力图。 (a) 结点 A,结点 B;(b) 圆柱 A 和 B 及整体;(c) 半拱 AB,半拱 BC 及整体;(d) 杠杆 AB, 切刀刀 CEF 及整体;(e) 秤杆 AB,秤盘架 BCD 及整体。
1m 1m
E D P
A F
B
C O
5m
W
解:(1) 研究跑⻋车与操作架、平臂 OC 以及料料斗斗 C,受力力力分析,画出受力力力图(平面面平行行行力力力系);
16
10
A FA
M1 M2 B
50
FB
解:(1) 取整体为研究对象,受力力力分析,A、B 的约束力力力组成一一个力力力偶,画受力力力图; (2) 列列平衡方方程:
3-5 四连杆机构在图示位置平衡。已知 OA=60cm,BC=40cm,作用用 BC 上的力力力偶的力力力偶矩大大 小小为 M2=1N.m ,试求作用用在 OA 上力力力偶的力力力偶矩大大小小 M1 和 AB 所受的力力力 FAB 所受的力力力。 各杆重量量不不计。 A C M1
6
4
F C
8
B
6
6
D A E
解:(1) 取 DE 为研究对象,DE 为二二力力力杆;FD = FE FD D E
FE
(2) 取 ABC 为研究对象,受力力力分析并画受力力力图;画封闭的力力力三⻆角形: B F FA D 3 3 A F’D 4 FA F’D F
2-7 在四连杆机构 ABCD 的铰链 B 和 C 上分别作用用有力力力 F1 和 F2,机构在图示位置平衡。试 求平衡时力力力 F1 和 F2 的大大小小之间的关系。 C B
工程力学 (静力学)单辉祖主编

Fy
F
F F F
2 x
2 y
Fx cos F
Fx
•两分力间任意夹角 先分解,再合成
第1章 静力学基础
二、载荷的移动、合成与分解
5.力偶的合成
作用在同一平 面(或平行平面) 内的力偶代数相加 即可
第1章 静力学基础
二、载荷的移动、合成与分解
例1:将C点载荷移至B点
y
y
F
F
O (a)
x
O
(b)
x
1-1-2 力的性质
例3:用图解法求合力
(a)
1-1-2 力的性质
例4:用图解法求Fx,Fy,Fz的合力
z Fz
Fy y
O
Fx
x
1-1-2 力的性质
例4:已知系统平衡,画出B、C两点的受力方向
1-1-2 力的性质
例5:已知构件处于平衡状态,求Fc的方向
Fc
(a)
F'
F
A rBA
B
F'
F B
以上结论对变形体不适用
§3.3 力偶系的简化与平衡条件
作用在刚体上的两个或两个以上的力偶组成力偶系。
平面力偶系
空间力偶系
M2
力偶系简化的结 果是合力偶
M1
II I
F2' r2 F1' r r1
M r F1
F1
r1 r2 F1 M1 M 2
i 1
n
力偶系的平衡条件:
M Mi 0
i 1 n
或
M x M ix 0 M y M iy 0 M z M iz 0
工程力学(教案)单辉祖-第八章-轴向拉伸与压缩

第八章轴向拉伸与压缩课型:新知课教学目标:1.掌握轴向拉压的概念;2.掌握轴力的计算和轴力图的绘制方法;3.掌握低碳钢Q235的应力应变图及其拉伸过程的四个阶段;4.熟记工作应力、极限应力和许用应力的概念及其关系式;5.掌握拉压杆的强度条件;!6.掌握弹性模量和泊松比的概念及其计算;重点:1. 轴力的计算和轴力图的绘制方法。
2. 低碳钢Q235的应力应变图及其拉伸过程的四个阶段。
3. 工作应力、极限应力和许用应力的概念及其关系式。
难点:1. 圣维南原理;2. 低碳钢Q235的应力应变图及其拉伸过程的四个阶段;3. 利用拉压杆的强度条件,解决一些强度问题。
教学手段、方法:结合应用实例进行理论讲授。
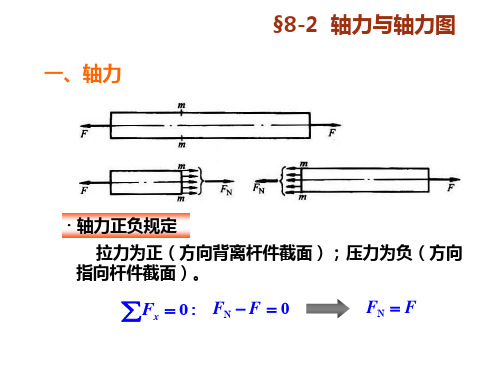
,教具:课件、板书教学过程:§8-1 引言作用线沿杆件轴线的载荷称为轴向载荷;以轴向伸长或缩短为主要特征的变形形式,称为轴向拉压;以轴向拉压为主要变形的杆件,称为拉压杆。
~§轴力与轴力图1、截面法求内力:(1) 假想沿m-m横截面将杆切开;(2) 留下左半段或右半段;(3) 将弃去部分对留下部分的作用用内力代替; (4) 对留下部分写平衡方程求出内力即轴力的值。
2、轴力:截面上的内力,由于外力的作用线与杆件的轴线重合,内力的作用线也与杆件的轴线重合。
所以称为轴力。
3、轴力正负号:拉为正、压为负。
4、轴力图:轴力沿杆件轴线的变化。
§ 拉压杆的应力与圣维南原理杆件的强度不仅与轴力有关,还与横截面面积有关。
必须用应力来比较和判断杆件的强度。
在拉(压)杆的横截面上,与轴力FN 对应的应力是正应力 。
根据连续性假设,横截面上到处都存在着内力。
于是得静力关系:N AF dA σ=⎰、观察变形:横向线ab 、cd 仍为直线,且仍垂直于杆轴线,只是分别平行移至a ’b ’、c ’d ’。
平面假设—变形前原为平面的横截面,变形后仍保持为平面且仍垂直于轴线。
从平面假设可以判断:(1)所有纵向纤维伸长相等;(2)因材料均匀,故各纤维受力相等;(3)内力均匀分布,各点正应力相等,为常量。
