(结构动力学讲义)运动方程的建立
合集下载
结构动力学第二章 运动方程的建立
h—框架结构的高度 E—弹性模量 Ib和Ic—梁和柱的截面惯性矩
ρ→∞：
k
24EIc h3
ρ→0
：
k
6EIc h3
2.1 基本动力体系
3. 阻尼力（Damping Force）
阻尼：引起结构能量的耗散，使结构振幅逐渐变小的一种作用 阻尼来源（物理机制）： (1)固体材料变形时的内摩擦，或材料快速应变引起的热耗散； (2)结构连接部位的摩擦，结构构件与非结构构件之间的摩擦； (3)结构周围外部介质引起的阻尼。例如，空气、流体等。
非保守力做功的变分等于0。
t2 (T V )dt t2 Wncdt 0
t1
t1
Wnc Pncju j
j
其中：
T —— 体系的总动能； V —— 体系的位能，包括应变能及任何保守力的势能； Wnc—— 作用于体系上非保守力（包括阻尼力及任意外荷载）所做的功； δ —— 指（在指定时间段内）所取的变分。
p(t) fI fD fs 0 fI mu fD cu fs ku
mu cu ku p(t)
图2.8 单质点体系的受力分析
2.2 运动方程的建立
3. 虚位移原理
虚位移原理的优点：虚位移原理是建立在对虚功分析的基础之 上，而虚功是一个标量，可以按代数方式运算，因 而比Newton第二定律，或D’Alembert原理中需要采 用的矢量运算更简便。
对如下图所示结构体系，用虚位移原理建立方程更简便一些
2.2 运动方程的建立
4. Hamilton原理
应用变分法来建立结构体系的运动方程。 动力学中广泛应用的变分法是Hamilton原理 体系的平衡位置是体系的稳定位置，在稳定位置，体系的能量取得极值, 一般是极小值。
结构动力学_运动控制方程_分段解析法
结构动力学运动控制方程分段解析法1. 引言1.1 概述在工程领域中，结构动力学是研究结构物体受外界力或激励下的响应和振动特性的一门学科。
结构动力学广泛应用于建筑、桥梁、飞机等领域，对于确保结构物的安全性和稳定性具有重要意义。
随着现代科技的发展，运动控制方程在结构动力学中扮演着至关重要的角色。
通过运动控制方程，我们可以深入理解和预测结构物运动的规律，并为其设计合适的控制策略。
因此，研究和解析这些方程是结构动力学研究中必不可少的一部分。
1.2 文章结构本文将按照以下顺序进行组织和阐述：首先，在第二部分中，我们将简要介绍结构动力学的定义和原理，以及涉及到的动力学方程。
接着，在第三部分中，我们将详细介绍分段解析法作为一种常见的求解方法，包括其基本原理、算法步骤以及相关应用案例。
在第四部分中，我们将描述所设计实验的参数设置，并对实验结果进行分析和讨论。
最后，在第五部分中，我们将总结本文的主要结论，并展望未来研究方向。
1.3 目的本文的主要目的是通过对结构动力学和运动控制方程的介绍，以及分段解析法的应用案例分析，进一步加深对相关理论和方法的理解。
同时，希望为研究者提供一个清晰、系统的框架，以便于更好地理解和应用这些内容。
鉴于分段解析法在结构动力学领域具有广泛应用和良好效果，本文还旨在为读者提供相关方法在实际工程问题中的指导参考。
2. 结构动力学2.1 定义和原理结构动力学是一门研究物体在受到外部力作用下的运动规律的领域。
它主要涉及质点的运动学和动力学，以及刚体与弹性体的运动特性。
在结构工程中，结构动力学用于分析和预测建筑物、桥梁、飞机等工程结构在自然环境或人为作用下的响应情况，并提供相应的设计依据。
2.2 动力学方程结构动力学理论通过牛顿定律和哈密顿原理等基本原理推导出结构系统的运动方程。
这些方程描述了结构物各个部分之间的相互关系，并包括质量、刚度、阻尼等参数。
根据实际工程问题，可以选择合适的数值解法求解这些方程，从而得到结构系统随时间变化的运动状态。
结构动力学第二章
∂T ∂V d ∂T ( )− + = Pncj (t ), & dt ∂u j ∂u j ∂u j
其中： T —— 体系的动能；
j = 1,2,L , N
V —— 体系的位能，包括应变能及任何保守力的势能； Pncj ——与 uj 相应的非保守力（包括阻尼力及任意外荷载）。
– 红色部分为引入动力自由度概念的目的，蓝色部分为实 现此目的的手段。 – 概念中的“全部”、“独立”两个条件非常关键。
• 严格来说，所以结构体系质量都是连续分布的，为无限自 由度体系，研究比较困难。但许多情况下，可以作一定的 简化，变为有限自由度体系。 • 简化并确定结构动力自由度最典型的方法：集中质量法
动能
1 & mu 2 转动质量 2
T =
1 &2 Jθ 2
1 2 V = ku 转动弹簧 2
1 &2 V = kθ θ 2
位能
1 1 & & &j T = ∑ ∑ mij u i u j = ∑ m j u 2 2 i j 2 j
V =
1 ∑ ∑ kij ui u j 2 i j
∫
1 体系的动能：T = mu 2 & 2
粘滞(性)阻尼力可表示为：
& f D = -cu
D — 表示阻尼（damping） c — 阻尼系数（Damping coefficient）
k c
u m
f S(t) m f D(t) f I (t)
& u — 质点的运动速度
阻尼系数 c 的确定：
• 不能像结构刚度 k 那样可通过结构几何尺寸、构件尺寸等 来获得，因为 c 是反映了多种耗能因素综合影响的系数， 阻尼系数一般是通过结构原型振动试验的方法得到。 • 粘性（滞）阻尼理论仅是多种阻尼中最为简单的一种。 • 其它常用的阻尼：
刘晶波结构动力学课件21w
线弹性体系：由线性弹簧(或线性构件)组成的体 系。
—最简单的理想化力学模型。
阻尼弹性体系：当线弹性系统中进一步考虑阻尼 影响时
15/45
2.1 基本概念
阻尼系数 c 的确定： 不能像结构刚度k那样可通过结构几何尺寸、构件尺寸和
材料的力学性质等来获得，因为c是反映了多种耗能因 素综合影响的系数，阻尼系数一般是通过结构原型振 动试验的方法得到。 粘性(滞)阻尼理论仅是多种阻尼中最为简单的一种。 其它常用的阻尼： 摩擦阻尼：阻尼力大小与速度大小无关，一般为常数； 滞变阻尼：阻尼力大小与位移成正比(相位与速度相同)； 流体阻尼：阻尼力与质点速度的平方成正比。
方向指向体系的平衡位置。
fs ku
fs
k
1
a
d
-u0
O
b
u u0
fs k
1
u
s— 表示弹簧(Spring)
c
(a)
k— 弹簧的刚度(Spring Stiffness)
u— 质点位移
(b)
11/45
2.1 基本概念
2.1.5 惯性力（Inertial Force）
惯性：保持物体运动状态的能力。 惯性力：大小等于物体的质量与加速度的乘积，
动力自由度的定义：结构体系在任意瞬时的一切可能的 变形中，决定全部质量位置所需的独立参数的数目称 为结构的动力自由度(数)。
4/45
2.1.1 广义坐标与动力自由度
静力自由度：确定结构体系在空间中位置所需的独立参 数的数目称为结构的自由度。
动力自由度：决定结构体系质量位置所需的独立参数的 数目称为结构的动力自由度(数)。
结构动力学
教师：刘晶波 助教：王东洋
清华大学土木工程系 2015年秋
—最简单的理想化力学模型。
阻尼弹性体系：当线弹性系统中进一步考虑阻尼 影响时
15/45
2.1 基本概念
阻尼系数 c 的确定： 不能像结构刚度k那样可通过结构几何尺寸、构件尺寸和
材料的力学性质等来获得，因为c是反映了多种耗能因 素综合影响的系数，阻尼系数一般是通过结构原型振 动试验的方法得到。 粘性(滞)阻尼理论仅是多种阻尼中最为简单的一种。 其它常用的阻尼： 摩擦阻尼：阻尼力大小与速度大小无关，一般为常数； 滞变阻尼：阻尼力大小与位移成正比(相位与速度相同)； 流体阻尼：阻尼力与质点速度的平方成正比。
方向指向体系的平衡位置。
fs ku
fs
k
1
a
d
-u0
O
b
u u0
fs k
1
u
s— 表示弹簧(Spring)
c
(a)
k— 弹簧的刚度(Spring Stiffness)
u— 质点位移
(b)
11/45
2.1 基本概念
2.1.5 惯性力（Inertial Force）
惯性：保持物体运动状态的能力。 惯性力：大小等于物体的质量与加速度的乘积，
动力自由度的定义：结构体系在任意瞬时的一切可能的 变形中，决定全部质量位置所需的独立参数的数目称 为结构的动力自由度(数)。
4/45
2.1.1 广义坐标与动力自由度
静力自由度：确定结构体系在空间中位置所需的独立参 数的数目称为结构的自由度。
动力自由度：决定结构体系质量位置所需的独立参数的 数目称为结构的动力自由度(数)。
结构动力学
教师：刘晶波 助教：王东洋
清华大学土木工程系 2015年秋
【结构动力学】第1章 运动方程 2020
12
承受动力荷载的任何线性结构体系的主要物理特性是体系的质量、弹 性特性（刚度或柔度）、能量耗散机理或阻尼、以及外部扰力或荷载
单自由度
c
体系模型
k
y (t )
F(t) m
▪ 质量块m，用来表示结构的质量和惯性特性 ▪ 自由度只有一个：水平位移 y(t) ▪ 无重弹簧，刚度为 k，提供结构的弹性恢复力 ▪ 无重阻尼器，阻尼系数c，表示结构的能量耗散，提供结
y P (FI FD )
改写成：
FI
FD
1
y
P
28
位移方程：
FI
FD
1
y
P
其中：
p为动荷载 q(t) 引起的质量沿y方向的位移：
q (t)y(t )
P
5l 4 384 EI
q(t )
惯性力： FI my 阻尼力： FD cy
为自由度方向加单位力所引起的位移，即柔度： 由此得到体系的运动方程：
my cy ky F(t) (2-3)
y(t )
EI l 1
my
cy
12EI
l13
12EI l23
y
FP (t)
12EI 12EI
令： k FS1 FS 2 l13 l23
；k 为（等效）刚度系数。
由此得到体系的运动方程： my cy ky FP (t)
运动方程与(2-3)的形式是一样的！
my cy ky F(t)
（2-3）
14
直接平衡法(达朗贝尔原理)
直接平衡法，又称动静法，将动力学问题转化为任 一时刻的静力学问题：根据达朗贝尔原理，把惯性 力作为附加的虚拟力，并考虑阻尼力、弹性力和作 用在结构上的外荷载，使体系处于动力平衡条件， 按照静力学中建立平衡方程的思路，直接写出运动 方程。
承受动力荷载的任何线性结构体系的主要物理特性是体系的质量、弹 性特性（刚度或柔度）、能量耗散机理或阻尼、以及外部扰力或荷载
单自由度
c
体系模型
k
y (t )
F(t) m
▪ 质量块m，用来表示结构的质量和惯性特性 ▪ 自由度只有一个：水平位移 y(t) ▪ 无重弹簧，刚度为 k，提供结构的弹性恢复力 ▪ 无重阻尼器，阻尼系数c，表示结构的能量耗散，提供结
y P (FI FD )
改写成：
FI
FD
1
y
P
28
位移方程：
FI
FD
1
y
P
其中：
p为动荷载 q(t) 引起的质量沿y方向的位移：
q (t)y(t )
P
5l 4 384 EI
q(t )
惯性力： FI my 阻尼力： FD cy
为自由度方向加单位力所引起的位移，即柔度： 由此得到体系的运动方程：
my cy ky F(t) (2-3)
y(t )
EI l 1
my
cy
12EI
l13
12EI l23
y
FP (t)
12EI 12EI
令： k FS1 FS 2 l13 l23
；k 为（等效）刚度系数。
由此得到体系的运动方程： my cy ky FP (t)
运动方程与(2-3)的形式是一样的！
my cy ky F(t)
（2-3）
14
直接平衡法(达朗贝尔原理)
直接平衡法，又称动静法，将动力学问题转化为任 一时刻的静力学问题：根据达朗贝尔原理，把惯性 力作为附加的虚拟力，并考虑阻尼力、弹性力和作 用在结构上的外荷载，使体系处于动力平衡条件， 按照静力学中建立平衡方程的思路，直接写出运动 方程。
结构动力学(运动方程)
p(t)
m
d
2u(t) dt 2
mu(t)
3.2.1.1-2
式中： mu(t) 称为抵抗质量加速度的惯性力。
直接平衡法
通过动力体系各质点的力矢量平衡关系建立运动方程 的方法。质量所产生的惯性力与它的加速度成正比，但方 向相反。这一概念称为达兰贝尔原理。借助该原理可以把 运动方程表示为动力平衡方程。方程中的力包括多种作用 于质量上的力，如抵抗位移的弹性恢复力、抵抗速度的粘 滞阻尼力以及其它独立确定的外荷载。因此，运动方程的 表达式仅仅是作用于质量上所有力（包含惯性力）的平衡 表达式。在许多简单问题中，直接平衡法是建立运动方程 的最直接而且方便的方法。
当结构体系相当复杂，且包含许多彼此联系的质量点 或有限尺寸的质量块时，直接写出作用于体系上的所有力 的平衡方程可能是困难的；尽管作用于体系的力可以容易 地用位移自由度来表示，但它们的平衡关系则可能十分复 杂。此时，利用虚位移原理建立运动方程更为方便。
例：假设给图 3.2.1.1（b）所示体系一个虚位移u （仅仅 是体系约束所允许的微小位移），则作用于体系的全部力都将做 功，体系所作的总功可写作
t2 [muδu cuδu kuδu p(t)δu]dt 0 t1
3.2.1.3-2
利用关系 δu d(δu) / dt ，上式中的第一项可表示为如下的分部积分：
t2 muδudt muδu t2 t2 muδudt
t1
t1
t1Biblioteka 3.2.1.3-3哈密尔顿原理假定变分 u 在积分限 t1 和 t2 时为零，故方程 3.2.1.3-3 右边第一项为
牛顿第二运动定律
任何质量 m 的动量变化率等于作用在这个质量上的力。这一关系在
结构动力学1
结构的动力自由度
结构动力学和静力学的一个本质区别：考虑惯性力的影响 结构产生动力反应的内因（本质因素）：惯性力 惯性力的产生是由结构的质量引起的 动力自由度（数目）：动力分析中为确定体系任一时刻全部质量的几何位置 所需要的独立参数的数目。
独立参数也称为体系的广义坐标，可以是位移、转角或其它广义量。
第5章 单自由度体系对任意荷载的反应
5.1 时域分析方法―Duhamel积分（脉冲荷载作为Duhamel积分法的应用） 5.2 频域分析方法―Fourier变换 5.3 数值积分法―时域逐步积分：中心差分法、Newmark-β法、Wilson-θ法 5.4非线性结构反应：非线性、增量平衡方程、逐步积分 5.5 结构地震反应初步：运动方程、反应谱
(a)与广义坐标法相似，有限元法采用了 形函数的概念，但不同于广义坐标法在全 部体系(结构)上插值(即定义形函数),而是 采用了分片的插值(即定义分片形函数)， 因此形函数的公式(形状)可以相对简单。 (b) 与集中质量法相比，有限元法中的 广义坐标也采用了真实的物理量，具有直 接、直观的优点，这与集中质量法相同。
nx u ( x, t ) bn sin L n 1
n 1
bn (t ) sin
nx L
sin(.)— 形函数（形状函数），给定函数，满足边界条件 bn(t)— 广义坐标，是一组待定参数，对动力问题是作为时间的函数
u ( x, t )
n 1
N
bn (t ) sin
nx L
结构动力学
第一章 概 述
1.1 动力问题的基本特征
动力问题：地震作用下建筑结构的震动； 风荷载作用下大型桥梁、高层结构的振动； 机器转动产生的不平衡力引起的大型机器基础的振动； 车辆运行中由于路面不平顺引起的车辆振动及车辆引起的路面振动； 爆炸荷载作用下防护工事的冲击动力反应； 海洋工程结构在波浪、冰激、台风等动力荷载作用下的反应； 等等，量大而面广 。
结构动力学-14
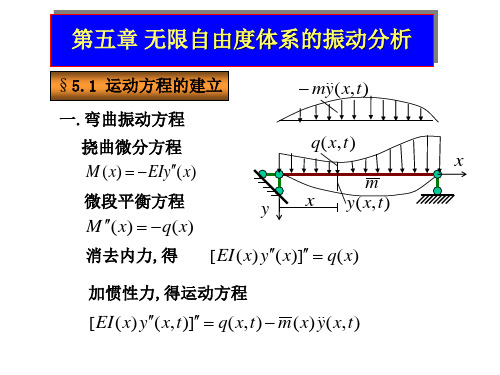
M MD Q 0 EIy(4) cb y (4)I q(x,t) ca y my
EIy(4) cb y (4)I q(x,t) ca y my
2.滞变阻尼 不计阻尼时 计阻尼时
EIy(4) q(x,t) my(x,t)
(1 i )EIy(4) q(x,t) my(x,t)
二.考虑轴力对弯曲的影响时的弯曲振动方程
Fy 0
dQ q(x) dx
M 0
dM Q N dy
dx
dx
y
Q dM N dy dx dx
dQ M (x) Ny(x)
N
dx
M (x) Ny(x) q(x)
q( x, t )
N
m
x
y( x, t )
dx
y
M
dy N
M dM
M (x) EIy(x) [EI (x) y(x)] q(x) Ny
习题：1.求剪切杆的运动方程。 2.求拉压杆的运动方程。
x
x
q( x, t )
ml GA
y
q( x, t )
m EA
l
A
m/A
mI
m
A
I
mr 2
dA A
zdA1
3.运动方程
Fy 0
（x, t)mr 2
M
my(x,t) q( x, t )
dQ q(x,t) my(x,Q
dM Q mr2(x,t)
dx
4.物理方程
M EI Q kGA
5.方程整理 几何方程： dy
dx
物理方程： M EI Q kGA
运动方程： dQ q(x,t) my(x,t) dx dM Q mr2(x,t)