小学数学 基本功训练 一课一练 6年级下册-6
(五四制) 鲁教版数学 6年级下册 配套练习册 一课一练 基本功训练_37
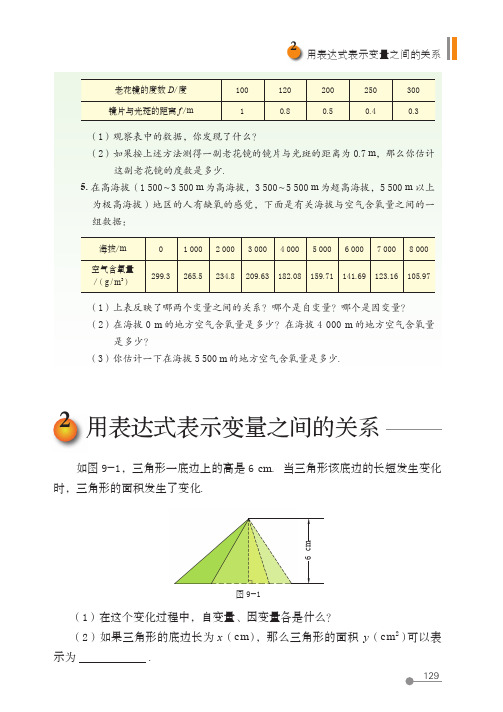
2用表达式表示变量之间的关系用表达式表示变量之间的关系如图 9-1,三角形一底边上的高是 6 cm . 当三角形该底边的长短发生变化时,三角形的面积发生了变化.老花镜的度数 D/ 度100120200250300镜片与光斑的距离 f / m10.80.50.40.3(1)观察表中的数据,你发现了什么?(2)如果按上述方法测得一副老花镜的镜片与光斑的距离为 0.7 m ,那么你估计这副老花镜的度数是多少.5. 在高海拔(1 500 ~ 3 500 m 为高海拔,3 500 ~ 5 500 m 为超高海拔,5 500 m 以上为极高海拔)地区的人有缺氧的感觉,下面是有关海拔与空气含氧量之间的一组数据:海拔/ m 01 0002 0003 0004 0005 0006 0007 0008 000空气含氧量 /(g / m 3)299.3265.5234.8209.63182.08159.71141.69123.16105.97(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)在海拔 0 m 的地方空气含氧量是多少?在海拔 4 000 m 的地方空气含氧量是多少?(3)你估计一下在海拔 5 500 m 的地方空气含氧量是多少.c 图 9-1(1)在这个变化过程中,自变量、因变量各是什么?(2)如果三角形的底边长为 x (cm ),那么三角形的面积 y (cm 2)可以表示为.用表2第九章变量之间的关系议一议做一做(3)当底边长从 12 cm 变化到 3 cm 时,三角形的面积从cm 2 变化到cm 2.y = 3x 表示了图 9-1 中三角形底边长 x 和面积 y 之间的关系,它是变量 y 随 x 变化的表达式.表达式是我们表示变量之间关系的另一种方法. 利用表达式,如 y = 3x ,我们可以根据任何一个自变量的值求出相应的因变量的值.如图 9-3,圆锥的高是 4 cm ,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳特别是二氧化碳的排放量的一种生活方式.图 9-2自变量 x因变量 y 表达式y = 3x图 9-3r cm O4 c m(1)在这个变化过程中,自变量、因变量各是什么?(2)如果圆锥的底面半径为 r (cm ),那么圆锥的体积 V (cm 3)与 r 的表达式为.(3)当底面半径由 1 cm 变化到 10 cm 时,圆锥的体积由cm3 变化到cm 3.2用表达式表示变量之间的关系随堂练习(2)在上述表达式中,耗电量每增加 1 kW ·h ,二氧化碳排放量增加kg . 当耗电量从 1 kW ·h 增加到 100 kW ·h ,二氧化碳排放量从 kg增加到kg .(3)小明家本月用电大约 110 kW ·h 、天然气 20 m 3、自来水 5 t 、油 75 L ,请你计算一下小明家这几项的二氧化碳排放量.1. 如图,一个长方形推拉窗,窗高 1.2 m ,当活动窗扇沿图中所示的方向移动时,随着窗扇拉开长度 b (m )的变化,窗户的通风面积 A (m 2)也发生了变化. (1)在这个变化过程中,自变量、因变量各是什么? (2)写出通风面积 A 与拉开长度 b 之间的表达式;(3)当拉开长度 b 从 0.2 m 变化到 0.4 m 时,通风面积 A 从m 2 变化到m 2.(1)家居用电的二氧化碳排放量可以用表达式表示为,其中的字母表示.(第 1 题)(第 2 题)自变量 d因变量 TT = 10 -d1502. 在地球某地,温度 T (℃)与高度 d (m )的关系可以近似地用表达式 T = 10 -d150来 表示. 根据这个表达式,当 d 的值分别是 0,200,400,600,800,1 000 时,计算相应的 T 值,并用表格表示所得结果.3. 仿照“议一议”中的(2),你能说一说家用自来水二氧化碳排放量随自来水使用吨数的变化而变化的情况吗?。
小学数学 基本功训练 一课一练 6年级下册-62

思考与探索 (1,9) (9,1) (2,8) (8,2) (3,7) (7,3) (4,6) (6,4) (5,5) 练习二 知识与技能 1.B (2,5) C (5,2) D (8,5) 3.(1)A (2,5) B (2,3) C (5,3) 思考与探索 (2)11-2=9 (个) 25×9=225 (千米)
225÷3=75 (千米) (3)75÷25=3 (个) 用 数 对 表 示 为 (11,
5) 三 正比例 反比例
练习一 知识与技能 1.成正比例 (4)不成正比例 (5) 不 成 正 比 例 3.(1)11240,36500,43620,64980; 比 值 相 等 , 均 为 720 (2) 比 值 就 是 飞 机 飞 行 的 速 度 。 (3) 航 程 和 飞 行 时 间 成 正 比 例, 因 为 它 们的比值一定。 思考与探索 (1) 杆 高 和 影 长 成 正 比 例 。 (2) 当 影 长 是 12 米 时 , 杆 高 是 16 米 。 (3) 当 杆 高 是 20 米 时 , 影 长 是 15 米 。 练习二 知识与技能 1.(3) 成 正 比 例。 因 为 流 掉 的 水 量 和 天 数 是两种相关联的量,且它们的比值一定, 所以成正比例。 (4)36升 2.(1)8 90
部分参考答案
课时部分
一 生活中的负数 练习一 知识与技能 3.(1)× (2)× (3)× (4)× 思考与探索 (1)上海 12℃ (2)长春 -12℃ (3)3℃ >0℃ > -1℃ > -12℃ 练习二 思考与探索 (1)-3 (2)东 8 (3)西 4 (4)-4 (5)4 练习三 思考与探索 (1)182 290 (2)四 (3)三 练习四 知识与技能 1.(1)82下 (2)0 -3 +10 -2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6 二 位 置
练 习 一
能用数对表示座位和涂色的方格,知道数对与位置是一一对应的
㊂1.认真填空㊂
(1)在确定位置时,竖向叫做( ),横向叫做( );确定第几列应该从( )往( )数,确定第几排应该从( )往( )数㊂(2)用数对表示位置时,一般先表示第几( ),再表示第几( )㊂(3)在同一平面内有两个点,点A (3,5)和点B (4,5),点( )
在点( )的右面㊂(4)确定物体的位置,需要确定物体的( )和( )
㊂2.仔细判断,正确的在括号里画ɿ,错误的画ˑ㊂(1)在确定物体的位置时,只需一个数即可㊂( )
(2)两个物体的位置分别是(3,4)和(3,7
),则这两个物体在同一列中㊂( )(3)(a ,3)和(b ,3)两点在同一列中㊂( )
3.你能用数对表示下面这些动物的位置吗?
T B )
>T 5T
小猴的位置是( ),大象的位置( ),小鹿的位置是( );( )的位置是(5,2),( )的位置是(6,3
)㊂。
