厦大附中2011小升初数学招生试卷(含答案)
2011年福建省厦大附中小升初数学真题试卷

周长是 6.28 厘米,那么中等的这个圆的周长是 厘米.
10.(3 分)有人民币 x 元,存两年定期,年利率为 y ,到期能取到 元. 11.(3 分)有甲、乙两个数,如果把甲数的小数点向右移一位,就是乙数的 1 ,那么,甲
n (n +1)
三、选一选(每题 2 分,共 10 分)
16.(2 分)从 A 站到 B 站,甲车要行 10 小时,乙车要行 8 小时,则甲车速度比乙车速度慢
()
A. 25%
B.125%
C. 2分)王大爷家新盖了一间房子,原打算在北墙上开一个长 1 米,高 7.5 分米的窗户,
一周形成圆锥甲,以 AB 边为轴旋转一周形成圆锥乙,那圆锥甲与圆锥乙的体积比是多 少?
25.(7 分)如图:两摞相同规格的碗整齐地叠放在桌面上,请根据图中给出的信息,解答 下列问题:
(1)一个碗的高度是多少厘米? (2)把这两摞碗整齐地摆成一摞时,这摞碗的高度是多少?
26.(7 分)在比例尺是 1 的地图上,量得甲城到乙城的图上距离是 9 厘米,现有一 6000000
后来嫌窗户小,又把长和高都增加了 2 分米,现在窗户的面积比原来增加了 ( ) 平方
分米.
A.39
B.4
C.15
D.28.5
18.(2 分)小明用一张梯形纸做折纸游戏.先上下对折,使两底重合,可得图 1,并测出未
重叠部分的两个三角形面积和是 20 平方厘米.然后再将图 1 中两个小三角形部分向内翻
折,得到图 2.经测算,图 2 的面积相当于图 1 的 5 .这张梯形纸的面积是 ( 6
2011年福建省厦大附中小升初数学试卷

2011年福建省厦大附中小升初数学试卷一、算一算(24分)1.(12分)用递等式计算,能简算的要简算(+)×17×258.1÷〔(﹣0.005×700)÷+3〕1234÷9999×2222+3334×3333.2.(6分)求未知数x的值16÷x=0.75:0.36÷5﹣=.3.(6分)看图计算如图,一个半圆在长方形中,长方形的宽是3厘米,求阴影部分的面积.二、填一填(共37分,1、2、4、5、7题每空1分,3、6、8-12题每空3分)4.(1分)在“、2、、、、、0.49”中,比大的有个.5.(3分)找规律,填一填:0.01a、0.04b、0.09a、、0.25a、、.6.(3分)一个长3厘米,宽2厘米的长方形,沿一条对角线对折后,得到如图几何图形,阴影部分的周长是厘米.7.(3分)用1、4、7三个数字组成任意一个三位数,这个三位数有因数2的可能性是,有因数3的可能性是,有因数5的可能性是.8.(2分)一个数省略“万”后面的尾数是8万,这个数在至之间.9.(3分)如图中三个圆的圆心在一条直线上,已知最大圆的周长是28.26厘米,最小圆的周长是6.28厘米,那么中等的这个圆的周长是厘米.10.(3分)有人民币x元,存两年定期,年利率为y,到期能取到元.11.(3分)有甲、乙两个数,如果把甲数的小数点向右移一位,就是乙数的,那么,甲数是乙数的倍.12.(6分)雨哗哗地下着不停,如在雨地里放一个图(1)中那样的长方体容器,雨水将它注满要用1小时.那么,同时雨水注满图(2)这个容器需要小时;注满图(3)这个容器需要小时.13.(3分)有红、黄、蓝三面旗,把这些旗挂在一个旗杆上做成各种信号,如果按照挂旗的面数及从上到下颜色的顺序区分信号,那么利用这三面旗能表示种不同信号.(不算不挂旗情况)14.(3分)对于两个自然数m、n,它们的最小公倍数与最大公因数的差记为m ⊕n,即:m⊕n=〔m,n〕﹣(m,n),如10⊕14=〔10,14〕﹣(10,14)=70﹣2=68,若8⊕k=32,则k=.15.(6分)阅读下面的材料:=1﹣;=﹣;=﹣…所以++=1﹣+﹣+﹣=1﹣=根据上面的规律解答下面的问题:(1)+++…+=(2)+++…+=.三、选一选(每题2分,共10分)16.(2分)从A站到B站,甲车要行10小时,乙车要行8小时,则甲车速度比乙车速度慢()A.25% B.125% C.20% D.80%17.(2分)王大爷家新盖了一间房子,原打算在北墙上开一个长1米,高7.5分米的窗户,后来嫌窗户小,又把长和高都增加了2分米,现在窗户的面积比原来增加了()平方分米.A.39 B.4 C.15 D.28.518.(2分)小明用一张梯形纸做折纸游戏.先上下对折,使两底重合,可得图1,并测出未重叠部分的两个三角形面积和是20平方厘米.然后再将图1中两个小三角形部分向内翻折,得到图2.经测算,图2的面积相当于图1的.这张梯形纸的面积是()平方厘米.A.50 B.60 C.100 D.12019.(2分)右面的立方体图形是由若干个同样的正方体积木堆积而成的,在这些正方体积木中恰好有4个面和其它积木相接的有()块.A.4 B.5 C.6 D.1220.(2分)试比较a和b的大小().A.a>b B.a<b C.a=b D.无法比较四、画一画,填一填(共8分)21.(2分)在如图涂两个小方格,使阴影部分对称.22.(6分)看图填空:(1)把图中的长方形绕M点逆时针旋转90°,画出旋转后的图形;旋转后P点的位置用数对表示是.(2)按1:2的比画出正方形放大后的图形.放大后的正方形与原来正方形的面积比是.(3)直角三角形的斜边BC是圆的直径,O是圆心,AO=AC.如果每个小格表示边长1厘米的小正方形.则A点在O点厘米处.五、看图回答问题(10分)23.(10分)小明和爸爸去北京香山游玩.如图是他们两人登山比赛情况的统计图.(1)10分钟时小明行了米,爸爸行了米.(2)在途中休息了分钟.(3)出发分钟后,两人行的路程相同,是米.(4)比早到达终点,早分钟.(5)爸爸登山的平均速度是每分钟米.六、实践运用(共61分,1--3题每题7分,4--8题每题8分)24.(7分)如图:直角三角形的两条直角边BC与AB的比是1:2,如果以BC 边为轴旋转一周形成圆锥甲,以AB边为轴旋转一周形成圆锥乙,那圆锥甲与圆锥乙的体积比是多少?25.(7分)如图:两摞相同规格的碗整齐地叠放在桌面上,请根据图中给出的信息,解答下列问题:(1)一个碗的高度是多少厘米?(2)把这两摞碗整齐地摆成一摞时,这摞碗的高度是多少?26.(7分)在比例尺是的地图上,量得甲城到乙城的图上距离是9厘米,现有一辆客车和一辆货车同时从甲乙两城相对开出,客车每小时行100千米,货车的速度是客车的.两车出发后几小时相遇?27.(7分)小明每天早晨6:50从家出发,7:20到校.老师要求他明天提早6分钟到校.如果小明明天早晨还是6:50从家出发,那么,每分钟必须比往常多走25米,才能按老师的要求准时到校.问:小明家距学校多远?28.(7分)某家电商场一次售出两种不同品牌的电视机,其中一台赚了12%,另一台赔了12%,且这次售出的两台电视机的售价都是3080元,那么,在这两次买卖中,这个商场是赚了还是赔了,赚了多少?如果赔了,赔了多少?29.(8分)如图所示,长方形草地ABCD被分成面积相等的甲、乙、丙、丁四块,其中图形甲的长和宽的比是a:b=5:2,问图形乙的长和宽的比是多少?30.(8分)甲乙两瓶盐水,甲瓶盐水的浓度是乙瓶盐水的3倍,将100克甲瓶盐水与300克乙瓶盐水混合后得到浓度为15%的新盐水,那么甲瓶盐水的浓度是多少?31.(8分)有两堆围棋子,A堆有500个白子和350个黑子,B堆有100个白子和400个黑子,为了使A堆中黑子占,B堆中黑子占,要从B堆中拿出黑、白子各多少个放入A堆?2011年福建省厦大附中小升初数学试卷参考答案与试题解析一、算一算(24分)1.(12分)用递等式计算,能简算的要简算(+)×17×258.1÷〔(﹣0.005×700)÷+3〕1234÷9999×2222+3334×3333.【解答】解:(1)(+)×17×25,=(+)×(17×25),=(×17×25)+(×25×17),=(4×25)+(1×17),=100+17,=117;(2)8.1÷[(﹣0.005×700)÷+3],=8.1÷[(﹣3.5)÷+3],=8.1÷[÷+3],=8.1÷[+3],=8.1÷3,=;(3)1234÷,=1234÷,=1234÷,=1234÷,=1234×,=;(4)9999×2222+3334×3333,=3333×6666+3334×3333,=3333×(6666+3334),=3333×10000,=33330000.2.(6分)求未知数x的值16÷x=0.75:0.36÷5﹣=.【解答】解:(1)16÷x=0.75:,16÷x=0.75÷,16÷x=0.4,16÷x×x=0.4×x,0.4x=16,0.4x÷0.4=16÷0.4,x=40;(2)0.36÷5﹣=,0.072﹣=,0.072﹣+x=+x,x+=0.072,x+﹣=0.072﹣,x=﹣0.728,x÷=﹣0.728÷,x=﹣.3.(6分)看图计算如图,一个半圆在长方形中,长方形的宽是3厘米,求阴影部分的面积.【解答】解:3×2×3÷2﹣(3×2×3﹣3.14×32÷2)÷2,=18÷2﹣(18﹣3.14×9÷2)÷2,=9﹣(18﹣28.26÷2)÷2,=9﹣(18﹣14.13)÷2,=9﹣(3.87÷2),=9﹣1.935,=7.065(平方厘米),答:阴影部分的面积是7.065平方厘米.二、填一填(共37分,1、2、4、5、7题每空1分,3、6、8-12题每空3分)4.(1分)在“、2、、、、、0.49”中,比大的有3个.【解答】解:因为=0.5,则2>0.5,0.49<0.5,因为5>×9,所以>,3×7,,12=24,=,1×3,,4×5,>,所以比大的数有:、2、;故答案为:3.5.(3分)找规律,填一填:0.01a、0.04b、0.09a、0.16b、0.25a、0.36b、0.49a.【解答】解:42=16,16÷100×b=0.16b,62÷100×b=0.36b,72÷100×a=0.49a;故答案为:0.16b,0.36b,0.49a.6.(3分)一个长3厘米,宽2厘米的长方形,沿一条对角线对折后,得到如图几何图形,阴影部分的周长是10厘米.【解答】解:由分析得出:阴影部分周长为:(3+2)×2=10(厘米).故答案为:10.7.(3分)用1、4、7三个数字组成任意一个三位数,这个三位数有因数2的可能性是,有因数3的可能性是100%,有因数5的可能性是0.【解答】解:这个三位数有因数2的可能性是:2÷6=;因为1+4+7=12,12是3的倍数,所以用1、4、7三个数字组成的所有三位数,都是3的倍数,即可能性是100%;因为没有5的倍数,所以有因数5的可能性是0;答:这个三位数有因数2的可能性是,有因数3的可能性是100%,有因数5的可能性是0;故答案为:,100%,0.8.(2分)一个数省略“万”后面的尾数是8万,这个数在75000至84999之间.【解答】解:8万可以由最小75000与最大84999省略“万”后面的尾数得来,所以这个数在75000至84999之间.故答案为:75000,84999.9.(3分)如图中三个圆的圆心在一条直线上,已知最大圆的周长是28.26厘米,最小圆的周长是6.28厘米,那么中等的这个圆的周长是21.98厘米.【解答】解:28.26﹣6.28=21.98(厘米),答:中等圆的周长为21.98厘米.故答案为:21.98.10.(3分)有人民币x元,存两年定期,年利率为y,到期能取到x+2xy元.【解答】解:x+x×y×2,=x+2xy(元),答:到期能取到x+2xy元;故答案为:x+2xy.11.(3分)有甲、乙两个数,如果把甲数的小数点向右移一位,就是乙数的,那么,甲数是乙数的倍.【解答】解:因为把甲数的小数点向右移一位,就是把甲数扩大到原来的10倍,它与乙数的相等.所以甲数×10=乙数×甲数×10×=乙数××甲数=乙数×答:甲数是乙数的故答案为:12.(6分)雨哗哗地下着不停,如在雨地里放一个图(1)中那样的长方体容器,雨水将它注满要用1小时.那么,同时雨水注满图(2)这个容器需要3小时;注满图(3)这个容器需要 1.5小时.【解答】解:在图(1)所示的容器中,容积:接水面积=(30×10×10):(30×10)=10:1,需1小时接满,所以在图(2)所示的容器中,容积:接水面积=(10×10×30):(10×10)=30:1,需3小时接满;在图(3)所示的容器中,容积:接水面积=(20×20×10﹣10×10×10):(20×10)=15:1,需1.5小时接满.答:雨水注满图(2)这个容器需要3小时;注满图(3)这个容器需要1.5小时.故答案为:3;1.5.13.(3分)有红、黄、蓝三面旗,把这些旗挂在一个旗杆上做成各种信号,如果按照挂旗的面数及从上到下颜色的顺序区分信号,那么利用这三面旗能表示15种不同信号.(不算不挂旗情况)【解答】解:3+3×2+3×2×1=3+6+6=15(种),答:利用这三面旗能表示15种不同信号.故答案为:15.14.(3分)对于两个自然数m、n,它们的最小公倍数与最大公因数的差记为m ⊕n,即:m⊕n=〔m,n〕﹣(m,n),如10⊕14=〔10,14〕﹣(10,14)=70﹣2=68,若8⊕k=32,则k=40.【解答】解:设8和k最大公因数为x,8=mx,k=nx,m,n互质,则8和k最小公倍数mnx,所以mnx﹣x=32,即x(mn﹣1)=32x为8,32的公因数,可能为1,2,4,8,①x=1则m=8,n=33÷8(舍去),②x=2则m=4,n=17÷4(舍去),③x=4则m=2,n=9÷2(舍去),④x=8则m=1,n=5,所以k=nx=5×8=40,故答案为:40.15.(6分)阅读下面的材料:=1﹣;=﹣;=﹣…所以++=1﹣+﹣+﹣=1﹣=根据上面的规律解答下面的问题:(1)+++…+=(2)+++…+=.【解答】解:(1)+++…+,=1﹣+﹣+﹣…+﹣,=1﹣,=;(2)+++…+,=1﹣+﹣+﹣…+﹣,=1﹣,=;故答案为:,.三、选一选(每题2分,共10分)16.(2分)从A站到B站,甲车要行10小时,乙车要行8小时,则甲车速度比乙车速度慢()A.25% B.125% C.20% D.80%【解答】解:(﹣)÷,=()÷,=×8,=0.2,=20%.答:甲车速度比乙车速度慢20%.故选:C.17.(2分)王大爷家新盖了一间房子,原打算在北墙上开一个长1米,高7.5分米的窗户,后来嫌窗户小,又把长和高都增加了2分米,现在窗户的面积比原来增加了()平方分米.A.39 B.4 C.15 D.28.5【解答】解:1米=10分米,(10+2)×(7.5+2)﹣10×7.5,=12×9.5﹣75,=114﹣75,=39(平方分米),=0.39(平方米),=39(平方分米);答:现在窗户的面积比原来增加了0.39平方米.故选:A.18.(2分)小明用一张梯形纸做折纸游戏.先上下对折,使两底重合,可得图1,并测出未重叠部分的两个三角形面积和是20平方厘米.然后再将图1中两个小三角形部分向内翻折,得到图2.经测算,图2的面积相当于图1的.这张梯形纸的面积是()平方厘米.A.50 B.60 C.100 D.120【解答】解:每个三角形的面积是:20÷2=10(平方厘米);图1的面积是:10÷(1﹣),=10÷,=60(平方厘米);图2的面积是:60×=50(平方厘米);梯形纸的面积是:50×2=100(平方厘米);答:梯形纸的面积是100平方厘米.故选:C.19.(2分)右面的立方体图形是由若干个同样的正方体积木堆积而成的,在这些正方体积木中恰好有4个面和其它积木相接的有()块.A.4 B.5 C.6 D.12【解答】解:根据题干分析可得:1+3+2=6(个),答:正方体积木中恰好有4个面和其它积木相接的小正方体有4个.故选:C.20.(2分)试比较a和b的大小().A.a>b B.a<b C.a=b D.无法比较【解答】解:由于=,则,<,同理,>,…,<b=,即a<b.故选:B.四、画一画,填一填(共8分)21.(2分)在如图涂两个小方格,使阴影部分对称.【解答】解:画图如下:22.(6分)看图填空:(1)把图中的长方形绕M点逆时针旋转90°,画出旋转后的图形;旋转后P点的位置用数对表示是(3,3).(2)按1:2的比画出正方形放大后的图形.放大后的正方形与原来正方形的面积比是4:1.(3)直角三角形的斜边BC是圆的直径,O是圆心,AO=AC.如果每个小格表示边长1厘米的小正方形.则A点在O点东偏北60°方向,3厘米处.【解答】解:根据题干分析画图如下:(1)观察图形可知:把小长方形逆时针旋转90度后,点P的位置是(3,3),(2)小正方形的面积是:2×2=4,放大后的正方形的面积是:4×4=16,所以放大后的正方形的面积与原正方形的面积之比是:16:4=4:1,(3)根据题干分析可得,三角形AOC是等边三角形,则∠AOC=60°,则A点在O点在东偏北60°方向,3厘米处.故答案为:(3,3);4:1;东偏北60°方向,3.五、看图回答问题(10分)23.(10分)小明和爸爸去北京香山游玩.如图是他们两人登山比赛情况的统计图.(1)10分钟时小明行了300米,爸爸行了200米.(2)小明在途中休息了5分钟.(3)出发15分钟后,两人行的路程相同,是300米.(4)爸爸比小明早到达终点,早 2.5分钟.(5)爸爸登山的平均速度是每分钟20米.【解答】解:(1)10分钟小明行了300米,爸爸行了200米;(2)15﹣10=5(分钟),答:小明在中途休息了5分钟;(3)根据折线统计图可知:出发后15分钟,两人行的路程相同,都是300米;(4)27.5﹣25=2.5(分钟),答:爸爸比小明早到达终点,早2.5分钟;(5)500÷25=20(米),答:爸爸登山的平均速度是每分钟20米.故答案为:(1)300,200,(2)小明,5,(3)15,300,(4)爸爸,小明,2.5,(5)20.六、实践运用(共61分,1--3题每题7分,4--8题每题8分)24.(7分)如图:直角三角形的两条直角边BC与AB的比是1:2,如果以BC 边为轴旋转一周形成圆锥甲,以AB边为轴旋转一周形成圆锥乙,那圆锥甲与圆锥乙的体积比是多少?【解答】解:(×π×22×1):(×π×12×2),=4:2,=2:1;答:圆锥甲与圆锥乙的体积比是2:1.25.(7分)如图:两摞相同规格的碗整齐地叠放在桌面上,请根据图中给出的信息,解答下列问题:(1)一个碗的高度是多少厘米?(2)把这两摞碗整齐地摆成一摞时,这摞碗的高度是多少?【解答】解:(1)每加上一只碗,则高度增加:(12﹣10.5)÷(5﹣4),=1.5÷1,=1.5(厘米);一只碗本身的高度为:10.5﹣(1.5×3),=10.5﹣4.5,=6(厘米);答:一个碗的高度是6厘米.(2)6+1.5×(9﹣1),=6+1.5×8,=6+12,=18(厘米);答:这摞碗的高度是18厘米.26.(7分)在比例尺是的地图上,量得甲城到乙城的图上距离是9厘米,现有一辆客车和一辆货车同时从甲乙两城相对开出,客车每小时行100千米,货车的速度是客车的.两车出发后几小时相遇?【解答】解:9÷,=54000000(厘米),=540(千米);100×+100,=80+100,=180(千米);540÷180=3(小时);答:两车出发后3小时相遇.27.(7分)小明每天早晨6:50从家出发,7:20到校.老师要求他明天提早6分钟到校.如果小明明天早晨还是6:50从家出发,那么,每分钟必须比往常多走25米,才能按老师的要求准时到校.问:小明家距学校多远?【解答】解:25×(30﹣6)÷6×30=25×24÷6×30=600÷6×30=100×30=3000(米).答:小明家距学校3000米.28.(7分)某家电商场一次售出两种不同品牌的电视机,其中一台赚了12%,另一台赔了12%,且这次售出的两台电视机的售价都是3080元,那么,在这两次买卖中,这个商场是赚了还是赔了,赚了多少?如果赔了,赔了多少?【解答】解:第一台电视机赚了:3080﹣3080÷(1+12%),=3080﹣3080÷112%,=3080﹣2750,=330(元);第二台电视机亏了:3080÷(1﹣12%)﹣3080,=3080÷88%﹣3080,=3500﹣3080,=420(元);330<420;420﹣330=90(元),答:亏了,亏了90元.29.(8分)如图所示,长方形草地ABCD被分成面积相等的甲、乙、丙、丁四块,其中图形甲的长和宽的比是a:b=5:2,问图形乙的长和宽的比是多少?【解答】解:设a是5,那么b就是2;长方形乙长是c,宽是d;由乙和丙的面积相等可知:c×d=×(a﹣d)×c,d=(a﹣d),2d=a﹣d,3d=a,a=5,所以d=;由甲与乙的面积相等可知:5×2=×c,c=6;所以c:d=6:=18:5.答:长方形乙长和宽的比是18:5.30.(8分)甲乙两瓶盐水,甲瓶盐水的浓度是乙瓶盐水的3倍,将100克甲瓶盐水与300克乙瓶盐水混合后得到浓度为15%的新盐水,那么甲瓶盐水的浓度是多少?【解答】解:设乙瓶盐水的浓度是x,则甲瓶盐水的浓度是3x,根据题意得100×3x+300×x=(100+300)×15%,300x+300x=60,600x=60,x=10%,3x=3×10%=30%.答:甲瓶盐水的浓度是30%.31.(8分)有两堆围棋子,A堆有500个白子和350个黑子,B堆有100个白子和400个黑子,为了使A堆中黑子占,B堆中黑子占,要从B堆中拿出黑、白子各多少个放入A堆?【解答】解:白子共:500+100=600个;黑子共:350+400=750个;黑白相差:750﹣600=150个;150÷(3﹣1)×3=150÷2×3,=225(个).100﹣75=25(个);400﹣225=175(个).答:B堆拿到A堆去的白子是25个,B堆拿到A堆去的黑子是175个.。
厦大附中2010年小升初数学试卷

1 / 3厦大附中“六年一贯制”实验班招生文化素质测试 数学试卷 (时间120分钟 满分150分)一、填一填(第11、14题每题4分,其余每题各2分,共32分)1、中国第二艘载人飞船“神舟六号”升空后的轨道约是三十五万四千米,写作( )km ,其中3在( )位上,表示3个( ),将它改写成用“万km ”做单位的数是( )万km 。
2、有a 吨化肥,每天用去1.2吨,用了b 天,还剩下( )吨。
3、分数单位为51的最大真分数与最小假分数的和是( ),再加上( )个这样的分数单位就可以得到一个最小的质数。
4、一个正方体,相交于一个顶点的三条棱之和是15cm ,这个正方体的表面积是( ),体积是( )。
5、右下图的钟面是从镜子里看到的,钟面上的实际时刻是( )。
6、27∶( )=45÷30=20)(=( )% 7、a ×7=5b,a 和b 成( )比例。
8、为了便于学籍管理,学校对每个学生进行了编号,设定用“1”表示男生,用“2”表示女生,表示的是“2003年入学的一年级二班的32号学生,是男生”。
林晓晓是2001年入学的,三年级一班的3号学生,是女生。
按照上面的编号规则,她的编号应是( )。
9、把7米长的钢筋,锯成每段一样长的小段,共锯6次,每段是全长的)()(,每段长( )米;如果锯成两段需2分,锯成6段共需( )分。
10、一个直角三角形的两条直角边分别长6dm 、8dm ,第三条边长10dm ,这条边(斜边)上的高是( )dm 。
11、甲、乙、丙、丁四位同学参加计算比赛,成绩如下:甲94分、乙86分、丙91分、丁93分。
①以90分为标准,即把90分记作0分,则甲、乙、丙、丁的成绩依次记作( )、( )、( )、( )。
计算四人总分的算式是( )×4+( )=( )。
②若以四人的平均成绩记作0分,则甲、乙、丙、丁的的成绩依次记作( )、( )、( )、( )。
12、一个圆柱体,高每减少1cm ,它的表面积就减少25.12cm 2,如果这个圆柱体的高是5cm ,那么它的体积是( )cm 3。
厦门市【小升初】小升初数学综合模拟试卷答案及详细解析(13)
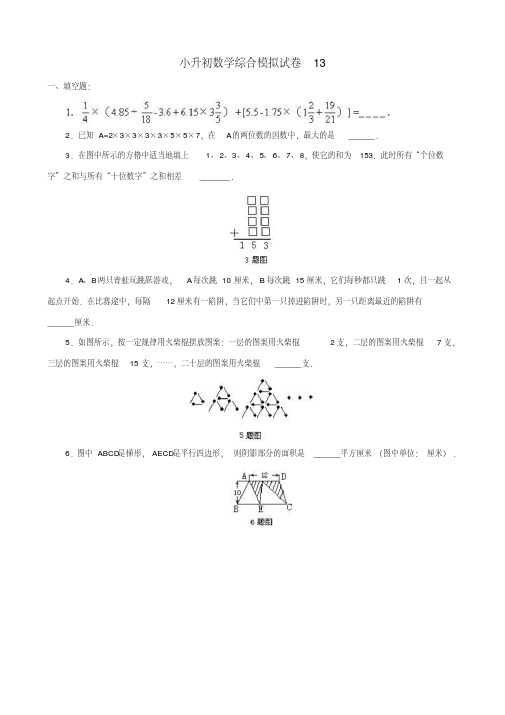
小升初数学综合模拟试卷13一、填空题:2.已知A=2×3×3×3×3×5×5×7,在A的两位数的因数中,最大的是______.3.在图中所示的方格中适当地填上1、2、3、4、5、6、7、8,使它的和为153.此时所有“个位数字”之和与所有“十位数字”之和相差_______.4.A、B两只青蛙玩跳跃游戏,A每次跳10厘米,B每次跳15厘米,它们每秒都只跳1次,且一起从起点开始.在比赛途中,每隔12厘米有一陷阱,当它们中第一只掉进陷阱时,另一只距离最近的陷阱有______厘米.5.如图所示,按一定规律用火柴棍摆放图案:一层的图案用火柴棍2支,二层的图案用火柴棍7支,三层的图案用火柴棍15支,……,二十层的图案用火柴棍______支.6.图中ABCD是梯形,AECD是平行四边形,则阴影部分的面积是______平方厘米(图中单位:厘米).7.用43个边长1厘米的白色小正方体和21个边长1厘米的黑色小正方体堆成如图所示的大正方体,使黑色的面向外露的面积要尽量大.那么这个立方体的表面积上有______平方厘米是黑色的.8.甲、乙、丙三人射击,每人打5发子弹,中靶的位置在图中用点表示.计算成绩时发现三人得分相同.甲说:“我头两发共打了8环.”乙说:“我头两发共打了9环.”那么唯一的10环是______打的.9.有三堆棋子,每堆棋子一样多,并且都有黑白两色棋子.第一堆里黑棋子和第二堆里白棋子的数目相等,第三堆里的黑棋_______分之_______.10.若干名战士排成八列长方形队列,若增加120人或减少120人都能组成一个新的正方形队列.那么,原有战士_______名.二、解答题:1.计算:2.甲有桌子若干张,乙有椅子若干把,如果乙用全部椅子换回数量同样多的桌子,则乙需补给甲320元,如乙不补钱,就要少换回5张桌子.已知3张桌子比5把椅子的价钱少48元,那么乙原有椅子多少把?3.有30个贰分硬币和8个伍分硬币,用这些硬币不能构成1分到1元之间的币值有多少种?4.快、中、慢三辆车同时从A地沿同一公路开往B地,途中有一骑车人也同方向行进.这三辆车分别用7分、8分、14分追上骑车人.已知快车每分行800米,慢车每分行600米,求中速车的速度.答案一、填空题:1.102.902×32×5=903.10所有“个位数字”之和=23,所有“十位数字”之和=13,所以23-13=10.4.410与12的最小公倍数是60,15和12的最小公倍数也是60.当第一只掉进陷阱时,第二只跳到10×(60÷15)=40厘米处,此时距离最近的陷阱有40-12×3=4(厘米).第一层:1×2第二层:1×2+1+2×2第三层:1×2+1+2×2+2+3×2第二十层:1×2+1+2×2+2+3×2+…+19+20×2=(1+2+…+19)+1×2+2×2+…+20×2=190+21×20=6106.60阴影部分的面积等于以12为底以10为高的平行四边形面积的一半,即12×10÷2=60(平方厘米).7.50八个顶点用去8个黑色小立方体,还剩13个黑色小立方体放在棱上,所以大立方体上黑色的面积为3×8+2×(21-8)=24+26=50(平方厘米)8.丙.从图中可以看出,总环数为1×2+2×6+4×3+7×3+10×1=57(环),每人五发子弹打(57÷3=)19环.从图中还可看出2+6+3+3+1=15,即每人五发子弹均中靶.因为甲、乙头两发子弹总成绩已分别为8环、9环,所以后三发中不可能有10环,否则总成绩将大于19环.由此可知,10环是丙打的.根据条件可知,第一、二堆中,白色棋子与黑色棋子数目相同,所以第一、二堆中的白棋子也可分成同样的3份,因为三堆棋子数相同,所以每堆棋子数相当于3份.根据第三堆中黑棋子占2份,可知第三堆中白棋子占1份.因为增加120人可构成大正方形(设边长为a),减少120人可构成小正方形(设边长为b),所以大、小正方形的面积差为240.利用弦图求大、小正方形的边长(只求其中一个即可),如右图所示,可知每个小长方形的面积为(240÷4)=60.根据60=2×30=3×20=4×15=5×12=6×10,试验.①长=30,宽=2,则b=30-2=28.原有人数=28×28+120=904(人),经检验是8的倍数(原有8列纵队),满足条件.②长=20,宽=3,则b=20-3=17.原有人数为奇数,不能排成8列纵队,舍。
厦门市重点小学小升初数学考试试卷(I卷) 含答案

厦门市重点小学小升初数学考试试卷(I卷)含答案班级:_________ 姓名:_________ 学号:_________试卷说明:1、测试时间90分钟,测试题满分100分。
2、答题前,请用黑色或蓝色钢笔、圆珠笔在密封区内写上学校、班别、姓名等内容。
3、答题时,请用黑色或蓝色钢笔、圆珠笔作答。
一、填空题(将正确答案填入空中,每题2分,共计16分)1、一根铁丝长25.12米,把它焊接成一个圆,圆的半径是(),面积是()平方米。
2、一项工程,甲单独做要6小时完成,乙单独做要9小时完成。
甲、乙合做,完成这项工程要()小时。
3、今年第一季度有()天。
4、在○里填上“>”“<”或“=”。
5、一个正方体的底面积是36平方厘米,这个正方体的体积是( )立方厘米。
6、一个圆柱的底面周长是9.42dm,它的高是直径的2倍,圆柱的侧面积是()dm2,它的表面积是()dm2。
7、按规律填数。
2、5、10、17、()、37。
8、小明集邮的数量占小华的2/3,把()看作单位“1”。
二、选择题(只有一个正确答案,每题1.5分,共计12分)1、在2、3、4、5这四个数中,一共可以找出()对互质数。
A、4B、5C、62、一个三角形至少有()个锐角。
A、1B、2C、33、甲是乙的2.5倍,那么甲与乙的最简比是()。
A、25:10B、10:25C、2:5D、5:24、一件商品,先提价20%,以后又降价20%,现在的价格与原来相比()。
A.提高了 B.降低了 C.不变 D.无法确定5、一根绳子,截下它的2/3后,还剩2/3米,那么()。
A、截去的多B、剩下的多C、一样多D、无法比较6、某商店实行“买四斤送一斤”的促销活动,“买四斤送一斤”相当于打( )折销售。
A.二 B.二五 C.八 D.七五7、甲、乙两数的比是5:4,乙数比甲数少()。
A.25% B.20% C.125%8、把一个边长3厘米的正方形按2:1放大后正方形的面积是()平方厘米。
小学升初中数学试卷

厦大附中“六年制”创新班招生考试数学试卷(考试时间:90分钟,满分120分)一、判断题(对的在括号里打“√”,错的打“×”。
)(每小题2分,共16分)1.一种彩票的中奖率是1%,买100张这种彩票,就一定能中奖.…( )2.某地当天的气温是-60C 到80C ,这天的温差是140C.…………( )3.两人以相同的速度合打一份稿件需要80分钟,如果其中一人的打字速度提高2倍, 那么两人合打这份稿件只要60分钟.…………………( )4.因为上海在北京的南偏东300的方向上,所以北京就在上海的东偏南300的方向上.………………………………………………………………… ( )。
5.小冬从一楼走到三楼用了 1.2分钟,如果用同样的速度再走到六楼,还要用0.03小时.……………………………………………………………( )6.除2以外所有的质数都是奇数. ………………………………( )7.一个长方形的长和宽各增加3米,它的面积就增加9平方米 .… ( )8.设C 为一个圆的周长,则C π ×12表示圆的半径.…………………( )二、选择题(每小题2分,共16分)1.把399.9万改写成以“亿”为单位的数,应该是( )亿.A. 0.0039B. 0.03999C. 0.3999D. 3.9992.已知平行四边形的两邻边长为5cm 和7cm.,且已知一边上的高是6cm ,则它的面积是( )cm 2.A. 30B. 42C. 30或42D. 无法确定3.如图,一个扇形的圆心角是1200,半径是r 。
用这个扇形围成一个高为锥(接缝处不计),圆锥的高h 与扇形的半径r 之间的关系是( )A. h >r B. h =r C. h <r D. 无法确定4.童装店以100元卖出两套不同的童装,结果一套赚20%,一套亏本20%,的来说,这个童装店是( ).A .亏本 B. 赚钱 C. 不亏也不赚 D. 以上都不对5.机器猫跑7步与机器狗跑5步的路程相同;机器狗跑11步与机器人跑7步路程相同。
厦门市【小升初】小升初数学综合模拟试卷答案及详细解析(8)

小升初数学综合模拟试卷8一、填空题:2.在下列的数字上加上循环点,使不等式能够变正确:0.9195<0.9195<0.9195<0.9195<0.91953.如图,O为△A1A6A12的边A1A12上的一点,分别连结OA2,OA3,…,OA11,图中共有______个三角形.4.今年小宇15岁,小亮12岁,______年前,小宇和小亮的年龄和是15.5.在前三场击球游戏中,王新同学得分分别为139,143,144,为使前4场的平均得分为145,第四场她应得______分.6.有这样的自然数:它加1是2的倍数,加2是3的倍数,加3是4的倍数,加4是5的倍数,加5是6的倍数,加6是7的倍数,在这种自然数中除了1以外最小的是______.7.如图,半圆S1的面积是14.13cm2圆S2的面积是19.625cm2那么长方形(阴影部分)的面积是______cm2.8.直角三角形ABC的三边分别为AC=3,AB=1.8,BC=2.4,ED垂直于AC,且ED=1,正方形的BFEG边长是______.9.有两个容器,一个容器中的水是另一个容器中水的2倍,如果从每个容器中都倒出8升水,那么一个容器中的水是另一个容器中水的3倍.有较少水的容器原有水______升.10.100名学生要到离校33千米处的少年宫活动.只有一辆能载25人的汽车,为了使全体学生尽快地到达目的地,他们决定采取步行与乘车相结合的办法.已知学生步行速度为每小时5千米,汽车速度为每小时55千米.要保证全体学生都尽快到达目的地,所需时间是______(上、下车所用的时间不计).二、解答题:1.一个四边形的广场,它的四边长分别是60米,72米,96米,84米.现在要在四边上植树,如果四边上每两树的间隔距离都相等,那么至少要种多少棵树?2.一列火车通过一条长1140米的桥梁(车头上桥直至车尾离开桥)用了50秒,火车穿越长1980米的隧道用了80秒,问这列火车的车速和车身长?3.能否把1,1,2,2,3,3,…,50,50这100个数排成一行,使得两个1之间夹着这100个数中的一个数,两个2之间夹着这100个数中的两个数,……两个50之间夹着这100个数中的50个数?并证明你的结论.4.两辆汽车运送每包价值相同的货物通过收税处.押送人没有带足够的税款,就用部分货物充当税款.第一辆车载货120包,交出了10包货物另加240元作为税金;第二辆车载货40包,交给收税处5包货,收到退还款80元,这样也正好付清税金.问每包货物销售价是多少元?答案一、填空题:3.(37)将△A1A6A12分解成以OA6为公共边的两个三角形.△OA1A6共有(5+4+3+2+1=)15个三角形,△OA6A12共有(6+5+4+3+2+1=)21个,所以图中共有(15+21+1=)37个三角形.4.(6年)今年年龄和15+12=27岁,比15岁多27-15=12,两人一年增长的年龄和是2岁,故12÷2=6年.5.(154)145×4-(139+143+144)=154.6.(421)这个数比2,3,4,5,6,7的最小公倍数大1,又2,3,4,5,6,7的最小公倍数为420,所以这个数为421.7.(5)由图示阴影部分的长是圆S2的直径,宽是半圆S1的直径与圆S2的直径9.(16升)由甲容器中的水是乙容器的2倍和它们均倒出8升水后变成3倍关系,设原甲容器中的水量为4份,则因2容器中的水量为2份,按题意画图如下:故较少容器原有水量8×2=16(升).把100名学生分成四组,每组25人.只有每组队员乘车和步行的时间都分别相等,他们才能同时到达目的地,用的时间才最少.如图,设AB=x千米,在第二组队员走完AB的同时,汽车走了由A到E,又由E返回B的路程,这一段路程为11x千米(因为汽车与步行速度比为55∶二、解答题:1.(26棵)要使四边上每两棵树间隔距离都相等,这个间隔距离必须能整除每一边长.要种的树尽可能少(间隔距离尽可能大),就应先求出四边长的最大公约数.60,72,96,84四数的最大公约数是12,种的棵数:(60+72+96+84)÷12=262.(28米/秒,260米)(1980-1140)÷(80-50)=28(米/秒)28×50-1140=260(米)3.不可能.反证法,假设存在某种排列,满足条件.我们把这100个数从左向右按1,2,3,…,99,100编号,则任何两个相等的偶数之间要插入偶数个数,则这两个偶数的序号的奇偶性是不同的;而任何两个相等的奇数之间要插入奇数个数,则这两个奇数的序号的奇偶性相同.由此,这100个数中有25对偶数(每对是两个相等的偶数),它们占去25个奇序号和25个偶序号;另外25对相等的奇数,它们中奇序号的个数一定是偶数.而在100个数中奇序号和偶序号各有50个,所以这25对相等的奇数中,奇序号个数只能是25个(因为25对偶数已占去了奇序号).25是奇数,由于奇数≠偶数,所以无法实现.4.(106元)(元).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011厦门大学附属实验中学“六年一贯制”实验班文化素质测试 数学试卷(120分钟)一、算一算(24分)1、用递等式计算,能简算的要简算(3×4=12分)(174+251)×17×25 8.1÷〔(714-0.005×700)÷721+3〕1234÷123512341234 9999×2222+3334×33332、求未知数x 的值(2×3=6分)16÷x =0.75∶815 0.36÷5-x 43=543、看图计算(6分)①如图,一个半圆在长方形中,长方形的宽是3厘米,求阴影部分的面积。
二、填一填(共37分,1、2、4、5、7题每空1分,3、6、8—12题每空3分)1、在“95、2、73、42、31、54、0.49”中,比21大的有( )个。
2、找规律,填一填:0.01a 、0.04b 、0.09a 、( )、0.25a 、( )、( )。
3、一个长3厘米,宽2厘米的长方形,沿一条对角线对折后, 得到如右图几何图形,阴影部分的周长是( )厘米。
4、用1、4、7三个数字组成任意一个三位数,这个三位数有因数2 的可能性是( ),有因数3的可能性是( ),有 因数5的可能性是( )。
5、一个数省略“万”后面的尾数约是5万,这个数在( )至( )之间。
6、右图中三个圆的圆心在一条直线上,已知最大圆的周长是28.26厘米, 最小圆的周长是6.28厘米,那么中等的这个圆的周长是( ) 厘米。
7、有人民币x 元,存两年定期,年利率为y ,到期能取到(8、有甲乙两个数,如果把甲的小数点向右移一位,就是乙数的41。
那么,甲数是乙数的()。
9、雨哗哗地下着不停,如在雨地里放一个图(1)中那样的长方体容器,雨水将它注满要用1小时。
那么,同时雨水注满图(2)这个容器需要( )小时;注满图(3)这个容器需要( )小时。
10、有红、黄、蓝三面旗,把这些旗挂在一个旗杆上做成各种信号,如果按照挂旗的面数及从上到下颜色的顺序区分信号,那么利用这三面旗能表示( )种不同的信号。
11、对于两个自然数m 、n ,它们的最小公倍数与最大公因数的差记为⊕,即:⊕=〔m ,n 〕-(m ,n ),如10⊕14=〔10,14〕-(10,14)=70-2=68,若8⊕k =32,则k =( )。
12、阅读下面的材料:211⨯=1-21;321⨯=21-31;431⨯=31-41…… 所以 211⨯+321⨯+431⨯=1-21+21-31+31-41=1-41=43根据上面的规律解答下面的问题:(1)211⨯+321⨯+431⨯+……+11101⨯=( )10 3010图(1)101030图(2)2020 101010 10图(3) 第6题第3题(2)211⨯+321⨯+431⨯+……+)+1(1n n ⨯=( )三、选一选(每题2分,共10分)1、从A 站到B 站,甲车要行10小时,乙车要行8小时,甲车的速度比乙车慢( )。
A 、25%B 、20%C 、80%2、王大爷家新盖了一间房子,原打算在北墙上开一个长1米,高7.5分米的窗户,后来嫌窗户小,又把长和高都增加了2分米,现在窗户的面积比原来增加了( )平方分米。
A 、39B 、4C 、15D 、28.53、小明用一张梯形纸做折纸游戏。
先上下对折,使两底重合,可得图1,并测出未重叠部分两个三角形的面积和是20平方厘米。
然后再将图1中的两个三角形部分向内翻折,得到图2。
经测算,图2(阴影部分)的面积相当于图1(实线内)的65。
这张梯形纸的面积是( )平方厘米。
A 、50B 、60C 、100D 、120 4、下面的立方体图形是由若干个同样的正方体积木堆积而成的,在这些正方体积木中恰好有4个面和其它积木相接的有( )块。
A 、4B 、5C 、6D 、125、试比较a 和b 的大小:( )。
99113121+++=⋯a 100199113121++++=⋯bA 、a >bB 、a < bC 、a =bD 、无法比较图1图2四、画一画,填一填(共8分)1、在下图涂两个小方格,使阴影部分对称。
2、看图填空(1)把图中的长方形绕M 点逆时针旋转90°,画出旋转后的图形;旋转后P 点的位置用数对表示是( )。
(2)按1∶2的比画出正方形放大后的图形。
放大后的正方形与原来正方形的面积比是( )。
(3)直角三角形的斜边是圆的直径,O 是圆心,=。
如果每个小格表示边长1厘米的小正方形。
则A 点在O 点( )( )厘米处。
五、看图回答问题(10分)小明和爸爸去北京香山游玩。
下图是他们两人登山比赛情况的统计图。
(1)10分钟时小明行了( )米,爸爸行了( )米。
(2)( )在途中休息了( )分钟。
(3)出发( )分钟后,两人行的路程相同,是( )米。
(4)( )比( )早到达终点,早( )分钟。
(5)爸爸登山的平均速度是每分钟( )米。
18 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 20 17时间/分六、实践运用(共61分,1——3题每题7分,4——8题每题8分)1、如图:直角三角形的两条直角边与的比是1∶2,如果以边为轴旋转一周形成圆锥甲,以边为轴旋转一周形成圆锥乙,那圆锥甲与圆锥乙的体积比是多少?2、如图:两摞相同规格的碗整齐地叠放在桌面上,请根据图中给出的信息,解答下列问题: (1)一个碗的高度是多少厘米?(2)把这两摞碗整齐地摆成一摞时,这摞碗的高度是多少?3、在比例尺为60000001的地图上,量得甲城到乙城的图上距离是9厘米,现在有一辆客车和一辆货车同时从甲、乙两城相对开出,客车每小时行100千米,相遇时货车和客车所行的路程比是4∶5,两车出发后几小时相遇?4、小明每天早晨6∶50从家里出发,7∶20到校。
老师要求他明天提早6分钟到校。
如果小明明天早晨还是6∶50从家里出发,那么,每分钟必须比往常多走25米,才能按老师的要求准时到校。
问:小明家距学校多远?5、某家电商场一次售出两种不同品牌的电视机,其中一台赚了12%,另一台赔了12%,A BC 10.5且这次售出的两台电视机的售价都是3080元,那么,在这两次买卖中,这个商场是赚了还是赔了,赚了多少?如果赔了,赔了多少?6、如图所示,长方形草地被分成面积相等的甲、乙、丙、丁四块,其中图形甲的长和宽的比是a ∶b =5∶2,问图形乙的长和宽的比是多少?7、甲乙两瓶盐水,甲瓶盐水的浓度是乙瓶盐水的3倍,将100克甲瓶盐水与300克乙瓶盐水混合后得到浓度为15%的新盐水,那么甲瓶盐水的浓度是多少?8、有两堆围棋子,A 堆有500个白子和350个黑子,B 堆有100个白子和400个黑子,为了使A 堆中黑子占21,B 堆中黑子占43,要从B 堆中拿出黑、白子各多少个放入A 堆?一、算一算(24分)1、用递等式计算,能简算的要简算甲 乙丙 丁 a b2、求未知数x的值(2×3=6分)3、看图计算(6分)①如图,一个半圆在长方形中,长方形的宽是3厘米,求阴影部分的面积。
分析:根据图和题意得出长方形的长是3×2=6厘米,半圆的半径是3厘米,所以先求出长方形的面积及半圆的面积,再用长方形的面积减去半圆的面积再除以2求出①的面积,再用长方形的面积的一半减去①的面积求出阴影部分的面积.六、实践运用(共61分,1——3题每题7分,4——8题每题8分)4..小明每天早晨6:50从家出发,7:20到校,用时30分钟,如果小明明天早晨还是6:50从家出发,要提早6分钟到校,所用时间是30-6=24分钟,根据每分钟必须比往常多走25米,这样可求出24分钟比往常多走25×24=600米,这600米相当于往常6分钟走的路程,即可求出往常的速读,600÷6=100米,再根据路程、速度、时间的关系即可解答.解:25×(30-6)÷6×30=25×24÷6×30=600÷6×30=100×30=3000(米).答:小明家距学校3000米.6. a:5:2,设a是5,那么b就是2;长方形乙长是c,宽是d,那么乙的面积就是c×d,直角三角形丙的面积是:1/2×()×c,由乙和丙的面积相等,求出d的长度;再根据甲乙的面积相等求出c,然后作比即可解:设a是5,那么b就是2;长方形乙长是c,宽是d;由乙和丙的面积相等可知:7..解:设乙瓶盐水的浓度是x,则甲瓶盐水的浓度是3x,根据题意得100×3300×(100+300)×15%,30030060,60060,10%,33×1030%.答:甲瓶盐水的浓度是30%.8.由题意可知,白子共500+100=600个,黑子共350+400=750个,A堆中黑子占1/2,则A堆中黑白一样多,所以黑白相差的750-600=150个出现在B堆,B堆黑子占3/4,即白1份,黑3份,每份是150÷(3-1)=75个,B堆中白子就是75个,黑子是75×3=225个,B堆拿到A堆去的白子是100-75=25个,B堆拿到A堆去的黑子是400-225=175个.此时A堆有白500+25=525个,黑350+175=525个,符合题意.解:白子共:500+100=600个;黑子共:350+400=750个;黑白相差:750-600=150个;150÷(3-1)×3=150÷2×3,=225(个).100-75=25(个);400-225=175(个).答:B堆拿到A堆去的白子是25个,B堆拿到A堆去的黑子是175个.。
