热力学双语练习
第二章 热力学第一定律

第二章 热力学第一定律英文习题1. Cooling of a hot fluid in a tankA rigid tank contains a hot fluid that is cooled while being stirred by apaddle wheel. Initially, the internal energy of the fluid is 800 kJ. During the cooling process, the fluid loses 500 kJ of heat, and the paddle wheel does 100 kJ of work on the fluid. Determine the final internal energy of the fluid. Neglect the energy stored in the paddlewheel.2. Heating of a gas by a resistance heaterA piston-cylinder device initially contains 0.5 m 3of nitrogen gas at 400 kPa and 27℃. An electric heater within the device is turned on and is allowed to pass a current of 2 A for 5 min from a 120-V source. Nitrogen expands at constant pressure, and a heat loss of 2800 J occursduring the process. Determine the final temperature of nitrogen.3. Cooling of an iron block by watercontains 0.5 A 50-kg iron block at 80℃ is dropped into an insulated tanks that equilibriumm 3of liquid water at 25℃. Determine the temperature when thermal is reached.4. Deceleration of air in a diffuserAir at 10℃ and 80 kPa enter the diffuser of a jet engine steadily with a velocity of 200 m/s. The inlet area of the diffuser is 0.4 m 2. The air leaves the diffuser with a velocity that isvery small compared with the inlet velocity. Determine (a) themass flow rate of the air and (b) the temperature of the air leaving the diffuser.5. Energy balance in turbineConsider a gas turbine power plant with air as the working fluid, Air enters at 100 kPa, 20ºC (ρ=1.19 kg/m 3), with a velocity of 130m/s through an opening 0.112 m 2cross-sectional area. After being compressed, heated and expanded through a turbine, the air leaves at 180 kPa, 150ºC (ρ=1.48 kg/m 3), through an opening of 0.100 m 2cross-sectional area. The power output of the plant is 375 kW. The internal energy and enthalpy of the air are given in kJ/kg byU=0.717T and h=1.004T, where T istemperature on the Kelvin scale. Determine the net amountofheatadded tothe air in kJ/kg.FIGURE 2-1FIGURE 2-2FIGURE 2-3FIGURE 2-42113111112.0/130/19.120100mA s m c m k g CT k Pa p f ===︒==ρ2112WsQ223222100.0/48.1150180m A m kg CT kPap ==︒==ρFIGURE 2-56. Air is compressed in a frictionless steady-flow processAir is compressed in a frictionless steady-flow process from 90 kPa, 150ºC (v=0.918 m 3/kg) to 130 kPa in such a manner that p(v+0.250)=constant, where v is in m 3/kg, inlet velocity is negligible small, and discharge velocity is 110 m/s. Calculate the work required per kilogram of air.7. Mixture processA mixture of air and water vapor with an enthalpy of 120 kJ/kg enters the dehumidifying section of an air-conditioning system at a rate of 320 kg/hr, liquid water drains out of the dehumidifier with an enthalpy of 42 kJ/kg at a rate of 7.0 kg/hr. An air vapor mixture leaves with an enthalpy of 47 kJ/kg.Determine the rate of heat removal from the fluids passing through the dehumidifier.8. Reviews problemA piston-cylinder device contains helium gas initially at 150 kPa, 20℃, and0.5 m 3. The helium is now compressed in a polytropic process (PV n=constant) to 400 kPa and 140℃. Determine the heat loss or gainduring this process.9. Two rigid tanks are connected by a valve. Tank Acontains 0.2 m 3of water at 400 kPa and 80 percent quality. Tank B contains 0.5 m 3of water at 200 kPa and 250℃. The valve is now opened, and the two tanks eventually come to the same state. Determine the pressure and the amount of heat transfer whenthe system reaches thermal equilibrium with the surrounding at 25 ℃.10. Consider a well-insulated horizontal rigid cylinder that isdividedm m 112233dehumidifierkgkJ h hrkg /126/32011==∙kgkJ h hr kg /42/0.722==∙kgkJ h /473=FIGURE 2-7FIGURE 2-8W in1122/918.0901311===f c kg m v kPa p sm c kPa p f /11013022==FIGURE 2-6FIGURE 2-9FIGURE 2-10into two compartments by a piston that is free to move but does not allow either gas to leak into the other side. Initially, one side of the piston contains 1 m 3of N 2 gas at 500 kPa and 80℃ while the other side contains 1 m 3of He gas at 500 kPa and 25℃. Now thermal equilibrium is established in the cylinder as a result of heat transfer through the piston. Using constant specific heats at room temperature, determine the final equilibrium temperature in the cylinder. What would your answer be if the piston were not free to move?工程热力学与传热学第二章 热力学第一定律 习题1. 一绝热刚性容器,中间用隔板分为两部分,左边盛有空气,右边为真空,抽掉搁板,空气将充满整个容器。
双语物理化学各章习题

第一章 气体的pVT 性质一、选择题1.在温度恒定为25℃,体积恒定为25dm 3的容器中,含有0.65mol 的理想气体A ,0.35mol 的理想气体B 。
若向容器中再加入0.4mol 的理想气体D ,则B 的分压力p B ( ),分体积V B *( )。
(A)变大;(B)变小;(C)不变;(D)无法确定2.由A(g)和B(g)形成的理想气体混合系统,总压p=p A +p B ,,V=V A *+V B *,n=n A +n B ,下列各式中,只有式( )是正确的(A) p B V B *=n B RT ;(B) pV A *=nRT ;(C) p B V=n B RT ;(D) p A V A *=n A RT3.(1)在一定的T,P 下(假设高于波义尔温度TB):V m (真实气体)( )V m (理想气体);(2) 在n ,T ,V 皆为定值的条件下p (范德华气体)( )p (理想气体);(3) 在临界状态下,范德华气体的的压缩因子Z C ( )1(A)>;(B)=;(C)<;(D)不能确定4.已知A(g)和B(g)的临界温度之间的关系为:T c (A)>T c (B);临界压力之间的关系为:p c(A)<p c (B),则A,B 气体的范德华常数a 和b 之间的关系必然是 a(A)( )a(B) ; b(A)( )b(B)。
(A)>;(B)<;(C)=;(D)不能确定5.在一个密闭的容器中放有足够多的某纯液态物质,在相当大的温度范围内皆存在气、液两相平衡。
当温度逐渐升高时液体的饱和蒸气压p*( ),饱和液体的摩尔体积 V m (l)( );饱和蒸气的摩尔体积V m (g)( );△V=V m (g)-V m (l)(A)变小;(B) 变大 ;(C) 不变; (D)无一定变化规律6.在t=-50℃,V=40dm 3的钢瓶内纯氢气的压力p=12.16×106Pa ,已知氢气的临界温度为-239.9℃,此时钢瓶内氢气的相态必然是( )。
工程热力学第三版答案【英文】第4章
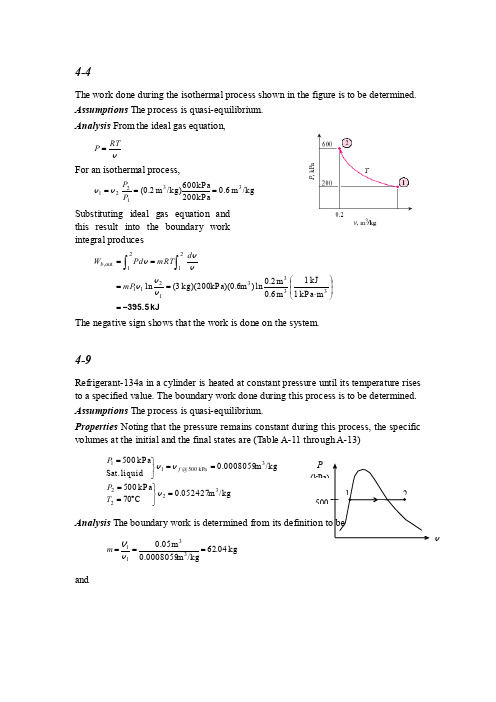
4-4The work done during the isothermal process shown in the figure is to be determined. Assumptions The process is quasi-equilibrium. Analysis From the ideal gas equation,vRTP =For an isothermal process,/kg m 0.6kP a200kP a 600/kg)m (0.2331221===P P v v Substituting ideal gas equation andthis result into the boundary work integral produceskJ395.5-=⎪⎪⎭⎫⎝⎛⋅====⎰⎰333312112121out ,m kP a 1kJ 1m 0.6m 0.2ln )m kP a)(0.6 kg)(200 (3lnv v v vvv mP d mRTd P W b The negative sign shows that the work is done on the system.4-9Refrigerant-134a in a cylinder is heated at constant pressure until its temperature risesto a specified value. The boundary work done during this process is to be determined. Assumptions The process is quasi-equilibrium.Properties Noting that the pressure remains constant during this process, the specific volumes at the initial and the final states are (Table A-11 through A-13)/kg m 0.052427C 07kP a 005/kg m 0.0008059liquid Sat.kP a 00532223kPa 005@11=⎭⎬⎫︒====⎭⎬⎫=v v v T P P fAnalysiskg 04.62/kgm 0.0008059m 0.053311===v V m andvPkJ1600=⎪⎪⎭⎫⎝⎛⋅-=-=-==⎰33121221out ,m kPa 1kJ1/kg m 0.0008059)427kPa)(0.052 kg)(500 (62.04)()( v v V VV mP P d P W b Discussion The positive sign indicates that work is done by the system (work output).4-23A saturated water mixture contained in a spring-loaded piston-cylinder device is heated until the pressure and temperature rises to specified values. The work done during this process is to be determined. Assumptions The process is quasi-equilibrium. Analysis The initial state is saturated mixture at 90︒C. The pressure and the specific volume at this state are (Table A-4),/kgm 23686.0)001036.03593.2)(10.0(001036.0kP a183.70311=-+=+==fgf x P v v vThe final specific volume at 800 kPa and 250°C is (Table A-6)/kg m 29321.032=vSince this is a linear process, the work done is equal to the area under the process line1-2:kJ24.52=⎪⎭⎫ ⎝⎛⋅-+=-+==331221out ,m kPa 1kJ 1)m 23686.01kg)(0.2932 (12)kPa 800(70.183)(2Area v v m P P W b4-29An insulated rigid tank is initially filled with a saturated liquid-vapor mixture of water. An electric heater in the tank is turned on, and the entire liquid in the tank is vaporized. The length of time the heater was kept on is to be determined, and the process is to be shown on a P-v diagram.Assumptions 1 The tank is stationary and thus the kinetic and potential energy changes are zero. 2 The device is well-insulated and thus heat transfer is negligible. 3The energy stored in the resistance wires, and the heat transferred to the tank itself is negligible.Analysis We take the contents of the tank as the system. This is a closed system since no mass enters or leaves. Noting that the volume of the system is constant and thus there is no boundary work, the energy balance for this stationary closed system can be expressed as)(V 0)=PE =KE (since )(1212in ,energiesetc. potential, kinetic,internal,in Change systemmassand work,heat,by nsfer energy tra Net out in u u m t I Q u u m U W E E E e -=∆=-=∆=∆=-The properties of water are (Tables A-4 through A-6)()[]()k J /k g 2569.7v a p o rs a t ./k g m 0.29065k J /k g980.032052.30.25466.97/km 0.290650.0010531.15940.250.001053k J/k g 3.2052,97.466/kgm 1.1594,001053.025.0kP a 150/kg m 0.29065@2312113113113==⎪⎭⎪⎬⎫===⨯+=+==-⨯+=+=====⎭⎬⎫==g fg f fg f fg f g f u u u x u u x u u x P v v v v v v v Substituting,min60.2==∆⎪⎪⎭⎫⎝⎛-=∆s 33613kJ/s 1VA 1000.03)kJ/kg 980kg)(2569.7 (2)A 8)(V 110(t t4-39A saturated water mixture contained in a spring-loaded piston-cylinder device isheated until the pressure and volume rise to specified values. The heat transfer and the work done are to be determined.Assumptions 1 The cylinder is stationary and thus the kinetic and potential energy changes are zero. 2 There are no work interactions involved other than the boundary work. 3 The thermal energy stored in the cylinder itself is negligible. 4 The compression or expansion process is quasi-equilibrium. Analysis We take the contents of the cylinder as the system. This is a closed system since no mass enters or leaves. The energy balance for this stationary closed system can be expressed asv)(0)=PE =KE (since )(12ou ,in 12ou ,in energiesetc. potential, kinetic,internal,in Change systemmassand work,heat,by nsfer energy tra Net out in u u m W Q u u m U W Q E E E t b t b -+=-=∆=-∆=-The initial state is saturated mixture at 75 kPa.The specific volume and internal energy at this state are (Table A-5),kJ/kg30.553)8.2111)(08.0(36.384/kgm 1783.0)001037.02172.2)(08.0(001037.0131=+=+==-+=+=fg f fg f xu u u x v v vThe mass of water iskg 22.11/kgm 1783.0m 23311===v V m The final specific volume is/kg m 4458.0kg22.11m 53322===m V vThe final state is now fixed. The internal energy at this specific volume and 225 kPa pressure is (Table A-6) kJ/kg 4.16502=u Since this is a linear process, the work done is equal to the area under the process line 1-2:kJ 450=⎪⎭⎫⎝⎛⋅-+=-+==331221out ,m kP a 1kJ 1)m 2(52)kP a 225(75)(2Area V V P P W b Substituting into energy balance equation giveskJ 12,750=-+=-+=kJ/kg )30.553kg)(1650.4 22.11(kJ 450)(12out ,in u u m W Q b4-43Two tanks initially separated by a partition contain steam at different states. Now thepartition is removed and they are allowed to mix until equilibrium is established. The temperature and quality of the steam at the final state and the amount of heat lost from the tanks are to be determined.Assumptions 1 The tank is stationary and thus the kinetic and potential energy changes are zero. 2 There are no work interactions.Analysis (a ) We take the contents of both tanks as the system. This is a closed system since no massenters or leaves. Noting that the volume of the system is constant and thus there is no boundary work, the energy balance for this stationary closed system can be expressed as[][]0)=PE =KE (since )()(1212out energiesetc. potential, kinetic,internal,in Change systemmassand work,heat,by nsfer energy tra Net out in =-+-=∆+∆=-∆=-W u u m u u m U U Q E E E B A B AThe properties of steam in both tanks at the initial state are (Tables A-4 through A-6)kJ/kg 7.2793/kg m 25799.0C 300kPa 1000,13,1,1,1==⎪⎭⎪⎬⎫︒==A A A A u T P v ()[]()kJ/kg4.15954.19270.50.66631/kg m 0.196790.0010910.392480.500.001091kJ/kg 4.1927,66.631/kgm .392480,001091.050.0C 1501,131,131,1=⨯+=+==-⨯+=+=====⎭⎬⎫=︒=fg f B fg f B fg f g f B u x u u x u u x T v v v v vThe total volume and total mass of the system arekg523m 106.1/kg)m 19679.0kg)( 3(/kg)m 25799.0kg)( 2(333,1,1=+=+==+=+=+=B A B B A A B A m m m m m v v V V VNow, the specific volume at the final state may be determined/kg m 22127.0kg5m 106.1332===m Vvwhich fixes the final state and we can determine other properties()kJ/kg8.12821.19820.3641.11561001073.060582.0001073.022127.0/kg m 22127.0kPa 0032222kPa 300 @sat 2322=⨯+=+==--=--=︒==⎪⎭⎪⎬⎫==fg f fg f u x u u x T T P 0.3641C 133.5v v v v v (b ) Substituting,[][]kJ 3959kJ/kg )4.15958.1282(kg) 3(kJ/kg )7.27938.1282(kg) 2()()(1212out -=-+-=-+-=∆+∆=-BA B A u u m u u m U U QorkJ 3959=out Q4-60The air in a rigid tank is heated until its pressure doubles. The volume of the tank and the amount of heat transfer are to be determined.Assumptions 1 Air is an ideal gas since it is at a high temperature and low pressure relative to its critical point values of -221︒F and 547 psia. 2 The kinetic and potential energy changes are negligible, ∆∆pe ke ≅≅0. 3 Constant specific heats at room temperature can be used for air. This assumption results in negligible error in heating and air-conditioning applications. Properties The gas constant of air is R = 0.3704 psia.ft 3/lbm.R (Table A-1E).Analysis (a3ft 80.0=⋅⋅==psia50R) R)(540/lbm ft psia 4lbm)(0.370 (20311P mRT V(b) We take the air in the tank as our system. The energy balance for this stationary closed system can be expressed as)()(1212in in energiesetc. potential, kinetic, internal,in Change systemmassand work,heat,by nsferenergy tra Net out in T T mc u u m Q UQ E E E -≅-=∆=∆=-vThe final temperature of air isR 1080R) (540211222211=⨯==−→−=T P P T T P T P V V The internal energies are (Table A-17E)u u u u 12====@@540R 1080R 92.04Btu /lbm 186.93Btu /lbmSubstituting, Q in = (20 lbm)(186.93 - 92.04)Btu/lbm = 1898 BtuAlternative solutions The specific heat of air at the average temperature of T avg = (540+1080)/2= 810 R = 350︒F is, from Table A-2Eb, c v ,avg = 0.175 Btu/lbm.R. Substituting,Q in = (20 lbm)( 0.175 Btu/lbm.R)(1080 - 540) R = 1890 BtuDiscussion Both approaches resulted in almost the same solution in this case.4-64A student living in a room turns her 150-W fan on in the morning. The temperature in the room when she comes back 10 h later is to be determined.Assumptions 1 Air is an ideal gas since it is at a high temperature and low pressure relative to its critical point values of -141︒C and 3.77 MPa. 2 The kinetic andQpotential energy changes are negligible, ∆∆ke pe ≅≅0. 3 Constant specific heats at room temperature can be used for air. This assumption results in negligible error in heating and air-conditioning applications. 4 All the doors and windows are tightly closed, and heat transfer through the walls and the windows is disregarded.Properties The gas constant of air is R = 0.287 kPa.m 3/kg.K (Table A-1). Also, c v = 0.718 kJ/kg.K for air at room temperature (Table A-2).Analysis We take the room as the system. This is a closed system since the doors and the windows are said to be tightly closed, and thus no mass crosses the system boundary during the process. The energy balance for this system can be expressed as)()(1212,,energiesetc. potential, kinetic,internal,in Change systemmassand work,heat,by nsfer energy tra Net T T mc u u m W UW E E E in e in e out in -≅-=∆=∆=-vThe mass of air iskg174.2K) K)(288/kg m kP a (0.287)m kP a)(144 (100m 14466433113=⋅⋅===⨯⨯=RT P m V VThe electrical work done by the fan isW W t e e==⨯= ∆(0.15kJ /s)(103600s)5400kJ Substituting and using the c v value at room temperature, 5400 kJ = (174.2 kg)(0.718 kJ/kg ⋅︒C)(T 2 - 15)︒CT 2 = 58.2︒CDiscussion Note that a fan actually causes the internal temperature of a confinedspace to rise. In fact, a 100-W fan supplies a room with as much energy as a 100-W resistance heater.4-69Carbon dioxide contained in a spring-loaded piston-cylinder device is heated. The work done and the heat transfer are to be determined.Assumptions 1 CO 2 is an ideal gas since it is at a high temperature relative to its critical temperature of 304.2 K. 2 The kinetic and potential energy changes are negligible, 0pe ke ≅∆≅∆. Properties The properties of CO 2 are R = 0.1889 kJ/kg ⋅K and c v = 0.657 kJ/kg ⋅K (Table A-2a ).PAnalysis We take CO 2 as the system. This is a closed system since no mass crosses the boundaries of the system. The energy balance for this system can be expressed as)(12out ,in energiesetc. potential, kinetic,internal,in Change systemmassand work,heat,by nsfer energy tra Net out in T T mc U W Q E E E b -=∆=-∆=-vThe initial and final specific volumes are33111m 5629.0k P a 100K) K)(298/kg m kPa kg)(0.1889 (1=⋅⋅==P mRT V 33222m 1082.0k P a1000K)K)(573/kg m kPa kg)(0.1889 (1=⋅⋅==P mRT V Pressure changes linearly with volume and the work done is equal to the area underthe process line 1-2:kJ1.250m kPa 1kJ 1)m 5629.0(0.10822)kPa1000(100)(2Area 331221out ,-=⎪⎪⎭⎫⎝⎛⋅-+=-+==V V P P W b Thus,kJ 250.1=in ,b WUsing the energy balance equation,kJ 4.69K )25K)(300kJ/kg 657.0(kg) 1(kJ 1.250)(12out ,in -=-⋅+-=-+=T T mc W Q b vThus,kJ 69.4=out Q4-76Air at a specified state contained in a piston-cylinder device with a set of stops is heated until a final temperature. The amount of heat transfer is to be determined.Assumptions 1 Air is an ideal gas since it is at a high temperature relative to its critical temperature of 304.2 K. 2 The kinetic and potential energy changes are negligible, 0pe ke ≅∆≅∆. Properties The properties of air are R = 0.287 kJ/kg ⋅K and c v = 0.718 kJ/kg ⋅K (Table A-2a ). Analysis We take air as the system. This is a closedsystem since no mass crosses the boundaries of the system. The energy balance for this system can be expressed as)(12out ,in energiesetc. potential, kinetic, internal,in Change systemmassand work,heat,by nsferenergy tra Net out in T T mc U W Q E E E b -=∆=-∆=-vThe volume will be constant until the pressure is 300 kPa:K 900kP a100kP a 300K) (3001212===P P T T The mass of the air iskg 4646.0K)K)(300/kg m kPa (0.287)m kPa)(0.4 (10033111=⋅⋅==RT P m V The boundary work done during process 2-3 iskJ04900)K -K)(1200/kg m kP a (0.287)kg 4646.0()()(323232out ,=⋅⋅=-=-=T T mR P W b V V Substituting these values into energy balance equation,kJ 340=-⋅+=-+=K )300K)(1200kJ/kg 718.0(kg) 4646.0(kJ 40)(13out ,in T T mc W Q b v4-85An egg is dropped into boiling water. The amount of heat transfer to the egg by the time it is cooked is to be determined.Assumptions 1 The egg is spherical in shape with a radius of r 0 = 2.75 cm. 2 The thermal properties of the egg are constant. 3 Energy absorption or release associated with any chemical and/or phase changes within the egg is negligible. 4 There are no changes in kinetic and potential energies.Properties The density and specific heat of the egg are given to be ρ = 1020 kg/m 3 and c p = 3.32 kJ/kg.︒C.Analysis We take the egg as the system. This is a closes system since no mass enters or leaves the egg. The energy balance for this closed system can be expressed as)()(1212egg in energiesetc. potential, kinetic,internal,in Change systemmassand work,heat,by nsfer energy tra Net out in T T mc u u m U Q E E E -=-=∆=∆=-Then the mass of the egg and the amount of heat transfer becomeBoilingPV (m 3)kJ 21.2=︒-︒=-=====C )880)(C kJ/kg. 32.3)(kg 0889.0()(kg0889.06m ) 055.0()kg/m 1020(612in 333T T mc Q D m p ππρρV。
工程热力学与传热学习题(英文版):第五章 水蒸气与湿空气

第五章 水蒸气和湿空气水蒸气 英文习题1. Volume and energy change during evaporationA mass of 200 g of saturated liquid water is completely vaporized at constant pressure of 100 kPa. Determine (a) the volume change and (b) the amount of energy added to the water.2.Pressureand volume of a mixtureA rigid tank contains 10 kg of water at 90℃. If 8 kg of the water is in the liquid form and rest is in thevapor form. Determine (a) the pressure in the tank and (b) the volume of the tank.3. Properties of saturated liquid-vapor mixtureAn 80-L vessel contains 4 kg of refrigerant-134a at a pressure of 160 kPa. Determine (a) the temperature of the refrigerant, (b) the quality, (c) the enthalpy of the refrigerant, and (d) the volume occupied by the vapor phase.4.Charging of a rigid tankby steamA rigid insulated tank that is initially evacuated is connected through a valve to a supply line that carries steam at 1 MPa and 300℃. Now the valve is opened, and steam is allowed to flow slowly into the tank until the pressure reaches 1 MPa, at which point the valve is closed.Determine the final temperatureFIGURE 5-1FIGURE 5-2FIGURE 5-3FIGURE 5-4of the steam in the tank.湿空气 英文习题1. The amount of water vapor in room air100 kPa A 5-m ×5-m×3-m room shown in Fig.5-1 contains air at 25℃ and at a relative humidity of 75 percent. Determine (a) the partial pressure of dry air, (b) the specific humidity, (c) the enthalpy per unit mass of the dry air,and (d) the masses of the dry air and water vapor in the room.2. Fogging of the windows in a houseIn cold weather, condensation frequently occurs on the inner surfaces of the windows due to the lower air temperatures near the window surface. Consider a house, shown in Fig.5-6, that contains air at 20℃ and 75 percent relative humidity. At what window temperature will themoisture in the air start condensing on the inner surfaces of thewindows?3. The specific and relative humidity of airThe dry and the wet-bulb temperatures of atmospheric air at 1 atm (101.325 kPa) pressure are measured with a sing psychrometer and determined to be 25℃ and 15℃, respectively. Determine (a0 the specific humidity, (b0 the relative humidity, and © the enthalpy of the air.4. Heating and humidification of airAn air-conditioning system is to take in outdoor air at 10℃ and 30 percent relative humidity at a steady rate of 45 m 3/min and to condition it to 25℃ and 60 percent relative humidity. The outdoor air is first then heated to 22℃ in the heating section and humidified by the injection of hot steam in the humidifying section. Assuming the entire process takes place at a pressure of 100 kPa, determine (a) the rate of heat supply in the heating section and (b) the mass flow rate of the steamrequired in the humidifying section.5. Cooling and dehumidification of airAir enters a window air conditioner at 1 atm, 30℃, and 80 percent relative humidity at rate of 10 m 2/min, and it leaves as saturated air at 14℃. Part of the moisture in the air that condenses during the process is also removed at 14℃. Determine the rates of heat and moisture removal from the air.工程热力学与传热学第五章 水蒸气与湿空气 习题FIGURE 5-5FIGURE 5-6FIGURE 5-7习题1.热水泵必须安装在热水容器下面距容器有一定高度的地方,而不能安装在热水容器的上面,为什么?2.锅炉产生的水蒸气在定温过程中是否满足q=w的关系?为什么?3.有无0℃或低于0℃的蒸汽存在?有无高于400℃的水存在,为什么?4.25MPa的水,是否也象1MPa的水那样经历汽化过程?为什么?5.dh=c p dT适用于任何工质的定压过程,水蒸气定压汽化过程中dT=0,由此得出结论,水定压汽化时dh=c p dT=0,此结论是否正确,为什么?6.试解释湿空气,湿蒸汽,饱和湿空气。
工程热力学与传热学习题(英文版):第四章 热力学第二定律

must be obtained or discarded into the river ?
3. Heat rejection by a refrigerator
The food compartment of a refrigerator, shown in Fig 4-2, is maintained at 4℃ by removing heat from it at a rate of 360 kJ/min. If the required power input to the refrigerator is 2 kW, determine (a) the coefficient of performance of the refrigerator and (b) the rate of heat rejection to the room that houses the refrigerator.
allowed process.
12. The concept of lost work
If 1000 kJ of energy is transferred from a work reservoir to a heat at 373K, determine (a) the amount of entropy generation and (b) amount of lost work with the environment at 300K.
The
power output of the heat engine is 180 kW. Determine the
reversible power and the irreversibility rate for this process.
《物理双语教学试题》Fundamentals of Physics - 大一 第2学期 Test 4 力学 热学 电学 计算

Fundamentals of Physics-Test 4EXAMINEE NAME:Solve 8 of the following 10 problems.1.The position of an electron is given by k j t i t r 0.20.40.32+-= (where t is inseconds and the coefficients have the proper units for r to be in meters). Find theexpressions for (1) its velocity )(t v , and (2) its acceleration )(t a .2.Several planets possess nearly circular surrounding rings.Consider a homogeneous ring of mass M and radius R. (1)What gravitational attraction does it exert on a particle ofmass m located a distance x from the center of the ringalong its axis? (2) Suppose the particle falls from rest asa result of the attraction of the ring of matter. Find an expression for the speed with which it passes through the center of the ring.3.Two blocks of mass 1m and 2m (21m m <) are connected by a massless cord thatis wrapped around a uniform disk of mass M and radius R,whose rotational inertia about the axis is 2/2MR I =. Thedisk can rotate without friction about a fixed horizontal axisthrough its center; the cord cannot slip on the disk. Thesystem is released from rest. Find (1) the magnitude of theacceleration of the blocks, (2) the tension 1T in the cord at the left, and (3) thetension 2T in the cord at the right.4.A sinusoid transverse wave is travelingalong a string toward decreasing x. Thefigure shows a plot of the displacement asa function of position at time t=0. Thestring tension is N 6.3, and its lineardensity is m g /25. Find (1) theamplitude, (2) the wavelength, (3) thewave speed, and the period of the wave. (4) Write an equation describing the traveling wave.5.Show that the ideal gas equation nRT pV =can be written in the following alternative form M RT p /ρ=, whereρ is the mass density of the gas and M the molar mass.6.One mole of an ideal mono-atomic gas is takenthrough the cycle in the Fig. (1) How much workis done by the gas in going from state a to state calong path abc? What are the changes in internalenergy and entropy in going from b to c? Expressall answers in terms of the pressure 0p , volume 0V , and temperature 0T of statea.7.4 electrons are equally spaced and fixed around a circle of radius R. Relative to V=0 at infinity, what are the electric potential and electric field at the center of the circle due to these electrons?8.A non-conducting rod of length Lhas charge -q uniformly distributedalong its length. (1) What is the linear charge density of the rod? (b) What is the electric field at point P, a distancea from the end of the rod?9.A particle of charge magnitude q and mass m moving perpendicular to a uniformmagnetic field B at speed v . The particle will move in a circle. Find (1) theradius of the circular path, (2) the period of the motion.10. A coil C of N turns is placed around a longsolenoid S of radius and n turns per unit length, asin the Fig. Show that the mutual inductance for thecoil-solenoid combination is given bynN R M 20πμ=.。
《物理双语教学试题》Fundam...

《物理双语教学试题》Fundam...Fundamentals of Physics-Test 2EXAMINEE NAME:I. Fill in each of the following blanks with an appropriate expression or quantity.(48)1. The position of an electron is given by k j t i t r 0.20.60.22+-= (where t is in seconds and the coefficients have the proper units for r to be in meters). (a) The velocity )(t v and the acceleration )(t a are (1) and (2) respectively for the electron. (b) In unit-vector notation, The velocity v and the acceleration a are, att=2.0s, (3) and (4) .2. A wheel rotates with an angular acceleration given by 2364bt at -=α, where t is the time and a and b are constant. If the wheel has an initial angular speed 0ω, then (a) the equation for the angular speed is (5) , and (b) the angular displacement of the wheel is (6) as functions of time.3. An oscillator consists of a block attached to a spring (k = 400 N/m). At some time t, the position (measured from the system’s equilibrium location), velocity, and acceleration of the block are ,/6.13,100.0s m v m x -== and 2/123s m a -=. Then(a) the frequency of the oscillation is (7) , (b) the mass of the block is (8) , and the amplitude of the motion is (9) .4. The equation of a transverse wave traveling along a very long string is given by ),0.402.0sin(0.6t x y ππ+= where x and y are expressed in centimeters and t is in seconds. So (a) the amplitude is (10) , (b) the wavelength is (11) , (c) the frequency is (12) , (d) the speed is (13) , (e) the maximum transverse speed of a particle in the string is (14) ,5. Suppose 2.00 mol of an ideal diatomic gas, with molecular rotation but not oscillation, experiences a temperature increase of 60.0 K under constant-pressure conditions. (a) The heat added to the gas is (15) . (b) The increase in internal the kinetic energy is(16) .II. Solve the following problems. (52)1.Force j N i xN F )4()3(+=, with x in meters, acts on a particle, changing only the kinetic energy of the particle. (a) How much work is done on the particle as it moves from coordinates (2m, 3m) to (3m, 0m)? (b) How much the kinetic energy of the particle is changed during the motion? (8)2. A uniform spherical shell of mass Mand radius R rotates about a vertical axison frictionless bearings as shown in thefigure. A massless cord passes around theequator of the shell, over a pulley ofrotational inertia I and radius r, and isattached to a small object of mass m.There is no friction on the pulley ’s axle; the cord does not slip on the pulley. Whatis the speed of the object after it has fallen a distance h from rest? Use work-energy consideration. (14)3. A string oscillates according to the equation].)40cos[(])3)[sin(50.0('11t s x cm cm y --=ππ(a) What are the amplitude and speed of the two waves (identical except for direction of travel) whose superposition gives this oscillation? (b) What is the distance between nodes? (c) What is the speed of a particle of the string at the position x = 1.5 cm when t = 9s/8? (15)4. One mole of an ideal gas is used as the working substance of an engine that operates on the cycle shown as the right figure. BC and DA are reversible adiabatic processes. (a) Is the gas monatomic, diatomic, or poly-atomic? (b) the heat added to the gas in one cycle. (c) the heat leaving the gas in one cycle. (d) the efficiency of the cycle, and (e) the change in entropy of the gas per cycle. (15)。
材料热力学习题答案2

材料热力学习题答案2The problems of the second law1 The solar energy flux is about 4J cm2/min. in no focusing collector the surface temperature can reach a value of about 900℃. If we operate a heat engine using the collector as the heat source and a low temperature reservoir at 25℃, calculate the area of collector needed if the heat engine is to produce 1 horse power. Assume the engine operates at maximum efficiency. (2.1)TH?TL(900?25)104W?QH??4?StTH900?27360SolutionP?W?746(W)tS?0.664(m2)2 A refrigerator is operated by 0.25 hp motor. If the interior of the box is to be maintained at -20℃ ganister a maximum exterior temperature of 35℃, what the maximum heat leak (in watts) into the box that can be tolerated if the motor runs continuously? Assume the coefficient of performance is 75% of the value for a reversible engine. (2.2)W?75%Solution:P?0.75TH?TLQHTHTH?TLPLTLPL?4273?20??0.25?746?1144(W)335?203 suppose an electrical motor supplies the work to operate a Carnot refrigerator. The interior of the refrigerator is at 0℃. Liquid water is taken in at 0℃ and converted to ice at 0℃. To convert 1 g of ice to 1 g liquid. △H=334J/g is required. If the temperature outside the box is 20℃, what mass of ice can be produced in one minute by a 0.25 hp motor running continuously? Assume that the refrigerator is perfectly insulated and that the efficiencies involved have their largest possible value. (2.3)P?TH?TLPLTLSolution: PL?273?0.25?746?334m 20M?60m?457(g)4 under 1 atm pressure, helium boils at 4.126K. The heat of vaporizationis 84 J/mol what sizemotor (in hp) is needed to run a refrigerator that must condense 2 mol of gaseous helium at 4.126k to liquid at the same temperature in one minute? Assume that the ambient temperature is 300K and that the coefficient of performance of the refrigerator is 50% of the maximum possible. (2.4)W?50%TH?TLQLTLTH?TL300?4.21684?2 PL??TL4.21660Solution:0.5P'?P?P'?393(W)?0.52(hp)5 if a fossil fuel power plant operating between 540 and 50℃ provides the electrical power torun a heat pum p that works between 25 and 5℃, what is the amount of heat pumped into the house per unit amount of heat extracted from the power plant boiler.(a) assume that the efficiencies are equal to the theoretical maximum values(b) assume the power plant efficiency is 70% of maximum and that coefficient of performance ofthe heat pump is 10% of maximum(c) if a furnace can use 80% of the energy in fossil foe to heat the house would it be moreeconomical in terms of overall fissile fuel consumption to use a heat pump or a furnace ? do the calculations for cases a and b (2.5)solution:TH,1?TL,1(a)PPH,11?TH,1P2?TH,2?TL,2PH,2TH,2(b)PH,2?0.6286PH,1P1?P2540?5025?5PH,1?PH,2540?273273?25PH,2?8.98PH,1(c)aisok,bisnot.6cal culate △U and △S when 0.5 mole of liquid water at 273 K is mixed with 0.5 mol of liquid water at 373 K and the system is allowed to reach equilibrium in an adiabatic enclosure. Assume that Cp is 77J /(mol K) from 273K to 373K (2.6) Solution:?U?0(J)TT323323?S?n1CPln(E)?n2CPln(E)?0.5CPln()?0.5CPln()?0.933(J/K)T1T23732737 A modern coal burning power plant operates with a steam out let from the boiler at 540℃ and acondensate temperature of 30℃.(a) what is the maximum electrical work that can be produced by the plant per joule of heatprovided to the boiler?(b) How many metric tons (1000kg) of coal per hour is required if the plant out put is to be500MW (megawatts). Assume the maximum efficiency for the plant. The heat of combustionof coal is 29.0 MJ/k g(c) Electricity is used to heat a home at 25℃ when the out door temperature is 10℃ by passinga current through resistors. What is the maximum amount of heat that can be added to the home per kilowatt-hour of electrical energy supplied? (2.7)(a)W?Solution:(b)TH?TL540?30QH?1?0.89(J)TH540?30TL?500?3600TH?TL(c)W?TH?TLQHTH273?251?19.9(J)25?1029.0mQH?m?69371(kg)?69.3(ton)8 an electrical resistor is immersed in water at the boiling temperature of water (100℃) th e electrical energy input into the resistor is at the rate of one kilowatt(a) calculate the rate of evaporation of the water in grams per second if the water container isinsulated that is no heat is allowed to flow to or from the water except for that provided by the resistor(b) at what rate could water could be evaporated if electrical energy were supplied at the rate of 1kw to a heat pump operating between 25 and 100℃data for water enthalpy of evaporation is 40000 J/mol at 100℃; m olecular weight is 18g/mol; density is 1g/cm3 (2.8)m40000?1000,m?0.45(g)18solution:m100?273(b)40000?1000,m?2.23(g)18100?25(a)9 some aluminum parts are being quenched (cooled rapidly ) from 480℃ to -20℃ by immersingthem in a brine , which is maintained at -20℃ by a refrigerator. The aluminum is being fed into the brine at a rate of one kilogram per minute. The refrigerator operates in an environment at 30℃; that is the refrigerator mayreject heat at 30℃. what is them minus power rating in kil owatts, of motor required to operate the refrigerator?Data for aluminum heat capacity is 28J/mol K; Molecular weight 27g/mol (2.9)100028?(480??20)27Solution:TH?TL30??20PW?PL?PL?102474(W)?102.5(kW)TL273?20PL?10 an electric power generating plant has a rated output of 100MW. The boiler of the plantoperates at 300℃. The condenser operates at 40℃(a) at what rate (joules per hour) must heat be supplied to the boiler?(b) The condenser is cooled by water, which may under go a temperaturerise of no more than10℃. What volume of cooling water in cubic meters per hour, is require to operate the plant?(c) The boiler tempeture is to be raised to 540℃,but the co ndensed temperature and electricoutput will remain the same. Will the cooling water requirement be increased, decreased, or remain the same?Data heat capacity 4.184, density 1g/cm3 (2.10)(a)PH?TH300?2738P?10TH?TL300?408(b)Solution: ?2.2?10(W)QL?4.3?1011(J)V?10?10?4.184?QLV?1.03?104(m3)6QH?PHt?7.9?1011(J)(c)PH?TH540?2738P?10TH?TL540?40?1.626?108(W)no11 (a) Heat engines convert heat that is available at different temperature to work. They have beenseveral proposals to generate electricity y using a heat engine that operate on the temperature differences available at different depths in the oceans. Assume that surface water is at 20℃, that water at a great depth is at 4℃, and that both may be con sidered to be infinite in extent. How many joules of electrical energy may be generated for each joule of energy absorbed from surface water? (b) the hydroelectric generation of electricity use the drop height of water as the energy source. in a particular region the level ofriver drops from 100m above sea level to 70m above the sea level . what fraction of the potential energy change between those two levels may be converted into electrical energy? how much electrical energy ,in kilowatt-hours, may be generated per cubic meter of water that undergoes such a drop? (2.11)(a)W?Solution:TH?TL20?4QH?1?0.055(J)TH20?273mg?h(b)P??3600?1.06?106(kW/h)100012 a sports facility has both an ice rink and a swimming pool. to keep the ice frozen during the summer requires the removal form the rink of 105 KJ of thermal energy per hour. It has been suggested that this task be performed by a thermodynamic machine, which would be use the swimming pool as the high temperature reservoir. The ice in the rink is to be maintain at a temperature of �C15℃, and the swimming pool operates at 20℃, (a) what is thetheoretical minimum power, in kilowatts, required to run the machine? (b) how much heat , in joule per hour , would be supplied t the pool by this machine?(2.12)(a)P?Solution:TH?TL20?155PL?10/3600?3.77(kW)TL273?15273?205(b)QH?10?1.14?105(kJ)273?1513(a)2Al?N2?2AlN(b)?H?152940(cal/mol)solution:(c)?S?4.82?2?6.77?2?45.77??49.67(c al/molK)(d)?H?152940(cal/mol)?S?4.82?2?6.77?2?45.77?8.314ln10??68.81(cal/molK) 1440CP,ICEC?Hm?S?m(?dT???P,WATERdT)?10TTmT00solution:?(2.1ln273336273?40??4.184ln)12000 263273273?22574(J/K)15W?TH?TL300?77QL?1000?2896(J)TL77W2?70428(J)16W?W? 17TH?TL300?4.2QL?83.3?5866.7(J)TL4.2TH?TL300?4.2QH?(83.3?1.5?8.314(300?4.2))?371 9.4(J)TH300(a)?T?0?U?OQ??W?n??pdV?1?8.314?298ln10?5704(J)P(b)?S?nRln0?1?8.314?ln10?19.1(J /K)P(c)Q?0(d)yes18500?60?TH?TL20?0335m?335mTL273m?1222(g)感谢您的阅读,祝您生活愉快。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1) one mole of a monatomic ideal gas in the initial state T=273K, P=1atm, is subject to the following three processes, each of which is conducted reversibly.a. a doubling of its volume at constant pressureb.Then a doubling of its pressure at constant volumec.Then a return to the initial state along the path p=6.643*10-4V2+0.6667 Calculate the heat and work effects, which occur during each of the process. Solution: a)2.27kJ; b)0J; c)-0.0149J2) The initial state of a quantity of monatomic ideal gas is P=1atm V=1liter and T=373K. The gas is isothermally expanded to a volume of 2 liters and is then cooled at constant pressure to the volume V. this volume is such that a reversible adiabatic compression to a pressure of 1 atm returns the system its initial state. All of the changes of state are conducted revisable adiabatic. Calculate the total work done on or by the gasSolution: 1.3J3)two moles of a monatomic ideal gas are at contained at a pressure of 1 atm and temperature of 300K, 34.166j of heat are transferred to the gas as a result of which the gas expands and does 1216 joules of work against its surroundings. The process is reversible. Calculate the final temperature of the gas.Solution: 252.5K4)one mole of N2 gas is contained at 273 K and a pressure of 1 atm. The addition of 3000 joules of heat to the gas at constant pressure causes 832 joules of work to be done during the expansion*(. Calculate (a) the final state of the gas, (b) the value of △U and △H for the change of state. And (c) the values of C V for N2 . Assume that nitrogen behaves as an ideal gas. and that the above change of state is conducted reversibly.Solution: a)P=1atm, T=373K, V=30.6L; b) △H=3000J, △U=2168J ; (c)C V= 2.5R 5) ten moles of ideal gas, in the initial state P1 =10 atm, T1 =300K, are taken round the following cycle:a) a revisable change of state along a line path on the P-V diagram t the stateP=1atm T=300Kb) a reversible isobaric (constant pressure) compression to V=24.6 liters andc) a reversible constant volume process to P=10 atmhow much work is done on or by the system during the cycle? Is this work done on the system or by the systemSolution: 35KJ6) one mole of an ideal gas at 25℃and 1atm undergoes the following reversible conducted cycle:a)an isothermal expansion to 0.5 atm, followed byb)an isobaric expansion to 100℃ followed byc) an isothermal compression to 1 atm followed byd) an isobaric compression to 25℃the system then undergoes the following reversible cyclic processe) an isobaric expansion to100℃, followed byf) a decrease in pressure at constant volume to the pressure P atm, followed by g) an isobaric compression at P atm 24.5 liters, followed byh) an increase in pressure at constant volume to 1 atmcalculate the value of P which makes the work done on the gas during the first cycle equal to the work done by the gas during the second cycle.Solution: P=1.7atm7) two moles of an equal gas, in an initial state P=10 atm, V= 5 liters are taken reversibly in a clockwise direction around a circular path give by (V-10)2+(P-10)2=25. Calculate the amount of work done by the gas as a result of the process, and calculate the maximum and minimum temperature attained by the gas during the cycle.Solution: )(53.21010132525min)](2/510[),](2/510[)](2/510[),](2/510[3kJ W T l V atm whenP MAXT l V atm whenP ππ=××==−=−==+=+=−8) one mole of monatomic ideal gas undergoes a reversible expansion at constant pressure during which the entropy of the gas increase by 14.4J/K, and the gas absorbs 6236 joules of heat. Calculate the initial and final temperatures of the gas. N mole of second monatomic ideal gas undergoes a reversible isothermal expansion during which it doubles its volume, performs 1729 joules of work and increases its entropy by 5.763 J/K. Calculate N and the temperature at which the expansion was conducted.Solution: 1) T 0=300K, T=600K 2)N=1,T=300K9)calculate the change in enthalpy and the change in entropy when 1 mole of SiC is heated from 25℃ to 1000℃. The constant pressure molar heat capacity of SiC varies with temperature asC P =50.79+1.97*10-3T-4.92*106 T -1+8.20*10 8T -2J/mol KSolution: △S=59.63J/K10) One mole of copper at a uniform temperature of 0 is placed in thermal ℃contact with a second mole of copper which, initially, is at a uniform temperature of 100. Calculate the temperature of the 2 mole system which is contained in ℃an adiabatic enclosure when thermal equilibrium is attained. Why the common uniform temperature not exactly 50? How much heat is transferred, and how ℃much entropy is produced by the transfer? The constan pressure molar heat capacity of solid copper varies with temperature asC P =22.64+6.28*10-3T J/mol KSolution:T Te T T TT T T S K T T T e e 3733-3733-2-32-3] 106.28T ln 64.22[] 106.28T ln 64.22[)?(0]103.1422.64T []103.1422.64T [11×++×+=Δ==×++×+11)An ideal gas at 25℃has a volume of 10 liters at a pressure of 15atm, the constant volume molar heat capacity of the gas C V =1.5R if undergoes a)a reversible isothermal expansion to a pressure of 1 atm b) a reversible adiabatic expansion to a pressure of 1 atmCalculate (1) the final volume (V)of the system(2) the work (W) done by the system(3) the heat entering or leaving the system(4) the change in the enthalpySolution :(a)1)1L; 2)23.3KJ; 3)23.3KJ; 4)0(b)1)39.8L; 2)9.13KJ; 3)0; 4)15.3KJ12) An ideal gas at 300K has a volume of 15 liters at a pressure of 15atm, the constant volum molar heat capacity of the gas C V =1.5R ,when the gas undergoes a)a reversible isothermal expansion to a pressure of 10 atm b) a reversible adiabatic expansion to a pressure of 10 atmCalculate (1)the final volume of the system(2)the work done by the system(3) the heat entering or leaving the system(4)the change in the enthalpySolution :(a)1)22.5L; 2)9.21KJ; 3)9.21KJ; 4)0(b)1)19.1L; 2)5.11KJ; 3)0; 4)-8.52KJ13) 5 moles of an ideal gas are contained adiabatically at 50atm pressure and 300K. The pressure is suddenly released to 10atm, and the gas undergoes an irreversible expansion during which it performs 4000 joules of work. Show that the final temperature of gas after the irreversible expansion is greater than that which the gas would attain if the expansion from 50 to 10atm had been conducted reversibly. Calculate the entropy produced as a result the irreversible expansion. The constant volume molar heat capacity of the gas C V has the value of 1.5RSolution:41.9J/K14) the initial state of one mole of monatomic ideal gas is p=10atm and T=300K.Calculate the change in the entropy of the gas for (a) an isothermal decrease in the pressure to 5 atm (c) constant –volume decrease in the pressure to 5 atmSolution: (a)5.79J/K (b)0 (c)-8.64K/J15) one mole of a monatomic ideal gas is subjected to the following sequence of stepsa) starting at 300K and 10 atm, the gas expands freely into a vacuum to triple its volumeb) the gas is next heated reversibly to 400K at constant volumec) the gas is reversibly expand as constant temperature until its volume is again tripledd) the gas is finally reversibly cooled to 300K at constant pressureCalculate the value of Q,W, and the change in U,H, SSolution: )(86.15)(83.2)(83.201−=Δ===Δ=ΔJK S kJ W kJ Q H U。
