新版高中数学人教A版选修2-2习题:第一章导数及其应用1-7-2(1)
人教A版选修2-2第一章 导数及其应用.docx

第一章 导数及其应用[基础训练A 组]一、选择题1.若函数()y f x =在区间(,)a b 内可导,且0(,)x a b ∈则000()()limh f x h f x h h→+--的值为( )A .'0()f xB .'02()f xC .'02()f x - D .02.一个物体的运动方程为21t t s +-=其中s 的单位是米,t 的单位是秒, 那么物体在3秒末的瞬时速度是( ) A .7米/秒 B .6米/秒 C .5米/秒 D .8米/秒 3.函数3y x x =+的递增区间是( )A .),0(+∞B .)1,(-∞C .),(+∞-∞D .),1(+∞4.32()32f x ax x =++,若'(1)4f -=,则a 的值等于( )A .319 B .316 C .313 D .310 5.函数)(x f y =在一点的导数值为0是函数)(x f y =在这点取极值的( )A .充分条件B .必要条件C .充要条件D .必要非充分条件6.函数344+-=x x y 在区间[]2,3-上的最小值为( )A .72B .36C .12D .0二、填空题1.若3'0(),()3f x x f x ==,则0x 的值为_________________;2.曲线x x y 43-=在点(1,3)- 处的切线倾斜角为__________; 3.函数sin xy x=的导数为_________________;4.曲线x y ln =在点(,1)M e 处的切线的斜率是_________,切线的方程为_______________; 5.函数5523--+=x x x y 的单调递增区间是___________________________。
三、解答题1.求垂直于直线2610x y -+=并且与曲线3235y x x =+-相切的直线方程。
高中数学人教A版选修2-2习题 第1章 导数及其应用1.7 Word版含答案

选修第一章一、选择题.曲线=(≤≤π)与两坐标轴所围成图形的面积为( )...[答案][解析]=,))-,))=-))=..一列车沿直线轨道前进,刹车后列车速度为()=-,则列车刹车后前进多少米才能停车?( )....[答案][解析]停车时()=,则-=,∴=,=∫()=∫(-)=(-)=..由曲线=-、直线=、=和轴围成的封闭图形的面积(如图)是( )(-).(-)-(-)+(-)[答案][解析]=-将轴下方阴影反折到轴上方,其定积分为正,故应选..曲线=-和=围成的图形面积为( )...[答案][解析]由(\\(=-,=,))解得(\\(=,=.))或(\\(=,=,))或(\\(=-,=-.))∵两函数=-与=均为奇函数,∴=[-(-)]=·(-)=(-)=,故选..一物体在力()=-(单位:)的作用下,沿着与力相同的方向,从=运动到=处(单位:),则力()所做的功为( )...[答案][解析]由变力做功公式有:=(-)=(-)=(),故应选..若某产品一天内的产量(单位:百件)是时间的函数,若已知产量的变化率为=,那么从小时到小时期间内的产量为( ).-.+.-[答案][解析]==-,故应选.二、填空题.由曲线=,=-所围图形的面积是[答案] [解析]如图,为了确定图形的范围,先求出这两条曲线交点的坐标,解方程组(\\(=,=-,))得交点坐标为(,-),().因此所求图形的面积=-(+-)取()=+-,则′()=+-,从而=()-(-)=..一物体沿直线以速度=运动,该物体运动开始后内所经过的路程是[答案](-)[解析]=∫=(+)=(-)..由两条曲线=,=与直线=围成平面区域的面积是[答案][解析]解法:如图,=与=交点(),=与=交点(),由对称性可知面积=(+-)=.。
高中新课程数学(新课标人教A版)选修2-2《第一章 导数及其应用》知识点、考点、及其例题

第一章导数及其应用知识点及练习题知识点1:导数概念的引入1. 导数的物理意义:瞬时速率。
一般的,函数()y f x =在0x x =处的瞬时变化率是000()()limx f x x f x x∆→+∆-∆,我们称它为函数()y f x =在0x x =处的导数,记作0()f x '或0|x x y =', 即0()f x '=000()()limx f x x f x x∆→+∆-∆2. 导数的几何意义:曲线的切线.通过图像,我们可以看出当点n P 趋近于P 时,直线PT 与曲线相切。
容易知道,割线n PP 的斜率是00()()n n n f x f x k x x -=-,当点n P 趋近于P 时,函数()y f x =在0x x =处的导数就是切线PT 的斜率k ,即000()()lim ()n x n f x f x k f x x x ∆→-'==-3. 导函数:当x 变化时,()f x '便是x 的一个函数,我们称它为()f x 的导函数. ()y f x =的导函数有时也记作y ',即0()()()limx f x x f x f x x∆→+∆-'=∆考点:导数的几何意义及其应用[例题] 已知曲线y =13x 3+43.(1)求曲线在点P (2,4)处的切线方程;(2)求曲线过点P (2,4)的切线方程; (3)求斜率为4的曲线的切线方程.[变式训练] 已知函数f(x)=x3+x -16.(1)求曲线y =f(x)在点(2,-6)处的切线的方程;(2)直线l 为曲线y =f(x)的切线,且经过原点,求直线l 的方程及切点坐标.知识点2:导数的计算1)基本初等函数的导数公式:1若()f x c =(c 为常数),则()0f x '=; 2 若()f x x α=,则1()f x xαα-'=;3 若()sin f x x =,则()cos f x x '=4 若()cos f x x =,则()sin f x x '=-;5 若()xf x a =,则()ln x f x a a '=6 若()x f x e =,则()xf x e '=7 若()log xa f x =,则1()ln f x x a '=8 若()ln f x x =,则1()f x x'=2)导数的运算法则1. [()()]()()f x g x f x g x '''±=±2. [()()]()()()()f x g x f x g x f x g x '''•=•+•3. 2()()()()()[]()[()]f x f xg x f x g x g x g x ''•-•'= 3)复合函数求导()y f u =和()u g x =,称则y 可以表示成为x 的函数,即(())y f g x =为一个复合函数 (())()y f g x g x '''=•考点:导数的求导及运算1、已知()22sin f x x x π=+-,则()'0f =2、若()sin x f x e x =,则()'f x =3.)(x f =ax 3+3x 2+2 ,4)1(=-'f ,则a=( )319.316.313.310.D C B A 4.过抛物线y=x 2上的点M )41,21(的切线的倾斜角是() A.30° B.45° C.60° D.90° 5.如果曲线2932y x =+与32y x =-在0x x =处的切线互相垂直,则0x =知识点3:导数在研究函数中的应用1.函数的单调性与导数:一般的,函数的单调性与其导数的正负有如下关系:在某个区间(,)a b 内,如果()0f x '>,那么函数()y f x =在这个区间单调递增; 如果()0f x '<,那么函数()y f x =在这个区间单调递减. 2.函数的极值与导数极值反映的是函数在某一点附近的大小情况. 求函数()y f x =的极值的方法是:(1) 如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么0()f x 是极大值;(2) 如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么0()f x 是极小值; 4.函数的最大(小)值与导数函数极大值与最大值之间的关系.求函数()y f x =在[,]a b 上的最大值与最小值的步骤 (1) 求函数()y f x =在(,)a b 内的极值;(2) 将函数()y f x =的各极值与端点处的函数值()f a ,()f b 比较,其中最大的是一个最大值,最小的是最小值.考点:1.导数在研究函数单调性中的应用2.导数在求函数极值与最值中的应用题型一:导数在研究函数单调性中的应用[例题] 设函数f (x )=x e a -x +bx ,曲线y =f (x )在点(2,f (2))处的切线方程为y=(e -1)x +4.(1)求a ,b 的值; (2)求f (x )的单调区间.[变式训练] 设函数f(x)=xekx(k ≠0).(1)讨论函数f(x)的单调性;(2)若函数f(x)在区间(-1,1)内单调递增,求k 的取值范围.题型二:导数在求函数极值与最值中的应用[例题]已知函数f(x)=-x3+ax2+bx在区间(-2,1)内,当x=-1时取极小值,当x=23时取极大值.(1)求函数y=f(x)在x=-2时的对应点的切线方程;(2)求函数y=f(x)在[-2,1]上的最大值与最小值.[变式训练] 设函数f(x)=[ax2-(4a+1)x+4a+3]e x.(1)若曲线y=f(x)在点(1,f(1))处的切线方程与x轴平行,求a;(2)若f(x)在x=2处取得极小值,求a的取值范围.知识点4:解决实际问题利用导数的知识,,求函数的最大(小)值,从而解决实际问题考点:1、导数在切线方程中的应用2、导数在单调性中的应用3、导数在极值、最值中的应用4、导数在恒成立问题中的应用题型一:导数在切线方程中的运用1.曲线3x y =在P 点处的切线斜率为k,若k=3,则P 点为( ) A.(-2,-8) B.(-1,-1)或(1,1)C.(2,8)D.(-21,-81)2.曲线53123+-=x x y ,过其上横坐标为1的点作曲线的切线,则切线的倾斜角为( ) A.6π B.4π C.3π D.π43题型二:导数在单调性中的运用1.函数32()31f x x x =-+是减函数的区间为( ) A.(2,)+∞ B.(,2)-∞ C.(,0)-∞ D.(0,2)2.关于函数762)(23+-=x x x f ,下列说法不正确的是( ) A .在区间(∞-,0)内,)(x f 为增函数 B .在区间(0,2)内,)(x f 为减函数 C .在区间(2,∞+)内,)(x f 为增函数 D .在区间(∞-,0)),2(+∞⋃内,)(x f 为增函数3.已知函数()y xf x '=的图象如右图所示(其中'()f x 是函数()f x 的导函数),下面四个图象中()y f x =的图象大致是( )4、(2010年山东21)(本小题满分12分)已知函数).(111)(R a xaax nx x f ∈--+-= (Ⅰ)当处的切线方程;在点时,求曲线))2(,2()(1f x f y a=-=(Ⅱ)当12a ≤时,讨论()f x 的单调性.题型三:导数在最值、极值中的运用1.函数93)(23-++=x ax x x f ,已知)(x f 在3-=x 时取得极值,则a =( ) A .2B. 3C. 4D.52.函数5123223+--=x x x y 在[0,3]上的最大值与最小值分别是( ) A.5 , - 15 B.5 , 4 C.- 4 , - 15 D.5 , - 163.已知函数)0()(3≠++=adcxaxxf是R上的奇函数,当1=x时)(xf取得极值-2.(1)试求a、c、d的值;(2)求)(xf的单调区间和极大值;4.设函数2312)(bxaxexxf x++=-,已知12=-=xx和为)(xf的极值点。
【人教A版数学选修2-2】导数及其应用1-7-2

功.
RJA·数学·选修2-2
进入导航
第一章 1.7 1.7.2 第14页
系列丛书
RJA·数学·选修2-2
进入导航
第一章 1.7 1.7.2 第15页
系列丛书
类型一
变速直线运动的路程
【例 1】 A、B 两站相距 7.2 km,一辆电车从 A 站开往 B 站,电车开出 t s 后到达途中 C 点,这一段的速度为 1.2t m/s,到 C 点的速度为 24 m/s,从 C 点到 B 点前的 D 点以等速行驶,从 D 点开始刹车,速度为(24-1.2t) m/s,经 t s 后,在 B 点恰好停 车,试求:
RJA·数学·选修2-2
进入导航
第一章 1.7 1.7.2 第25页
系列丛书
【解】 (1)由 v(t)=8t-2t2≥0 得 0≤t≤4, 即当 0≤t≤4 时,P 点向 x 轴正方向运动,t>4 时,P 点向 x 轴负方向运动. 故 t=3 时,点 P 离开原点的路程 s1=∫30(8t-2t2)dt=(4t2-23t3)|30=18. (2)s2=∫50(8t-2t2)dt=(4t2-23t3)|50=530. ∴点 P 在 x 轴正方向上距原点530处.
则
DB=
20(24-1.2t)dt=(24t-0.6t2)|200=240(m).
0
RJA·数学·选修2-2
进入导航
第一章 1.7 1.7.2 第17页
系列丛书
求变速直线运动的路程、位移应关注三点 1分清运动过程中的变化情况; 2如果速度方程是分段函数,那么要用分段的定积分表示; 3明确是求位移还是求路程,求位移可以正负抵消,求路 程不能正负抵消.
RJA·数学·选修2-2
2018版数学人教A版选修2-2学案:第一章 导数及其应用 1-7-2 含答案 精品

1.7.2 定积分在物理中的应用学习目标 1.能利用定积分解决物理中的变速直线运动的路程、变力做功问题.2.通过定积分在物理中的应用,学会用数学工具解决物理问题,进一步体会定积分的价值.知识点一 变速直线运动的路程思考 变速直线运动的路程和位移相同吗?答案 不同.路程是标量,位移是矢量,路程和位移是两个不同的概念. 梳理 (1)当v (t )≥0时,求某一时间段内的路程和位移均用()21d t t t t ⎰v 求解.(2)当v (t )<0时,求某一时间段内的位移用()21d t t t t ⎰v 求解,这一时段的路程是位移的相反数,即路程为-()21d t t t t ⎰v .做变速直线运动的物体所经过的路程s ,等于其速度函数v =v (t )(v (t )≥0)在时间区间[a ,b ]上的定积分,即ʃb a v (t )d t .知识点二 变力做功问题思考 恒力F 沿与F 相同的方向移动了s ,力F 做的功为W =Fs ,那么变力做功问题怎样解决?答案 与求曲边梯形的面积一样,物体在变力F (x )作用下运动,沿与F 相同的方向从x =a 到x =b (a <b ),可以利用定积分得到W =ʃb a F (x )d x .梳理 如果物体在变力F (x )的作用下做直线运动,并且物体沿着与F (x )相同的方向从x =a 移动到x =b (a <b ),那么变力F (x )所做的功为ʃb a F (x )d x .类型一 求变速直线运动的位移、路程例1 (1)一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度v (t )=7-3t +251+t (t 的单位:s ,v 的单位:m/s)行驶至停止,则在此期间汽车继续行驶的距离(单位:m)是( ) A .1+25ln5 B .8+25ln 113C .4+25ln5D .4+50ln2答案 C解析 令v (t )=0,得t =4或t =-83(舍去),∴汽车行驶距离s =ʃ40(7-3t +251+t)d t =7t 40|-32t 240|+25ln(1+t )40|=28-24+25ln5=4+25ln5.(2)有一动点P 沿x 轴运动,在时间t 时的速度v (t )=8t -2t 2(速度的正方向与x 轴正方向一致).求:①P 从原点出发,当t =6时,求点P 离开原点的路程和位移; ②P 从原点出发,经过时间t 后又返回原点时的t 值.解 ①由v (t )=8t -2t 2≥0,得0≤t ≤4,即当0≤t ≤4时,P 点向x 轴正方向运动,当t >4时,P 点向x 轴负方向运动. 故当t =6时,点P 离开原点的路程s 1=ʃ40(8t -2t 2)d t -ʃ64(8t -2t 2)d t= ⎪⎪⎝⎛⎭⎫4t 2-23t 340-⎪⎪⎝⎛⎭⎫4t 2-23t 364=1283. 当t =6时,点P 的位移s 2=ʃ60(8t -2t 2)d t =⎪⎪⎝⎛⎭⎫4t 2-23t 360=0. ②依题意得ʃt 0(8t -2t 2)d t =0, 即4t 2-23t 3=0,解得t =0或t =6,t =0对应于P 点刚开始从原点出发的情况,t =6是所求的值.反思与感悟 (1)用定积分计算做直线运动物体的路程,要先判断速度v (t )在时间区间内是否为正值,若v (t )>0,则运动物体的路程s =ʃb a v (t )d t ;若v (t )<0,则运动物体的路程s =ʃb a |v (t )|d t=-ʃb a v (t )d t .(2)若已知做直线运动物体的速度—时间图象,可以先求出速度—时间函数式,再转化为定积分计算路程;也可以直接计算曲边梯形的面积得到路程;若速度—时间函数是分段函数,要利用定积分的性质进行分段积分再求和.跟踪训练1 一质点在直线上从时刻t =0(s)开始以速度v (t )=t 2-4t +3(m/s)运动.求: (1)在时刻t =4时,该点的位置; (2)在时刻t =4时,该点运动的路程. 解(1)由ʃ40(t 2-4t +3)d t =⎪⎪⎝⎛⎭⎫t 33-2t 2+3t 4=43知,在时刻t =4时,该质点离出发点43m. (2)由v (t )=t 2-4t +3>0,得t ∈(0,1)∪(3,4).这说明t ∈(1,3)时质点运动方向与t ∈(0,1)∪(3,4)时运动方向相反.故s =ʃ40|t 2-4t +3|d t =ʃ10(t 2-4t +3)d t +ʃ31(4t -t 2-3)d t +ʃ43(t 2-4t +3)d t =4.即在时刻t =4时,该质点运动的路程为4m.类型二 求变力做功例2 如图所示,一物体沿斜面在拉力F 的作用下由A 经B 、C 运动到D ,其中AB =50m ,BC =40m ,CD =30m ,变力F =⎩⎪⎨⎪⎧14x +5,0≤x ≤90,20,90<x ≤120(单位:N),在AB 段运动时,F 与运动方向成30°角.在BC 段运动时,F 与运动方向成45°角.在CD 段运动时,F 与运动方向相同,求物体由A 运动到D 所做的功.(3≈1.732,2≈1.414,精确到1J)解 在AB 段运动时,F 在运动方向上的分力F 1=F cos30°,在BC 段运动时,F 在运动方向上的分力F 2=F cos45°. 由变力做功公式得W =ʃ500⎝⎛⎭⎫14x +5cos30°d x +ʃ9050⎝⎛⎭⎫14x +5cos45°d x +600 =⎪⎪38⎝⎛⎭⎫12x 2+20x 500+⎪⎪28⎝⎛⎭⎫12x 2+20x 9050+600 =112543+4502+600≈1723(J).所以物体由A 运动到D ,变力F 所做的功为1723J. 反思与感悟 解决变力做功注意以下两个方面(1)首先要将变力用其方向上的位移表示出来,这是关键的一步. (2)根据变力做功的公式将其转化为求定积分的问题.跟踪训练2 一物体在力F (x )=⎩⎪⎨⎪⎧2,0≤x ≤2,2x -2,x >2,(单位:N)的作用下沿与力F 相同的方向,从x =0处运动到x =4(单位:m)处,则力F (x )做的功为( ) A .10J B .12J C .14J D .16J答案 B解析 从x =0处运动到x =4(单位:m)处,力F (x )做的功为ʃ202d x +ʃ42(2x -2)d x =2x |20+(x 2-2x )|42=12(J).故选B.1.一列车沿直线轨道前进,刹车后列车速度v (t )=27-0.9t ,则列车从开始刹车到停车所行驶的路程为( )A .405米B .540米C .810米D .945米 答案 A解析 停车时v (t )=0,由27-0.9t =0,得t =30,∴s =ʃ300v (t )d t =ʃ300(27-0.9t )d t =(27t -0.45t 2)|300=405(米).2.一个物体在力F (x )=1+e x 的作用下,沿着与力F (x )相同的方向从x =0处运动到x =1处,力F (x )所做的功是( ) A .1+e B .e -1 C .1-e D .e答案 D解析 W =ʃ10(1+e x )d x =(x +e x +c )|10=1+e -1=e.故选D.3.一质点运动时速度与时间的关系为v (t )=t 2-t +2,质点作直线运动,则此质点在[1,2]时间内的位移为________. 答案176解析 由题意可知s =ʃ21(t 2-t +2)d t=⎪⎪⎝⎛⎭⎫13t 3-12t 2+2t 21=176.4.已知作用于某一质点的力F (x )=⎩⎪⎨⎪⎧x ,0≤x ≤1,x +1,1<x ≤2(单位:N),则力F 从x =0处运动到x=2处(单位:m)所做的功为________J. 答案 3解析 W =ʃ20F (x )d x =ʃ10x d x +ʃ21(x +1)d x= ⎪⎪12x 210+⎪⎪⎝⎛⎭⎫12x 2+x 21=12+12×22+2-12×12-1=3(J).1.已知变速运动方程,求在某段时间内物体运动的位移或者经过的路程,就是求速度方程的定积分.解这类问题需注意三点:(1)分清运动过程中的变化情况;(2)如果速度方程是分段函数,那么要用分段的定积分表示;(3)明确是求位移还是求路程,求位移可以正负抵消,求路程不能正负抵消.2.利用定积分求变力做功问题,关键是求出变力与位移之间的函数关系,确定好积分区间.求变力做功时,要注意单位,F(x)单位:N,x单位:m.课时作业一、选择题1.一辆汽车做变速直线运动,在时刻t的速度为v(t)=2+sin t(t的单位:h,v的单位:km/h),那么它在0≤t≤1这段时间内行驶的路程s(单位:km)是()A.3-cos1 B.3+cos1C.1+cos1 D.1-cos1答案 A解析由v(t)=2+sin t>0,故这辆车行驶的路程s=ʃ10v(t)d t=ʃ10(2+sin t)d t=(2t-cos t)|10=(2-cos1)-(-cos0)=3-cos1,故选A.2.一物体从A处向B处运动,速度为1.4t m/s(t为运动的时间),到B处时的速度为35 m/s,则AB间的距离为()A.120m B.437.5mC.360m D.480m答案 B解析从A处到B处所用时间为25s,所以|AB|=ʃ2501.4t d t=0.7t2|250=437.5(m).3.物体A以速度v=3t2+1(m/s)在一直线l上运动,物体B在直线l上,且在物体A的正前方5 m处,同时以v=10t(m/s)的速度与A同向运动,出发后物体A追上物体B所用的时间t(s)为()A.3 B.4C.5 D.6答案 C解析因为物体A在t秒内行驶的路程为ʃt0(3t2+1)d t,物体B在t秒内行驶的路程为ʃt010t d t,所以ʃt0(3t2+1-10t)d t=(t3+t-5t2)|t0=t3+t-5t2=5⇒(t-5)(t2+1)=0,即t=5.故选C.4.沿x 轴正方向运动的质点,在任意位置x 米处,所受的力为F (x )=3x 2牛顿,则质点从坐标原点运动到4米处,力F (x )所做的功是( ) A .74焦耳 B .72焦耳 C .70焦耳 D .64焦耳答案 D解析 根据定积分的物理意义可知,力F (x )所做的功为ʃ403x 2d x =x 3|40=64(焦耳).故选D.5.以初速度40m/s 竖直向上抛一物体,t s 时刻的速度v =40-10t 2,则此物体达到最高时的高度为( )A.1603mB.803mC.403mD.203m 答案 A解析 达到最高点时速度v =40-10t 2=0, 得t =2.∴此物体达到最高时的高度为ʃ20(40-10t 2)d t =⎪⎪⎝⎛⎭⎫40t -103t 320=1603. 6.如果用1N 的力能拉长弹簧1cm ,则将弹簧拉长6cm ,克服弹力所做的功为( ) A .0.18JB .0.26JC .0.12JD .0.28J 答案 A解析 设F (x )=kx ,当F (x )=1时,x =0.01,则k =100,W =ʃ0.060100x d x =50x 2|0.060=0.18(J).7.一物体在变力F (x )=5-x 2(力单位:N ,位移单位:m)的作用下,沿与F (x )成30°方向做直线运动,则由x =1 (m)运动到x =2 (m)时,F (x )做的功为( ) A .1J B.3J C.433J D .2J答案 C解析 由于F (x )与位移方向成30°角.如图,F 在位移方向上的分力F ′=F ·cos30°,W =ʃ21(5-x 2)·cos30°d x =32ʃ21(5-x 2)d x =32(5x -13x 3)|21=433.故选C. 二、填空题8.若某产品一天内的产量(单位:百件)是时间t 的函数,若已知产量的变化率为a =36t,那么从3小时到6小时期间内的产量为________百件. 答案 6-3 2 解析ʃ6336td t =⎪⎪66 t 63=6-3 2. 9.做变速直线运动的物体的速度为v (t )=4-t 2,初始位置s (0)=1,则3秒时所处的位置s (3)为________. 答案 4解析 由题意可知,s (3)=ʃ30v (t )d t +1=ʃ30(4-t 2)d t +1=⎪⎪⎝⎛⎭⎫4t -13t 330+1=4. 10.一物体做直线运动的速度与时间成正比,5s 时速度为20m/s ,则物体开始运动10s 内所经过的路程为________m. 答案 200解析 ∵v =4t ,∴s =ʃ1004t d t =(2t 2)|100=200(m).11.在原点O 处有一个带电量为+q 的点电荷,它所产生的电场对周围有作用力.现有一个单位正电荷从距O 点的距离为a 处沿着射线方向移至距O 点为b (a <b )的地方,则电场力F =k ·qr 2(k 为常数)做的功为________.答案 k q a -k qb解析 W =ʃb a k qr 2d r =⎪⎪-k q r b a =k q a -k q b . 三、解答题12.物体按x =2t 2(m)做直线运动,设介质的阻力与速度成正比,且速度等于8m/s 时,阻力为2N ,求物体从x =0m 运动到x =2m 时,克服阻力所做的功. 解 设阻力F =k v ,因为v =x ′=4t ,所以F =4kt . 由题意得v =4t =8,所以t =2, 所以8k =2,即k =0.25, 所以F =4×0.25t =t . 又x =2t 2,t >0,所以t =x 2, 所以F (x )=x2.所以阻力所做的功W =-ʃ2012x d x =-12×23×32x |20=-43(J).故物体从x =0m 运动到x =2m 时克服阻力所做的功为43J.13.已知A ,B 两站相距7.2km ,一辆电车从A 站开往B 站,电车开出t s 后到达途中C 点,这一段的速度为1.2t m /s ,到C 点的速度为24 m/s ,从C 点到B 点前的D 点以等速行驶,从D 点开始刹车,经t s 后,速度为(24-1.2t ) m/s ,在B 点恰好停车,试求: (1)A ,C 间的距离; (2)B ,D 间的距离;(3)电车从A 站到B 站所需的时间. 解 (1)设A 到C 的时间为t 1, 则1.2t 1=24,所以t 1=20(s),则AC =ʃ2001.2t d t =0.6t 2|200=240(m).(2)设D 到B 的时间为t 2, 则24-1.2t 2=0,t 2=20(s).则BD =ʃ200(24-1.2t )d t =(24t -0.6t 2)|200=240(m).(3)CD =7200-2×240=6720(m), 则从C 到D 的时间为672024=280(s),则所求时间为20+280+20=320(s).。
人教A版选修2-2第一章 导数及其应用

高中数学学习材料(灿若寒星精心整理制作)第一章导数及其应用1.1变化率与导数1.1.1变化率问题1.1.2导数的概念双基达标(限时20分钟)1.已知函数f(x)=2x2-4的图象上一点(1,-2)及邻近一点(1+Δx,-2+Δy),则ΔyΔx等于().A.4 B.4xC.4+2Δx D.4+2(Δx)2解析ΔyΔx=f(1+Δx)-f(1)Δx=2(1+Δx)2-2Δx=4+2Δx.答案 C2.如果质点M按规律s=3+t2运动,则在一小段时间[2,2.1]中相应的平均速度是().A.4 B.4.1 C.0.41 D.3解析v=(3+2.12)-(3+22)0.1=4.1.答案 B3.如果某物体的运动方程为s =2(1-t 2)(s 的单位为m ,t 的单位为s),那么其在1.2 s 末的瞬时速度为( ).A .-4.8 m /sB .-0.88 m/sC .0.88 m /sD .4.8 m/s解析 物体运动在1.2 s 末的瞬时速度即为s 在1.2处的导数,利用导数的定义即可求得.答案 A4.已知函数y =2+1x ,当x 由1变到2时,函数的增量Δy =________.解析 Δy =⎝ ⎛⎭⎪⎫2+12-(2+1)=-12. 答案 -125.已知函数y =2x ,当x 由2变到1.5时,函数的增量Δy =________.解析 Δy =f (1.5)-f (2)=21.5-22=43-1=13.答案 136.利用导数的定义,求函数y =1x 2+2在点x =1处的导数.解 ∵Δy =⎣⎢⎡⎦⎥⎤1(x +Δx )2+2-⎝⎛⎭⎪⎫1x 2+2=-2x Δx -(Δx )2(x +Δx )2·x 2, ∴Δy Δx =-2x -Δx (x +Δx )2·x 2, ∴y ′=lim Δx →0 Δy Δx =lim Δx →0-2x -Δx (x +Δx )2·x 2=-2x 3, ∴y ′|x =1=-2.综合提高 (限时25分钟)7.已知函数y =f (x )=x 2+1,则在x =2,Δx =0.1时,Δy 的值为( ).A.0.40 B.0.41 C.0.43 D.0.44 解析Δy=(2+0.1)2-22=0.41.答案 B8.设函数f(x)可导,则limΔx→0f(1+Δx)-f(1)3Δx等于().A.f′(1) B.3f′(1)C.13f′(1) D.f′(3)解析根据导数的定义:limΔx→0f(1+Δx)-f(1)Δx=f′(1),lim Δx→0f(1+Δx)-f(1)3Δx=13f′(1).答案 C9.一做直线运动的物体,其位移s与时间t的关系是s=3t-t2,则物体的初速度是________.解析v初=s′|t=0=limΔt→0s(0+Δt)-s(0)Δt=limΔt→0(3-Δt)=3.答案 310.某物体作匀速运动,其运动方程是s=v t,则该物体在运动过程中其平均速度与任何时刻的瞬时速度的关系是________.解析v0=limΔt→0ΔsΔt=limΔt→0s(t0+Δt)-s(t0)Δt=limΔt→0v(t0+Δt)-v t0Δt=limΔt→0v·ΔtΔt=v.答案相等11.子弹在枪筒中的运动可以看作是匀变速运动,如果它的加速度是a=5×105 m/s2,子弹从枪口射出时所用的时间为t0=1.6×10-3s,求子弹射出枪口时的瞬时速度.解运动方程为s=12at2.∵Δs =12a (t 0+Δt )2-12at 20=at 0Δt +12a (Δt )2,∴Δs Δt =at 0+12a Δt ,∴ lim Δt →0Δs Δt =at 0.由题意知a =5×105,t 0=1.6×10-3,故at 0=8×102=800(m/s).即子弹射出枪口时的瞬时速度为800 m/s.12.(创新拓展)已知f (x )=x 2,g (x )=x 3,求满足f ′(x )+2=g ′(x )的x 的值. 解 由导数的定义知,f ′(x )=lim Δx →0(x +Δx )2-x 2Δx =2x , g ′(x )=lim Δx →0(x +Δx )3-x 3Δx =3x 2. ∵f ′(x )+2=g ′(x ),∴2x +2=3x 2.即3x 2-2x -2=0,解得x =1-73或x =1+73.。
2017年春高中数学人教A版选修2-2习题课件-第1章 导数及其应用 1-7-12

4.由抛物线y=x2-x,直线x=-1及x轴围成的图形的面
积为( )
2 A.3
B.1
4
5
C.3
D.3
第十一页,编辑于星期六:二点 四十二分。
解析:S=0 (x2-x)dx+1(x-x2)dx
-1
0
=13x3-12x20-1+12x2-13x310=1.
答案:B
第十二页,编辑于星期六:二点 四十二分。
第三十页,编辑于星期六:二点 四十二分。
U′=a2-12, 令U′=0,得a= 22, 当a∈0, 22时,U′<0; 当a∈ 22,1时,U′>0.
第三十一页,编辑于星期六:二点 四十二分。
图(2)
第三十二页,编辑于星期六:二点 四十二分。
故当a= 22时,U取最小值为2-6
2 .
(2)当a<0时,如图(2),
限时:40分钟 满分:90分
第四页,编辑于星期六:二点 四十二分。
一、选择题:每小题5分,共30分.
1.已知二次函数y=f(x)的图象如图所示,则它与x轴所围
图形的面积为( )
2π
4
A. 5
B.3
3
π
C.2
D.2
第五页,编辑于星期六:二点 四十二分。
解析:由题中图象易知f(x)=-x2+1,则所求面积为 201-x2+1dx=2-x33+x01=43.
所以函数y=U(a)在(-∞,0)上单调递减.
故函函数y=U(a)无最小值.
(3)当a=0时,无最小值.
综上可知,a=
2 2.
第三十四页,编辑于星期六:二点 四十二分。
由yy==axx2,, 得交点(0,0)和(a,a2), S=a0(ax-x2)dx=a2x2-x330a =-a23+a33=-a63,
高中数学选修2-2(人教A版)第一章导数及其应用1.7知识点总结含同步练习及答案
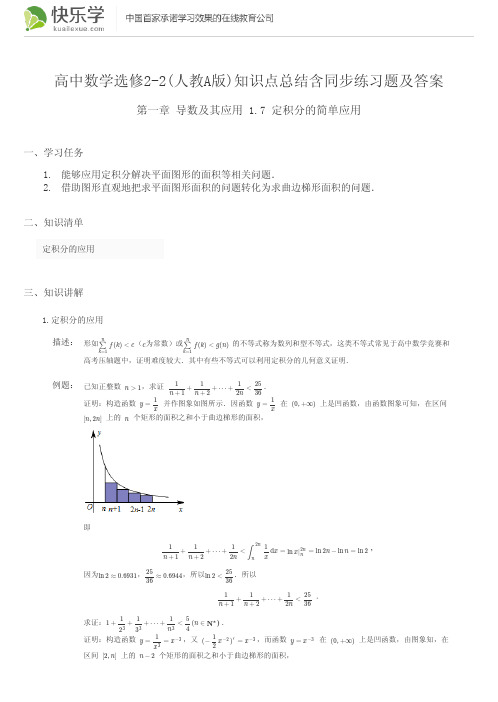
若 n ∈ N,n ⩾ 2 ,求证: 1 + 1 + ⋯ + 1 < ln n < 1 + 1 + 1 + ⋯ +
3 n 2 3 证明:构造函数 y = 1 ,因为 (ln x) ′ = 1 ,作 y = 1 的图象, x x x 2
由图知,在区间 [n − 1, n](n ≥ 2) 上曲边梯形的面积大小在以区间长度 1 为一边长,以左右端点对应的函数值为 另一边长的两个矩形面积之间,即
由累加法可得 1 + 1 + ⋯ + 1 < ln n < 1 + 1 + 1 + ⋯ +
2 3 n 2 3
1 成立. n−1
四、课后作业
(查看更多本章节同步练习题,请到快乐学)
1. 如图中阴影部分的面积是 (
).
A.2√3
答案: C
B.9 − 2√3
C.
32 3
D.
35 3
n 1 1 1 <∫ dx < , n n−1 n−1 x
而
∫
n n−1
1 dx = ln x| n n−1 = ln n − ln(n − 1), x
故不等式
1 1 < ln n − ln(n − 1) < n n−1
成立,从而当 n ⩾ 2 时,
1 < ln 2 − ln 1 < 1, 2 1 1 < ln 3 − ln 2 < , 3 2 ⋯ 1 1 < ln n − ln(n − 1) < , n n−1
1 1 x, g (x) = cos x ;② f (x) = x + 1, g (x) = x − 1 ;③ 2 2 f (x) = x, g (x) = x2 .其中为区间 [−1, 1] 的正交函数的组数是 ( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.7.2定积分在物理中的应用
课时过关·能力提升
基础巩固
1若某质点沿直线以v=3t+2(t的单位:s,v的单位:m/s)的速度运动,则该质点在第3 s到第6 s间的运动路程s为()
A.46 m
B.46.5 m
C.87 m
D.47 m
解析s=v d t=(3t+2)d t=
==46.5(m).
答案B
2已知一物体在力F(x)=(单位:N)的作用下沿与力F(x)相同的方向,由x=0 m处直线运动到x=4 m处,则力F(x)所做的功为() A.44 J B.46 J C.48 J D.50 J
答案B
3物体以速度v(t)=3t2-2t+4做直线运动,它在第3秒内的位移是()
A.12
B.14
C.16
D.18
解析其位移为s=(3t2-2t+4)d t=(t3-t2+4t)
=(27-9+12)-(8-4+8)=18.
答案D
4若火车紧急刹车的速度为v(t)= m/s,则刹车后火车行驶的距离约为 m.(精确到0.1 m)
解析停止时车速为0,由v(t)=10-t+=0,解得刹车所用的时间为t=16(s)(t=-8(s)舍去),
所以s=d t
==32+216ln 3
≈269.3(m).
答案269.3
5若某物体以v(t)=t2-3t+8(t的单位:s,v的单位:m/s)的速度运动,则其在前30 s内的平均速度为.
解析由定积分的物理意义,得
s=(t2-3t+8)d t=
=7 890(m),=263(m/s).
答案263 m/s
6在弹性限度内,拉伸(或压缩)弹簧所需的力F(x)(单位:N)与弹簧拉伸(或压缩)的长度x(单位:m)成正比,如果用1 N的力能拉长弹簧1 cm,那么为了将弹簧拉长6 cm需做功 J.
解析设F(x)=kx(常数k是比例系数),由题意知,当F(x)=1 N时,x=0.01 m,可得k=100.
由变力做功公式,得到将弹簧拉长6 cm需做的功W=100x d x=50x2=0.18(J).
答案0.18
7
某物体在力F(x)(单位:N)的作用下沿与力F相同的方向运动,力—位移曲线如图所示.求该物体从x=0处运动到x=4(单位:m)处,力
F(x)做的功.
分析先根据图象确定力关于位移的函数关系式,再利用定积分求解.
解由力—位移曲线可知F(x)=因此该物体从x=0处运动到x=4处力F(x)做的功为10d x+(3x+4)d x=10x=46(J).
能力提升
1如果某质点以初速度v(0)=1(v的单位:m/s),加速度a(t)=6t(a的单位:m/s2)做直线运动,则质点在t=2 s时的瞬时速度为() A.5 m/s B.7 m/s C.9 m/s D.13 m/s
解析v(2)-v(0)=a(t)d t=6t d t=3t2,
所以v(2)=v(0)+3×22=1+12=13(m/s).。
