实验5 脉冲响应不变法设计IIR数字滤波器
IIR数字滤波器设计实验报告

实验三IIR数字滤波器设计实验报告一、实验目的:1.通过仿真冲激响应不变法和双线性变换法2.掌握滤波器性能分析的基本方法二、实验要求:1.设计带通IIR滤波器2.按照冲激响应不变法设计滤波器系数3. 按照双线性变换法设计滤波器系数4. 分析幅频特性和相频特性5. 生成一定信噪比的带噪信号,并对其滤波,对比滤波前后波形和频谱三、基本原理:㈠IIR模拟滤波器与数字滤波器IIR数字滤波器的设计以模拟滤波器设计为基础,常用的类型分为巴特沃斯(Butterworth)、切比雪夫(Chebyshev)Ⅰ型、切比雪夫Ⅱ型、贝塞尔(Bessel)、椭圆等多种。
在MATLAB信号处理工具箱里,提供了这些类型的IIR数字滤波器设计子函数。
(二)性能指标1.假设带通滤波器要求为保留6000hz~~7000hz频段,滤除小于2000hz和大宇9000hz频段2.通带衰减设为3Db,阻带衰减设为30dB,双线性变换法中T取1s.四、实验步骤:1.初始化指标参数2.计算模拟滤波器参数并调用巴特沃斯函数产生模拟滤波器3.利用冲激响应不变法和双线性变换法求数字IIR滤波器的系统函数Hd (z)4.分别画出两种方法的幅频特性和相频特性曲线5.生成一定信噪比的带噪信号6.画出带噪信号的时域图和频谱图6.对带噪信号进行滤波,并画出滤波前后波形图和频谱图五、实验结果模拟滤波器的幅频特性和相频特性:101010101Frequency (rad/s)P h a s e (d e g r e e s )1010101011010-5100Frequency (rad/s)M a g n i t u d e在本实验中,采用的带通滤波器为6000-7000Hz ,换算成角频率为4.47-0.55,在上图中可以清晰地看出到达了题目的要求。
冲击响应不变法后的幅频特性和相频特性:0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )双线性变换法的幅频特性和相频特性:0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )00.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )通过上图比较脉冲响应不变法双线性变换法的幅频特性和相频特性,而在在幅频曲线上几乎没有差别,都能达到相同的结果。
二IIR数字滤波器的设计

五、实验报告要求
1.简述实验原理及目的。 2.按照实验步骤及要求,比较各种情况下的 滤波性能。 3.总结实验所得主要结论。 4.简要回答思考题。
1
s平面的虚轴单值地映射于z平面的单位圆上,s平面 的左半平面完全映射到z平面的单位圆内。双线性变 换不存在混叠问题。 双线性变换是一种非线性变换,这种非线性引起的 幅频特性畸变可通过预畸而得到校正。
二、实验原理
以低通数字滤波器为例,将设计步骤归纳如下: (1)确定数字滤波器的性能指标:通带临界频率fp、阻带临界 频率fs;通带内的最大衰减Ap;阻带内的最小衰减As; (2)确定相应的数字角频率,ωp=2πfp/Fs;ωs=2πfs/Fs; (3)计算经过预畸的相应模拟低通原型的频率,; (4)根据Ωp和Ωs计算模拟低通原型滤波器的阶数N,并求 得低通原型的传递函数Ha(s); (5)用上面的双线性变换公式代入Ha(s),求出所设计的传 递函数H(z); (6)分析滤波器特性,检查其指标是否满足要求。
实验二 IIR数字滤波器的设计
一、实验目的
1.掌握双线性变换法及脉冲相应不变法设计 IIR数字滤波器的具体设计方法及其原理,熟 悉用双线性变换法及脉冲响应不变法设计低 通、高通和带通IIR数字滤波器的计算机编程。 2.观察双线性变换及脉冲响应不变法设计的 滤波器的频域特性,了解双线性变换法及脉 冲响应不变法的特点。
二、实验原理
1.脉冲响应不变法 用数字滤波器的单位脉冲响应序列h(n)模仿 模拟滤波器的冲激响应ha(t),让h(n)正好等于 ha(t)的采样值,即h(n)=ha(nT),其中T为采 样间隔。
二、实验原理
用脉冲响应不变法设计数字滤波器

用脉冲响应不变法设计数字滤波器(总22页)-本页仅作为预览文档封面,使用时请删除本页-皖西学院《数字信号处理》课程设计报告题目用脉冲响应不变法设计数字滤波器学院信息工程学院专业通信工程专业班级(*** )班学生姓名陈* 孙**指导教师吴**二 0一二年十二月《数字信号处理》课程设计是在学生完成数字信号处理和MATLAB结合后的基本实验后开设的,本课程设计的目的是为了让学生综合数字信号处理和MATLAB并实现一个较为完整的小型滤波系统。
这一点与验证性的基本实验有本质性的区别。
开设课程设计环节的主要目的是通过系统设计、软件仿真、程序安排与调试、写实习报告等步骤,使学生初步掌握工程设计的具体步骤和方法,提高分析问题和解决问题的能力,提高实际应用水平。
IIR数字滤波器具有无限宽的冲激响应,与模拟滤波器相匹配,所以IIR滤波器的设计可以采用在模拟滤波器设计的基础上进一步变换的方法。
其设计方法主要有间接设计法、直接设计法和最大平滑滤波器设计方法。
间接法是借助于模拟滤波器的设计方法进行的。
其设计步骤是:先设计过度模拟滤波器得到系统函数,然后将其按某种方法转换成数字滤波器的系统函数。
这是因为模拟滤波器的设计方法已经成熟,不仅有完整的设计公式,还有完善的图表和曲线供查阅;另外还有一些优良的滤波器可供我们使用。
直接法直接在频域或者时域中设计数字滤波器,由于要解联立方程,设计时需要计算机辅助设计。
FIR数字滤波器的单位脉冲响应应是有限长序列。
它的设计问题实质上是确定能满足要求的转移序列或脉冲响应的常数问题,它不能采用间接法,设计方法主要有窗函数法、频率采样法和等波纹最佳逼近法等。
第1章绪论........................................................................................................ 错误!未定义书签。
课程设计的目的及意义.............................................................................. 错误!未定义书签。
第5章无限长单位脉冲响应(IIR)数字滤波器的设计方法

|ω|≤ωp
在阻带内,幅度响应以误差小于δ2而逼近于零,即
| H ( e jω ) |≤ δ 2
ωs≤|ω|≤π
式中,ωp, ωs分别为通带截止频率和阻带截止频率,它们都是 数字域频率。幅度响应在过渡带(ωs-ωp)中从通带平滑地下降 到阻带,过渡带的频率响应不作规定。
第5章 无限长单位脉冲响应(IIR)数字滤波器的设计方法
第5章 无限长单位脉冲响应(IIR)数字滤波器的设计方法
5.1.2 滤波器的技术指标 理想滤波器(如理想低通滤波器)是非因果的, 其单位脉冲响 应从-∞延伸到+∞, 因此,无论用递归还是非递归方法, 理想滤 波器是不能实现的, 但在概念上极为重要。 一般来说,滤波器的性能要求往往以频率响应的幅度特性的 允许误差来表征。以低通滤波器为例,如图5-2(称容限图)所 示, 频率响应有通带、 过渡带及阻带三个范围(而不是理想的 陡截止的通带、阻带两个范围)。图中δ1为通带的容限,δ2为阻 带的容限。
第5章 无限长单位脉冲响应(IIR)数字滤波器的设计方法
无限长单位脉冲响应(IIR) 第5章 无限长单位脉冲响应(IIR) 数字滤波器的设计方法
5.1 基本概念 5.2 IIR滤波器设计的特点 滤波器设计的特点 5.3 常用模拟低通滤波器的设计方法 5.4 用脉冲响应不变法设计 用脉冲响应不变法设计IIR数字滤波器 数字滤波器 5.5 用双线性变换法设计IIR数字滤波器 用双线性变换法设计 数字滤波器 5.6 设计 设计IIR滤波器的频率变换法 滤波器的频率变换法 5.7 Z平面变换法 平面变换法
第5章 无限长单位脉冲响应(IIR)数字滤波器的设计方法
5.1.3 FIR型滤波器和 型滤波器 型滤波器和IIR型滤波器 型滤波器和 数字滤波器按单位脉冲响应h(n)的时域特性可分为无限长脉 冲响应IIR(Infinite Impulse Response)滤波器和有限长脉冲响应 FIR(Finite Impulse Response)滤波器。 IIR滤波器一般采用递归型的实现结构。其N阶递归型数字滤 波器的差分方程为
无限冲激响应数字滤波器设计实验报告

实验5 无限冲激响应数字滤波器设计一、实验目的1、掌握双线性变换法及脉冲相应不变法设计IIR数字滤波器的具体设计方法;2、熟悉用双线性变换法及脉冲响应不变法设计低通、高通和带通IIR数字滤波器的计算机编程。
二、实验原理在MATLAB中,可以用下列函数辅助设计IIR数字滤波器:1)利用buttord和cheb1ord可以确定低通原型巴特沃斯和切比雪夫滤波器的阶数和截止频率;如:求阶数[N, Wn] = cheb1ord (Wp, Ws, Rp, Rs,’s’)选择项说明:high-类别。
缺省为low; s-模/数,缺省为数Rp即p, Rs即s ; Wn-Chebyshev自然频率(3dB频率),数字设计: Wp =p/ Ws=s/ 。
2)[num,den]=butter(N,Wn)(巴特沃斯)和[num,den]=cheby1(N,Wn),[num,den]=cheby2(N,Wn)(切比雪夫1型和2型)可以进行滤波器的设计;3)lp2hp,lp2bp,lp2bs可以完成低通滤波器到高通、带通、带阻滤波器的转换;4)使用bilinear可以对模拟滤波器进行双线性变换,求得数字滤波器的传输函数系数;5)利用impinvar可以完成脉冲响应不变法的模拟滤波器到数字滤波器的转换。
三、实验内容利用MATLAB编程,用脉冲响应不变法和双线性变换法设计一个数字带通滤波器,指标要求如下:通带边缘频率:,,通带峰值起伏:;阻带边缘频率:,,最小阻带衰减:。
1.采用切比雪夫程序:%%%%%%%%%%%采用切比雪夫%%%%%%%%%%脉冲响应format compactfs=1000;%%%%%%%%%%采样频率wp1=0.45*pi*fs;wp2=0.65*pi*fs;ws1=0.3*pi*fs;ws2=0.8*pi*fs;[N,wn]=cheb1ord([wp1 wp2],[ws1 ws2],1,40,'s');[B,A]=cheby1(N,1,wn,'s');[num,den]=impinvar(B,A,fs);[h1,w]=freqz(num,den);%%%%%%%%%%双线性法wp3=2*fs*tan(pi*0.45/2);wp4=2*fs*tan(pi*0.65/2);ws3=2*fs*tan(pi*0.3/2);ws4=2*fs*tan(pi*0.8/2);[N,wn]=cheb1ord([wp1 wp2],[ws1 ws2],1,40,'s');[B,A]=cheby1(N,1,wn,'s');[num,den]=bilinear(B,A,fs);[h2,w]=freqz(num,den);f=w/pi*fs/2;plot(f,20*log10(abs(h1)),'-.',f,20*log10(abs(h2)),'-'); axis([0,600,-80,10]);grid;title('采用切比雪夫')xlabel('f')ylabel('幅度/dB')图形:2.采用巴特沃斯的程序:%%%%%%%%%%%%%%%%采用巴特沃斯format compactfs=1000;%%%%%%%%%%采样频率wp1=0.45*pi*fs;wp2=0.65*pi*fs;ws1=0.3*pi*fs;ws2=0.8*pi*fs;[N,wn]=buttord([wp1 wp2],[ws1 ws2],1,40,'s'); [B,A]=butter(N,wn,'s');[num,den]=impinvar(B,A,fs);[h1,w]=freqz(num,den);%%%%%%%%%%双线性法wp3=2*fs*tan(pi*0.45/2);wp4=2*fs*tan(pi*0.65/2);ws3=2*fs*tan(pi*0.3/2);ws4=2*fs*tan(pi*0.8/2);[N,wn]=buttord([wp1 wp2],[ws1 ws2],1,40,'s');[B,A]=butter(N,wn,'s');[num,den]=bilinear(B,A,fs);[h2,w]=freqz(num,den);f=w/pi*fs/2;plot(f,20*log10(abs(h1)),'-.',f,20*log10(abs(h2)),'-');axis([0,600,-80,10]);grid;title('采用巴特沃斯')xlabel('f')ylabel('幅度/dB')图形:四.小结双线性变换法采用非线性频率压缩方法,它克服了频率混叠的现象,它适合低通,高通,带通,带阻滤波器的设计;用脉冲响应不变法设计的优点是频率坐标变换是线性的,它可以很好的重现原模拟滤波器的频率特性,但它只适合低通和带通滤波器的设计。
脉冲响应不变法与双线性变换发设计IIR滤波器.doc

实验四 脉冲响应不变法和双线性变换法设计IIR 滤波器⏹ 实验学时:2学时⏹ 实验类型:设计、验证一 、实验目的1、熟悉脉冲响应不变法和双线性变换法设计IIR 滤波器的原理2、掌握脉冲响应不变法和双线性变换法设计IIR 滤波器的具体设计方法、步骤。
3、观察实验现象,比较脉冲响应不变法和双线性变换法设计IIR 滤波器的特点4、熟悉impinvar ,freqz ,butter ,bilinear 等函数的应用二、实验原理1. 脉冲响应不变法用数字滤波器的单位脉冲响应序列)(n h 模仿模拟滤波器的冲激响应)(t h a ,让)(n h 正好等于)(t h a 的采样值,即)()(nT h n h a =,其中T 为采样间隔,如果以)(s H a 及)(z H 分别表示)(t h a 的拉式变换及)(n h 的Z 变换,则)2(1)(m Tj s H T z H m a e z sT ∑∞-∞==+=π2.双线性变换法S 平面与z 平面之间满足以下映射关系:);(,2121,11211ωωσj re z j s s T s T z z z T s =+=-+=+-⋅=-- s 平面的虚轴单值地映射于z 平面的单位圆上,s 平面的左半平面完全映射到z 平面的单位圆内。
双线性变换不存在混叠问题。
双线性变换是一种非线性变换,这种非线性引起的幅频特性畸变可通过预畸而得到校正。
以低通数字滤波器为例,将设计步骤归纳如下:1. 确定数字滤波器的性能指标:通带临界频率c f 、阻带临界频率r f 、通带波动δ、阻带内的最小衰减At 、采样周期T 、采样频率s f ;2. 确定相应的数字角频率,T f c c πω2=;T f r r πω2=;3. 计算经过预畸的相应模拟低通原型的频率,)2(2c c tg T ω=Ω,)2(2r r tg T ω=Ω; 4. 根据Ωc 和Ωr 计算模拟低通原型滤波器的阶数N ,并求得低通原型的传递函数)(s H a ;5. 用上面的双线性变换公式代入)(s H a ,求出所设计的传递函数)(z H ;6. 分析滤波器特性,检查其指标是否满足要求。
使用脉冲响应不变法设计切比雪夫I型IIR滤波器

语音信号滤波去噪—脉冲响应不变法设计的并联型切比雪夫I型滤波器学生姓名:指导老师:摘要本课程设计主要内容是使用脉冲响应不变法设计的并联型切比雪夫I型IIR滤波器,对一段含噪语音信号进行滤波去噪处理并根据滤波前后的波形和频谱分析滤波性能。
本课程设计仿真平台为MATLAB7.0,开发工具是M语言编程。
首先利用录音工具录制一段语音信号,并人为加入一单频噪声,然后对信号进行频谱分析以确定所加噪声频率,并设计滤波器进行滤波去噪处理,最后比较滤波前后的波形和频谱并进行分析。
由分析结果可知,滤波器后的语音信号与原始信号基本一致,即设计的切比雪夫I型IIR 滤波器能够去除信号中所加单频噪声,达到了设计目的。
关键词滤波去噪;脉冲响应不变法;切比雪夫I型;IIR滤波器;MATLAB1 引言本课程设计主要解决在含噪情况下对语音信号的滤波去噪处理,处理时采用的是利用脉冲响应不变法设计的切比雪夫I型IIR滤波器。
1.1 课程设计目的(1)熟悉使用MATLAB语言来解决一些简单的课程问题。
(2)锻炼动手能力及独立思考并解决问题的能力(3)增加对书本知识的理解以及掌握,如:IIR滤波器的工作原理,切比雪夫滤波器的设计,脉冲响应法的应用等等;(4)对录制好的音频行加噪和过滤,比较前后语音变化;1.2 课程设计内容(1)使用录音软件;录制一段语音信号,要求为PCM 编码格式 单声道8K 8位 7k/s 的语音信号,绘制波形并观察频谱特点;(2)加上噪声并绘制加噪信号波形及观察其频谱特点; (3)设计滤波器,绘制出滤波器的频谱并检验滤波器是否合格;(4)最后使用设计好的滤波器对噪声信号进项过滤,绘制过滤后的波形及观察滤波前后频谱变化;(5)绘制滤波器的并联型结构图;2 设计原理录制一段语音信号,绘制波形并观察其频谱,给定相应技术指标,用脉冲响应不变法设计的一个满足指标的切比雪夫I 型IIR 滤波器,对该语音信号进行滤波去噪处理,比较滤波前后的波形和频谱并进行分析。
实验五:双线性变换法的设计IIR-数字滤波器
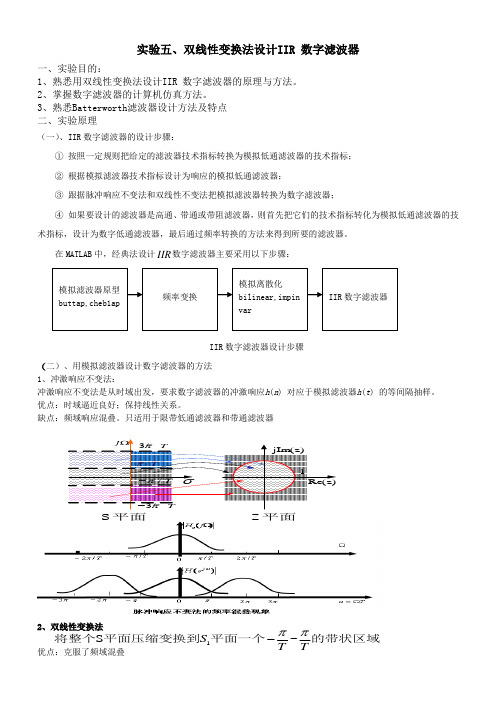
实验五、双线性变换法设计IIR 数字滤波器一、实验目的:1、熟悉用双线性变换法设计IIR 数字滤波器的原理与方法。
2、掌握数字滤波器的计算机仿真方法。
3、熟悉Batterworth 滤波器设计方法及特点 二、实验原理(一)、IIR 数字滤波器的设计步骤:① 按照一定规则把给定的滤波器技术指标转换为模拟低通滤波器的技术指标; ② 根据模拟滤波器技术指标设计为响应的模拟低通滤波器;③ 跟据脉冲响应不变法和双线性不变法把模拟滤波器转换为数字滤波器;④ 如果要设计的滤波器是高通、带通或带阻滤波器,则首先把它们的技术指标转化为模拟低通滤波器的技术指标,设计为数字低通滤波器,最后通过频率转换的方法来得到所要的滤波器。
在MATLAB 中,经典法设计IIR 数字滤波器主要采用以下步骤:IIR 数字滤波器设计步骤(二)、用模拟滤波器设计数字滤波器的方法 1、冲激响应不变法:冲激响应不变法是从时域出发,要求数字滤波器的冲激响应h (n ) 对应于模拟滤波器h (t ) 的等间隔抽样。
优点:时域逼近良好;保持线性关系。
缺点:频域响应混叠。
只适用于限带低通滤波器和带通滤波器2、双线性变换法优点:克服了频域混叠模拟滤波器原型 buttap,cheb1ap频率变换 模拟离散化 bilinear,impin varIIR 数字滤波器/Tπ/T π-3/Tπ3/Tπ-j ΩσjIm (z)Re(z)1S 平面Z 平面1S ~S T Tππ-将整个平面压缩变换到平面一个的带状区域缺点:高频时会引起畸变1)冲激响应不变法impinvar格式:[BZ,AZ]= impinvar (B,A,Fs )功能:把具有[B,A]模拟滤波器传递函数模型转换为采样频率为Fs 的数字滤波器的传递函数模型[BZ,AZ],Fs 默认值为1。
例:一个4阶的Butterworth 模拟低通滤波器的系统函数如下:12251)(234++++=s s s s s H a试用冲激响应不变法求出Butterworth 模拟低通数字滤波器的系统函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
标准 文案 实验5脉冲响应不变法设计IIR数字滤波器
一、实验目的 1.掌握利用脉冲响应不变法设计IIR数字滤波器的原理及具体方法。 2.加深理解数字滤波器和模拟滤波器之间的技术指标转化。 3.掌握脉冲响应不变法设计IIR数字滤波器的优缺点及适用范围。 二、实验设备及环境
计算机、matlab软件环境。 三、实验基础理论
1.基本原理 从时域响应出发,是数字录波器的单位脉冲响应h(n)模仿模拟滤波器的单位冲击响应ha(t),h(n)等于ha
(t)的取样值。
2变换方法 Ha(s)拉氏反变换→ ha(t)时域采样→ ℎa(nT)=h(n)z变换→ H(z) 将Ha
(s)进行部分分式展开
Ha(s)=∑
Ak
s−pk
N
k=1 (2)对Ha
(s)进行拉式变换
ha(t)=∑Akepku(t)Nk=1 标准 文案 (3)对ha
(t)时域采样得到h(n)
h(n)=∑AkepknTu(nT)Nk=1=∑Ak(epkT)nu(n)N
k=1 (4)对h(n)进行z变换
H(z)=∑
Ak
1−epkz−1
N
k=1 3.设计步骤
(1)确定数字滤波器性能指标ωp,ωst,Rp和As。 (2)将数字滤波器频率指标转换成相应的模拟滤波器频率指标 Ωp=ωpTΩst=ωst
T
(3)根据指标ωp,ωst,Rp和As设计模拟滤波器Ha
(s)。
(4)将Ha
(s)展成部分分式形式
Ha(s)=∑
Ak
s−pk
N
k=1 (5)将模拟极点Pk转换成数字极点ePkT,得到数字滤波器
Ha(s)=∑
Ak
1−epkTz−1
N
k=1 可见Ha
(s)至H(z)间的变换关系为
1s−sk<=>11−eskTz−1=zz−eskT
在MATLAB中有两种方法可以实现上述变换。 方法1:利用residue函数和residuez函数实现脉冲响应不变法,这两个函数的使用方法如下 标准 文案 [r,p,k]=residue(b,a) [b,a]=reisdue(r,p,k) 实现多项式形式
H(s)=bMsM+bM−1sM−1+⋯+b0
aNsN+aN−1sN−1+⋯+a0
和部分分式形式
H(s)=r1s−p1+r2s−p2+⋯+rNs−pN+k(s) 之间的转换。 [r,p,k]=residuez(b,a) [b,a]=reisduez(r,p,k) 实现多项式形式
H(z)=b0+b1z−1+⋯+bMz−Ma0+a1z−1+⋯+aNz−N
和部分分式形式 H(z)=r11−p1z−1+r21−p2z−1+⋯+rk1−pkz−1+k1+k2z−1+⋯ 之间的转换。
方法2:MATLAB提供了impinvar函数采用脉冲响应不变法实现模拟滤波器到数字滤波器的变换,其使用方法如下 [bz,az]=impinvar(b,a,fs)采用脉冲响应不变法将模拟滤波器系统函数的系数向量b和a变换成为数字滤波器系统函数的系统向量bz和az,fs为采样频率。 标准 文案 [bz,az]=impinvar(b,a)采样频率默认为1的情况下,采用脉冲响应不变法将模拟滤波器变换为数字滤波器。
四、实验内容 1.设采用率为fs
=4kHz,采用脉冲响应不变法设计一个三阶巴特
沃斯数字低通滤波器,其3dB截止频率为fc
=1kHz。
实验代码及结果: >> [b, a] = butter(3, 0.5*pi, 's')
b = 0 0 0 3.8758
a = 1.0000 3.1416 4.9348 3.8758 >> [bz, az] = impinvar(b, a) bz = 0 0.5813 0.2114 0
az = 1.0000 -0.3984 0.2475 -0.0432 >> w = [0:500]*pi/500; >> [H, w] = freqz(bz, az); >>subplot(211); >>plot(w/pi, abs(H)); 标准 文案 >>xlabel('\omega(\pi)'); >>ylabel('|H(e^j^\omega)|'); >>subplot(212); >>plot(w/pi, angle(H)/pi); >>xlabel('\omega(\pi)'); >>ylabel('Phase of H(e^j^\omega)(\pi)');
2.设采用频率为fs=10kHz,设计数字低通滤波器,满足如下指标: 通带截止频率:fp=1kHz,通带波动:Rp
=1dB
阻带截止频率:fst=1.5kHz,阻带衰减:As
=15dB
要求分别采用巴特沃斯、切比雪夫1型、切比雪夫2型和椭圆模拟原型滤波器及脉冲响应不变法进行设计。结合实验结果,分别讨论采用上述方法设计的数字滤波器是否都能满足给定指标要求,分析脉冲响应不变法设计IIR数字滤波器的优缺点及适用范围。 实验代码及结果:
00.10.20.30.40.50.60.70.80.910.20.40.60.81()
|H(ej)|
00.10.20.30.40.50.60.70.80.91-1-0.500.51()
Phase of H(ej)()标准
文案 Butterworth滤波器: >> [N, Wn] = buttord(0.2*pi, 0.3*pi, 1, 15, 's')
N = 6
Wn = 0.7087 >> [b, a] = butter(N, Wn, 's') b = 0 0 0 0 0 0 0.1266
a = 1.0000 2.7380 3.7484 3.2533 1.8824 0.6905 0.1266
>> [bz, az] = impinvar(b, a) bz = -0.0000 0.0007 0.0105 0.0167 0.0042 0.0001 0
az = 1.0000 -3.3443 5.0183 -4.2190 2.0725 -0.5600 0.0647 标准 文案 >> w = [0:500]*pi/500; [H, w] = freqz(bz, az); subplot(211); plot(w/pi, abs(H)); xlabel('\omega(\pi)'); ylabel('|H(e^j^\omega)|'); subplot(212); plot(w/pi, angle(H)/pi); xlabel('\omega(\pi)'); ylabel('Phase of H(e^j^\omega)(\pi)');
(2) Chebyshev I型 >> [N, Wn] = cheb1ord(0.2*pi, 0.3*pi, 1, 15, 's')
N = 4
00.10.20.30.40.50.60.70.80.9100.51()
|H(ej)|
00.10.20.30.40.50.60.70.80.91-1-0.500.51()
Phase of H(ej)()标准
文案 Wn = 0.6283 >> [b, a] = cheby1(N, 1, Wn, 's') b = 0 0 0 0 0.0383
a = 1.0000 0.5987 0.5740 0.1842 0.0430 >> [bz, az] = impinvar(b, a) bz = -0.0000 0.0054 0.0181 0.0040 0
az = 1.0000 -3.0591 3.8323 -2.2919 0.5495 >> w = [0:500]*pi/500; >> [H, w] = freqz(bz, az); >>subplot(211); >>plot(w/pi, abs(H)); >>grid on; >>xlabel('\omega(\pi)'); >>ylabel('|H(e^j^\omega)|'); >>subplot(212); >>plot(w/pi, angle(H)/pi); >>grid on;
