二次函数综合大题压轴题Word版
二次函数单元综合测试(Word版 含答案)

二次函数单元综合测试(Word版含答案)一、初三数学二次函数易错题压轴题(难)1.如图,二次函数y=ax2+bx+c交x轴于点A(1,0)和点B(3,0),交y轴于点C,抛物线上一点D的坐标为(4,3)(1)求该二次函数所对应的函数解析式;(2)如图1,点P是直线BC下方抛物线上的一个动点,PE//x轴,PF//y轴,求线段EF的最大值;(3)如图2,点M是线段CD上的一个动点,过点M作x轴的垂线,交抛物线于点N,当△CBN是直角三角形时,请直接写出所有满足条件的点M的坐标.【答案】(1)y=x2﹣4x+3;(2)EF的最大值为24;(3)M点坐标为可以为(2,3),(552+,3),(552-,3).【解析】【分析】(1)根据题意由A、B两点坐标在二次函数图象上,设二次函数解析式的交点式,将D点坐标代入求出a的值,最后将二次函数的交点式转化成一般式形式.(2)由题意可知点P在二次函数图象上,坐标为(p,p2﹣4p+3).又因为PF//y轴,点F 在直线BC上,P的坐标为(p,﹣p+3),在Rt△FPE中,可得FE2PF,用纵坐标差的绝对值可求线段EF的最大值.(3)根据题意求△CBN是直角三角形,分为∠CBN=90°和∠CNB=90°两类情况计算,利用三角形相似知识进行分析求解.【详解】解:(1)设二次函数的解析式为y=a(x﹣b)(x﹣c),∵y=ax2+bx+与x轴r的两个交点A、B的坐标分别为(1,0)和(3,0),∴二次函数解析式:y=a(x﹣1)(x﹣3).又∵点D(4,3)在二次函数上,∴(4﹣3)×(4﹣1)a=3,∴解得:a=1.∴二次函数的解析式:y=(x﹣1)(x﹣3),即y=x2﹣4x+3.(2)如图1所示.因点P 在二次函数图象上,设P (p ,p 2﹣4p+3).∵y =x 2﹣4x+3与y 轴相交于点C ,∴点C 的坐标为(0,3).又∵点B 的坐标为B (3,0),∴OB =OC∴△COB 为等腰直角三角形.又∵PF//y 轴,PE//x 轴,∴△PEF 为等腰直角三角形.∴EF 2PF .设一次函数的l BC 的表达式为y =kx+b ,又∵B (3,0)和C (0,3)在直线BC 上,303k b b +=⎧⎨=⎩, 解得:13k b =-⎧⎨=⎩, ∴直线BC 的解析式为y =﹣x+3.∴y F =﹣p+3.FP =﹣p+3﹣(p 2﹣4p+3)=﹣p 2+3p .∴EF 2p 22.∴线段EF 的最大值为,EF max 42-24. (3)①如图2所示:若∠CNB =90°时,点N 在抛物线上,作MN//y 轴,l//x 轴交y 轴于点E ,BF ⊥l 交l 于点F .设点N 的坐标为(m ,m 2﹣4m+3),则点M 的坐标为(m ,3),∵C 、D 两点的坐标为(0,3)和(4,3),∴CD ∥x 轴.又∵∠CNE =∠NBF ,∠CEN =∠NFB =90°,∴△CNE ∽△NBF .∴CE NE =NF BF, 又∵CE =﹣m 2+4m ,NE =m ;NF =3﹣m ,BF =﹣m 2+4m ﹣3,∴24m m m-+=2343m m m --+-, 化简得:m 2﹣5m+5=0.解得:m 1=552+,m 2=552-. ∴M 点坐标为(55+,3)或(55-,3) ②如图3所示:当∠CBN =90°时,过B 作BG ⊥CD ,∵∠NBF =∠CBG ,∠NFB =∠BGC =90°,∴△BFN ∽△CGB .∵△BFN 为等腰直角三角形,∴BF =FN ,∴0﹣(m 2﹣4m+3)=3﹣m .∴化简得,m 2﹣5m+6=0.解得,m =2或m =3(舍去)∴M 点坐标为,(2,3). 综上所述,满足题意的M 点坐标为可以为(2,3),(552+,3),(552-,3). 【点睛】本题考查待定系数法求解函数解析式,二次函数和三角函数求值,三角形相似等相关知识点;同时运用数形结合和分类讨论的思想探究点在几何图形上的位置关系.2.在平面直角坐标系中,抛物线22(0)y ax bx a =++≠经过点(2,4)A --和点(2,0)C ,与y 轴交于点D ,与x 轴的另一交点为点B .(1)求抛物线的解析式;(2)如图1,连接BD ,在抛物线上是否存在点P ,使得2PBC BDO ∠=∠?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)如图2,连接AC ,交y 轴于点E ,点M 是线段AD 上的动点(不与点A ,点D 重合),将CME △沿ME 所在直线翻折,得到FME ,当FME 与AME △重叠部分的面积是AMC 面积的14时,请直接写出线段AM 的长. 【答案】(1)22y x x =-++;(2)存在,(23,209)或(103,529-);(3)5或 【解析】【分析】(1)根据点A 和点C 的坐标,利用待定系数法求解;(2)在x 轴正半轴上取点E ,使OB=OE ,过点E 作EF ⊥BD ,垂足为F ,构造出∠PBC=∠BDE ,分点P 在第三象限时,点P 在x 轴上方时,点P 在第四象限时,共三种情况分别求解;(3)设EF 与AD 交于点N ,分点F 在直线AC 上方和点F 在直线AC 下方时两种情况,利用题中所给面积关系和中线的性质可得MN=AN ,FN=NE ,从而证明四边形FMEA 为平行四边形,继而求解.【详解】解:(1)∵抛物线22(0)y ax bx a =++≠经过点A (-2,-4)和点C (2,0),则44220422a b a b -=-+⎧⎨=++⎩,解得:11a b =-⎧⎨=⎩, ∴抛物线的解析式为22y x x =-++;(2)存在,理由是:在x 轴正半轴上取点E ,使OB=OE ,过点E 作EF ⊥BD ,垂足为F ,在22y x x =-++中,令y=0,解得:x=2或-1,∴点B 坐标为(-1,0),∴点E 坐标为(1,0),可知:点B 和点E 关于y 轴对称,∴∠BDO=∠EDO ,即∠BDE=2∠BDO ,∵D (0,2),∴=,在△BDE 中,有12×BE ×OD=12×BD ×EF ,即2×EF ,解得:,∴,∴tan ∠BDE=EF DF =55÷=43, 若∠PBC=2∠BDO ,则∠PBC=∠BDE ,∵BE=2,则BD 2+DE 2>BE 2,∴∠BDE 为锐角,当点P 在第三象限时,∠PBC 为钝角,不符合;当点P 在x 轴上方时,∵∠PBC=∠BDE ,设点P 坐标为(c ,22c c -++),过点P 作x 轴的垂线,垂足为G ,则BG=c+1,PG=22c c -++,∴tan ∠PBC=PG BG =221c c c -+++=43, 解得:c=23, ∴22c c -++=209, ∴点P 的坐标为(23,209);当点P 在第四象限时,同理可得:PG=22c c --,BG=c+1,tan ∠PBC=PG BG =221c c c --+=43, 解得:c=103, ∴22c c -++=529-, ∴点P 的坐标为(103,529-), 综上:点P 的坐标为(23,209)或(103,529-);(3)设EF 与AD 交于点N ,∵A (-2,-4),D (0,2),设直线AD 表达式为y=mx+n ,则422m n n -=-+⎧⎨=⎩,解得:32m n =⎧⎨=⎩, ∴直线AD 表达式为y=3x+2,设点M 的坐标为(s ,3s+2),∵A (-2,-4),C (2,0),设直线AC 表达式为y=m 1x+n 1,则11114202m n m n -=-+⎧⎨=+⎩,解得:1112m n =⎧⎨=-⎩, ∴直线AC 表达式为y=x-2,令x=0,则y=-2,∴点E 坐标为(0,-2),可得:点E 是线段AC 中点,∴△AME 和△CME 的面积相等,由于折叠,∴△CME ≌△FME ,即S △CME =S △FME ,由题意可得:当点F 在直线AC 上方时,∴S △MNE =14S △AMC =12S △AME =12S △FME , 即S △MNE = S △ANE = S △MNF ,∴MN=AN ,FN=NE ,∴四边形FMEA 为平行四边形, ∴CM=FM=AE=12AC=221442+22 ∵M (s ,3s+2), ()()2223222s s -++=解得:s=45-或0(舍),∴M (45-,25-), ∴AM=22422455⎛⎫⎛⎫-++-+ ⎪ ⎪⎝⎭⎝⎭=6105,当点F 在直线AC 下方时,如图,同理可得:四边形AFEM 为平行四边形,∴AM=EF ,由于折叠可得:CE=EF ,∴AM=EF=CE=22,综上:AM 的长度为105或22 【点睛】 本题是二次函数综合题,涉及到待定系数法,二次函数的图像和性质,折叠问题,平行四边形的判定和性质,中线的性质,题目的综合性很强.难度很大,对学生的解题能力要求较高.3.如图,抛物线()250y ax bx a =+-≠经过x 轴上的点1,0A 和点B 及y 轴上的点C ,经过B C 、两点的直线为y x n =+.(1)求抛物线的解析式.(2)点P 从A 出发,在线段AB 上以每秒1个单位的速度向B 运动,同时点E 从B 出发,在线段BC 上以每秒2个单位的速度向C 运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t 秒,求t 为何值时,PBE △的面积最大并求出最大值. (3)过点A 作AM BC ⊥于点M ,过抛物线上一动点N (不与点B C 、重合)作直线AM 的平行线交直线BC 于点Q .若点A M N Q 、、、为顶点的四边形是平行四边形,求点N 的横坐标.【答案】(1)265y x x =-+- (2)2t =;2(3)5412或4或5412【解析】【分析】(1)先确定A 、B 、C 三点的坐标,然后用待定系数法解答即可;(2)先求出AB 、BC 的长并说明△BOC 是等腰直角三角形,再求出点P 到BC 的高d 为()24542d BP sin t =⋅︒=-,则12PBE S BE d =⨯⨯)()122244222t t t =⨯⨯-=-,再根据二次函数的性质即可确定最大值; (3)先求出2454222AM AB sin =⋅︒=⨯=N 作直线AM 的平行线交直线BC 于点,Q 则,再说明四边形AMNQ 是平行四边形,得到22NQ AM ==;再过点N 作NH x ⊥轴,交x 轴于点,G 交BC 于点,H 结合题意说明NQH 为等腰直角三角形,求得22884NH NQ HQ =+=+=;设()2,65N m m m -+-,则(),0G m , (),5H m m -,最后分点N 在x 轴上方时、点N 在x 轴下方且5m >时和1m <三种情况解答即可.【详解】解:()1因为直线y x n =+经过B C 、两点,且点B 在x 轴上,点C 在y 轴上, ∵()(),,00,B n C n -∴抛物线25y ax bx =+-经过点1,0A ,点(),0B n -,点()0,C n ,∴250505a b an bn n +-=⎧⎪--=⎨⎪-=⎩,解得51,6n a b =-⎧⎪=-⎨⎪=⎩所以抛物线的解析式为265y x x =-+-.()2∵()()()1,05,0,0,,5,A B C -∴4,AB BC BOC ==为等腰直角三角形,∴45,ABC ∠=由题意得4,2,02BP t BE t t =-=<≤点P 到BE的距离()4542d BP sin t =⋅︒=- 所以12PBE S BE d =⨯⨯)()1244222t t t t =⨯⨯-=-; ∵二次函数()()42f t t =-的函数图象开口向下,零点为0和4, ∴0422t +==时, ∴()()()22422maxf t f ==⨯⨯-=即2t =时,PBE △的面积最大,且最大值为()3由题意得454AM AB sin =⋅︒== 过点N 作直线AM 的平行线交直线BC 于点,Q 则,NQ BC ⊥ ∵点,A M N Q 、、为顶点的四边形是平行四边形,∴NQ AM ==过点N 作NH x ⊥轴,交x 轴于点,G 交BC 于点,H∵:5BC l y x =-,∴NQH 为等腰直角三角形,∴22884,NH NQ HQ =+=+=设()2,65N m m m -+-, 则(),0G m ,(),5H m m -,①点N 在x 轴上方时,此时()()2655,NH m m m =-+---∴()()26554m m m -+---=,即()()140,m m --=解得1m =(舍,因为此时点N 与点A 重合)或4m =;②点N 在x 轴下方且5m >时,此时()()2565,NH m m m =---+- ∴()()25654m m m ---+-=,即2540,m m --=解得54152m -=<(舍)或5412m +=③点N 在x 轴下方且1m <时,此时()()2565,NH m m m =---+- ∴()()25654m m m ---+-=,即2540,m m --=解得5412m -=或5412m +=(舍)综上所述,5414,2m m +==,5412m -=符合题意, 即若点,A M N Q 、、为顶点的四边形是平行四边形, 点N 的横坐标为541-或4或541+.【点睛】本题主要考查了二次函数的性质、平行四边形的判定与性质,掌握二次函数的性质以及分类讨论思想是解答本题的关键4.对于函数y =ax 2+(b+1)x+b ﹣2(a ≠0),若存在实数x0,使得a 20x +(b+1)x 0+b ﹣2=x0成立,则称x 0为函数y =ax 2+(b+1)x+b ﹣2(a ≠0)的不动点. (1)当a =2,b =﹣2时,求y =ax 2+(b+1)x+b ﹣2(a ≠0)的不动点;(2)若对于任何实数b ,函数y =ax 2+(b+1)x+b ﹣2(a ≠0)恒有两相异的不动点,求实数a 的取值范围;(3)在(2)的条件下,若y =ax 2+(b+1)x+b ﹣2(a ≠0)的图象上A ,B 两点的横坐标是函数y =ax 2+(b+1)x+b ﹣2(a ≠0)的不动点,且直线y =﹣x+2121a +是线段AB 的垂直平分线,求实数b 的取值范围.【答案】(1)不动点是﹣1或2;(2)a 的取值范围是0<a <2;(3)b 的取值范围是﹣4≤b <0. 【解析】 【分析】(1)将a =2,b =﹣2代入函数y =ax 2+(b+1)x+b ﹣2(a ≠0),得y =2x 2﹣x ﹣4,然后令x =2x 2﹣x ﹣4,求出x 的值,即y =ax 2+(b+1)x+b ﹣2(a ≠0)的不动点;(2)对于任何实数b ,函数y =ax 2+(b+1)x+b ﹣2(a ≠0)恒有两相异的不动点,可以得到x =ax 2+(b+1)x+b ﹣2(a ≠0)时,对于任何实数b 都有△>0,然后再设t =△,即可求得a 的取值范围;(3)根据y =ax 2+(b+1)x+b ﹣2(a ≠0)的图象上A ,B 两点的横坐标是函数y =ax 2+(b+1)x+b ﹣2(a ≠0)的不动点,可知点A 和点B 均在直线y =x 上,然后设出点A 和点B 的坐标,从而可以得到线段AB 的中点坐标,再根据直线y =﹣x+2121a +是线段AB 的垂直平分线,从而可以求得b 的取值范围. 【详解】解:(1)当a =2,b =﹣2时, 函数y =2x 2﹣x ﹣4, 令x =2x 2﹣x ﹣4, 化简,得x 2﹣x ﹣2=0 解得,x 1=2,x 2=﹣1,即y =ax 2+(b+1)x+b ﹣2(a ≠0)的不动点是﹣1或2; (2)令x =ax 2+(b+1)x+b ﹣2, 整理,得 ax 2+bx+b ﹣2=0,∵对于任何实数b ,函数y =ax 2+(b+1)x+b ﹣2(a ≠0)恒有两相异的不动点,∴△=b 2﹣4a (b ﹣2)>0,设t =b 2﹣4a (b ﹣2)=b 2﹣4ab+8a ,对于任何实数b ,t >0, 故(﹣4a )2﹣4×1×8a <0, 解得,0<a <2,即a 的取值范围是0<a <2; (3)由题意可得, 点A 和点B 在直线y =x 上, 设点A (x 1,x 1),点B (x 2,x 2),∵A ,B 两点的横坐标是函数y =ax 2+(b+1)x+b ﹣2(a ≠0)的不动点, ∴x 1,x 2是方程ax 2+bx+b ﹣2=0的两个根, ∴x 1+x 2=﹣b a, ∵线段AB 中点坐标为(122x x +,122x x+), ∴该中点的坐标为(2b a -,2b a-), ∵直线y =﹣x+2121a +是线段AB 的垂直平分线,∴点(2b a -,2ba -)在直线y =﹣x+2121a +上, ∴2ba -=21221b a a ++∴﹣b =221a a ≤+4,(当a =2时取等号)∴0<﹣b∴﹣4≤b <0,即b 的取值范围是﹣4≤b <0. 【点睛】本题是一道二次函数综合题、主要考查新定义、二次函数的性质、二次函数图象上点的坐标特征、一次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.5.在平面直角坐标系中,二次函数22y ax bx =+-的图象与x 轴交于点(4,0)A -,(1,0)B ,与y 轴交于点C .(1)求此抛物线的解析式;(2)点P 是抛物线22y ax bx =+-上的任意一点,过点P 作x 轴的垂线PD ,直线PD交直线AC 于点D .①是否存在点P ,使得PAC ∆的面积是ABC ∆面积的45?若存在,求出点P 的坐标;若不存在,请说明理由.②点Q 是坐标平面内的任意一点,若以O ,C ,Q ,D 为顶点的四边形是菱形时,请直接写出点Q 的坐标. 【答案】(1)213222y x x =+- (2)①存在,点P 的坐标为(22,12)-+-,(222,12)--+,(2,3)--②1816,55Q ⎫⎛-- ⎪⎝⎭,2(2,1)Q -,34525Q ⎝⎭,44525Q ⎛ ⎝⎭【解析】 【分析】(1)将(4,0)A -,(1,0)B 两点坐标代入解析式中求解即可; (2)①先求出△PAC 的面积为4,再求出直线AC 的解析式为122y x =--.设点P 的横坐标为(t ,213222t t +-),利用21442∆∆∆=-=⋅=+=PAC PDC PDA S S S OA PD t t 即可求解; ②先设出D 点坐标,然后再按对角线分成三种情况讨论即可求解. 【详解】解:(1)由题意得,将(4,0)A -,(1,0)B 两点坐标代入解析式中:1642020a b a b --=⎧⎨+-=⎩,解得:1232a b ⎧=⎪⎪⎨⎪=⎪⎩. ∴此抛物线的解析式为213222y x x =+-, 故答案为213222y x x =+-. (2)①存在点P ,使得PAC ∆的面积是ABC ∆面积的45.理由如下: 作出如下所示示意图:∵点(4,0)A -,(1,0)B , ∴4OA =,5AB =, 令0x =,则2y =-, ∴(0,2)C -,∴2OC =, ∴1152522ABC S AB OC ∆=⋅=⨯⨯=, ∴445545PAC ABC S S ∆∆==⨯=, 设直线AC 的解析式为y mx n =+,则有402m n n -+=⎧⎨=-⎩,解得:122m n ⎧=-⎪⎨⎪=-⎩,∴直线AC 的解析式为122y x =--.设点P 的横坐标为t ,则其纵坐标为213222t t +-, 即213,222P t t t ⎫⎛+- ⎪⎝⎭. ∵PD x ⊥轴,则点D 的坐标为1,22t t ⎫⎛-- ⎪⎝⎭. ∴2213112222222PD t t t t t ⎫⎛=+----=+ ⎪⎝⎭. ∵22111424222PAC PDC PDA S S S OA PD t t t t ∆∆∆=-=⋅=⨯⨯+=+. ∴244t t +=,即2440t t +-=或2440t t ++=, 解得:1222t =-+,2222t =--,32t =-.∴点P 的坐标为(222,12)-+-,(222,12)--+,(2,3)--, 故答案为:(222,12)-+-或(222,12)--+或(2,3)--. ②分类讨论:情况一:当OC 为菱形的对角线时,此时DO=DC ,即D 点在线段OC 的垂直平分线, ∴D 点坐标(-2,-1),将△OCD 沿y 轴翻折,此时四边形ODCQ 为菱形,故此时Q 点坐标为(2,-1),如下图一所示,情况二:当OQ 为对角线时,DO=DQ ,如下图二所示,DQ=OC=OD=2,设D 点坐标1,22⎛⎫-- ⎪⎝⎭x x ,则EO=-x ,DE=122x +,在Rt △EDO 中,由勾股定理可知:EO²+ED²=DO², 故221(2)42++=x x ,解得80(),5舍==-x x ,此时Q 点坐标为816,55⎛⎫-- ⎪⎝⎭,情况三:当OD 为对角线时,OC=OQ=2,如下图三所示:设D 点坐标1,22⎛⎫-- ⎪⎝⎭m m ,则EO=|m|,DE=122m +,QE=2-(122m +)=12m , 在Rt △QDO 中,由勾股定理可知:QE²+EO²=QO², 故221()()42+=m m ,解得124545,==-m m ,此时Q 点坐标为4525,⎛⎫- ⎪ ⎪⎝⎭或4525,55⎛⎫- ⎪ ⎪⎝⎭, 综上所述,Q 点的坐标为1816,55Q ⎫⎛-- ⎪⎝⎭,2(2,1)Q -,34525,55Q ⎫⎛-⎪ ⎝⎭,44525,Q ⎫⎛-⎪ ⎝⎭.故答案为1816,55Q ⎫⎛-- ⎪⎝⎭,2(2,1)Q -,34525,Q ⎫⎛-⎪ ⎝⎭,44525,Q ⎫⎛-⎪ ⎝⎭.【点睛】本题考查了待定系数法求二次函数解析式,三角形的面积问题,菱形的存在性问题等,属于综合题,具有一定的难度,熟练掌握二次函数的图形及性质是解决本题的关键.6.如图,已知点()1,2A 、()()5,0B n n >,点P 为线段AB 上的一个动点,反比例函数()0ky x x=>的图像经过点P .小明说:“点P 从点A 运动至点B 的过程中,k 值逐渐增大,当点P 在点A 位置时k 值最小,在点B 位置时k 值最大.”(1)当1n =时.①求线段AB 所在直线的函数表达式.②你完全同意小明的说法吗?若完全同意,请说明理由;若不完全同意,也请说明理由,并求出正确的k 的最小值和最大值.(2)若小明的说法完全正确,求n 的取值范围.【答案】(1)①1944y x =-+;②不完全同意小明的说法;理由见详解;当92x =时,k 有最大值8116;当1x =时,k 有最小值2;(2)109n ≥;【解析】 【分析】(1)①直接利用待定系数法,即可求出函数的表达式; ②由①得直线AB 为1944y x =-+,则21944k x x =-+,利用二次函数的性质,即可求出答案;(2)根据题意,求出直线AB 的直线为21044n n y x --=+,设点P 为(x ,kx),则得到221044n n k x x --=-,讨论最高项的系数,再由一次函数及二次函数的性质,得到对称轴52ba -≥,即可求出n 的取值范围. 【详解】解:(1)当1n =时,点B 为(5,1), ①设直线AB 为y ax b =+,则251a b a b +=⎧⎨+=⎩,解得:1494a b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴1944y x =-+; ②不完全同意小明的说法;理由如下: 由①得1944y x =-+, 设点P 为(x ,kx),由点P 在线段AB 上则 1944k x x =-+, ∴22191981()444216k x x x =-+=--+; ∵104-<,∴当92x =时,k 有最大值8116; 当1x =时,k 有最小值2;∴点P 从点A 运动至点B 的过程中,k 值先增大后减小,当点P 在点A 位置时k 值最小,在92x =的位置时k 值最大. (2)∵()1,2A 、()5,B n , 设直线AB 为y ax b =+,则25a b a b n +=⎧⎨+=⎩,解得:24104n a n b -⎧=⎪⎪⎨-⎪=⎪⎩, ∴21044n ny x --=+, 设点P 为(x ,kx),由点P 在线段AB 上则 221044n n k x x --=-, 当204n -=,即n=2时,2k x =,则k 随x 的增大而增大,如何题意; 当n≠2时,则对称轴为:101042242n n x n n --==--;∵点P 从点A 运动至点B 的过程中,k 值逐渐增大,当点P 在点A 位置时k 值最小,在点B 位置时k 值最大.即k 在15x ≤≤中,k 随x 的增大而增大; 当204n ->时,有 ∴20410124n n n -⎧>⎪⎪⎨-⎪≤⎪-⎩,解得:26n n >⎧⎨≥-⎩,∴不等式组的解集为:2n >; 当204n -<时,有∴2410524nnn-⎧<⎪⎪⎨-⎪≥⎪-⎩,解得:1029n≤<,∴综合上述,n的取值范围为:109n≥.【点睛】本题考查了二次函数的性质,反比例函数的性质,一次函数的性质,以及解不等式组,解题的关键是熟练掌握所学的知识,掌握所学函数的性质进行解题,注意利用分类讨论的思想进行分析.7.定义:函数l与l'的图象关于y轴对称,点(),0P t是x轴上一点,将函数l'的图象位于直线x t=左侧的部分,以x轴为对称轴翻折,得到新的函数w的图象,我们称函数w是函数l的对称折函数,函数w的图象记作1F,函数l的图象位于直线x t=上以及右侧的部分记作2F,图象1F和2F合起来记作图象F.例如:如图,函数l的解析式为1y x=+,当1t=时,它的对称折函数w的解析式为()11y x x=-<.(1)函数l的解析式为21y x=-,当2t=-时,它的对称折函数w的解析式为_______;(2)函数l的解析式为1²12y x x=--,当42x-≤≤且0t=时,求图象F上点的纵坐标的最大值和最小值;(3)函数l的解析式为()2230y ax ax a a=--≠.若1a=,直线1y t=-与图象F有两个公共点,求t的取值范围.【答案】(1)()212y x x=+<-;(2)F的解析式为2211(0)211(0)2y x x xy x x x⎧=--≥⎪⎪⎨⎪=--+<⎪⎩;图象F上的点的纵坐标的最大值为32y=,最小值为3y=-;(3)当3t=-,312t<≤,352t+<<时,直线1y t=-与图象F有两个公共点.【解析】【分析】(1)根据对折函数的定义直接写出函数解析式即可;(2)先根据题意确定F的解析式,然后根据二次函数的性质确定函数的最大值和最小值即可;(3)先求出当a=1时图像F的解析式,然后分14t-=-、点(),1t t-落在223()y x x x t=--≥上和点(),1t t-落在()223y x x x t=--+<上三种情况解答,最后根据图像即可解答.【详解】解:(1)()212y x x=+<-(2)F的解析式为2211(0)211(0)2y x x xy x x x⎧=--≥⎪⎪⎨⎪=--+<⎪⎩当4x=-时,3y=-,当1x=-时,32y=,当1x=时,32y=-,当2x=时,1y=,∴图象F上的点的纵坐标的最大值为32y=,最小值为3y=-.(3)当1a=时,图象F的解析式为2223()23()y x x x ty x x x t⎧=--≥⎨=--+<⎩∴该函数的最大值和最小值分别为4和-4;a:当14t-=-时,3t=-,∴当3t=-时直线1y t=-与图象F有两个公共点;b:当点(),1t t-落在223()y x x x t=--≥上时,2123t t t-=--,解得1t=232t=c:当点(),1t t-落在()223y x x x t=--+<上时,2123t t t-=--+,解得34t=-(舍),41t=14t-=,∴55t=∴当31712t -<≤或31752t +<<时,直线1y t =-与图象F 有两个公共点; 综上所述:当3t =-,3171t -<≤,3175t +<<时,直线1y t =-与图象F 有两个公共点.【点睛】 本题属于二次函数综合题,考查了“称折函数”的定义、二次函数的性质、解二元一次方程等知识,弄清题意、灵活运用所学知识是解答本题的关键.8.如图,在平面直角坐标系中,抛物线2(0)y ax bx c a =++≠交x 轴于点(2,0),(3,0)A B -,交y 轴于点C ,且经过点(6,6)D --,连接,AD BD .(1)求该抛物线的函数关系式;(2)△ANM 与ABD ∆是否相似?若相似,请求出此时点M 、点N 的坐标;若不存在,请说明理由;(3)若点P 是直线AD 上方的抛物线上一动点(不与点,A D 重合),过P 作//PQ y 轴交直线AD 于点Q ,以PQ 为直径作⊙E ,则⊙E 在直线AD 上所截得的线段长度的最大值等于 .(直接写出答案)【答案】(1)2113442y x x =--+;(2)点M (0,32)、点N (34,0)或点M (0,32),N (-3,0)或点M (-1,32)、点N (-3,0)或N (14-,0)、M (-1,32);(3)QH 有最大值,当x=2-时,其最大值为125. 【解析】【分析】(1)用交点式函数表达式得:y=a (x-2)(x+3),将点D 坐标代入上式即可求解; (2)分∠MAB=∠BAD 、∠MAB=∠BDA ,两种大情况、四种小情况,分别求解即可; (3)根据题意,利用二次函数的性质和三角函数,QH=PQcos ∠PQH=35PQ=352113(442x x --+33)42x -+=23392055x x --+,即可求解.【详解】解:(1)用交点式函数表达式得:y=a (x-2)(x+3),将点D 坐标代入上式并解得:14a =-, 故函数的表达式为:2113442y x x =--+…①, 则点C (0,32);(2)由题意得:AB=5,AD=10,BD=,①∠MAN=∠ABD 时,(Ⅰ)当△ANM ∽△ABD 时,直线AD 所在直线的k 值为34,则直线AM 表达式中的k 值为34-, 则直线AM 的表达式为:3(2)4y x =--,故点M (0,32), AD AB AM AN =,则AN=54,则点N (34,0); (Ⅱ)当△AMN ∽△ABD 时,同理可得:点N (-3,0),点M (0,32), 故点M (0,32)、点N (34,0)或点M (0,32),N (-3,0); ②∠MAN=∠BDA 时,(Ⅰ)△ABD ∽△NMA 时, ∵AD ∥MN ,则tan ∠MAN=tan ∠BDA=12, AM :y=12-(x-2),则点M (-1,32)、点N (-3,0); (Ⅱ)当△ABD ∽△MNA 时,AD BDAM AN ==, 解得:AN=94, 故点N (14-,0)、M (-1,32); 故:点M (-1,32)、点N (-3,0)或N (14-,0)、M (-1,32);综上,点M (0,32)、点N (34,0)或点M (0,32),N (-3,0)或点M (-1,32)、点N (-3,0)或N (14-,0)、M (-1,32); (3)如图所示,连接PH ,由题意得:tan ∠PQH=43,则cos ∠PQH=35, 则直线AD 的表达式为:y=3342x -, 设点P (x ,2113442x x --+),则点Q (x ,3342x -), 则QH=PQcos ∠PQH=35PQ=352113(442x x --+33)42x -+ =23392055x x --+ =2312(2)205x -++, ∵3020-<, 故QH 有最大值,当x=2-时,其最大值为125. 【点睛】本题考查的是二次函数综合应用,涉及到一次函数、圆的基本知识,解直角三角形,相似三角形的判定和性质,其中(2)需要分类求解共四种情况,避免遗漏.9.如图,直线3y x 与x 轴、y 轴分别交于点A ,C ,经过A ,C 两点的抛物线2y ax bx c =++与x 轴的负半轴的另一交点为B ,且tan 3CBO ∠=(1)求该抛物线的解析式及抛物线顶点D 的坐标;(2)点P 是射线BD 上一点,问是否存在以点P ,A ,B 为顶点的三角形,与ABC 相似,若存在,请求出点P 的坐标;若不存在,请说明理由【答案】(1)243y x x =++,顶点(2,1)D --;(2)存在,52,33P ⎛⎫-- ⎪⎝⎭或(4,3)-- 【解析】【分析】(1)利用直线解析式求出点A 、C 的坐标,从而得到OA 、OC ,再根据tan ∠CBO=3求出OB ,从而得到点B 的坐标,然后利用待定系数法求出二次函数解析式,整理成顶点式形式,然后写出点D 的坐标;(2)根据点A 、B 的坐标求出AB ,判断出△AOC 是等腰直角三角形,根据等腰直角三角形的性质求出AC ,∠BAC=45°,再根据点B 、D 的坐标求出∠ABD=45°,然后分①AB 和BP 是对应边时,△ABC 和△BPA 相似,利用相似三角形对应边成比例列式求出BP ,过点P 作PE ⊥x 轴于E ,求出BE 、PE ,再求出OE 的长度,然后写出点P 的坐标即可;②AB 和BA 是对应边时,△ABC 和△BAP 相似,利用相似三角形对应边成比例列式求出BP ,过点P 作PE ⊥x 轴于E ,求出BE 、PE ,再求出OE 的长度,然后写出点P 的坐标即可.【详解】解:(1)令y=0,则x+3=0,解得x=-3,令x=0,则y=3,∴点A (-3,0),C (0,3),∴OA=OC=3,∵tan ∠CBO=3OC OB=, ∴OB=1,∴点B (-1,0),把点A 、B 、C 的坐标代入抛物线解析式得, 93003a b c a b c c -+=⎧⎪-+=⎨⎪=⎩,解得:143a b c =⎧⎪=⎨⎪=⎩,∴该抛物线的解析式为:243y x x =++,∵y=x 2+4x+3=(x+2)2-1,∴顶点(2,1)D --;(2)∵A (-3,0),B (-1,0),∴AB=-1-(-3)=2,∵OA=OC,∠AOC=90°,∴△AOC是等腰直角三角形,∴AC=2OA=32,∠BAC=45°,∵B(-1,0),D(-2,-1),∴∠ABD=45°,①AB和BP是对应边时,△ABC∽△BPA,∴AB ACBP BA=,即2322BP=,解得BP=223,过点P作PE⊥x轴于E,则BE=PE=23×22=23,∴OE=1+23=53,∴点P的坐标为(-53,-23);②AB和BA是对应边时,△ABC∽△BAP,∴AB ACBA BP=,即2322=,解得BP=32过点P作PE⊥x轴于E,则BE=PE=32×22=3, ∴OE=1+3=4, ∴点P 的坐标为(-4,-3);综合上述,当52,33P ⎛⎫--⎪⎝⎭或(4,3)--时,以点P ,A ,B 为顶点的三角形与ABC ∆相似;【点睛】本题是二次函数综合题型,主要利用了直线与坐标轴交点的求解,待定系数法求二次函数解析式,等腰直角三角形的判定与性质,相似三角形的判定与性质,难点在于(2)要分情况讨论.10.在平面直角坐标系中,二次函数y =ax 2+bx +2的图象与x 轴交于A (﹣3,0),B (1,0)两点,与y 轴交于点C .(1)求这个二次函数的关系解析式;(2)点P 是直线AC 上方的抛物线上一动点,是否存在点P ,使△ACP 的面积最大?若存在,求出点P 的坐标;若不存在,说明理由;(3)在平面直角坐标系中,是否存在点Q ,使△BCQ 是以BC 为腰的等腰直角三角形?若存在,直接写出点Q 的坐标;若不存在,说明理由;【答案】(1)224233y x x =--+;(2)存在,点P 35,22⎛⎫- ⎪⎝⎭,使△PAC 的面积最大;(3)存在点Q ,使△BCQ 是以BC 为腰的等腰直角三角形.Q 点坐标为:Q 1(2,3),Q 2(3,1),Q 3(﹣1,﹣1),Q 4(﹣2,1).【解析】【分析】(1)直接把点A (﹣3,0),B (1,0)代入二次函数y =ax 2+bx+2求出a 、b 的值即可得出抛物线的解析式;(2)设点P 坐标为(m ,n ),则n =﹣23m 2﹣43m+2,连接PO ,作PM ⊥x 轴于M ,PN ⊥y 轴于N .根据三角形的面积公式得出△PAC 的表达式,再根据二次函数求最大值的方法得出其顶点坐标即可;(3)以BC 为边,在线段BC 两侧分别作正方形,正方形的其他四个顶点均可以使得“△BCQ 是以BC 为腰的等腰直角三角形”,因此有四个点符合题意要求,再过Q 1点作Q 1D ⊥y 轴于点D ,过点Q 2作Q 2E ⊥x 轴于点E ,根据全等三角形的判定定理得出△Q 1CD ≌△CBO ,△CBO ≌△BQ 2E ,故可得出各点坐标.【详解】(1)∵抛物线y =ax 2+bx+2过点A (﹣3,0),B (1,0),∴093202a b a b =-+⎧⎨=++⎩ 2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩解得 ∴二次函数的关系解析式为y =﹣23x 2﹣43x+2; (2)存在.∵如图1所示,设点P 坐标为(m ,n ),则n =﹣23m 2﹣43m+2. 连接PO ,作PM ⊥x 轴于M ,PN ⊥y 轴于N .则PM =﹣23m 2﹣43m+2.,PN =﹣m ,AO =3. ∵当x =0时,y =﹣23×0﹣43×0+2=2, ∴OC =2,∴S △PAC =S △PAO +S △PCO ﹣S △ACO =12AO•PM+12CO•PN ﹣12AO•CO =12×3×(﹣23m 2﹣43m+2)+12×2×(﹣m )﹣12×3×2 =﹣m 2﹣3m∵a =﹣1<0∴函数S △PAC =﹣m 2﹣3m 有最大值∴当m =﹣2b a =﹣32时,S △PAC 有最大值. ∴n =﹣23m 2﹣43m+2=﹣23×(﹣32)2﹣43×(﹣32)+2=52, ∴存在点P (﹣32,52),使△PAC 的面积最大.(3)如图2所示,以BC 为边在两侧作正方形BCQ 1Q 2、正方形BCQ 4Q 3,则点Q 1,Q 2,Q 3,Q 4为符合题意要求的点.过Q 1点作Q 1D ⊥y 轴于点D ,过点Q 2作Q 2E ⊥x 轴于点E , ∵∠1+∠2=90°,∠2+∠3=90°,∠3+∠4=90°,∴∠1=∠3,∠2=∠4,在△Q 1CD 与△CBO 中,∵11324Q C BC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△Q 1CD ≌△CBO ,∴Q 1D =OC =2,CD =OB =1,∴OD =OC+CD =3,∴Q 1(2,3);同理可得Q 4(﹣2,1);同理可证△CBO ≌△BQ 2E ,∴BE =OC =2,Q 2E =OB =1,∴OE =OB+BE =1+2=3,∴Q 2(3,1),同理,Q 3(﹣1,﹣1),∴存在点Q ,使△BCQ 是以BC 为腰的等腰直角三角形.Q 点坐标为:Q 1(2,3),Q 2(3,1),Q 3(﹣1,﹣1),Q 4(﹣2,1).【点睛】本题考查的是二次函数综合题,涉及到用待定系数法求二次函数解析式,二次函数极值、全等三角形的判定与性质,正方形及等腰直角三角形的性质等知识,涉及面较广,难度较大.。
九年级数学中考压轴题 二次函数综合题(附答案)

B铅垂高水平宽haA专题五中考压轴试题——二次函数综合训练一 .二次函数求最值问题(一)求线段最值1.平行于x轴的线段最值问题首先用自变量(如m)表示出线段两个端点的坐标,用右端点的横坐标减去左端点的横坐标(大横-小横),得到一个线段长关于自变量的二次函数,将其化为顶点式,根据m的正负及其取值范围判断最值.2.平行于y轴的线段最值问题首先用自变量(如m)表示出线段两个端点的坐标,用上端点的纵坐标减去下端点的纵坐标(大纵-小纵),得到一个线段长关于自变量的二次函数,将其化为顶点式,并根据m的正负及其取值范围判断最值.3.既不平行于x轴,又不平行于y轴的线段最值问题将斜线段用竖直线段(或水平线段)表示(一般用到相似或三角函数知识,如补充1和补充2)(二)求周长最值建立周长与动点的横坐标之间的二次函数关系式,利用二次函数的性质求其最值.(三)求面积最值问题1.规则图形面积最值(规则图形指三角形有一边平行于坐标轴,四边形有一组对边平行于坐标轴)首先用自变量(如m)表示出所需的边长及高,利用面积公式表示出面积,得到一个面积关于自变量的二次函数,将其化为顶点式,并根据m的正负及其取值范围判断最值.2.不规则图形面积最值法一:分割;法二:铅直高度与水平高度积的一半(针对三角形而言).二.存在性问题问题或AB2=(x1-x2)2+(y1-y2)21.等腰三角形(分类讨论用距离公式)2.直角三角形(分类讨论用距离公式)3.相似三角形(分类讨论列比例)4.平行四边形(分“两定两动”和“三定一动”两种情况,用全等三角形知识)三.补充知识1.二次函数存在性问题中,往往会用到两点间的距离公式,在使用该公式时,如果出现平方的平方(即4次方),一般改设动点的坐标为(x,y),即设两个变量x和y,根据满足的条件(比如直角三角形、等腰三角形)先得到y 与x函数关系式,再联立已知的二次函数关系式,解方程组即可(如补充3)。
2.解二次函数问题,要关注数形结合,当用代数法所列式子比较复杂或思路受阻,可观察图形中是不是有特殊的图形(如等腰三角形、含有特殊角的直角三角形、等腰直角三角形),可以利用相似等几何知识进行求解;当几何图形复杂,难以画出符合条件的图形,可以直接列式子用代数法求解.一最值问题 (面积最值)1.如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.(1)求抛物线的解析式.(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.2.如图,抛物线的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.3.如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.一最值问题(线段最值)4.如图:已知抛物线265y x x=-+与x轴交于A、B两点,(A在B的左边),与y轴交于点C,若M是抛物线在x轴下方图像上一动点,过点M作MN∥y轴交直线BC于N,求线段MN的最大值。
(完整word)中考数学中二次函数压轴题分类总结,推荐文档

yBE AFNx关于二次函数的压轴题一、抛物线关于三角形面积问题例题 二次函数 y = (x + m )2 + k 的图象,其顶点坐标为 M(1, -4 ).(1) 求出图象与 x 轴的交点 A ,B 的坐标;(2) 在二次函数的图象上是否存在点 P ,使S请说明理由;∆PAB= 5 S4∆MAB ,若存在,求出 P 点的坐标;若不存在, (3) 将二次函数的图象在 x 轴下方的部分沿 x 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线 y = x + b (b < 1) 与此图象有两个公共点时, b 的取值范围.练习: 1.如图.平面直角坐标系 xOy 中,点 A 的坐标为(-2,2),点 B 的坐标为(6,6),抛物线经过 A 、O 、B 三点,线段 AB 交 y 轴与点 E .(1) 求点 E 的坐标; (2) 求抛物线的函数解析式;(3) 点 F 为线段 OB 上的一个动点(不与 O 、B 重合),直线 EF 与抛物线交与 M 、N 两点(点N 在 y 轴右侧),连结 ON 、BN ,当点 F 在线段 OB 上运动时,求∆ BON 的面积的最大值,并求出此时点 N 的坐标;xAOEQ P F y B2. 如图,已知抛物线 y = - 1x 2 + x + 4 交 x 轴的正半轴于点 A ,交 y 轴于点 B .2(1) 求 A 、B 两点的坐标,并求直线 AB 的解析式;(2) 设 P (x , y ) ( x > 0 )是直线 y = x 上的一点,Q 是 OP 的中点(O 是原点),以 PQ 为对角线作正方形 PEQF .若正方形 PEQF 与直线 AB 有公共点,求 x 的取值范围;(3) 在(2)的条件下,记正方形 PEQF 与△OAB 公共部分的面积为 S ,求 S 关于 x 的函数解析式,并探究 S 的最大值.二、抛物线中线段长度最小问题例题如图,对称轴为直线 x =-1 的抛物线 y =ax 2+bx +c (a ≠0)与 x 轴相交于 A 、B 两点,其中点 A 的坐标为(-3,0).(1) 求点 B 的坐标;(2) 已知 a =1,C 为抛物线与 y 轴的交点.①若点 P 在抛物线上,且 S △POC =4S △BOC ,求点 P 的坐标;②设点 Q 是线段 AC 上的动点,作 QD ⊥x 轴,QD 交抛物线于点 D ,求线段 QD 长度的最大值.yBCN MAODEx练习:1. 如图, Rt △ABO 的两直角边 OA 、OB 分别在 x 轴的负半轴和 y 轴的正半轴上,O 为坐标原点, A 、B 两点的坐标分别为( -3 ,0)、(0,4),抛物线 y = 2x 2 + bx + c 经过 B 点,且顶点在直线3 x =5 上.2(1) 求抛物线对应的函数关系式;(2) 若△DCE 是由△ABO 沿 x 轴向右平移得到的,当四边形 ABCD 是菱形时,试判断点 C 和点D 是否在该抛物线上,并说明理由;(3) 若 M 点是 CD 所在直线下方该抛物线上的一个动点,过点 M 作 MN 平行于 y 轴交 CD 于点N .设点 M 的横坐标为 t ,MN 的长度为 l .求 l 与 t 之间的函数关系式,并求 l 取最大值时,点 M 的坐标.三、抛物线与线段和最小的问题例题 如图,已知抛物线 y = 1(x - 2)(x + a )(a > 0)与 x 轴交于点 B 、C ,与 y 轴交于点 E ,且点 Ba在点 C 的左侧.(1) 若抛物线过点 M (﹣2,﹣2),求实数 a 的值; (2) 在(1)的条件下,解答下列问题;①求出△BCE 的面积;②在抛物线的对称轴上找一点 H ,使 CH+EH 的值最小,直接写出点 H 的坐标.练习:1.如图,已知二次函数y =ax2- 4x +c 的图象与坐标轴交于点A(-1,0)和点B(0,-5).(1)求该二次函数的解析式;(2)已知该函数图象的对称轴上存在一点P,使得△ABP 的周长最小.请求出点P 的坐标.2.如图,抛物线y = ax2 + bx + 4 与x 轴的两个交点分别为A(-4,0)、B(2,0),与y 轴交于点C,顶点为D.E(1,2)为线段BC 的中点,BC 的垂直平分线与x 轴、y 轴分别交于F、G.(1)求抛物线的函数解析式,并写出顶点D 的坐标;(2)在直线EF 上求一点H,使△CDH 的周长最小,并求出H 的坐标;(3)若点K 在x 轴上方的抛物线上运动,当K 运动到什么位置时,△EFK 的面积最大?并求出最大面积.四、抛物线与等腰三角形例题:已知抛物线y=ax2+bx+c 经过A(-1,0)、B(3,0)、C(0,3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P 是直线l 上的一个动点,当△PAC 的周长最小时,求点P 的坐标;(3)在直线l 上是否存在点M,使△MAC 为等腰三角形?若存在,直接写出所有符合条件的点M 的坐标;若不存在,请说明理由.练习:1..如图,抛物线与x 轴交于A、B 两点,与y 轴交C 点,点A 的坐标为(2,0),点C 的坐标为1(0,3)它的对称轴是直线x =-2(1)求抛物线的解析式;(2)M 是线段AB 上的任意一点,当△MBC 为等腰三角形时,求M 点的坐标.2.如图,在平面直角坐标系中,点A 的坐标为(m,m),点B 的坐标为(n,﹣n),抛物线经过A、O、B 三点,连接OA、OB、AB,线段AB 交y 轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0 的两根.(1)求抛物线的解析式;(2)若点P 为线段OB 上的一个动点(不与点O、B 重合),直线PC 与抛物线交于D、E 两点(点D 在y 轴右侧),连接OD、BD.①当△OPC 为等腰三角形时,求点P 的坐标;②求△BOD 面积的最大值,并写出此时点D 的坐标.3.如图1,在直角坐标系中,已知△AOC 的两个顶点坐标分别为A(2,0),C(0,2).(1)请你以AC 的中点为对称中心,画出△AOC 的中心对称图形△ABC,此图与原图组成的四边形OABC 的形状是,请说明理由;(2)如图2,已知D( 1,0),过A,C,D 的抛物线与(1)所得的四边形OABC 的边BC 交2于点E,求抛物线的解析式及点 E 的坐标;(3)在问题(2)的图形中,一动点P 由抛物线上的点A 开始,沿四边形OABC 的边从A﹣B ﹣C 向终点C 运动,连接OP 交AC 于N,若P 运动所经过的路程为x,试问:当x 为何值时,△AON 为等腰三角形(只写出判断的条件与对应的结果)?4.如图,已知抛物线于x 轴交于A(-1,0)、B(3,0)两点,与y 轴交于点C(0,3).(1)求抛物线的解析式;(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC 是等腰三角形,若存在,求出符合条件的点P 的坐标;若不存在,请说明理由:(3)若点M 是抛物线上一点,以B、C、D、M 为顶点的四边形是直角梯形,试求出点M 的坐标。
(完整版)二次函数压轴题(带详细答案)(可编辑修改word版)

二次函数压轴题强化训练(带详细答案)一.解答题(共30 小题)1.(2016•深圳模拟)已知:如图,在平面直角坐标系xOy 中,直线与x 轴、y轴的交点分别为A、B,将∠OBA 对折,使点O 的对应点H 落在直线AB 上,折痕交x 轴于点C.(1)直接写出点C 的坐标,并求过A、B、C 三点的抛物线的解析式;(2)若抛物线的顶点为D,在直线BC 上是否存在点P,使得四边形ODAP 为平行四边形?若存在,求出点P 的坐标;若不存在,说明理由;(3)设抛物线的对称轴与直线BC 的交点为T,Q 为线段BT 上一点,直接写出|QA﹣QO|的取值范围.2.(2015•枣庄)如图,直线y=x+2 与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P 是线段AB 上异于A、B 的动点,过点P 作PC⊥x 轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P 点,使线段PC 的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC 为直角三角形时点P 的坐标.3.(2007•玉溪)如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m 与该二次函数的图象交于A、B 两点,其中A 点的坐标为(3,4),B 点在y 轴上.(1)求m 的值及这个二次函数的关系式;(2)P 为线段AB 上的一个动点(点P 与A、B 不重合),过P 作x 轴的垂线与这个二次函数的图象交于点E,设线段PE 的长为h,点P 的横坐标为x,求h 与x 之间的函数关系式,并写出自变量x 的取值范围;(3)D 为直线AB 与这个二次函数图象对称轴的交点,在线段AB 上是否存在一点P,使得四边形DCEP 是平行四边形?若存在,请求出此时P 点的坐标;若不存在,请说明理由.4.(2013•凉ft州)如图,抛物线y=ax2﹣2ax+c(a≠0)交x 轴于A、B 两点,A 点坐标为(3,0),与y 轴交于点C(0,4),以OC、OA 为边作矩形OADC 交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l 在边OA(不包括O、A 两点)上平行移动,分别交x 轴于点E,交CD 于点F,交AC 于点M,交抛物线于点P,若点M 的横坐标为m,请用含m 的代数式表示PM 的长;(3)在(2)的条件下,连结PC,则在CD 上方的抛物线部分是否存在这样的点P,使得以P、C、F 为顶点的三角形和△AEM 相似?若存在,求出此时m 的值,并直接判断△PCM 的形状;若不存在,请说明理由.5.(2009•綦江县)如图,已知抛物线y=a(x﹣1)2+3(a≠0)经过点A(﹣2,0),抛物线的顶点为D,过O 作射线OM∥AD.过顶点平行于x 轴的直线交射线OM 于点C,B 在x 轴正半轴上,连接BC.(1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1 个长度单位的速度沿射线OM 运动,设点P 运动的时间为t(s).问当t 为何值时,四边形DAOP 分别为平行四边形,直角梯形,等腰梯形?(3)若OC=OB,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1 个长度单位和2 个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t(s),连接PQ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.6.(2013•天水)如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.(1)求抛物线的解析式;(2)将直线OB 向下平移m 个单位长度后,得到的直线与抛物线只有一个公共点D,求m 的值及点D 的坐标;(3)如图2,若点N 在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB 的点P 坐标(点P、O、D 分别与点N、O、B 对应).7.(2014•河南)如图,抛物线y=﹣x2+bx+c 与x 轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣x+3 与y 轴交于点C,与x 轴交于点D.点P 是x 轴上方的抛物线上一动点,过点P作PF⊥x 轴于点F,交直线CD 于点E.设点P 的横坐标为m.(1)求抛物线的解析式;(2)若PE=5EF,求m 的值;(3)若点E′是点E 关于直线PC 的对称点,是否存在点P,使点E′落在y 轴上?若存在,请直接写出相应的点P 的坐标;若不存在,请说明理由.8.(2013•德州)如图,在直角坐标系中有一直角三角形AOB,O 为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O 逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c 经过点A、B、C.(1)求抛物线的解析式;(2)若点P 是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l 与x 轴交于一点E,连接PE,交CD 于F,求出当△CEF 与△COD 相似时,点P 的坐标;②是否存在一点P,使△PCD 的面积最大?若存在,求出△PCD 的面积的最大值;若不存在,请说明理由.9.(2013•河南)如图,抛物线y=﹣x2+bx+c 与直线y=x+2 交于C、D 两点,其中点C 在y轴上,点D 的坐标为(3,).点P 是y 轴右侧的抛物线上一动点,过点P 作PE⊥x 轴于点E,交CD 于点F.(1)求抛物线的解析式;(2)若点P 的横坐标为m,当m 为何值时,以O、C、P、F 为顶点的四边形是平行四边形?请说明理由.(3)若存在点P,使∠PCF=45°,请直接写出相应的点P 的坐标.10.(2013•重庆)如图,已知抛物线y=x2+bx+c 的图象与x 轴的一个交点为B(5,0),另一个交点为A,且与y 轴交于点C(0,5).(1)求直线BC 与抛物线的解析式;(2)若点M 是抛物线在x 轴下方图象上的一动点,过点M 作MN∥y 轴交直线BC 于点N,求MN 的最大值;(3)在(2)的条件下,MN 取得最大值时,若点P 是抛物线在x 轴下方图象上任意一点,以BC 为边作平行四边形CBPQ,设平行四边形CBPQ 的面积为S1,△ABN 的面积为S2,且S1=6S2,求点P 的坐标.11.(2013•徐州)如图,二次函数y=x2+bx﹣的图象与x 轴交于点A(﹣3,0)和点B,以AB为边在x 轴上方作正方形ABCD,点P 是x 轴上一动点,连接DP,过点P 作DP 的垂线与y 轴交于点E.(1)请直接写出点D 的坐标:;(2)当点P 在线段AO(点P 不与A、O 重合)上运动至何处时,线段OE 的长有最大值,求出这个最大值;(3)是否存在这样的点P,使△PED 是等腰三角形?若存在,请求出点P 的坐标及此时△PED 与正方形ABCD 重叠部分的面积;若不存在,请说明理由.12.(2013•泰安)如图,抛物线y=x2+bx+c 与y 轴交于点C(0,﹣4),与x 轴交于点A,B,且B 点的坐标为(2,0).(1)求该抛物线的解析式.(2)若点P 是AB 上的一动点,过点P 作PE∥AC,交BC 于E,连接CP,求△PCE 面积的最大值.(3)若点D 为OA 的中点,点M 是线段AC 上一点,且△OMD 为等腰三角形,求M 点的坐标.13.(2014•广元)如图甲,四边形OABC 的边OA、OC 分别在x 轴、y 轴的正半轴上,顶点在B 点的抛物线交x 轴于点A、D,交y 轴于点E,连接AB、AE、BE.已知tan∠CBE=,A(3,0),D(﹣1,0),E(0,3).(1)求抛物线的解析式及顶点B 的坐标;(2)求证:CB 是△ABE 外接圆的切线;(3)试探究坐标轴上是否存在一点P,使以D、E、P 为顶点的三角形与△ABE 相似,若存在,直接写出点P 的坐标;若不存在,请说明理由;(4)设△AOE 沿x 轴正方向平移t 个单位长度(0<t≤3)时,△AOE 与△ABE 重叠部分的面积为s,求s 与t 之间的函数关系式,并指出t 的取值范围.14.(2014•成都)如图,已知抛物线y=(x+2)(x﹣4)(k 为常数,且k>0)与x 轴从左至右依次交于A,B 两点,与y 轴交于点C,经过点B 的直线y=﹣x+b 与抛物线的另一交点为D.(1)若点D 的横坐标为﹣5,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点P,使得以A,B,P 为顶点的三角形与△ABC 相似,求k 的值;(3)在(1)的条件下,设F 为线段BD 上一点(不含端点),连接AF,一动点M 从点A 出发,沿线段AF 以每秒1 个单位的速度运动到F,再沿线段FD 以每秒2 个单位的速度运动到D 后停止,当点F 的坐标是多少时,点M 在整个运动过程中用时最少?15.(2014•南宁)在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k 与直线y=kx+1 交于A,B两点,点A 在点B 的左侧.(1)如图1,当k=1 时,直接写出A,B 两点的坐标;(2)在(1)的条件下,点P 为抛物线上的一个动点,且在直线AB 下方,试求出△ABP 面积的最大值及此时点P 的坐标;(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x 轴交于点C、D 两点(点C 在点D 的左侧),在直线y=kx+1 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k 的值;若不存在,请说明理由.16.(2013•防城港)如图,抛物线y=﹣(x﹣1)2+c 与x 轴交于A,B(A,B 分别在y 轴的左右两侧)两点,与y 轴的正半轴交于点C,顶点为D,已知A(﹣1,0).(1)求点B,C 的坐标;(2)判断△CDB 的形状并说明理由;(3)将△COB 沿x 轴向右平移t 个单位长度(0<t<3)得到△QPE.△QPE 与△CDB 重叠部分(如图中阴影部分)面积为S,求S 与t 的函数关系式,并写出自变量t 的取值范围.17.(2014•重庆)如图,抛物线y=﹣x2﹣2x+3 的图象与x 轴交于A、B 两点(点A 在点B 的左边),与y 轴交于点C,点D 为抛物线的顶点.(1)求A、B、C 的坐标;(2)点M 为线段AB 上一点(点M 不与点A、B 重合),过点M 作x 轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P 作PQ∥AB 交抛物线于点Q,过点Q 作QN⊥x 轴于点N.若点P 在点Q 左边,当矩形PMNQ 的周长最大时,求△AEM 的面积;(3)在(2)的条件下,当矩形PMNQ 的周长最大时,连接DQ.过抛物线上一点F 作y 轴的平行线,与直线AC 交于点G(点G 在点F 的上方).若FG=2DQ,求点F 的坐标.18.(2014•钦州)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c 与x 轴交于A、D 两点,与y 轴交于点B,四边形OBCD 是矩形,点A 的坐标为(1,0),点B 的坐标为(0,4),已知点E(m,0)是线段DO 上的动点,过点E 作PE⊥x 轴交抛物线于点P,交BC 于点G,交BD 于点H.(1)求该抛物线的解析式;(2)当点P 在直线BC 上方时,请用含m 的代数式表示PG 的长度;(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G 为顶点的三角形与△DEH 相似?若存在,求出此时m 的值;若不存在,请说明理由.19.(2014•昆明)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x 轴交于点A(﹣2,0)、B(4,0)两点,与y 轴交于点C.(1)求抛物线的解析式;(2)点P 从A 点出发,在线段AB 上以每秒3 个单位长度的速度向B 点运动,同时点Q 从B 点出发,在线段BC 上以每秒1 个单位长度的速度向C 点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ 存在时,求运动多少秒使△PBQ 的面积最大,最大面积是多少?(3)当△PBQ 的面积最大时,在BC 下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K 点坐标.20.(2013•恩施州)如图所示,直线l:y=3x+3 与x 轴交于点A,与y 轴交于点B.把△AOB 沿y 轴翻折,点A 落到点C,抛物线过点B、C 和D(3,0).(1)求直线BD 和抛物线的解析式.(2)若BD 与抛物线的对称轴交于点M,点N 在坐标轴上,以点N、B、D 为顶点的三角形与△MCD 相似,求所有满足条件的点N 的坐标.(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P 的坐标;若不存在,说明理由.21.(2013•毕节地区)如图,抛物线y=ax2+b 与x 轴交于点A、B,且A 点的坐标为(1,0),与y 轴交于点C(0,1).(1)求抛物线的解析式,并求出点B 坐标;(2)过点B 作BD∥CA 交抛物线于点D,连接BC、CA、AD,求四边形ABCD 的周长;(结果保留根号)(3)在x 轴上方的抛物线上是否存在点P,过点P 作PE 垂直于x 轴,垂足为点E,使以B、P、E 为顶点的三角形与△CBD 相似?若存在请求出P 点的坐标;若不存在,请说明理由.22.(2014•德州)如图,在平面直角坐标系中,已知点A 的坐标是(4,0),并且OA=OC=4OB,动点P 在过A,B,C 三点的抛物线上.(1)求抛物线的解析式;(2)是否存在点P,使得△ACP 是以AC 为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,说明理由;(3)过动点P 作PE 垂直于y 轴于点E,交直线AC 于点D,过点D 作x 轴的垂线.垂足为F,连接EF,当线段EF 的长度最短时,求出点P 的坐标.23.(2014•吉林)如图①,直线l:y=mx+n(m<0,n>0)与x,y 轴分别相交于A,B 两点,将△AOB 绕点O 逆时针旋转90°得到△COD,过点A,B,D 的抛物线P 叫做l 的关联抛物线,而l 叫做P 的关联直线.(1)若l:y=﹣2x+2,则P 表示的函数解析式为;若P:y=﹣x2﹣3x+4,则l 表示的函数解析式为.(2)求P 的对称轴(用含m,n 的代数式表示);(3)如图②,若l:y=﹣2x+4,P 的对称轴与CD 相交于点E,点F 在l 上,点Q 在P 的对称轴上.当以点C,E,Q,F 为顶点的四边形是以CE 为一边的平行四边形时,求点Q 的坐标;(4)如图③,若l:y=mx﹣4m,G 为AB 中点,H 为CD 中点,连接GH,M 为GH 中点,连接OM.若OM=,直接写出l,P 表示的函数解析式.24.(2013•武汉)如图,点P 是直线l:y=﹣2x﹣2 上的点,过点P 的另一条直线m 交抛物线y=x2于A、B 两点.(1)若直线m 的解析式为y=﹣x+,求A,B 两点的坐标;(2)①若点P 的坐标为(﹣2,t).当PA=AB 时,请直接写出点A 的坐标;②试证明:对于直线l 上任意给定的一点P,在抛物线上能找到点A,使得PA=AB 成立.(3)设直线l 交y 轴于点C,若△AOB 的外心在边AB 上,且∠BPC=∠OCP,求点P 的坐标.25.(2013•遂宁)如图,抛物线y= x2+bx+c 与x 轴交于点A(2,0),交y 轴于点B(0,).直线y=kx 过点A 与y 轴交于点C,与抛物线的另一个交点是D.(1)求抛物线y= x2+bx+c 与直线y=kx 的解析式;(2)设点P 是直线AD 上方的抛物线上一动点(不与点A、D 重合),过点P 作y 轴的平行线,交直线AD 于点M,作DE⊥y 轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P 的坐标;若不存在,请说明理由;(3)在(2)的条件下,作PN⊥AD 于点N,设△PMN 的周长为l,点P 的横坐标为x,求l与x 的函数关系式,并求出l 的最大值.26.(2013•舟ft)如图,在平面直角坐标系xOy 中,抛物线y=(x﹣m)2﹣m2+m 的顶点为A,与y 轴的交点为B,连结AB,AC⊥AB,交y 轴于点C,延长CA 到点D,使AD=AC,连结BD.作AE∥x 轴,DE∥y 轴.(1)当m=2 时,求点B 的坐标;(2)求DE 的长?(3)①设点D 的坐标为(x,y),求y 关于x 的函数关系式?②过点D 作AB 的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m 为何值时,以A,B,D,P 为顶点的四边形是平行四边形?27.(2006•重庆)已知:m、n 是方程x2﹣6x+5=0 的两个实数根,且m<n,抛物线y=﹣x2+bx+c的图象经过点A(m,0)、B(0,n).(1)求这个抛物线的解析式;(2)设(1)中抛物线与x 轴的另一交点为C,抛物线的顶点为D,试求出点C、D 的坐标和△BCD 的面积;(3)P 是线段OC 上的一点,过点P 作PH⊥x 轴,与抛物线交于H 点,若直线BC 把△PCH 分成面积之比为2:3 的两部分,请求出P 点的坐标.28.(2015•阜新)如图,抛物线y=﹣x2+bx+c 交x 轴于点A(﹣3,0)和点B,交y 轴于点C(0,3).(1)求抛物线的函数表达式;(2)若点P 在抛物线上,且S△AOP=4S BOC,求点P 的坐标;(3)如图b,设点Q 是线段AC 上的一动点,作DQ⊥x 轴,交抛物线于点D,求线段DQ长度的最大值.29.(2014•白银)如图,在平面直角坐标系xOy 中,顶点为M 的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的,它与y 轴负半轴交于点A,点 B 在该抛物线上,且横坐标为3.(1)求点M、A、B 坐标;(2)连接AB、AM、BM,求∠ABM 的正切值;(3)点P 是顶点为M 的抛物线上一点,且位于对称轴的右侧,设PO 与x 正半轴的夹角为α,当α=∠ABM 时,求P 点坐标.30.(2014•宿迁)如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x 轴于点A,B,交y 轴于点C,设过点A,B,C 三点的圆与y 轴的另一个交点为D.(1)如图1,已知点A,B,C 的坐标分别为(﹣2,0),(8,0),(0,﹣4);①求此抛物线的表达式与点D 的坐标;②若点M 为抛物线上的一动点,且位于第四象限,求△BDM 面积的最大值;(2)如图2,若a=1,求证:无论b,c 取何值,点D 均为定点,求出该定点坐标.二次函数压轴题强化答案一.解答题(共30 小题)1.(2016•深圳模拟)已知:如图,在平面直角坐标系xOy 中,直线与x 轴、y轴的交点分别为A、B,将∠OBA 对折,使点O 的对应点H 落在直线AB 上,折痕交x 轴于点C.(1)直接写出点C 的坐标,并求过A、B、C 三点的抛物线的解析式;(2)若抛物线的顶点为D,在直线BC 上是否存在点P,使得四边形ODAP 为平行四边形?若存在,求出点P 的坐标;若不存在,说明理由;(3)设抛物线的对称轴与直线BC 的交点为T,Q 为线段BT 上一点,直接写出|QA﹣QO|的取值范围.【考点】二次函数综合题.【专题】压轴题;开放型.【分析】(1)点A 的坐标是纵坐标为0,得横坐标为8,所以点A 的坐标为(8,0);点B 的坐标是横坐标为0,解得纵坐标为6,所以点B 的坐标为(0,6);由题意得:BC 是∠ABO 的角平分线,所以OC=CH,BH=OB=6∵AB=10,∴AH=4,设OC=x,则AC=8﹣x由勾股定理得:x=3∴点C 的坐标为(3,0)将此三点代入二次函数一般式,列的方程组即可求得;(2)求得直线BC 的解析式,根据平行四边形的性质,对角相等,对边平行且相等,借助于三角函数即可求得;(3)如图,由对称性可知QO=QH,|QA﹣QO|=|QA﹣QH|.当点Q 与点B 重合时,Q、H、A 三点共线,|QA﹣QO|取得最大值4(即为AH 的长);设线段OA 的垂直平分线与直线BC 的交点为K,当点Q 与点K 重合时,|QA﹣QO|取得最小值0.【解答】解:(1)点C 的坐标为(3,0).(1 分)∵点A、B 的坐标分别为A(8,0),B(0,6),∴可设过A、B、C 三点的抛物线的解析式为y=a(x﹣3)(x﹣8).将x=0,y=6 代入抛物线的解析式,得.(2 分)∴过A、B、C 三点的抛物线的解析式为.(3 分)(2)可得抛物线的对称轴为直线,顶点D 的坐标为,设抛物线的对称轴与x 轴的交点为G.直线BC 的解析式为y=﹣2x+6.4 分)设点P 的坐标为(x,﹣2x+6).解法一:如图,作OP∥AD 交直线BC 于点P,连接AP,作PM⊥x 轴于点M.∵OP∥AD,∴∠POM=∠GAD,tan∠POM=tan∠GAD.∴,即.解得.经检验是原方程的解.此时点P 的坐标为.(5 分)但此时,OM<GA.∵,∴OP<AD,即四边形的对边OP 与AD 平行但不相等,∴直线BC 上不存在符合条件的点P(6 分)解法二:如图,取OA 的中点E,作点D 关于点E 的对称点P,作PN⊥x 轴于点N.则∠PEO=∠DEA,PE=DE.可得△PEN≌△DEG.由,可得E 点的坐标为(4,0).NE=EG= ,ON=OE﹣NE= ,NP=DG= .∴点P 的坐标为.(5 分)∵x= 时,,∴点P 不在直线BC 上.∴直线BC 上不存在符合条件的点P.(6 分)(3)|QA﹣QO|的取值范围是.(8 分)当Q 在OA 的垂直平分线上与直线BC 的交点时,(如点K 处),此时OK=AK,则|QA﹣QO|=0,当Q 在AH 的延长线与直线BC 交点时,此时|QA﹣QO|最大,直线AH 的解析式为:y=﹣x+6,直线BC 的解析式为:y=﹣2x+6,联立可得:交点为(0,6),∴OQ=6,AQ=10,∴|QA﹣QO|=4,∴|QA﹣QO|的取值范围是:0≤|QA﹣QO|≤4.【点评】此题考查了二次函数与一次函数以及平行四边形的综合知识,解题的关键是认真识图,注意数形结合思想的应用.2.(2015•枣庄)如图,直线y=x+2 与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P 是线段AB 上异于A、B 的动点,过点P 作PC⊥x 轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P 点,使线段PC 的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC 为直角三角形时点P 的坐标.【考点】二次函数综合题.【专题】几何综合题;压轴题.【分析】(1)已知B(4,m)在直线y=x+2 上,可求得m 的值,抛物线图象上的A、B 两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC 的长,实际是直线AB 与抛物线函数值的差.可设出P 点横坐标,根据直线AB 和抛物线的解析式表示出P、C 的纵坐标,进而得到关于PC 与P 点横坐标的函数关系式,根据函数的性质即可求出PC 的最大值.(3)当△PAC 为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.【解答】解:(1)∵B(4,m)在直线y=x+2 上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx+6 上,∴,解得,∴抛物线的解析式为y=2x2﹣8x+6.(2)设动点P 的坐标为(n,n+2),则C 点的坐标为(n,2n2﹣8n+6),∴PC=(n+2)﹣(2n2﹣8n+6),=﹣2n2+9n﹣4,=﹣2(n﹣)2+ ,∵PC>0,∴当n=时,线段PC 最大且为.(3)∵△PAC 为直角三角形,i)若点P 为直角顶点,则∠APC=90°.由题意易知,PC∥y 轴,∠APC=45°,因此这种情形不存在;ii)若点A 为直角顶点,则∠PAC=90°.如答图3﹣1,过点A(,)作AN⊥x 轴于点N,则ON=,AN= .过点A 作AM⊥直线AB,交x 轴于点M,则由题意易知,△AMN 为等腰直角三角形,∴MN=AN= ,∴OM=ON+MN= +=3,∴M(3,0).设直线AM 的解析式为:y=kx+b,则:,解得,∴直线AM 的解析式为:y=﹣x+3 ①又抛物线的解析式为:y=2x2﹣8x+6 ②联立①②式,解得:x=3 或x=(与点A 重合,舍去)∴C(3,0),即点C、M 点重合.当x=3 时,y=x+2=5,∴P1(3,5);iii)若点C 为直角顶点,则∠ACP=90°.∵y=2x2﹣8x+6=2(x﹣2)2﹣2,∴抛物线的对称轴为直线x=2.如答图3﹣2,作点A(,)关于对称轴x=2 的对称点C,则点C 在抛物线上,且C(,).当x=时,y=x+2=.∴P2(,).∵点P1(3,5)、P2(,)均在线段AB 上,∴综上所述,△PAC 为直角三角形时,点P 的坐标为(3,5)或(,).【点评】此题主要考查了二次函数解析式的确定、二次函数最值的应用以及直角三角形的判定、函数图象交点坐标的求法等知识.3.(2007•玉溪)如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m 与该二次函数的图象交于A、B 两点,其中A 点的坐标为(3,4),B 点在y 轴上.(1)求m 的值及这个二次函数的关系式;(2)P 为线段AB 上的一个动点(点P 与A、B 不重合),过P 作x 轴的垂线与这个二次函数的图象交于点E,设线段PE 的长为h,点P 的横坐标为x,求h 与x 之间的函数关系式,并写出自变量x 的取值范围;(3)D 为直线AB 与这个二次函数图象对称轴的交点,在线段AB 上是否存在一点P,使得四边形DCEP 是平行四边形?若存在,请求出此时P 点的坐标;若不存在,请说明理由.【考点】二次函数综合题.【专题】压轴题.【分析】(1)因为直线y=x+m 过点A,将A 点坐标直接代入解析式即可求得m 的值;设出二次函数的顶点式,将(3,4)代入即可;(2)由于P 和E 的横坐标相同,将P 点横坐标代入直线和抛物线解析式,可得其纵坐标表达式,h 即为二者之差;根据P、E 在二者之间,所以可知x 的取值范围是0<x<3;(3)先假设存在点P,根据四边形DCEP 是平行四形的条件进行推理,若能求出P 点坐标,则证明存在点P,否则P 点不存在.【解答】解:(1)∵点A(3,4)在直线y=x+m 上,∴4=3+m.∴m=1.设所求二次函数的关系式为y=a(x﹣1)2.∵点A(3,4)在二次函数y=a(x﹣1)2的图象上,∴4=a(3﹣1)2,∴a=1.∴所求二次函数的关系式为y=(x﹣1)2.即y=x2﹣2x+1.(2)设P、E 两点的纵坐标分别为y P 和y E.∴PE=h=y P﹣y E=(x+1)﹣(x2﹣2x+1)=﹣x2+3x.即h=﹣x2+3x(0<x<3).(3)存在.解法1:要使四边形DCEP 是平行四边形,必需有PE=DC.∵点D 在直线y=x+1 上,∴点D 的坐标为(1,2),∴﹣x2+3x=2.即x2﹣3x+2=0.解之,得x1=2,x2=1(不合题意,舍去)∴当P 点的坐标为(2,3)时,四边形DCEP 是平行四边形.解法2:要使四边形DCEP 是平行四边形,必需有BP∥CE.设直线CE 的函数关系式为y=x+b.∵直线CE 经过点C(1,0),∴0=1+b,∴b=﹣1.∴直线CE 的函数关系式为y=x﹣1.∴得x2﹣3x+2=0.解之,得x1=2,x2=1(不合题意,舍去)∴当P 点的坐标为(2,3)时,四边形DCEP 是平行四边形.【点评】此题考查了用待定系数法求函数解析式以及函数图象上点的坐标特征,结合图形有利于解答;(3)是一道存在性问题,有一定的开放性,需要先假设点P 存在,然后进行验证计算.4.(2013•凉ft州)如图,抛物线y=ax2﹣2ax+c(a≠0)交x 轴于A、B 两点,A 点坐标为(3,0),与y 轴交于点C(0,4),以OC、OA 为边作矩形OADC 交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l 在边OA(不包括O、A 两点)上平行移动,分别交x 轴于点E,交CD 于点F,交AC 于点M,交抛物线于点P,若点M 的横坐标为m,请用含m 的代数式表示PM 的长;(3)在(2)的条件下,连结PC,则在CD 上方的抛物线部分是否存在这样的点P,使得以P、C、F 为顶点的三角形和△AEM 相似?若存在,求出此时m 的值,并直接判断△PCM 的形状;若不存在,请说明理由.【考点】二次函数综合题.【专题】压轴题.【分析】(1)将A(3,0),C(0,4)代入y=ax2﹣2ax+c,运用待定系数法即可求出抛物线的解析式;(2)先根据A、C 的坐标,用待定系数法求出直线AC 的解析式,进而根据抛物线和直线AC 的解析式分别表示出点P、点M 的坐标,即可得到PM 的长;(3)由于∠PFC 和∠AEM 都是直角,F 和E 对应,则若以P、C、F 为顶点的三角形和△AEM相似时,分两种情况进行讨论:①△PFC∽△AEM,②△CFP∽△AEM;可分别用含m 的代数式表示出AE、EM、CF、PF 的长,根据相似三角形对应边的比相等列出比例式,求出m的值,再根据相似三角形的性质,直角三角形、等腰三角形的判定判断出△PCM 的形状.【解答】解:(1)∵抛物线y=ax2﹣2ax+c(a≠0)经过点A(3,0),点C(0,4),∴ ,解得,∴抛物线的解析式为y=﹣x2+ x+4;(2)设直线AC 的解析式为y=kx+b,∵A(3,0),点C(0,4),∴ ,解得,∴直线AC 的解析式为y=﹣x+4.∵点M 的横坐标为m,点M 在AC 上,∴M 点的坐标为(m,﹣m+4),∵点P 的横坐标为m,点P 在抛物线y=﹣x2+ x+4 上,∴点P 的坐标为(m,﹣m2+ m+4),∴PM=PE﹣ME=(﹣m2+m+4)﹣(﹣m+4)=﹣m2+4m,即PM=﹣m2+4m(0<m<3);(3)在(2)的条件下,连结PC,在CD 上方的抛物线部分存在这样的点P,使得以P、C、F 为顶点的三角形和△AEM 相似.理由如下:由题意,可得AE=3﹣m,EM=﹣m+4,CF=m,若以P、C、F 为顶点的三角形和△AEM 相似,情况:①P 点在F 上,PF=﹣m2+m+4﹣4=﹣m2+m.若△PFC∽△AEM,则PF:AE=FC:EM,即(﹣m2+m):(3﹣m)=m:(﹣m+4),∵m≠0 且m≠3,∴m= .∵△PFC∽△AEM,∴∠PCF=∠AME,∵∠AME=∠CMF,∴∠PCF=∠CMF.在直角△CMF 中,∵∠CMF+∠MCF=90°,∴∠PCF+∠MCF=90°,即∠PCM=90°,∴△PCM 为直角三角形;②P 点在F 下,PF=4﹣(﹣m2+m+4)= m2﹣m若△PFC∽△AEM,则PF:AE=FC:EM,即(m2﹣m):(3﹣m)=m:(﹣m+4),∵m≠0 且m≠3,∴m=(不合题意舍去).∵∠CFP=90°,∴∠CPM=∠CFP+FCM>90°,∴△CPM 为钝角三角形;③若△CFP∽△AEM,则CF:AE=PF:EM,即m:(3﹣m)=(﹣m2+m):(﹣m+4),∵m≠0 且m≠3,∴m=1.∵△CFP∽△AEM,∴∠CPF=∠AME,∵∠AME=∠CMF,∴∠CPF=∠CMF.∴CP=CM,∴△PCM 为等腰三角形.综上所述,存在这样的点P 使△PFC 与△AEM 相似.此时m 的值为或1,△PCM 为直角三角形或等腰三角形.【点评】此题是二次函数的综合题,其中涉及到运用待定系数法求二次函数、一次函数的解析式,矩形的性质,相似三角形的判定和性质,直角三角形、等腰三角形的判定,难度适中.要注意的是当相似三角形的对应边和对应角不明确时,要分类讨论,以免漏解.5.(2009•綦江县)如图,已知抛物线y=a(x﹣1)2+3(a≠0)经过点A(﹣2,0),抛物线的顶点为D,过O 作射线OM∥AD.过顶点平行于x 轴的直线交射线OM 于点C,B 在x 轴正半轴上,连接BC.(1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1 个长度单位的速度沿射线OM 运动,设点P 运动的时间为t(s).问当t 为何值时,四边形DAOP 分别为平行四边形,直角梯形,等腰梯形?(3)若OC=OB,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1 个长度单位和2 个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t(s),连接PQ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.【考点】二次函数综合题.【专题】压轴题.【分析】(1)将A 的坐标代入抛物线y=a(x﹣1)2+3(a≠0)可得a 的值,即可得到抛物线的解析式;(2)易得D 的坐标,过D 作DN⊥OB 于N;进而可得DN、AN、AD 的长,根据平行四边形,直角梯形,等腰梯形的性质,用t 将其中的关系表示出来,并求解可得答案;(3)根据(2)的结论,易得△OCB 是等边三角形,可得BQ、PE 关于t 的关系式,将四边形的面积用t 表示出来,进而分析可得最小值及此时t 的值,进而可求得PQ 的长.【解答】解:(1)∵抛物线y=a(x﹣1)2+3(a≠0)经过点A(﹣2,0),∴0=9a+3 ,∴a=﹣(1 分)∴二次函数的解析式为:y=﹣x2+ x+;(3 分)(2)①∵D 为抛物线的顶点,∴D(1,3),过D 作DN⊥OB 于N,则DN=3,AN=3,∴AD= =6,∴∠DAO=60°.(4 分)∵OM∥AD,①当AD=OP 时,四边形DAOP 是平行四边形,∴OP=6,∴t=6(s).(5 分)②当DP⊥OM 时,四边形DAOP 是直角梯形,过O 作OH⊥AD 于H,AO=2,则AH=1(如果没求出∠DAO=60°可由Rt△OHA∽Rt△DNA(求AH=1)∴OP=DH=5,t=5(s)(6 分)③当PD=OA 时,四边形DAOP 是等腰梯形,易证:△AOH≌△DPP′,∴AH=CP,∴OP=AD﹣2AH=6﹣2=4,∴t=4(s)综上所述:当t=6、5、4 时,对应四边形分别是平行四边形、直角梯形、等腰梯形;(7 分)(3)由(2)及已知,∠COB=60°,OC=OB,△OCB 是等边三角形则OB=OC=AD=6,OP=t,BQ=2t,∴OQ=6﹣2t(0<t<3)过P 作PE⊥OQ 于E,则PE= t(8 分)。
二次函数压轴题精选40道(word含答案)

二次函数压轴题精选40道(word含答案)上文和下面资料在QQ群653794940下载1.分享:200个精美几何画板文件2.再分享:149个精美几何画板文件3.二次函数压轴题精选40道(word含答案)4.最全的“一线三等角”模型解析(ppt)5.重磅:2G多初中数学赛课好资料(打包分享)6.中考满分之路—必刷的30个专题(word分享)7.史上最全:初高中数学衔接教材(word分享)8.重磅分享:中考数学压轴题十大题型(word含详细答案)9.初中数学满分讲义10.重磅分享:最新旋转中考题精粹11.精品分享:将军饮马六大模型12.破解中考数学压轴题12讲(上word)13.破解中考数学压轴题12讲(下word)14.中考必备的15个word好专题(上)15.中考必备的15个word好专题(下)16.重磅分享:1991-2018年初中数学联赛试题及答案17.重磅分享:各类型全等三角形专题78页125题18.燃炸分享:初中数学选择通关题19.重磅:中考数学压轴题12讲(word分享)20.初中数学选择题精选400题(含答案)21.九年级数学暑假专用资料22.八年级最实用讲义23.勾股定理及逆定理专题(电子版分享)24.必看:中考数学考前指导(ppt)25.初高中数学衔接——超好教材(word)26.燃爆分享:初中数学综合复习资料27.相似三角形模型(word分享)28.旋转型相似三角形(word分享)29.收藏:一文搞定二次函数30.史上最全:初高中数学衔接教材(word分享)31.初中数学选择题精选400题(含答案)32.初中数学选择题精选300题(含答案)33.一张图读懂“代数几何”模型34.刚刚,第11届全国赛课一等奖获奖资料打包分享!35.word分享:四边形通关题36.将军饮马的六种常见模型37.重磅分享:初中数学几何模型38.初中数学解题技巧大全39.重磅word分享:学霸必备的23讲word40.1991-2018年初中数学联赛试题及答案(打包分享)41.81套2019年全国各地中考真题(word含答案)42.分享:初中几何辅助线大全43.学霸拥有满分无忧44.收藏:常见的线段最值问题45.最新:二次函数压轴题及答案(word分享)46. 最全初中数学几何动点问题专题分类归纳汇总47.word分享:12个专题模型(word分享)48.特殊平行四边形专题(word含详细答案)49.最值问题和路径问题精选(word分享)50.初中好题难题总动员(word分享)51.最全:2018年全国中考数学真题汇编(word含答案)52.助力中考:旋转专题53.最短路径12个基本问题(PPT分享)54.平移和旋转专题含答案(word分享)55.助力中考:相似三角形56.助力中考:半角模型(word分享)57.助力中考:手拉手模型(word分享)58.初中数学模型解题策略59.截长补短模型(word分享)60.共顶点模型(word分享)61.费马点最值模型(word分享)62.胡不归最值模型(word分享)63.隐圆模型(word分享)64.收藏:初中经典几何模型大全65.阿氏圆最值模型(word分享)66.角含半角模型(word分享)67.轴对称最值模型(word分享)68.弦图模型(word分享)69.对角互补模型(word分享)70.中考数学考前指导!最后一课!(PPT)71.全国各市中考真题111套(word含解析)72.中点模型(word分享)73.构造平行四边形解题(word分享)74.中考押题:等边三角形(word分享)75.主从联动模型(word分享)76.二次函数与几何综合(word分享)77.一题30问及解答78.中考二次函数压轴题汇总(163页word含详细解析)79.最全:中考总复习知识点总结(word分享)80.函数“存在性”问题(word分享)81.初中数学培优资料1-10讲(word分享)82.探索性问题(74页word分享)83.折叠问题(word分享)84.中数学培优资料11-20讲(word分享)85.初中数学培优资料21-26(word分享)86.初中数学常用几何模型及构造方法大全87.重磅:几何应用题(word分享)88.100多套2020年中考真题(word分享)89.章建跃教授:我们应该如何教几何(PPT分享)90.2020年中考数学试题分类汇编(word分享)91.一文搞定初中数学几何模型92.初中数学第一课:迷人的数学(PPT分享)93.对初中数学复习教学的思考(PPT分享)94.常见几何基本图形及结论95.三角形的中位线(ppt分享)96.大树理论和工匠精神(PPT分享)97.初三复习建议(PPT分享)98.初中第一课:走进数学世界(PPT分享)99.动找规律,静下结论(PPT分享)100.一文搞定瓜豆原理101.最全的将军饮马模型(word分享)102.图形变换背景下的轨迹思想的研究(ppt分享)103.相似三角形六大证明技巧(word分享)104.角平分线解题模型(word分享)105.18个经典几何模型(word400多页)106.三垂直模型(word分享)107.酷酷的:手拉手模型(word分享)108.酷酷的:半角模型(word分享)109.几何推理的秘密(ppt分享)110.酷酷的:对角互补模型(word分享)111.初中数学优秀获奖教案(word分享)112.再谈一线三等角(ppt分享)113.初中数学葵花宝典114.初中数学知识点全总结(word分享)115.酷酷的:线段求最值模型(word分享)116.圆精选50题(120页word分享)117.酷酷的:相似三角形模型(word分享)118.最经典的折叠题(word分享)119.最全的中点专题(PPT分享)120.最全的角平分线专题(ppt分享)121.最全的面积专题(ppt分享)122.如何教会学生?(ppt分享)123.最全的全等模型(ppt分享)124.最全的相似模型(ppt分享)125.最全的辅助圆模型(ppt分享)126.最全的折叠问题(ppt分享)127.最全的线段最值问题(ppt分享)128.核心专题:函数(word分享)129.核心专题:相似三角形(word分享)130. 初中数学的折叠问题(word分享)131.最全的解直角三角形模型(ppt分享)132.核心专题:圆(word分享)133.最全的函数与几何图形问题(ppt分享)134.权威专家谈教学的设计(ppt分享)135.十大专题12个模型54种考法上(ppt分享)136.十大专题12个模型54种考法下(ppt分享)137.初中数学全学段思维导图138.初中数学必备的72个二级结论139.角度计算的11个经典模型(word分享)140.2022中考数学应试技巧(ppt分享)141.收藏:中考必备的知识总结142.超级精品:初中数学几何模型143.倍长中线模型(word分享)144.重磅分享:数学竞赛精品资料30讲145.半角模型十五个结论及证明(word分享)146.半角模型的前世今生(word分享)147.秘籍:数学思想方法(word分享)148.初中几何基本图形及证明(word分享)149.初中数学公式定理大全(word分享)150.中考案例分析与解题技巧(word分享)151.精品专题:旋转相似(word分享)152.面积最值问题的2个重要模型(word分享)153.精品专题:旋转的6个命题角度(word分享)154.平面几何一题百变(word分享)155.因式分解的六大绝招(word分享)156.应用图形的旋转巧解难题(word分享)157.初中数学思想方法(ppt分享)158.精品专题:中心对称的6个命题角度(word分享)159.经典几何证明模型(word含答案)160.7个反比例函数常见几何模型(word分享)161.巧用数形结合妙解中考题(word分享)162.精品专题:瓜豆原理(word分享)163.十大专题12个模型54种考法(ppt分享)164.手把手教你几何画板10个经典案例(word分享)165.中考数学最易出错的61个知识点(word分享)166.中考数学必备手册(word分享)167.必看:中考数学36个秒懂(word分享)168.选择填空题的21个解题方法技巧169.二次函数精选12题(word分享)170.31个模型搞定中考几何(word分享)171.中考数学36个几何模型(word分享)172.中考必看的28个考点及60个易错点173.超好专题:相似三角形(word分享)174.9种常见的解题方法(word分享)175.精品收藏:胡不归专题(word分享)176.精品专题:将军饮马专题(word分享)177.精品收藏:瓜豆原理(word分享)178.精品收藏:费马点专题(word分享)179.12345模型(ppt分享)180.2021年安徽中考数学试题及答案(word分享)181.托勒密定理的应用(ppt分享)182.手拉手(ppt分享)183.重磅:2021年中考真题120份(word分享)184.三垂直模型(ppt分享)185.旋转的性质(ppt分享)186.半角模型(ppt分享)187.正方形与45度的基本图(word分享)188.最全的对称折叠专题(ppt分享)189.最全的相似模型(ppt分享)190.二次函数几何定义(ppt分享)191.强化模型意识,提高复习效率(ppt分享)192.最全的中考数学知识点总结(word分享)193.正方形对称、旋转(ppt分享)194.七种方法求最大值(word分享)195.中考必备的知识方法和模型196.从全等到相似(ppt分享)197.初中数学全学段思维导图198.圆中十四图(word分享)199.三弦图的应用(ppt分享)200.半角遇到三垂直(ppt分享)201.三角形中位线定理(word分享)202.初中数学各章节知识图解(ppt分享)203.神奇正方形(ppt分享)204.中考必备的知识框架图205.配方法的7大应用206.207.数形结合思想(word分享)208.圆中的相似(ppt分享)209.八大几何模型专题(word分享)210.动圆相切(ppt分享)211.旋转在中考压轴题中的应用(word分享)212.4个旋转常见模型(word分享)213.初中几何证明技巧及例题(word)214.圆切线的判定(ppt分享)215.中考几何解题策略18个专题(ppt)216.平行线的五大模型(word分享)217.中考必备的几何综合题(word分享)218.巧用翻折妙解几何题(word分享)219.二次函数与直角三角形(word)220.二次函数压轴十大类型题(word分享)221.三角形面积专题精选24题(word分享)222.反比例函数与面积综合题(word)223.中考必备的代数几何综合题(word)224.共端点共直线的两条线段的数量关系(word)225.旋转相似专题(word分享)226.精品:12个几何专题(word分享)227.隐形圆的4个模型(word分享)228.垂直精品小专题(word)229.初中几何辅助线做法大全230.二次函数与半角倍角等角问题(word分享)231.利用辅助圆求最值专题(word分享)232.阿波罗尼斯圆专题(word分享)233.最值问题的9个类型题(word分享)234.2022届数学思维导图(word分享)235.精品收藏:旋转专题(word分享)236.反比例函数与三角形(word分享)237.精品收藏:阿氏圆专题(word分享)238.精品收藏:路径专题(word分享)239.精品收藏:翻折专题(word分享)240.角存在专题(word分享)241.米勒角最大问题。
二次函数压轴题(含答案)[1]
![二次函数压轴题(含答案)[1]](https://img.taocdn.com/s3/m/b01b5993f242336c1fb95e16.png)
二次函数压轴题(含答案)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(二次函数压轴题(含答案)(word 版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为二次函数压轴题(含答案)(word版可编辑修改)的全部内容。
面积类1.如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.(1)求抛物线的解析式.(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.考点:二次函数综合题.专题:压轴题;数形结合.分析:(1)已知了抛物线上的三个点的坐标,直接利用待定系数法即可求出抛物线的解析式.(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长.(3)设MN交x轴于D,那么△BNC的面积可表示为:S△BNC=S△MNC+S△MNB=MN(OD+DB)=MN•OB,MN 的表达式在(2)中已求得,OB的长易知,由此列出关于S△BNC、m的函数关系式,根据函数的性质即可判断出△BNC是否具有最大值.解答:解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:a(0+1)(0﹣3)=3,a=﹣1;∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.(2)设直线BC的解析式为:y=kx+b,则有:,解得;故直线BC的解析式:y=﹣x+3.已知点M的横坐标为m,MN∥y,则M(m,﹣m+3)、N(m,﹣m2+2m+3);∴故MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).(3)如图;∵S△BNC=S△MNC+S△MNB=MN(OD+DB)=MN•OB,∴S△BNC=(﹣m2+3m)•3=﹣(m﹣)2+(0<m<3);∴当m=时,△BNC的面积最大,最大值为.2.如图,抛物线的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.考点:二次函数综合题.。
中考数学专题复习《二次函数综合压轴题》测试卷(附带参考答案)

中考数学专题复习《二次函数综合压轴题》测试卷(附带参考答案)学校:___________班级:___________姓名:___________考号:___________1.定义:对于函数 当自变量0x x = 函数值0y x =时 则0x 叫做这个函数的不动点.(1)直接写出反比例函数1y x=的不动点是__________.(2)如图 若二次函数2y ax bx =+有两个不动点 分别是0与3 且该二次函数图象的顶点P 的坐标为()2,4.①求该二次函数的表达式①连接OP M 是线段OP 上的动点(点M 不与点O P 重合) N 是该二次函数图象上的点 在x 轴正半轴上是否存在点(),0Q m 满足MOQ MPN NMQ ∠=∠=∠ 若存在 求m 的最大值 若不存在 请说明理由.2.如图 抛物线21103y x bx =-++分别交x 轴于点A 和B (A 在B 左侧) 交y 轴于点C 直线192y x =-+交x 轴于点E 交y 轴于点D 连接AD ADE 的面积是1892.(1)如图1 求b 的值(2)如图2 点P 为第一象限抛物线上一点 点P 的横坐标为t 连接AP 和BP ABP 的面积为S 求S 与t 之间的函数关系式(不要求写出自变量t 的取值范围)(3)如图3 在(2)的条件下 65S = 直线AP 和直线DE 相交于点F G 为AP 延长线上一点 连接GE AED DEG ∠=∠ 点M 为GE 上一点 连接FM FN 、 MN FM ⊥交x 轴于点N BN NE < 且GM NE = 在y 轴负半轴上一点H 使90MFN FEH ∠+∠=︒ 若求点H 的坐标.3.在平面直角坐标系xOy 中 已知线段PQ 和直线1l 2l 线段PQ 关于直线1l 2l 的“垂点距离”定义如下:过点P 作1⊥PM l 于点M 过点Q 作2QN l ⊥于点N 连接MN 称MN 的长为线段PQ 关于直线1l 和2l 的“垂点距离” 记作d .(1)已知点()2,1P ()1,2Q 则线段PQ 关于x 轴和y 轴的“垂点距离”d 为______(2)如图1 线段PQ 在直线3y x =-+上运动(点P 的横坐标大于点Q 的横坐标)若2PQ = 则线段PQ 关于x 轴和y 轴的“垂点距离”d 的最小值为______(3)如图2 已知点(0,23A A 的半径为1 直线33y x b 与A 交于P Q 两点(点P 的横坐标大于点Q 的横坐标) 直接写出线段PQ 关于x 轴和直线3y x =-的“垂点距离”d 的取值范围.4.如图 在平面直角坐标系中 抛物线23y ax bx =++过点(2,3) 且交x 轴于点(1,0)A - B 两点 交y 轴于点C .(1)求抛物线的表达式(2)点P 是直线BC 上方抛物线上的一动点 过点P 作PD BC ⊥于点D 过点P 作y 轴的平行线交直线BC 于点E :①当点P 运动到抛物线顶点时 求此时PDE △的面积①点P 在运动的过程中 是否存在PDE △周长的最大值 若存在 请求出PDE △周长的最大值及此时点P 的坐标 若不存在 请说明理由.5.如图1 抛物线2y x bx c =++交x 轴于A B 两点 其中点A 的坐标为()1,0与y 轴交于点C 1tan 3ACO ∠=.(1)求抛物线的函数解析式(2)点P 为直线BC 下方抛物线上一点 PD BC ⊥ PE y 轴 求PDE △周长的最大值(3)如图2 连接AC 点P 在抛物线上 且满足2PAB ACO ∠=∠ 求点P 的坐标.6.如图 在平面直角坐标系xOy 中 抛物线2y ax bx c =++与抛物线21y x x =-+-的形状相同 且与x 轴交于点()10-,和()40,.直线2y kx =+分别与x 轴 y 轴交于点A B 与2y ax bx c =++于点C D ,(点C 在点D 的左侧).(1)求抛物线的解析式(2)点P 是直线2y kx =+上方抛物线上的任意一点 当2k =时 求PCD 面积的最大值(3)若抛物线2y ax bx c =++与线段AB 有公共点 结合函数图象请直接写出k 的取值范围.7.如图 已知抛物线()()36y a x x =-+过点()1,5A -和点()5,B m - 与x 轴的正半轴交于点 C .(1)求a m 的值和点C 的坐标(2)若点P 是x 轴负半轴上的点 连接PB PA 当PA PB =时 求点P 的坐标(3)在抛物线上是否存在点M 使A B 两点到直线MC 的距离相等?若存在 求出满足条件的点M 的横坐标 若不存在 请说明理由.8.如图 在平面直角坐标系中 抛物线2y ax bx =++x 轴交于点()1,0A - ()5,0B 与y 轴交于点C 连接BC AC .(1)求抛物线的表达式(2)P 为直线BC 上方抛物线上一点 过点P 作PD BC ⊥于点D 过点P 作PE x 轴交抛物线于点E 的最大值及此时点P 的坐标(3)点C关于抛物线对称轴对称的点为Q将抛物线沿射线CA3新抛物线y'新抛物线y'与y轴交于点M新抛物线y'的对称轴与x轴交于点N连接AM MN点R在直线BC上连接QR.当QR与AMN一边平行时直接写出点R的坐标并写出其中一种符合条件的解答过程.9.如图国家会展中心的大门的截面图是由抛物线ADB和矩形ABCO构成的矩形ABCO的边34OA=米9OC=米以OC所在直线为x轴以OA所在直线为y轴建立平面直角坐标系抛物线顶点D的坐标为924,25⎛⎫ ⎪⎝⎭.(1)求此抛物线对应的函数表达式(2)近期需要对大门进行粉刷工人师傅搭建一木板OM点M正好在抛物线上支撑MN 垂直x轴7.5ON=米工人师傅站在木板OM上他能刷到的最大垂直高度是2.4米.①判断工人师傅能否刷到顶点D①设点E是OM上方抛物线上的一点且点E的横坐标为m直接写出他不能刷到大门顶部的对应点E的横坐标的范围.10.在平面直角坐标系中 抛物线()()()160y a x x a =+-≠分别交x 轴于A B 两点(A 在B 左边) 交y 轴于点C 连接AC 且12tan 5OAC ∠=.(1)如图1 求a 的值(2)如图2 点Q 是第四象限内抛物线上的一点 过点Q 作QD x ⊥轴于D 连接AQ 点E 在AQ 上 过E 点作EF x ⊥轴于F 点H 在EF 上 纵坐标为2- 连接HD 若5tan tan 2DHF QAF ∠=∠ 点Q 的横坐标为t DF 的长为d 求d 与t 之间的函数关系式并直接写出自变量t 的取值范围(3)如图3 在(2)的条件下 延长EF 交抛物线于点G 连接CG 延长至点M 过点M 作x 轴的垂线 交抛物线于点N 点P 为抛物线顶点 连接NP 并延长交y 轴于点K 连接KM并延长分别交EG HD 的延长线于点R T 连接ED 若5tan ,6EDQ RT ∠== 求点K 的坐标.11.如图 已知抛物线2y x bx c =++与x 轴交于0()1,A - B 两点 与y 轴交于点C (0,3)-.(1)求抛物线的解析式(2)如图1 点P 是抛物线上位于第四象限内一动点 PD BC ⊥于点D 求PD 的最大值及此时点P 的坐标(3)如图2 点E 是抛物线的顶点 点M 是线段BE 上的动点(点M 不与B 重合) 过点M 作MN x ⊥轴于N 是否存在点M 使CMN 为直角三角形?若存在 求出点M 的坐标 若不存在 请说明理由.12.如图 抛物线2y x bx c =-++与x 轴交于1,0A ()5,0B -两点 与y 轴交于点C .P 是抛物线上的任意一点(不与点C 重合) 点P 的横坐标为m 抛物线上点C 与点P 之间的部分(包含端点)记为图象G .(1)求抛物线的解析式(2)当m 符合什么条件时 图象G 的最大值与最小值的差为4?(3)将线段AB 先向左平移1个单位长度 再向上平移5个单位长度 得到线段A B ''.若抛物线2y x bx c =-++平移后与线段A B ''有两个交点 且这两个交点恰好将线段A B ''三等分 求抛物线平移的最短路程(4)当0m <时 若图象G 与平行于x 轴的直线23=-+y m 有且只有一个公共点 直接写出m 的取值范围.13.如图 二次函数()240y ax bx a =++≠的图象与x 轴交于点()1,0A - ()4,0B 与y 轴交于点C 抛物线的顶点为D(1)求二次函数的表达式及顶点D 的坐标(2)若点P 为直线BC 上方的抛物线上的一点 过点P 作垂直于x 轴的直线l 交直线BC 于点.F 是否存在点P 使四边形OCPF 为平行四边形?若存在 求出点P 的坐标 若不存在 请说明理由(3)若N 为抛物线上一个动点 连接NC 过点N 作NQ NC ⊥交抛物线对称轴于点Q 当tan 1NCQ ∠=时 请直接写出点N 的横坐标.14.如图 抛物线23y ax bx =+0a ≠)与x 轴交于点()1,0A -和点B 与y 轴交于点C 抛物线的对称轴交x 轴于点()1,0D 过点B 作直线l x ⊥轴 过点D 作DE CD ⊥ 交直线l 于点E .(1)求抛物线的解析式(2)点P 为第四象限内抛物线上的点 直线BP 与DE 交于点Q 当12BQ PQ =时 求点P 的坐标 (3)坐标轴上是否存在点F 使得75DEF ∠=︒ 若存在 请求出点F 的坐标 若不存在 请说明理由.15.如图 已知抛物线214y x bx c =-++交x 轴于点()2,0A ()8,0B - 交y 轴于点C 过点A B C 三点的M 与y 轴的另一个交点为D .(1)求此抛物线的表达式及圆心M 的坐标(2)设P 为弧BC 上一点 且⊥AP MC 交MC 于点N 求P 点坐标(3)延长线段BD 交抛物线于点E 设点F 是线段BE 上的任意一点(不含端点) 连接AF .动点Q 从点A 出发 沿线段AF 以每秒1个单位的速度运动到点F 再沿线段FB 单位的速度运动到点B 后停止 问当点F 的坐标是多少时 点Q 在整个运动过程中所用时间最少?参考答案:1.(1)1和1- (2)①42033=-+y x ①m 的最大值为942.(1)73b =(2)213916566S t t =-++ (3)()0,6H -3.(1)(2)222121d <≤4.(1)223y x x =-++(2)①PDE △的面积为1 ①存在 PDE △929+ 点P 的坐标为315,24⎛⎫ ⎪⎝⎭5.(1)223y x x =+- (2))9214 (3)1557,416⎛⎫- ⎪⎝⎭939,416⎛⎫-- ⎪⎝⎭6.(1)234y x x =-++(2)PCD 面积的最大值为278(3)k 的取值范围为02k <<或102k -<<7.(1)14a =- 2m = ()3,0C (2)3,08P ⎛⎫- ⎪⎝⎭(3)()9,9--或1135,39⎛⎫- ⎪⎝⎭8.(1)22422y x = (2)当154t =时 332292 151924P ⎛ ⎝⎭(3)R 点的坐标为22⎛ ⎝⎭或26,⎛ ⎝⎭或(2.9.(1)21924525y x ⎛⎫=--+ ⎪⎝⎭(2)①不能 ①31122m <<10.(1)25- (2)()2126d t t =->(3)()0,8K11.(1)223y x x =--(2)当32m =时 PD 取得最大值为8315,24P ⎛⎫- ⎪⎝⎭(3)CMN 为直角三角形时 点M 的坐标为:3,32⎛⎫- ⎪⎝⎭或()1212.(1)245y x x =--+(2)42m -≤≤-或2m =(4)3m =-或11m <≤-13.(1)234y x x =-++ 325,24D ⎛⎫ ⎪⎝⎭(2)存在 点P 的坐标为()2,6(3)11或2或214.(1)2y x x =-(2)P 1,⎛ ⎝⎭(3)F 的坐标为⎫⎪⎪⎝⎭或0,⎛ ⎝⎭.15.(1)213442y x x =--+ ()3,0M - (2)3224,55P ⎛⎫- ⎪⎝⎭(3)()2,3F --。
中考数学压轴题专练之二次函数综合(含20题)
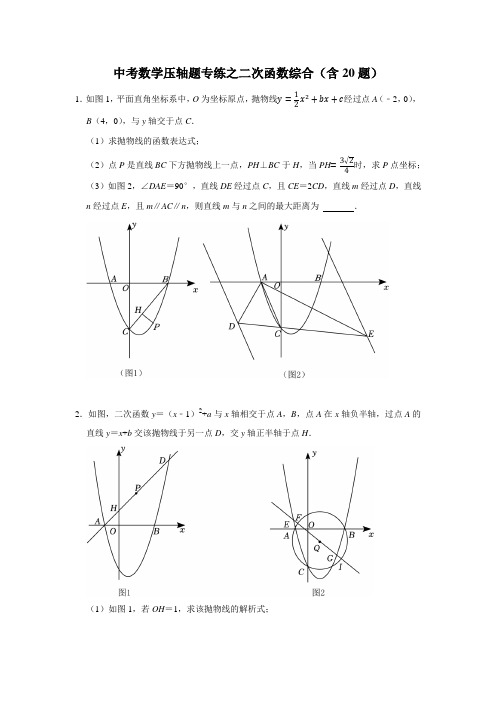
中考数学压轴题专练之二次函数综合(含20题)1.如图1,平面直角坐标系中,O为坐标原点,抛物线y=12x2+bx+c经过点A(﹣2,0),B(4,0),与y轴交于点C.(1)求抛物线的函数表达式;(2)点P是直线BC下方抛物线上一点,PH⊥BC于H,当PH=3√24时,求P点坐标;(3)如图2,∠DAE=90°,直线DE经过点C,且CE=2CD,直线m经过点D,直线n经过点E,且m∥AC∥n,则直线m与n之间的最大距离为.2.如图,二次函数y=(x﹣1)2+a与x轴相交于点A,B,点A在x轴负半轴,过点A的直线y=x+b交该抛物线于另一点D,交y轴正半轴于点H.(1)如图1,若OH=1,求该抛物线的解析式;(2)如图1,若点P是线段HD上一点,当1AH +1AD=3AP时,求点P的坐标(用含b的代数式表示);(3)如图2,在(1)的条件下,设抛物线交y轴于点C,过A,B,C三点作⊙Q,经过点Q的直线y=hx+q交⊙Q于点F,I,交抛物线于点E,G.当EI=GI+FI时,求2h2的值.3.如图1,在平面直角坐标系中,直线y=1与抛物线y=4x2相交于A,B两点(点B在第一象限),点C在AB的延长线上.且BC=n•AB(n为正整数).过点B,C的抛物线L,其顶点M在x轴上.(1)A点的坐标为;B点的坐标为;(2)当n=1时,抛物线L的函数表达式为;(3)如图2,抛物线E:,经过B、C两点,顶点为P.且O、B、P三点在同一直线上,求a n与n的关系式.4.如图,在平面直角坐标系中,二次函数y=14x2+bx+c的图象经过点A(6,0)、C(0,﹣3),点P为抛物线上一动点,其横坐标为m(m≥1).(1)求该抛物线对应的函数表达式.(2)若此抛物线在点P右侧部分(包括点P)的最低点的纵坐标为﹣5+m时,求m的值.(3)已知点M(m,m﹣3),点N(m﹣1,m﹣4),以MP、MN为邻边作▱PMNQ.①当抛物线在▱PMNQ 内部的部分的函数值y 随x 的增大而增大时,直接写出m 的取值范围;②当抛物线在▱PMNQ 内部的部分的函数值y 随x 的增大而增大或y 随x 的增大而减小时,抛物线与▱PMNQ 的边交点的纵坐标之差为12时,直接写出m 的值.5.综合与探究如图1,平面直角坐标系xOy 中,抛物线y =−38x 2+bx +3与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,点A 的坐标为(﹣2,0),抛物线上有一动点P ,点P 在第一象限,过点P 作y 轴的平行线分别交x 轴和直线BC 于点D 和点E . (1)求抛物线及直线BC 的函数关系式;(2)当点E 为线段DP 的中点时,求点E 的坐标;(3)如图2,作射线OP ,交直线BC 于点F ,当△OBF 是等腰三角形时,求点F 的坐标.6.如图,抛物线y=ax2+bx﹣4(a≠0).与x轴交于A(4,0)和B(﹣1,0)两点,与y 轴交于点C,点P是直线AC下方的抛物线上一动点.(1)求抛物线的解析式;(2)过点P作PD⊥x轴于点D,交直线AC于点E,求线段PE的最大值及此时点P的坐标;(3)取(2)中PE最大值时的P点,在坐标平面内是否存在点Q,使得以点A、C、P、Q为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标,若不存在,请说明理由.7.如图,在平面直角坐标系中,抛物线y=−12x2+bx+c与x轴交于A(﹣2,0)、B(4,0)两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点P为直线BC上方抛物线上一动点,连接OP交BC于点Q.(1)求抛物线的函数表达式;(2)当PQOQ 的值最大时,求点P的坐标和PQOQ的最大值;(3)把抛物线y=−12x2+bx+c向右平移1个单位,再向上平移2个单位得新抛物线y',M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,写出所有符合条件的N点的坐标,并写出求解点N的坐标的其中一种情况的过程.8.如图,△ABC的三个顶点坐标分别为A(﹣1,0),B(0,32),C(3,0),抛物线y=ax2+bx+c(a≠0)经过△ABC的三个顶点.(1)求抛物线y=ax2+bx+c(a≠0)的函数表达式;(2)点M是抛物线在第一象限上一点.①连接AM与BC相交于点E,即将△ABC分为两个三角形,若这两个三角形的面积之比为1:2时,则点M的坐标为,直线AM的函数表达式为;②将△ABO沿着x轴正方向平移,当点B与点M重合时停止,点A的对应点为A',点O 的对应点为点O'.求出△A'MO'与△BOC重合部分的图形的周长;(3)在抛物线y=ax2+bx+c(a≠0)的对称轴上取一点K,连接CK,使∠ACK+∠BAO =90°,延长CK交抛物线于点P,连接AK.动点Q从C点出发,沿射线CA以每秒1个单位长度的速度运动,是否存在某一时刻,使∠AQP=∠AKP?若存在,请直接写出此时t的值;若不存在,请说明理由.9.在平面直角坐标系中,抛物线y=x2+bx+c(b、c为常数)与x轴交点坐标为(1,0),与y轴交点的坐标为(0,3),点A、点B均在这个抛物线上,点A的横坐标为m,点B 的横坐标为1﹣m.当B在A的左侧时,抛物线上A、B两点之间的部分(包括A、B两点)记为图象G.(1)求此抛物线对应的函数表达式;(2)当图象G对应的函数值y随x的增大而减小时,求m的取值范围;(3)图象G最大值与最小值差为h,求h与m之间的函数关系式;(4)设点E的坐标为(m﹣3,2),点F的坐标(m﹣3,m﹣3),连结EF,以EF为边长向右作正方形EFPQ,当抛物线与正方形EFPQ的边只有两个交点,且交点的纵坐标之差为1时,直接写出m的值.10.如图,在平面直角坐标系中,抛物线y=x2+bx+c与直线AB交于点A(0,﹣2),B(2,0).(Ⅰ)求该抛物线的解析式;(Ⅱ)点P是直线AB下方抛物线上的一动点,过点P作x轴的平行线交AB于点C,过点P作y轴的平行线交x轴于点D,交线段AB于点H.求PC的最大值及此时点P的坐标;(Ⅲ)若点M是抛物线的顶点,在x轴上存在一点N,使△AMN的周长最小,求此时点N的坐标.11.在平面直角坐标系中,∠ACB=90°,AB∥x轴,如图1,C(1,0),且OC:OA=AC:BC=1:2.(1)求点A、点B的坐标;(2)已知抛物线y=ax2+bx+c(a≠0)过A、B、C三点,求该抛物线的表达式;(3)如图2,抛物线对称轴与AB交于点D,现有一点P从点A出发,以每秒1个单位的速度在AB上向点B运动,另一点Q从点D与点P同时出发,以每秒5个单位在抛物线对称轴上运动.当点P到达B点时,点P、Q同时停止运动,问点P、Q运动到何处时,△PQB面积最大,并求出最大面积.12.如图,抛物线y =ax 2+bx +2与x 轴交于点A (﹣1,0)、B (4,0)两点,与y 轴交点C ,连接AC ,BC .抛物线的对称轴交x 轴于点E ,交BC 于点F ,顶点为M . (1)求抛物线的解析式及顶点M 的坐标;(2)若D 是直线BC 上方抛物线上一动点,连接OD 交BC 于点E ,当DE OE的值最大时,求点D 的坐标;(3)已知点G 是抛物线上的一点,连接CG ,若∠GCB =∠ABC ,求点G 的坐标.13.如图,抛物线y =ax 2﹣8ax +12a (a <0)与x 轴交于A ,B 两点(点A 在点B 的左侧),抛物线上另有一点C 在第一象限,满足∠ACB 为直角,且使∠OCA =∠OBC . (1)求线段OC 的长;(2)求该抛物线的函数关系式;(3)在抛物线的对称轴上是否存在一点P ,使得△BCP 是以BC 为腰的等腰三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,请说明理由.14.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0),B (4,0)两点,与y轴交于点C,且OC=2OA.(1)试求抛物线的解析式;(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线在第一象限交于点P,与直线BC交于点M,记m=S△CPMS△CDM,试求m的最大值及此时点P的坐标;(3)在(2)的条件下,m取最大值时,是否存在x轴上的点Q及坐标平面内的点N,使得P,D,Q,N四点组成的四边形是矩形?若存在,请直接写出所有满足条件的Q点和N点的坐标;若不存在,请说明理由.15.已知:y=12x2+bx+c经过点A(﹣2,﹣1),B(0,﹣3).(1)求函数的解析式;(2)平移抛物线使得新顶点为点P(m,n).①当m>0时,若S△OPB=3,且在直线x=k的右侧,两函数值y都随x的增大而增大,求k的取值范围;②点P在原抛物线上,新抛物线与y轴交于点Q,当∠BPQ=120°时,求点P的坐标.16.已知抛物线y =﹣x 2+bx +c 与x 轴交于A (﹣1,0),B (3,0)两点,交y 轴于点C ,M 是抛物线顶点.(1)直接写出抛物线的函数解析式;(2)如图1,点P 在抛物线上,若直线AP 经过△CBM 外接圆的圆心,判断△CBM 的形状并求点P 的横坐标;(3)以点P (1,t )为圆心的⊙P 与x 轴相切且与抛物线只有两个公共点,求t 的取值范围.17.如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 与x 轴交于点A (4,0),C (﹣1,0)与y 轴交于点B ,已知tan ∠BAC =34. (1)求抛物线的函数表达式;(2)如图1,点P 为抛物线上的点,且点P 的横坐标为3,F 是抛物线上异于点P 的点,连接P A ,PB ,当S △P AB =S △F AB ,求点F 的横坐标;(3)如图2,点Q 为直线AB 上方抛物线上一点,OQ 交AB 于点D ,QE ∥BO 交AB 于点E .记△QDE ,△QDB ,△BDO 的面积分别为S 1,S 2,S 3.求S 1S 2+S 2S 3的最大值.18.如图1,对于平面上小于或等于90°的∠MON,我们给出如下定义:若点P在∠MON 的内部或边上,作PE⊥OM于点E,PF⊥ON于点F,则将PE+PF称为点P与∠MON 的“点角距”,记作d(∠MON,P).如图2,在平面直角坐标系xOy中,x、y正半轴所组成的角记为∠xOy.(1)已知点A(4,0)、点B(3,1),则d(∠xOy,A)=,d(∠xOy,B)=.(2)若点P为∠xOy内部或边上的动点,且满足d(∠xOy,P)=4,在图2中画出点P 运动所形成的图形.(3)如图3与图4,在平面直角坐标系xOy中,射线OT的函数关系式为y=43x(x≥0).①在图3中,点C的坐标为(4,1),试求d(∠xOT,C)的值;②在图4中,抛物线y=−12x2+2x+c经过A(5,0),与射线OT交于点D,点Q是A,D两点之间的抛物线上的动点(点Q可与A,D两点重合),求c的值和当d(∠xOT,Q)取最大值时点Q的坐标.19.如图,已知抛物线y=ax2+bx+c(a>0)与x轴交于A、B两点,与y轴交于点C(0,2),抛物线的对称轴为直线x=52,且OB=2OC.连接BC,点D是线段OB上一点(不与点O、B重合),过点D作x轴的垂线,交BC于点M,交抛物线于点N.(1)求抛物线的表达式;(2)当线段MN最大时,求点M的坐标;(3)连接BN,以B、D、N为顶点的三角形是否能够与△OBC相似?若能,请求出点N 的坐标;若不能,请说明理由.20.如图,已知抛物线y=﹣x2﹣2x+3的顶点为D点,且与x轴交于B,A两点(B在A的左侧),与y轴交于点C.点E为抛物线对称轴上的一个动点:(1)当点E在x轴上方且CE∥BD时,求sin∠DEC的值;(2)若点P在抛物线上,是否存在以点B,E,C,P为顶点的四边形是平行四边形?请求出点P的坐标;(3)若抛物线对称轴上有点E,使得AE+√55DE取得最小值,连接AE并延长交第二象限抛物线为点M,从请直接写出AM的长度.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名学生姓名填写时间
学科数学年级初三教材版本人教版
阶段观察期□:第()周维护期□本人课时统计第()课时共( 2)课时
课题名称二次函数综合大题(压轴题)
课时计划
第( 1、2 )
课时
共( 4 )课时
上课时间
教学目标
同步教学知识内容学校同步学到圆周角,1对1提前学到圆结束
个性化学习问题解决二次函数综合大题(压轴题)
教学过程
教师活动
二次函数综合大题(压轴题)
一、经典例题精讲
面积类
例1.如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.
(1)求抛物线的解析式.
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.
考点:二次函数综合题.
专题:压轴题;数形结合.
分析:
(1)已知了抛物线上的三个点的坐标,直接利用待定系数法即可求出抛物线的解析式.
(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长.
(3)设MN交x轴于D,那么△BNC的面积可表示为:S△BNC=S△MNC+S△MNB=MN(OD+DB)=MN•OB,MN的表达式在(2)中已求得,OB的长易知,由此列出关于S△BNC、m的函数关系式,根据函数的性质即可判断出△BNC是否具有最大值.
解答:
解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:
a(0+1)(0﹣3)=3,a=﹣1;
∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.
(2)设直线BC的解析式为:y=kx+b,则有:
,
解得;
故直线BC的解析式:y=﹣x+3.
已知点M的横坐标为m,MN∥y,则M(m,﹣m+3)、N(m,﹣m2+2m+3);
∴故MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).
(3)如图;
∵S△BNC=S△MNC+S△MNB=MN(OD+DB)=MN•OB,
∴S△BNC=(﹣m2+3m)•3=﹣(m﹣)2+(0<m<3);
∴当m=时,△BNC的面积最大,最大值为.
练习1
如图,抛物线的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.
考点:二次函数综合题..
专题:压轴题;转化思想.
平行四边形类
例2如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,﹣3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
考点:二次函数综合题;解一元二次方程-因式分解法;待定系数法求一次函数解析式;待定系数法求二次函数解析式;三角形的面积;平行四边形的判定..
专题:压轴题;存在型.
分析:
(1)分别利用待定系数法求两函数的解析式:把A(3,0)B(0,﹣3)分别代入y=x2+mx+n与y=kx+b,得到关于m、n的两个方程组,解方程组即可;
(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),用P点的纵坐标减去M的纵坐标得到PM的长,即PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,然后根据二次函数的最值得到
当t=﹣=时,PM最长为=,再利用三角形的面积公式利用S△ABM=S△BPM+S△APM计算即可;
(3)由PM∥OB,根据平行四边形的判定得到当PM=OB时,点P、M、B、O为顶点的四边形为平行四边形,然后讨论:当P在第四象限:PM=OB=3,PM最长时只有,所以不可能;当P在第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3;当P在第三象限:PM=OB=3,t2﹣3t=3,分别解一元二次方程即可得到满足条件的t的值.
解答:
解:(1)把A(3,0)B(0,﹣3)代入y=x2+mx+n,得
解得,所以抛物线的解析式是y=x2﹣2x﹣3.
设直线AB的解析式是y=kx+b,
把A(3,0)B(0,﹣3)代入y=kx+b,得,解得,
所以直线AB的解析式是y=x﹣3;
(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),
因为p在第四象限,
所以PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,
当t=﹣=时,二次函数的最大值,即PM最长值为=,
则S△ABM=S△BPM+S△APM==.
(3)存在,理由如下:
∵PM∥OB,
∴当PM=OB时,点P、M、B、O为顶点的四边形为平行四边形,
①当P在第四象限:PM=OB=3,PM最长时只有,所以不可能有PM=3.
②当P在第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3,解得t1=,t2=(舍去),所以P点的横坐标是;
③当P在第三象限:PM=OB=3,t2﹣3t=3,解得t1=(舍去),t2=,所以P点的横坐标是
.
所以P点的横坐标是或.
练习2
如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.
(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;
(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O 面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.
考点:二次函数综合题..
专题:压轴题.
周长类
例3.如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B 两点的坐标分别为(﹣3,0)、(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线x=上.
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
考点:二次函数综合题..
专题:压轴题.
分析:(1)根据抛物线y=经过点B(0,4),以及顶点在直线x=上,得出b,c即可;(2)根据菱形的性质得出C、D两点的坐标分别是(5,4)、(2,0),利用图象上点的性质得出x=5或2时,y的值即可.
(3)首先设直线CD对应的函数关系式为y=kx+b,求出解析式,当x=时,求出y即可;
解:(1)∵抛物线y=经过点B(0,4)∴c=4,∵顶点在直线x=上,∴﹣=﹣=,∴b=﹣;
∴所求函数关系式为;
(2)在Rt△ABO中,OA=3,OB=4,∴AB=,∵四边形ABCD是菱形,∴BC=CD=DA=AB=5,
∴C、D两点的坐标分别是(5,4)、(2,0),
当x=5时,y=,
当x=2时,y=,
∴点C和点D都在所求抛物线上;
(3)设CD与对称轴交于点P,则P为所求的点,
设直线CD对应的函数关系式为y=kx+b,
则,解得:,∴,
当x=时,y=,∴P(),
三.随堂练习
练习3、如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P 的坐标;若不存在,请说明理由.
考点:二次函数综合题..
专题:压轴题;分类讨论.
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
