二次函数符号判断
二次函数abc组合的符号判断

二次函数abc组合的符号判断对于二次函数中abc组合的符号判断套路掌握情况,分为三个层次,首先根据函数图象确定a,b,c符号以及对称轴信息,其次是找特殊点的函数值,获取等式和不等式,最后在判断残缺型符号时,将等式代入不等式。
过程中考查学生读图,数形结合以及逻辑分析能力。
单选题(本大题共7小题,共100分)1.(本小题12分)如图,二次函数的图象开口向上,对称轴为直线x=1,且图象经过点(3,0),则下列结论正确的是( )∙ A.∙ B.∙ C.∙ D.核心考点: 二次函数图象与系数的关系 abc组合的符号判断2.(本小题12分)已知二次函数的图象如图所示,下列结论:①;②;③;④b+2a=0;⑤.其中正确的有( )∙ A. 1个∙ B. 2个∙ C. 3个∙ D. 4个核心考点: 二次函数图象与系数的关系abc组合的符号判断3.(本小题12分)已知二次函数的图象如图所示,下列结论:①;②;③;④.其中正确的是( )∙ A. ②③∙ B. ③④∙ C. ②④∙ D. ①④核心考点: 二次函数图象与系数的关系 abc组合的符号判断4.(本小题16分)如图所示,二次函数的图象中,王刚同学观察得出了下面四条结论:①;②;③;④.其中错误的有( )∙ A. 1个∙ B. 2个∙ C. 3个∙ D. 4个核心考点: 二次函数图象与系数的关系abc组合的符号判断5.(本小题16分)已知二次函数的图象如图所示,其对称轴为直线,则下列结论正确的是( )∙ A.∙ B. a+b=0∙ C.∙ D.核心考点: 二次函数图象与系数的关系 abc组合的符号判断6.(本小题16分)如图,二次函数图象的顶点在第一象限,且过点(0,1)和(-1,0).下列结论:①;②;③;④当时,.其中正确的有( )∙ A. 1个∙ B. 4个∙ C. 3个∙ D. 2个核心考点: 二次函数图象与系数的关系abc组合的符号判断7.(本小题16分)已知二次函数的图象如图所示,下列结论:①;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④;⑤.其中正确的是( )∙ A. ②③⑤∙ B. ①②③⑤∙ C. ①②④⑤∙ D. ①③④⑤核心考点: 二次函数图象与系数的关系 abc组合的符号判断单选题(本大题共6小题,共100分)1.(本小题15分)二次函数图象的一部分如图所示,其对称轴为直线x=-1,且过点(-3,0).下列说法:①;②2a-b=0;③;④若,是抛物线上的两点,则.其中正确的是( )∙ A. ①②∙ B. ②③∙ C. ①②④∙ D. ②③④核心考点: 二次函数图象与系数的关系 abc组合的符号判断2.(本小题15分)二次函数的图象如图所示,下列结论:①;②;③;④.其中正确的是( )∙ A. ①②∙ B. ②③∙ C. ③④∙ D. ①④核心考点: 二次函数图象与系数的关系abc组合的符号判断3.(本小题15分)如图所示,二次函数的图象中,小轩同学观察得出了如下四条结论:①;②;③;④.其中正确的是( )∙ A. ①②∙ B. ②③∙ C. ①②③∙ D. ①②③④核心考点: 二次函数图象与系数的关系 abc组合的符号判断4.(本小题15分)已知二次函数的图象如图所示,有下列结论:①;②2a+b=0;③;④.其中正确的有( )个.∙ A. 1 ∙ B. 2 ∙ C. 3 ∙D. 4核心考点: 二次函数图象与系数的关系 abc 组合的符号判断5.(本小题20分) 已知二次函数的图象如图所示,它与x 轴的两个交点分别为 (-1,0),(3,0).下列结论:①;②b-2a=0;③;④.其中正确的是( )∙A. ③ ∙B. ②③ ∙C. ③④ ∙D. ①②核心考点: 二次函数图象与系数的关系 abc 组合的符号判断6.(本小题20分)已知二次函数的图象经过,(2,0)两点,且,图象与y轴正半轴的交点在(0,2)的下方,则下列结论:①;②;③;④.其中正确的是( )∙ A. ①②∙ B. ②③∙ C. ①②④∙ D. ①②③④核心考点: 二次函数图象与系数的关系abc组合的符号判断。
二次函数a.b.c等的符号的确定

-1 o 1 x
(5)△=b2-4ac决定抛物线与x轴交点情况:
① △>0 ② △=0
抛物线与x轴有两个交点; 抛物线与x轴有唯一的公共点;
③ △<0 抛物线与x轴无交点。
y ox
y ox
y ox
勇攀高峰
1. 二次函数y=ax2+bx+c的图象如图所示,下列结论中:
①abc>0;② a+b+c<0 ③ a-b+c>0 ;
o1 特殊值法
x
y aabb cc 0 0
y=ax2+bx+c 当x 1时 y=a-b+c
y aabbcc0 0 y
y aabbcc00
-1 o
x
y aabbcc00
x=-1
比拼速度
二次函数y ax2 bx c的图象如图,用(< , >或 =)填空: a< 0,b < 0,c > 0,a+b+c< 0,a-b+c> 0, Nhomakorabeay
开口向下
a<0
数形结合法
x
⑵c决定抛物线与y轴交点(0,c)的位置:
① 图象与y轴交点在y轴正半轴;
c>0
② 图象过原点
c=0
③ 图象与y轴交点在y轴负半轴
c<0
y
指出下列二次函数与y轴交点的坐标.
(1) y=x2-8x+7 (2) y=-2x2+9x-17
x
⑶a,b决定抛物线对称轴的位置: 对称轴是直线x =
转化 + 特殊值
根据抛物线y=ax2+bx+c图象位置,你 会判断那些字母或代数式的符号?
二次函数中根据图像判断代数式符号归类

(1)决定开口方向:a>0时开口向上,a<0时开口向下.(2)决定形状: ︱a︱相同,则形状相同.︱a︱不同,则形状不同.(3)决定开口大小: ︱a︱越大,则开口越小. ︱a︱越小,则开口越大.(4)决定最值:a>0时,有最低点,有最小值.a<0时,有最高点,有最大值.(5)决定增减性:a>0时,在对称轴左侧,y随x的增大而减小,在对称轴右侧,y随x的增大而增大.a<0时,在对称轴左侧,y随x的增大而增大在对随x的增大而减小.a、b同号时对称轴在y轴左侧a、b异号时对称轴在y轴右侧y轴y轴的交点:c>0时,抛物线交于y轴的正半轴c=0时,抛物线过原点y轴的负半轴:与x轴有两个交点点在x轴上方a+b+c>0,点在x轴下方a+b+c<0点在x轴上方a-b+c>0,点在x轴下方a-b+c<0点在x轴上a-b+c=0决定开口方向:a>0时开口向上,a<0时开口向下.(2)决定形状: ︱a︱相同,则形状相同.︱a︱不同,则形状不同.(3)决定开口大小: ︱a︱越大,则开口越小.︱a︱越小,则开口越大.(4)决定最值:a>0时,有最低点,有最小值.a<0时,有最高点,有最大值.(5)决定增减性:a>0时,在对称轴左侧,y随x的增大而减小,在对称轴右侧,y随x的增大而增大.a<0时,在对称轴左侧,y随x的增大而增大在对随x的增大而减小.a、b同号时对称轴在y轴左侧a、b异号时对称轴在y轴右侧y轴y轴的交点:c>0时,抛物线交于y轴的正半轴c=0时,抛物线过原点y轴的负半轴:与x轴有两个交点点在x轴上方a+b+c>0,点在x轴下方a+b+c<0点在x轴上方a-b+c>0,点在x轴下方a-b+c<0点在x轴上a-b+c=0。
二次函数符号abc的判定练习

二次函数y=ax2+bx+c系数符号的确定方法一、知识点二次函数y=ax2+bx+c系数符号的确定:(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0.(2)b由对称轴和a的符号确定:由对称轴公式x=判断符号.(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.(4)b2-4ac的符号由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.(5)当x=1时,可确定a+b+c的符号,当x=-1时,可确定a-b+c的符号.(6)由对称轴公式x=,可确定2a+b的符号.二、基础练习1、已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中,正确的是()A、a>0B、b<0C、c<0D、a+b+c>02、二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a-b+c<0,则正确的结论是()A、①②③④B、②④⑤C、②③④D、①④⑤3、如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为( 1/2,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确结论的个数是()A、1B、2C、3D、44、已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是()A、ac>0B、方程ax2+bx+c=0的两根是x1=-1,x2=3C、2a-b=0D、当x>0时,y随x的增大而减小5、已知二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,有下列结论:①abc>0,②b2-4ac<0,③a-b+c>0,④4a-2b+c<0,其中正确结论的个数是()A、1B、2C、3D、46、如图所示的二次函数y=ax2+bx+c的图象中,下面四条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.错误的有()A、2个B、3个C、4个D、1个7、抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列说法正确的是()A、b2-4ac<0B、abc<0C、 -b/2a<-1D、a-b+c<08、已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2-4ac>0 ②abc>0 ③8a+c>0 ④9a+3b+c<0,则其中结论正确的个数是()A、2个 B、3个 C、4个 D、5个9、已知二次函数y=ax2的图象开口向上,则直线y=ax-1经过的象限是()A、第一、二、三象限B、第二、三、四象限C 、第一、二、四象限D 、第一、三、四象限10、二次函数y=ax 2+bx+c 的图象如图示,则下列结论正确的是( )A 、a <0,b <0,c >0,b 2-4ac >0B 、a >0,b <0,c >0,b 2-4ac <0C 、a <0,b >0,c <0,b 2-4ac >0D 、a <0,b >0,c >0,b 2-4ac >011、已知二次函数y=ax 2+bx+c 的图象如图所示,那么下列判断不正确的是( )A 、ac <0B 、a-b+c >0C 、b=-4aD 、关于x 的方程ax 2+bx+c=0的根是x 1=-1,x 2=512、已知二次函数y=ax 2+bx+c 的图象如图所示,则a ,b ,c 满足( )A 、a <0,b <0,c >0,b 2-4ac >0B 、a <0,b <0,c <0,b 2-4ac >0C 、a <0,b >0,c >0,b 2-4ac <0D 、a >0,b <0,c >0,b 2-4ac >013、已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,有下列4个结论, 其中正确的结论是( )A 、abc >0B 、b >a+cC 、2a-b=0D 、b 2-4ac <014、(已知二次函数y=y=ax 2+bx+c (a ≠0)的图象如图所示,则下列结论:①ac >0;②a-b+c <0;③当x <0时,y <0;④方程ax 2+bx+c=0(a ≠0)有两个大于-1的实数根.其中错误的结论有( )A 、②③ B 、②④ C 、①③ D 、①④15、如图所示为二次函数y=ax 2+bx+c (a ≠0)的图象,在下列选项中错误的是( )A 、ac <0B 、x >1时,y 随x 的增大而增大C 、a+b+c >0D 、方程ax 2+bx+c=0的根是x 1=-1,x 2=316、二次函数y=ax 2+bx+c 的图象如图所示,下列结论错误的是( )A 、ab <0B 、ac <0C 、当x <2时,函数值随x 增大而增大;当x >2时,函数值随x 增大而减小D 、二次函数y=ax 2+bx+c 的图象与x 轴交点的横坐标就是方程ax 2+bx+c=0的根17、已知二次函数y=ax 2+bx+c 的图象如图所示,则下列结论正确的是( )A 、a >0B 、c <0C 、b 2-4ac <0D 、a+b+c >018、二次函数y=ax 2+bx+c (a ≠0)的图象如图示,下列结论①a ,b 异号;②当x=1和x=3时,函数值相等;③4a+b=0;④当y=4时,x 的取值只能为0,结论正确的个数有( )个. A 、1 B 、2 C 、3 D 、419、二次函数y=-x 2+bx+c 的图象如图所示,下列几个结论:①对称轴为x=2;②当y ≤0时,x <0或x >4;③函数解析式为y=-x (x-4);④当x ≤0时, y 随x 的增大而增大.其中正确的结论有( )A 、①②③④B 、①②③C 、①③④D 、①③三、能力练习1.已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,下列结论:①abc >0;②b <a+c ;③2a+b=0;④a+b >m (am+b )(m ≠1的实数).其中正确的结论有( )A 、1个B 、2个C 、3个D 、4个2.如图,抛物线y=ax 2+bx+c 的对称轴是x=1,下列结论:①b <0;②(a+c )2>b 2;③2a+b-c >0;④3b <2c .其中正确的结论有( )(填上正确结论的序号).3、二次函数2(0)y ax bx c a =++≠的图象如图所示,则①20a b +>. .C A y x O 图2 O xy-1 1 y 0 11 x-1 图1 ②20a b +<③02b a-< ④20a b -<⑤20a b ->中正确的有( )4、如图,是二次函数 y=ax 2+bx+c (a ≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b >2a ③ax 2+bx+c=0的两根分别为-3和1;④a-2b+c >0. 其中正确的命题是( )5、如图7是二次函数)0(2≠++=a c bx ax y 在平面直角坐标系中的图象,根据图形判断 ① c >0;② a +b +c <0; ③ 2a -b <0;④ b 2+8a >4a c 中正确的是(填写序号) .6、抛物线y=ax 2+bx+c 的图象如图,OA=OC ,则( )(A ) ac+1=b; (B ) ab+1=c; (C )bc+1=a; (D )以上都不是7、已知二次函数c bx ax y ++=2的图象如图2所示,那么下列判断不正确的是( )(A)abc >0; (B )ac b 42->0;(C)2a+b >0; (D )c b a +-24<08、二次函数c bx ax y ++=2的图象如图所示,则 abc ,ac b 42-,b a +2,c b a ++这四个式子中,值为正数的有( )A .4个 B .3个 C .2个 D .1个9、二次函数c bx ax y ++=2的图象如图1所示,则下列结论中,正确的个数是( ) ①0<++c b a ;②0>+-c b a ;③0>abc ;④a b 2=A.4B.3C.2D.1图7。
二次函数中的符号问题

基础回顾:
1、抛物线y=ax2+bx+c的开口方向、形状与什么 有关?
a>0时,开口向上;a<0时,开口向下。
a 相等
抛物线的形状相同
2、抛物线y=ax2+bx+c与y轴的交点是(0、c).
3、抛物线y=ax2+bx+c的对称轴是 X=- b .
2a
2
归纳知识点:
抛物线y=ax2+bx+c的符号问题:
y
根据图像可得:
1、a>0
2、- b >0
2a
o
x 3、△=b²-4ac>0
4、C>0
6
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的 符号:
y
根据图像可得:
1、a>0
b
2、-
<0
2a
o
x 3、△=b²-4ac>0
4、C=0
7
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的 符号:
M
B 1
Ax
O
1
17
再想一想:
5.如图,在平面直角坐标系中,二次函数y=ax2+c(a<0)的
图象过正方形ABOC的三个顶点A、B、C,则ac的值是 -2 .
设正方形的对角线长为2n, 根据图像可得:
∵A(0、2n)、B(-n、n)、 C(n、n) ∴n=a(±n)²+2n、c=2n,
∴a=- 1 ,∴ac=2n*(-
②如图2a+b _______0 4a+2b+c_______0
12
根据图象填空:
(1)a_____0; (2)b_____0; (3)c______0; (4)b2 4ac _____0; (5)a+b+c_____0; (6)a-b+c_____0; (7)2a+b_____0;
期末专题复习(一)二次函数的符号判断

的图象与 轴交于点
, 两点,与 轴交于点 ,对称轴为直线 숸 ,点 的坐标为 ,则下列
结论:① 숸 ;② t t ;③ t ;④ t t ,其中正确的结
论有
个.
A. 个
B. 个
C. 个
D. 个
7. 如 图 10 , 二 次 函 数 숸 t t
的部分图象如图所示,图象过点
,对称轴为直线 숸 ,下列结论:(1) t 숸 ;(2) t t;
...
与 b (对称轴)和 a b c,3a b,2a 2b,2a b... 等特殊符号判断 2a
2a c,2a b, a b, a b 将对称轴与常数大小作比较/通过代入消元法解决.
温馨提示:每完成一次专题复习记得留意复习此栏内容哦!
期末专题复习·九年级·数学
图象的一部分,对称轴为 숸 ,且
经过点
.有 下列 说法 :① tt ; ② t 숸 ;③ t t ; ④若
,
是抛物线上的两点,则 숸 .上述说法正确的是
A. ①②④
B. ③④
C. ①③④
D. ①②
图2
例题 3. (2018·深圳中考)如图 3,二次函数 숸 t
A. tt
B. t
C. t
A.
B.
C.
D.
10. 当 t 时, 숸 与 숸 t 的图象大致是
A.
B.
C.
D.
11. ,函数 숸 与 숸 在同一直角坐标系中的大致图象可能是
图 12
A.
B.
C.
D.
12. 如图 13,二次函数 숸 t t 的图象经过点
二次函数abc10条口诀

二次函数abc10条口诀二次函数是中学数学中一个重要的概念,在学习二次函数时,了解关于二次函数的性质和特点是非常重要的。
为了帮助大家更好地记忆和理解二次函数的内容,下面给出了10条关于二次函数的口诀,助您轻松掌握二次函数的重要知识点。
口诀一:二次的意志在二次函数中,二次项的系数a代表了二次函数的开口方向和大小,关于a的取值有三条重要的规则需要记住:1.当a>0时,二次函数开口向上;2.当a<0时,二次函数开口向下;3.当a=0时,二次函数就退化成了一次函数。
口诀二:顶峰或底谷二次函数的顶点是函数图像的最高点或最低点,顶点的横坐标就是二次项的系数b的相反数,纵坐标则是带入该横坐标得到的函数值。
口诀三:顺时针或逆时针?二次函数的抛物线在坐标系中的开口方向由二次项的系数a和平方数的系数c的正负号决定:1.当a>0且c>0时,抛物线开口向上;2.当a<0且c>0时,抛物线开口向下;3.当a>0且c<0时,抛物线开口向下;4.当a<0且c<0时,抛物线开口向上。
口诀四:判别式开局判别式是判断二次函数的根的性质的一个重要指标,其值为b2−4ac。
根据判别式的值,可以得到以下结论:1.当判别式>0时,二次函数有两个不相等的实根;2.当判别式=0时,二次函数有两个相等的实根,此时二次函数的抛物线与x轴只有一个交点;3.当判别式<0时,二次函数没有实根,此时二次函数的抛物线与x轴没有交点。
口诀五:根公式最牛根据判别式的值,二次函数的根可以通过以下公式计算得到:1.当判别式>0时,根的公式为$x=\\frac{-b\\pm\\sqrt{b^2-4ac}}{2a}$;2.当判别式=0时,根的公式为$x=\\frac{-b}{2a}$;3.当判别式<0时,没有实根。
口诀六:对称性二次函数的图像具有关于顶点对称的性质,这意味着如果将顶点的横坐标记为ℎ,则对称轴方程为x=ℎ。
判定二次函数中的a,b,c的符号
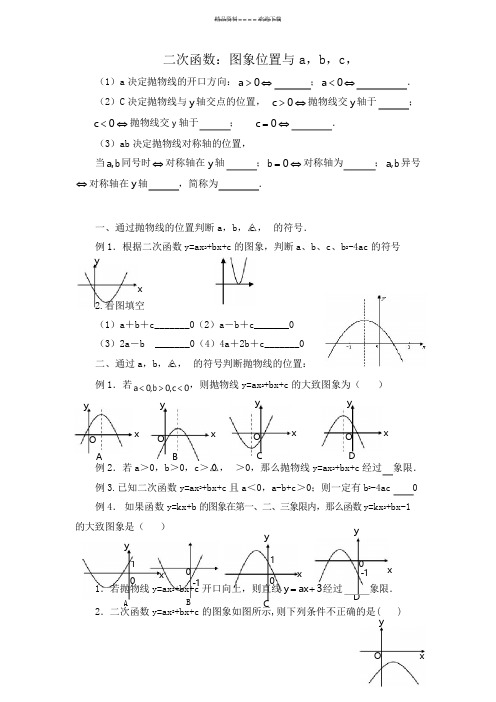
10A B C D二次函数:图象位置与a,b,c,(1)a决定抛物线的开口方向:a>0⇔;a<0⇔.(2)C决定抛物线与y轴交点的位置,c>0⇔抛物线交y轴于;c<0⇔抛物线交y轴于;c=0⇔.(3)ab决定抛物线对称轴的位置,当a,b同号时⇔对称轴在y轴;b=0⇔对称轴为;a,b异号⇔对称轴在y轴,简称为.一、通过抛物线的位置判断a,b,△c,的符号.例1.根据二次函数y=ax2+bx+c的图象,判断a、b、c、b2-4ac的符号yx2.看图填空(1)a+b+c_______0(2)a-b+c_______0(3)2a-b_______0(4)4a+2b+c_______0二、通过a,b,△c,的符号判断抛物线的位置:例1.若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为()y y y yOx O x O x O xA B C D例2.若a>0,b>0,c>△0,>0,那么抛物线y=ax2+bx+c经过象限.例3.已知二次函数y=ax2+bx+c且a<0,a-b+c>0;则一定有b2-4ac0例4.如果函数y=kx+b的图象在第一、二、三象限内,那么函数y=kx2+bx-1的大致图象是()y yy 1x0x-1x 0-101.若抛物线y=ax2+bx+c开口向上,则直线y=ax+3经过象限.2.二次函数y=ax2+bx+c的图象如图所示,则下列条件不正确的是()yO x3.二次函数 y=ax 2+bx+c 的图象如图,则点, ⎪ 在.( )⎝ b 2 - 4ac b ⎭y yA 、 a < 0, b > 0, c < 0B 、 b 2 - 4ac < 0C 、 a + b + c < 0D 、 a - b + c > 0⎛ a + b ac ⎫yA 、第一象限B 、第二象限C 、第三象限D 、第四象限O4.二次函数 y=ax 2+bx+c 与一次函数 y = ax + c 在同一坐标系中的图象大致是() yyO xO xO x OxABCD5.二次函数 y=ax 2+bx+c (a ≠ 0)的图象,如图,下列结论①c < 0 ② b > 0 ③ 4a + 2b + c > 0 ④ (a + c )2 < b 2 其中正确的有()A 、1 个B 、2 个C 、3 个D 、4 个6.已知函数 y=ax 2+bx+c 的图象如图所示,关于系数 a, b , cyOxx = 1y有下列不等式① a < 0 ② b < 0 ③ c > 0 ④ 2a + b < 0 ⑤ a + b + c > 0 其中正确个数为 .7.已知直线 y=ax 2+bx+c 不经过第一象限,则抛物线y = ax 2 + bx 一定经过()A .第一、二、四象限B .第一、二、三象限C .第一、二象限D .第三、四象限8. 如图所示的抛物线是二次函数 y =ax 2-3x +a 2-1 的图象,那么 a 的值是__.- O 1x.. 轴正半轴相交,其顶点坐标为,1⎪ ,下列结论:①ac<0;② 精品资料 欢迎下载9. 若抛物线 y =x 2-bx +9 的顶点在 x 轴上,则 b 的值为______若抛物线 y =x 2-bx +9 的顶点在 y 轴上,则 b 的值为______10.已知二次函数 y =ax 2+bx +c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b +c=2; ③a >结论是( )1 2;④b<1.其中正确的A .①②B .②③C .②④D .③④11.二次函数 y =ax 2+bx +c(a≠0)的图象开口向上,图象经过点(-1,2)和(1,0),且与 y 轴负半轴交于一点,给出以下结论①abc<0;②2a+b >0;③a+c =1;④a>1.其中正确的结论是()A 、1 个B 、2 个C 、3 个D 、4 个12. 二次函数 y =ax 2 -2x -1 与 x 轴有交点,则 k 的取值范围________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)
A.2 个 B.3 个 C.4 个 D.5 个
-1 O 1 x
4. 抛物线 y ax2 bx c 图象如图所示,给出下列四
个结论:① abc >0;② a b c 2 ;③ a 1 ;
2
④ b <1.其中正确的结论是 (
)
(A)①② (B)②③ (C)②④ (D)③④
5. 函数y=x2+bx+c与y=x的图象如图所示,有以下 结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0; ④当1<x<3时,x2+(b﹣1)x+c<0.其中正确 的个数为( )
A1 B 2 C3 D 4
6.小轩从如图所示的二次函数y=ax2+bx+c
(a≠0)的图象中,观察得出了下面五条信
8.如图,二次函数y=ax2+bx+c(a≠0)的图象的顶 点在第一象限,且过点(0,1)和(﹣1,0) 下列结论:①ab<0,②b2>4a,③0<a+b+c<2, ④0<b<1,⑤当x>﹣1时,y>0,其中正确结 论的个数是( )
A5个 B4个 C3个 D2个
9. 对于对称轴为 x=-1 的抛物线 y ax2 bx c(a 0) ,
有下面五条信息:① b 3 ; ②b=2a ; c2
③ b2 4ac >0;④3a+b+c<0;⑤当 x<-3
时,y<0.其中正确信息的个数为 (
)
y
A.2 个 B.3 个 C.4 个 D.5 个
-1 O 1 x
第 9 题图
10.如图,抛物线 y ax2 bx c ( a 0 )的对称轴为直线 x 2 ,
二次函数符号判断
1. 如图是二次函数y=ax2+bx+c图象的一部分, 其对称轴为x=﹣1,且过点(﹣3,0).下列说 法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④ 若(﹣5,y1),(1,y2)是抛物线上两点,则 y1>y2.其中说法正确的是( ) A①② B②③ C①②④ D②③④
与 x 轴的一个交点在 (3, 0) 和 (4, 0) 之间,其部分图象如图所示,则
下列结论:① 4a b 0 ;② c 0 ;③3a c 0 ;④4a 2b at2 bt
(t
为实数);⑤点
(
9 2
,
y1
)
,
(
5 2
,
y2
)
,
(
1 2
,
y3
)
是该抛物线上的点,
2.如图,抛物线y=ax2+bx+c(a≠0)的顶点为D(-1, 2),与x轴的一个交点A在点(-3,0)和(-2,0)之 间,有四个结论:①b2-4ac<0; ②a+b+c<0; ③2c-b =4;④方程ax2+bx+c-2=0有两个不相等 的实数根.其中正确结论有 ( ) A.1个 B.2个 C.3个 D.4个
A4个 B3个 C2个 D1个
则 y1 y2 y3 ,正确的个数有( ).
A.4 个 B.3 个 C.2 个 D.1 个
11.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线 x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象 如图所示,下列结论:①4ac<b2;②方程x2+bx+c=0的 两个根是x1=﹣1,x2=3;③3a+c>0④当y>0时,x的取 值范围是﹣1≤x<3⑤当x<0时,y随x增大而增大,其中 结论正确的个数是( )
y
D
A
-3 -2 -1
Ox
3.二次函数 y ax2 bx c (a≠0 )的图象如图,其
对称轴为 x=-1,有下面五个结论:①b>0;
② b2 4ac >0; ③c=-3a ; ④4a-2b+c>0;
⑤对于图象上的两个不同的点(m, n)、
(-1, k),有 n k .其中正确结论有 y (
息:①ab>0;②a+b+c<0;③b+2c>0;
④a﹣2b+4c>0;⑤
a
3 2
b
你认为其中正确信息的个数有( )
A.2 B.3 C.+c (a≠0)的图象如图 所示,有下列5个结论:①abc<0; ②b<a+c; ③4a+2b+c>0④2c<3b;⑤a+b<m (am+b)( m≠1的实数)其中正确结论的序号有 .
