Rotation topological factors of minimal $ZM^{d}$-actions on the cantor set
结晶和去润湿竞争条件下分子结构对超薄膜表面形貌的影响(英文)

209; 。 0 02 清华大学化学工程 系, 北京
摘要 : 将星形支化结构的聚己内酯, 包括六臂 星形 聚己内酯 ( C ) HP L 和树枝状星形聚 己内酯( P L, D C ) 以及线形
聚己内酯(P L 室温旋涂于云母片上, LC ) 通过原子力显微镜 ( M) AV 观察分子结构对星形支化聚己内酯超薄膜 的润 湿一 去润湿性质的影响. 在旋涂过程 中, 薄膜的形成受去润湿和结晶竞争的控制 . 差示 扫描量热( c 测试结果表 Ds ) 明, 当相对分子质量相 同时, 晶性 的顺 序是: C 结 DP L最弱, C HP L次弱, P L最强. LC 依据分子结构和相对分子质 量 的影响, 即去润湿和结 晶竞争的结果, P L H C L C 、 P L和 D C P L的超薄膜表现 出不同的表面形 态, 包括尺寸不同 的完整的球 晶、 口的球晶、 开 树枝状片 、 分散 的颗粒. 关键词 : 润湿; 分子结构 ; 去润湿: 结 晶; 超薄膜 中图分类号 : 0 4 67
物 理化学 学报( lHuxe ubo Wui a u ea ) X
中科院上海分院科学家发现斑马鱼中β-Arrestin1蛋白是胚胎造血系统发育的重要调控因子

牛的碱基 对数 量。克斯 廷说 , 马有 9 多 种遗 传病与 人类相 o
似, 如果能确定马的这些遗传 病 的基 因根 源 , 就会帮 助人类 加深对 自身相关遗传病 的认识 。
国 际 科学 家共 同破 译 家 猪 基 因组 序 列 。
D一 氨基 酸氧化 酶是 首个 由 中国学 者发 现的 神经 性慢 性疼
・
7 ・ 4
生 物学 教学 21 年( 5 第4 0 0 第3 卷) 期
乳香 酸提取于卡 氏乳香树的橡胶脂中 , 氏乳 香树广泛 卡 分布于热带区域。我国海南省、 台湾南部 、 东南部 、 广 广西南
秘, 为后续兰花功能和进 化基 因组 学研 究打 下基础 , 而且 会
为我国宝 贵兰花品种的种质资 源保 护提供科学 依据 , 为兰 花 科植物基因资源的开发 和利用提供重要 资源 和技术平 台。
有助 于研发人类疾病治疗的新方法 据 20 0 9年 l 3日《 1月 参考消 息》 引美联社 芝加哥 1 援 1 月 2日电 , 由美国伊诺伊 大学 厄巴纳一 尚佩思 分校生物学 教
授拉 里 ・ 斯库克领 导的国 际研 究 团队完成 了该项 研究 。科
型氨基酸氧化酶在神经源性慢 性疼痛 中的作用 , 明它是治 证 疗神经源性疼痛 的新 的作 用靶 分子 , 对欧美传统学 术观点和
上海交通大学科学家发现一个治疗 神 经源性疼痛 的新的分子 靶点
据 20 09年 1 月 l 《 1 1日 上海科 技报 》 消息 , 上海交 通大 学药学 院王永 祥教授领衔 的研究 团队在神 经源性 疼痛 调节
研究 中取得了重要突破 , 首次发现脊髓 D一型氨基 酸氧化酶
贵赛 马品种 , 后引入一些 欧美和亚 洲 国家 , 主要用 于赛 马 和
移动机器人路径规划和导航(英文)
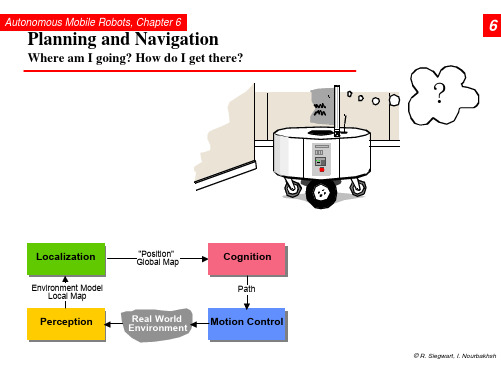
Autonomous Mobile Robots, Chapter 6
6.2.1
Road-Map Path Planning: Voronoi Diagram
• Easy executable: Maximize the sensor readings • Works also for map-building: Move on the Voronoi edges
© R. Siegwart, I. Nourbakhsh
Autonomous Mobile Robots, Chapter 6
6.2.1
Road-Map Path Planning: Adaptive Cell Decomposition
© R. Siegwart, I. Nourbakhsh
Autonomous Mobile Robots, Chapter 6
© R. Siegwart, I. Nourbakhsh
Autonomous Mobile Robots, Chapter 6
6.2.1
Road-Map Path Planning: Voronoi, Sysquake Demo
© R. Siegwart, I. Nourbakhsh
Autonomous Mobile Robots, Chapter 6
Ø Topological or metric or a mixture between both.
• First step:
Ø Representation of the environment by a road-map (graph), cells or a potential field. The resulting discrete locations or cells allow then to use standard planning algorithms.
超材料翻译

Naturematerials LETTERSPublished online : 18 APRIL 2010| DOI:10.1038/NMAT2747A single-layer wide-angle negative-index metamaterial at visible frequencies在可见光频率的一种单层广角负折射率超材料Metamaterials are materials with artificial electromagnetic properties defined by their sub-wavelength structure rather than their chemical composition.基于亚波长结构而非化学结构,超材料也叫人工电磁材料。
Negative-index materials(NIMs) are a special class of metamaterials characterized by an effective negative index that give rise to such unusual wave behavior as backwards phase propagation and negative refraction.负折射率材料(NIMs)是一类具有有效负折射率的特殊超材料,能够产生逆向传播和负折射的不同寻常的波行为。
These extraordinary properties lead to many interesting functions such as sub-diffraction imaging and invisibility cloaking.这些非凡的性能使得有有趣的功能,如子衍射成像和隐蔽伪装So far ,NIMs have been realized through layering of resonant structures,such as spilt-ring resonators ,and have been demonstrated at microwave to infrared frequencies over a narrow range of angles-of-incidence and polarization.到目前,负折射率材料(NIMs)已经通过谐振结构层实现,例如开环谐振器,而且在较窄范围的红外频率内的入射角和偏振也可以证明。
固体物理专业术语

费密能级 Fermi level 费密球 Fermi sphere 费密面 Fermi surface 费密温度 Fermi temperature 费密速度 Fermi velocity 费密半径 Fermi radius 恢复力常数 Constant of restorable force 绝热近似 Adiabatic approximation
反演 Inversion 分子晶体 Molecular Crystal 切变模量 Shear module 双原子链 Diatomic linear chain 介电常数 Dielectric constant 化学势 Chemical potential 内能 Internal energy
分布函数 Distribution function 夫伦克耳缺陷 Frenkel defect 比热 Specific heat 中子散射 Neutron scattering
纯金属 Ideal metal 体心立方 Body-centered cubic 体心四方布喇菲格子 Body-centered tetragonal Bravais lattices 卤化碱晶体 Alkali-halide crystal 劳厄衍射 Laue diffraction 间隙原子 Interstitial atom 间隙式扩散 Interstitial diffusion 肖特基缺陷 Schottky defect
有效电荷 Effective chaБайду номын сангаасges 弛豫时间 Relaxation time 弛豫时间近似 Relaxation-time approximation 扩展能区图式 Extended zone scheme 自由电子模型 Free electron model 自由能 Free energy 杂化轨道 Hybrid orbit
C4_旋转对称光子晶体平板中的对称保护连续谱束缚态

第40卷第3期Vol.40㊀No.3重庆工商大学学报(自然科学版)J Chongqing Technol &Business Univ(Nat Sci Ed)2023年6月Jun.2023C4旋转对称光子晶体平板中的对称保护连续谱束缚态张铭洋重庆工商大学数学与统计学院,重庆400067摘㊀要:在光子晶体平板中,连续谱束缚态关于C2和C6旋转对称的依赖性已经在数值上进行了广泛研究,但是缺少严格的理论分析过程,此外还缺少对C4旋转对称的研究,鉴于此,构建了系统分析连续谱束缚态关于所有旋转对称的依赖性的理论,并且重点研究了C4旋转对称的情况;首先,通过分析具有旋转对称的结构中麦克斯韦方程组特征解的性质,将连续谱束缚态的存在性问题转变为旋转矩阵的特征值是否与一个简单代数方程的解相同的问题;其次,给出了C4旋转对称的结构中连续谱束缚态存在时所对应的条件;然后,证明了破坏C4旋转对称保持C2旋转对称时,连续谱束缚态依然存在;最后,利用有限元软件FreeFEM 进行了大量的数值验证;上述理论可适用于所有旋转对称的情况,深入揭示了旋转对称对连续谱束缚态存在的重要性,深入揭示了高阶旋转对称性与低阶旋转对称性之间的依赖关系,为连续谱束缚态的实际应用提供了理论指导㊂关键词:光子晶体;旋转对称;连续谱束缚态中图分类号:O436㊀㊀文献标识码:A㊀㊀doi:10.16055/j.issn.1672-058X.2023.0003.09㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀收稿日期:2022-05-13㊀修回日期:2022-06-20㊀文章编号:1672-058X(2023)03-0064-07基金项目:重庆市自然科学基金面上项目(CSTC2019JCYJ -MSXMX0717).作者简介:张铭洋(1997 ),女,重庆忠县人,硕士研究生,从事光子晶体㊁麦克斯韦方程组数值计算研究.引用格式:张铭洋.C4旋转对称光子晶体平板中的对称保护连续谱束缚态[J].重庆工商大学学报(自然科学版),2023,40(3):64 70.ZHANG Mingyang.Symmetry-protected bound states in the continuum in C4rotationally symmetric photonic crystal plates J .Journal of Chongqing Technology and Business University Natural Science Edition 2023 40 3 64 70.Symmetry-protected Bound States in the Continuum in C 4Rotationally Symmetric Photonic Crystal Plates ZHANG MingyangSchool of Mathematics and Statistics Chongqing Technology and Business University Chongqing 400067 ChinaAbstract The dependence of bound states in the continuum BICs on C2and C6rotational symmetry in photonic crystalplates has been extensively studied numerically.However a rigorous theoretical analysis process is lacking and there is alack of studies on C4rotational symmetries.In view of this a theory of systematic analysis of the dependence of BICs on all rotational symmetries was constructed and the case of C4rotational symmetry was mainly studied.Firstly by analyzingthe characteristic solutions of Maxwell s equations with rotationally symmetric structure the problem of the existence of BICs was transformed into the question of whether the eigenvalue of the rotation matrix was the same as the solution of asimple algebraic equation.Secondly the conditions for the existence of BICs in C4rotationally symmetric structures weregiven.Then it was proved that the BICs still existed when C4rotation symmetry was destroyed and C2rotatory symmetrywas maintained.Finally the finite element software FreeFEM was used to do a lot of numerical verifications.The abovetheory can be applied to all cases of rotational symmetries revealing the importance of rotational symmetry for the existenceof BICs.The dependence between high-order and low-order rotational symmetries was revealed providing theoretical guidance for applying BICs.Keywords photonic crystal rotational symmetry bound states in the continuum第3期张铭洋,等:C4旋转对称光子晶体平板中的对称保护连续谱束缚态1㊀引㊀言光学连续谱束缚态(bound states in the continuum, BIC)是指位于连续谱中的导模,其不能与辐射场耦合,没有能量辐射,被完美地束缚在结构中[1-3]㊂数学上,光学连续谱束缚态是指开结构中麦克斯韦方程组的一类频率位于连续谱内的平方可积特征解㊂通常,导模(即平方可积特征解)的特征频率位于连续谱外㊂1929年冯诺依曼等[4]从数学模型上发现在一些特殊的结构中存在特征频率位于连续谱内的导模㊂直到1985年文献[5]才构造出具有连续谱束缚态的真实物理系统㊂2008年,文献[3]研究了光子晶体结构中的连续谱束缚态㊂此后,连续谱束缚态受到广泛关注,与之有关的研究快速发展㊂目前,连续谱束缚态的概念和研究已推广到水波㊁声波等其他波动现象[1]㊂连续谱束缚态可看成为品质因子为无穷大的共振,只存在于若干离散的频率上㊂连续谱束缚态由共振模式所包围㊂通过扰动波矢,可在连续谱束缚态附近找到任意大小品质因子的共振模式[6]㊂此性质使得连续谱束缚态在光学㊁光子学等领域都拥有广阔的应用前景㊂目前,连续谱束缚态已在波导㊁光栅㊁光子晶体及超材料等结构中被广泛研究[7],光子晶体中的连续谱束缚态现在已经被用于传感器,激光器和滤波器的设计当中[8-10]㊂通常,共振模式的品质因子与波矢之差的平方成反比㊂文献[6]证明了存在特殊的连续谱束缚态使得附近共振模式的品质因子与波矢之差的四次方和六次方成反比,并给出了两类特殊连续谱束缚态的条件㊂从实际应用角度来讲,在这些特殊的连续谱束缚态附近更容易构造出高品质因子的共振模式㊂连续谱束缚态可以大致分为两类:对称保护的连续谱束缚态[11-15]和非对称保护的连续谱束缚态[2,16-19]㊂对称保护的连续谱束缚态(Symmetry Protected Bound states in the continuum,SPBIC)的机理是:在对称结构中,布洛赫模的对称性与结构中辐射场的对称性不相容,从而与辐射场不耦合,变成一个连续谱束缚态[3]㊂而非对称保护连续谱束缚态的存在机理是:共振模式的辐射场之间发生干涉相消现象,造成没有辐射,成为连续谱束缚态[3]㊂连续谱束缚态的存在性与结构的对称性具有密切联系㊂早期研究结果都是在对称结构中研究连续谱束缚态,学术界一度认为连续谱束缚态只存在于对称结构中㊂目前数学上还没有非对称保护连续谱束缚态的存在性理论㊂非对称保护连续谱束缚态关于结构对称性的依赖关系非常复杂㊂文献[20-23]从数值和实验上演示了破坏二维结构的C2旋转对称性后,连续谱束缚态演化为共振模式㊂这间接说明了结构的对称性对非对称保护连续谱束缚态的存在性具有重要影响㊂但是破坏对称性后连续谱束缚态是否一定会演化为共振模式并没有明确的结论㊂最近,文献[24-26]证明了只要引入足够多的结构扰动参数,连续谱束缚态可以连续存在于非对称的结构中,且对于不同类型的连续谱束缚态,所需要引入的最小参数的数量是不同的㊂上述结论表明,非对称保护连续束缚态可以存在于非对称结构中,只要结构的自由参数足够多㊂对称保护连续谱束缚态只存在于对称结构中㊂光子晶体平板可具有四类旋转对称性:C2㊁C3㊁C4和C6旋转对称性,即分别旋转180㊁120㊁90和60度后结构不变㊂文献[11-12]首先从数学理论上证明了在具有C2旋转对称的二维介质结构中对称保护连续谱束缚态的存在性,在非对称结构中一定不存在对称保护连续谱束缚态㊂研究对称保护连续谱束缚态对上述四种不同类型对称性的连续依赖性具有十分重要的意义㊂文献[21]研究了C6旋转对称性对具有拓扑电荷为q=-2的对称保护连续谱束缚态存在性的影响㊂通过数值计算发现破坏C6对称保持C2对称,对称保护连续谱束缚态依然存在,但是变成拓扑电荷q=-1;破坏C6对称保持C3对称,对称连续谱束缚态演化为共振模式,而且会产生两个非对称保护连续谱束缚态㊂上述研究结果给出了一种产生非对称保护连续谱束缚态的方法㊂目前,对于拓扑电荷为q=-1或q=1的对称保护连续谱束缚态关于结构对称性的依赖关系没有进行系统讨论,缺乏严格系统的依赖性理论㊂研究C4旋转对称结构中对称保护连续谱束缚态关于对称性的依赖关系㊂建立了严格数学理论证明破坏C4对称保持C2对称,对称保护连续谱依然存在㊂并利用有限元软件FreeFEM进行数值验证㊂相比于以前的研究,研究既有严格的数学理论,又有数值验证㊂研究成果具有一般性,可推广到分析对称保护连续谱束缚态关于C6对称性的依赖性,有利于深入理解连续谱束缚态关于对称性的依赖关系,为其实际应用提供理论指导㊂2㊀连续谱束缚态考虑一个在x与y方向为周期,在z方向上厚度有限的光子晶体平板㊂光子晶体平板通过在平板上构造正方形空气柱晶格所构成㊂设平板厚度为2D,晶格常数为L,平板的介电常数为ε1,空气的介电常数为ε0= 1㊂记整个结构的介电常数为ε(r),其中r=(x,y,z),则z>D时有ε(r)=1,且ε(r)满足ε(r)=ε(x+mL,y+nL,z)(1)其中,m与n为任意整数㊂设光子晶体平板是无磁性㊁各向同性的,由麦克斯56重庆工商大学学报(自然科学版)第40卷韦方程组可知,具有时间依赖e -iwt 的时谐波的电场E 满足如下的控制方程:∇ˑ∇ˑE -k 2εE =0∇㊃(εE )=0其中k =ωc为真空中的波速,ω为角频率,c 为真空中的光速㊂光子晶体平板中的布洛赫模(即麦克斯韦方程组的特征解)可写成:E (r )=Φ(r )e ik ㊃r其中,k =(α,β,0)为布洛赫波矢,实数α与β分别为x 与y 方向的布洛赫波速,Φ(r )满足周期条件式(1)㊂由于在z >D 时,结构是均匀的,由傅立叶展开式与分离变量法可知,满足向外辐射条件的布洛赫模可以展开为[18]E (r )=ð+ɕm ,n =-ɕd ʃm ,neik ʃm ,n㊃r ʃz >D (2)其中,常数向量d ʃm ,n满足d ʃm ,n ㊃k ʃm ,n =0,k ʃm ,n=(αm ,βn ,ʃγm ,n ),αm =α+2m πL ,βn =β+2n πL,γm ,n =k 2-α2m -β2n ㊂若结构是无耗散的,即ε(r )为非负实函数,则布洛赫模可以分为三类:导模㊁共振以及连续谱束缚态㊂(1)若k 为实数,则布洛赫模为导模㊂可以证明k 为实数等价于E (r )满足lim z ңɕE (r )=0,即没有能量辐射,没有能量损失㊂当波速和布洛赫波矢满足条件0<k <α2+β2时,导模关于α与β连续存在㊂在上述条件下,γm ,n 的虚部都大于0,所以展开式(2)中每一个平面波都在无穷远出衰退到0,即E (r )自动满足lim z ңɕE (r )=0,从而是一个导模㊂(2)若k 为复数,则布洛赫模为共振模式㊂共振模式的波速k 满足[Re(k )]2-[lm(k )]2>α2+β2㊂由于共振的波速k 为复数且满足向外辐射条件,共振满足条件lim z ңɕE (r )=ɕ,即在空间上是无限增大,但随时间指数衰退㊂共振波速k (或共振频率ω)的虚部小于零,即lm(k )<0,它表示共振随着时间衰退的速度㊂共振的品质因子Q 定义为Q =-12Re(k )lm(k ),表示共振模式的振幅衰退到原来的e -1时所需要的振荡周期㊂共振模式关于α与β也是连续存在的㊂(3)若k 为实数且满足k >α2+β2,则布洛赫模是一个连续谱束缚态㊂连续谱束缚态可以看成是一个Q 因子为无穷大的共振,只在离散的(α,β)点上存在,在连续谱束缚态的附近,通过调整α与β可以获得任意大小Q 因子的共振㊂由于k 为实数等价于条件limz ңɕE (r )=0,在展开式(2)中,若lm(γm ,n )ȡ0,则e ikm ,n㊃r可向z ңɕ辐射能量,(m ,n )是对应一个开放的辐射通道㊂若lm(γm ,n )<0,则eik ʃn ,m ㊃r在z ңɕ时衰退到零,对应一个关闭的辐射通道㊂若Re(k )>α2+β2,则至少有lm(γ0,0)ȡ0,即(0,0)处辐射通道是开放的㊂记Z 0表示所有开放的辐射通道,即Z 0=(m ,n )lm(γm ,n )ȡ0{},则条件lim z ңɕE (r )=0等价于d ʃm ,n=0,∀(m ,n )ɪZ 0(3)式(3)是布洛赫模的一个附加条件,在一般情况下,连续谱束缚态不容易存在㊂3 对称保护连续谱束缚态当光子晶体平板具有旋转对称性时,可能存在对称保护连续谱束缚态㊂下面给出具有C n 旋转对称的光子晶体平板中对称保护连续谱束缚态的定义,并分析其关于对称性的依赖关系㊂利用旋转对称性下布洛赫模的性质,将连续谱束缚态的存在性问题转变为旋转矩阵的特征值是否与一个简单代数方程的解相同的问题;其次,给出了C4旋转对称的结构中连续谱束缚态存在时所对应的条件;然后,证明了破坏C4旋转对称保持C2旋转对称时,连续谱束缚态依然存在;具有C n 旋转对称性结构的介电函数ε(r )满足条件ε(r )=ε(T -1r )其中,T =cos φ-sin φ0sin φcos φ0001éëêêêùûúúú表示旋转矩阵,φ=2πn ,只考虑n =2与n =4的情况㊂其理论可推广到n =3与n =6的情况㊂C n 旋转对称光子晶体平板中的布洛赫模具有以下性质[24]:若E (r )=Φ(r )e ik ㊃r 是一个对应于波矢k =(α,β,0)和波速k 的布洛赫模,则TE (T -1r )是一个对应于波矢Tk 和波速k 的布洛赫模㊂特别地,取α=β=0,即k =(0,0,0),有Tk =k ,此时E (r )与TE (T -1r )是对应同一个波矢与波速的两个布洛赫模㊂若特征值问题是非退化的,则E (r )与TE (T -1r )线性相关,即存在常数τ使得:TE (T -1r )=τE (r )(4)由于任何结构旋转n 次2πn角度(即2π)后都不变,有T n=I ,其中I 表示单位算子㊂所以有τn=1,即τ=e i 2πn j,j =0,1,2, ,n -1㊂更具体地,当n =2时,τ=ʃ1;当n =4时,τ=ʃ1,ʃi ㊂注意到τ的取值对应于C n 点群的不可约表示的特征㊂设布洛赫模的波矢为k =(0,0,0)且频率满足0<Re(k )ε0<2πL,即只有(0,0)处辐射通道是开放的,则当n =2时,对应于τ=1以及当n =4时,对66第3期张铭洋,等:C4旋转对称光子晶体平板中的对称保护连续谱束缚态应于τ=ʃ1的布洛赫模一定是连续谱束缚态,称为对称保护连续谱束缚态㊂在上述条件下,布洛赫模是一个连续谱束缚态的充要条件是d ʃ0,0=0㊂下面证明当n =2时,τ=1以及当n =4时,τ=ʃ1,有d ʃ0,0=0㊂将展开式(2)代入条件式(4)得:Td ʃ0,0=τd ʃ0,0(5)令,d ʃ0,0=d ʃx ,d ʃy ,d ʃz []T ,T ^=cos φ-sin φsin φcos φéëêêùûúú,d ʃʅ=d ʃx ,d ʃy []T 表示d ʃ0,0的x 与y 分量所构成的向量㊂由d ʃ0,0㊃k ʃ0,0=0且α=β=0,知d ʃz k =0,即d ʃz =0㊂所以d ʃ0,0=0等价于d ʃʅ=0㊂由式(5)得:T ^d ʃʅ=τd ʃʅ若τ不是T ^的特征值,则必有d ʃʅ=0㊂当n =2时,T ^=-100-1éëêêùûúú,T ^只有一个特征值-1㊂所以当τ=1时,有d ʃʅ=0㊂当n =4时,T ^=0-110éëêêùûúú,此时T ^的特征值为ʃi ㊂所以当τ=ʃ1时有d ʃʅ=0㊂由上面的证明过程可知,条件d ʃ0,0=0是由C n 对称性所保证的㊂在具有C4旋转对称的结构中,对称保护连续谱束缚态对应的τ=1或-1㊂注意到无论是τ=1还是-1,都有τ2=1,即这些连续谱束缚态也同时由C2旋转对称所保护㊂有以下结论:具有C4旋转对称结构中的对称保护连续谱束缚态都是由C2旋转对称所保护的,即破坏C4旋转对称,保持C2旋转对称,这些连续谱束缚态依然存在㊂4㊀拓扑电荷连续谱束缚态对应于动量空间中辐射场的漩涡,因此其存在性与拓扑性质有关㊂前面提到了布洛赫模是一个连续谱束缚态的充要条件是d ʃ0,0=0,通过d ʃ0,0的x 与y 分量可以计算得到辐射场的极化角㊂极化椭圆的长轴与y 轴的夹角称之为极化角度,记为θ㊂θ可以看成是α与β的函数,即θ=θ(α,β)㊂在αβ平面上,任意给定一条曲线Γ,让(α,β)沿着Γ绕一圈重新定义θ,使其为连续函数㊂拓扑电荷的定义为q =12πɥΓd θ=12πɥΓ∇θ㊃ n d s拓扑电荷q 表示αβ上的一点绕Γ走一圈后,极化角度旋转了q 圈,q 是一个整数㊂若Γ所围区域内无圆极化与连续谱束缚态,则q =0;若Γ所围区域内有且仅有一个连续谱束缚态则q =ʃ1,ʃ2,ʃ3, ;若Γ所围区域内只有一个圆极化,则q =ʃ12㊂需要注意的是圆极化和连续谱束缚态是αβ平面中的一个极化奇点㊂5㊀数值实验由于辐射边界条件下的特征值问题定义在无穷区间上,无法用数值方法来计算㊂所以在实际计算连续谱束缚态的时候,可以用完美匹配层的方法来将无穷区域截断为有限区域㊂用完美匹配层截断后的特征值问题是原特征值问题的一个近似,它们之间的误差关于完美匹配层的参数σ∗㊁H 2-H 1(即完美匹配层的厚度)指数衰退到零㊂所以只需要选择合适的σ∗与H 2-H 1,便可以得到足够精确的特征解,即可以计算得到连续谱束缚态的频率㊂相对于拟周期边界条件,在有限元方法中周期边界条件更容易实现㊂用有限元方法求解偏微分方程最重要的是弄清楚解空间和变分形式㊂在用有限元求解时,变分问题被近似为下列代数方程的特征值问题:A Φ=k 2B Φ其中,A 与B 为矩阵㊂考虑如图1所示的具有正方形晶格空气柱的光子晶体平板,其俯视图如图2所示㊂平板是由空气所包围的㊂平板的厚度为2D =0.5L ,介电常数为ε1=4,空气中的介电常数ε0=1㊂空气柱体横截面参数分别为w =0.2L ,a =w2㊂若h 1=h 2,则结构具有C4旋转对称性㊂若h 1ʂh 2,则结构只有C2旋转对称性㊂为了验证前面得到的理论,用完美匹配层[27]的方法将无穷区域上的特征值问题转化为有限区域上的特征值问题,并用有限元[28]的方法求解㊂数值计算时,需要用完美匹配层方法将z 方向截断为-H 2,H 2[],如图3所示㊂取完美匹配层的厚度为H 2-H 1=L ,σ∗=18ˑm +1β0(H 2-H 1)[29],β0=k 20ε0-α2-γ2,m =3㊂其中H 1-D 表示完美匹配层的远近㊂采用基于FreeFEM 软件的有限元方法来数值求解特征值问题,以计算对称保护连续谱束缚态的频率㊂计算时在平板的每个边界的离散点个数取N =10,PML 层的离散点个数也取N =10㊂考虑如此复杂结构的原因是为了避免其他对称性(例如镜面反射对称)对结果的影响㊂ε=ε0ε=ε0z =D z =-Dzxy图1㊀光子晶体平板结构图Fig.1㊀Structure diagram of photonic crystal plates76重庆工商大学学报(自然科学版)第40卷h 2h 1h 1h 2L Lαωωxy图2㊀光子晶体平板结构的俯视图Fig.2㊀Top view of the photonic crystal flat plate structurez=H2z=H1z=D z=-Dz=-H1z=-H2ε=εε=εzxy 图3㊀PML截断后的计算区域Fig.3㊀Computation region after PML truncation 若取h1=h2=0.15L,这时结构具有C4旋转对称性㊂通过数值计算,可以找到5个TM-Like模式下(即E z是z变量的奇函数)的对称保护连续谱束缚态,其频率如表1的第2列所示㊂图4(a) 图8(a)分别是SPBIC1-SPBIC5在具有C4旋转对称的结构中log10Q 关于α与β的值㊂可以通过观察得到当(α,β)ң(0, 0)时,Q的值趋近于无穷大㊂图4(c) 图8(c)分别是SPBIC1到SPBIC5在C4旋转对称结构中的磁场z分量H z在z=0时的场图㊂从下面的场图可以观察得到, SPBIC1与SPBIC5对应于τ=1,其他3个对称保护连续谱束缚态对应于τ=-1㊂表1的最后一列表示为对称保护连续谱束缚态的拓扑电荷㊂若保持h1=0.15L,令h2=0.1L,参数扰动后结构的C4旋转对称性被破坏,但保持了C2旋转对称性㊂通过数值计算表明,SPBIC1-SPBIC5在扰动后的结构中依然存在,其频率如表1的第三列所示,可以发现两种结构下连续谱束缚态的频率近乎相等㊂图4(b) 图8(b)分别是SPBIC1到SPBIC5在具有C2旋转对称的结构中log10Q关于α与β的值㊂可以通过观察得到当(α,β)ң(0,0)时,Q的值趋近于无穷大,并且可以发现两种结构下,log10Q关于α与β的值很相近㊂图4(d) 图8(d)分别代表的是扰动后SPBIC1-SPBIC5在C2旋转对称结构中的磁场z分量H z在z=0时的场图㊂从下面的场图可以观察得到,SPBIC1与SPBIC5仍然对应于τ=1,其他3个对称保护连续谱束缚态也依旧对应于τ=-1㊂通过对比,可以发现两种结构下的场图几乎一模一样,并且可以发现结构扰动不改变对称保护连续谱束缚态的拓扑电荷㊂表1㊀C4与C2旋转对称结构中对称保护连续谱束缚态的频率ωL2πc的值Table1㊀Value ofωL2πc the frequency of symmetrically protected bound states in the continuum in the rotationallysymmetric structure of C4and C2C4C2q SPBIC10.61590.6101+1 SPBIC20.63670.6282-1 SPBIC30.85690.8485-1 SPBIC40.93830.9338-1 SPBIC50.95140.9492+10.05-0.05-0.0500.05βL/(2π)Q f a c t o rαL/(2π)8640.05-0.05-0.0500.05αL/(2π)864βL/(2π)Q f a c t o r㊀㊀(a)(b )0.5-0.5-0.500.5y/LR e/H zx/L0.5-0.5-0.500.5R e/H zx/L㊀㊀(c)(d)图4㊀SPBIC1的Q因子图和场图Fig.4㊀Q factor diagram and field diagram of SPBIC10.05-0.05-0.0500.05βL/(2π)Q f a c t o rαL/(2π)8765430.05-0.05-0.0500.05αL/(2π)βL/(2π)Q f a c t o r876543㊀㊀(a)(b)86第3期张铭洋,等:C4旋转对称光子晶体平板中的对称保护连续谱束缚态0.50-0.5-0.50.5y /LR e /H zx /L0.5-0.5-0.50.5y /LR e /H zx /L㊀㊀(c )(d )图5㊀SPBIC2的Q 因子图和场图Fig.5㊀Q factor diagram and field diagram of SPBIC20.010-0.01-0.010.01βL /(2π)Q f a c t o rαL /(2π)8765430.010-0.01-0.0100.01αL /(2π)βL /(2π)Q f a c t o r76543㊀㊀(a )(b )0.5-0.5-0.50.5y /LR e /H zx /L0.5-0.5-0.50.5y /LR e /H zx /L㊀㊀(c )(d )图6㊀SPBIC3的Q 因子图和场图Fig.6㊀Q factor diagram and field diagram of SPBIC30.010-0.01-0.010.01βL /(2π)Q f a c t o rαL /(2π)76540.010-0.01-0.0100.01αL /(2π)βL /(2π)Q f a c t o r7654㊀㊀(a )(b )0.5-0.5-0.50.5y /LR e /H zx /L0.5-0.5-0.50.5y /LR e /H zx /L㊀㊀(c )(d )图7㊀SPBIC4的Q 因子图和场图Fig.7㊀Q factor diagram and field diagram of SPBIC40.020-0.02-0.0200.02βL /(2π)Q f a c t o rαL /(2π)8640.020-0.02-0.0200.02αL /(2π)βL /(2π)Q f a c t o r6543㊀㊀(a )(b )0.5-0.5-0.50.5y /LR e /H zx /L0.5-0.5-0.500.5y /LR e /H zx /L㊀㊀(c )(d )图8㊀SPBIC5的Q 因子图和场图Fig.8㊀Q factor diagram and field diagram of SPBIC5经过数值计算,从扰动前后不同结构下对称保护连续谱束缚态的频率以及对比分析它们的Q 因子图和场图可以观察得到具有C4旋转对称结构的光子晶体平板中的对称保护连续谱束缚态都是由C2旋转对称性所保护的㊂即若破坏C4旋转对称但保持C2旋转对称,原有的对称保护连续谱束缚态依然存在㊂进一步反映了C4旋转对称与C2旋转对称之间的依赖关系㊂6㊀结束语构建了系统分析连续谱束缚态关于旋转对称性的依赖理论,并且重点研究了C4旋转对称的情况,分别从理论和数值两个方面证明了具有C4旋转对称光子晶体平板中的对称保护连续谱束缚态都是由C2旋转对称性所保护的㊂即破坏C4旋转对称但是保持C2旋转对称性,原对称保护连续谱束缚态依然存在㊂虽然只考虑了C4旋转对称光子晶体平板中的对称保护连续谱束缚态,但提出的理论和数值分析方法都可以用于研究具有C6旋转对称的光子晶体平板,不过由于此结构同时具有C2与C3旋转对称性,对称保护连续谱束缚态与对称性的依赖关系可能会更加复杂㊂提出的理论分析方法也可以适用于所有旋转对称的情况㊂由于是从麦克斯韦方程组出发,没有引入模型近似,并且分析过程根据严格㊂研究结果有利于深入理解对称保护连续谱束缚态的性质,为其理论分析和实际应用提供指导㊂96重庆工商大学学报(自然科学版)第40卷参考文献References1 ㊀HSU C W ZHEN B STONE A D et al.Bound states in thecontinuum J .Nature Reviews Materials 2016 1 9 1 13.2 ㊀HSU C W ZHEN B LEE J et al.Observation of trappedlight within the radiation continuum J .Nature 2013 4997457 188 191.3 ㊀MARINICA D C BORISOV A G SHABANOV S V.Boundstates in the continuum in photonics J .Physical Review Letters 2008 100 18 1 4.4 ㊀NEUMANN J WIGNER E P.Über merkwürdige diskreteEigenwerte M .Berlin Heidelberg Springer 1993.5 ㊀FRIEDRICH H WINTGEN D.Interfering resonances andbound states in the continuum J .Physical Review A 198532 6 3231 3239.6 ㊀YUAN L LU Y Y.Bound states in the continuum on periodicstructures surrounded by strong resonances J .Physical Review A 2018 97 4 1 8.7 ㊀AZZAM S I KILDISHEV A V.Photonic bound states in thecontinuum from basics to applications J .Advanced Optical Materials 2020 9 1 1469 1477.8 ㊀KODIGALA A LEPETIT T GU Q et sing action fromphotonic bound states in continuum J .Nature 2017 5417636 196 199.9 ㊀JIN J YIN X NI L et al.Topologically enabled ultrahigh-Qguided resonances robust to out-of-plane scattering J .Nature 2019 574 7779 501 504.10 HAN S CONG L SRIVASTAVA Y K et al.All-dielectricactive terahertz photonics driven by bound states in the continuum J .Advanced Materials 2019 31 37 1 28.11 BONNET-BENDHIA A S STARLING F.Guided waves byelectromagnetic gratings and non-uniqueness examples for the diffraction problem J .Mathematical Methods in the Applied Sciences 1994 17 5 305 338.12 VENAKIDES S SHIPMAN S P.Resonance and bound statesin photonic crystal slabs J .SIAM Journal on Applied Mathematics 2003 64 1 322 342.13 SHIPMAN S VOLKOV D.Guided modes in periodic slabsexistence and nonexistence J .SIAM Journal on Applied Mathematics 2007 67 3 687 713.14 LEE J ZHEN B CHUA S L et al.Observation anddifferentiation of unique high-Q optical resonances near zero wave vector in macroscopic photonic crystal slabs J .Physical Review Letters 2012 109 6 1 5.15 HU Z LU Y Y.Standing waves on two-dimensional periodicdielectric waveguides J .Journal of Optics 2015 176065601 065608.16 YANG Y PENG C LIANG Y et al.Analytical perspective for bound states in the continuum in photonic crystal slabs J . Physical Review Letters 2014 113 3 1 5.17 YUAN L LU Y Y.Propagating bloch modes above the lightline on a periodic array of cylinders J .Journal of Physics B Atomic Molecular and Optical Physics 2017 505 1 5.18 KANG M ZHANG S XIAO M et al.Merging bound states in the continuum at off-high symmetry points J .Physical Review Letters 2021 126 11 1 7.19 YUAN L LU Y Y.Conditional robustness of propagating bound states in the continuum in structures with two-dimensional periodicity J .Physical Review A 2021 1034 1 10.20 OVERVIG A C MALEK S C CARTER M J et al.Selection rules for quasibound states in the continuum J .Physical Review B 2020 102 3 1 30.21 YODA T NOTOMI M.Generation and annihilation of topologically protected bound states in the continuum and circularly polarized states by symmetry breaking J .Physical Review Letters 2020 125 5 1 12.22 LI S ZHOU C LIU T et al.Symmetry-protected bound states in the continuum supported by all-dielectric metasurfaces J . Physical Review A 2019 100 6 1 6.23 LI L LI Y ZHU Y et al.Rotational symmetry of photonic bound states in the continuum J .Scientific Reports 2020 101 1 8.24 SAKODA K.Optical properties of photonic crystals M . Berlin Springer Science&Business Media 2004.25 YUAN L LU Y Y.Parametric dependence of bound states in the continuum on periodic structures J .Physical Review A 2020 102 3 1 9.26 YUAN L LUO X LU Y Y.Parametric dependence of bound states in the continuum in periodic structures vectorial cases J .Physical Review A 2021 104 2 1 11.27 LU Y Y.Minimizing the discrete reflectivity of perfectly matched layers J .IEEE Photonics Technology Letters 2006 18 3 487 489.28 LI Y J JIN J M.Fast full-wave analysis of large-scale three-dimensional photonic crystal devices J .JOSA B 2007 249 2406 2415.29 ZHEN B HSU C W LU L et al.Topological nature of optical bound states in the continuum J .Physical Review Letters 2014 113 25 1 20.责任编辑:田㊀静07。
ros膨胀半径

ros膨胀半径
【最新版】
目录
1.ROS 膨胀半径的概念
2.ROS 膨胀半径的计算方法
3.ROS 膨胀半径的应用领域
正文
1.ROS 膨胀半径的概念
ROS(Reactive Oxygen Species,反应性氧类物质)膨胀半径是指在ROS 生成过程中,由于 ROS 的生成使得细胞膜的脂质过氧化,导致细胞膜的物理性质发生改变,从而影响到细胞内外物质的交换和细胞功能的正常发挥。
ROS 膨胀半径可以用来衡量细胞在 ROS 作用下的生物学效应。
2.ROS 膨胀半径的计算方法
ROS 膨胀半径的计算方法通常基于细胞膜的脂质过氧化程度。
常用的指标包括丙二醛(MDA)和共轭亚油酸(CLA)等。
这些指标的浓度与 ROS 生成量呈正相关,可以通过测量这些指标的浓度来推算 ROS 膨胀半径。
3.ROS 膨胀半径的应用领域
ROS 膨胀半径在生物学和医学研究中有着广泛的应用。
首先,ROS 膨胀半径可以用来评估氧化应激的程度,帮助研究者了解生物体在氧化应激条件下的生理和病理变化。
其次,ROS 膨胀半径可以用来评估药物的抗氧化效果,为药物研发和评价提供实验依据。
此外,ROS 膨胀半径还可以作为生物标志物,用于疾病的早期诊断和疗效监测。
第1页共1页。
脊柱手术导航中分步式2D_3D图像配准方法

计算机辅助设计与图形学学报J O U RNAL O F COM P U T E R 2A I D E D D E SI G N & COM P U T E R GRA P H ICSVol 119 , No 19Sep 1 , 2007第 19 卷 第 9 期 2007 年 9 月脊柱手术导航中分步式 2D Π3D 图像配准方法张 翼 王满宁 宋志坚( 复旦大学数字医学研究中心 上海 200032) ( 1145 @so hu 1c o m )摘 要 为实现微创脊柱手术导航 ,提出一种将脊柱术前 C T 与其术中 X 射线图像配准的方法1 首先基于一种最近点迭代法进行快速粗配准 ;然后提取图像的梯度特征 ,根据投影变换原理 ,采用寻找具有 C T 最大梯度投影位置的方 法进行精配准1 在模拟数据及临床标本上进行实验的配准率分别为 92 %和 78 %1 实验结果表明 :该方法鲁棒性强 、 人工干预少 、适合于临床应用1关键词 2D Π3D 配准 ;数字 X 射线图像 ;计算机断层扫描 ;手术导航 中图法分类号 TP39117Mul t i 2Step 2D Π3D Image R egistrat i on in Image 2G uided Spine SurgeryZhang Y i Wang Manning So n g Zhijian( Di gi t al M edical Resea r ch Center , Fu d a n U ni versi t y , S ha n g hai 200032)Abstract A novel regist r ati o n met h o d of p r eoperative C T images and int r a 2operative X 2ray images is p r o 2po s ed fo r minimally invasive image 2guided spine surgery 1 Firstly , an Iterative Cl o s est Point algo r it h m is ap 2 plied fo r coarse regist rati o n 1 Seco ndly , gradient feat ure is e xt racted f ro m image 1 Based o n t he p rinci pl e of p rojective t ransfo r mati o n , t he fine regist rati o n is perfo r med by finding t he ma ximum C T gradient p r oj ec 2 ti o ns 1 The co rrect rate of regist rati o n was of 92 % and 78 % respectively o n simulated data and clinical p h an 2 to m research 1 Experimental result s show t hat p ropo sed met ho d is suitable fo r clinical applicati o n wi t h goo d ro b ust n ess and less degree of human interventi o n 1K ey w ords 2D Π3D regist r ati o n ; digital X 2ray ; co m p u ted to m ograp h y ; image 2guided surgery手术导航是指以 C T , M R I 等医学影像数据为 基础 ,通过虚拟现实技术 ,借助光学定位仪跟踪并显 示手术器械相对于病变组织的位置关系 ,从而实现 对手术过程的实时引导1 该技术应用于脊柱外科 , 对提高定位精度 、减少术中创伤1 降低手术失误率 有重要意义1 图像空间与病人参考空间配准是手术 导航的关键步骤1 在基于 C T 图像的脊柱手术导航 中 ,欲获得上述配准关系 ,需要在脊柱表面放置标记 物 ,或暴露脊柱选取表面点 ,这种做法不利于微创治疗的开展11 C 型臂 X 射线机作为脊柱手术中的常 用辅助设备 ,其图像可以利用视觉标定技术与病人进行无创配准 ,但由于其为 2D 图像 ,提供的导航信息有限1 因此 ,寻找一种 C T 图像 ( 3D ) 与 X 射线图像 (2D ) 的配准方法 ,间接获得 C T 与病人的配准关系 ,是解决该问题的一条有效途径1目前 ,2D Π3D 图像配准方法大致分为 3 类2 23: 1) 基于几何特征 ,通过寻找待配准物体上 2 组特征间的最短空间距离进行配准1 按特征来源分为外加特征与内在特征1 前者配准精度高 , 但因需要侵入性植入标记物 ,临床应用受到限制 ;后者需要对边界收稿日期 :2006 - 12 - 18 ;修回日期 :2007 - 04 - 231 基金项目 :上海市科技攻关项目 ( 05DZ19511) 1 张 翼 ,男 ,1976 年生 ,博士研究生 ,主要 研究方向为计算机辅助手术 、医学图像处理1 王满宁 , 男 , 1977 年生 , 博士研究生 , 讲师 , 主要 研 究 方 向 为 计 算 机 辅 助 手 术 、医 学 图 像 处 理1 宋志坚 ,男 ,1960 年生 ,博士 ,教授 ,博士生导师 ,主要研究方向为计算机辅助手术 、医学图像处理 、模式识别 (zjso ng @f udan 1edu 1cn ) 1定位仪直接得到 ; T X 2ray为 CT 到 X 射线图像的空间 进行精确的分割 ,在实际应用中误差较大1 2) 基于 图像密度特征 ,通常是采用 DRR (digitally reconstructed radi ograp h s ) 算法 ,利用 C T 数据重建的 X 射线图像 与实际 X 射线图像密度的相似性进行配准 ,其精度 较高 ;但由于该算法耗时 、捕捉范围有限且需要划分 兴趣区域 ,因此效率不高1 3) 基于上述 2 种特征结 合的方法 ,通过寻找 2 类图像中对应的几何特征 ,如 梯度特征 ,利用相似性原理进行配准 ,可同时获得较 高的配准精度与速度 ; 该算法的关键在于几何特征 及最优化函数的选取 ,其捕捉范围较小及鲁棒性较 弱是目前存在的问题1针对上述特点 ,本文提出一种基于不同特征的 分步配准方法1 首先根据几何特征 , 采用最近点迭 代法 (iterative cl o sest point , ICP ) 算法进行快速粗配 准 ,将误差限制到一定范围之内 ,以解决捕捉范围有 限的问题1 精配准基于一种我们改进后的图像梯度 特征的配准算法 ,根据 C T 梯度在成像平面的投影 强度构造最优化函数 ,能获得较稳定的局部极值 ,减 小了 X 射线图像对配准精度的影响 ,提高了系统的 鲁棒性1 另外 ,由于本文算法只对形成图像边缘的 光线进行追踪 ,因此配准速度也得到了大幅提升1C T 转换矩阵 , 是本文研究的核心内容1 配准前需要获得 2~ 3 幅不同角度的 X 射线图像 , 根据病人体位调整 C T 模型的姿态 ,使两者角度误差小于 10°,距离误差小于 30 mm , 以满足粗配准的初始条件1111 基于几何特征的粗配准ICP 算法[ 4 ]是解决 2 类点集配准的常用算法 ,其基本思想是寻找从浮动点集 q 到参考点集 p 的一个转换矩阵 T , 使得 2 组点集之间对应点的平均 距离达到最小 , 即T ^ = arg T min∑‖pi- T q i ‖( 1)该算法从初始的对应关系 C 0 开始迭代1 在每 次迭代中 , 根据参考点的位置寻找最近的浮动点 , 建立起对应关系 C i , 用点配准法计算出 T i , 将 T i 应用于原浮动点集 q 后 , 再寻找新的对应关系 C i + 11 我 们对原始 ICP 算法进行改动 , 将参考点设置成为活动状态 :在 X 射线图像中的脊柱轮廓上 , 随机选取 200 个点 , 参考点位于焦点到这些点的射线上1 浮动点位于 C T 脊柱表面 :采用 Marching Cube 算法生成 脊柱表面三角网格模型 , 利用三角片折叠的方法进 行网格动态化简 , 将精简后的三角网格的顶点作为浮动点集1 配准过程如下 :对于每条射线 , 在浮动点集中查找与之相切的最近点作为 q i , 根据 q i 计算出 在该射线上与之距离最近的点 p i , 按照式 ( 1) 进行迭代1由于 C T 表面顶点的数目庞大 , 本文采用构建1 配准方法在 C 型臂 系 统 中 , X 射 线 由 焦 点 发 出 , 穿 越 病 人后 在 影 像 增 强 器 上 形 成 X 射 线 图 像 ( 如 图 1 所 示) 1 C T 图像空间到病人空间坐标转换矩阵经由 C 型臂系统间接得到[ 5 ]顶点最小外接球树的方法 加 快 最 近 浮 动 点 的 搜 索速度1 首先对所有顶点生成一个最小外接球作为根节点 , 然后将该球的外接盒分成 8 份 , 对每份外接 盒中包含的顶点再生成一个最 小 外 接 球 作 为 子 节 点1这样逐渐细分 , 直到外接球的半径小于设定的阈值 ( 如图 2 所示) 1 搜索初始时 , 对每条射线构造一 个以外接球为元素的堆 , 并按照外接球边界到射线 的距离进行排序 , 堆的根一直是具有最短距离的外接球1 我们利用顶点所在三角片的法向量进行相切判断 , 当其中一个与射线方向相同 、另一个相反时 , 则认为该顶点与射线相切1 搜索步骤如下 :S t ep 11 初始化最近点 ^v , 其到射线的距离设为 ∞; S t ep 21 构造排序堆 H ,将外接球树的根节点元素插入 H; S t ep 31 while H 不为空1) 从 H 中取出根节点元素 u ;2) 如果 u 的距离大于 v^到射线的距离 则搜索结束 , 最近点为 ^v ;3) 如果 u 包含子节点则在 H 中插入 u 的全部子节点 ;T patient X 2rayintensifier senso r senso r - 1 1 T C T ·T X 2ray ·T intensifier ·( T patient ) = C T 其中 , T intensifier为 X 射线空间 到 增 强 器 空 间 的 转 换 X 2ray 矩阵 , 可利用视觉标定方法获得 ; T sens o r 与 T senso r intensifierpatient 分别为增强器及病人到定位仪空间的转换矩阵 , 由计算机辅助设计与图形学学报 2007 年1156的距离判断是否替换 ^v ;end while为准确提取 X 射线图像中对应的脊柱轮廓 ,本文采用 Live Wire 交互式分割方法[ 6 ] ( 如图 3 所示) 1针对透视图像噪声多 、目标轮廓强弱不均的特点 , 我们使用高斯 函 数 的 一 种 变 体 构 造 相 邻 像 素 p 和 q 间的代价函数( f - m ean ) 2e-C ( p , q ) = 1 - 12σ2 其中 , f 为 C anny 算子边缘检测后的像素值 ; m e a n和σ是通过分割前人工选取图像上局部较弱边缘作 为训练区域 , 并以该训练区域的 f 值统计得出1图 2 脊柱表面顶点外接球连续细分的结果图 3 Live Wire 交互式分割方法提取脊柱轮廓112 基于密度梯度特征的精配准11211 原理根据 X 射线成像原理 ,对于到达成像平面上任 意像素的 X 射线强度 , 有p (λ) = r s + λ( p - r s ) ,λ ∈ [ 0 ~ 1 ;r ( p ) = ‖p - r s ‖, 则式 ( 3) 变为I ( p ) ∝ r ( p )∫V ( p (λ) ) d λ设 ( 4)u 方向对式 ( 4) 求导得在 E 0e -∫L μ( p ) d r ;E ( u , v ) = 5 I ( p ) I ( p+Δ u ) - I ( p ) = lim Δ u →0∝ 其中 ,μ为组织对 X 射线的衰减系数 , r 为组织的深度 , E 0 为 射 线 L 发 出 时 的 强 度 , p 为 L 上 任 意 一 点 , p 是 L 与成像平面的交点 , u , v 是成像平面坐 标 ( 如图 4 所示) 15 u Δ u lim ∫{ r ( p +Δ u) V ( r s + λ( p +Δ u - r s )-Δ u →0r ( p ) V ( r s + λ( p - r s ) ) } Π{ Δ u } d λ∝λV ( p (λ) + λΔ u ) - V ( p (λ) ) d λ∝ Δu →0∫ r ( p ) lim λΔ u r ( p )∫λ V ( p (λ) ) ·u Td λ∝ r ( p )∫λ同理 ,V ( p (λ) ) d λ ·u T( 5)5I ( p ) ∫V ( p (λ) ) d λ ·v T ( 6) ∝ r ( p ) 图 4 X 射线梯度投影模型λ 5 v 由于接收器对 X 射线呈对数响应特征 , 因此其 图像灰度 I 与衰减系数之间存在线性关系将式 ( 5) , ( 6) 合并 , 得到 X 射线图像梯度与 C T 梯度投影的关系为5 I ( p )I ( p ) = a ∫μ( p ) d r + b( 2)T5 u 5 I ( p ) Luv ∝ r ( p )∫λ V ( p (λ) ) d λ ·I ( p ) =根据 C T 值 V ( p ) 与衰减系数间的线性关系 , 由式 ( 2) 推导出5 v( 7)I ( p ) ∝∫V ( p ) d r( 3)11212 算法实现L将 p 表示成参数形式一般算法是根据 C T 梯度投影与 X 射线图像梯度的相似程度进行最优解搜索 , 如 Wein 等7 采用 两者互相关性为测度函数 ; To m azevic 等8 提出将 X 射线图像梯度在射线上的反投影与 C T 梯度比较的 方法1 但我们在研究中发现 : X 射线图像梯度方向 会随射线能量的 ( k V ) 不同产生变化 , 因此文献 7 28 方法鲁棒性不高1 根据投射原理 , X 射线图像边缘的产生是由于射线经过了相应投照物体的边缘 , 因此在配准情况下 ,这部分形成边缘的射线也必然 与 C T 模型的边缘相切1 在 2D 图像中 ,位于图像边 缘的像素具有最大的梯度值 ,根据式 (7) 的梯度对应 关系可以得到结论 : 在以配准点为中心的局部范围 内 ,C T 数据场在这部分射线上的梯 度 投 影 必 然 在 配准点上取得最大值1 我们定义射线的梯度投影函 数为为 10 - 3 与 10 - 21 梯度场采用 C T 数据场同高斯微分 函数卷积 (σ= 015 mm ) 获得 ,以减小非骨骼梯度信息对配准的影响1 X 射线图像边缘由 C anny 算子在粗配准中得到的脊柱边界内自动提取1 提取的边缘 可能包含有其他非脊柱的信息 ,如手术器械等 ,由于在 C T 模型中没有与之对应的物体 ,所以这部分光线的 G P 值很小 , 可以设定一个阈值将其过滤1 每次迭代时 ,对经过图像边缘的每条射线以 T - 1 变换到 C T 图像空间 ,并按照光线投射法原理对梯度场 采样 ,采样间隔 1 mm 12 实 验C 型臂采用 GE 公司的 O EC9800 ,空间分辨率为 1024 ×768 ,灰度分辨率 12 bit 1 C T 的扫描参数如下 :准直器宽度 2 mm ,螺距 110 ,视野 20 cm ×20 c m 1光学跟踪设备采用 ND I 公司的 Polaris 以及配套的跟踪器械 , 定位误差 ≤0135 mm 1 所有程序运行于Dell 650 工作站 ( Xeo n 218 GHz , 1 G B RA M ) 1 我们以腰椎为例设计了 2 步实验进行验证1 配准精度应 用表面配准误差及 T 的各分量误差评估 ,表面配准误差为TuvGP ( T , p ;其中 T , 包含 3 个平移及; 式中 省略了 r G P , 成一个多参数最优化过程 , 并避免了 X 射线图像梯 度方向变化对配准的影响 , 即T ^ = arg T ma x∑ ‖G P ( T , p ) ‖1s T R E = ‖T p ‖ - T p C T gold C T p ∈e dges本文采用 Powell 多参数优化算法 ,在每一维内使用 Brent 搜索算法9 1 初始搜索方向设为共轭的 单位向量 , Powell 与 Brent 算法的收敛值分别设定其中 , T 为本文算法得到的坐标转换关系 , T gold 为标 准坐标转换关系 , p C T 为 C T 脊柱模型的表面点1 实 验结果如表 1 所示 , s T R E ≤3 mm 则认为配准成功1表 1 配准实验结果s T R E Πmm ΔxΔyΔzΔθxΔθyΔθz时间Πs成功率Π%步骤 粗配准 精配准 粗配准精配准5150 1136 512721283118 0179 217911082166 0165 219911313131 0157 219111061137 0130 210911141169 0124 115501980194 0147 215411272116 4213 20176211实验 192实验 278距离误差单位 mm ,角度误差单位°实验 11 为排除 C 型臂系统标定误差的影响 , 采用临床病人的脊柱 C T 数据及由它生成的模拟 X射线图像进行配准1 首先人工设定 T gold 及射线投影 参数 ,然后将 C T 数据以 D RR 方式生成 2 ~ 3 幅不 同角度的模拟 X 射线图像 ,最后随机生成 C T 模型 位置进行配准实验1 为了进一步检验精配准算法 , 我们以 C T 模型经 T gold 的转换后的标准位置为中 心 ,对 6 个空间变换方向分别进行最优化函数值统 计 ,如图 5 所示 ,纵轴为函数值 ,横轴分别为沿坐标数具有单一的极值 ,并出现在标准位置附近 ,曲线呈 现出较好的收敛特性1实验 21 在 C 型臂系统上采用人体脊柱标本模拟实际手术1 术前将 5 个人工标记物附着在标本上进行 C T 扫描 ; 术中将利用标记物点配准方法获得 的空间转换关系作为 T gold ,同时 X 射线图像经不同 方位采集后经 B 样条校正10 ;利用直接线性变换法进行系统标定 ,获得射线投影参数1 图 6 所示为一配准实例 ,我们将 C T 投影到 X 射线图像上以显示两者配准情况1计算机辅助设计与图形学学报 2007 年1158错误的术中定位1 总之 ,本文提出的 2D Π3D 图像配 准方法在精度与速度上取得了较好的平衡 ,并且操 作简便 ,能满足脊柱外科手术导航的临床需要1讨 论3 本文采用基于不同特 征 的 分 步 2D Π3D 配 准 方 法 ,较好地克服了单一配准方法的局限性1 整个配 准过程采用简单的交互操作 ,有利于配准效率的提 高1 由于本文算法只利用了 X 射线图像边缘的位置 信息 ,因此放宽了对成像条件的限制 ,方便与不同类 型的 C 形臂系统配套使用1 在配准精度方面 ,参照 国外手术导航系统的临床应用情况11 ,配准误差一 般要求小于 5 mm ,因此本文算法的配准精度处于临 床可接受范围内1 在配准成功率方面 , 虽然模拟实 际手术的成功率有所下降 ,但部分原因是由于人工 估计初始位置的角度误差较大造成的 ,而在实际应 用中可以采用根据病人体表解剖标志点进行初始位 置估计的方法加以避免5 1 同时 , 由于手术导航系 统要求术前采用标记点定位来验证配准精度 ,因此 在配准误差较大时需要重新进行配准 ,从而避免了参 考 文 献Zhang Y ing , Y uan Wen 1 The current st at us and develop ment ofc o mp ut er 2assist ed spinal surgery J 1 Jo urnal of Spine Surgery , 2005 , 3 ( 1) : 51 - 53 (in Chinese )(张 颖 , 袁 文1 计算机辅助脊柱外科手术的应用现状及进展J 1 脊柱外科杂志 , 2005 , 3 ( 1) : 51 - 53)Fitz pat ri ck J M , West J B , Maurer C R 1 Predicting erro r inrigid 2bo dy point 2based regist ratio n J 1 I EEE Transactio ns o nMedical Imaging , 1998 , 17 ( 5) : 694 - 702To mazevic D , Li kar B , Pernus F 1 32D Π22D regist ratio n by int e 2grating 22D inf o r matio n in 32D J 1 I EEE Transactio ns o n Med 2ical Imaging , 2006 , 25 ( 1) : 17 - 27Besl P J , Mckay N D 1 A met ho d f o r regist ratio n of 32D shapesJ 1 I EEE Transactio ns o n Pat t ern Analysis and Machine Int el 2ligence , 1992 , 14 ( 2) : 239 - 256(下转第 1165 页)1 ]2 ]3 ]4 ]4 ] K aucic Branko , Zali k Bo rut 1 An overview of visi bilit y p ro blemalgo rit hms in 1 , 5D C ΠΠProceedings of t he 10t h Int ernatio na l Co nference in Cent ral Europe o n Co m p ut er G rap hics , Visualiza2tio n and Co mp ut er Visio n’20021 Plzen , 2002 : 241 - 274K i m Y o ung2H oo n , Rana Sanjay , Wise St eve1 Explo ring multi2 ple viewshed analysis using t errain feat ures and opti misatio n t echniques J 1 Co mp u t ers and Ge o sciences , 2004 , 30 ( 9Π10) :1019 - 1032L ee J ay , St ucky Dan1 On applying viewshed analysis f o r det er2 mining least2c o st pat hs o n digit al elevatio n mo dels J 1 Int erna2 tio nal Jo urnal of G e ograp hical Inf o r matio n Syst ems , 1998 , 12 ( 8) : 891 - 950Zhang J infang , Li L ei , Wang Yuxin1 Terrain visibilit y analysis J 1 Jo urnal of Syst em Si mulatio n , 2005 , 17 (8 ) : 1916 - 1921 (in Chinese)( 张金方, 李磊, 王宇心1 地形可视性分析J 1 系统仿真学报, 2005 , 17 ( 8) : 1916 - 1921)L u Pin , Zhang J infang , L u Min1 An optimal met ho d f o r multi2 ple o bservers sit ting o n t errain based o n i mp roved s i mulat ed a n2 nealing t echniques C ΠΠProceedings of t he 19t h Int ernatio nal Co nference o n Indust rial , Engineering & Ot her Applicatio ns ofA pplied Int elligent Syst ems , Annecy , 2006 : 373 - 382Li Zhilin , Zhu Qing1 Digit al elevatio n mo del M 1 Wuhan : Wuhan U niversit y Press , 2000 : 5 - 59 (in Chinese)(李志林, 朱庆1 数字高程模型M 1 武汉:武汉大学出版社, 2000 : 5 - 59) 10 ] To mlin C Dana1 G e ograp hic inf o r matio n syst ems and carto2grap hic mo deling M 1 Englewoo d Cliff s : Prentice Hall , 1990 :85 - 112Cha o Qingyu , L ee J ay , Munro2St asiuk Mandy J 1 Ext ensio ns toleast2c o st pat h algo rit hms f o r roadway planning J 1 Int erna2tio nal Jo urnal of G e ograp hical Inf o r matio n Science , 2003 , 17( 4) : 361 - 376Saha A K , Aro ra M K , G upt a R P , et al 1 GIS2based ro uteplanning in landslide2p ro ne areas J 1 Int ernatio nal Jo urnal ofGe ograp hical Inf o r matio n Science , 2005 , 19 ( 10) : 1149 - 1175Wang Ling1 Int elligent opti mizatio n algo rit hm and it s applicatio nM 1 Be ijing : Tsinghua U niversit y Press , 2001 : 17 - 33 (inChinese)( 王凌1 智能优化算法M 1 北京: 清华大学出版社, 2001 :17 - 33)Minet er M J , D owers A , Caldwell D R , et al 1H igh2t hro ugh2p ut c o mp uting to enhance invervisi bilit y analysis OL 1 (2003209208) 2006 210225 1 ht tp :ΠΠwww . ge oc o mp ut atio n . o rgΠ2003ΠCaldwell D R , Mine t er M J , D owers S , et al 1 Analysis and vi2sualizatio n of visibilit y surfaces OL 1 ( 2003209208 ) 2006 210225 1 ht tp :ΠΠwww1ge oc o mp ut atio n1o rgΠ2003ΠMinet er M J , D owers S , Caldwell D R1 A multic o mp uting sof t2ware enviro nment f o r Arc Info int ervisi bilit y analysis OL 1( 2003209208) 2006 210225 1 ht tp :ΠΠwww1ge oc o mp ut atio n1o rgΠ2003Π11 ]5 ]12 ] 6 ]13 ] 7 ]14 ]8 ]15 ]16 ] 9 ](上接第1158 页)5 ] Livyat an H , Y aniv Z , Jo skowicz L 1 Gradient2based 2DΠ3D ri gidregist ratio n of fluo ro sc opic X2ray to C T J 1 I EEE Transactio n s o n Medical Imaging , 2003 , 22 ( 11) : 1395 - 14066 ] Cho do rowski A , Mat t sso n U, L angille M , et al 1 Colo ur le s io nbo undary det ectio n using live wire C ΠΠProceedings of SP I E , San Diego , 2005 , 5747 : 1589 - 15967 ] Wein W , Roper B , Navab N1 2DΠ3D regist ratio n based o n vol2ume gradi ent s C ΠΠProceedings of SP I E , San Diego , 2005 ,5747 : 144 - 1508 ] To mazevic D , Li kar B , Pernus F1 Rigid 2DΠ3D regist ratio n ofint ra operative digit al X2ray i mages and p re operative C T and MRi mages C ΠΠProceedings of SP I E , Milan , 2002 : 507 - 517Press W H , Flannery B P , Teukolo sky S A , et al 1 Numerica lrecipes in C M ΠΠ2nd ed1 Cambridge , U K : Cambridge U ni2versit y Press , 1992 : 412 - 419Livyat an H , Y aniv Z , Jo skowicz L 1 Ro bust auto matic C2ar mcalibratio n f o r f l uo ro sc opy2based navigatio n : a p ractical app roac hC ΠΠProceedings of Int ernatio nal Co nference o n Medical ImageCo mp uting and Co mp ut er2Assist ed Int erventio n , To k yo , 2002 :60 - 68H erring J L , Dawant B M , Maurer C R1 Surface2based regist ra2tio n of C T i mages to p hysical space f o r i mage2guided surgery oft he spine : a sensitivit y st udy J 1 I EEE Transactio n s o n Medi2cal Imaging , 1998 , 17 ( 5) : 743 - 7529 ]10 ]11 ]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Date: February 1, 2008. 1
2
M.I. Cortez, J.-M. Gambaudo and A. Maass
the coordinates of θ¯ are independent on Q, the set O1 is the 1-torombinatorics of return times
Let us start this section with some general considerations. Let Rd be the Euclidean d-space and − its Euclidean norm. Consider two positive numbers r and R. An (r, R)-Delone set is a subset D of the d-space Rd equipped with the Euclidean norm − , which satisfies the following two properties:
Abstract. In this paper we study conditions under which a free minimal Zdaction on the Cantor set is a topological extension of the action of d rotations, either on the product Td of d 1-tori or on a single 1-torus T1. We extend the notion of linearly recurrent systems defined for Z-actions on the Cantor set to Zd-actions and we derive in this more general setting, a necessary and sufficient condition, which involves a natural combinatorial data associated with the action, allowing the existence of a rotation topological factor of one these two types.
Notice that a complete combinatorial answer to this question is given in [BDM] in the particular case when the dimension d = 1 and when the free minimal Zaction is linearly recurrent. The linear recurrence of a given Z-action is a property that involves the combinatorics of return times associated with a nested sequence of clopen sets (for further references on linearly recurrent Z-actions see [CDHM],[Du1] and [Du2]). The notion of return time to a clopen set can be generalized to Zd-actions when d ≥ 2. In this case, the combinatorics of the return times associated with a nested sequence of clopen sets inherits a richer structure than in the case d = 1 . However, as for d = 1, there exists a natural definition of linearly recurrent Zd-action. These generalizations are developed in Section 2 which is devoted to the combinatorics of return times (for further references on the structure of return times associated with a Zd-action see [BG] where the hierarchical ideas used in this paper are introduced, see also [S] and [SW] for related topics). This combinatorial approach allows us to derive a necessary condition on the action to be an extension of an action of one of the two rotations described above. In the case of a linearly recurrent action this condition is sufficient. This result is given in Section 3 (Theorem 3.1) together with its proof.
• First consider the Zd-action generated by d rotations on the product d-torus Td = Rd/Zd = T1 × · · · × T1, each rotation acting on T1. More precisely, take θ¯ = (θ1, . . . , θd) ∈ Rd and let Adθ¯ : Zd × Td → Td be the map defined by: Adθ¯(n¯, x) = x + [n¯, θ¯] mod Zd , for n¯ = (n1, . . . , nd) ∈ Zd, x ∈ Td and where [n¯, θ¯] = (n1 · θ1, . . . , nd · θd). This construction yields a minimal Zd-action (Od, Adθ¯) on the closure Od of the orbit of 0 in the d-torus Td. When the coordinates of θ¯ are rationally independent, the set Od is the d-torus Td and the action is free.
1. Introduction
Let (X, A) be a Zd-action (by homeomorphisms) on a compact metric space X. The action is free if A(n¯, x) = x for some n¯ ∈ Zd and x ∈ X implies n¯ = 0 and is minimal if the orbit of any point x ∈ X, OA(x) = {A(n¯, x) : n¯ ∈ Zd}, is dense in X. The simplest non trivial examples of free minimal Zd-actions on a compact metric space are given by “rotation-type” actions on compact topological groups. This type of factors play a central role in topological dynamics of Zd-actions since in particular they determine weak mixing property through the existence of continuous eigenvalues. In this paper, we focus on two kinds of “rotation-type” factors that we describe now.
Assume X is a Cantor set, i.e., it has a countable basis of closed and open (clopen) sets and has no isolated points (or equivalently, it is a totally disconnected compact metric space with no isolated points).
• The same θ¯ can be used to define a Zd-action on T1. Consider the map A1θ¯ : Zd × T1 → T1 given by A1θ¯(n¯, t) = t+ < n¯, θ¯ > mod Z, where < ·, · > is the usual inner product in Rd. The Zd-action (O1, A1θ¯) on the closure O1 of the orbit of 0 in the 1-torus T1 is again minimal. When
