高考数学小题狂做冲刺训练(详细解析)(共15套)(最新整理)
高三理科数学小题狂做3
高三理科数学小题狂做(3)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}250x x x M =->,{}2,3,4,5,6N =,则MN =( )A .{}2,3,4B .{}2,3,4,5C .{}3,4D .{}5,62、已知复数z 满足()135i z i -=+,则复数z 在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3、已知点()3,4P ,()Q 2,6,向量()F 1,λE =-.若Q//F P E ,则实数λ的值为( )A .12B .2C .12-D .2- 4、“5m <”是“5m <”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 5、下列函数既是奇函数又是()0,1上的增函数的是( ) A .y x =-B .2y x =C .sin y x =D .cos y x =6、某几何体的正(主)视图和侧(左)视图如图所示,则该几何体的体积不可能是( )A .13B .6πC .23D .1 7、已知圆222410x y x y +-++=和两坐标轴的公共点分别为A ,B ,C ,则C ∆AB 的面积为( )A .4B .2C .23D .38、执行下面的程序框图,则输出的m 的值为( ) A .9B .7C .5D .119、已知函数()()2cos f x x ωϕ=+(0ω>,2πϕ<)的部分图象如下图所示,其中12,3y ⎛⎫⎪⎝⎭与220,3y ⎛⎫⎪⎝⎭分别为函数()f x 图象的一个最高点和最低点,则函数()f x 的一个单调增区间为( ) A .1420,33⎛⎫⎪⎝⎭B .10,03⎛⎫- ⎪⎝⎭C .40,3⎛⎫ ⎪⎝⎭D .1610,33⎛⎫-- ⎪⎝⎭10、已知()621x a x x ⎛⎫+- ⎪⎝⎭(R a ∈)的展开式中常数项为5,则该展开式中2x 的系数为( )A .252-B .5-C .252D .5 11、已知双曲线C :22221x y a b-=(0a >,0b >)的右焦点为2F ,()00,x y M (00x >,00y >)是双曲线C 上的点,()00,x y N --.连接2F M 并延长2F M 交双曲线C 于P ,连接2F N ,PN ,若2F ∆N P 是以2F ∠N P 为顶角的等腰直角三角形,则双曲线C 的渐近线方程为( )A .2y x =±B .4y x =±C .62y x =±D .102y x =± 12、已知函数()f x 的图象在点()()00,x f x 处的切线方程为:l ()y g x =,若函数()f x 满足x ∀∈I (其中I 为函数()f x 的定义域),当0x x ≠时,()()()00f x g x x x --<⎡⎤⎣⎦恒成立,则称0x x =为函数()f x 的“分界点”.已知函数()f x 满足()15f =,()462f x x x'=--,则函数()f x 的“分界点”的个数为( ) A .0个 B .1个 C .2个 D .无数个 二、填空题(本大题共4小题,每小题5分,共20分.) 13、某健康协会从某地区睡前看手机的居民中随机选取了270人进行调查,得到如右图所示的频率分布直方图,则可以估计睡前看手机在4050分钟的人数为.14、若实数x ,y 满足约束条件4210440y x x y x y ≤-⎧⎪-+≥⎨⎪--≤⎩,则2z x y=-的最大值是.15、已知六棱柱111111CD F C D F AB E -A B E 的底面是正六边形,侧棱与底面垂直,若该六棱柱的侧面积为48,底面积为123,则该六棱柱外接球的表面积等于. 16、如图,空间四边形CD AB 中,C D 45∠A =,15cos C 5∠A B =,C 1510A =+,D 25A =,C 6B =.若点E 在线段C A 上运动,则D EB +E 的最小值为.高三理科数学小题狂做(3)参考答案一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案ABCBCDDADACB13、81 14、4 15、32π 16、7高考理科数学试题及答案(考试时间:120分钟试卷满分:150分)一、选择题:本题共12小题,每小题5分,共60分。
高三数学高考小题冲刺训练(详细解析)(十三)

高考数学小题狂做冲刺训练(详细解析)姓名:__________班级:__________考号:__________题号 一 二 总分 得分、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.已知集合A={x|x 2-2x-3≤0},B={x|x 2+px+q <0},满足A∩B={x|-1≤≤x<2},则p 与q 的关系为( )A.p-q=0B.p+q=0C.p+q=-5D.2p+q=-4解析:A={x|-1≤x≤3},∵A∩B 非空,∴B 非空,设B={x|x 1<x <x 2},观察数轴,有x 1<-1,x 2=2,即x=2是方程x 2+px+q=0的一根,把x 2=2代入x 2+px+q=0,有4+2p+q=0.故选择D.答案:D2.如图,四边形ABCD 中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB 沿BD 折起,使平面ABD⊥平面BCD,构成三棱锥A —BCD.则在三棱锥A —BCD 中,下列命题正确的是( )A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC解析:∵在四边形ABCD 中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,∴BD⊥CD. 又平面ABD⊥平面BCD,且平面ABD∩平面BCD =BD, 故CD⊥平面ABD,则CD⊥AB. 又AD⊥AB,故AB⊥平面ADC. ∴平面ABC⊥平面ADC. 答案:D3.用数字1,2,3,4,5可以组成没有重复数字,并且比20 000大的五位偶数共有( )A .48个B .36个C .24个D .18个解析:个位数是2的有333A =18个,个位数是4的有33A =18个,所以共有36个. 答案:B 4.3ln )1()(--=x xx x f 的零点个数为( )A.1B.2C.3D.0 解析:∵f(x)=0,∴(x -1)lnx =0.∴x=1. ∴f(x)零点为1. 答案:A5.以点(2,-1)为圆心且与直线3x-4y+5=0相切的圆的方程为( )A.(x-2)2+(y+1)2=3B.(x+2)2+(y-1)2=3C.(x-2)2+(y+1)2=9D.(x+2)2+(y-1)2=3解析:343|5)1(423|22=++-⨯-⨯=r ,故选C.答案:C6.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 、N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成的角为( )A.arccos23 B.arccos 1010C.arccos53 D.arccos 52 解析:如图建立空间直角坐标系,把D 点视作原点O ,分别沿DA 、DC 、1DD 方向为x 轴、y轴、z 轴的正方向,则A (1,0,0),M (1,21,1),C (0,1,0),N (1,1,21),∴AM=(1,21,1)-(1,0,0)=(0,21,1), CN=(1,1,21)-(0,1,0)=(1,0,21). 故AM ·CN =0×1+21×0+1×21=21.又|AM|=251)21(0222=++, |CN|=25)21(01222=++, 设α为直线AM 与CN 所成的角,∴cosα=52252521||||=•=•CN AM CNAM . ∴α=arccos 52.答案:D7.△ABC 中,a 、b 、c 分别为∠A、∠B、∠C 的对边,如果a 、b 、c 成等差数列,∠B=30°,△ABC 的面积为23,那么b 等于( ) A.231+ B.31+ C.232+ D.32+解析:∵a、b 、c 成等差数列,∴2b=a+c.平方,得a 2+c 2=4b 2-2ac.又△ABC 的面积为23,∠B=30°,故由234130sin 21sin 21==︒==∆ac ac B ac S ABC ,得ac=6.∴a 2+c 2=4b 2-12.由余弦定理,得2344621242cos 222222=-=⨯--=-+=b b b ac b c a B ,解得3242+=b .又b 为边长,∴31+=b .答案:B8.一对酷爱运动的年轻夫妇,让刚满十个月大的婴儿把“0,0,2,8,北,京”六张卡片排成一行,若婴儿能使得排成的顺序为“北京”或“北京”,则受到父母的夸奖,那么婴儿受到父母夸奖的概率为( )A.1801 B.2401 C.3601 D.7201 解析:婴儿受到父母夸奖的概率180122266==A A P . 答案:A9.已知双曲线122=-ny m x (mn≠0)的离心率为2,有一个焦点恰好是抛物线y 2=4x 的焦点,则此双曲线的渐近线方程是( )A.03=±y xB.03=±y xC.3x±y=0D.x±3y=0 解析:抛物线y 2=4x 的焦点为(1,0). ∴m+n=1.又双曲线的离心率为2,∴21=m. ∴41=m ,43=n . ∴双曲线的方程为134422=-y x . ∴其渐近线方程为03=±y x . 答案:A10.)(lim 11413122242322nnn C C C C n C C C C ++++++++∞→ 等于( )A.3B.31 C.61D.6 解析:∵2243422423332242322n n n C C C C C C C C C C C +++=++++=++++ 31+==n C ,2)1)(2()(1141312-+=++++n n nC C C C n n ,∴312)2)(1(6)1()1(lim 2)2)(1(lim )(lim 3111413122242322=+--+=+-=++++++++∞→+∞→∞→n n n n n n n n n C C C C C n C C C C n n n nn n . 答案:B、填空题(本大题共5小题,每小题5分,共25分)11.如图(1),正四棱柱ABCD —A′B′C′D′中,AA′=2AB,则异面直线A′B 与AD′所成的角的余弦值是______________.解析:如图(2),连结D′C、AC,则A′B∥D′C, ∴异面直线A′B 与AD′所成的角等于∠AD′C. 令AB =a,∴AA′=2AB =2a. ∴AD′=D′C=a 5,a AC 2=.△AD′C 中,AD′=D′C=a 5,a AC 2=,∴cos∠AD′C=54108222222=='•'-'+'a a C D D A AC C D D A .答案:54 12.口袋内装有10个相同的球,其中5个球标有数字0,5个球标有数字1,若从袋中摸出5个球,那么摸出的5个球所标数字之和小于2或大于3的概率是________.(用数值作答)解析:随机变量ξ=i 表示摸出的5个球所标数字之和为i (i =0,1,2,3,4,5),则5101)0(C P =,510510451551045151)5(,)4(,)1(C P C C C P C C C P ===,故摸出的5个球所标数字之和小于2或大于3的概率为6313252262)(2)5()4()1()0(510451505=⨯=+=+++C C C C P P P P . 答案:631313.若不等式|x-4|+|3-x|<a 的解集是空集,则实数a 的取值范围为______________.解析:不等式|x-4|+|3-x|<a 的解集为⇔|x-3|+|x-4|<a 的解集为.又|x-3|+|x-4|的最小值为1,故a∈(-∞,1]. 答案:(-∞,1]14.(上海高考,理10)某海域内有一孤岛,岛四周的海平面(视为平面)上有一浅水区(含边界),其边界是长轴长为2a 、短轴长为2b 的椭圆.已知岛上甲、乙导航灯的海拔高度分别为h 1、h 2,且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上.现有船只经过该海域(船只的大小忽略不计),在船上测得甲、乙导航灯的仰角分别为θ1、θ2,那么船只已进入该浅水区的判别条件是_______________. 解析:依题意作图,如右图,知|MF 1|+|MF 2|<2a h 1·cotθ1+h 2·cotθ2<2a.答案:h 1·cotθ1+h 2·cotθ2<2a15.在x 、y 值都是不小于0的整数点(x,y)中,满足x+y≤4的点的个数为__________.解析:如图所示,用数形结合法知共有15个.答案:15。
高中数学小题狂做(一)及答案
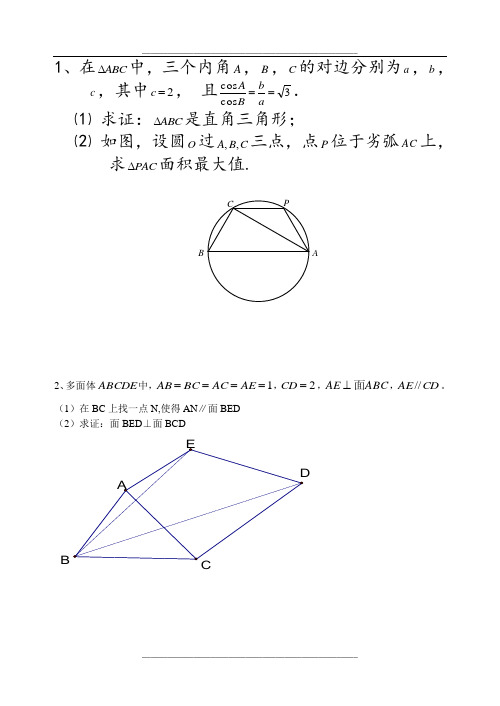
1、在ABC ∆中,三个内角A ,B ,C 的对边分别为a ,b ,c ,其中2c =, 且3cos cos ==ab B A . ⑴ 求证:ABC ∆是直角三角形;⑵ 如图,设圆O 过,,A B C 三点,点P 位于劣弧AC 上,求PAC ∆面积最大值.2、多面体ABCDE 中,1====AE AC BC AB ,2=CD ,ABC AE 面⊥,CD AE //。
(1)在BC 上找一点N,使得AN ∥面BED(2)求证:面BED ⊥面BCD BA1、⑴ 证明:由正弦定理得cos sin cos sin A B B A =,整理为sin cos sin cos A A B B =,即sin 2sin 2A B = 又因为02,22A B π<<∴22A B =或22A B π+=,即A B =或2A B π+=∵31b a =, ∴A B =舍去,故2A B π+=由2A B π+=可知2C π=,∴ABC ∆是直角三角形⑵ 解法一:由(1)及2c =,得1a =,3b =,分设()62PAB ππθθ∠=<<,则6PAC πθ∠=-, 在Rt PAB ∆中,cos 2cos PA AB θθ=⋅= 所以11sin()2cos 3sin()2626PAC S PA AC ππθθθ∆=⋅⋅-=⋅⋅⋅⋅-3cos sin()6πθθ=⋅⋅-313cos (sin cos )22θθθ=⋅-⋅233cos sin cos 22θθθ=- 331cos 2sin 2422θθ+=-⨯3sin(2)26πθ=-34- 因为62ππθ<<所以52666πππθ<-<,当262ππθ-=,即3πθ=时,PAC S ∆最大值等于34. 解法二:设p 到AC 的距离为h ,h 取到最大值时,PAC S 取得最大值;过o 作AC 的垂线交AC 于P 点,此时h 最大,11122h =-=,所以PAC S =342、证明:(1)令BC 中点为N ,BD 中点为M ,连结MN 、EN∵MN 是△ABC 的中位线∴ MN ∥CD 由条件知AE ∥CD ∴MN ∥AE 又MN=12CD=AE ∴四边形AEMN 为平行四边形∴AN ∥EM ∵AN ⊄面BED, EM ⊆面BED∴AN ∥面BED (2) ∵AE ⊥面ABC, AN ⊂面ABC∴AE ⊥AN 又∵AE ∥CD,AN ∥EM ∴EM ⊥CD ∵N 为BC 中点,AB=AC ∴AN ⊥BC ∴EM ⊥BC ∴EM ⊥面BCD ∵EM ⊂面BED ∴ 面BED ⊥面BCD。
高三理科数学小题狂做15

高三理科数学小题狂做(1)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知全集{}2U 1x x =>,集合{}2430x x x A =-+<,则UA =( )A .()1,3B .()[),13,-∞+∞C .()[),13,-∞-+∞D .()(),13,-∞-+∞2、221i i ⎛⎫= ⎪-⎝⎭( )A .2i -B .4i -C .2iD .4i3、已知抛物线的焦点()F ,0a (0a <),则抛物线的标准方程是( ) A .22y ax =B .24y ax =C .22y ax =-D .24y ax =- 4、命题:p x ∃∈N ,32x x <;命题:q ()()0,11,a ∀∈+∞,函数()()log 1a f x x =-的图象过点()2,0,则( )A .p 假q 真B .p 真q 假C .p 假q 假D .p 真q 真 5、执行右边的程序框图,则输出的A 是( ) A .2912B .7029C .2970D .169706、在直角梯形CD AB 中,//CD AB ,C 90∠AB =,2C 2CD AB =B =,则cos D C ∠A =( )A .1010B .31010C .55D .255 7、已知2sin 21cos 2αα=+,则tan 2α=( ) A .43-B .43C .43-或0D .43或0 8、32212x x ⎛⎫+- ⎪⎝⎭展开式中的常数项为( )A .8-B .12-C .20-D .209、函数()sin 2cos f x x x =+的值域为( ) A .1,5⎡⎤⎣⎦B .[]1,2C .2,5⎡⎤⎣⎦D .5,3⎡⎤⎣⎦10、F 是双曲线C :22221x y a b-=(0a >,0b >)的右焦点,过点F 向C 的一条渐近线引垂线,垂足为A ,交另一条渐近线于点B .若2F F A =B ,则C 的离心率是( ) A .2B .2C .233D .14311、直线y a =分别与曲线()21y x =+,ln y x x =+交于A ,B ,则AB 的最小值为( ) A .3B .2C .324D .3212、某几何体的三视图如图所示,则该几何体的表面积为( ) A .4B .213+ C .3312+D .33122+ 二、填空题(本大题共4小题,每小题5分,共20分.) 13、已知()1,3a =-,()1,b t =,若()2a b a -⊥,则b =.14、为了研究某种细菌在特定环境下,随时间变化繁殖情况,得如下实验数据,计算得回归直线方程为ˆ0.850.25yx =-.由以上信息,得到下表中c 的值为. 天数t (天) 345 67繁殖个数y (千个)2.5 3 44.5 c,若C D 2AB =A =A =,则平面CD B 被球所截得图形的面积为.16、已知x ,R y ∈,满足22246x xy y ++=,则224z x y =+的取值范围为.高三理科数学小题狂做(1)参考答案一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CABABBDCACDC13、5 14、6 15、16π 16、[]4,12高考数学(文)一轮:一课双测A+B精练(四十)空间几何体的结构特征及三视图和直观图1.(·青岛摸底)如图,在下列四个几何体中,其三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是( )A.②③④B.①②③C.①③④D.①②④2.有下列四个命题:①底面是矩形的平行六面体是长方体;②棱长相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体.其中真命题的个数是( )A.1B.2C.3D.43.一个锥体的正视图和侧视图如图所示,下面选项中,不可能是该锥体的俯视图的是( )4.如图是一几何体的直观图、正视图和俯视图.在正视图右侧,按照画三视图的要求画出的该几何体的侧视图是( )5.如图△A′B′C′是△ABC的直观图,那么△ABC是( )A.等腰三角形B.直角三角形C.等腰直角三角形D.钝角三角形6.(·东北三校一模)一个几何体的三视图如图所示,则侧视图的面积为( )A.2+3B.1+3C.2+23D.4+37.(·昆明一中二模)一个几何体的正视图和侧视图都是边长为1的正方形,且体积为1,则这个几何体的俯视图可能是下列图形中的________.(填入所有可能的图形前的编号) 2①锐角三角形;②直角三角形;③四边形;④扇形;⑤圆8.(·安徽名校模拟)一个几何体的三视图如图所示,则该几何体的体积为________.9.正四棱锥的底面边长为2,侧棱长均为3,其正视图(主视图)和侧视图(左视图)是全等的等腰三角形,则正视图的周长为________.10.已知:图1是截去一个角的长方体,试按图示的方向画出其三视图;图2是某几何体的三视图,试说明该几何体的构成.11.(·银川调研)正四棱锥的高为3,侧棱长为7,求侧面上斜高(棱锥侧面三角形的高)为多少?12.(·四平模拟)已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示.(1)画出该三棱锥的直观图;(2)求出侧视图的面积.1.(·江西八所重点高中模拟)底面水平放置的正三棱柱的所有棱长均为2,当其正视图有最大面积时,其侧视图的面积为( )A.23B.3C.3D.42.(·深圳模拟)如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE=3,且当规定正视方向垂直平面ABCD时,该几何体的侧视图的面积为22.若M,N分别是线段DE,CE上的动点,则AM+MN+NB的最小值为________.3.一个多面体的直观图、正视图、侧视图如图1和2所示,其中正视图、侧视图均为边长为a的正方形.(1)请在图2指定的框内画出多面体的俯视图;(2)若多面体底面对角线AC,BD交于点O,E为线段AA1的中点,求证:OE∥平面A1C1C;(3)求该多面体的表面积.[答题栏]A级1._________2._________3._________4._________5._________6._________B级 1.______2.______ 7.__________8.__________9.__________答案高考数学(文)一轮:一课双测A+B精练(四十)A级1.A2.A3.C4.B5.选B由斜二测画法知B正确.6.选D依题意得,该几何体的侧视图的面积等于22+12×2×3=4+ 3.7.解析:如图1所示,直三棱柱ABE-A1B1E1符合题设要求,此时俯视图△A BE是锐角三角形;如图2所示,直三棱柱ABC-A1B1C1符合题设要求,此时俯视图△ABC是直角三角形;如图3所示,当直四棱柱的八个顶点分别是正方体上、下各边的中点时,所得直四棱柱ABCD-A1B1C1D1符合题设要求,此时俯视图(四边形ABCD)是正方形;若俯视图是扇形或圆,体积中会含有π,故排除④⑤.答案:①②③8.解析:结合三视图可知,该几何体为底面边长为2、高为2的正三棱柱除去上面的一个高为1的三棱锥后剩下的部分,其直观图如图所示,故该几何体的体积为12×2×2sin60°×2-13×12×2×2sin60°×1=533.答案:5339.解析:由题意知,正视图就是如图所示的截面PEF ,其中E 、F 分别是AD 、BC 的中点,连接AO ,易得AO =2,而PA =3,于是解得PO =1,所以PE =2,故其正视图的周长为2+2 2.答案:2+2210.解:图1几何体的三视图为:图2所示的几何体是上面为正六棱柱,下面为倒立的正六棱锥的组合体. 11.解:如图所示,正四棱锥S -ABCD 中, 高OS =3,侧棱SA =SB =SC =SD =7, 在Rt △SOA 中,OA =SA2-OS2=2,∴AC =4. ∴AB =BC =CD =DA =2 2. 作OE ⊥AB 于E ,则E 为AB 中点. 连接SE ,则SE 即为斜高, 在Rt △SOE 中,∵OE =12BC =2,SO =3,∴SE =5,即侧面上的斜高为 5.12.解:(1)三棱锥的直观图如图所示. (2)根据三视图间的关系可得BC =23, ∴侧视图中VA =42-⎝ ⎛⎭⎪⎫23×32×232=12=23,∴S △VBC =12×23×23=6.B 级1.选A 当正视图的面积达最大时可知其为正三棱柱某个侧面的面积,可以按如图所示位置放置,此时侧视图的面积为2 3.2.解析:依题意得,点E 到直线AB 的距离等于32-⎝ ⎛⎭⎪⎫222=2,因为该几何体的左(侧)视图的面积为12·BC ×2=22,所以BC =1,DE =EC =DC =2.所以△DEC 是正三角形,∠DEC =60°,tan ∠DEA =AD AE =33,∠DEA =∠CEB =30°.把△DAE ,△DEC 与△CEB 展在同一平面上,此时连接AB ,AE =BE =3,∠AEB =∠DEA +∠DEC +∠CEB =120°,AB2=AE2+BE2-2AE ·BEcos120°=9,即AB =3,即AM +MN +NB 的最小值为3.答案:33.解:(1)根据多面体的直观图、正视图、侧视图,得到俯视图如下:(2)证明:如图,连接AC ,BD ,交于O 点,连接OE. ∵E 为AA1的中点,O 为AC 的中点, ∴在△AA1C 中,OE 为△AA1C 的中位线. ∴OE ∥A1C.∵OE ⊄平面A1C1C ,A1C ⊂平面A1C1C , ∴OE ∥平面A1C1C.(3)多面体表面共包括10个面,SABCD =a2, SA1B1C1D1=a22,S △ABA1=S △B1BC =S △C 1DC =S △ADD1=a22,S △AA1D1=S △B1A1B =S △C1B1C =S △DC1D1 =12×2a 2×32a 4=3a28, ∴该多面体的表面积S =a2+a22+4×a22+4×3a28=5a2.高考数学(文)一轮:一课双测A+B精练(四十八) 直线与圆、圆与圆的位置关系1.(·人大附中月考)设m>0,则直线2(x+y)+1+m=0与圆x2+y2=m的位置关系为( )A.相切B.相交C.相切或相离D.相交或相切2.(·福建高考)直线x+3y-2=0与圆x2+y2=4相交于A,B两点,则弦AB的长度等于( )A.25B.23C.3D.13.(·安徽高考)若直线x-y+1=0与圆(x-a)2+y2=2有公共点,则实数a的取值范围是( )A.[-3,-1]B.[-1,3]C.[-3,1]D.(-∞,-3]∪[1,+∞)4.过圆x2+y2=1上一点作圆的切线与x轴,y轴的正半轴交于A,B两点,则|AB|的最小值为( )A.2B.3C.2D.35.(·兰州模拟)若圆x2+y2=r2(r>0)上仅有4个点到直线x-y-2=0的距离为1,则实数r的取值范围为( )A.(2+1,+∞) B.(2-1, 2+1)C.(0, 2-1) D.(0, 2+1)6.(·临沂模拟)已知点P(x,y)是直线kx+y+4=0(k>0)上一动点,PA,PB是圆C:x2+y2-2y=0的两条切线,A,B是切点,若四边形PACB的最小面积是2,则k的值为( )A.2B.21 2C.22D.27.(·朝阳高三期末)设直线x-my-1=0与圆(x-1)2+(y-2)2=4相交于A、B两点,且弦AB的长为23,则实数m的值是________.8.(·东北三校联考)若a,b,c是直角三角形ABC三边的长(c为斜边),则圆C:x2+y2=4被直线l:ax+by+c=0所截得的弦长为________.9.(·江西高考)过直线x +y -22=0上点P 作圆x2+y2=1的两条切线,若两条切线的夹角是60°,则点P 的坐标是________.10.(·福州调研)已知⊙M :x2+(y -2)2=1,Q 是x 轴上的动点,QA ,QB 分别切⊙M 于A ,B 两点.(1)若|AB|=423,求|MQ|及直线MQ 的方程; (2)求证:直线AB 恒过定点.11.已知以点C ⎝ ⎛⎭⎪⎫t ,2t (t ∈R ,t ≠0)为圆心的圆与x 轴交于点O 、A ,与y 轴交于点O 、B ,其中O 为原点.(1)求证:△AOB 的面积为定值;(2)设直线2x +y -4=0与圆C 交于点M 、N ,若|OM|=|ON|,求圆C 的方程.12.在平面直角坐标系xOy 中,已知圆x2+y2-12x +32=0的圆心为Q ,过点P(0,2),且斜率为k 的直线与圆Q 相交于不同的两点A 、B.(1)求k 的取值范围;(2)是否存在常数k ,使得向量OA +OB 与PQ ―→共线?如果存在,求k 值;如果不存在,请说明理由.1.已知两圆x2+y2-10x -10y =0,x2+y2+6x -2y -40=0,则它们的公共弦所在直线的方程为________________;公共弦长为________.2.(·上海模拟)已知圆的方程为x2+y2-6x -8y =0,a1,a2,…,a11是该圆过点(3,5)的11条弦的长,若数列a1,a2,…,a11成等差数列,则该等差数列公差的最大值是________.3.(·江西六校联考)已知抛物线C :y2=2px(p >0)的准线为l ,焦点为F ,圆M 的圆心在x 轴的正半轴上,圆M 与y 轴相切,过原点O 作倾斜角为π3的直线n ,交直线l 于点A ,交圆M 于不同的两点O 、B ,且|AO|=|BO|=2.(1)求圆M 和抛物线C 的方程;(2)若P 为抛物线C 上的动点,求PM ―→,·PF ―→,的最小值;(3)过直线l 上的动点Q 向圆M 作切线,切点分别为S 、T ,求证:直线ST 恒过一个定点,并求该定点的坐标.[答 题 栏]A 级 1._________2._________3._________4._________5B 级 1.______2.______.__________6._________ 7.__________8.__________9.__________答 案高考数学(文)一轮:一课双测A+B 精练(四十八)A 级1.C2.B3.C4.C5.选A 计算得圆心到直线l 的距离为22= 2>1,如图.直线l :x -y -2=0与圆相交,l1,l2与l 平行,且与直线l 的距离为1,故可以看出,圆的半径应该大于圆心到直线l2的距离2+1.6.选D 圆心C(0,1)到l 的距离d =5k2+1,所以四边形面积的最小值为2×⎝ ⎛⎭⎪⎫12×1×d2-1=2, 解得k2=4,即k =±2.又k >0,即k =2.7.解析:由题意得,圆心(1,2)到直线x -my -1=0的距离d =4-3=1,即|1-2m -1|1+m2=1,解得m =±33. 答案:±33 8.解析:由题意可知圆C :x2+y2=4被直线l :ax +by +c =0所截得的弦长为24-⎝ ⎛⎭⎪⎫c a2+b22,由于a2+b2=c2,所以所求弦长为2 3. 答案:239.解析:∵点P 在直线x +y -22=0上,∴可设点P(x0,-x0+22),且其中一个切点为M.∵两条切线的夹角为60°,∴∠OPM =30°.故在Rt △OPM 中,有OP =2OM =2.由两点间的距离公式得OP =x20+-x0+222=2,解得x0= 2.故点P 的坐标是( 2,2).答案:( 2, 2) 10.解:(1)设直线MQ 交AB 于点P ,则|AP|=223,又|AM|=1,AP ⊥MQ ,AM ⊥AQ ,得|MP|=12-89=13, 又∵|MQ|=|MA|2|MP|,∴|MQ|=3. 设Q(x,0),而点M(0,2),由x2+22=3,得x =±5,则Q 点的坐标为(5,0)或(-5,0).从而直线MQ 的方程为2x +5y -25=0或2x -5y +25=0.(2)证明:设点Q(q,0),由几何性质,可知A ,B 两点在以Q M 为直径的圆上,此圆的方程为x(x -q)+y(y -2)=0,而线段AB 是此圆与已知圆的公共弦,相减可得AB 的方程为qx -2y +3=0,所以直线AB 恒过定点⎝ ⎛⎭⎪⎫0,32. 11.解:(1)证明:由题设知,圆C 的方程为(x -t)2+⎝ ⎛⎭⎪⎫y -2t 2=t2+4t2, 化简得x2-2tx +y2-4ty =0, 当y =0时,x =0或2t ,则A(2t,0);当x =0时,y =0或4t ,则B ⎝ ⎛⎭⎪⎫0,4t , 所以S △AOB =12|OA|·|OB| =12|2t|·⎪⎪⎪⎪⎪⎪4t =4为定值. (2)∵|OM|=|ON|,则原点O 在MN 的中垂线上,设MN 的中点为H ,则CH ⊥MN , ∴C 、H 、O 三点共线,则直线OC 的斜率k =2t t =2t2=12,∴t =2或t =-2. ∴圆心为C(2,1)或C(-2,-1),∴圆C 的方程为(x -2)2+(y -1)2=5或(x +2)2+(y +1)2=5,由于当圆方程为(x +2)2+(y +1)2=5时,直线2x +y -4=0到圆心的距离d >r ,此时不满足直线与圆相交,故舍去,∴圆C 的方程为(x -2)2+(y -1)2=5.12.解:(1)圆的方程可写成(x -6)2+y2=4,所以圆心为Q(6,0).过P(0,2)且斜率为k 的直线方程为y =kx +2,代入圆的方程得x2+(kx +2)2-12x +32=0,整理得(1+k2)x2+4(k -3)x +36=0.①直线与圆交于两个不同的点A 、B 等价于Δ=[4(k -3)]2-4×36(1+k2)=42(-8k2-6k)>0,解得-34<k<0,即k 的取值范围为⎝ ⎛⎭⎪⎫-34,0. (2)设A(x1,y1)、B(x2,y2) 则OA +OB =(x1+x2,y1+y2),由方程①得x1+x2=-4k -31+k2.②又y1+y2=k(x1+x2)+4.③因P(0,2)、Q(6,0),PQ =(6,-2),所以OA +OB 与PQ 共线等价于-2(x1+x2)=6(y1+y2),将②③代入上式,解得k =-34. 而由(1)知k ∈⎝ ⎛⎭⎪⎫-34,0,故没有符合题意的常数k. B 级1.解析:由两圆的方程x2+y2-10x -10y =0,x2+y2+6x -2y -40=0,相减并整理得公共弦所在直线的方程为2x +y -5=0.圆心(5,5)到直线2x +y -5=0的距离为105=25,弦长的一半为50-20=30,得公共弦长为230.答案:2x +y -5=02302.解析:容易判断,点(3,5)在圆内部,过圆内一点最长的弦是直径,过该点与直径垂直的弦最短,因此,过(3,5)的弦中,最长为10,最短为46,故公差最大为10-4610=5-265. 答案:5-2653.解:(1)易得B(1,3),A(-1,-3),设圆M 的方程为(x -a)2+y2=a2(a >0),将点B(1,3)代入圆M 的方程得a =2,所以圆M 的方程为(x -2)2+y2=4,因为点A(-1,-3)在准线l 上,所以p 2=1,p =2,所以抛物线C 的方程为y2=4x.(2)由(1)得,M(2,0),F(1,0),设点P(x ,y),则PM ,=(2-x ,-y),PF ,=(1-x ,-y),又点P 在抛物线y2=4x 上,所以PM ,·PF ,=(2-x)(1-x)+y2=x2-3x +2+4x =x2+x +2,因为x ≥0,所以PM ,·PF ,≥2,即PM ,·PF ,的最小值为2.(3)证明:设点Q(-1,m),则|QS|=|QT|=m2+5,以Q 为圆心,m2+5为半径的圆的方程为(x +1)2+(y -m)2=m2+5,即x2+y2+2x -2my -4=0,①又圆M 的方程为(x -2)2+y2=4,即x2+y2-4x =0,②由①②两式相减即得直线ST 的方程3x -my -2=0,显然直线ST 恒过定点⎝ ⎛⎭⎪⎫23,0.。
(整理版)高考数学小题狂做冲刺训练(详细解析)

高考数学小题狂做冲刺训练〔详细解析〕、选择题〔本大题共10小题,每题5分,共50分。
在每题给出的四个选项中,只有一个选项是符合题目要求的〕 1.点P 在曲线323+-=x x y 上移动,设点P 处切线的倾斜角为α,那么角α的取值范围是( )A.[0,2π]B.[0,2π〕∪[43π,π) C.[43π,π) D.(2π,43π]解析:∵y′=3x 2-1,故导函数的值域为[-1,+∞). ∴切线的斜率的取值范围为[-1,+∞〕. 设倾斜角为α,那么tanα≥-1. ∵α∈[0,π),∴α∈[0,2π)∪[43π,π).答案:B2.假设方程x 2+ax+b =0有不小于2的实根,那么a 2+b 2的最小值为( )A.3B.516 C.517 D.518 解析:将方程x 2+ax+b =0看作以(a,b)为动点的直线l:xa+b+x 2=0的方程,那么a 2+b 2的几何意义为l 上的点(a,b)到原点O(0,0)的距离的平方,由点到直线的距离d 的最小性知a 2+b 2≥d 2=211)1(1)100(2224222-+++=+=+++x x x x x x (x ≥2), 令u =x 2+1,易知21)(-+=u u u f (u ≥5)在[5,+∞)上单调递增,那么f(u)≥f(5)=516, ∴a 2+b 2的最小值为516.应选B. 答案:B3.国际上通常用恩格尔系数来衡量一个国家或地区人民生活水平的状况,它的计算公式为yxn =(x:人均食品支出总额,y:人均个人消费支出总额),且y =2x+475.各种类型家庭情相同的情况下人均少支出75元,那么该家庭属于( )解析:设1998年人均食品消费x 元,那么人均食品支出:x(1-7.5%)=92.5%x,人均消费支出:2×92.5%x+475,由题意,有2×92.5%x+475+75=2x+475,∴x=500. 此时,14005.462475%5.922%5.92=+⨯=x x x ≈0.3304=33.04%,应选D.答案:D4.(海南、宁夏高考,文4)设f(x)=xlnx,假设f′(x 0)=2,那么x 0等于( )2B.eC.22ln 解析:f′(x)=lnx+1,令f′(x 0)=2, ∴lnx 0+1=2.∴lnx 0=1.∴x 0=e. 答案:B5.n =log n+1 (n+2)(n∈N *).定义使a 1·a 2·a 3·…·a k 为整数的实数k 为奥运桔祥数,那么在区间[1,2 008]内的所有奥运桔祥数之和为( )A.1 004B.2 026C.4 072D.2 044解析:a n =log n+1 (n+2)=)1lg()2lg(++n n ,a 1·a 2·a 3·…·a k =2lg )2lg()1lg()2lg(4lg 5lg 3lg 4lg 2lg 3lg +=++••k k k . 由题意知k+2=22,23,…,210,∴k=22-2,23-2,…,210-2.∴S=(22+23+…+210)-2×9=20261821)21(49=---. 答案:B6.从2 004名学生中选取50名组成参观团,假设采用下面的方法选取,先用简单随机抽样法从2 004人中剔除4人,剩下的 2 000人再按系统抽样的方法进行,那么每人入选的概率〔 〕A .不全相等B .均不相等C .都相等且为002125D .都相等且为401解析:抽样的原那么是每个个体被抽到的概率都相等,所以每人入选的概率为002125. 答案:C7.将数字1,2,3,4,5,6拼成一列,记第i 个数为a i 〔i =1,2,…,6〕,假设a 1≠1,a 3≠3,5≠5,a 1<a 3<a 5,那么不同的排列方法种数为〔 〕A .18B .30C .36D .48 解析:∵a 1≠1且a 1<a 3<a 5,∴〔1〕当a 1=2时,a 3为4或5,a 5为6,此时有12种; 〔2〕当a 1=3时,a 3仍为4或5,a 5为6,此时有12种; 〔3〕当a 1=4时,a 3为5,a 5为6,此时有6种. ∴共30种. 答案:B8.在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.假设从中任选3人,那么选出的火炬手的编号能组成以3为公差的等差数列的概率为〔 〕A .511 B .681 C .3061 D .4081 解析:属于古典概型问题,根本领件总数为318C =17×16×3,选出火炬手编号为a n =a 1+3〔n -1〕〔1≤n ≤6〕,a 1=1时,由1,4,7,10,13,16可得4种选法; a 1=2时,由2,5,8,11,14,17可得4种选法; a 1=3时,由3,6,9,12,15,18可得4种选法. 故所求概率68131617444444318=⨯⨯++=++=C P . 答案:B9.复数i 3(1+i)2等于( )A.2B.-2 C解析:i 3(1+i)2=-i(2i)=-2i 2=2. 答案:A 10.(全国高考卷Ⅱ,4)函数x xx f -=1)(的图象关于( ) A.y 轴对称 B.直线y =-x 对称 C.坐标原点对称 D.直线y =x 对称 解析: x xx f -=1)(是奇函数,所以图象关于原点对称. 答案:C、填空题〔本大题共5小题,每题5分,共25分〕11.垂直于直线2x-6y+1=0且与曲线y=x 3+3x 2-5相切的直线方程为___________________.解析:与直线2x-6y+1=0垂直的直线的斜率为k=-3,曲线y=x 3+3x 2-5的切线斜率为y ′=3x 2+6x.依题意,有y ′=-3,即3x 2+6x=-3,得x=-1.当x=-1时,y=(-1)3+3·(-1)2-5=-3.故所求直线过点(-1,-3),且斜率为-3,即直线方程为y+3=-3(x+1), 即3x+y+6=0. 答案:3x+y+6=0 12.函数13)(--=a axx f (a≠1).假设f(x)在区间(0,1]上是减函数,那么实数a 的取值范围是______________. 解析:由03)1(2)('<--=axa a x f ,⎪⎩⎪⎨⎧<->-②,0)1(2①,03a aax由①,得a <x3≤3. 由②,得a <0或a >1,∴当a =3时,f(x)在x∈(0,1)上恒大于0,且f(1)=0,有f(x)>f(1). ∴a 的取值范围是(-∞,0)∪(1,3]. 答案:(-∞,0)∪(1,3] 13.平面上三点A 、B 、C满足3||=AB ,5||=CA ,4||=BC ,那么AB CA CA BC BC AB •+•+•的值等于________________.解析:由于0=++CA BC AB ,∴)(2||||||)(2222AB CA CA BC BC AB CA BC AB CA BC AB •+•+•+++=++0)(225169=•+•+•+++=AB CA CA BC BC AB ,即可求值.答案:-2514.设一次试验成功的概率为p,进行100次独立重复试验,当p=_________________时,成功次数的标准差的值最大,其最大值为___________________________________.解析:4)2(2n q p n npq D =+≤=ξ,等号在21==q p 时成立,此时Dξ=25,σξ=5. 答案:215 15.设z 1是复数,112z i z z -=(其中1z 表示z 1的共轭复数),z 2的实部是-1,那么z 2的虚部为___________________.解析:设z 1=x+yi(x,y ∈R),那么yi x z -=1. ∴z 2=x+yi-i(x-yi)=x-y+(y-x)i. ∵x-y=-1, ∴y-x=1. 答案:1。
高考数学小题专项训练及答案解析

小题专项训练小题专项训练1 集合与简易逻辑一、选择题1.(2019年河南模拟)已知集合A ={x |x 2<4},B ={x |x <2-x },则A ∪B =( )A .{x |-2<x <2}B .{x |x <2}C .{x |x >-1}D .{x |x >-2}【答案】B【解析】由x 2<4得-2<x <2,则A ={x |-2<x <2}.由x <2-x 得x <1,则B ={x |x <1}.所以A ∪B ={x |x <2}.故选B .2.命题p :“∀x ∈N *,⎝ ⎛⎭⎪⎫12x ≤12”的否定为( )A .∀x ∈N *,⎝ ⎛⎭⎪⎫12x >12B .∀x ∉N *,⎝ ⎛⎭⎪⎫12x >12C .∃x 0∉N *,⎝ ⎛⎭⎪⎫12x 0>12D .∃x 0∈N *,⎝ ⎛⎭⎪⎫12x 0>12【答案】D【解析】命题p 的否定是把“∀”改成“∃”,再把“⎝ ⎛⎭⎪⎫12x ≤12”改为“⎝ ⎛⎭⎪⎫12x 0>12”即可. 3.若集合A ={2,3,4},B ={x |x =n ·m ,m ,n ∈A ,m ≠n },则集合B 中元素个数为( )A .3B .4C .5D .6【答案】A【解析】由题意,B 中的元素有:2×3=6,2×4=8,3×4=12,所以B ={6,8,12}.故选A .4.(2019年浙江模拟)设a ,b 是两个平面向量,则“a =b ”是“|a|=|b|”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】相等向量的模一定相等,模相等的向量不一定相等(因为方向可能不同),所以“a=b”是“|a|=|b|”的充分不必要条件.故选A.5.(2018年山东济宁模拟)设全集U=A∪B,定义A-B={x|x∈A,且x∉B},集合A,B分别用圆表示,则下列图中阴影部分表示A -B的是()A BC D【答案】C【解析】A-B={x|x∈A,且x∉B},即A-B表示集合A中的元素去掉集合A∩B中的元素.故选C.6.下列命题正确的是()A.“x<1”是“x2-3x+2>0”的必要不充分条件B.若给定命题p:∃x∈R,x2+x-1<0,则¬p:∀x∈R,x2+x -1≥0C.若p∧q为假命题,则p,q均为假命题D.命题“若x2-3x+2=0,则x=2”的否命题为“若x2-3x+2=0,则x≠2”【答案】B【解析】由x<1,可得x2-3x+2>0,而由x2-3x+2>0,可得x<1或x>2,所以“x<1”是“x2-3x+2>0”的充分不必要条件,A错误;易知B正确;C中还有可能p与q一真一假,C错误;D中条件“若x2-3x+2=0”也应该否定.故选B.7.设集合A={x|y=lg(-x2+x+2)},B={x|x-a>0},若A⊆B,则实数a的取值范围是()A.(-∞,2)B.(-∞,2]C.(-∞,-1)D.(-∞,-1]【答案】D【解析】A={x|y=lg(-x2+x+2)}={x|-1<x<2},B={x|x>a}.因为A⊆B,所以a≤-1.8.(2019年四川成都模拟)命题p:∀x∈R,x2+1>0,命题q:∃θ∈R,sin2θ+cos2θ=1.5,则下列命题中是真命题的是() A.p∧q B.(¬p)∧qC.(¬p)∨q D.p∨(¬q)【答案】D【解析】x∈R时,x2+1>0恒成立,故p是真命题.对任意θ∈R,sin2θ+cos2θ=1,不可能等于1.5,故q是假命题.所以p∧q,(¬p)∧q,(¬p)∨q都是假命题,p∨(¬q)是真命题.故选D.9.(2019年浙江模拟)设a>0,b>0,则“lg(ab)>0”是“lg(a+b)>0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】当lg(ab)>0时,ab>1,结合a>0,b>0可知a,b中至少有一个大于1,则a+b>1,可以推出lg(a+b)>0.当lg(a+b)>0时,a+b>1,则ab>1不一定成立,如a=b=23时,a+b>1但ab<1,所以推不出lg(ab)>0.综上所述,“lg(ab)>0”是“lg(a+b)>0”的充分不必要条件.10.(2018年山东师大附中模拟)已知函数f(x)=x2-2x+3,g(x)=kx-1,则“|k|≤1”是“f(x)≥g(x)在R上恒成立”的() A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】若f(x)≥g(x),则x2-(2+k)x+4≥0,所以f(x)≥g(x)在R上恒成立⇔(2+k)2-16≤0⇔-6≤k≤2;而|k|≤1⇔-1≤k≤1.所以“|k|≤1”是“f(x)≥g(x)在R上恒成立”的充分不必要条件.故选A.11.设集合S={A0,A1,A2,A3},在S上定义运算⊕:A i⊕A j =A k,k为i+j除以4的余数(i,j=0,1,2,3),则满足关系式(x⊕x)⊕A2=A0的x(x∈S)的个数为()A.4B.3C.2D.1【答案】C【解析】因为x∈S={A0,A1,A2,A3},故x的取值有四种情况.若x=A0,根据定义得(x⊕x)⊕A2=A0⊕A2=A2,不符合题意,同理可以验证x=A1,x=A2,x=A3三种情况,其中x=A1,x=A3符合题意.故选C.12.在下列结论中,正确的是()①命题p:“∃x0∈R,x20-2≥0”的否定形式为¬p:“∀x∈R,x2-2<0”;②O 是△ABC 所在平面上一点,若OA →·OB →=OB →·OC →=OC →·OA →,则O 是△ABC 的垂心;③“M >N ”是“⎝ ⎛⎭⎪⎫23M >⎝ ⎛⎭⎪⎫23N ”的充分不必要条件;④命题“若x 2-3x -4=0,则x =4”的逆否命题为“若x ≠4,则x 2-3x -4≠0”.A .①③B .②④C .①②③D .①②④【答案】D【解析】由特称(存在性)命题与全称命题的关系可知①正确;∵OA→·OB →=OB →·OC →,∴OB →·(OA →-OC →)=0,即OB →·CA →=0,∴OB →⊥CA →,同理可知OA→⊥BC →,OC →⊥BA →,故点O 是△ABC 的垂心,②正确;∵y =⎝ ⎛⎭⎪⎫23x 是减函数,∴当M >N 时,⎝ ⎛⎭⎪⎫23M <⎝ ⎛⎭⎪⎫23N ,当⎝ ⎛⎭⎪⎫23M >⎝ ⎛⎭⎪⎫23N 时,M <N ,∴“M >N ”是“⎝ ⎛⎭⎪⎫23M >⎝ ⎛⎭⎪⎫23N”的既不充分也不必要条件,③错误;由逆否命题的写法可知④正确.综上,正确的结论是①②④.二、填空题13.已知A ={y |y =10x -1},B ={x |y =lg(4-x 2)},则(∁R A )∩B =________.【答案】(-2,-1]【解析】∵A ={y |y =10x -1}={y |y >-1}, ∴∁R A ={y |y ≤-1}.又B ={x |-2<x <2}, ∴(∁R A )∩B =(-2,-1].14.(2018年广西防城港期末)若“∀x ∈⎣⎢⎡⎦⎥⎤0,π3,m ≥2tan x ”是真命题,则实数m 的最小值为________.【答案】23【解析】当x ∈⎣⎢⎡⎦⎥⎤0,π3时,2tan x 的最大值为2tan π3=23,∴m ≥23,实数m 的最小值为2 3.15.已知集合A ={x |1≤x <5},C ={x |-a <x ≤a +3},若C ∩A =C ,则a 的取值范围是________.【答案】(-∞,-1]【解析】由C ∩A =C ,可得C ⊆A .①当C =∅时,满足C ⊆A ,此时-a ≥a +3,解得a ≤-32;②当C ≠∅时,要使C ⊆A ,需满足⎩⎪⎨⎪⎧-a <a +3,-a ≥1,a +3<5,解得-32<a ≤-1.由①②得a ≤-1.16.设命题p :2x -1x -1<0;命题q :关于x 的不等式x 2-(2a +1)x+a (a +1)≤0.若p 是q 的充分不必要条件,则实数a 的取值范围是________.【答案】⎣⎢⎡⎦⎥⎤0,12【解析】由2x -1x -1<0,得(2x -1)(x -1)<0,解得12<x <1.由x 2-(2a+1)x +a (a +1)≤0,解得a ≤x ≤a +1.由题意得⎝ ⎛⎭⎪⎫12,1[a ,a +1],故⎩⎨⎧a ≤12,a +1≥1,解得0≤a ≤12. 小题专项训练2 函数的图象与性质一、选择题1.函数f (x )=1x -1+x 的定义域为( )A .[0,+∞)B .(1,+∞)C .[0,1)∪(1,+∞)D .[0,1)【答案】C【解析】由题意知x ≥0且x ≠1.故选C .2.(2019年福建厦门模拟)设函数f (x )=⎩⎪⎨⎪⎧2x ,x ≥3,f (x +1),x <3,则f (log 26)的值为( )A .3B .6C .8D .12【答案】D【解析】因为log 24<log 26<log 28,即2<log 26<3,所以f (log 26)=f (log 26+1)=2log 26+1=2log 212=12.故选D .3.(2019年北京)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m 2-m 1=52lg E 1E 2,其中星等为m k的星的亮度为E k (k =1,2).已知太阳的星等是-26.7,天狼星的星等是-1.45,则太阳与天狼星的亮度的比值为A .1010.1B .10.1C .lg 10.1D .10-10.1【答案】A【解析】设太阳的星等是m 1=-26.7,天狼星的星等是m 2=-1.45,由题意可得-1.45-(-26.7)=52lg E 1E 2,所以lg E 1E 2=10.1,则E 1E 2=1010.1.故选A .4.(2019年上海)已知ω∈R ,函数f (x )=(x -6)2·sin ωx ,存在常数a ∈R ,使得f (x +a )为偶函数,则ω可能的值为( )A .π2B .π3 C .π4D .π5【答案】C【解析】若f (x +a )为偶函数,则f (x )的图象关于直线x =a 对称.又y =(x -6)2关于x =6对称,所以a =6且y =sin ωx 也关于x =6对称.所以6ω=π2+k π,k ∈Z .当k =1时,得ω=π4.故选C .5.(2019年浙江)在同一直角坐标系中,函数y =1a x ,y =log a ⎝ ⎛⎭⎪⎫x +12(a >0且a ≠1)的图象可能是( )A B C D【答案】D【解析】当0<a <1时,y =1a x 是增函数,图象恒过(0,1),y =log a⎝ ⎛⎭⎪⎫x +12是减函数,图象恒过⎝ ⎛⎭⎪⎫12,0,排除A ,B ;当a >1时,y =1a x 是减函数,图象恒过(0,1),y =log a ⎝ ⎛⎭⎪⎫x +12是增函数,图象恒过⎝ ⎛⎭⎪⎫12,0,排除C .故选D .6.若f (x )=⎩⎪⎨⎪⎧2x -3,x >0,g (x ),x <0,是奇函数,则f (g (-2))的值为( )A .1B .-1C .52 D .-25【答案】A【解析】因为f (x )是奇函数,所以当x <0时,g (x )=-12x +3.所以g (-2)=-1,f (g (-2))=f (-1)=g (-1)=1.7.函数y =f (x )在区间[0,2]上单调递增,且函数f (x +2)是偶函数,则下列结论成立的是( )A .f (1)<f ⎝ ⎛⎭⎪⎫52<f ⎝ ⎛⎭⎪⎫72B .f ⎝ ⎛⎭⎪⎫72<f (1)<f ⎝ ⎛⎭⎪⎫52C .f ⎝ ⎛⎭⎪⎫72<f ⎝ ⎛⎭⎪⎫52<f (1)D .f ⎝ ⎛⎭⎪⎫52<f (1)<f ⎝ ⎛⎭⎪⎫72【答案】B【解析】∵f (x +2)是偶函数,∴f (x +2)=f (-x +2),即f (x )的图象关于x =2对称.又∵y =f (x )在区间[0,2]上单调递增,∴y =f (x )在区间[2,4]上单调递减.∵f (1)=f (3),72>3>52,∴f ⎝ ⎛⎭⎪⎫72<f (3)<f ⎝ ⎛⎭⎪⎫52,即f ⎝ ⎛⎭⎪⎫72<f (1)<f ⎝ ⎛⎭⎪⎫52.8.如图,动点P 在正方体ABCD -A 1B 1C 1D 1的体对角线BD 1上,过点P 作垂直于平面BB 1D 1D 的直线,与正方体的表面相交于M ,N 两点,设BP =x ,MN =y ,则函数y =f (x )的图象大致是( )ABC D【答案】B【解析】设正方体的棱长为1,当P 移动到体对角线BD 1的中点O 时,函数y =MN =AC =2取得唯一的最大值,排除A ,C ;当P 在BO 上时,分别过M ,N ,P 作底面的垂线,垂足分别为M 1,N 1,P 1,则y =MN =M 1N 1=2BP 1=2x cos ∠D 1BD =263x ,是一次函数,排除D .故选B .9.若函数f (x )=x 2-2ax +a 在区间(-∞,1)上有最小值,则函数g (x )=f (x )x 在区间(1,+∞)上一定( )A .有最大值B .有最小值C .是增函数D .是减函数【答案】C【解析】∵f (x )=x 2-2ax +a 在区间(-∞,1)上有最小值,图象开口向上,对称轴为x =a ,∴a <1.g (x )=f (x )x =x +ax -2a .若a ≤0,则g (x )=x +ax -2a 在(-∞,0),(0,+∞)上单调递增;若0<a <1,则g (x )=x +ax -2a 在(a ,+∞)上单调递增,故g (x )在(1,+∞)上单调递增.综上可得g (x )=x +ax -2a 在(1,+∞)上一定是增函数.10.(2018年湖南名校高三联考)已知函数f (x )=(e x -e -x )x 2,若实数m 满足f (log 3m )-f (log 13m )≤2f (1),则实数m 的取值范围为( )A .(0,3]B .⎣⎢⎡⎦⎥⎤13,3 C .(0,9] D .⎝ ⎛⎭⎪⎫0,13∪(3,+∞) 【答案】A【解析】由题意得函数的定义域为R ,∵f (-x )=(e -x -e x )(-x )2=-f (x ),∴f (x )为奇函数.又当x ≥0时,f ′(x )=(e x +e -x )x 2+(e x -e-x)·2x ≥0,∴f (x )在[0,+∞)上单调递增,则在R 上奇函数f (x )为增函数,∴f (log 3m )-f (log 13m )=f (log 3m )-f (-log 3m )=2f (log 3m )≤2f (1),即f (log 3m )≤f (1),∴log 3m ≤1,解得0<m ≤3.故选A .11.已知定义在D =[-4,4]上的函数f (x )=⎩⎪⎨⎪⎧|x 2+5x +4|,-4≤x ≤0,2|x -2|,0<x ≤4,若存在x 1,x 2∈D ,对任意x ∈D ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最大值与最小值之和为( )A .7B .8C .9D .10【答案】C【解析】作出f (x )的图象如图所示,由任意x ∈D ,f (x 1)≤f (x )≤f (x 2),知f (x 1),f (x 2)分别为f (x )的最小值和最大值,由图可知|x 1-x 2|max =8,|x 1-x 2|min =1,所以|x 1-x 2|的最大值与最小值之和为9.12.(2019年新课标Ⅱ)设函数f (x )的定义域为R ,满足f (x +1)=2f (x ),且当x ∈(0,1]时,f (x )=x (x -1).若对任意x ∈(-∞,m ],都有f (x )≥-89,则m 的取值范围是A .⎝ ⎛⎦⎥⎤-∞,94 B .⎝ ⎛⎦⎥⎤-∞,73 C .⎝ ⎛⎦⎥⎤-∞,52 D .⎝ ⎛⎦⎥⎤-∞,83 【答案】B【解析】因为f (x +1)=2f (x ),所以f (x )=2f (x -1).因为x ∈(0,1]时,f (x )=x (x -1)∈⎣⎢⎡⎦⎥⎤-14,0,所以x ∈(1,2]时,x -1∈(0,1],f (x )=2f (x-1)=2(x -1)(x -2)∈⎣⎢⎡⎦⎥⎤-12,0,所以x ∈(2,3]时,x -1∈(1,2],f (x )=2f (x -1)=4(x -2)(x -3)∈[-1,0].f (x )的大致图象如图所示.由4(x -2)(x -3)=-89,解得x =73或x =83.若对任意x ∈(-∞,m ],都有f (x )≥-89,则由图象可知m ≤73.二、填空题13.已知函数f (x )=x 2+ax (a >0)在(2,+∞)上为单调递增函数,则实数a 的取值范围为________.【答案】(0,4]【解析】f (x )=x +a x ,则f ′(x )=1-ax 2.由题意知在(2,+∞)上f ′(x )≥0,所以a ≤x 2,则0<a ≤4.14.已知函数f (x )是定义在R 上且周期为4的偶函数,当x ∈[2,4]时,f (x )=⎪⎪⎪⎪⎪⎪log 4⎝ ⎛⎭⎪⎫x -32,则f ⎝ ⎛⎭⎪⎫12的值为________.【答案】12【解析】∵f (x )是定义在R 上且周期为4的偶函数,∴f ⎝ ⎛⎭⎪⎫12=f ⎝⎛⎭⎪⎫-12=f ⎝⎛⎭⎪⎫4-12=f ⎝ ⎛⎭⎪⎫72.又当x ∈[2,4]时,f (x )=⎪⎪⎪⎪⎪⎪log 4⎝ ⎛⎭⎪⎫x -32,∴f ⎝ ⎛⎭⎪⎫12=f ⎝ ⎛⎭⎪⎫72=⎪⎪⎪⎪⎪⎪log 4⎝ ⎛⎭⎪⎫72-32=|log 42|=12.15.(2018年新课标Ⅲ)已知函数f (x )=ln(1+x 2-x )+1,f (a )=4,则f (-a )=________.【答案】-2【解析】f (a )+f (-a )=ln(1+a 2-a )+ln(1+a 2+a )+2=2,则f (-a )=2-f (a )=2-4=-2.16.已知函数f (x )的定义域为A ,若x 1,x 2∈A 且f (x 1)=f (x 2)时总有x 1=x 2,则称f (x )为单函数,例如函数f (x )=2x +1(x ∈R )是单函数.给出下列命题:①函数f(x)=x2(x∈R)是单函数;②指数函数f(x)=2x(x∈R)是单函数;③若f(x)为单函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2);④在定义域上具有单调性的函数一定是单函数.其中真命题的序号是________.【答案】②③④【解析】对于①,当x1=2,x2=-2时,f(x1)=4=f(x2),①错误;对于②,f(x)=2x为单调递增函数,②正确;③④显然正确.故真命题的是②③④.小题专项训练3不等式一、选择题1.(2019年山东临沂模拟)已知集合A={x|x2<x+2},B={x|x<a},若A⊆B,则实数a的取值范围为()A.(-∞,-1]B.(-∞,2]C.[2,+∞)D.[-1,+∞)【答案】C【解析】解不等式x2<x+2,得-1<x<2,则A={x|x2<x+2}={x|-1<x<2}.又B={x|x<a},要使A⊆B,则a≥2.故选C.2.(2018年山西运城模拟)若a>b>0,c<d<0,则一定有()A.ac>bd B.ac<bdC.ad<bc D.ad>bc【答案】B3.(2019年北京)若x,y满足|x|≤1-y,且y≥-1,则3x+y的最大值为()A.-7B.1C .5D .7【答案】C【解析】由|x |≤1-y ,可得y -1≤x ≤1-y ,即x -y +1≥0且x +y -1≤0.作出不等式组⎩⎪⎨⎪⎧x -y +1≥0,x +y -1≤0,y ≥-1表示的平面区域,解相应的方程组可得A (2,-1),B (-2,-1),C (0,1).令z =3x +y ,化为y =-3x +z ,由图可知,当直线y =-3x +z 过点A (2,-1)时,z 有最大值为3×2-1=5.故选C .4.(2019年湖南模拟)周长为20的矩形绕其一边旋转形成一个圆柱,该圆柱的侧面积的最大值是( )A .25πB .50πC .100πD .200π【答案】B【解析】设矩形的两邻边长分别为x ,y 且y 为圆柱的高,则x+y =10,圆柱的侧面积S =2πxy ≤2π⎝ ⎛⎭⎪⎫x +y 22=50π,当x =y =5时等号成立,所以该圆柱侧面积的最大值为50π.故选B .5.若关于x 的不等式x 2-2ax -8a 2<0(a >0)的解集为(x 1,x 2),且x 2-x 1=15,则a 的值为( )A .52 B .72 C .152 D .172【答案】A【解析】由x 2-2ax -8a 2<0,得(x +2a )(x -4a )<0.因为a >0,所以不等式的解集为(-2a,4a ),即x 2=4a ,x 1=-2a .由x 2-x 1=15,得4a -(-2a )=15,解得a =52.6.若实数x ,y 满足条件⎩⎪⎨⎪⎧x ≥1,x -2y +3≥0,y ≥x ,则z =yx +1的最小值为( )A .1B .34 C .13 D .12【答案】D【解析】作出实数x ,y 满足条件的平面区域如图.z =yx +1的几何意义是点P (x ,y )与点D (-1,0)连线的斜率.易求得A (1,1),由图可知当P 经过A 时,z 取得最小值11+1=12.7.已知a >0,函数f (x )=ax 2-(a 2+1)x +a ,若f (x )<0在x ∈(1,2)时恒成立,则实数a 的取值范围是( )A .⎝ ⎛⎦⎥⎤0,12B .⎝ ⎛⎦⎥⎤0,12∪[2,+∞)C .(0,2]D .[2,+∞)【答案】B【解析】由题意知⎩⎪⎨⎪⎧f (1)≤0,f (2)≤0,解得0<a ≤12或a ≥2.8.已知正数x ,y 满足x +y =1,则4x +2+1y +1的最小值为( )A .1B .2C .94 D .92【答案】C【解析】令x +2=a ,y +1=b ,则a +b =4(a >2,b >1),所以4x +2+1y +1=4a +1b =14(a +b )⎝ ⎛⎭⎪⎫4a +1b =14⎝ ⎛⎭⎪⎫5+4b a +a b ≥14(5+4)=94,当且仅当a =83,b =43,即x =23,y =13时取等号,所以4x +2+1y +1的最小值为94.9.(2018年甘肃兰州诊断)设变量x ,y 满足不等式组⎩⎪⎨⎪⎧x +y ≥3,x -y ≥-1,2x -y ≤3,则x 2+y 2的最小值是( )A .92B .25C .322 D .5【答案】A【解析】约束条件所表示的可行域为一个三角形,而目标函数可视为可行域内的点到原点的距离的平方,其距离的最小值为原点到直线x +y =3的距离.∵原点到直线x +y =3的距离为32,∴x 2+y 2的最小值为92.10.某厂生产的甲、乙两种产品每件可获利润分别为30元、20元,生产甲产品每件需用A 原料2千克、B 原料4千克,生产乙产品每件需用A 原料3千克、B 原料2千克.A 原料每日供应量限额为60千克,B 原料每日供应量限额为80千克.要求每天生产的乙种产品不能比甲种产品多10件以上,则合理安排生产可使每日获得的最大利润为( )A .500元B .550元C .600元D .650元【答案】D【解析】设每日生产甲、乙两种产品分别为x ,y 件,则x ,y 满足⎩⎪⎨⎪⎧2x +3y ≤60,4x +2y ≤80,y -x ≤10,x ∈N ,y ∈N .设每日获得的利润z =30x +20y ,画出不等式组所表示的平面区域如图所示.根据目标函数z =30x +20y 的几何意义知,当目标函数对应的直线20y +30x -z =0,过B 点时z 取最大值.由⎩⎪⎨⎪⎧2x +3y =60,4x +2y =80,解得B (15,10),所以z max =30×15+20×10=650.故选D .11.(2018年河北邢台检测)若a ,b 是正数,直线2ax +by -2=0被圆x 2+y 2=4截得的弦长为23,则t =a 1+2b 2取得最大值时a 的值为( )A .12B .32 C .34 D .34【答案】C【解析】∵圆心到直线的距离d =24a 2+b 2,则直线被圆截得的弦长L =2r 2-d 2=24-44a 2+b 2=23,∴4a 2+b 2=4.t =a 1+2b 2=122×(22a )×1+2b 2≤122×12×[](22a )2+(1+2b 2)2=142 (8a 2+1+2b 2)=942,当且仅当⎩⎪⎨⎪⎧8a 2=1+2b 2,4a 2+b 2=4时等号成立,此时a =34.12.(2018年江苏联考)已知对满足x +y +4=2xy 的任意正实数x ,y ,都有x 2+2xy +y 2-ax -ay +1≥0,则实数a 的取值范围为( )A .(5,6)B .(3,4)C .(1,2)D .⎝ ⎛⎦⎥⎤-∞,174 【答案】D【解析】由x +y +4=2xy ≤(x +y )22,得(x +y )2-2(x +y )-8≥0,又x ,y 是正实数,得x +y ≥4.由x 2+2xy +y 2-ax -ay +1≥0,可得(x +y )2-a (x +y )+1≥0,则a ≤x +y +1x +y.易得当x +y =4时,x +y+1x +y取得最小值174,所以a ≤174.故选D . 二、填空题13.不等式x -12x +1≤0的解集为________.【答案】⎝ ⎛⎦⎥⎤-12,1【解析】原不等式等价于⎩⎪⎨⎪⎧(x -1)(2x +1)≤0,2x +1≠0,解得-12<x ≤1.14.(2018年广东惠州模拟)已知实数x ,y 满足⎩⎪⎨⎪⎧x +3y +5≥0,x +y -1≤0,x +a ≥0,若z =x +2y 的最小值为-4,则实数a 的值为________.【答案】2【解析】作出不等式组表示的平面区域如图中阴影部分所示,当直线z =x +2y 经过点C ⎝⎛⎭⎪⎫-a ,a -53时,z 取得最小值-4,所以-a +2×a -53=-4,解得a =2.15.(2018年江苏扬州中学检测)已知二次函数f (x )=ax 2-(a +2)x +1(a ∈Z ),且函数f (x )在(-2,-1)上恰有一个零点,则不等式f (x )>1的解集为________.【答案】(-1,0)【解析】因为f (x )=ax 2-(a +2)x +1(a ≠0),Δ=(a +2)2-4a =a 2+4>0,所以f (x )必有两个不同的零点.所以f (-2)f (-1)<0,即(6a +5)(2a +3)<0,解得-32< a <-56.又a ∈Z ,所以a =-1.不等式f (x )>1,即-x 2-x >0,解得-1<x <0.16.(2019年天津)设x >0,y >0,x +2y =5,则(x +1)(2y +1)xy 的最小值为________.【答案】43【解析】(x +1)(2y +1)xy =2xy +x +2y +1xy =2xy +6xy =2xy +6xy≥22xy ·6xy =43,当且仅当2xy =6xy ,即⎩⎪⎨⎪⎧x =3,y =1或⎩⎨⎧x =2,y =32时等号成立,所以(x +1)(2y +1)xy的最小值为4 3.小题专项训练4 函数与导数一、选择题1.(2019年天津模拟)下列求导运算正确的是( ) A .(cos x )′=sin x B .(log 2x )′=xln 2 C .(2x )′=12xD .(3x )′=3x log 3e【答案】C【解析】(cos x )′=-sin x ,A 错误;(log 2x )′=1x ln 2,B 错误;(2x )′=2(x )′=2×12·1x =12x ,C 正确;(3x )′=3x ln 3,D 错误.故选C .2.(2018年江西模拟)已知函数f (x )=ln(ax -1)的导函数是f ′(x ),且f ′(2)=2,则实数a 的值为( )A .12 B .1 C .34 D .23【答案】D【解析】因为f (x )=ln(ax -1),所以f ′(x )=aax -1.所以f ′(2)=a 2a -1=2,解得a =23.3.(2019年福建宁德模拟)函数f (x )=3+x ln x 的单调递减区间是( )A .⎝ ⎛⎭⎪⎫1e ,eB .⎝ ⎛⎭⎪⎫0,1eC .⎝ ⎛⎭⎪⎫-∞,1eD .⎝ ⎛⎭⎪⎫1e ,+∞【答案】B【解析】由f (x )=3+x ln x ,得定义域为(0,+∞)且f ′(x )=ln x +1,令ln x +1<0,解得0<x <1e .故选B .4.已知函数y =f (x )满足f (1)=2,f ′(1)=-1,则曲线g (x )=e x f (x )在x =1处的切线斜率是( )A .-eB .eC .2eD .3e【答案】B【解析】∵g ′(x )=e x f (x )+e x f ′(x ),∴g ′(1)=e f (1)+e f ′(1)=e.5.设x =-2与x =4是函数f (x )=x 3+ax 2+bx 的两个极值点,则a -b 的值为( )A .21B .-21C .27D .-27【答案】A【解析】因为f ′(x )=3x 2+2ax +b ,所以⎩⎪⎨⎪⎧-2+4=-2a 3,-2×4=b3⇒⎩⎪⎨⎪⎧a =-3,b =-24.所以a -b =-3+24=21. 6.(2019年内蒙古模拟)函数f (x )=x sin x 的图象在点⎝⎛⎭⎪⎫3π2,f ⎝ ⎛⎭⎪⎫3π2处的切线的倾斜角为( )A .π6B .π4 C .3π4 D .5π6【答案】C【解析】由f (x )=x sin x ,得f ′(x )=sin x +x cos x ,则f ′⎝⎛⎭⎪⎫3π2=sin 3π2+3π2cos 3π2=-1.由导数的几何意义可得切线的斜率k =-1,则切线的倾斜角为3π4.故选C .7.f (x )是一次函数,过点(2,3),且⎠⎛01f (x )d x =0,则函数f (x )的图象与坐标轴围成的三角形的面积为( )A .1B .12 C .14 D .18【答案】C【解析】设f (x )=kx +b (k ≠0),由题意得2k +b =3,①⎠⎛01(kx +b )d x =0,⎝ ⎛⎭⎪⎫12kx 2+bx ⎪⎪⎪10=0,即12k +b =0,②联立①②,解得k =2,b =-1,所以f (x )=2x -1.直线y =f (x )与坐标轴的交点分别为⎝ ⎛⎭⎪⎫12,0与(0,-1),所以所求的面积为12×12×1=14.8.某银行准备设一种新的定期存款业务,经预测,存款额与存款利率的平方成正比,比例系数为k (k >0),贷款的利率为4.8%,假设银行吸收的存款能全部放贷出去,若存款利率为x (x ∈(0,4.8%)),则使银行获得最大收益的存款利率为( )A .3.1%B .3.2%C .3.4%D .3.5%【答案】B【解析】依题意知存款额是kx 2,银行应支付的存款利息是kx 3,银行应获得的贷款利息是0.048kx 2,所以银行的收益是y =0.048kx 2-kx 3(0<x <0.048),故y ′=0.096kx -3kx 2.令y ′=0,解得x =0.032或x =0(舍去).当0<x <0.032时,y ′>0;当0.032<x <0.048时,y ′<0.∴当x =0.032时,y 取得极大值也是最大值,即当存款利率为3.2%时,银行可获得最大收益.9.(2018年宁夏银川二模)设f (x )是定义在非零实数集上的函数,f ′(x )为其导函数,且x >0时,xf ′(x )-f (x )<0,记a =f (20.2)20.2,b =f (0.22)0.22,c =f (log 25)log 25,则( )A .a <b <cB .c <a <bC .b <a <cD .c <b <a【答案】B【解析】令g (x )=f (x )x ,则g ′(x )=xf ′(x )-f (x )x 2.∵x >0时,xf ′(x )-f (x )<0,∴g (x )在(0,+∞)上单调递减.又log 25>log 24=2,1<20.2<2,0.22=0.04,∴log 25>20.2>0.22,∴g (log 25)<g (20.2)<g (0.22),∴c <a <b .10.已知函数f (x )=x 3+bx 2+cx +d 的图象如图所示,则函数y =log 2⎝⎛⎭⎪⎫x 2+23bx +c 3的单调递减区间为( )A .⎝⎛⎭⎪⎫12,+∞B .(3,+∞)C .⎝ ⎛⎭⎪⎫-∞,-12D .(-∞,-2)【答案】D【解析】∵f (x )=x 3+bx 2+cx +d ,∴f ′(x )=3x 2+2bx +c =3⎝ ⎛⎭⎪⎫x 2+23bx +c 3.由f (x )的图象,可得f ′(x )在(-∞,-2)上大于0且单调递减,故y =log 2⎝⎛⎭⎪⎫x 2+23bx +c 3的单调递减区间为(-∞,-2).故选D .11.(2019年浙江)设a ,b ∈R ,函数f (x )=⎩⎨⎧x ,x <0,13x 3-12(a +1)x 2+ax ,x ≥0,若函数y =f (x )-ax -b 恰有3个零点,则( )A .a <-1,b <0B .a <-1,b >0C .a >-1,b <0D .a >-1,b >0【答案】C【解析】当x <0时,由y =f (x )-ax -b =(1-a )x -b =0,得x =b 1-a,y =f (x )-ax -b 有一个零点;当x ≥0时,y =f (x )-ax -b =13x 3-12(a +1)x 2+ax -ax -b =13x 3-12(a +1)x 2-b ,y ′=x 2-(a +1)x ,当a +1≤0,即a ≤-1时,y ′≥0,y =f (x )-ax -b 在[0,+∞)上递增,y =f (x )-ax -b 最多有一个零点,不合题意;当a +1>0,即a >-1时,令y ′=0,得x =a +1,易知函数在(a +1,+∞)上递增,在(0,a +1)上递减,函数最多有2个零点.函数恰有3个零点,则y =f (x )-ax -b 在(-∞,0)上有一个零点,在(0,+∞)上有2个零点.所以b1-a <0且⎩⎨⎧-b >0,13(a +1)3-12(a +1)(a +1)2-b <0,即⎩⎨⎧b <0,-16(a +1)3<b ,得b <0,-1<a <1.故选C .12.(2019年天津)已知a ∈R .设函数f (x )=⎩⎪⎨⎪⎧x 2-2ax +2a ,x ≤1,x -a ln x ,x >1.若关于x 的不等式f (x )≥0在R 上恒成立,则a 的取值范围为( )A .[0,1]B .[0,2]C .[0,e]D .[1,e]【答案】C【解析】当x =1时,f (1)=1-2a +2a =1>0恒成立;当x <1时,f (x )=x 2-2ax +2a ≥0恒成立,等价于2a ≥x2x -1恒成立.令g (x )=x 2x -1=-x 21-x =-(1-x -1)21-x =-(1-x )2-2(1-x )+11-x=-⎝⎛⎭⎪⎫1-x +11-x -2≤-⎝ ⎛⎭⎪⎫2(1-x )·11-x -2=0,∴2a ≥g (x )max =0,∴a ≥0.当x >1时,f (x )=x -a ln x ≥0恒成立,等价于a ≤xln x 恒成立.令h (x )=xln x ,则h ′(x )=ln x -1(ln x )2.当x >e 时,h ′(x )>0,h (x )递增;当1<x <e 时,h ′(x )<0,h (x )递减.∴x =e 时,h (x )取得最小值h (e)=e.∴a ≤h (x )min =e.综上,a 的取值范围是[0,e].二、填空题13.(2019年浙江台州模拟)已知函数f (x )=13x 3-f ′(1)x 2+2x +5,则f ′(1)=__________,f ′(2)=__________.【答案】1 2【解析】显然f ′(1)为常数,则f ′(x )=x 2-2f ′(1)x +2,可得f ′(1)=1-2f ′(1)+2,解得f ′(1)=1.所以f ′(x )=x 2-2x +2,则f ′(2)=2.14.(2018年云南昆明模拟)已知函数f (x )=ax ln x +b (a ,b ∈R ),若f (x )的图象在x =1处的切线方程为2x -y =0,则a +b =________.【答案】4【解析】由题意得f ′(x )=a ln x +a ,∴f ′(1)=a .∵f (x )的图象在x =1处的切线方程为2x -y =0,∴a =2.又f (1)=b ,∴2×1-b =0,解得b =2.故a +b =4.15.已知函数f (x )=e x -ax (a ∈R ),若函数f (x )在区间[2,4]上是单调增函数,则实数a 的取值范围为________.【答案】[-e 2,+∞)【解析】∵f (x )在区间[2,4]上是单调递增函数,∴f ′(x )≥0在区间[2,4]上恒成立,即(x -1)e x +a ≥0在区间[2,4]上恒成立.记g (x )=(x -1)e x +a ,则g ′(x )=x e x .∵x ∈[2,4],∴g ′(x )>0,故g (x )在[2,4]递增,∴g (x )min =g (2)=e 2+a ≥0,解得a ≥-e 2.16.(2018年东北三校联考)已知函数f (x )=x ln x +12x 2,x 0是函数f (x )的极值点,给出以下几个命题:①0<x 0<1e ;②x 0>1e ;③f (x 0)+x 0<0; ④f (x 0)+x 0>0.其中正确的命题是________.(填出所有正确命题的序号) 【答案】①③【解析】由已知得f ′(x )=ln x +x +1(x >0),显然的f ′(x )在(0,+∞)上单调递增,且f ′⎝ ⎛⎭⎪⎫1e =1e >0,x →0时,f ′(x )<0.x 0是f (x )的极值点,∴f ′(x 0)=0,则0<x 0<1e ,①正确,②错误;∵ln x 0+x 0+1=0,∴f (x 0)+x 0=x 0ln x 0+12x 20+x 0=x 0(ln x 0+x 0+1)-12x 20=-12x 20<0,③正确,④错误.综上,①③正确.小题专项训练5 三角函数与三角恒等变换一、选择题1.若点⎝ ⎛⎭⎪⎫sin 5π6,cos 5π6在角α的终边上,则sin α的值为( ) A .-12 B .12 C .32 D .-32【答案】D【解析】因为点⎝ ⎛⎭⎪⎫sin 5π6,cos 5π6在单位圆上,所以sin α=cos 5π6=-32.2.已知α为锐角,且sin α=45,则cos(π+α)=( ) A .35 B .-35 C .-45 D .45【答案】B【解析】因为α为锐角,所以cos α=1-sin 2α=35,所以cos(π+α)=-cos α=-35.3.函数y =4sin x cos x -1的最小正周期T 和最大值M 分别为( )A .π,1B .2π,1C .π,2D .2π,2【答案】A【解析】y =4sin x cos x -1=2sin 2x -1,故其最小正周期T =2π2=π,最大值M =2-1=1.4.(2019年河南模拟)若sin ⎝⎛⎭⎪⎫α-π3=-3cos ⎝⎛⎭⎪⎫α-π6,则tan 2α=( )A .-43B .-32 C .43 D .32【答案】A【解析】由sin ⎝ ⎛⎭⎪⎫α-π3=-3cos ⎝ ⎛⎭⎪⎫α-π6,可得12sin α-32cos α=-3⎝ ⎛⎭⎪⎫32cos α+12sin α,则2sin α=-3cos α,所以tan α=-32.所以tan 2α=2tan α1-tan 2α=-4 3.故选A .5.(2018年四川泸州模拟)已知函数y =sin(2x +φ)在x =π6处取得最大值,则函数y =cos(2x +φ)的图象( )A .关于点⎝ ⎛⎭⎪⎫π6,0对称 B .关于点⎝ ⎛⎭⎪⎫π3,0对称 C .关于直线x =π6对称 D .关于直线x =π3对称【答案】A【解析】∵y =sin(2x +φ)在x =π6处取得最大值,∴sin ⎝ ⎛⎭⎪⎫π3+φ=1.∴cos ⎝ ⎛⎭⎪⎫π3+φ=0.∴y =cos(2x +φ)的图象过点⎝ ⎛⎭⎪⎫π6,0,则关于点⎝ ⎛⎭⎪⎫π6,0对称.故选A .6.已知sin β=35⎝ ⎛⎭⎪⎫π2<β<π,且sin(α+β)=cos α,则tan(α+β)=( )A .-12 B .12 C .-2 D .2【答案】C【解析】∵sin β=35,且π2<β<π,∴cos β=-45,tan β=-34.∵sin(α+β)=sin αcos β+cos αsin β=cos α,∴tan α=-12,∴tan(α+β)=tan α+tan β1-tan αtan β=-2.7.若函数f (x )=sin ωx +3cos ωx (ω>0)满足f (α)=-2,f (β)=0,且|α-β|的最小值为π2,则函数f (x )的解析式为( )A .f (x )=2sin ⎝ ⎛⎭⎪⎫x -π6B .f (x )=2sin ⎝ ⎛⎭⎪⎫x +π6C .f (x )=2sin ⎝ ⎛⎭⎪⎫x -π3D .f (x )=2sin ⎝ ⎛⎭⎪⎫x +π3 【答案】D【解析】f (x )=sin ωx +3cos ωx =2sin ⎝ ⎛⎭⎪⎫ωx +π3.因为f (α)=-2,f (β)=0,且|α-β|min =π2,所以T 4=π2,得T =2π.故ω=2πT =1,所以f (x )=2sin ⎝ ⎛⎭⎪⎫x +π3.8.(2018年山西太原模拟)已知函数f (x )=2cos ⎝ ⎛⎭⎪⎫πx 3+φ的一个对称中心是(2,0),且f (1)>f (3),要得到函数f (x )的图象,可将函数y =2cos πx3的图象( )A .向左平移12个单位长度B .向左平移π6个单位长度 C .向右平移12个单位长度 D .向右平移π6个单位长度 【答案】C【解析】∵f (x )=2cos ⎝ ⎛⎭⎪⎫πx 3+φ的一个对称中心是(2,0),∴2π3+φ=k π+π2,k ∈Z ,故可取φ=-π6,f (x )=2cos ⎝ ⎛⎭⎪⎫πx 3-π6=2cos ⎣⎢⎡⎦⎥⎤π3⎝ ⎛⎭⎪⎫x -12,满足f (1)>f (3).故选C .9.若θ∈⎣⎢⎡⎦⎥⎤π4,π2,sin 2θ=378,则sin θ=( )A .74 B .34 C .35 D .45【答案】B【解析】由已知得(sin θ+cos θ)2=1+sin 2θ=1+378,于是sin θ+cos θ=3+74.又(sin θ-cos θ)2=1-sin 2θ=1-378,所以sin θ-cos θ=3-74.可得sin θ=34.10.已知f (x )=2sin ωx (cos ωx +sin ωx )(ω>0)的图象在x ∈[0,1]上恰有一条对称轴和一个对称中心,则实数ω的取值范围为( )A .⎝⎛⎭⎪⎫3π8,5π8B .⎣⎢⎡⎭⎪⎫3π8,5π8C .⎝ ⎛⎦⎥⎤3π8,5π8D .⎣⎢⎡⎦⎥⎤3π8,5π8【答案】B【解析】f (x )=2sin ωx cos ωx +2sin 2 ωx =sin 2ωx -cos 2ωx +1=2sin ⎝ ⎛⎭⎪⎫2ωx -π4+1.设g (x )=2ωx -π4,g (0)=-π4,g (1)=2ω-π4,f (x )的图象在x ∈[0,1]上恰有一条对称轴和一个对称中心,∴π2≤2ω-π4<π,解得3π8≤ω<5π8.故选B .11.已知函数f (x )=3sin(ωx +φ)(ω>0)的部分图象如图所示,若AB→·BC →=-|AB →|2,则ω等于( )A .π2B .π3 C .π4 D .π6 【答案】A【解析】由三角函数的对称性知AB→·BC →=AB →·2BD →=2AB →·BD →=2|AB →|2cos(π-∠ABD )=-|AB →|2,所以cos ∠ABD =12,即∠ABD =π3.|AD |=23tan π6=2,所以f (x )的最小正周期T =4.所以ω=2π4=π2.故选A .12.已知函数f (x )=3sin(ωx +φ)⎝⎛⎭⎪⎫ω>0,|φ|≤π2的部分图象如图所示,A ,B 两点之间的距离为10,且f (2)=0.若将函数f (x )的图象向右平移t (t >0)个单位长度后所得函数图象关于y 轴对称,则t 的最小值为( )A .4B .3C .2D .1【答案】C【解析】由题图可设A (x 1,3),B (x 2,-3),∴|AB |=(x 1-x 2)2+62=10,得|x 1-x 2|=8.∴T =2|x 1-x 2|=16.∴2πω=16,ω=π8,则f (x )=3sin ⎝ ⎛⎭⎪⎫π8x +φ.由f (2)=0,得3sin ⎝ ⎛⎭⎪⎫π4+φ=0.又-π2≤φ≤π2,∴φ=-π4,f (x )=3sin ⎝ ⎛⎭⎪⎫π8x -π4.将f (x )的图象向右平移t (t >0)个单位长度,得对应的函数g (x )=f (x -t )=3sin ⎣⎢⎡⎦⎥⎤π8x -⎝ ⎛⎭⎪⎫π8t +π4.由题意得g (x )的图象关于y 轴对称,∴π8t +π4=k π+π2(k ∈Z ),解得t =8k +2(k ∈Z ),故正数t 的最小值为2.二、填空题13.(2018年山东日照二模)已知sin ⎝ ⎛⎭⎪⎫x +π6=14,则cos 2⎝ ⎛⎭⎪⎫π3-x 的值为________.【答案】116【解析】cos 2⎝⎛⎭⎪⎫π3-x =cos 2⎣⎢⎡⎦⎥⎤π2-⎝⎛⎭⎪⎫x +π6=sin 2⎝⎛⎭⎪⎫x +π6=116.14.已知函数f (x )=2sin(ωx +φ)对任意的x 都有f ⎝ ⎛⎭⎪⎫π6+x =f ⎝ ⎛⎭⎪⎫π6-x ,则f ⎝ ⎛⎭⎪⎫π6=________.【答案】±2【解析】由题意可得f (x )的图象的对称轴为x =π6,所以f ⎝ ⎛⎭⎪⎫π6=±2.15.(2019年广东中山模拟)函数y =2sin ⎝ ⎛⎭⎪⎫π3-2x 的单调递增区间为________.【答案】⎣⎢⎡⎦⎥⎤k π+5π12,k π+11π12(k ∈Z ) 【解析】y =2sin ⎝ ⎛⎭⎪⎫π3-2x =-2sin ⎝ ⎛⎭⎪⎫2x -π3,令2k π+π2≤2x -π3≤2k π+3π2(k ∈Z ),得k π+5π12≤x ≤k π+11π12(k ∈Z ),即函数y =2sin ⎝ ⎛⎭⎪⎫π3-2x 的单调递增区间为⎣⎢⎡⎦⎥⎤k π+5π12,k π+11π12(k ∈Z ). 16.(2019年山西运城模拟)给出下列四个语句: ①函数y =sin ⎝ ⎛⎭⎪⎫x +π4在区间⎣⎢⎡⎦⎥⎤-3π4,π4上为增函数;②函数y =cos 2x 的最小正周期为2π;③函数y =tan x 的图象关于点⎝ ⎛⎭⎪⎫π2,0对称;④若sin ⎝ ⎛⎭⎪⎫2x 1-π4=sin ⎝ ⎛⎭⎪⎫2x 2-π4,则x 1-x 2=k π,其中k ∈Z .以上四个语句中正确的有________(填写正确语句前面的序号). 【答案】①③【解析】x ∈⎣⎢⎡⎦⎥⎤-3π4,π4时,x +π4∈⎣⎢⎡⎦⎥⎤-π2,π2,故①正确.y =cos 2x=cos 2x +12的最小正周期为π,故②不正确.由正切函数y =tan x 的图象可得③正确.若sin ⎝ ⎛⎭⎪⎫2x 1-π4=sin ⎝ ⎛⎭⎪⎫2x 2-π4,则⎝ ⎛⎭⎪⎫2x 1-π4-⎝ ⎛⎭⎪⎫2x 2-π4=2k π或⎝ ⎛⎭⎪⎫2x 1-π4+⎝ ⎛⎭⎪⎫2x 2-π4=2⎝ ⎛⎭⎪⎫k π+π2,即x 1-x 2=k π或x 1+x 2=k π+3π4(k ∈Z ),故④不正确.综上所述,正确的有①③.小题专项训练6 解三角形一、选择题1.在锐角△ABC 中,角A ,B 所对的边长分别为a ,b,2a sin B =b ,则A 等于( )A .π3B .π4 C .π6 D .π12【答案】C【解析】由2a sin B =b 及正弦定理,得2sin A sin B =sin B ,故sin A =12.又△ABC 为锐角三角形,则A =π6.2.(2019年四川模拟)△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若(a 2+c 2-b 2)tan B =ac ,则角B 的值为( )A .π6B .π3 C .π6或5π6 D .π3或2π3 【答案】C【解析】由余弦定理cos B =a 2+c 2-b 22ac 结合已知可得cos B =12tan B ,则cos B =cos B 2sin B .由tan B 有意义,可知B ≠π2,则cos B ≠0,所以sin B =12,则B =π6或5π6.故选C .3.如图,设A ,B 两点在河的两岸,一测量者在A 的同侧,在所在的河岸边选定一点C ,测出AC 的距离为50 m ,∠ACB =45°,∠CAB =105°后,就可以计算出A ,B 两点的距离为( )A .50 2 mB .50 3 mC .25 2 mD .2522 m【答案】A【解析】由正弦定理得AB sin ∠ACB=ACsin B ,所以AB =AC ·sin ∠ACB sin B =50 sin 45°sin 30°=502(m).4.(2019年吉林四平模拟)在△ABC 中,D 为AC 边上一点,若BD =3,CD =4,AD =5,AB =7,则BC =( )A .22B .23C .37D .13【答案】D【解析】如图,∠ADB +∠CDB =180°,则cos ∠ADB =-cos ∠CDB ,即32+52-722×3×5=-32+42-BC 22×3×4,解得BC =13.故选D .5.在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若c =2a ,b sin B -a sin A =12a sin C ,则sin B 为( )A .74B .34C .73 D .13【答案】A【解析】由b sin B -a sin A =12a sin C ,可得b 2-a 2=12ac ,又c =2a ,得b =2a .∵cos B =a 2+c 2-b 22ac =a 2+4a 2-2a 24a 2=34,∴sin B =1-⎝ ⎛⎭⎪⎫342=74. 6.(2018年江西南昌模拟)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且cos 2A =sin A ,bc =2,则△ABC 的面积为( )A .14B .12 C .1 D .2【答案】B【解析】由cos 2A =sin A ,得1-2sin 2A =sin A ,解得sin A =12(负值舍去).又bc =2,得S △ABC =12bc sin A =12.7.若△ABC 的三个内角满足sin B -sin A sin B -sin C =ca +b ,则A =( )A .π6B .π3 C .2π3 D .π3或2π3【答案】B 【解析】由sin B -sin A sin B -sin C =c a +b 及结合正弦定理,得b -a b -c =ca +b,整理得b 2+c 2-a 2=bc ,所以cos A =b 2+c 2-a 22bc =12.由A 为三角形的内角,知A =π3.8.(2018年河南开封一模)已知锐角三角形ABC ,角A ,B ,C 的对边分别为a ,b ,c ,若b 2=a (a +c ),则sin 2Asin (B -A )的取值范围是( )A .(0,1)B .⎝ ⎛⎭⎪⎫0,22C .⎝ ⎛⎭⎪⎫12,22D .⎝ ⎛⎭⎪⎫12,1 【答案】C【解析】由b 2=a (a +c )及余弦定理,得c -a =2a cos B .由正弦定理,得sin C -sin A =2sin A cos B .∵A +B +C =π,∴sin(A +B )-sin A =2sin A cos B ,∴sin(B -A )=sin A .∵△ABC 是锐角三角形,∴B -A =A ,即B =2A .∴π6<A <π4,则sin 2A sin (B -A )=sin A ∈⎝ ⎛⎭⎪⎫12,22.9.△ABC 中,三边长a ,b ,c 满足a 3+b 3=c 3,那么△ABC 的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .以上均有可能【答案】A【解析】由题意可知c 边最大,即c >a ,c >b ,则a 2c +b 2c >a 3+b 3=c 3,则a 2+b 2-c 2>0.由余弦定理得cos C >0,∴0<C <π2.∴△ABC为锐角三角形.10.设a ,b ,c 分别是△ABC 的角A ,B ,C 所对的边,若tan A tan Btan A +tan B =1 009tan C ,且a 2+b 2=mc 2,则m =( )A .1 008B .1 009C .2 018D .2 019【答案】D【解析】由tan A tan B tan A +tan B=1 009tan C ,得1tan A +1tan B =11 009×1tan C ,即cos A sin A +cos B sin B =11 009×cos C sin C ,sin 2C sin A sin B =cos C1 009.根据正、余弦定理,得c 2ab =11 009×a 2+b 2-c 22ab ,即a 2+b 2-c 2c 2=2 018,则a 2+b 2c 2=2 019,所以m =2 019.11.(2019年贵州模拟)在锐角三角形ABC 中,已知a ,b ,c 分别是角A ,B ,C 的对边,且3b =2a sin B ,a =4,则△ABC 面积的最大值为( )A .23B .43C .83D .163【答案】B【解析】由3b =2a sin B 结合正弦定理得3sin B =2sin A sin B ,由锐角三角形知sin B ≠0,所以sin A =32,则cos A =12.由余弦定理得a 2=b 2+c 2-2bc cos A ,即16=b 2+c 2-bc ,所以16≥2bc -bc =bc ,当b =c 时等号成立.所以S =12bc sin A ≤12×16×32=43,即△ABC 面积的最大值为4 3.故选B .12.(2018年辽宁沈阳五校联考)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知sin A -sin B =13sin C ,3b =2a,2≤a 2+ac ≤18.设△ABC 的面积为S ,p =2a -S ,则p 的最大值是( )A .529 B .729 C .928 D .1128 【答案】C【解析】在△ABC 中,由sin A -sin B =13sin C 及正弦定理,得c =3a -3b .再根据3b =2a ,2≤a 2+ac ≤18,得a =c,1≤a ≤3.由余弦定。
高考数学模拟试卷复习试题高三数学小题狂做15理7

高考数学模拟试卷复习试题高三数学小题狂做(15)理一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}24x x M =<,{}1x x N =<,则MN =( )A .{}21x x -<<B .{}2x x <-C .{}1x x <D .{}2x x <2、设i 是虚数单位,若复数z 满足()11z i i +=-,则复数z 的模z =( ) A .1-B .1C .2D .23、在C ∆AB 中,45∠A =,C 105∠=,C 2B =,则边长C A 为( )A .31-B .1C .2D .31+4、椭圆C 的中心在原点,焦点在x 轴上,离心率等于12,且它的一个顶点恰好是抛物线283x y =的焦点,则椭圆C 的标准方程为( )A .22142x y +=B .22143x y +=C .221129x y +=D .2211612x y +=5、下列程序框图中,输出的A 的值是( )A .128B .129C .131D .1346、将函数()()sin 2f x x ϕ=+(2πϕ<)的图象向左平移6π个单位后的图形关于原点对称,则函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的最小值为( ) A .32B .12C .12-D .32- 7、函数cos 622x xxy -=-的图象大致为( )A .B .C .D .8、已知不等式组110x y x y y +≤⎧⎪-≥-⎨⎪≥⎩所表示的平面区域为D ,若直线3y kx =-与平面区域D 有公共点,则k 的取值范围是( )A .[]3,3-B .11,,33⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭C .(][),33,-∞-+∞D .11,33⎡⎤-⎢⎥⎣⎦9、某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( ) A .203B .163C .86π-D .83π-10、()421x x x ⎛⎫+- ⎪⎝⎭的展开式中x 的系数是( )A .1B .2C .3D .1211、如图,1F 、2F 是双曲线22221x y a b-=(0a >,0b >)的左、右焦点,过1F 的直线l 与双曲线的左右两支分别交于点A 、B .若2F ∆AB 为等边三角形,则双曲线的离心率为( )A .4B .7C .233D .3 12、已知函数()11,14ln ,1x x f x x x ⎧+≤⎪=⎨⎪>⎩,则方程()f x ax =恰有两个不同的实根时,实数a 的取值范围是( )A .10,e ⎛⎫ ⎪⎝⎭B .11,4e ⎡⎫⎪⎢⎣⎭C .10,4⎛⎤ ⎥⎝⎦D .1,4e ⎛⎫ ⎪⎝⎭二、填空题(本大题共4小题,每小题5分,共20分.)13、已知()0,απ∈,4cos 5α=,则()sin πα-=. 14、在C ∆AB 中,90∠B =,C 1AB =B =,点M 满足2BM =AM ,则C C M ⋅A =.15、如图,在边长为1的正方形C OAB 中任取一点,则该点落在阴影部分中的概率为.16、已知直三棱柱111C C AB -A B 中,C 90∠BA =,侧面11CC B B 的面积为2,则直三棱柱111C C AB -A B 外接球表面积的最小值为.高三理科数学小题狂做(15)参考答案一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案ABBDCDACACBB13、35 14、3 15、1316、4π高考数学高三模拟试卷试题压轴押题重庆市高考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.1.(5分)已知全集U={1,2,3,4},集合A={1,2},B={2,3},则∁U(A∪B)=()A.{1,3,4} B.{3,4} C.{3} D.{4}2.(5分)命题“对任意x∈R,都有x2≥0”的否定为()A.对任意x∈R,都有x2<0 B.不存在x∈R,都有x2<0C.存在x0∈R,使得x02≥0D.存在x0∈R,使得x02<03.(5分)(﹣6≤a≤3)的最大值为()A.9 B.C.3 D.4.(5分)以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为()A.2,5 B.5,5 C.5,8 D.8,85.(5分)某几何体的三视图如图所示,则该几何体的体积为()A.B.C.200 D.2406.(5分)若a<b<c,则函数f(x)=(x﹣a)(x﹣b)+(x﹣b)(x﹣c)+(x﹣c)(x ﹣a)的两个零点分别位于区间()A.(a,b)和(b,c)内B.(﹣∞,a)和(a,b)内C.(b,c)和(c,+∞)内D.(﹣∞,a)和(c,+∞)内7.(5分)已知圆C1:(x﹣2)2+(y﹣3)2=1,圆C2:(x﹣3)2+(y﹣4)2=9,M,N 分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.﹣1 B.5﹣4 C.6﹣2D.8.(5分)执行如图所示的程序框图,如果输出S=3,那么判断框内应填入的条件是()A.k≤6B.k≤7C.k≤8D.k≤99.(5分)4cos50°﹣tan40°=()A.B.C.D.2﹣110.(5分)在平面上,⊥,||=||=1,=+.若||<,则||的取值范围是()A.(0,] B.(,] C.(,] D.(,]二、填空题:本大题共3小题,考生作答5小题,每小题5分,共25分,把答案填写在答题卡相应位置上.11.(5分)已知复数z=(i是虚数单位),则|z|=.12.(5分)已知{an}是等差数列,a1=1,公差d≠0,Sn为其前n项和,若a1,a2,a5成等比数列,则S8=.13.(5分)从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有1人的选派方法种数是(用数字作答).14,15,16三题为选做题,请从中任选两题作答,若三题全做,则按前两题给分:14.(5分)如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为.15.(5分)在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若极坐标方程为ρcosθ=4的直线与曲线(t为参数)相交于A,B两点,则|AB|=.16.若关于实数x的不等式|x﹣5|+|x+3|<a无解,则实数a的取值范围是.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(13分)设f(x)=a(x﹣5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).(1)确定a的值;(2)求函数f(x)的单调区间与极值.18.(13分)某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球,根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:奖级摸出红、蓝球个数获奖金额一等奖3红1蓝200元二等奖3红0蓝50元三等奖2红1蓝10元其余情况无奖且每次摸奖最多只能获得一个奖级.(1)求一次摸奖恰好摸到1个红球的概率;(2)求摸奖者在一次摸奖中获奖金额x的分布列与期望E(x).19.(13分)如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=,F为PC的中点,AF⊥PB.(1)求PA的长;(2)求二面角B﹣AF﹣D的正弦值.20.(12分)在△ABC中,内角A,B,C的对边分别是a,b,c,且a2+b2+ab=c2.(1)求C;(2)设cosAcosB=,=,求tanα的值.21.(12分)如图,椭圆的中心为原点O,长轴在x轴上,离心率,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.(Ⅰ)求该椭圆的标准方程;(Ⅱ)取垂直于x轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若PQ⊥P'Q,求圆Q的标准方程.22.(12分)对正整数n,记In={1,2,3…,n},Pn={|m∈In,k∈In}.(1)求集合P7中元素的个数;(2)若Pn的子集A中任意两个元素之和不是整数的平方,则称A为“稀疏集”.求n的最大值,使Pn能分成两个不相交的稀疏集的并集.重庆市高考数学试卷(理科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.1.(5分)已知全集U={1,2,3,4},集合A={1,2},B={2,3},则∁U(A∪B)=()A.{1,3,4} B.{3,4} C.{3} D.{4}【分析】根据A与B求出两集合的并集,由全集U,找出不属于并集的元素,即可求出所求的集合.【解答】解:∵A={1,2},B={2,3},∴A∪B={1,2,3},∵全集U={1,2,3,4},∴∁U(A∪B)={4}.故选:D.【点评】此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.2.(5分)命题“对任意x∈R,都有x2≥0”的否定为()A.对任意x∈R,都有x2<0 B.不存在x∈R,都有x2<0C.存在x0∈R,使得x02≥0D.存在x0∈R,使得x02<0【分析】直接利用全称命题的否定是特称命题,写出命题的否定命题即可.【解答】解:因为全称命题的否定是特称命题,所以命题“对任意x∈R,都有x2≥0”的否定为.存在x0∈R,使得x02<0.故选:D.【点评】本题考查命题的否定,全称命题与特称命题的否定关系,基本知识的考查.3.(5分)(﹣6≤a≤3)的最大值为()A.9 B.C.3 D.【分析】令f(a)=(3﹣a)(a+6)=﹣+,而且﹣6≤a≤3,利用二次函数的性质求得函数f(a)的最大值,即可得到所求式子的最大值.【解答】解:令f(a)=(3﹣a)(a+6)=﹣+,而且﹣6≤a≤3,由此可得当a=﹣时,函数f(a)取得最大值为,故(﹣6≤a≤3)的最大值为=,故选:B.【点评】本题主要考查二次函数的性质应用,体现了转化的数学思想,属于中档题.4.(5分)以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为()A.2,5 B.5,5 C.5,8 D.8,8【分析】求乙组数据的平均数就是把所有乙组数据加起来,再除以5.找甲组数据的中位数要把甲组数据按从小到大的顺序排列,位于最中间的一个数为中位数.据此列式求解即可.【解答】解:乙组数据平均数=(9+15+18+24+10+y)÷5=16.8;∴y=8;甲组数据可排列成:9,12,10+x,24,27.所以中位数为:10+x=15,∴x=5.故选:C.【点评】本题考查了中位数和平均数的计算.平均数是指在一组数据中所有数据之和再除以数据的个数.将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.5.(5分)某几何体的三视图如图所示,则该几何体的体积为()A.B.C.200 D.240【分析】如图所示,该几何体是棱长分别为4,8,10的长方体砍去两个小三棱柱得到一个四棱柱,据此即可计算出体积.【解答】解:如图所示,该几何体是棱长分别为4,8,10的长方体砍去两个小三棱柱得到一个四棱柱,由图知V==200.故选:C.【点评】由三视图正确恢复原几何体是解题的关键.6.(5分)若a<b<c,则函数f(x)=(x﹣a)(x﹣b)+(x﹣b)(x﹣c)+(x﹣c)(x ﹣a)的两个零点分别位于区间()A.(a,b)和(b,c)内B.(﹣∞,a)和(a,b)内C.(b,c)和(c,+∞)内D.(﹣∞,a)和(c,+∞)内【分析】由函数零点存在判定定理可知:在区间(a,b),(b,c)内分别存在一个零点;又函数f(x)是二次函数,最多有两个零点,即可判断出.【解答】解:∵a<b<c,∴f(a)=(a﹣b)(a﹣c)>0,f(b)=(b﹣c)(b﹣a)<0,f(c)=(c﹣a)(c﹣b)>0,由函数零点存在判定定理可知:在区间(a,b),(b,c)内分别存在一个零点;又函数f(x)是二次函数,最多有两个零点,因此函数f(x)的两个零点分别位于区间(a,b),(b,c)内.故选:A.【点评】熟练掌握函数零点存在判定定理及二次函数最多有两个零点的性质是解题的关键.7.(5分)已知圆C1:(x﹣2)2+(y﹣3)2=1,圆C2:(x﹣3)2+(y﹣4)2=9,M,N 分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.﹣1 B.5﹣4 C.6﹣2D.【分析】求出圆C1关于x轴的对称圆的圆心坐标A,以及半径,然后求解圆A与圆C2的圆心距减去两个圆的半径和,即可求出|PM|+|PN|的最小值.【解答】解:如图圆C1关于x轴的对称圆的圆心坐标A(2,﹣3),半径为1,圆C2的圆心坐标(3,4),半径为3,由图象可知当P,M,N,三点共线时,|PM|+|PN|取得最小值,|PM|+|PN|的最小值为圆C3与圆C2的圆心距减去两个圆的半径和,即:|AC2|﹣3﹣1=﹣4=﹣4=5﹣4.故选:B.【点评】本题考查圆的对称圆的方程的求法,两个圆的位置关系,两点距离公式的应用,考查转化思想与计算能力.8.(5分)执行如图所示的程序框图,如果输出S=3,那么判断框内应填入的条件是()A.k≤6B.k≤7C.k≤8D.k≤9【分析】根据程序框图,写出运行结果,根据程序输出的结果是S=3,可得判断框内应填入的条件.【解答】解:根据程序框图,运行结果如下:S k第一次循环 log23 3第二次循环log23•log34 4第三次循环log23•log34•log45 5第四次循环log23•log34•log45•log56 6第五次循环log23•log34•log45•log56•log67 7第六次循环log23•log34•log45•log56•log67•log78=log28=3 8故如果输出S=3,那么只能进行六次循环,故判断框内应填入的条件是k≤7.故选:B.【点评】本题考查程序框图,尤其考查循环结构.对循环体每次循环需要进行分析并找出内在规律.本题属于基础题.9.(5分)4cos50°﹣tan40°=()A.B.C.D.2﹣1【分析】原式第一项利用诱导公式化简,第二项利用同角三角函数间的基本关系切化弦,通分后利用同分母分式的减法法则计算,再利用诱导公式及两角和与差的正弦函数公式化简,整理后利用两角和与差的余弦函数公式化为一个角的余弦函数,约分即可得到结果.【解答】解:4cos50°﹣tan40°=4sin40°﹣tan40°======.故选:C.【点评】此题考查了两角和与差的正弦、余弦函数公式,同角三角函数间的基本关系,以及诱导公式的作用,熟练掌握公式是解本题的关键.10.(5分)在平面上,⊥,||=||=1,=+.若||<,则||的取值范围是()A.(0,] B.(,] C.(,] D.(,]【分析】建立坐标系,将向量条件用等式与不等式表示,利用向量模的计算公式,即可得到结论.【解答】解:根据条件知A,B1,P,B2构成一个矩形AB1PB2,以AB1,AB2所在直线为坐标轴建立直角坐标系,设|AB1|=a,|AB2|=b,点O的坐标为(x,y),则点P的坐标为(a,b),由=1,得,则∵||<,∴∴∴∵(x﹣a)2+y2=1,∴y2=1﹣(x﹣a)2≤1,∴y2≤1同理x2≤1∴x2+y2≤2②由①②知,∵||=,∴<||≤故选:D.【点评】本题考查向量知识的运用,考查学生转化问题的能力,考查学生的计算能力,属于难题.二、填空题:本大题共3小题,考生作答5小题,每小题5分,共25分,把答案填写在答题卡相应位置上.11.(5分)已知复数z=(i是虚数单位),则|z|=.【分析】通过复数的分子与分母同时求模即可得到结果.【解答】解:|z|===.故答案为:.【点评】本题考查复数的模的求法,考查计算能力.12.(5分)已知{an}是等差数列,a1=1,公差d≠0,Sn为其前n项和,若a1,a2,a5成等比数列,则S8=64.【分析】依题意,a1=1,=a1•(a1+4d),可解得d,从而利用等差数列的前n项和公式即可求得答案.【解答】解:∵{an}是等差数列,a1,a2,a5成等比数列,∴=a1•(a1+4d),又a1=1,∴d2﹣2d=0,公差d≠0,∴d=2.∴其前8项和S8=8a1+×d=8+56=64.故答案为:64.【点评】本题考查等差数列的前n项和,考查方程思想与运算能力,属于基础题.13.(5分)从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有1人的选派方法种数是590(用数字作答).【分析】不同的组队方案:选5名医生组成一个医疗小组,要求其中骨科、脑外科和内科医生都至少有1人,方法共有6类,他们分别是:3名骨科、1名脑外科和1名内科医生;1名骨科、3名脑外科和1名内科医生,…,在每一类中都用分步计数原理解答.【解答】解:直接法:3名骨科、1名脑外科和1名内科医生,有C33C41C51=20种,1名骨科、3名脑外科和1名内科医生,有C31C43C51=60种,1名骨科、1名脑外科和3名内科医生,有C31C41C53=120种,2名骨科、2名脑外科和1名内科医生,有C32C42C51=90种,1名骨科、2名脑外科和2名内科医生,有C31C42C52=180种,2名骨科、1名脑外科和2名内科医生,有C32C41C52=120种,共计20+60+120+90+180+120=590种间接法:﹣﹣﹣+1=590故答案为:590.【点评】本题主要考查了排列、组合及简单计数问题,解答关键是利用直接法:先分类后分步.14,15,16三题为选做题,请从中任选两题作答,若三题全做,则按前两题给分:14.(5分)如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为5.【分析】利用直角△ABC的边角关系即可得出BC,利用弦切角定理可得∠BCD=∠A=60°.利用直角△BCD的边角关系即可得出CD,BD.再利用切割线定理可得CD2=DE•DB,即可得出DE.【解答】解:在△ABC中,∠C=90°,∠A=60°,AB=20,∴BC=AB•sin60°=.∵CD是此圆的切线,∴∠BCD=∠A=60°.在Rt△BCD中,CD=BC•cos60°=,BD=BC•sin60°=15.由切割线定理可得CD2=DE•DB,∴,解得DE=5.故答案为5.【点评】熟练掌握直角三角形的边角关系、弦切角定理、切割线定理是解题的关键.15.(5分)在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若极坐标方程为ρcosθ=4的直线与曲线(t为参数)相交于A,B两点,则|AB|=16.【分析】先将直线极坐标方程ρcosθ=4化成直角坐标方程,再代入曲线(t为参数)中得A,B两点的直角坐标,最后利用两点间的距离公式即可得出|AB|.【解答】解:将直线极坐标方程ρcosθ=4化成直角坐标方程为x=4,代入曲线(t为参数)中得A,B两点的直角坐标为(4,8),(4,﹣8),则|AB|=16.故答案为:16.【点评】本题考查参数方程、极坐标方程、直角坐标方程间的转化,两点间的距离公式,考查转化、计算能力.16.若关于实数x的不等式|x﹣5|+|x+3|<a无解,则实数a的取值范围是(﹣∞,8].【分析】利用绝对值的意义求得|x﹣5|+|x+3|最小值为8,由此可得实数a的取值范围.【解答】解:由于|x﹣5|+|x+3|表示数轴上的x对应点到5和﹣3对应点的距离之和,其最小值为8,再由关于实数x的不等式|x﹣5|+|x+3|<a无解,可得a≤8,故答案为:(﹣∞,8].【点评】本题主要考查绝对值的意义,绝对值不等式的解法,求得|x﹣5|+|x+3|最小值为8,是解题的关键,属于中档题.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(13分)设f(x)=a(x﹣5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).(1)确定a的值;(2)求函数f(x)的单调区间与极值.【分析】(1)先由所给函数的表达式,求导数fˊ(x),再根据导数的几何意义求出切线的斜率,最后由曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6)列出方程求a的值即可;(2)由(1)求出的原函数及其导函数,求出导函数的零点,把函数的定义域分段,判断导函数在各段内的符号,从而得到原函数的单调区间,根据在各区间内的单调性求出极值点,把极值点的横坐标代入函数解析式求得函数的极值.【解答】解:(1)因f(x)=a(x﹣5)2+6lnx,故f′(x)=2a(x﹣5)+,(x>0),令x=1,得f(1)=16a,f′(1)=6﹣8a,∴曲线y=f(x)在点(1,f(1))处的切线方程为y﹣16a=(6﹣8a)(x﹣1),由切线与y轴相交于点(0,6).∴6﹣16a=8a﹣6,∴a=.(2)由(I)得f(x)=(x﹣5)2+6lnx,(x>0),f′(x)=(x﹣5)+=,令f′(x)=0,得x=2或x=3,当0<x<2或x>3时,f′(x)>0,故f(x)在(0,2),(3,+∞)上为增函数,当2<x<3时,f′(x)<0,故f(x)在(2,3)上为减函数,故f(x)在x=2时取得极大值f(2)=+6ln2,在x=3时取得极小值f(3)=2+6ln3.【点评】本小题主要考查利用导数研究曲线上某点切线方程、利用导数研究函数的单调性、函数的极值及其几何意义等基础知识,考查运算求解能力,考查分类讨论思想、化归与转化思想.属于中档题.18.(13分)某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球,根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:奖级摸出红、蓝球个数获奖金额一等奖3红1蓝200元二等奖3红0蓝50元三等奖2红1蓝10元其余情况无奖且每次摸奖最多只能获得一个奖级.(1)求一次摸奖恰好摸到1个红球的概率;(2)求摸奖者在一次摸奖中获奖金额x的分布列与期望E(x).【分析】(1)从7个小球中取3的取法为,若取一个红球,则说明第一次取到一红2白,根据组合知识可求取球的种数,然后代入古典概率计算公式可求(2)先判断随机变量X的所有可能取值为200,50,10,0根据题意求出随机变量的各个取值的概率,即可求解分布列及期望值【解答】解:(1)设Ai表示摸到i个红球,Bi表示摸到i个蓝球,则Ai与Bi相互独立(i=0,1,2,3)∴P(A1)==(2)X的所有可能取值为0,10,50,200P(X=200)=P(A3B1)=P(A3)P(B1)=P(X=50)=P(A3)P(B0)==P(X=10)=P(A2)P(B1)==P(X=0)=1﹣=∴X的分布列为x 0 10 50 200PEX==4元【点评】本题主要考查了古典概型及计算公式,互斥事件、离散型随机变量的分布列及期望值的求解,考查了运用概率知识解决实际问题的能力.19.(13分)如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=,F为PC的中点,AF⊥PB.(1)求PA的长;(2)求二面角B﹣AF﹣D的正弦值.【分析】(I)连接BD交AC于点O,等腰三角形BCD中利用“三线合一”证出AC⊥BD,因此分别以OB、OC分别为x轴、y轴建立空间直角坐标系如图所示.结合题意算出A、B、C、D各点的坐标,设P(0,﹣3,z),根据F为PC边的中点且AF⊥PB,算出z=2,从而得到=(0,0,﹣2),可得PA的长为2;(II)由(I)的计算,得=(﹣,3,0),=(,3,0),=(0,2,).利用垂直向量数量积为零的方法建立方程组,解出=(3,,﹣2)和=(3,﹣,2)分别为平面FAD、平面FAB的法向量,利用空间向量的夹角公式算出、夹角的余弦,结合同角三角函数的平方关系即可算出二面角B﹣AF﹣D的正弦值..【解答】解:(I)如图,连接BD交AC于点O∵BC=CD,AC平分角BCD,∴AC⊥BD以O为坐标原点,OB、OC所在直线分别为x轴、y轴,建立空间直角坐标系O﹣xyz,则OC=CDcos=1,而AC=4,可得AO=AC﹣OC=3.又∵OD=CDsin=,∴可得A(0,﹣3,0),B(,0,0),C(0,1,0),D(﹣,0,0)由于PA⊥底面ABCD,可设P(0,﹣3,z)∵F为PC边的中点,∴F(0,﹣1,),由此可得=(0,2,),∵=(,3,﹣z),且AF⊥PB,∴•=6﹣=0,解之得z=2(舍负)因此,=(0,0,﹣2),可得PA的长为2;(II)由(I)知=(﹣,3,0),=(,3,0),=(0,2,),设平面FAD的法向量为=(x1,y1,z1),平面FAB的法向量为=(x2,y2,z2),∵•=0且•=0,∴,取y1=得=(3,,﹣2),同理,由•=0且•=0,解出=(3,﹣,2),∴向量、的夹角余弦值为cos<,>===因此,二面角B﹣AF﹣D的正弦值等于=【点评】本题在三棱锥中求线段PA的长度,并求平面与平面所成角的正弦值.着重考查了空间线面垂直的判定与性质,考查了利用空间向量研究平面与平面所成角等知识,属于中档题.20.(12分)在△ABC中,内角A,B,C的对边分别是a,b,c,且a2+b2+ab=c2.(1)求C;(2)设cosAcosB=,=,求tanα的值.【分析】(1)利用余弦定理表示出cosC,将已知等式变形后代入求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数;(2)已知第二个等式分子两项利用两角和与差的余弦函数公式化简,再利用同角三角函数间的基本关系弦化切,利用多项式乘多项式法则计算,由A+B的度数求出sin(A+B)的值,进而求出cos(A+B)的值,利用两角和与差的余弦函数公式化简cos(A+B),将cosAcosB的值代入求出sinAsinB的值,将各自的值代入得到tanα的方程,求出方程的解即可得到tanα的值.【解答】解:(1)∵a2+b2+ab=c2,即a2+b2﹣c2=﹣ab,∴由余弦定理得:cosC===﹣,又C为三角形的内角,则C=;(2)由题意==,∴(cosA﹣tanαsinA)(cosB﹣tanαsinB)=,即tan2αsinAsinB﹣tanα(sinAcosB+cosAsinB)+cosAcosB=tan2αsinAsinB﹣tanαsin(A+B)+cosAcosB=,∵C=,A+B=,cosAcosB=,∴sin(A+B)=,cos(A+B)=cosAcosB﹣sinAsinB=﹣sinAsinB=,即sinAsinB=,∴tan2α﹣tanα+=,即tan2α﹣5tanα+4=0,解得:tanα=1或tanα=4.【点评】此题考查了余弦定理,两角和与差的余弦函数公式,同角三角函数间的基本关系,熟练掌握余弦定理是解本题的关键.21.(12分)如图,椭圆的中心为原点O,长轴在x轴上,离心率,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.(Ⅰ)求该椭圆的标准方程;(Ⅱ)取垂直于x轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若PQ⊥P'Q,求圆Q的标准方程.【分析】(Ⅰ)利用点A(﹣c,2)在椭圆上,结合椭圆的离心率,求出几何量,即可求得椭圆的标准方程;(Ⅱ)设出圆Q的圆心坐标及半径,由PQ⊥P'Q得到P的坐标,写出圆的方程后和椭圆联立,化为关于x的二次方程后由判别式等于0得到关于t与r的方程,把P点坐标代入椭圆方程得到关于t与r的另一方程,联立可求出t与r的值,经验证满足椭圆上的其余点均在圆Q外,结合对称性即可求得圆Q的标准方程.【解答】解:(Ⅰ)由题意知点A(﹣c,2)在椭圆上,则,即①∵离心率,∴②联立①②得:,所以b2=8.把b2=8代入②得,a2=16.∴椭圆的标准方程为;(Ⅱ)设Q(t,0),圆Q的半径为r,则圆Q的方程为(x﹣t)2+y2=r2,不妨取P为第一象限的点,因为PQ⊥P'Q,则P()(t>0).联立,得x2﹣4tx+2t2+16﹣2r2=0.由△=(﹣4t)2﹣4(2t2+16﹣2r2)=0,得t2+r2=8又P()在椭圆上,所以.整理得,.代入t2+r2=8,得.解得:.所以,.此时.满足椭圆上的其余点均在圆Q外.由对称性可知,当t<0时,t=﹣,.故所求圆Q的标准方程为.【点评】本题考查椭圆的标准方程,考查椭圆的几何性质,考查方程组的解法,考查学生的计算能力,属于中档题.22.(12分)对正整数n,记In={1,2,3…,n},Pn={|m∈In,k∈In}.(1)求集合P7中元素的个数;(2)若Pn的子集A中任意两个元素之和不是整数的平方,则称A为“稀疏集”.求n的最大值,使Pn能分成两个不相交的稀疏集的并集.【分析】(1)对于集合P7 ,有n=7.当k=4时,根据Pn中有3个数与In={1,2,3…,n}中的数重复,由此求得集合P7中元素的个数.(2)先用反证法证明证当n≥15时,Pn不能分成两个不相交的稀疏集的并集,再证P14满足要求,从而求得n的最大值.【解答】解:(1)对于集合P7 ,有n=7.当k=1时,m=1,2,3…,7,Pn={1,2,3…,7},7个数,当k=2时,m=1,2,3…,7,Pn对应有7个数,当k=3时,m=1,2,3…,7,Pn对应有7个数,当k=4时,Pn={|m∈In,k∈In}=Pn={,1,,2,,3,}中有3个数(1,2,3)与k=1时Pn中的数重复,当k=5时,m=1,2,3…,7,Pn对应有7个数,当k=6时,m=1,2,3…,7,Pn对应有7个数,当k=7时,m=1,2,3…,7,Pn对应有7个数,由此求得集合P7中元素的个数为 7×7﹣3=46.(2)先证当n≥15时,Pn不能分成两个不相交的稀疏集的并集.假设当n≥15时,Pn可以分成两个不相交的稀疏集的并集,设A和B为两个不相交的稀疏集,使A∪B=Pn⊇In .不妨设1∈A,则由于1+3=22,∴3∉A,即3∈B.同理可得,6∈A,10∈B.又推出15∈A,但1+15=42,这与A为稀疏集相矛盾.再证P14满足要求.当k=1时,P14={|m∈I14,k∈I14}=I14,可以分成2个稀疏集的并集.事实上,只要取A1={1,2,4,6,9,11,13},B1={3,5,7,8,10,12,14},则A1和B1都是稀疏集,且A1∪B1=I14.当k=4时,集合{|m∈I14}中,除整数外,剩下的数组成集合{,,,…,},可以分为下列3个稀疏集的并:A2={,,,},B2={,,}.当k=9时,集合{|m∈I14}中,除整数外,剩下的数组成集合{,,,,…,,},可以分为下列3个稀疏集的并:A3={,,,,},B3={,,,,}.最后,集合C═{|m∈I14,k∈I14,且k≠1,4,9 }中的数的分母都是无理数,它与Pn中的任何其他数之和都不是整数,因此,令A=A1∪A2∪A3∪C,B=B1∪B2∪B3,则A和B是不相交的稀疏集,且A∪B=P14.综上可得,n的最大值为14.【点评】本题主要考查新定义,集合间的包含关系,体现了分类讨论的数学思想,属于中档题.高考数学高三模拟试卷试题压轴押题统考数学理试卷第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)复数313ii+=- (A )i (B )i - (C )2i (D )2i -(2)已知()f x 是定义在R 上的奇函数,且当0x >时,()23xf x =-,则(2)f -=(A )1 (B )1- (C )14 (D )114- (3)已知数列{}n a 为等差数列,若23a =,1612a a +=,则789a a a ++=(A )27 (B )36 (C )45 (D )63(4)已知抛物线24x y =上一点A 的纵坐标为4,则点A 到抛物线焦点的距离为(A )10 (B )4 (C )15 (D )5 (5)给出下列四个命题:①,sin cos 1R ααα∀∈+>-②3,sin cos 2R ααα∃∈+=③1,sin cos 2R ααα∀∈≤④3,sin cos 4R ααα∃∈=其中正确命题的序号是①②③④(A )①② (B )①③ (C )③④ (D )②④(6)如图是一个容量为200的样本频率分布直方图,则样本数据落在范围[13,17)的频数为(A )81 (B )36 (C )24 (D )12(7)已知椭圆221:12x y C m n +=+与双曲线222:1x y C m n-=共焦点,则椭圆1C 的离心率e 的取值范围为(A )2(,1) (B )2(0,) (C )(0,1) (D )1(0,)2(8)已知O为坐标原点,A,B两点的坐标均满足不等式组3103010x yx yx-+≤⎧⎪+-≤⎨⎪-≥⎩,则tan AOB∠的最大值等于(A)12(B)34(C)47(D)94(9)设函数()3cos(2)sin(2)(||)2f x x xπϕϕϕ=+++<,且其图象关于直线0x=对称,则(A)()y f x=的最小正周期为π,且在(0,)2π上为增函数(B)()y f x=的最小正周期为π,且在(0,)2π上为减函数(C)()y f x=的最小正周期为2π,且在(0,)4π上为增函数(D)()y f x=的最小正周期为2π,且在(0,)4π上为减函数(10)某几何体的三视图入图所示,则此几何体对应直观图中△PAB的面积是(A)7(B)2 (C)3(D)5(11)根据如图所示程序框图,若输入2146m=,1813n=,则输出m的值为(A)1 (B)37 (C)148 (D)333(12)已知函数|21|,2()3,21x xf xxx⎧-<⎪=⎨≥⎪-⎩,若方程()0f x a-=有三个不同的实数根,则实数a的取值范围为(A )(1,3) (B )(0,3) (C )(0,2) (D )(0,1)第Ⅱ卷本卷包括必考题和选考题两部分。
高三数学理小题狂做精选

高三理科数学小题狂做(11)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知全集U R =,集合{}0x x A =≤,{}1x x B =>-,则集合AB =()A .{}10x x -<≤B .{}10x x -≤≤C .{}10x x x ≤->或D .{}10x x x ≤-≥或2、设()102,0xx f x x ⎧-≥⎪=⎨<⎪⎩,则()2f f -=⎡⎤⎣⎦() A .1-B .14C .12D .323、下列命题中,真命题是()A .0R x ∃∈,00x e ≤B .R x ∀∈,22x x >C .0a b +=的充要条件是1ab=-D .1a >,1b >是1ab >的充分条件 4、设()sin f x x x =-,则()f x ()A .既是奇函数又是减函数B .既是奇函数又是增函数C .是有零点的减函数D .是没有零点的奇函数 5、已知()f x 是R 上的奇函数,且当(],0x ∈-∞时,()()lg 3f x x x =--,则()1f =()A .0B .lg 3C .lg 3-D .lg 4- 6、已知函数()321f x x ax x =-+--在R 上是单调函数,则实数a 的取值范围是() A.(),3,⎡-∞+∞⎣B.⎡⎣C .((),3,-∞+∞D.(7、若()2x x e e f x --=,()2x xe e g x -+=,则()2f x 等于()A .()2fx B .()()2f x g x +⎡⎤⎣⎦C .()2g x D .()()2f x g x ⋅8、函数()2log 2xf x =的图象大致是()A .B .C .D . 9、函数()22ln f x x x bx a =+-+(0b >,R a ∈)在点()(),b fb 处的切线斜率的最小值是()A ..2C D .110、定义在R 上的函数()f x 满足:()()()111f x f x f x -=+=-成立,且()f x 在[]1,0-上单调递增,设()3a f =,b f=,()2c f =,则a 、b 、c 的大小关系是()A .a b c >>B .a c b >>C .c b a >>D .b c a >>11、定义在R 上的函数()f x 满足()()6f x f x +=,当[)3,1x ∈--时,()()22f x x =-+,当[)1,3x ∈-时,()f x x =,则()()()()1232015f f f f +++⋅⋅⋅+=()A .336B .355C .1676D .201512、已知函数()2,0ln ,0kx x f x x x +≤⎧=⎨>⎩(R k ∈),若函数()y f x k =+有三个零点,则实数k 的取值范围是() A .2k≤B .2k ≤-C .21k -≤≤-D .10k -<<二、填空题(本大题共4小题,每小题5分,共20分.)13、151lg 2lg 222-⎛⎫+-= ⎪⎝⎭.14、若命题“R x ∃∈,使得22390x ax -+<成立”为假命题,则实数a 的取值范围是. 15、若函数()6,23log ,2a x x f x x x -+≤⎧=⎨+>⎩(0a >且1a ≠)的值域是[)4,+∞,则实数a 的取值范围是.16、函数()()221sin 1x xf x x ++=+的最大值为M ,最小值为m ,则m M +=.高三理科数学小题狂做(11)参考答案一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)13、1-14、⎡-⎣15、(]1,216、2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学小题狂做冲刺训练(详细解析)高中数学姓名:__________班级:__________考号:__________题号一二总分得分、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.已知两个等差数列{a n }和{b n }的前n 项和分别为A n 和B n ,且,则使得为3457++=n n B A n n n n b a 整数的正整数n 的个数是( )A.2B.3C.4D.5解析:,nn n n n n n n b a b a a a n B A ==+∙-+∙-=----2222)()12(1211211212∴31245)12(71212+-+-==--n n B A b a n n n n =.11271197++=++n n n 当n =1,2,3,5,11时,是正整数.n n b a 答案:D2.已知数列{a n }的前n 项和(n∈N *),则a 4等于( )21++=n n S n A. B. C. D.301341201321解析:由已知,得a 4=S 4-S 3=.3015465=-答案:A3.若△ABC 的内角A 满足,则sinA+cosA 等于( )322sin =A A. B. C. D.315315-3535-解析:在△ABC 中,,032cos sin 2>=A A ∴sinA>0,cosA >0.∴2)cos (sin cos sin A A A A +=+AA A A cos sin 2cos sin 22++=.31535321==+=答案:A4.若a <0,则( )A.2a >()a >(0.2)a B.(0.2)a >()a >2a 2121C.()a >(0.2)a >2a D.2a >(0.2)a >()a2121解析:∵a<0,∴2a<0,()a >1,0.2a >1.21而=()a ∈(0,1),a a )2.0()21(25∴()a <0.2a .21答案:B5.下列各组向量中不平行的是( )A.a =(1,2,-2),b =(-2,-4,4)B.c =(1,0,0),d =(-3,0,0)C.e =(2,3,0),f =(0,0,0)D.g =(-2,3,5),h =(16,24,40)解析:向量平行的充要条件是:存在实数λ,使a =λb.g,h 不满足要求,故D 中的两个向量不平行.答案:D6.由等式x 3+a 1x 2+a 2x+a 3=(x+1)3+b 1(x+1)2+b 2(x+1)+b 3,定义一个映射:f(a 1,a 2,a 3)=(b 1,b 2,b 3),则f(2,1,-1)等于( )A.(-1,0,-1)B.(-1,-1,0)C.(-1,0,1)D.(-1,1,0)解析:由题意知x 3+2x 2+x-1=(x+1)3+b 1(x+1)2+b 2(x+1)+b 3,令x =-1,得-1=b 3,即b 3=-1;再令x =0与x =1,得⎩⎨⎧+++=+++=-,2483,11321321b b b b b b 解得b 1=-1,b 2=0,故选A.答案:A7.下列两个变量之间是相关关系的是( )A.圆的面积与半径B.球的体积与半径C.角度与它的正弦值D.一个考生的数学成绩与物理成绩解析:相关关系不是确定的函数关系,这里A 、B 、C 都是确定的函数关系.答案:D8.已知集合A ={x|x 2-x-2>0},B ={x||x-a|≤1},若A∩B=∅,则实数a 的取值范围是( )A.(0,1)B.(-∞,1)C.(0,+∞)D.[0,1]解析:A ={x|x >2或x <-1},B ={x|a-1≤x≤a+1}.又A∩B=∅,∴⎩⎨⎧-≥-≤+.11,21a a ∴0≤a≤1.答案:D9.已知(ax +1)n 的展开式中,二项式系数和为32,各项系数和为243,则a 等于( )A .-2B .2C .-3D .3解析:由二项式系数和为2n =32,得n =5,又令x =1,得各项系数和为(a +1)5=243,所以a +1=3,故a =2.答案:B10.如果一个三位数的十位数字既大于百位数字也大于个位数字,则这样的三位数共有( )A.240个B.285个C.231个D.243个解析:当十位数字是9时,百位数字有8种取法,个位数字有9种取法,此时取法种数为8×9;当十位数字是8时,百位数字有7种取法,个位数字有8种取法,此时取法种数为7×8,依此类推,直到当十位数字是2时,百位数字有1种取法,个位数字有2种取法,此时取法种数为1×2,所以总的个数为1×2+2×3+3×4+…+8×9=240.答案:A、填空题(本大题共5小题,每小题5分,共25分)11.已知函数f(x)=2+log 3x,x∈[1,9],则函数y =[f(x)]2+f(x 2)的值域为___________.解析:∵f(x)=2+log 3x,x∈[1,9],∴y=[f(x)]2+f(x 2)的定义域为⎩⎨⎧≤≤≤≤.91,912x x 解得1≤x ≤3,即定义域为[1,3].∴0≤log 3x ≤1.又y =[f(x)]2+f(x 2)=(2+log 3x)2+2+log 3x 2=(log 3x)2+6log 3x+6=(log 3x+3)2-3,∵0≤log 3x ≤1,∴6≤y ≤13.故函数的值域为[6,13].答案:[6,13]12.过抛物线x 2=2py(p>0)的焦点F 作倾斜角为30°的直线,与抛物线分别交于A 、B 两点(点A 在y 轴左侧),则______________.=||||FB AF 解析:由已知,得直线方程为y=与x 2=2py 联立消x,得12y 2-20py+3p 2=0,233p x +∵A 在y 轴左侧,∴.如图所示,过A 、B 分别作准线的垂线AM 、BN,由抛物线定义知p y P y B A 23,6==|AF|=|AM|,|BF|=|BN|,故.3123222||||||||==++==p p y p y BN AM FB AF B A 答案:3113.下列四个命题中的真命题是____________.①经过定点P 0(x 0,y 0)的直线都可以用方程y-y 0=k(x-x 0)表示②经过任意两个不同的点P 1(x 1,y 1),P 2(x 2,y 2)的直线都可以用方程(y-y 1)·(x 2-x 1)=(x-x 1)(y 2-y 1)表示③不经过原点的直线都可以用方程表示1=+by a x ④经过定点A (0,b)的直线都可以用方程y =kx+b 表示答案:②14.给出下列5个命题:①函数f(x)=-sin(k π+x)(k ∈Z)是奇函数;②函数f(x)=tanx 的图象关于点( ,0)(k ∈Z)对称;③函数f(x)=sin|x|是最小正周期为π的周期函数;④设θ是第二象限角,则 > ,且 > ;⑤函数y=cos2x+sinx 的最小值是-1.其中正确的命题是___________.解析:∵y=-sin(k π+x)(n∈Z),故f(x)是奇函数,∴①正确;对f(x)=tanx,(kπ,0)、( ,0)都是对称中心(前者在曲线上,后者不在),∴②正确;f(x)=sin|x|不是周期函数,∴③不正确;对④, 必满足> ,但是第三象限角时, < ,∴④不正确;∵y=cos2x+sinx=1-sin2x+sinx,当sinx=-1时,ymin=-1,∴⑤正确.答案:①②⑤15.函数y=f(x)的图象与直线x=a、x=b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积.已知函数y=sinnx在[0, ]上的面积为 (n∈N*),则(1)函数y=sin3x在[0, ]上的面积为____________;(2)函数y=sin(3x-π)+1在[ , ]上的面积为________.解析:(1)令n=3,则y=sin3x在[0, ]上的面积为 .又∵y=sin3x在[0, ]和[ , ]上的面积相等,∴y=sin3x在[0, ]上的面积为 .(2)由y=sin(3x-π)+1,设3φ=3x-π,∴y=sin3φ+1.又∵x∈[ , ],∴3φ∈[0,3π].∴φ∈[0,π].由(1)y=sin3φ在[0, ]上的面积为 ,y=sin3φ在[0,π]上的面积为S1+S2+S3-S4 ,∵ ,∴y=sin(3x-π)+1在[ , ]上的面积为 .答案:(1) (2)“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
