Cha4-4渐近线及作图
chap-4

经数学变换,两组颜色空间色度坐标的相互转换
关系为:
x=(0.490r+0.310g+0.200b)/(0.667r+1.132g+1.200b) y=(0.177r+0.812g+0.010b)/(0.667r+1.132g+1.200b)
z=(0.000r+0.010g+0.990b)/(0.667r+1.132g+1.200b)
1931 CIE-RGB系统标准色度观察者光谱三刺
激值,简称 1931 CIE-RGB系统标准观察者
用很多观察者 来实验,匹配 光谱的各个颜 色,得到很多 组不同的三刺 激值,最后取 它们三刺激值 的平均结果。
1931CIE-RGB系统的光谱三刺激值是从实验得出来
的,本来可以用于颜色测量和标定以及色度学计算, 但是实验结果得到的用来标定光谱色的原色出现了 负值(有些颜色纯度太高),正负交替十分不便,不 宜理解。
2、颜色光的混合
调节上方 三原色光 到适应的 比例,即 可混合出 下方的待 匹配的色 光。
同色异谱:二个颜色在视觉上感觉相同,但光 谱组成却不一样。
二、颜色方程:
用数学的方程形式来描述颜色的匹配实验。 C≡R(R)+G(G)+B(B) ≡:代表匹配,即视觉上相等。 R、G、B代表)、(B)代表混合所用的三原色
在颜色转盘实验中,若处在中间位置的被匹
配的颜色很饱和,那么很难用前面的颜色转 盘实现颜色的匹配。
可把处在外圈的一种原色加到中心被匹配的
颜色上,相当于只用外周的二种颜色来与中 心的颜色匹配。
这样的话,方程 中就可能出现了 负值,但用这种 方法,可使各种 色调和饱和度的 颜色也能匹配的 出来。
4-2函数的凸性4-4作图

x
2
x
0
4.拐点
称连续函数f ( x ) 凹凸性的分界点为曲线 y = f ( x ) 的拐点.
表示法 x0 , f ( x0 )
曲线的弯曲方向——凹凸性; 改变弯曲方向的点——拐点; (1) 拐点的必要条件:
曲线的拐点必是二阶导数为零或二阶导数不存在的点.
(2) 拐点的充分条件:
若 f ( x)在 x0左右异号,则 x0 , f ( x0 )是曲线y = f ( x )
f
( x)
4( x x3
2)
,
f
( x)
8( x x4
1
x2
e 2 的图像.
2
【解】 定义域: (, ) 偶函数
(x)
1
x2
xe 2 ,
( x)
( x 1)( x 1) x2 e2
2
2
( x) 0 x1 0, ( x) 0 x2 1, x3 1
x (, 1) 1 (1, 0) 0 (0,1) 1 (1, )
A oa
曲线的纵坐标
x0 b x
切线的纵坐标
证明:
f (x)
f ( x0 )
f ( x0 )( x x0 )
f
(
2!
)
(
x
x0
)2
介于x与x0之间
由 f ( x) 0 得 f ( x) f ( x0 ) f ( x0 )( x x0 )
(2) 若f ( x ) 是[a, b]上二阶可导的凸函数,则
f ( x) cos x 2 , f ( x) sin x 0
ch4-4

−2
2 9 −5 3 −4 5 3 − 3 −2 2 9 −5 =B 1 −6 1 0 0
于是 R(A = A的列秩 = R )
( B ) =3<5, 1
故,向量组 A的秩为3,且向量组 A 线性相关. (2)由于行阶梯形 B的三个非零行的非零首元 1 在1,2,4三列, 故 a , a2, a4为向量组 A的一个最大无关组. 1 这是因为
α L 向 组 则 量 α1, 2, αn线 相 的 分 要 件 : 性 关 充 必 条是
T 阵 αT L T 的 小 向 的 数 矩 A = (α1 , 2 , ,αn ) 秩 于 量 个 n.
等价定理: 等价定理:
于 行 量 , , 对 n维 向 α j = (a1 j , a2 j ,L anj )( j = 1,2L n)
线性表示;
a , 则称 A: 1, a2,L ar 为 A 的一个最大线性 0
无关向量组(简称最大无关组).
例如,向量组
a1 = (1 ) , a2 = ( 0,1) , a3 = (1 ) ,0 ,1
T T
T
a , a2线性无关, 3 = a +a2 ; a 1 1 a , a3线性无关, 2 =−a +a3 ; a 1 1 a2, a3线性无关, 1 =−a2 +a3 . a
T T
T
1 a4 = ( −2,1 −1 ) , a5 = 2,3,0, , ,1 3
T
T
(1)求向量组 A的秩并判定 A的线性相关性; (2)求向量组 A 的一个最大无关组; (3)将 A中的其余向量用所求出的最大无关组 线性表示.
, 解 (1)以 a , a2, a , a4, a 为列向量作矩阵 A 1 3 5 用初等行变换将矩阵 A 化为行阶梯形
过四点的曲线系方程

过四点的曲线系方程在数学中,当我们谈论过特定数量点的曲线时,我们实际上是在寻找一个方程,该方程能够描述这些点之间的关系。
对于过四点的曲线,通常我们考虑的是二次曲线(如圆、椭圆、双曲线或抛物线)或更高阶的多项式曲线。
然而,需要注意的是,并非所有四个点都可以通过单一的二次曲线或多项式曲线连接。
如果我们假设这四个点不共线(即它们不在同一条直线上),那么我们可以找到一个三次多项式曲线(或更高阶)来穿过这四个点。
但是,如果我们想要一个二次曲线(例如圆或椭圆)穿过这四个点,那么这四个点必须满足特定的条件。
对于一般情况,我们可以使用拉格朗日插值法来找到一个穿过给定点的多项式曲线。
但是,请注意,拉格朗日插值并不保证生成的曲线具有特定的形状(如圆或椭圆)。
如果我们确实想要一个特定类型的曲线(例如圆),那么我们需要使用与该曲线类型相关的特定数学工具。
例如,如果我们想要找到一个穿过四个特定点的圆,我们可以使用以下步骤:1.选择三个点,并使用它们来找到一个圆。
这可以通过找到这三个点的外接圆来完成。
2.检查第四个点是否也在这个圆上。
如果不在,那么不存在一个圆可以同时穿过这四个点。
3.如果第四个点确实在圆上,那么我们找到了一个解。
但是,请注意,可能存在多个不同的圆可以同时穿过这四个点(特别是当这四个点共圆时)。
对于更复杂的曲线类型(如椭圆或双曲线),找到穿过四个特定点的曲线将需要更复杂的数学工具和技术。
然而,如果你只是想要一个多项式曲线穿过四个点,并且不关心它的具体形状,那么拉格朗日插值法是一个很好的选择。
这种方法可以生成一个穿过给定点的多项式曲线,但请注意,生成的多项式可能具有很高的阶数(特别是当给定的点数量很大时)。
水平渐近线

y=4(x-1)/X^2的水平渐近线需过程解:当x->+∞/-∞时,lim[4(x-1)/X^2]=lim4/(2x)=0=>y=0故y=4(x-1)/X^2的水平渐近线为y=0渐近线编辑词条编辑摘要摘要目录1渐近线编辑本段渐近线渐近线特点:无限接近,永不相交定义当曲线上一点M沿曲线无限远离原点时,如果M到一条直线的距离无限趋近于零,那么这条直线称为这条曲线的渐近线。
例如,直线是双曲线}-的渐近线,因为双曲线上的点M到直线的距离MQ< MN;当MN无限趋近于0时,MQ也无限趋近于0。
所以按照定义,直线是该双曲线的渐近线。
同理,直线也是该双曲线的渐近线。
对于来说,如果当时,有,就把x = a叫做的垂直渐近线;如果当时,有,就把y = b 叫做的水平渐近线。
例如,y = 3是曲线xy = 3x + 2的水平渐近线。
求渐近线,可以依据以下结论:若极限存在,且极限也存在,那么曲线具有渐近线y = ax + b。
例:求的渐近线。
解:(1)x = - 1为其垂直渐近线。
(2),即a = 1;,即b = - 1;所以y = x - 1也是其渐近线。
例如,直线是双曲线的渐近线,因为双曲线上的点M到直线的距离MQ < MN;当MN无限趋近于0时,MQ也无限趋近于0。
所以按照定义,直线是该双曲线的渐近线。
同理,直线也是该双曲线的渐近线。
对于来说,如果当时,有,就把x = a叫做的垂直渐近线;如果当时,有,就把y = b叫做的水平渐近线。
例如,y = 3是曲线xy = 3x + 2的水平渐近线。
求渐近线,可以依据以下结论:若极限存在,且极限也存在,那么曲线具有渐近线y = ax + b。
例:求的渐近线。
解:(1)x = - 1为其垂直渐近线。
(2),即a = 1;,即b = - 1;所以y = x - 1也是其渐近线。
函数作图的基本步骤与方法(精)

(3)当x 1时, y , 所以 x 1 是一条铅垂渐近线. b2 4ac
a lim f ( x) 2 lim(1 2 )1 x x x x 1 2x 而b lim[ f ( x ) ax ] lim( x 2 x) 0 x x x 1
(5)根据以上讨论, 列表、描点并作出函数 y = ƒ(x)的 图形.
2
例32 作函数 f ( x )
1 2
e
x2 2
的图形.
解 (1)定义域 D (, ) (2)因ƒ(–x) = ƒ(x), 则ƒ(x)为偶函数, 其图形关于 y 轴对 称, 从而只讨论 ƒ(x) 在 [0, ) 的情形
y 0.4 0.3 0.2 0.1 o
•
•
–2 –1
•
1 2
5
x
例32 作函数
f ( x) x
2x x2 1
的图形.
解 (1)定义域 D (, 1) (1,1) (1, ) (2) x = ±1 为无穷间断点. 而ƒ(–x) = –ƒ(x),则ƒ(x)为奇函数, 其图形关于原点对称, 从而只讨论ƒ(x)在 (0,1) (1, ) 的情形.
x
f ( x) f ( x)
0
0
(0, 1)
1
(1, )
–
极大值
ƒ(x)
1 2
– –
拐点
–
0
(1, 1 2 e )
– +
4
(5)描出点(0,
1 2
),(1,
1 2 e
)
(6)综合上述讨论, 可画出函数 在 y 轴右侧的图形, 再按图形 关于y轴对称, 画出y轴左侧的 图形. 如左图:
函数渐近线及函数图形的描绘

使用图形计算器绘制函数图形
简单易用、无需额外设置
图形计算器的操作通常非常简单,只需要选择相应的函数 类型或输入函数表达式,就可以自动绘制出相应的图形。 用户无需进行复杂的设置或调整参数,使得绘图过程更加 快速和简便。
使用图形计算器绘制函数图形
功能相对有限
VS
相对于数学软件,图形计算器的功能 相对有限。它们通常只能绘制基本的 函数图形,如直线、二次函数、三角 函数等,而无法绘制更复杂的函数图 形或进行高级的图形定制。
功能强大、精确度高
数学软件如Matlab、Mathematica和Maple等,提供了强大的绘图工具和函数 库,可以绘制各种复杂的函数图形,包括三维图形和极坐标图形。这些软件通常 具有高精度的计算和绘图能力,能够准确地表示函数的形状和变化趋势。
使用数学软件绘制函数图形
操作简便、可视化效果好
这些软件通常具有直观的用户界面和易于操作的命令语言,使得用户可以轻松地绘制函数图形。同时,这些软件还提供了丰 富的颜色、线条样式和标记工具,使得绘制的图形更加生动和易于理解。
验证模型
通过比较函数渐近线和实际数据,可以验证数学模型的准确 性和可靠性。
在科学计算中的应用
数据拟合
在科学实验中,利用函数渐近线可以 对实验数据进行拟合,得到更准确的 结论。
理论推导
在理论推导中,函数渐近线可以作为 理论依据,帮助推导出新的科学理论。
04 函数图形的描绘工具和技 术
使用数学软件绘制函数图形
平移变换
对称变换
将函数图像沿x轴或y轴方向平移一定 的距离。
将函数图像关于原点、x轴或y轴进行 对称。
伸缩变换
将函数图像在x轴或y轴方向上伸缩一 定的比例。
函数作图知识
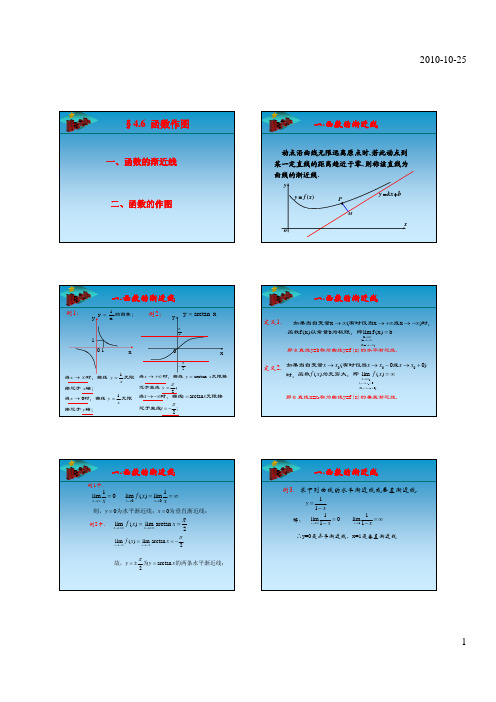
例2 :
y
2
定义1.
如果当自变量x (有时仅当x 或x )时, 函数f ( x )以常量b为极限,即 lim f ( x ) b
x
(x 或x )
1 01 x 0
2
x
那么直线y=b称为曲线y=f(x)的水平渐近线 那么直线y=b称为曲线y=f(x)的水平渐近线.
定义2. 如果当自变量x x0 (有时仅当x x0 0或x x0 0)
时,函数 f ( x )为无穷大,即 lim f ( x )
(x x0 0 或x x0 0)
x x0
那么直线x=x0称为曲线y=f(x)的垂直渐近线.
一.函数的渐近线
例1 中.
一.函数的渐近线
例5. 求曲线y
一.函数的渐近线
1 的渐近线. x 1
如上图, lim
x 1
1 , x 1
故直线x 1为曲线y
如上图, lim ln x ,
x 0 0
1 又 lim 0, x x 1
1 的垂直渐近线. x 1 1 的水平渐近线. x 1
故直线x 0为曲线y ln x的垂直渐近线.
求出方程 f " ( x ) 0 在函数定义域内的全部实 根, 用这些根同函数的间断点或导数不存在的点把 函数的定义域划分成几个凸性区间,求其拐点。 函数的定义域划分成几个凸性区间 求其拐点
( 2 ) 求函数的单调区间 , 极值 ;
求出方程 f ' ( x ) 0 在函数定义域内的全部 实根, 用这些根同函数的间断点或导数不存在的点 把函数的定义域划分成几个单调区间, 并求其极值
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
A 2 2 1
−2 D
0
3
x
C
B
( 3) y" = 6 x − 12 , 令 y" = 0 , 得 x3 = 2 .
(4)
x
( −∞ , 1)
+
1
(1 , 2)
−
2
( 2, 3 )
3 0
+
极小 值
(3 , + ∞)
+
y' y"
y
0
−
0
拐点
−
−
极大 值
−
+
+
极大值 A(1,2) ; 极小值 B( 3,−2) ; 拐点 C ( 2,0) . 补充: D ( 0, − 2 ) .
( 2) 求出 f ' ( x )、f '' ( x ) 的零点和不存在的点;
(3) 讨论单调区间、极值、凸性区间、拐点; (4) 渐近线、变化趋势; (5) 增补点、作图。
例 1. 作函数 解
f ( x) = e
−1
x
的图形.
(1) 定义域 ( −∞ , 0) U (0 ,+∞ ) 值域 (0 , 1) U (1 , + ∞ )
= e
1
1 x
< 1.
y
1
0
x
例 2. 作函数 解
y = x 3 − 6 x 2 + 9 x − 2 的图形.
(1) 定义域: ( −∞,+∞ ).
( 2) y' = 3 x 2 − 12 x + 9 = 3( x − 1)( x − 3)
令 y' = 0 , 解得 x1 = 1 , x2 = 3 .
2. 水平渐近线
若 lim f ( x ) = b 或 lim f ( x ) = b,则称 y = b 为 f ( x ) 的水平渐近线.
x → +∞ x → −∞
例如
y = arctan x
水平渐近线为 y = ±
π
2
二. 函数图形的描绘 函数作图的一般步骤
(1) 定义域 ( 值域 )、奇偶性、周期性、间断点、与坐标轴的交点;
f ( x)
0
−
1 −2 ( ,e ) 拐点 2
(4)
x →0
lim e
−
−1
x
= +∞
∴ 垂直渐近线为
x=0
x →0+ x →∞
lim e
−1
x
=0
lim e
−1
x
=1
∴ 水平渐近线为
y = 1.
− 1 x
1 − > 0, 当 x < 0 时, x
(5) 作图
e
−
1 x
> 1;
当 x > 0 时, e
间断点
x=0
−1 x
(2)
1 f '( x ) = 2 e x
令 f ' ' ( x ) = 0,
> 0,
得 x= 1 2
f ''( x ) =
e
−1
x
x
4
(1 − 2 x )
(3)
x
( −∞ , 0)
+ +
1 (0 , ) 2
+ +
1 2
+
1 ( , + ∞) 2
+
f '( x ) f '' ( x )
§ 4.4 渐近线及函数作图
一. 渐近线
1. 垂直渐近线
若 lim f ( x ) = ∞ 或 lim f ( x ) = ∞ ,则称 x = x0 为 y = f ( x ) 的
x → x0 + x → x0 −
垂直渐近线.
例如 y= 1 ( x + 1)( x − 3)
垂直渐近线为 x = −1,x = 3
