科大610分析与代数2015大纲
中国科技大学610分析代数2020年考研专业课初试大纲

2020年硕士研究生招生考试自命题科目考试大纲
考试科目代码及名称 610分析与代数
一、考试范围及要点
数学分析部分
1. 数列和函数的极限
2. 函数的单调性、连续性、凹凸性和极值
3. 一元函数的微分、不定积分和定积分
4. 多变量函数的微分和重积分
5. 无穷级数的收敛性
6. 广义积分和含参变量积分
线性代数部分
1. 行列式的计算
2. 矩阵的代数运算
3. 线性方程组的求解
4. 线性空间和线性变换
5. 方阵的特征值和特征向量
6. 矩阵相合与相似(欧式空间、正交化、二次型、正定阵、标准型等)
二、考试形式与试卷结构
考试形式
1.试卷满分为150分, 考试时间为3小时
2.闭卷、笔试
3.不使用计算器
试卷结构
1.题型为计算题和证明题
2.分析部分80分、代数部分70分
参考书目名称 作者 出版社 版次 年份 微积分 谢盛刚等 科学出版社 第二版 2011 线性代数 李尚志 高等教育出版社 第一版 2006。
教学大纲_实变函数与泛函分析

《实变函数与泛函分析》教学大纲课程编号:120233B课程类型:□通识教育必修课□通识教育选修课□专业必修课□专业选修课□√学科基础课总学时:48 讲课学时:48 实验(上机)学时:0学分:3适用对象:经济统计学先修课程:数学分析、高等代数、空间解析几何毕业要求:1.应用专业知识,解决数据分析问题2.可以建立统计模型,获得有效结论3.掌握统计软件及常用数据库工具的使用4.关注国际统计应用的新进展5.基于数据结论,提出决策咨询建议6.具有不断学习的意识一、课程的教学目标本课程以实变函数与泛函分析基本理论为基础,教学的目的是丰富学生的知识和培养学生解决实际问题的能力。
本课程就其实质来说是方法性的,但对于应用学科的学生来说,作为授课的目的,则是知识性的,故在教学方法和内容的选择上来说,只能让学生了解那些体现实变函数与泛函分析基本特征的思想内容,冗难的证明过程应尽量避免。
本课程基本目标为:能理解、掌握Lebesgue测度和Lebesgue积分,赋范空间和Hilbert空间一些基本概念、基本理论和基本方法。
本课程的难点在于学生初次涉及众多的抽象概念,并且论证的部分很多,教学中应密切结合数学分析中学到的相对来说比较直观的内容讲解,并督促学生下工夫理解。
二、教学基本要求(一)教学内容及要求《实变函数与泛函分析》在理解数学分析思想及基本知识和线性代数的基本知识后将其拓展到实数域上,进而讨论集合,欧氏空间,Lebesgtle测度,Lebesgue 可测函数,Lebesgue积分,测度空间,测度空间上的可测函数和积分,L^p空间,L^2空间,卷积与Fourier变换,Hilbert空间理论,Hilbert空间上的有界线性算子,Banach空间,Banach空间上的有界线算子,Banach空间上的连续线性泛函、共轭空间与共轭算子,Banach空间的收敛性与紧致性。
其中要求同学们:1. 理解和掌握集合间的关系和集与映射间的关系,了解度量空间的相关概念和Lebesgue可测集的有关内容和性质。
考研数学一大纲变化与趋势分析

考研数学一大纲变化与趋势分析近年来,考研数学一科目的大纲发生了一些变化,本文将对这些变化进行分析,并且展望未来的趋势。
第一部分:大纲变化一、知识点调整从过去的大纲来看,考研数学一科目的知识点主要分为数学分析和线性代数两个部分。
然而,最新的大纲调整在这两个部分中进行了细化和调整。
数学分析中的微积分、极限和级数等内容得到了更加详细的规定,要求考生对这些概念和方法有更深入的理解。
线性代数中的矩阵和行列式、向量空间以及线性变换等内容也有所调整,要求考生能掌握更多的线性代数的基本概念和技巧。
二、题型改革考研数学一科目的题型一直以来都是以计算为主。
然而,随着考研数学一科目的知识点的增加和知识要求的提高,在最新的大纲中对题型进行了相应的改革。
除了传统的计算题外,还增加了多项式插值、数列极限、极值与最值以及概率与统计等题型。
这些题型更注重考察考生对数学概念的理解和应用能力,帮助考生培养出解决实际问题的能力。
第二部分:趋势分析一、综合能力的考察随着社会对综合素质人才的需求越来越大,未来考研数学一科目的趋势将更注重考察考生的综合能力。
除了对数学概念和方法的理解和应用,还将注重数学建模和解决实际问题的能力。
这意味着考生需要不仅掌握数学知识,还要培养出实际运用数学解决问题的能力。
二、难度提升为了选拔更优秀的考生,考研数学一科目的难度将会不断提升。
这不仅体现在知识点的增加和题型的改革上,还体现在对考生数学思维能力和逻辑推理能力的要求上。
未来的考研数学一科目将更加注重对考生深层次的思考能力和创新能力的考察,希望考生能够在解决复杂问题时展现出扎实的数学素养。
三、技巧的培养随着考研数学一科目的难度提升,考生在备考过程中需要不断提升解题的技巧。
未来的趋势将更加注重考察考生的数学思维方法和解题技巧。
考生需要通过大量的练习和解题经验的积累,培养自己解决各类数学问题的技巧,并且能够在考场上熟练应用。
结论:综上所述,考研数学一大纲在知识点调整和题型改革方面发生了一些变化。
新课标“数与代数”内容分析:从结构到要求

和!#!!年颁布的-义务教育数学课程标准 题整合成%数与运算&%数量关系&两个主题!
"!#!!年版#."以下简称%新课标&#也保持了这 初中部分的%数与式&%方程与不等式&%函数&
一做法(在前两版课标中!%数与代数&领域的 三个主题保持不变(
内容逐步丰富和完善!但是!依然存在数的概 将%数的认识&%数的运算&整合为%数与
"二#%数量关系&内容要求分析 %数量关系&主题贯穿于小学阶段的三个 学段(与!#""年版课标相比!新课标这一主 题的变化主要是$将%方程&%反比例&调整到 初中阶段!增加了%能用字母表示运算律&%认
算'运算律等!充分体现了%研究对象)&的设 计理念( 这样的呈现将数的认识与数的运 算的学习统一起来!因为数的运算最终是要
数量关系的延伸和扩展
位的含义知道用算盘可以表示多位数了
综上可知通过主题整合突出了不同阶 解符号"-#的含义会比较万以内数的
段的核心内容使得数与代数领域的内容结 大小通过数的大小比较感悟相等和不等关
构更具统整性同时也加强了小学与初中内 系这清晰地指出了第一学段数内容的学
学习领域(同时!小学数学课程中逐步渗透 代数的内容!如"*(,年的小学数学教学大纲
"!#!!年版吕#世.课虎程教内授容团深队度的分-析义系务列教文育章数之学三课(程标准
!%! 教育研究与评论 中学教育教学年月
Copyright©博看网. All Rights Reserved.
标准"!#""年版#."以下简称%!#""年版课标&# 索规律&%式与方程&%正比例'反比例&六个主
《高等代数与解析几何》教学大纲
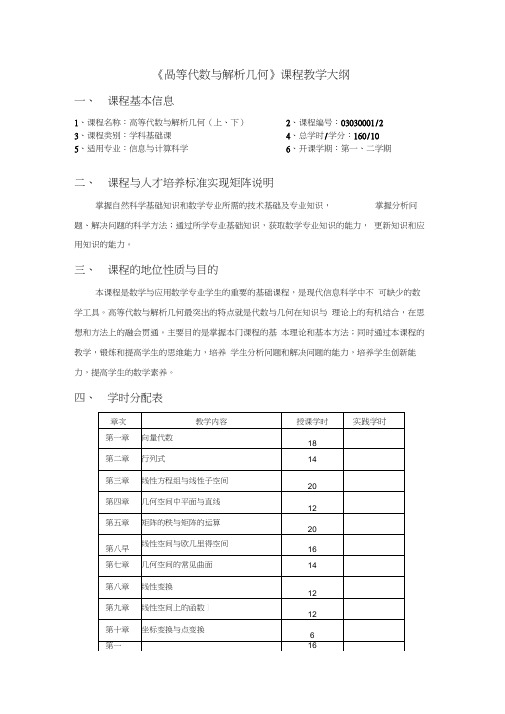
《咼等代数与解析几何》课程教学大纲一、课程基本信息1、课程名称:高等代数与解析几何(上、下)2、课程编号:03030001/23、课程类别:学科基础课4、总学时/学分:160/105、适用专业:信息与计算科学6、开课学期:第一、二学期二、课程与人才培养标准实现矩阵说明掌握自然科学基础知识和数学专业所需的技术基础及专业知识,掌握分析问题、解决问题的科学方法;通过所学专业基础知识,获取数学专业知识的能力,更新知识和应用知识的能力。
三、课程的地位性质与目的本课程是数学与应用数学专业学生的重要的基础课程,是现代信息科学中不可缺少的数学工具。
高等代数与解析几何最突出的特点就是代数与几何在知识与理论上的有机结合,在思想和方法上的融会贯通。
主要目的是掌握本门课程的基本理论和基本方法;同时通过本课程的教学,锻炼和提高学生的思维能力,培养学生分析问题和解决问题的能力,培养学生创新能力,提高学生的数学素养。
四、学时分配表五、课程教学内容和基本要求总的目标:通过本课程的学习要求学生对高等代数与解析几何的基本概念、基本定理有比较全面、系统认识,能把几何的观点与代数的方法结合起来,“代数为几何提供研究方法,几何为代数提供直观背景”,逐步培养学生运用几何与代数相结合的方法分析问题、解决问题的能力,培养学生抽象的思维能力及空间想象能力。
本课程各章的教学内容和基本要求如下:第一章向量代数【教学内容】1、向量的线性运算2、向量的共线与共面3、用坐标表示向量4、线性相关性与线性方程组5、n维向量空间6、几何空间向量的内积7、几何空间向量的外积8、几何空间向量的混合积【基本要求】理解向量的概念,掌握向量的线性运算、内积、外积、混合积运算;熟悉向量间垂直、共线、共面的条件;会用坐标进行向量的运算。
【教学重点及难点】重点:向量的概念,向量的线性运算、内积、外积、混合积运算;用坐标进行向量的运算。
难点:向量间垂直、共线、共面的条件。
第二章行列式【教学内容】1、映射与变换2、置换的奇偶性3、矩阵4、行列式的定义理解n阶行列式的概念及性质,掌握常见类型的行列式的计算;熟悉克拉默法则。
数学分析610研究生入学考试大纲

《数学分析》(610)研究生入学考试大纲一、参考书目:1.《数学分析》第四版(上、下册)华东师范大学数学系编(高等教育出版社)。
2.《数学分析》(上、下册)盛炎平等编(机械工业出版社)。
二、考试大纲:(第一章~第二十二章,所有带*号的部分不用看)第一章实数集与函数数集的确界,确界原理.第二章数列极限极限定义,收敛数列性质,单调有界原理,重要极限.第三章函数极限函数极限定义,函数极限性质,两个重要极限,无穷大量与无穷小量,渐近线.第四章函数连续性函数连续概念,间断点分类,连续函数的性质,一致连续的概念.第五章导数与微分导数概念,导数几何意义,求导法则,基本求导公式,参变量函数求导,高阶导数,微分的概念,几何意义.第六章微分中值定理及其应用罗尔定理,拉格朗日定理,函数单调性的判定,柯西中值定理,不定式极限的罗必达法则,泰勒公式,,函数极值的判定,最值问题,函数凹凸性的判定.第七章实数的完备性了解刻画实数完备性定理的内容.第八章不定积分原函数与不定积分概念,基本积分公式,换元法与分部积分法.第九章定积分定积分概念,定积分性质,牛顿-莱布尼兹公式,变限积分和原函数存在定理,积分中值定理,计算积分的换元法与分部积分法.第十章定积分应用计算平面图形面积,立体体积,曲线弧长,旋转曲面面积.第十一章反常积分无穷积分和瑕积分的概念和性质,非负无穷积分和瑕积分的比较判别法,一般无穷积分和瑕积分的狄立克莱判别法和阿贝尔判别法.第十二章数项级数级数收敛的定义,级数的性质,正项级数的比较、根值、比值判别法,一般项级数的阿贝尔判别法和狄立克雷判别法.第十三章函数列与函数项级数函数列的一致收敛性,一致收敛的柯西准则及充要条件,一致收敛函数列的极限函数的性质,函数项级数一致收敛概念,判别法,一致收敛函数项级数的性质.第十四章幂级数幂级数的收敛半径、收敛区间、收敛域,收敛半径的计算,幂级数的性质,泰勒级数,初等函数的幂级数展开.第十五章傅立叶级数三角级数,正交系,收敛定理,周期函数的傅里叶展开,偶函数与奇函数的傅里叶级数与展开.第十六章多元函数的极限与连续二元函数的极限与连续.第十七章多元函数微分学偏导数的概念,全微分的概念,偏导数的几何意义,复合函数的求导法则,方向导数与梯度的概念,多元函数的极值问题.第十八章隐函数定理及其应用了解隐函数定理,会隐函数求导,曲线的切线,曲面的切平面与法线,条件极值问题.第十九章含参积分该章不考察.第二十章曲线积分第一型曲线积分定义与计算,第二型曲线积分的定义与计算,两类积分的联系.第二十一章重积分二重积分的概念、性质,直角坐标计算,极坐标计算,格林公式,曲线积分与路径的无关性,三重积分的定义,性质,利用直角坐标计算,柱坐标计算,球坐标计算.第二十二章曲面积分第一型曲面积分定义与计算,第二型曲面积分的定义与计算,高斯公式与斯托克斯公式三、试卷结构:1.概念简答题;2.计算题;3.证明题.。
601《数学分析》考试大纲

601《数学阐发》测验大纲一、大纲综述数学阐发是大学数学系本科学生的最根本课程之一,也是大都理工科专业学生的必修根底课。
为帮忙考生明确测验范围和有关要求,特制订《数学阐发》测验大纲。
《数学阐发》测验大纲按照北京林业大学数学与应用数学本科《数学阐发》教学大纲编制而成,适用于报考北京林业大学数学学科各专业〔根底数学、概率论与数理统计、计算数学、应用数学〕硕士学位研究生的考生。
参考书目以华东师范大学数学系编写的教材为主,其他两个参考书目为辅。
二、测验内容1.实数集与函数〔1〕确界概念,确界道理〔2〕函数概念与运算,初等函数2.数列极限〔1〕数列极限的ε一N定义〔2〕收敛数列的性质〔3〕数列的单调有界法那么,柯西收敛准那么,重要极限3.函数极限(1) 函数极限的ε一M定义和ε一δ定义,单侧极限(2) 函数极限的性质(3) 海涅定理〔归结原那么〕,柯西收敛准那么,两个重要极限(4) 无穷小量与无穷大量的定义、性质,无穷小〔大〕量阶的比拟4.函数的持续性(1) 函数在一点持续,单侧持续和在区间上持续的定义,间断点的类型(2) 持续函数的局部性质。
复合函数的持续性,反函数的持续性。
闭区间上持续函数的性质。
(3) 一致持续的定义,初等函数的持续性5.导数与微分(1) 导数的定义,导数的几何意义(2) 导数四那么运算、反函数导数、复合函数导数,求导法那么与求导公式(3) 参数方程所确定的函数的导数,高阶导数(4) 微分概念、微分根本公式,微分法那么,一阶微分形式的不变性。
微分在近似计算中的应用,高阶微分6.微分中值定理及其应用(1) 费马定理,罗尔定理,拉格朗日定理(2) 柯西中值定理,罗比达法那么,不定式极限(3) 泰勒公式(4) 函数的单调性、凸性与拐点、极值与最值(5)渐近线,函数作图。
7.实数的完备性〔1〕区间套定理,柯西收敛准那么,聚点定理,有限覆盖定理,致密性定理〔2〕闭区间上持续函数的性质及证明8.不定积分〔1〕原函数与不定积分的概念,根本积分表,线性运算法那么〔2〕换元积分法,分部积分法〔3〕有理函数的积分法。
中科大数学考研参考书

中科大数学考研参考书
1. 《数学分析》(第三版) 作者: 陈纪修
2. 《高等代数》(第三版) 作者: 杨宝森
3. 《常微分方程教程》(第二版) 作者: 郑蕴良
4. 《概率论与数理统计》(第二版) 作者: 陈希孺
5. 《复变函数与积分变换》(第二版) 作者: 陈纪修
6. 《数学物理方程(高等数学)》(第二版) 作者: 张家荣
7. 《数学物理方程(偏微分方程)》(第二版) 作者: 刘石泉
8. 《泛函分析初步》(第二版) 作者: 吴赛凤
9. 《实变函数与泛函分析》(第二版) 作者: 杨维国
10. 《拓扑学导论》(第二版) 作者: 何士晋
11. 《数值分析》(第二版) 作者: 吴建平
12. 《非线性泛函分析及其应用》(第三版) 作者: 马昭宏
13. 《微分几何及其应用》(第三版) 作者: 李文博
14. 《偏微分方程及其应用》(第二版) 作者: 高洪岩
15. 《代数拓扑学》(第二版) 作者: 周民强。
- 1 -。
