图像距离
图聚类的概念

图聚类的概念图聚类是一种数据挖掘技术,主要用于将大量的图像数据分组,将相似的图像归为一类。
图聚类涉及多个领域,如计算机视觉、模式识别、机器学习等,是一项非常有挑战性的任务,因为相比于传统的向量数据,图像数据的特征维度更高,信息更丰富,因此,如何在保持图像特征的完整性和高维性的前提下实现快速有效的分组,是图聚类的一项重要目标。
图聚类可以应用于很多领域。
例如,一个电影网站可能会使用图聚类来推荐电影,将用户拥有相似喜好的电影进行分组,并对用户进行推荐。
另一个例子是,用于医学图像分析,通过对医学图像进行聚类,可以帮助医生快速准确地诊断疾病。
在图聚类中,最基本的任务是寻找图像之间的相似性。
这可以通过测量图像之间的距离或相似性度量来实现。
图像距离通常是指两张图像之间的欧几里德距离,其中每个像素的颜色和位置的差异都会影响距离。
然而这种方法效率较低,当数据量较大、高维时,可能会导致结果不准确、耗时较长。
因此,一些研究者将此问题转化为计算每个图像之间的相似性。
这种方法使用相似性度量,其结果是图像相似性矩阵。
相似性度量定义的多种方式可以用于不同的图像表示方法和算法。
图聚类可以归入两个主要的框架:基于子图的方法和基于图谱的方法。
基于子图的方法将相似的节点集合合并为子图,并使用一些度量方法对子图进行聚类。
基于图谱的方法则将图像之间相似性表示为图谱,并利用图嵌入方法对图像进行聚类。
两种方法各有优缺点,在实际应用中需要根据具体的需求来选择。
图聚类还需要面对许多挑战。
其中一个挑战是运行成本。
由于数据维度和对象数量的增加,计算时间和内存需求也会随之增加。
通常,在图聚类之前需要进行一些预处理操作,如降维、缩放、去噪等,以减少维度和保持图像特征,同时提高运行效率。
另一个挑战是聚类结果的可解释性。
除了聚类的精确率之外,如果聚类算法不能解释结果,从而使得用户难以理解结果,也会降低算法的可接受度。
总体而言,图聚类是一项非常有挑战性和实用性的任务。
已知像素大小和焦距 计算最小成像距离的公式

题目:已知像素大小和焦距计算最小成像距离的公式一、概述在计算机视觉和图像处理领域,如何准确地计算图像的成像距离一直是一个重要的问题。
图像的成像距离与像素大小和焦距有着密切的关系。
本文将从已知像素大小和焦距出发,探讨如何计算图像最小成像距离的公式。
二、像素大小和焦距的关系1. 像素大小:在数字图像中,像素是图像的最小单元,每个像素代表图像中的一个小点。
像素大小通常用长度单位表示,比如毫米、微米等。
2. 焦距:在光学系统中,焦距是指从凸透镜或凹透镜的光心到使平行光线在其上焦同一点的距离。
焦距通常用长度单位表示,比如毫米、厘米等。
3. 成像距离:成像距离是指物体到透镜的距离,也是图像在光学系统中的具体位置。
三、计算最小成像距离的公式已知像素大小p和焦距f,可以通过以下公式计算最小成像距离d:其中,d为最小成像距离,p为像素大小,f为焦距。
四、应用举例以下以实际应用举例说明如何利用已知像素大小和焦距计算最小成像距离。
假设已知某数码相机的像素大小p为5μm(微米),焦距f为25mm,在拍摄距离为100mm的情况下,计算其最小成像距离。
根据公式d = p * f,代入已知数值进行计算:d = 5μm * 25mm= 0.005mm * 25mm= 0.125mm此数码相机在拍摄距离为100mm时的最小成像距离为0.125mm。
五、结论本文通过讨论已知像素大小和焦距计算最小成像距离的公式,阐明了像素大小和焦距对图像成像距离的影响。
在实际应用中,掌握这一公式可以帮助我们准确地计算图像的成像距离,为图像采集和处理提供六、展望未来随着图像处理和计算机视觉的发展,对成像距离的需求将会更加广泛和迫切,通过对像素大小和焦距的进一步研究,可能会提出更加精确和实用的成像距离计算模型,为图像领域的发展带来更多的可能性和机遇。
七、参考文献[1] 高等物理学教程(第3版),北京:高等教育出版社,2008年。
[2] 红外焦平面阵列成像系统的成像质量检测,光学仪器与技术,2015年,第11期。
平面镜知识点

平面镜知识点摘要:本文旨在阐述平面镜的基本原理、成像特性以及在日常生活和科学技术中的应用。
通过对平面镜的物理特性进行分析,可以帮助读者更好地理解反射现象以及平面镜在不同领域的实际用途。
1. 平面镜的定义平面镜是一种具有平滑反射表面的镜子,它能够反射光线,形成清晰的图像。
平面镜的反射面可以是玻璃背面涂上反射层,也可以是金属涂层。
在理想情况下,平面镜的表面是完全平整的,这样可以确保光线按照可预测的方式反射。
2. 反射定律平面镜的工作原理基于光的反射定律,该定律包含两个主要内容:- 入射光线、反射光线和法线都位于同一平面内。
- 入射光线与法线之间的角度等于反射光线与法线之间的角度,这个角度称为入射角和反射角。
3. 平面镜成像特性- 对称性:平面镜所形成的图像是对称的,即物体与图像关于镜面对称。
- 大小:图像的大小与物体相同。
- 距离:图像距离镜面的距离与物体距离镜面的距离相等。
- 虚像:平面镜产生的是虚像,即图像不能在屏幕上捕捉到,它看起来像是在镜子后方。
4. 平面镜的应用- 光学仪器:平面镜在望远镜、显微镜等光学仪器中有广泛应用。
- 装饰:在室内装饰中,使用平面镜可以增加空间感。
- 安全:后视镜和安全反光镜等利用平面镜来扩大视野,提高安全性。
- 科学实验:在物理学实验中,平面镜用于研究光的反射和光学路径。
5. 平面镜的制造和维护- 制造:高质量的平面镜需要精确的抛光和涂层技术,以确保反射面的平整度和反射率。
- 维护:为了保持平面镜的清晰度和反射效果,需要定期清洁镜面,并避免刮擦和破损。
6. 结论平面镜是物理学中的一个基本概念,它不仅在科学研究中有重要应用,也是日常生活中不可或缺的工具。
了解平面镜的工作原理和特性,可以帮助我们更好地利用这一技术,并在各种场合发挥其作用。
以上是关于平面镜知识点的简要介绍。
文章的结构清晰,内容连贯,并且避免了不必要的背景信息。
文档格式规范,无乱码或错乱字符段落,可供阅读者下载后进行编辑和修改。
ai条件对象间距

ai条件对象间距
AI条件对象间距是指条件对象之间的相似度或差异度。
在AI 中,条件对象是指一个具体的实例或事物,可以是文本、图像、音频等形式。
条件对象间距离通常通过计算它们之间的相似性或差异性来确定。
常见的计算条件对象间距的方法包括:
1. 欧氏距离:对于数值型的条件对象,可以使用欧氏距离来计算其差异度。
欧氏距离是指两个对象之间的直线距离。
例如,对于两个二维坐标点A(x1, y1)和B(x2, y2),欧氏距离可以通
过计算sqrt((x2-x1)^2 + (y2-y1)^2)来得到。
2. 余弦相似度:对于文本或向量型的条件对象,可以使用余弦相似度来计算它们的相似度。
余弦相似度是通过计算两个向量之间的夹角来确定的。
相似度的取值范围在0到1之间,值越接近1表示越相似,值越接近0表示越不相似。
3. 编辑距离:对于文本型的条件对象,可以使用编辑距离来计算它们的相似度。
编辑距离是指从一个文本转换到另一个文本所需的最小编辑操作数,如插入、删除、替换等。
编辑距离越小表示两个文本越相似。
4. 图像距离:对于图像型的条件对象,可以使用图像特征提取方法,如卷积神经网络,来提取图像的特征向量,然后计算特征向量之间的距离来确定图像之间的相似度。
以上只是一些常见的计算条件对象间距的方法,实际应用中可以根据具体的需求和条件对象的特征选择适合的方法来计算距离。
谷歌地图的级别与对应比例尺及分辨率探究

谷歌地图的级别与对应比例尺及分辨率探究谷歌推出的免费在线卫星地图、电子地图也已经有些年头了,无论是出于个人爱好还是商业目的,大家都在分享谷歌提供的这份丰盛的免费午餐。
至于如何获取谷歌的免费地图,这个不用多讲,百度一下就能找到各种谷歌地图下载器工具。
以截屏方式获取的,或直接从谷歌服务器上下载的,收费的,免费的,应用尽有,这个不是今天我们要讨论的主题!谷歌的免费地图是容易下载的,但没有哪款地图下载器工具是有比例显示的,这个问题很严重!即便是简单的应用,如打印个挂图什么的也需要有比例尺作参照,如果要作深层次的专业应用,比例尺就更重要了,是必须的,也是必不可缺少的。
目前谷歌地图大概分为22个层级(国内一般只到20级,国外有20级以上的),每个层级比例尺不相同,如果我们能知道每个图层的比例尺对于我们下载来说也是件很轻松的事,可以直接选择下载适合自已应用比例的层级,何乐而不为?为了方便他人,也方便自已,今天就来分析解决这一问题:探究谷歌地图各层级的对应比例尺和分辨率!一、什么是比例尺?比例尺是表示图上距离比实地距离缩小的程度,也叫缩尺。
公式为:比例尺=图上距离/实地距离。
比例尺有三种表示方法:数字式,线段式,和文字式。
三种表示方法可以互换。
根据地图的用途,所表示地区范围的大小、图幅的大小和表示内容的详略等不同情况,制图选用的比例尺有大有小。
地图比例尺中,通常大于二十万分之一的地图称为大比例尺地图;比例尺介于二十万分之一至一百万分之一之间的地图,称为中比例尺地图;比例尺小于一百万分之一的地图,称为小比例尺地图。
在同样图幅上,比例尺越大,地图所表示的范围越小,图内表示的内容越详细,精度越高;比例尺越小,地图上所表示的范围越大,反映的内容越简略,精确度越低。
一般讲,大比例尺地图,内容详细,几何精度高,可用于图上测量。
小比例尺地图,内容概括性强,不宜于进行图上测量。
二、什么是分辨率我们这里探讨的分辨率是指卫星影像分辨率。
追及 vt图像 距离极值 微解题
追及vt图像距离极值微解题
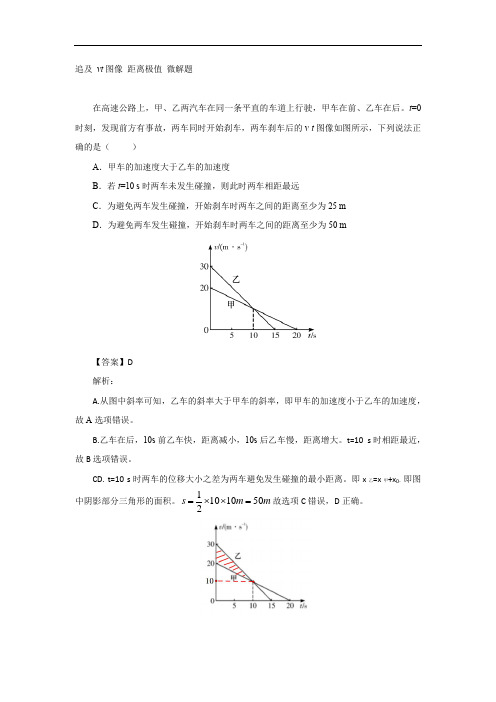
在高速公路上,甲、乙两汽车在同一条平直的车道上行驶,甲车在前、乙车在后。
t=0时刻,发现前方有事故,两车同时开始刹车,两车刹车后的v-t图像如图所示,下列说法正确的是()
A.甲车的加速度大于乙车的加速度
B.若t=10 s时两车未发生碰撞,则此时两车相距最远
C.为避免两车发生碰撞,开始刹车时两车之间的距离至少为25 m
D.为避免两车发生碰撞,开始刹车时两车之间的距离至少为50 m
【答案】D
解析:
A.从图中斜率可知,乙车的斜率大于甲车的斜率,即甲车的加速度小于乙车的加速度,故A选项错误。
B.乙车在后,10s前乙车快,距离减小,10s后乙车慢,距离增大。
t=10 s时相距最近,故B选项错误。
CD. t=10 s时两车的位移大小之差为两车避免发生碰撞的最小距离。
即x乙=x甲+x0,即图中阴影部分三角形的面积。
m
m
s50
10
10
2
1
=
⨯
⨯
=故选项C错误,D正确。
像素距离

class Point
{
public:
Point(int xValue=0,int yValue=0)
{
x = xValue;
y = yValue;
}
int getX()
{
{
pointA = pointValueA;
pointB = pointValueB;
distanceType = distanceTypeValue;
}
pixelDistance(){};
double getPixelDistance();
对于像素p(x , y),q(s , t),z(v , w),用D(p , q)来表示像素p , q间的距离,有:
一 像素间距离的定义(D(x , y)应满足的条件)
1 D(p , q) ≥ 0.(当且仅当p = q);
2 D(p , q) = D(q , p);
3 D(p , q) + D(q , z) ≥ D(p , z);
cin >> dType >> p1x >> p1y >> p2x >> p2y;
while ((dType>3) || (dType <0)) {
Байду номын сангаас cout << "Sorry! You choice wrongly. Please choice again."<< endl;
break;
case 2:
dTypeStr = "Chess Board Distance";
距离变换算法原理

距离变换算法原理距离变换是图像处理中的一种重要算法,主要用于分析和测量图像中不同对象之间的距离。
距离变换算法可以将图像中的每一个像素点转化为该点到最近背景像素点的距离,从而实现对图像中不同对象的距离测量和分析。
距离变换算法的原理基于两个基本假设:第一,物体的边缘和内部的像素点应该被区分开来;第二,距离越近的像素点应该被赋予更小的值。
基于这两个假设,距离变换算法将图像中的每一个像素点分为两类:前景像素点和背景像素点。
前景像素点指的是对象的像素点,背景像素点指的是非对象的像素点。
距离变换算法分为两种方式:欧几里得距离和曼哈顿距离。
欧几里得距离指的是两点之间的直线距离,而曼哈顿距离则是两点之间的曼哈顿距离,即两点在水平和垂直方向上的距离之和。
两种距离方式都可以实现距离变换,但是在某些情况下,需要根据实际需求选择合适的距离方式。
距离变换算法的实现过程包括以下三个步骤:1. 对图像进行二值化处理,将图像中的前景和背景像素点分离出来。
2. 对二值化后的图像进行距离变换,将每个前景像素点转化为到最近背景像素点的距离。
3. 对距离变换后的图像进行归一化处理,使得距离值在0和255之间,从而便于后续处理。
距离变换算法可以应用于不同领域的图像处理,例如医学图像分析、机器视觉、目标跟踪等领域。
在医学图像分析领域中,距离变换算法可以用于分析肿瘤的大小和形状,从而实现对肿瘤的诊断和治疗。
在机器视觉领域中,距离变换算法可以用于物体的定位和跟踪,从而实现对物体的自动识别和分析。
距离变换算法是一种重要的图像处理算法,可以用于分析和测量图像中不同对象之间的距离。
距离变换算法的实现过程包括二值化、距离变换和归一化处理三个步骤,可以应用于不同领域的图像处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
2 2 .
d
2 IME
( x, y)
1 2
2
i , j 1
2 i i j j exp P P / 2 ( x y )( x y ). i j
MN
图像欧氏距离
将IMED嵌入图像识别算法: 对一种图像距离而言,一个十分重要的性质是它是否能 与有力的图像识别算法相结合。
其中, h( A, B) max min a b , h( B, A) max min b a .
a A bB
bB a A
H ( A, B) 称为双向Hausdorff 距离,h( A, B ) 称为从点集 A 到
点集 B 的单向Hausdorff 距离,相应地 h( B, A)称为从点集 A
( x y) G( x y) G
T 12
x G
12
y G
T
12
x G1 2 y .
12 T 其中, G1 2 ,G T .
变换基图像
图像欧氏距离
实验:将IMED嵌入两种标准人脸识别算法,检验它对算法识
别率提高的效果:
嵌入Eigenface (特征脸方法); 嵌入Bayes相似度识别算法; 实验在FERET人脸识别数据库上完成。
街区距离和棋盘距离都是欧式距离的一种近似。
Hausdorff 距离
二值图像可以看作二维图像平面上的点集。 B b1 , b2 , , A a1 , a2 ,, 给定欧氏空间中两个点集, Hausdorff 距离就是用来衡量这两个点集间的距离。
H ( A, B) maxh( A, B), h( B, A).
马氏距离
Mahalanobis距离是由一位印度统计学 者Mahalanobis于1963年提出。 它是一种有效的计算两个未知样本集的相似 度的方法。与欧式距离不同的是它考虑到各 种特性之间的联系(例如:一条关于身高的 信息会带来一条关于体重的信息,因为两者 是有关联的)并且是尺度无关的(scaleinvariant),即独立于测量尺度。
bB a A
表示点集B 到点集 A 的最大距离。
双向Hausdorff 距离H ( A, B) 是单向距离h( A, B )和h( B, A) 两者中的 较大者,显然它度量了两个点集间的最大不匹配程度。
Hausdorff 距离
部分Hausdorff距离定义
由于Hausdorff距离易受突发噪声的影响, 当图像受到噪声污染或存在遮挡等情况时, 原始的Hausdorff距离容易造成误匹配。所 以在1993年,Huttenlocher提出了部分 Hausdorff距离的概念
C2: f 是连续函数,而且随 Pi Pj 增加而单调减小;
C3: f 是普适函数,也就是说它适用于任意大小和分辨
率的图像。 IMED的特殊性以及对 f 的要求: C1-C3决定了必须 f 是正定函数。
图像欧氏距离
IMED的典型例子:
g ij f ( Pi Pj )
1 2
2
exp Pi Pj
th aA bB
在计算 hK ( A, B) 时,K值并不是固定的,K的求取是通过K=[f×q] 来得到的,f(0<fμ1)是给定的一个分数,q是集合B中的点数,[] 表示向下取整运算。
部分的双向Hausdorff距离定义为:
H K ( A, B) max(hK ( A, B), hK ( B, A)).
图像欧氏距离
Probe4(称作fc)上的结果:
欧式距离的缺点
我们熟悉的欧氏距离虽然很有用,但也有明 显的缺点。它将样品的不同属性(即各指标 或各变量)之间的差别等同看待,这一点有 时不能满足实际要求。例如,在教育研究中, 经常遇到对人的分析和判别,个体的不同属 性对于区分个体有着不同的重要性。因此, 有时需要采用不同的距离函数。
FERET人脸数据库: 1.一个gallery:已知身份的人脸图像; 2.四个probe:未知身份的人脸图像; 3.独立于gallery, probe的训练集;
图像欧氏距离
Probe1(称作FB)上的结果:
图像欧氏距离
Probe2(称作duplicate1)上的结果:
图像欧氏距离
Probe3(称作duplicate2)上的结果:
1 (1 2 ) 2
1 2
1 2 1 1 DBA (G1 , G2 ) ( 1 2 )( 1 ) ( 1 2 )T ln 8 2 2 1
2
1
2
目标图像有一定角度的旋转变化,或图像 会受噪声的影响时的结果
灰度图像距离
图像的欧氏空间表示: 一幅 M N 的图像被看作 M N 维欧氏图像空间中的一 个点,每个坐标值对应一个像素的灰度值。 传统欧氏距离: 两幅图像 x, y 间的距离定义为:
2 d E ( x, y ) ( x k y k ) 2 . k 1 MN 1
图像距离
姓名:刘宁海 学号:201120602016
定义
距离是描述像素间关系的基本参数,也是目标物几 何特征和相似性的重要测度。 1.距离的定义 给定三个像素p(m ,n ),q(m ,n ),r(m ,n ),若 D(p,q) 满足 (1)非负性:D(p,q) ≥0 ,当且仅当p=q时, D(p,q)=0 ; (2)对称性:D(p,q)=D(q,p) ; (3)三角不等式:D(p,q) ≤D(p,r)+D(r,q); 则 D(p,q)称为距离的度量函数。
图像欧氏距离
传统欧氏距离缺乏对图像的空间性质的考虑,物理意义 不明确,对图像形变十分敏感。
2 dE (a, b) 54
2 dE (a, c) 49
图像欧氏距离
图像空间的构造:
代数:图像空间以 e1 , e2 ,, eMN 作为空间的一组基,其中 ekN l 对应 于位于 的一个理想点信号源。于是一幅图像 x ( x1 , x 2 ,, x MN ) ( k , l) (其中 x kN l 是像素 的灰度值)就对应于图像空间中的一个点。图 ( k , l) 像空间的原点代表一幅灰度值处处为零的图像。 度量:度量系数矩阵 G gij MN MN 决定了图像空间中两幅图像的距 离:
1 ) ( 1 2 )T 2
即两者均值数值完全相同时,
2
1943年,Bhattacharrya提出的Bhattacharrya距离解决了Mahalanobis 距离无法计算的问题。 假设给定两个高斯分布, G1 G( 1 , 1 ) 及 G2 G(2 , 2 ) ,则两者 间的Bhattacharrya距离可以表示为:
假计算公式可以表示为:
1 , 2
表示均值向量,
G1 G(1, 1 )
及
1 , 2
表示共变异矩阵,则两者间的
G2 G(2 , 2 )
,
D(G1 , G2 ) ( 1 2 )(
由上式可以发现,当 1 Mahalanobis距离无法计算。
d E ( x, y) gii ( x i y i ) 2 g jj ( x j y j ) 2 2 gij ( x i y i )(x j y j ) 2.
构造2:ij 很小,gij cosij 1,
d E ( x, y ) g ii g jj 2 g ij 0.
gij ei , e j
2 E MN
ei , ei
e j , e j cosij.
d ( x, y) g ( xi y i )(x j y j ) ( x y)T G( x y).
i , j 1
图像欧氏距离
示例——度量系数对图像距离的影响 gii g jj 1 构造1:ij 2 , gij cosij 0,
距离的分类
常见的距离 Hausdorff 距离——二值图像距离 Euclidean 距离(欧氏距离)——灰度图像距离 Mahalanobis 距离(马氏距离) Bhattachayya 距离(巴氏距离)
计算点(i,j)和(h,k)间距离常采用的几种方法:
(1) 欧氏距离:
(2) 4-邻域距离, d s [(i, j ), (h, k )] | i h | | j k | 也称为街区 距离: (3)8-邻域距离, 也称为棋盘 距离:
对于距离很近的像素,给它们所对应的度量系数一个较大 的值就能使诱导的欧氏距离对小的形变很鲁棒!
图像欧氏距离
图像欧氏距离(IMED)的定义: C1:度量系数 gij 完全由像素 Pi , Pj 间距离决定。我们用 来表示 f 这一函数关系:
g ij f ( Pi Pj ), i, j 1,2, MN .
到点集 B 的单向Hausdorff 距离。
Hausdorff 距离
h( A, B) max min a b .
a A bB
表示点集 A 到点集 B 的最大距离。即首先计算点集 A中每个点a i 到点集 B 中距离点b j 最近的点的距离值,然后取出这些距离中的最大 值作为点集 A 到点集 B 的单向Hausdorff 距离。 同理 h( B, A) max min b a
IMED可以嵌入的图像识别算法: • 径向基函数支撑向量机(SVM); • PCA,人脸识别系统中又称Eigenface(人脸特征)方法; • Bayes相似度人脸识别算法; 以上方法都基于欧氏距离,用IMED代替传统欧氏距离 即可。
图像欧氏距离
IMED嵌入的快速算法原理:做一个变换,如下所示:
Hausdorff距离图像匹配并行算法设计步 骤
(1)读取模板图A和目标图B,并分别求出图A和图B的行和列; (2)定义一个矩阵C,大小为图A在图B上所能移动的最大的行 数和列数,用以记录每次移动的模板图和对应下方目标图中的 搜索子图的Hausdorff距离值; (3)按从上到下,从左到右的顺序在目标图上并行移动模板图; (4)并行计算模板图与对应下方搜索子图的像素点的Hausdorff 距离,并行结果保存在矩阵C中的对应坐标上; (5)重复第3,4步,直到计算出所有模板图和对应搜索子图的 Hausdorff距离,取最小值作为最佳匹的位置。然后对得到的 匹配图进行定位搜索,确定精确匹配位置。
