2016高三数学复习(人教A版)_第三章_第3讲_两角和与差的正弦、余弦和正切公式(含答案)
高考数学(文通用)一轮复习课件:第三章第3讲两角和与差的正弦、余弦和正切公式

第三章三角函数、解三角形第3讲两角和与差的正弦、余弦和正切公式教材回顾▼夯实基础知谋梳理〉1.两角和与差的正弦、余弦和正切公式cos acos 0土sinasin Bcos(aT B )= _________________tan a土tan B1+tan atan B(a±0, a , 0均不为佥兀+于,kE: Z 课本温故追根求源sin(a±/?)=sin acos “土cos asin p tan(m±Q=2.二倍角的正弦、余弦、• a2sin acos a sm 2 a = cos 2 a = cos%—si,疣2tan atan 2“a,正切公式2a—1 2cos1Tl\2 a均不为E兀+亍,kWZ、1—2sin2a3. 三角公式关系令0 = a 「 以-0代0C 2a ------------------- 匕十) -----------两式相除两式相除两式相除T(a + B)v 利用cos 任±0 利用cos 任土 a) 令 0二a I ^2a 3(a + 0) v 以-仔代07T 利用 cos(—±a a S(a_Q) T (—p )£要点整食71.辨明两个易误点(1)在使用两角和与差的余弦或正切公式时运算符号易错.、伍(2)在(0,兀)范围内,sin(d+")=专所对应的角不是唯一的.2・有关公式的逆用及变形用(l)tan a 土 tan B = tan(a±/?)(1+tan a tan 0); (3)1+ sin 2 a = (sin a +cos a )2, 1—sin 2 a =(sin a — cosa )2, sin a 土 cos a ⑵ cos? 1 + cos 2 a 2sin 2 1 —cos 2 a3.角的变换技巧a =(a+fl)_ 卩;a =卩_ a);a =^[(«+^)+ (a—fi)];0=扌仗+沟_@_创;JI JI A JI A3★暉自测卩a 解析:因为sin —2=11.若 sin贝!)cos a=( CDi=申,所以COSa—= 1— 2■2X32. (2015•高考全国卷 I )sin 20° cos 10°解析:sin 20° cos 10° —cos 160° sin 10° =sin 20° cosc.—cos 160° sin 10°10° + cos 20° sin 10° = sin(20°+ 10° )=sin 30° =|.(a )¥卵冰"+〃)呵|M 'lhp+訂1引¥=(罟一町呵昵•£=(“+巧11引4.已知解析:因为以COS X—sinx=^, 则11_sin 2x=巧 —sin2r=五'所以 sin 2x=-.所以^COS X ——sin x= 2JI a sin —= sin3 JI----- c os asin —,所以 tan a = l5.已知 a +yj=sin^a,贝i tan a = ____ ]解析:因为 所以 cos a cosJI----- s in3典例剖析▼考点突破+名师导悟以例说法考点一三角函数公式的直接应用典例対(2015•高考广东卷)已知tan a =2⑴求tan@+£的值;⑵求.2亠.心―的值.sm a +sm a cos a — cos 2 a — 12+1 _1-2X1 = _Xsin 2 aa cos a —cos 2 a —12sin a cos a _ 2tan asin 2 a +sin a cos a — 2cos 2 a tan 2a +tan a —2 2X2 4+2-2兀tan a+tan — JT1—tan fftan —⑵sii? a +sin两角和与差的三角函数公式可看作是诱导公式的推广,可用«> 0的三角函数表示Q土〃的三角函数,在使用两角和与差的三角函数公式时,特别要注意角与角之间的关系,完成统一角和角与角转换的目的.O'2aW (0,兀),tan 2 a =|>0, ,所以 sin 2 a =扌,cos 2 a =7JIJI=sin 2 a cos —+cos 2 a sin —_4 J 亠 3 V5_4+3 萌 一5%2十5* 2 _10 •腹歸训绣]1•已知,tan a =-,求 tan 2 Q 和sin (2 ff+yj 的值.解:tan 22tan a CL —~ 51—tan a2Xi 4 2 一亍1_©因为圧 5’所以2圧 所以考点二三角函数公式的活用(高频考点)三角函数公式的活用是高考的热点,高考多以选择题或填空题的形式出现,在解答题中考查三角函数的性质和解三角形时也应用三角函数公式.高考对三角函数公式的考查主要有以下三个命题角度:(1)应用正切公式的变形;(2)降幕公式的应用;(3)二倍角公式的逆用.\/3tan 12° —3 sin12° (4COS 212° —2)(1)(2015-高考重庆卷)若tan 兀a = 2tan —,5A. 1C. 3B. 2 D. 4 (2)求值:[解]⑴选C ・因为cos ( a—脅)JI JIsin a cos —+cos a sin —JI兀sin a cos ——cos a sin —IJI JIcosl a +T~2f JI =sinl a+—tan a +ta又因为tan兀a =2tan —,兀 兀2tan ----- t an —5 5tan兀所以原式= JI JI 2tan —+tair^-厂sin 12°V3X--------- -3—cos 12。
高考数学一轮复习 第三章 三角函数、解三角形 第3讲 两角和与差的正弦、余弦和正切公式课件 文

12/11/2021
第十八页,共四十五页。
2cos 1.
10°-sin sin 70°
20°的值是___3_____.
[解析] 原式=2cos(30°-sin207°0°)-sin 20°
=2(cos
30°·cos
20°+sin 30°·sin sin 70°
20°)-sin
20°
= c3ocsos202°0°= 3.
12/11/2021
第二十二页,共四十五页。
三角函数的给值求值、给值求角(高频考点)
(1)已 知
0
<
β<
π 2
<
α
<
π
,
且
cos
α-β2
=
-
1 9
,
sinα2-β=23,求 cos(α+β)的值;
(2)已知 α,β∈(0,π),且 tan(α-β)=12,tan β=-17,求 2α
-β 的值.
12/11/2021
12/11/2021
第十九页,共四十五页。
2.已知函数 f(x)=2sin13x-π6,x∈R. (1)求 f54π的值; (2)设 α,β∈0,π2,f3α+π2=1103,f(3β+2π)=65,
求 cos(α+β)的值.
12/11/2021
第二十页,共四十五页。
[解] (1)f54π=2sin 13×54π-π6=2sinπ4= 2. (2)由 f3α+π2=2sin α=1130,
12/11/2021
第二十四页,共四十五页。
=-19× 35+4 9 5×23=7275,
所以 cos(α+β)=2cos2α+2 β-1=2×497×295-1=-722399.
人教A版高中数学必修一 《三角恒等变换》三角函数(第3课时两角和与差的正弦、余弦、正切公式)

当堂达标 固双基
31
1.思考辨析 (1)存在 α,β∈R,使 tan(α+β)=tan α+tan β 成立.( ) (2)对任意 α,β∈R,tan(α+β)=1t-antαan+αttaannββ都成立.( ) (3)tan(α+β)=1t-antαan+αttaannββ等价于 tan α+tan β=tan(α+β)·(1-tan αtan β).( )
3.熟悉两角和与差的正切公式的常 素养.
见变形,并能灵活应用.(难点)
2
自主预习 探新知
3
两角和与差的正切公式
名称 简记符号
公式
使用条件
两角和 的正切 T(α+β)
tan(α+β)=1t_-a_n_t_αa_n+_α_t_taa_nn_β_β α,β,α+β≠kπ+π2(k∈Z) 且 tan α·tan β≠1
两角差 T(α-β)
的正切
tan(α-β)=1t_+a_n_t_αa_n-_α_t_taa_nn_β_β α,β,α-β≠kπ+π2(k∈Z) 且 tan α·tan β≠-1
4
1.已知 tan α+tan β=2,tan(α
C [∵tan(α+β)=1t-antαan+αttaannββ
+β)=4,则 tan αtan β 等于( ) =4,且 tan α+tan β=2,
A.2
B.1
∴1-tan2αtan β=4,解得 tan αtan
C.12
D.4
β=12.]
5
2.求值:tan1112π=________.
-2+ 3Biblioteka [tan11π 12
=-tan
π 12
=
-tanπ4-π6
高考数学复习第三章三角函数解三角形第三课时两角和与差的正弦余弦和正切公式理市赛课公开课一等奖省名师优

(1)给角求值的关键是正确地选用公式,以便把非特殊角的三 角函数相约或相消,从而化为特殊角的三角函数.
(2)给值求值的关键是找出已知式与待求式之间的联系及函数 的差异,一般可以适当变换已知式,求得另外某些函数式的值, 以备应用.同时也要注意变换待求式,便于将已知式求得的函数 值代入,从而达到解题的目的.
cos 10° 3)·sin 50°
=(tan
10°-tan
cos 60°)·sin
10° 50°
=csoins
1100°°-csoins
60° cos 60°·sin
10° 50°
=cossi1n0-°·c5o0s°60°·csoins 5100°°=-2.
18/54
法二:(tan 10°-
cos 10° 3)·sin 50°
14/54
1.(2015·高考课标卷Ⅰ)sin 20°cos 10°-cos 160°sin 10°=
()
A.-
3 2
3 B. 2
C.-12
D.12
15/54
解析:sin 20°cos 10°-cos 160°sin 10°=sin 20°cos 10°+cos 20°sin 10°=sin(20°+10°)=sin 30°=12,故选D.
36/54
(1)由f(α)=353,得sin α=35. 又α是第一象限角,所以cos α>0. 从而g(α)=1-cos α=1- 1-sin2α=1-45=15.
37/54
(2)f(x)≥g(x)等价于 3sin x≥1-cos x,
即 3sin x+cos x≥1,于是sinx+π6≥12,
答案:D
16/54
2.化简:(1)(tan 10°-
人教A版高中数学必修四课件第三章3.1.2两角和与差的正弦余弦正切公式(一)

S(α+β):sin(α+β)= sin αcos β+cos αsin β
.
S(α-β):sin(α-β)= sin αcos β-cos αsin β
.
前置学习
3.两角互余或互补 π
(1)若 α+β= 2 ,其 α、β 为任意角,我们就称 α、β 互余.例 如:π4-α 与 π4+α 互余,π6+α 与 π3-α 互余.
解 ∵α∈0,2π,β∈-2π,0,∴α-β∈(0,π). ∵cos(α-β)=35,∴sin(α-β)=45.
∵β∈-π2,0,sin β=-102,∴cos β=7102.
∴sin α=sin[(α-β)+β]=sin(α-β)cos β+cos(α-β)sin β
=45×7102+35×- 102=
解析
f(x)=212sin
x-
3 2 cos
x=2sinx-3π.
∴f(x)∈[-2,2].
前置学习
4.已知锐角
α、β
满足
sin
α=2 5 5,cos
β=
1100,则
3π α+β=__4___.
解析 ∵α,β 为锐角,sin α=255,cos β= 1100,
∴cos α= 55,sin β=31010. cos(α+β)=cos αcos β-sin αsin β
B.-2 5 5
C.
5 5
D.-
5 5
解析 sin C=sin[π-(A+B)]=sin(A+B)
=sin Acos B+cos Asin B
=
2 2 (cos
B+
1-cos2B)
=
22×
1100+3
10 10
=2
高中数学 第三章 三角恒等变换 3.1 两角和与差的正弦、余弦和正切公式 3.1.3 二倍角的正弦、
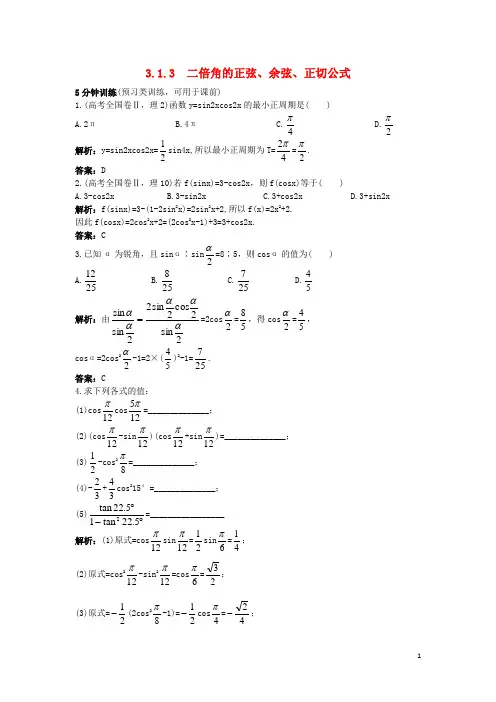
3.1.3 二倍角的正弦、余弦、正切公式5分钟训练(预习类训练,可用于课前)1.(高考全国卷Ⅱ,理2)函数y=sin2xcos2x 的最小正周期是( )A.2πB.4πC.4π D.2π 解析:y=sin2xcos2x=21sin4x,所以最小正周期为T=42π=2π.答案:D2.(高考全国卷Ⅱ,理10)若f(sinx)=3-cos2x ,则f(cosx)等于( )A.3-cos2xB.3-sin2xC.3+cos2xD.3+sin2x解析:f(sinx)=3-(1-2sin 2x)=2sin 2x+2,所以f(x)=2x 2+2.因此f(cosx)=2cos 2x+2=(2cos 2x-1)+3=3+cos2x. 答案:C3.已知α为锐角,且sinα∶sin 2α=8∶5,则cosα的值为( ) A.2512 B.258 C.257 D.54 解析:由2sin2cos2sin 22sin sin ααααα==2cos 2α=58,得cos 2α=54, cosα=2cos 22α-1=2×(54)2-1=257. 答案:C4.求下列各式的值:(1)cos 12πcos 125π=______________; (2)(cos 12π-sin 12π)(cos 12π+sin 12π)=______________;(3)21-cos 28π=______________; (4)-32+34cos 215°=______________;(5)︒-︒5.22tan 15.22tan 2=_________________解析:(1)原式=cos 12πsin 12π=21sin 6π=41;(2)原式=cos212π-sin 212π=cos 6π=23; (3)原式=21-(2cos 28π-1)=21-cos 4π=42-;(4)-32+34cos 215°=32(2cos 215°-1)=32cos30°=33;(5)原式=21tan45°=21. 答案:(1)41 (2)23 (3)42- (4)33 (5)2110分钟训练(强化类训练,可用于课中) 1.若tanx=2,则tan2(x-4π)等于( ) A.34 B.-34 C.43 D.43- 解析:tan(2x-2π)=-tan(2π-2x)=-cot2x=x 2tan 1-,而tan2x=4122-⨯=-34,∴原式=43.答案:C2.当0<x <2π时,函数f(x)=x x x 2sin sin 82cos 12++的最小值为( )A.2B.32C.4D.34解析:f(x)=x x x x cos sin 2sin 8cos 222+=x tan 1+4tanx≥42=4,当且仅当tanx=21时,取“=”.答案:C3.化简cos72°cos36°=________________. 解析:原式=︒︒=︒︒︒=︒︒•︒︒36sin 4144sin 36sin 472sin 72cos 236sin 236sin 236cos 72cos =41. 答案:414.在△ABC 中,tanA+tanB+33+tanAtanB 且sinAcosA=43,判断三角形的形状. 解:由sinAcosA=43,得21sin2A=43,即sin2A=23, ∴2A=60°或120°.∴A=30°或60°.又由tanA+tanB=3-(1-tanAtanB),得tan(A+B)=3tan tan 1)tan tan 1(3-=---BA B A ,∴A+B=120°.当A=30°时,B=90°,tanB 无意义,∴A=60°,B=60°,即三角形为等边三角形. 5.平面上两塔相距120 m ,一人分别在两塔的底部测得一塔顶的仰角为另一塔顶仰角的2倍,又在两塔底的连线中点测得两塔顶的仰角互余.求两塔的高.解析:如图所示,设两塔的高分别为x m 、y m ,且∠ADB=α,∠AMB=θ.由题意,得∠CBD=2α,∠AMC=90°, ∠AMB=∠MCD=θ, 所以x=60tanθ,y=θtan 60, x=120tan α,y=120tan2α.所以⎪⎪⎩⎪⎪⎨⎧-==.12012,360022x x y xy 解得x=40,y=90.答:两塔高分别是90 m 和40 m.6.(2006高考北京卷,理15)已知函数f(x)=xx cos )42sin(21π--, (1)求f(x)的定义域;(2)设α是第四象限的角,且tanα=-34,求f(α)的值. 解:(1)由cosx≠0,得x≠kπ+2π(k ∈Z ). 故f(x)的定义域为{x|x≠kπ+2π,k ∈Z }.(2)因为tanα=54-,cosα=53,且α为第四象限的角,所以sinα=54-,cosα=53.故f(α)=αααααααπαcos 2cos 2sin 1cos )2cos 222sin 22(21cos )42sin(21+-=--=--=ααααcos cos sin 2cos 22-=2(cosα-sinα)=514. 30分钟训练(巩固类训练,可用于课后) 1.已知θ是第三象限的角,若sin 4θ+cos 4θ=95,那么sin2θ等于( ) A.322 B.322- C.32 D.-32解析:(sin 2θ+cos 2θ)2=sin 4θ+cos 4θ+2sin 2θcos 2θ=sin 4θ+cos 4θ+21(sin2θ)2,而(sin 2θ+cos 2θ)2=1,可以得到sin2θ=±322,又由于θ是第三象限的角,所以sin2θ=322. 答案:A2.已知tanα=71,tanβ=2π,0<α<β<2π,则α+2β等于( ) A.45π B.4π C.45π或4π D.47π解析:∵tan2β=43tan 1tan 2=-ββ,∴tan(α+2β)=28314371-+=1.∵tanα=71<1,∴0<α<4π.tan2β=43<1,∴0<2β<4π.∴0<α+2β<43π.∴α+2β=4π.答案:B3.(2006高考上海卷,理17)求函数y=2cos(x+4π)cos(x-4π)+3sin2x 的值域和最小正周期.解:y=2(cosxcos4π-sinxsin 4π)(cosxcos 4π-sinxsin 4π)+3sin2x =cos 2x-sin 2x+3sin2x=cos2x+3sin2x=2sin(2x+6π).∴原函数的值域是[-2,2],周期T=22π=π. 4.化简︒-+︒+10sin 110sin 1. 解:原式=︒︒-︒+︒+︒︒+︒+︒5cos 5sin 25cos 5sin 5cos 5sin 25cos 5sin 2222=|sin5°+cos5°|+|sin5°-cos5°|=sin5°+cos5°+cos5°-sin5°=2cos5°. 5.求sin10°sin30°sin50°sin70°的值.解:原式=21cos20°cos40°cos80° =︒︒︒=︒︒︒=︒︒︒︒︒20sin 1680cos 80sin 2880cos 40cos 40sin 220sin 480cos 40cos 20cos 20sin 2 =16120sin 16160sin =︒︒. 6.已知sin 22α+sin2αcos α-cos2α=1,α∈(0,2π),求sin α,tan α.解:由题意知4sin 2αcos 2α+2sin αcos 2α-2cos 2α=0,即2cos 2α(2sin α-1)(sin α+1)=0. 又α∈(0,2π),∴sinα+1≠0,cos 2α≠0. 由2sin α-1=0得sin α=21,∴α=6π,tan α=33.7.已知sin(α-4π)=1027,cos2α=257,求sin α及tan(α+3π).解:由sin(α-4π)=1027,得22(sin α-cos α)=1027,即sin α-cos α=57. ① 又由cos2α=257得cos 2α-sin 2α=257,即(cos α+sin α)(cos α-sin α)=257,∴cosα+sin α=-51. ②由①②得sin α=53,cos α=54-,∴tanα=-43.tan(α+3π)=1132548343344331433tan 313tan -=+-=+-=-+αα. 8.当x∈[-2π,2π]时,求f(x)=sin 2x+2sinxcosx+3cos 2x 的周期、最大值及此时的x 值. 解:f(x)=1+cos2x+1+sin2x=2sin(2x+4π)+2.周期T=π.当x ∈[-2π,2π]时,2x+4π∈[-43π,45π],sin(2x+4π)∈[-1,1]. ∴f(x)∈[22-,22+].∴f(x)max =22+.由2x+4π=2k π+2π得x=k π+8π. 又∵x∈[-2π,2π],∴x=8π,即当x=8π时,f(x)的最大值为22+.9.(2006高考安徽卷,理17)已知43π<α<π,tanα+cosα=310-.(1)求tanα的值;(2)求)4sin(282cos 112cos2sin82sin 522πααααα--++的值.解:(1)∵tanα+cosα=310-,∴3tan 2α+10tanα+3=0,解得tanα=-31或tanα=-3.∵43π<α<π,∴-1<tanα<0.∴tanα=-31.(2)∵tanα=-31,∴)4(sin 282cos 112cos2sin82sin 522παααααα--++=451tan 3tan 4cos sin 82cos 16sin 4)2cos 2(sin 522-=-+=--+•+++αααααααα. 10.(2006高考四川卷,理17)已知A 、B 、C 是△ABC 三内角,向量m =(-1,3),n =(cosA,sinA),且m ·n =1. (1)求角A ; (2)若BB B22sin cos 2sin -+1=-3,求tanC. 解:(1)∵m ·n =1,∴(-1,3)·(cosA,sinA)=1,即3sinA-cosA=1,2(sinA·23-cosA·21)=1,sin(A-6π)=21. ∵0<A <π,-6π<A-6π<65π,∴A-6π=6π.∴A=3π.(2)由题知BB B B 22sin cos cos sin 21-+=-3,整理得sin 2B-sinBcosB-2cos 2B=0. ∵cosB≠0,∴tan 2B-tanB-2=0. ∴tanB=-2或tanB=-1.而tanB=-1使cos 2B-sin 2B=0,舍去. ∴tanB=2.∴tanC=tan[π-(A+B)]=-tan(A+B)=11358321322tan tan 1tan tan +=-+⨯-=-+-B A B A .。
【人教a版】高中数学:第三章3.1-3.1.2两角和与差的正弦、余弦、正切公式
第三章 三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.1.2 两角和与差的正弦、余弦、正切公式A 级 基础巩固一、选择题1.sin 45°cos 15°+cos 225°sin 15°的值为( )A .-32B .-12 C.12 D.32解析:原式=sin 45°cos 15°-cos 45°sin 15°=sin 30°=12. 答案:C2.1-tan 27°tan 33°tan 27°+tan 33°等于( ) A.33 B. 3C .tan 6°D.1tan 6° 解析:因为tan 27°+tan 33°1-tan 27°·tan 33°=tan(27°+33°)=tan 60°,所以原式=1tan 60°=33.答案:A3.在△ABC 中,若sin(B +C)=2sin Bcos C ,则△ABC 是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形解析:因为sin(B +C)=2sin Bcos C ,所以sin Bcos C +cos Bcos C =2sin Bcos C ,即sin Bcos C -cos Bsin C =0,所以sin(B -C)=0,所以B =C ,所以△ABC 是等腰三角形.答案:D4.3sin x -3cos x =23sin(x +φ),φ∈(-π,π),则φ的值是( )A .-π6 B.π6C .-5π6 D.5π6解析:3sin x -3cos x=23⎝ ⎛⎭⎪⎪⎫32sin x -12cos x=23⎝ ⎛⎭⎪⎫sin xcos π6-cos xsin π6=23sin ⎝ ⎛⎭⎪⎫x -π6=23sin(x +φ).因为φ∈(-π,π),所以φ=-π6.答案:A5.已知α, β均为锐角,且cos(α+ β )=sin(α- β ),则角α的值为() A.π4 B .-π4C.0 D.无法确定解析:由题意得cos αcos β-sin αsin β=sin αcos β-cos αsin β,即cos α(cos β+sin β )=sin α(sin β+cos β ),因为α、β均为锐角,所以sin β+cos β≠0,所以cos α=sin α,所以α=π4. 答案:A 二、填空题6.(2018·江苏卷)已知tan α=-2,tan(α+β )=17,则tan β的值为________.解析:tan β=tan[(α+β)-α]=tan(α+β)-tan α1+tan(α+β)tan α=17-(-2)1+17×(-2)=3.答案:37.计算1-tan 15°3+tan 60°tan 15°=________.解析:原式=tan 45°-tan 15°3(1+tan 45°·tan 15°)=1 3tan(45°-15°)=13.。
高中数学第三章三角恒等变换3.1.2两角和与差的正弦、余弦、正切公式(1)课件新人教A版必修4
2
2
(2) 3 sin x cos x.
解:(1)1 cos x 3 sin x (2) 3 sin x cos x
2
2
sin 30 cos x cos 30 sin x
2( 3 sin x 1 cos x)
2
2
sin(30 x);
2(sin x cos 30 cos x sin 30 )
解:原式 sin(72 18 ) sin 90 1.
第十三页,共31页。
例1 已知 sin 3 , 是第四象限角,求 sin( ),
5
4
cos( )的值.
4
解:由sin=-
3 5
,
是第四象限角,得
cos 1 sin2 1 ( 3)2 4 , 55
于是有sin( ) sin cos cos sin
第七页,共31页。
探究(tànjiū)二:两角和与差的正弦公式
1.利用哪些公式可以实现正弦(zhèngxián)、余弦的互 化?
提示(tíshìs)i:n cos( ) 2
sin(
)
cos
2
(
)
第八页,共31页。
2.由两角和与差的余弦公式如何推导两角和与 差的正弦(zhèngxián)公式?
(2) 2 cos x 6 sin x.
解:(1)原式 (2 2 sin x 2 cos x)
2
2
2sin(x ).
4
(2)原式 2 (2 1 cos x 3 sin x)
2
2
2 2 sin( x).
6
第二十一页,共31页。
1.(2015·四川高考)下列函数中,最小正周期为π且图象关
高考数学一轮复习第3章三角函数解三角形3.5两角和与差的正弦余弦与正切公式课件理
(2)将三角变换与代数变换密切结合:三角变换主要是 灵活应用相应的三角公式,对于代数变换主要有因式分解、 通分、提取公因式、利用相应的代数公式等,例如,sin4x +cos4x=(sin2x+cos2x)2-2sin2xcos2x=1-12sin22x.
第八页,共45页。
[诊断自测] 1.概念思辨 (1)两角和与差的正弦、余弦公式中的角 α,β 是任意 的.( √ ) (2)存在实数 α,β,使等式 sin(α+β)=sinα+sinβ 成 立.( √ ) (3)在锐角△ABC 中,sinAsinB 和 cosAcosB 大小关系不 确定.( × ) (4)公式 tan(α+β)=1t-anαta+nαttaannββ可以变形为 tanα+tanβ =tan(α+β)(1-tanαtanβ),且对任意角 α,β 都成立.( × )
第二十页,共45页。
冲关针对训练
已知锐角 α,β 满足 sinα= 55,cosβ=31010,则 α+β
等于( )
3π A. 4
B.π4或34π
π C.4
D.2kπ+π4(k∈Z)
第二十一页,共45页。
解析 由 sinα= 55,cosβ=31010,且 α,β 为锐角,可
知 cosα=255,sinβ= 1100,
(1)求函数 f(x)的最小正周期和单调递增区间;
(2)若函数 g(x)=f(x)-m 在0,π2上有两个不同的零点 x1,x2,求实数 m 的取值范围,并计算 tan(x1+x2)的值.
本题采用转化法、数形结合思想.
第二十三页,cosx+ 3, 化简可得 f(x)=2sinxcosx-2 3cos2x+ 3 =sin2x-2 312+21cos2x+ 3 =sin2x- 3cos2x =2sin2x-π3.
高中数学第三章三角恒等变换3.1.2两角和与差的正弦、余弦、正切公式(1)课件新人教A版必修4
∴T=2ωπ=2π,值域[-2,2].
由-π2+2kπ≤x-π6≤π2+2kπ 得,递增区间[-π3+2kπ,23π+2kπ],k∈Z.
解析答案
类型三 公式的变形应用 例 3 已知 sin(α+β)=12,sin(α-β)=13,求ttaann αβ的值.
解 ∵sin(α+β)=12,∴sin αcos β+cos αsin β=12.
123 45
解析答案
2.化简 2cos x- 6sin x 等于( D )
A.2 2sinπ6+x
B.2 2cosπ6-x
C.2 2sinπ3-x
D.2 2cosπ3+x
解析
2cos x-
6sin x=2
212cos
x-
3 2 sin
123 45
解析答案
123 45
5.已知
α,β
9
均为锐角,且
sin
α=35,tan(α-β)=-13,则
sin(α-β)=
-
10 10
,
cos β=
50
10
.
解析 ∵α,β∈(0,π2),从而-π2<α-β<π2. 又∵tan(α-β)=-13<0,
∴-π2<α-β<0. ∴sin(α-β)=- 1100,cos(α-β)=31010.
达标检测
1.sin 245°sin 125°+sin 155°sin 35°的值是( B )
A.-
3 2
B.-12
1
3
C.2
D. 2
解析 原式=-sin 65°sin 55°+sin 25°sin 35° =-cos 25°cos 35°+sin 25°sin 35°
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3讲 两角和与差的正弦、余弦和正切公式2016高考导航知识梳理1.两角和与差的正弦、余弦和正切公式 sin(α±β)=sin_αcos__β±cos_αsin__β; cos(α∓β)=cos_αcos__β±sin_αsin__β;tan(α±β)=tan α±tan β1∓tan αtan β.(α±β,α,β均不为k π+π2,k Z ∈)2.二倍角的正弦、余弦、正切公式sin 2α=2sin_αcos__α;cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α; tan 2α=2tan α1-tan 2α.(α,2α均不为k π+π2,k Z ∈) 3.三角公式关系[做一做]1.若sin α2=33,则cos α=( )A .-23B .-13C .13D .232.若sin α+cos αsin α-cos α=12,tan β=13,则tan(α+β)等于( )A .-34B .34C .-43D .43要点整合1.辨明两个易误点(1)在使用两角和与差的余弦或正切公式时运算符号易错. (2)在(0,π)范围内,sin(α+β)=22所对应的角α+β不是唯一的. 2.熟悉公式的逆用及变形用 (1)tan α±tan β=tan(α±β)(1∓tan αtan β); (2)cos 2α=1+cos 2α2,sin 2α=1-cos 2α2;(3)1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)2,sin α±cos α=2sin ⎝⎛⎭⎫α±π4. 3.角的变换技巧α=(α+β)-β;α=β-(β-α);α=12[(α+β)+(α-β)];β=12[(α+β)-(α-β)];π4+α=π2-⎝⎛⎭⎫π4-α. [做一做]3.sin 68°sin 67°-sin 23°cos 68°的值为( ) A .-22 B .22 C .32D .1 4.已知tan ⎝⎛⎫α-π6=37,tan ⎝⎛⎭⎫π6+β=25,则tan(α+β)的值为( ) A .2941 B .129 C .141D .1典例剖析考点一__三角函数公式的直接应用__________(2014·高考广东卷)已知函数f (x )=A sin ⎝⎛⎭⎫x +π4,x R ∈,且f ⎝⎛⎭⎫5π12=32. (1)求A 的值;(2)若f (θ)+f (-θ)=32,θ∈⎝⎛⎭⎫0,π2,求f ⎝⎛⎭⎫3π4-θ. [规律方法] 两角和与差的三角函数公式可看作是诱导公式的推广,可用α、β的三角函数表示α±β的三角函数,在使用两角和与差的三角函数公式时,特别要注意角与角之间的关系,完成统一角和角与角转换的目的.1.已知α∈ (0,π2),tan α=12,求tan 2α和sin(2α+π3)的值.考点二__三角函数公式的活用(高频考点)________三角函数公式的活用是高考的热点,高考多以选择题或填空题的形式出现,在解答题中考查三角函数的性质和解三角形时也应用三角公式.高考对三角公式的考查主要有以下三个命题角度:(1)应用正切公式的变形; (2)降幂公式的应用;(3)二倍角公式的逆用.求值:(1)3tan 12°-3sin 12°(4cos 212°-2); (2)tan 20°+tan 40°+3tan 20°tan 40°.[规律方法] 运用两角和与差的三角函数公式时,不但要熟练、准确,而且要熟悉公式的逆用及变形,如tan α+tan β=tan(α+β)·(1-tan αtan β)和二倍角的余弦公式的多种变形等.公式的逆用和变形应用更能开拓思路,培养从正向思维向逆向思维转化的能力,只有熟悉了公式的逆用和变形应用后,才能真正掌握公式的应用.2.(1)(2015·洛阳市高三年级统考)已知sin 2α=13,则cos 2⎝⎛⎭⎫α-π4=( ) A .-13 B .-23 C .13 D .23(2)若α+β=3π4,则(1-tan α)(1-tan β)的值是________.(3)cos π9·cos 2π9·cos ⎝⎛⎫-23π9=( ) A .-18 B .-116 C .116D .18考点三__角的变换______________________________(1)设tan(α+β)=25,tan ⎝⎛⎭⎫β-π4=14,则tan ⎝⎛⎭⎫α+π4=( ) A .1318 B .1322 C .322 D .16(2)(2015·贵州六盘水二模)已知cos α=13,cos(α+β)=-13,且α、β∈⎝⎛⎭⎫0,π2,则cos(α-β)的值等于( ) A .-12 B .12C .-13D .2327本例(2)条件不变,求cos 2β的值.[规律方法] (1)当“已知角”有两个时,一般把“所求角”表示为两个“已知角”的和或差的形式;(2)当“已知角”有一个时,此时应着眼于“所求角”与“已知角”的和或差的关系,然后应用诱导公式把“所求角”变成“已知角”.3.已知α∈⎝⎛⎭⎫π2,π,且sin α2+cos α2=62. (1)求cos α的值;(2)若sin(α-β)=-35,β∈⎝⎛⎭⎫π2,π,求cos β的值.名师讲坛考题溯源——二倍角公式的应用(2013·高考四川卷)设sin 2α=-sin α,α∈⎝⎛⎭⎫π2,π,则tan 2α的值是________. [考题溯源] 本考题源于教材人教A 版必修4 P 135练习T 3“已知sin 2α=-sin α,α∈⎝⎛⎭⎫π2,π,求tan α的值.”的变式而成.1.(2015·东北三校联考)已知sin α+cos α=13,则sin 2⎝⎛⎭⎫π4-α=( ) A .118 B .1718 C .89 D .292.(2015·唐山市第一次模拟)若sin ⎝⎛⎭⎫π6-α=13,则cos ⎝⎛⎭⎫2π3+2α=( ) A .-79 B .79 C .-29 D .29知能训练1.(2014·郑州模拟)计算cos42°cos18°-cos48sin18°的结果等于( ) A .12B .33 C .22 D .322.(2014·湖州模拟)已知sin ⎝⎛⎭⎫π2+α=13,则cos(π+2α)的值为( ) A .-79B .79C .29D .-233.(2015·山东实验中学诊断)已知cos ⎝⎛⎭⎫π4-x =35,则sin2x =( ) A .1825 B .725 C .-725 D .-16254.(2014·成都模拟)已知α∈⎝⎛⎭⎫π,32π,且cos α=-45,则tan ⎝⎛⎭⎫π4-α等于( ) A .7 B .17 C .-17D .-75.(2015·金华十校模拟)已知tan ⎝⎛⎭⎫α+π4=-12,且π2<α<π,则sin2α-2cos 2αsin ⎝⎛⎭⎫α-π4等于( ) A .255 B .-3510 C .-255 D .-310106.(2015·娄底模拟)已知tan α,tan β是方程x 2+33x +4=0的两根,若α,β∈⎝⎛⎭⎫-π2,π2,则α+β=( ) A .π3 B .π3或-23π C .-π3或23πD .-23π7.(2015·大连市第一次模拟)若角α的终边过点(-1,2),则cos(π-2α)的值为( ) A .35 B .-35 C .55 D .-558.已知cos ⎝⎛⎭⎫x -π6=-33,则cos x +cos ⎝⎛⎭⎫x -π3的值是( ) A .-233 B .±233C .-1D .±19.(2015·衡水中学高三第二学期二调)3cos 10°-1sin 170°=( )A .4B .2C .-2D .-4 10.(2015·山西晋中名校高三联合测试)对于集合{a 1,a 2,…,a n }和常数a 0,定义:ω=sin 2(a 1-a 0)+sin 2(a 2-a 0)+…+sin 2(a n -a 0)n为集合{a 1,a 2,…,a n }相对a 0的“正弦方差”,则集合⎩⎨⎧⎭⎬⎫π2,5π6,7π6相对a 0的“正弦方差”为( ) A .12 B .13 C .14D .与a 0有关的一个值11.已知:α,β∈⎝⎛⎭⎫0,π2,满足tan(α+β)=4tan β,则tan α的最大值是( ) A .14 B .34 C .342 D .3212.[2015·重庆模拟]设tan α,tan β是方程x 2-3x +2=0的两根,则tan(α+β)的值为( ) A. -3 B. -1 C. 1 D. 313.[2015·长春月考]已知sin α=55,sin(α-β)=-1010,α,β均为锐角,则角β等于( )A .5π12B .π3C .π4D .π614.(2014年郑州模拟)若0<α<π2,-π2<β<0,cos ⎝⎛⎭⎫π4+α=13,cos ⎝⎛⎭⎫π4-β2=33,则cos ⎝⎛⎭⎫α+β2=( ) A .33 B .-33 C .539D .-6915.化简sin15°cos9°-cos66°sin15°sin9°+sin66°的结果是( )A .tan9°B .-tan9°C .tan15°D .-tan15° 16.(2015·河南洛南联考)已知f (x )=sin x -cos x ,则f (π12)的值是( )A .-62 B.12 C .-22 D.2217.(2014·湖北重点中学联考)若tan α=lg(10a ),tan β=lg(1a ),且α+β=π4,则实数a 的值为( )A .1B .110C .1或110D .1或1018. (2014·河北衡水中学五调)已知sin(α+π3)+sin α=-435,-π2<α<0,则cos(α+2π3)等于( )A .-45B .-35C .45D .3519.命题:∀x ∈ [0,π3],使3cos 2x 2+3sin x 2cos x 2<a +32成立,则实数a 的取值范围是( )A .(1,+∞)B .(32,+∞) C .(32,+∞) D .(3,+∞) 20.C B A 、、是∆ABC 的三个内角,且B A tan ,tan 是方程01532=+-x x 的两个实数根,则∆ABC是( )A .钝角三角形B .锐角三角形C .等腰三角形D .等边三角形二、填空题1.计算:3-tan15°1+3tan15°=________.2.(2014·宜昌模拟) 计算:sin50°(1+3tan10°)-cos20°cos80°1-cos20°=__________.3.(2015·南京模拟)已知sin ⎝⎛⎭⎫π4-x =513,0<x <π4,则cos2x cos ⎝⎛⎭⎫π4+x =__________. 4.(2015·烟台模拟)已知角α,β的顶点在坐标原点,始边与x 轴的正半轴重合,α、β∈(0,π),角β的终边与单位圆交点的横坐标是-13,角α+β的终边与单位圆交点的纵坐标是45,则cos α=________.5.设α为锐角,若cos ⎝⎛⎭⎫α+π6=45,则sin ⎝⎛⎭⎫2α+π12的值为________. 6.已知sin(α-45°)=-210,0°<α<90°,则cos α=________. 7.已知α,β均为锐角,且tan β=cos α-sin αcos α+sin α,则tan(α+β)=________.8.已知cos 4α-sin 4α=23,且α∈⎝⎛⎭⎫0,π2,则cos ⎝⎛⎭⎫2α+π3=________. 三、解答题1.(2014·江苏卷)已知α∈⎝⎛⎭⎫π2,π,sin α=55. (1)求sin ⎝⎛⎭⎫π4+α的值; (2)求cos ⎝⎛⎭⎫5π6-2α的值. 2.(2014·济南模拟)已知0<α<π2<β<π,tan α2=12,cos(β-α)=210.(1)求sin α的值. (2)求β的值.3.(2015·浙大附中模拟)已知函数f (x )=cos ⎝⎛⎭⎫x -π3-sin ⎝⎛⎭⎫π2-x . (1)求函数f (x )的最小正周期;(2)若α∈⎝⎛⎭⎫0,π2,且f ⎝⎛⎭⎫α+π6=35,求f (2α)的值.4.(选做题)已知sin α+cos α=355,α∈⎝⎛⎭⎫0,π4,sin ⎝⎛⎭⎫β-π4=35,β∈⎝⎛⎭⎫π4,π2. (1)求sin 2α和tan 2α的值;(2)求cos(α+2β)的值.5.(2014·惠州模拟)已知函数f (x )=cos 2x +sin x cos x ,x R ∈. (1)求f ⎝⎛⎭⎫π6的值;(2)若sin α=35,且α∈⎝⎛⎭⎫π2,π,求f ⎝⎛⎭⎫α2+π24. 6.[2014·广东高考]已知函数f (x )=A sin ⎝⎛⎭⎫x +π3,x R ∈,且f ⎝⎛⎭⎫5π12=322. (1)求A 的值;(2)若f (θ)-f (-θ)=3,θ∈⎝⎛⎭⎫0,π2,求f ⎝⎛⎭⎫π6-θ. 7.已知A ,B ,C 是△ABC 的三个内角,向量m =(-1,3),n =(cos A ,sin A ),且m ·n =1. (1)求角A ;(2)若1+sin 2Bcos 2B -sin 2B =2+3,求角B .两角和与差的正弦、余弦和正切公式参考答案1. C 2. C 3. B4. D 考点一_[解] (1)∵f ⎝⎛⎭⎫5π12=A sin ⎝⎛⎭⎫5π12+π4=A sin 2π3=A sin π3=32A =32,∴A = 3. (2)由(1)知f (x )=3sin ⎝⎛⎭⎫x +π4, 故f (θ)+f (-θ)=3sin ⎝⎛⎭⎫θ+π4+3sin ⎝⎛⎭⎫-θ+π4=32, ∴3⎣⎡⎦⎤22(sin θ+cos θ)+22(cos θ-sin θ)=32,∴6cos θ=32,∴cos θ=64.又θ∈⎝⎛⎭⎫0,π2,∴sin θ=1-cos 2θ=104,∴f ⎝⎛⎭⎫3π4-θ=3sin(π-θ)=3sin θ=304. 1.解:tan 2α=2tan α1-tan 2α=2×121-(12)2=43. ∵α∈(0,π2),2α∈(0,π),tan 2α=43>0,∴2α∈(0,π2),∴sin 2α=45,cos 2α=35,∴sin(2α+π3)=sin 2α·cos π3+cos 2α·sin π3=45×12+35×32=4+3310.考点二[解] (1)原式=3×sin 12°cos 12°-3sin 12°(4cos 212°-2)=3sin 12°-3cos 12°2sin 12°cos 12°(2cos 212°-1)=23⎝⎛⎭⎫12sin 12°-32cos 12°sin 24°cos 24°=23sin (12°-60°)12sin 48°=-4 3.(2)∵tan 60°=3=tan(20°+40°)=tan 20°+tan 40°1-tan 20°tan 40°,∴tan 20°+tan 40°=tan(20°+40°)(1-tan 20°tan 40°)=3(1-tan 20°tan 40°).∴tan 20°+tan 40°+3tan 20°tan 40°=3(1-tan 20°tan 40°)+3tan 20°tan 40°= 3.答案:(1)D(2)2 (3)A考点三_[答案] (1)C (2)D解:∵cos α=13,cos(α+β)=-13,且α,β∈⎝⎛⎭⎫0,π2, ∴sin α=223,sin(α+β)=223, cos β=cos[(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α=-13×13+223×223=79.∴cos 2β=2cos 2β-1=2×⎝⎛⎭⎫792-1=1781. 3. 解:(1)因为sin α2+cos α2=62,两边同时平方,得sin α=12.又π2<α<π,所以cos α=-32. (2)因为π2<α<π,π2<β<π.所以-π<-β<-π2,故-π2<α-β<π2.又sin(α-β)=-35,得cos(α-β)=45.cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=-32×45+12×⎝⎛⎭⎫-35=-43+310.名师讲坛[答案] 31.选B.2.A.知能训练参考答案ABCBC D ACDA BA CCB CCCD二、填空题1.1 2. 2 3.24134.3+82155.172506.457.1 8.2-156三、解答题1.解析:(1)因为α∈⎝⎛⎭⎫π2,π,sinα=55,所以cosα=-1-sin2α=-255.故sin⎝⎛⎭⎫π4+α=sinπ4cosα+cosπ4sinα=22×⎝⎛⎭⎫-255+22×55=-1010.(2)由(1)知sin2α=2sinαcosα=2×55×⎝⎛⎭⎫-255=-45,cos2α=1-2sin2α=1-2×⎝⎛⎭⎫552=35,所以cos⎝⎛⎭⎫5π6-2α=cos5π6cos2α+sin5π6sin2α=⎝⎛⎭⎫-32×35+12×⎝⎛⎭⎫-45=-4+3310.2.解析:(1)因为tanα2=12,所以sinα=sin⎝⎛⎭⎫2·α2=2sinα2cosα2=2sinα2cosα2sin2α2+cos2α2=2tanα21+tan2α2=2×121+⎝⎛⎭⎫122=45.(2)因为0<α<π2,sinα=45,所以cosα=35.又0<α<π2<β<π,所以0<β-α<π.由cos(β-α)=210,得0<β-α<π2.所以sin(β-α)=9810=7210,所以sinβ=sin[(β-α)+α]=sin(β-α)cosα+cos(β-α)sinα=7210×35+210×45=25250=22.由π2<β<π,得β=34π.⎝⎛⎭⎫或求cosβ=-22,得β=34π.3.解析:(1)f(x)=12cos x+32sin x-cos x=32sin x-12cos x=sin⎝⎛⎭⎫x-π6.∴f(x)的最小正周期为2π.(2)由(1)知f(x)=sin⎝⎛⎭⎫x-π6.所以f⎝⎛⎭⎫α+π6=sin⎝⎛⎭⎫α+π6-π6=sinα=35,∵α∈⎝⎛⎭⎫0,π2,∴cosα=1-sin2α=1-⎝⎛⎭⎫352=45.∴sin2α=2sinαcosα=2×35×45=2425,cos2α=2cos2α-1=2×⎝⎛⎭⎫452-1=725,∴f(2α)=sin⎝⎛⎭⎫2α-π6=32sin2α-12cos2α=32×2425-12×725=243-750.4.解:(1)由题意得(sin α+cos α)2=95,即1+sin 2α=95,∴sin 2α=45.又2α∈⎝⎛⎭⎫0,π2.∴cos 2α=1-sin22α=35,∴tan 2α=sin 2αcos 2α=43.(2)∵β∈⎝⎛⎭⎫π4,π2,β-π4∈⎝⎛⎭⎫0,π4,sin⎝⎛⎭⎫β-π4=35,∴cos⎝⎛⎭⎫β-π4=45,于是sin 2⎝⎛⎭⎫β-π4=2sin⎝⎛⎭⎫β-π4·cos⎝⎛⎭⎫β-π4=2425.又sin 2⎝⎛⎭⎫β-π4=-cos 2β,∴cos 2β=-2425,又2β∈⎝⎛⎭⎫π2,π,∴sin 2β=725,又cos2α=1+cos 2α2=45,α∈⎝⎛⎭⎫0,π4,∴cos α=255,sin α=55.∴cos(α+2β)=cos αcos 2β-sin αsin 2β=255×⎝⎛⎭⎫-2425-55×725=-11525.5.解(1)f ⎝⎛⎭⎫π6=cos2π6+sinπ6cosπ6=⎝⎛⎭⎫322+12×32=3+34.(2)因为f(x)=cos2x+sin x cos x=1+cos 2x2+12sin 2x=12+12(sin 2x+cos 2x)=12+22sin⎝⎛⎭⎫2x+π4.所以f ⎝⎛⎭⎫α2+π24=12+22sin⎝⎛⎭⎫α+π12+π4=12+22sin⎝⎛⎭⎫α+π3=12+22⎝⎛⎭⎫12sin α+32cos α.又因为sin α=35,且α∈⎝⎛⎭⎫π2,π,所以cos α=-45, 所以f ⎝⎛⎭⎫α2+π24=12+22⎝⎛⎭⎫12×35-32×45=10+32-4620. 6.解:(1)由f ⎝⎛⎭⎫5π12=322, 得A sin ⎝⎛⎭⎫5π12+π3=322⇒A sin 3π4=322⇒22A =322⇒A =3. (2)由f (θ)-f (-θ)=3,得3sin ⎝⎛⎭⎫θ+π3-3sin ⎝⎛⎭⎫-θ+π3=3, 即3sin ⎝⎛⎭⎫θ+π3+3sin ⎝⎛⎭⎫θ-π3=3, 化简整理得6sin θcos π3=3,∴3sin θ=3,∴sin θ=33.∵θ∈⎝⎛⎭⎫0,π2,∴cos θ=63,∴f ⎝⎛⎭⎫π6-θ=3sin ⎝⎛⎭⎫π6-θ+π3=3sin ⎝⎛⎭⎫π2-θ=3cos θ= 6. 7.解析:(1)∵m ·n =(-1,3)·(cos A ,sin A )=3sin A -cos A =2sin ⎝⎛⎭⎫A -π6=1, ∴sin ⎝⎛⎭⎫A -π6=12. 又∵0<A <π,∴-π6<A -π6<5π6,∴A -π6=π6,∴A =π3.(2)∵1+sin 2B cos 2B -sin 2B =2+3,∴(sin B +cos B )2(cos B -sin B )(cos B +sin B )=2+3,∴cos B +sin B cos B -sin B =2+3,∴tan B +11-tan B=2+3,∴tan B =33.又0<B <π,∴B =π6.。
