2016年春季新版沪科版八年级数学下学期第19章、四边形单元复习试卷2

合集下载

沪科版数学八年级下册第19章四边形单元检测

沪科版数学八年级下册第19章四边形单元检测一、选择题(本题共10小题，每小题3分，共30分)1．正方形具有而菱形不一定具有的性质是( )．A ．对角线互相垂直B ．对角线互相平分C ．对角线相等D ．对角线平分一组对角2．下列说法中，不正确的是( )．A ．有三个角是直角的四边形是矩形B ．对角线相等的四边形是矩形C ．对角线互相垂直的矩形是正方形D ．对角线互相垂直的平行四边形是菱形3．已知一四边形的对角线互相垂直，那么顺次连接这个四边形四边中点所得的四边形是( )．A ．矩形B ．菱形C ．等腰梯形D ．正方形4．用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是( )．A ．①②③B ．①④⑤C ．①②⑤D ．②⑤⑥5．已知菱形的周长为9.6 cm ，两个邻角的比是1∶2，这个菱形较短的对角线的长是( )．A ．2.1 cmB ．2.2 cmC ．2.3 cmD ．2.4 cm6．一个正方形的对角线长为2 cm ，则它的面积是( )．A ．2 cm2B ．4 cm2C ．6 cm2D ．8 cm27．如图，在正方形ABCD 中，CE ＝MN ，∠BCE ＝40°，则∠ANM 等于( )．A ．70°B ．60°C ．50°D ．40°8．如图，四边形ABCD 是正方形，延长BC 至点E ，使CE ＝CA ，连接AE 交CD 于点F ，则∠AFC 的度数是( )．A ．150°B ．125°C ．135°D ．112.5°9．正方形ABCD 的边长为3，以CD 为一边向两旁作等边△PCD 和等边△QCD, 那么PQ 的长为（）A ．323 B.332 C.33 D. 36 10．将一张矩形纸对折再对折(如图)，然后沿着图中的虚线剪下，得到①②两部分，将①展开后得到的平面图形是( )．A ．矩形B ．三角形C ．梯形D ．菱形（第7题）（第8题）（第10题）二、填空题(本题共5小题，每小题3分，共15分)11．把“直角三角形，等腰三角形，等腰直角三角形”填入下列相应的空格上．(1)正方形可以由两个能够完全重合的__________拼合而成；(2)菱形可以由两个能够完全重合的__________拼合而成；(3)矩形可以由两个能够完全重合的__________拼合而成．12．在ABCD 中，若添加一个条件__________，则四边形ABCD 是矩形；若添加一个条件_________则四边形ABCD 是菱形；若对角线满足______________，则四边形ABCD 是正方形。

沪科版八年级数学下册第19章四边形单元测试题

沪科版⼋年级数学下册第19章四边形单元测试题第19章四边形⼀、选择题(每题4分,共40分)1. 五边形的内⾓和为( )A.720°B.540°C.360°D.180°2.从n边形的⼀个顶点出发可以引出8条对⾓线,则n= ( )A.8B.9C.10D.113.如图,?ABCD的对⾓线AC,BD相交于点O,E是AB的中点,且AE+EO=4,则?ABCD的周长为( )A.20B.16C.12D.8第3题图第5题图第6题图4.下列给出的是四边形ABCD中∠A,∠B,∠C,∠D的度数之⽐,其中能够判定四边形ABCD是平⾏四边形的是( )A.2∶3∶2∶3B.1∶2∶3∶4C.2∶2∶3∶4D.1∶2∶2∶15.如图,正⽅形ABCD的边长为1,点E,F分别是对⾓线AC上的两点,EG⊥AB, EI⊥AD,FH⊥AB,FJ⊥AD,垂⾜分别为点G,I,H,J,则图中阴影部分的⾯积等于( )A.12 C.13D.146.如图,在四边形ABCD中,∠DAB=90°,∠DCB=90°,E,F分别是BD,AC的中点.若AC=6,BD=10,则EF的长为( )A.3B.4C.5D.√77.如图,正⽅形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,过点A作FA⊥AE,交CB延长线于点F,则EF的长为( ) A.6 B.6√2C.6√3D.6√5第7题图第8题图第9题图8.矩形ABCD与矩形CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH= ( )A.1B.23 C.√22D.√529.如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学⽣在⼀次数学活动课中,通过动⼿实践,探索出如下结论,其中错误的是( )A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形C.当E,F,G,H不是各边中点时,四边形EFGH可以为平⾏四边形D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形10.如图,在矩形ABCD中,BC=√2AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列结论:①∠AEB=∠AEH;②DH=2√2EH;③OH=1AE;④BC-BF=√2EH.其中正确结论的序号为( )A.①②③B.②③④C.②④D.①③⼆、填空题(每题5分,共20分)11.⼀个正多边形的每个外⾓都是36°,这个正多边形是.12.如图,已知矩形ABCD的对⾓线长为8 cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长等于cm.第12题图第13题图第14题图13.如图,在?ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为.14.如图1,在正⽅形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.将正⽅形ABCD沿线段EG,HF 剪开,再把得到的四个四边形按图2的⽅式拼接成⼀个四边形.若正⽅形ABCD的边长为3,HA=EB=FC=GD=1,则图2中阴影部分的⾯积为.三、解答题(共90分)15.(8分)如图,⼀个正五边形和⼀个正⽅形都有⼀边在直线l上,且有⼀个公共顶点B,求∠ABC的度数.16.(8分)如图,在?ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.求证:四边形ACDF是平⾏四边形.17.(8分)如图,BD为矩形ABCD的⼀条对⾓线,延长BC⾄E,使CE=BD,连接AE,若AB=1,∠E=15°,求AD的长度.18.(8分)如图,在菱形ABCD 中,点E,O,F 分别为AB,AC,AD的中点,连接CE,CF,OE,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满⾜什么关系时,四边形AEOF是正⽅形?请说明理由.19.(10分)如图,在菱形ABCD中,E,F分别是边BC,AD上的点,已知AE⊥BC,∠1=∠2.(1)判断四边形AECF的形状,并证明你的结论;(2)若AE=4,AF=2,试求菱形ABCD的⾯积.20.(10分)如图,在平⾏四边形ABCD中,AB=3 cm,BC=5 cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.(1)求证:四边形CEDF是平⾏四边形;(2)①当AE=cm时,四边形CEDF是矩形;②当AE=cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)21.(12分)如图,AD是△ABC的⾓平分线,线段AD的垂直平分线分别交AB和AC于点E,F,连接DE,DF.(1)试判断四边形AEDF的形状,并证明你的结论;(2)若AE=5,AD=8,求四边形AEDF的⾯积;(3)△ABC满⾜什么条件时,四边形AEDF是正⽅形?22.(12分)如图,在Rt△ABC中,∠ACB=90°,过点C作直线MN,且MN∥AB,D为AB边上⼀点,过点D作DE⊥BC,交直线MN于点E,垂⾜为点F,连接CD,BE.(1)求证:CE=AD;(2)当D为AB的中点时,判断四边形BECD的形状,并说明理由;(3)若D为AB的中点,则当∠A为多少度时,四边形BECD是正⽅形.请简要证明.23.(14分)在菱形ABCD中,∠ABC=60°,点P是射线BD上⼀动点,以AP为边向右侧作等边三⾓形APE,点E的位置随着点P的位置变化⽽变化.(2)当点E在菱形ABCD外部时,(1)中的结论是否仍然成⽴?若成⽴,请予以证明;若不成⽴,请说明理由(选择图2,图3中的⼀种情况予以证明或说理).(3)如图4,当点P在线段BD的延长线上时,连接BE,若AB=2√3,BE=2√19,求四边形ADPE的⾯积.图1图2图3图4答案题号 1 2 3 4 5 6 7 8 9 10答案 B D B A B B B C D D11.正⼗边形12.1613.30°14.1=108°,∠CBF=90°,∠BFE=90°,∠BEF=360°÷5=72°, 15.如图,根据题意,得∠ABE=(5-2)×180°5∴∠EBF=180°-∠BEF -∠BFE=180°-72°-90°=18°,∴∠ABC=360°-∠ABE-∠EBF -∠CBF=360°-108°-18°-90°=144°.16.∵四边形ABCD是平⾏四边形,∴AB∥CD,即AF∥CD,∴∠FAE=∠CDE,∵点E是AD的中点,∴AE=DE,⼜∵∠FEA=∠CED,∴△FAE≌△CDE(ASA),∴CD=FA,⼜∵CD∥AF,∴四边形ACDF是平⾏四边形.17.连接AC,∵四边形ABCD是矩形,∴AD∥BE,AC=BD.∵BD=CE,∴CE=CA,∴∠E=∠CAE=15°.∵∠ACB=∠CAE+∠E=30°,AB=1,∴AC=2AB=2,∴AD=BC=√AC2-AB2=√3.18.(1)∵四边形ABCD为菱形,⼜∵点E,F分别是AB,AD的中点,∴BE=DF,∴△BCE≌△DCF.(2)当AB⊥BC时,四边形AEOF为正⽅形.理由如下:∵点E,O分别是AB,AC的中点,∴EO∥BC.∵四边形ABCD为菱形,∴BC∥AD,∴OE∥AD,即OE∥AF. 同理可证OF∥AE,∴四边形AEOF为平⾏四边形.由(1)可得,AE=AF,∴平⾏四边形AEOF为菱形.∵BC⊥AB,∴∠B=90°,∴∠BAD=90°,∴菱形AEOF为正⽅形.19.(1)四边形AECF是矩形.证明如下:∵四边形ABCD是菱形,∴AD∥BC,∠BAD=∠BCD,∵AE⊥BC,∴AE⊥AD,∴∠FAE=∠AEC=90°,∵∠1=∠2,∴∠BAD-∠1=∠BCD-∠2,∴∠EAF=∠FCB=90°=∠AEC,∴四边形AECF是矩形.(2)∵四边形AECF是矩形,∴AF=EC=2.∵四边形ABCD是菱形,∴AB=BC,∴BE=BC-CE=AB-2. 在Rt△ABE中,AB2=AE2+BE2,∴AB2=16+(AB-2)2,∴AB=5,∴菱形ABCD的⾯积=BC×AE=AB×AE=5×4=20.20.(1)∵四边形ABCD是平⾏四边形,∴CF∥ED,∴∠FCG=∠EDG,∵G是CD的中点,∴CG=DG,在△FCG和△EDG中,∠FCG=∠EDG,CG=DG,∠CGF=∠DGE,∴△FCG≌△EDG,∴FG=EG,⼜∵CG=DG,∴四边形CEDF是平⾏四边形.(2)①3.5如图,过点A作AM⊥BC于M.∵∠B=60°,AB=3 cm,∴BM=1.5 cm.∵四边形ABCD是平⾏四边形,∴AD=BC=5 cm,∴MC=BC-BM=5-1.5=3.5(cm),∵四边形CEDF是矩形,∴∠AEC=∠ECM=90°,∴四边形AECM是矩形,∴MC=AE=3.5 cm.∵四边形CEDF是菱形,∴CE=ED,∠CEG=12∠CED,CD⊥EF.∵∠CDA=60°,∴△CED是等边三⾓形,∠CEG=30°,在Rt△CEG中,CE=2CG=CD=AB=3 cm,∴AE=AD-ED=AD-CE=5-3=2(cm).21.(1)四边形AEDF是菱形.证明如下:∵AD平分∠BAC,∴∠1=∠2,⼜∵EF⊥AD,∴∠AOE=∠AOF=90°.在△AEO和△AFO中,∵∠1=∠2,AO=AO,∠AOE=∠AOF,∴△AEO≌△AFO,∴EO=FO,⼜∵OA=OD,∴四边形AEDF是平⾏四边形,⼜∵EF⊥AD,∴平⾏四边形AEDF为菱形.(2)由(1)得,AO=12AD=4,∠AOE=90°,EF=2EO,在Rt△AOE中,∵AE=5,∴EO=√AE2-AO2=3,EF=2EO=6.∵四边形AEDF是菱形,所以四边形AEDF的⾯积为12EF×AD=12×6×8=24.(3)当△ABC是直⾓三⾓形且∠BAC=90°时,四边形AEDF是正⽅形.22.(1)∵DE⊥BC,∴∠DFB=90°,∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,∵MN∥AB,即CE∥AD,∴四边形ADEC是平⾏四边形,∴CE=AD.(2)四边形BECD是菱形.理由如下:∵D为AB的中点,∴AD=BD,∵CE=AD,∴BD=CE,∵BD∥CE,∴四边形BECD是平⾏四边形,∵∠ACB=90°,D为AB的中点,∴CD=BD,∴四边形BECD是菱形.(3)∠A=45°时,四边形BECD是正⽅形.证明如下:由(2)可知,四边形BECD是菱形,∴∠ABC=∠CBE=45°,∴∠DBE=90°,∴四边形BECD是正⽅形.23.(1)相等(或BP=CE) 垂直(或CE⊥AD)(2)成⽴.选择题图2中的情况.证明如下:如图1,连接AC,交BD于点O,图1∵四边形ABCD为菱形,∠ABC=60°,∴AB=BC,∠ABD=30°,∴△ABC为等边三⾓形,∴∠BAC=60°.∵△APE为等边三⾓形,∴AP=AE,∠PAE=60°,∴∠BAC+∠PAC=∠PAE+∠PAC,即∠BAP=∠CAE.在△ABP与△ACE中,{AB=AC,∠BAP=∠CAE, AP=AE,∴△ABP≌△ACE,∴BP=CE,∠ACE=∠ABP=30°. 易得△ACD为等边三⾓形,∴∠CAD=60°,∴CE⊥AD.(3)如图2,连接AC,CE,设AD与CE交于点M,图2由(2)可得BP=CE,CE⊥AD,∠ACE=∠ABP=30°. ∵△ABC为等边三⾓形,∴∠ACB=60°,∴∠BCE=90°.∵BC=AB=2√3,BE=2√19,∴CE=√BE2-BC2=√76?12=8,∴BP=8.∵△ADC为等边三⾓形,AD=2√3,∴AM=√3,CM=3,∴EM=CE-CM=5,∴AE=√AM2+EM2=√(√3)2+52=√28=2√7,∴S△AEP=√34设AC与BD交于点O,∵AB=2√3,∴BD=6,AO=√3,∴DP=BP-BD=8-6=2,∴S△ADP=12DP·AO=12×2×√3=√3,∴S四边形ADPE=S△AEP+S△ADP=7√3+√3=8√3.。

八年级数学下册《第十九章四边形》单元测试卷及答案解析-沪科版

八年级数学下册《第十九章四边形》单元测试卷及答案解析-沪科版一、单选题1．若一个n 边形内角和为540︒，则n 的值为（）A ．5B ．6C ．7D ．82．在ABC 中，点D ，E 分别是AB ，AC 上的点，且DE BC ，点F 是DE 延长线上一点，连接CF ．添加下列条件后，不能判断四边形BCFD 是平行四边形的是（）A ．BD CFB ．DF BC = C ．BD CF = D ．=B F ∠∠3．菱形的边长为5，它的一条对角线的长为6，则菱形的另一条对角线的长为（）A ．8B ．6C ．5D ．44．如图，菱形ABCD 的对角线相交于点O ，AC=5cm ，10cm BD =则菱形的面积为（）A ．25cmB ．210cmC ．225cmD ．250cm5．已知一个多边形的内角和是它的外角和的3倍，则这个多边形是（）A ．九边形B ．八边形C ．七边形D ．六边形6．如图，在平行四边形ABCD 中120BAD ∠=︒连接BD ，作AE //BD 交CD 延长线于点E ，过点E 作EF BC ⊥交BC 的延长线于点F ，且1CF =，则AB 的长是（）A ．1B ．2C 3D 27．如图，在矩形ABCD 中，AB=3，BC=6，对角线AC 的垂直平分线分别交AD 、AC 于点M ，N ，则AM 的长为（）A ．154B ．153C ．254D ．2538．如图，在菱形ABCD 中，E ，F 分别是边CD ，BC 上的动点，连接AE ，EF ，G ，H 分别为AE ，EF 的中点，连接GH ．若45B ∠=︒，23BC =则GH 的最小值为（）A 3B ．22C 6D 69．如图，在边长为5的正方形ABCD 中，点M 为线段CD 上一点，且23CM DM =，点P 是对角线AC 上一动点，过点P 作PE AD ⊥于点E ，PF CD ⊥于点F ，则PM EF +的最小值为（）A 21B ．52C 29D ．213+10．正多边形通过镶嵌能够密铺成一个无缝隙的平面，下列组合中不能镶嵌成一个平面的是（） A ．正三角形和正方形B ．正三角形和正六边形C ．正方形和正六边形D ．正方形和正八边形二、填空题11．已知一个多边形的每个外角都是45°，则这个多边形的边数为12．如图，在▱ABCD 中，▱B ＝75°，AC ＝AD ，则▱DAC 的度数是 °．13．如图，在菱形ABCD 中，过点A 作AE BC ⊥于点E ，交对角线BD 于点F ，点G 为DF 的中点．若90BAG ∠=︒，则DBC ∠= °．14．用两类不同形状的正多边形密铺地面，除了正三角形与正六边形可供选择外，还可以选择与来密铺．三、解答题15．在四边形ABCD 中，▱D=60°，▱B 比▱A 大20°，C 是▱A 的2倍，求▱A ，▱B ，▱C 的大小。

沪科版八年级数学下《第19章四边形》单元测试卷含答案

四边形测试题一、选择题(本大题共5小题，每小题5分，共25分；在每小题列出的四个选项中，只有一项符合题意)1．若菱形的周长为48 cm，则其边长是()A．24 cmB．12 cmC．8 cmD．4 cm2．如图3－G－1，在矩形ABCD中，对角线AC，BD相交于点O，∠ACB＝30°，则∠AOB的大小为()图3－G－1A．30°B．60°C．90°D．120°3.如图3－G－2所示，在菱形ABCD中，不一定成立的是()图3－G－2A．四边形ABCD是平行四边形B．AC⊥BDC．△ABD是等边三角形D．∠CAB＝∠CAD4．如图3－G－3，在矩形ABCD中，O是对角线AC，BD的交点，点E，F分别是OD，OC的中点．如果AC＝10，BC＝8，那么EF的长为()A．6 B．5 C．4 D．3图3－G－35．如图3－G－4，菱形ABCD的周长为16，∠ABC＝120°，则AC的长为()图3－G－4A．4 3B．4C．2 3D．2二、填空题(本大题共5小题，每小题5分，共25分)6．在菱形ABCD中，若对角线AC＝8 cm，BD＝6 cm，则边长AB＝________ cm.7．矩形两对角线的夹角为120°，矩形的宽为3，则矩形的面积为__________．8．如图3－G－5所示，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD，BC于点E，F，AB＝2，BC＝3，则图中阴影部分的面积为________．图3－G－59．已知菱形ABCD的面积为24 cm2，若对角线AC＝6 cm，则这个菱形的边长为________cm.10．如图3－G－6，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE＝DF.给出下列条件：①BE⊥EC；②BF∥CE；③AB＝AC.从中选择一个条件使四边形BECF是菱形，你认为这个条件是________(只填写序号)．图3－G－6三、解答题(本大题共5小题，共50分)11．(6分)如图3－G－7所示，已知四边形ABCD是菱形，对角线AC与BD相交于点O，AB＝5，AO＝4，求BD的长．图3－G－712．(8分)如图3－G－8，在△ABC中，AB＝AC＝5，BC＝6，AD是BC边上的中线，四边形ADBE是平行四边形．(1)求证：四边形ADBE是矩形；(2)求矩形ADBE的面积．图3－G－813.(12分)如图3－G－9①，在△ABC和△EDC中，AC＝CE＝CB＝CD，∠ACB＝∠DCE＝90°，AB与CE交于点F，ED与AB，BC分别交于M，H.(1)求证：CF＝CH；(2)如图②，△ABC不动，将△EDC绕点C旋转到∠BCE＝45°时，试判断四边形ACDM 是什么四边形？并证明你的结论．图3－G－914．(12分)如图3－G－10，在四边形ABCD中，对角线AC，BD相交于点O，AO＝CO，BO＝DO，且∠ABC＋∠ADC＝180°.(1)求证：四边形ABCD是矩形．(2)若∠ADF∶∠FDC＝3∶2，DF⊥AC，则∠BDF的度数是多少？图3－G－1015．(12分)如图3－G－11，▱ABCD的对角线AC，BD相交于点O，BD＝12 cm，AC＝6 cm，点E在线段BO上从点B以1 cm/s的速度运动，点F在线段OD上从点O以2 cm/s 的速度运动．(1)若点E，F同时运动，设运动时间为t秒，当t为何值时，四边形AECF是平行四边形？(2)在(1)的条件下，①当AB为何值时，四边形AECF是菱形？②四边形AECF可以是矩形吗？为什么？图3－G－111．B 2．B3．C [解析] 灵活掌握菱形的性质定理即可判断．4．D [解析] ∵四边形ABCD 是矩形，∴AB ＝CD ，∠ABC ＝90°.∵AC ＝10，BC ＝8，由勾股定理得AB ＝102－82＝6，∴CD ＝AB ＝6.∵点E ，F 分别是OD ，OC 的中点，∴EF ＝12CD ＝3.故选D . 5．A [解析] 设AC 与BD 交于点E ，则∠ABE ＝60°.根据菱形的周长求出AB ＝16÷4＝4.在Rt △ABE 中，求出BE ＝2，根据勾股定理求出AE ＝42－22＝2 3，故可得AC ＝2AE ＝4 3.6．5 [解析] 如图，∵在菱形ABCD 中，对角线AC ＝8 cm ，BD ＝6 cm ，∴AO ＝12AC＝4 cm ，BO ＝12BD ＝3 cm .∵菱形的对角线互相垂直，∴在Rt △AOB 中，AB ＝AO 2＋BO 2＝42＋32＝5(cm )．7．9 3 [解析] 根据勾股定理求得矩形的另一边长为3 3，所以面积是9 3.8．3 [解析] 可证得△AOE ≌△COF ，所以阴影部分的面积就是△BCD 的面积，即矩形面积的一半．9．5 [解析] 菱形ABCD 的面积＝12AC·BD.∵菱形ABCD 的面积是24 cm 2，其中一条对角线AC 长6 cm ，∴另一条对角线BD 的长为8 cm .边长＝32＋42＝5 (cm )．10．③ [解析] 由题意得BD ＝CD ，ED ＝FD ，∴四边形EBFC 是平行四边形．①BE ⊥EC ，根据这个条件只能得出四边形EBFC 是矩形；②BF ∥CE ，根据EBFC 是平行四边形已可以得出BF ∥CE ，因此不能根据此条件得出▱EBFC 是菱形；③AB ＝AC ，∵⎩⎨⎧AB ＝AC ，DB ＝DC ，AD ＝AD ，∴△ADB ≌△ADC(SSS)，∴∠BAD ＝∠CAD ，∴△AEB ≌△AEC(SAS)，∴BE ＝CE ，∴四边形BECF 是菱形． 11．解：∵四边形ABCD 是菱形， ∴AC ⊥BD ，DO ＝BO. ∵AB ＝5，AO ＝4，∴BO ＝AB 2－AO 2＝52－42＝3， ∴BD ＝2BO ＝6.12．解：(1)证明：∵AB ＝AC ，AD 是BC 边上的中线， ∴AD ⊥BC ， ∴∠ADB ＝90°.∵四边形ADBE 是平行四边形， ∴▱ADBE 是矩形．(2)∵AB ＝AC ＝5，BC ＝6，AD 是BC 边上的中线，∴BD ＝DC ＝6×12＝3.在Rt △ACD 中，AD ＝AC 2－DC 2＝52－32＝4， ∴S 矩形ADBE ＝BD·AD ＝3×4＝12.13．解：(1)证明：∵AC ＝CE ＝CB ＝CD ，∠ACB ＝∠ECD ＝90°， ∴∠A ＝∠B ＝∠D ＝∠E ＝45°. 在△BCF 和△ECH 中， ⎩⎨⎧∠B ＝∠E ，BC ＝EC ，∠BCF ＝∠ECH ，∴△BCF ≌△ECH(ASA)， ∴CF ＝CH.(2)四边形ACDM 是菱形．证明：∵∠ACB ＝∠DCE ＝90°，∠BCE ＝45°， ∴∠ACE ＝∠DCH ＝45°.∵∠E ＝45°，∴∠ACE ＝∠E ，∴AC ∥DE ， ∴∠AMH ＝180°－∠A ＝135°＝∠ACD. 又∵∠A ＝∠D ＝45°，∴四边形ACDM 是平行四边形． ∵AC ＝CD ，∴四边形ACDM 是菱形．14．解：(1)证明：∵AO ＝CO ，BO ＝DO ， ∴四边形ABCD 是平行四边形， ∴∠ABC ＝∠ADC.∵∠ABC ＋∠ADC ＝180°， ∴∠ABC ＝∠ADC ＝90°， ∴四边形ABCD 是矩形．(2)∵∠ADC ＝90°，∠ADF ∶∠FDC ＝3∶2， ∴∠FDC ＝36°.∵DF ⊥AC ，∴∠DCO ＝90°－36°＝54°. ∵四边形ABCD 是矩形，∴OC ＝OD ，∴∠ODC ＝54°， ∴∠BDF ＝∠ODC －∠FDC ＝18°.15．解：(1)若四边形AECF 是平行四边形，则AO ＝OC ，EO ＝OF.∵四边形ABCD 是平行四边形， ∴BO ＝OD ＝6 cm ， ∴EO ＝6－t ，OF ＝2t ， ∴6－t ＝2t ，∴t ＝2，∴当t ＝2时，四边形AECF 是平行四边形． (2)①若四边形AECF 是菱形， ∴AC ⊥BD ，∴AO2＋BO2＝AB2，∴AB＝36＋9＝3 5，即当AB＝3 5时，四边形AECF是菱形．②不可以．理由：若四边形AECF是矩形，则EF＝AC，∴6－t＋2t＝6，∴t＝0，则此时点E在点B处，点F在点O处，显然四边形AECF不可以是矩形．。

沪科版八年级下《第19章四边形》单元测试卷含答案

沪科版八年级下《第19章四边形》单元测试卷含答案一、选择题(每题4分,共40分)1.正多边形的一个内角是120°,则这个正多边形的边数为()A.4B.8C.6D.122.菱形具有而一般平行四边形不具有的性质是()A.对边相等B.对角相等C.对角线互相平分D.对角线互相垂直3.在▱ABCD中,AB=3,BC=4,连接AC,BD,当▱ABCD的面积最大时,下列结论正确的有()①AC=5;②∠BAD+∠BCD=180°;③AC⊥BD;④AC=BD.A.①②③B.①②④C.②③④D.①③④4.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是()A.6B.7C.8D.95.菱形的周长是它的高的4倍,则菱形中较大的一个角是()A.100°B.120°C.135°D.150°6.以三角形一条中位线和第三边上的中线为对角线的四边形是()A.平行四边形B.矩形C.菱形D.正方形7.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是()A.20B.15C.10D.58.如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则AE的长为()A.4B.C.D.59.如图,梯形ABCD中,AB∥CD,点E,F,G分别是BD,AC,DC的中点.已知两底之差是6,两腰之和是12,则△EFG的周长是()A.8B.9C.10D.1210.如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC 的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE是菱形;③四边形ABCD的面积为EF·BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有()A.5个B.4个C.3个D.2个二、填空题(每题5分,共20分)11.如图,在矩形ABCD中,E,F,G,H分别是边AB,CD,BC,DA的中点,则四边形EGFH是______________形.12.如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC.若AB=10,则EF的长是__________.13.如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论中一定成立的是__________.(把所有正确结论的序号都填在横线上)①∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.14.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是__________.三、解答题(22,23题每题9分,其余每题6分,共60分)15.如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AB=5,OA=4,求BD的长.16.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.猜想线段CD与线段AE的位置关系和大小关系,并加以证明.17.如图,▱ABCD中,点E,F在直线AC上(点E在点F左侧),BE∥DF.(1)求证:四边形BEDF是平行四边形;(2)若AB⊥AC,AB=4,BC=2,当四边形BEDF为矩形时,求线段AE 的长.18.如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A 按顺时针方向旋转得到的,连接BE,CF,相交于点D.(1)求证:BE=CF;(2)当四边形ACDE为菱形时,求BD的长.19.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC的外角∠CAM的平分线,CE⊥AN,垂足为点E.(1)求证:四边形ADCE为矩形.(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.20.若a,b,c,d是四边形ABCD的四条边长,且满足a4+b4+c4+d4=4abcd,试判断四边形ABCD的形状,并说明理由.21.已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.(1)若CE=1,求BC的长;(2)求证:AM=DF+ME.22.如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.23.如图①所示,在正方形ABCD和正方形CGEF中,点B,C,G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM.易证DM=FM,DM⊥FM.(不需写证明过程)(1)如图②,当点B,C,F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明.(2)如图③,当点E,B,C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.参考答案一、1.【答案】C 2.【答案】D3.【答案】B解：根据题意得,当▱ABCD的面积最大时,四边形ABCD为矩形,∴∠BAD=∠ABC=∠BCD=90°,AC=BD.∴AC==5.①正确,②正确,③不正确,④正确.故选B.4.【答案】C解：根据从一个n边形的某个顶点出发,可以引(n-3)条对角线,把n边形分为(n-2)个三角形列出方程n-2=6,解得n=8.5.【答案】C6.【答案】A7.【答案】D8.【答案】C解：设BE=x.∵四边形ABCD是菱形,∴BC=AB=5,∴CE=5-x,根据勾股定理得52-x2=62-(5-x)2,解得x=,∴AE==.9.【答案】B解：由三角形中位线定理得EG=BC,FG=AD,EF是两底之差的一半,所以△EFG的周长=×12+×6=9.10.【答案】B解：①正确,根据三角形的面积公式可得到结论.②根据已知条件利用菱形的判定定理可证得其正确.③正确,根据菱形的面积等于对角线乘积的一半即可求得.④不正确,根据已知可求得∠FDO=∠EDO,∠ADE=∠CDF,而无法求得∠ADE=∠EDO.⑤正确,由已知可证得△DEO≌△DFO,从而可推出此结论正确.二、11.【答案】菱12.【答案】513.【答案】①②④解：在▱ABCD中,AB=CD,AB∥CD,AD∥BC.∵F是AD的中点,AD=2AB,∴DF=DC,∴∠DFC=∠DCF.∵AD∥BC,∴∠DFC=∠BCF,∴∠DCF=∠BCF,∴∠DCF=∠BCD,①正确;延长EF交CD的延长线于点M.∵AB∥CD,∴∠A=∠MDF.在△AEF和△DMF中,∴△AEF≌△DMF,∴EF=FM.∵CE⊥AB,AB∥CD,∴CE⊥CD,∴CF= EM=EF,②正确;∵EF=FM,∴S△CEF=S△CMF.∵CM>BE,∴S△BEC<S△CEM=2S△CEF,③错误;设∠FEC=x,则∠FCE=x,∴∠DCF=90°-x,∠EFC=180°-2x,∴∠DFE=90°-x+180°-2x=27 0°-3x.∵∠AEF=90°-x,∴∠DFE=3∠AEF,④正确.14.【答案】10解：如图,连接DE,交AC于P',连接BP',则P'B+P'E即为PB+PE的最小值.∵四边形ABCD是正方形,∴B,D关于直线AC对称,∴P'B=P'D,∴P'B+P'E=P'D+P'E=DE.∵BE=2,AE=3BE,∴AE=6,∴AD =AB=8,∴DE==10,故PB+PE的最小值是10.三、15.解:∵四边形ABCD是菱形,∴OD=OB,AC⊥BD,∴在Rt△AOB中,OB===3,∴BD=2OB=6.16.解:线段CD与线段AE的位置关系和大小关系是平行且相等.证明:∵CE∥AB,∴∠ADO=∠CEO,∠DAO=∠ECO.又∵OA=OC,∴△ADO≌△CEO,∴AD=CE,∴四边形ADCE是平行四边形,∴CD∥AE,CD=AE.17.(1)证明:连接BD,交AC于点O,∵四边形ABCD是平行四边形,∴OB=OD.∵BE∥DF,∴∠BEO=∠DFO.又∵∠EOB=∠FOD,∴△BEO≌△DFO.∴BE=DF.又BE∥DF,∴四边形BEDF是平行四边形.(2)解:∵AB⊥AC,AB=4,BC=2,∴AC=6,∴OA=3,∴BO==5.又∵四边形BEDF是矩形,∴OE=OB=5,∴点E在OA的延长线上,且AE=2.18.(1)证明:由旋转可知,∠EAF=∠BAC,AF=AC,AE=AB.∴∠EAF+∠BAF=∠BAC+∠BAF,即∠BAE=∠CAF.又∵AB=AC,∴AE=AF.∴△ABE≌△ACF,∴BE=CF.(2)解:∵四边形ACDE是菱形,AB=AC=1,∴AC∥DE,DE=AE=AB=1.又∵∠BAC=45°,∴∠AEB=∠ABE=∠BAC=45°.∵∠AEB+∠BAE+∠ABE=180°,∴∠BAE=90°,∴BE===.∴BD=BE-DE=-1.19.(1)证明:在△ABC中,AB=AC,AD⊥BC,∴∠BAD=∠DAC.∵AN是△ABC的外角∠CAM的平分线,∴∠MAE=∠CAE,∴∠DAE=∠DAC+∠CAE=×180°=90°.又∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形.(2)解:当∠BAC=90°时,四边形ADCE是正方形,证明如下:∵∠BAC=90°,AB=AC,AD⊥BC于D,∴∠ACD=∠DAC=45°,∴DC=AD.由(1)知四边形ADCE是矩形,∴四边形ADCE是正方形.解：(2)题答案不唯一.20.解:四边形ABCD是菱形.理由:因为a4+b4+c4+d4=4abcd,所以a4-2a2b2+b4+c4-2c2d2+d4+2a2b2-4abcd+2c2d2=0,所以(a2-b2)2+(c2-d2)2+2(ab-cd)2=0,所以a2-b2=0且c2-d2=0且ab-cd=0.因为a,b,c,d是四边形ABCD的四条边长,所以a>0,b>0,c>0,d>0,所以a=b=c=d,所以四边形ABCD是菱形.21.(1)解:∵四边形ABCD是菱形,∴CB=CD,AB∥CD,∴∠1=∠ACD.∵∠1=∠2,∴∠2=∠ACD,∴MC =MD.∵ME⊥CD,∴CD=2CE=2,∴BC=CD=2.(2)证明:如图,延长DF交AB的延长线于点G.∵四边形ABCD是菱形,∴∠BCA=∠DCA,BC=CD.∵BC=2CF,CD=2CE,∴CE=CF.∵CM=CM,∴△CEM≌△CFM,∴ME=MF.∵AB∥CD,∴∠2=∠G,∠BCD=∠GBF.∵CF=BF,∴△CDF≌△BGF,∴DF=GF.∵∠1=∠2,∠G=∠2,∴∠1=∠G ,∴AM=GM=MF+GF=DF+ME.分析：利用三角形全等来解决线段的有关问题是常见的思考方法,遇到中点延长一倍,是常见的辅助线作法.22.(1)证明:∵AF∥BC,∴∠AFE=∠ECD.又∵E为AD的中点,∴AE=DE.在△AFE与△DCE中,∵∴△AFE≌△DCE(AAS),∴AF=CD.又∵AF=BD,∴BD=CD.(2)解:当AB=AC时,四边形AFBD是矩形.证法一:由(1)知,D为BC的中点,又∵AB=AC,∴AD⊥BC.∵AF∥BC,∴∠DAF=∠ADB=90°.∵△AFE≌△DCE(已证),∴CE=EF.∴DE为△BCF的中位线,∴DE∥BF.∴∠FBD=∠EDC=90°,∴四边形AFBD是矩形.证法二:∵AF=BD,AF∥BD,∴四边形AFBD是平行四边形.由(1)知,D为BC的中点,又∵AB=AC,∴AD⊥BC(三线合一),即∠BDA=90°.∴▱AFBD是矩形.23.解:(1)DM=FM,DM⊥FM.证明:连接DF,NF.如图.∵四边形ABCD和四边形CGEF都是正方形, ∴AD∥BC,BC∥GE.∴AD∥GE.∴∠DAM=∠NEM.∵M是AE的中点,∴AM=EM.∵∠AMD=∠EMN,∴△MAD≌△MEN.∴DM=NM,AD=EN.∵AD=CD,∴CD=EN.∵CF=EF,∠FCD=∠FEN=90°,∴△DCF≌△NEF.∴DF=NF,∠CFD=∠EFN.∵∠EFN+∠CFN=90°,∴∠CFD+∠CFN=90°,即∠DFN=90°.∴DM=FM,DM⊥FM.(2)DM=FM,DM⊥FM.。

难点详解沪科版八年级数学下册第19章四边形章节训练试题(含答案及详细解析)

沪科版八年级数学下册第19章四边形章节训练考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、若一个直角三角形的周长为31，则此直角三角形的面积为（）A B C．3D．2、下列测量方案中，能确定四边形门框为矩形的是（）A．测量对角线是否互相平分B．测量两组对边是否分别相等C．测量对角线是否相等D．测量对角线交点到四个顶点的距离是否都相等3、如图，小明从点A出发沿直线前进10m到达点B，向左转30，后又沿直线前进10m到达点C，再向左转30°后沿直线前进10m到达点．．．照这样走下去，小明第一次回到出发点A，一共走了（）米．A．80 B．100 C．120 D．1404、将一张长方形纸片ABCD按如图所示的方式折叠，AE、AF为折痕，点B、D折叠后的对应点分别为∠''＝10°，则∠EAF的度数为（）B′、D'，若B ADA．40°B．45°C．50°D．55°5、菱形ABCD的周长是8cm，∠ABC＝60°，那么这个菱形的对角线BD的长是（）A B．C．1cm D．2cm6、如果一个多边形的外角和等于其内角和的2倍，那么这个多边形是（）A．三角形B．四边形C．五边形D．六边形7、在平面直角坐标系中，平行四边形ABCD的顶点A、B、D的坐标分别是(0，0)，(5，0)，(2，3)，则顶点C的坐标是（）A．（7，3）B．（8，2）C．（3，7）D．（5，3）8、如图，直角三角形纸片ABC中，∠ACB=90°，∠A=50°，将其沿边AB上的中线CE折叠，使点A 落在点A'处，则∠A'EB的度数为（）A．10°B．15°C．20°D．40°9、如图，平行四边形ABCD的周长为36，对角线AC，BD相交于点O，点E是CD的中点，BD＝12，则△DOE的周长是（）A．12 B．15 C．18 D．2410、下列四个命题中，正确的是（）A．对角线相等的四边形是矩形B．有一个角是直角的四边形是矩形C．两组对边分别相等的四边形是矩形D．四个角都相等的四边形是矩形第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、在矩形ABCD中，点E在AD边上，△BCE是以BE为一腰的等腰三角形，若AB＝4，BC＝5，则线段DE的长为 _____．2、平行四边形ABCD中，∠BAD的平分线交BC边于点E，∠ADC的平分线交BC边于点F，AB=5，EF=1，则BC=______ ．3、如图，菱形ABCD的对角线AC，BD相交于点O，E为DC的中点，若2OE ，则菱形的周长为__________．4、如图，四边形ABCD和四边形OMNP都是边长为4的正方形，点O是正方形ABCD对角线的交点，正方形OMNP绕点O旋转过程中分别交AB，BC于点E，F，则四边形OEBF的面积为______．5、如图，在正方形ABCD 中，AB ＝AC ，以点C 为圆心、AC 长为半径画弧，点E 在BC 的延长线上，则阴影部分的面积为 _____．三、解答题（5小题，每小题10分，共计50分）1、如图，在Rt△ABC 中，∠ACB ＝90°，D 为AB 中点，,BE CD CE AB ∥∥．（1）试判断四边形BDCE 的形状，并证明你的结论；（2）若∠ABC ＝30°，AB ＝4，则四边形BDCE 的面积为．2、如图，正方形ABCD 的边长为4，连接对角线AC ，点E 为BC 边上一点，将线段AE 绕点A 逆时针旋转45°得到线段AF ，点E 的对应点F 恰好落在边CD 上，过F 作FM ⊥AC 于点M ．（1）求证：BE ＝FM ；（2）求BE 的长度．3、如图，▱ABCD的对角线AC，BD相交于点O，点E，点F在线段BD上，且DE＝BF．求证：AE∥CF．4、阅读材料，回答下列问题：（材料提出）“八字型”是数学几何的常用模型，通常由一组对顶角所在的两个三角形构成．（探索研究）探索一：如图1，在八字形中，探索∠A、∠B、∠C、∠D之间的数量关系为；探索二：如图2，若∠B＝36°，∠D＝14°，求∠P的度数为；探索三：如图3，CP、AG分别平分∠BCE、∠FAD，AG反向延长线交CP于点P，则∠P、∠B、∠D之间的数量关系为．（模型应用）应用一：如图4，在四边形MNCB中，设∠M＝α，∠N＝β，α+β＞180°，四边形的内角∠MBC与外角∠NCD的角平分线BP，CP相交于点P．则∠A＝（用含有α和β的代数式表示），∠P ＝．（用含有α和β的代数式表示）应用二：如图5，在四边形MNCB中，设∠M＝α，∠N＝β，α+β＜180°，四边形的内角∠MBC与外角∠NCD 的角平分线所在的直线相交于点P ，∠P ＝．（用含有α和β的代数式表示）（拓展延伸）拓展一：如图6，若设∠C ＝x ，∠B ＝y ，∠CAP ＝13∠CAB ，∠CDP ＝13∠CDB ，试问∠P 与∠C 、∠B 之间的数量关系为．（用x 、y 表示∠P ）拓展二：如图7，AP 平分∠BAD ，CP 平分∠BCD 的邻补角∠BCE ，猜想∠P 与∠B 、∠D 的关系，直接写出结论．5、Rt ABC ∆中，90ACB ∠=︒，点D 、E 分别为边AB 、BC 上的点，且CD CA =，DE AB ⊥，联结AE 交CD 与点F ，点M 是AE 的中点，联结CM 并延长与AB 交于点H ．（1）点F 是CD 中点时，求证：AE CD ⊥；（2）求证：222+=MH HD AM-参考答案-一、单选题1、B【分析】根据直角三角形斜边上中线的性质，可得斜边为2，然后利用两直角边之间的关系以及勾股定理求出两直角边之积，从而确定面积．【详解】解：根据直角三角形斜边上中线的性质可知，斜边上的中线等于斜边的一半，得AC=2BD=2．∵一个直角三角形的周长为∴AB+BC等式两边平方得（AB+BC）2 2，即AB2+BC2+2AB•BC∵AB2+BC2=AC2=4，∴2AB•BC AB•BC即三角形的面积为12×AB •BC 故选：B ．【点睛】本题考查直角三角形斜边上的中线，勾股定理，三角形的面积等知识点的理解和掌握，巧妙求出AC •BC 的值是解此题的关键，值得学习应用．2、D【分析】由平行四边形的判定与性质、矩形的判定分别对各个选项进行判断即可．【详解】解：A 、∵对角线互相平分的四边形是平行四边形，∴对角线互相平分且相等的四边形才是矩形，∴选项A 不符合题意；B 、∵两组对边分别相等是平行四边形，∴选项B 不符合题意；C 、∵对角线互相平分且相等的四边形才是矩形，∴对角线相等的四边形不是矩形，∴选项C 不符合题意；D 、∵对角线交点到四个顶点的距离都相等，∴对角线互相平分且相等，∵对角线互相平分且相等的四边形是矩形，∴选项D 符合题意；故选：D ．【点睛】本题考查了矩形的判定、平行四边形的判定与性质、解题的关键是熟记矩形的判定定理．3、C【分析】由小明第一次回到出发点A，则小明走过的路程刚好是一个多边形的周长，由多边形的外角和为360︒，每次的转向的角度的大小刚好是多边形的一个外角，则先求解多边形的边数，从而可得答案. 【详解】解：由360=12,30可得：小明第一次回到出发点A，一个要走1210=120⨯米，故选C【点睛】本题考查的是多边形的外角和的应用，掌握“由多边形的外角和为360︒得到一共要走12个10米”是解本题的关键.4、A【分析】可以设∠EAD′＝α，∠FAB′＝β，根据折叠可得∠DAF＝∠D′AF，∠BAE＝∠B′AE，用α，β表示∠DAF＝10°+β，∠BAE＝10°+α，根据四边形ABCD是矩形，利用∠DAB＝90°，列方程10°+β+β+10°+10°+α+α＝90°，求出α+β＝30°即可求解．【详解】解：设∠EAD′＝α，∠FAB′＝β，根据折叠性质可知：∠DAF＝∠D′AF，∠BAE＝∠B′AE，∵∠B′AD′＝10°，∴∠DAF＝10°+β，∠BAE＝10°+α，∵四边形ABCD是矩形∴∠DAB＝90°，∴10°+β+β+10°+10°+α+α＝90°，∴α+β＝30°，∴∠EAF＝∠B′AD′+∠D′AE+∠FAB′，＝10°+α+β，＝10°+30°，＝40°．则∠EAF的度数为40°．故选：A．【点睛】本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．5、B【分析】由菱形的性质得AB＝BC＝2（cm），OA＝OC，OB＝OD，AC⊥BD，再证△ABC是等边三角形，得AC＝AB＝2（cm），则OA＝1（cm），然后由勾股定理求出OB cm），即可求解．【详解】解：∵菱形ABCD的周长为8cm，∴AB＝BC＝2（cm），OA＝OC，OB＝OD，AC⊥BD，∵∠ABC＝60°，∴△ABC是等边三角形，∴AC＝AB＝2cm，∴OA＝1（cm），在Rt△AOB中，由勾股定理得：OB cm），∴BD＝2OB＝cm），故选：B．【点睛】此题考查了菱形的性质，勾股定理，等边三角形的性质和判定，解题的关键是熟练掌握菱形的性质，勾股定理，等边三角形的性质和判定方法．6、A【分析】多边形的外角和是360度，多边形的外角和是内角和的2倍，则多边形的内角和是180度，则这个多边形一定是三角形．【详解】解：多边形的外角和是360度，又多边形的外角和是内角和的2倍，∴多边形的内角和是180度，∴这个多边形是三角形．故选：A．【点睛】考查了多边形的外角和定理，解题的关键是掌握多边形的外角和定理．7、A【分析】利用平行四边形的对边平行且相等的性质，先利用对边平行，得到D点和C点的纵坐标相等，再求出CD=AB=5，得到C点横坐标，最后得到C点的坐标．【详解】解：四边形ABCD为平行四边形。

沪科版八年级数学下册19章四边形单元测试(含答案)

沪科版八年级数学下册19章四边形单元测试学校:___________姓名：___________班级：___________考号：___________一、单选题1．一个多边形的每个内角均为120°，则这个多边形是（）A ．四边形B ．五边形C ．六边形D ．七边形2．菱形的两条对角线长分别为6，8，则它的周长是（）A ．5B ．10C ．20D ．243．能判定四边形ABCD 是平行四边形的是（）A ．AD//BC ，AB=CDB ．∠A=∠B ，∠C=∠DC ．∠A=∠C ，∠B=∠D D ．AB=AD ，CB=CD4．小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板，他购买的瓷砖形状不可能．．．是（） A ．正三角形 B ．正方形 C ．正五边形 D ．正六边形5．如图，已知平行四边形ABCD 中，4,B A ∠=∠则C ∠=( )A ．18oB ．36oC ．72oD ．114o6．将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD ，转动这个四边形，使它形状改变，当90B ︒∠=时，如图1，测得AC=2，当60B ︒∠=时，如图2，则AC 的值为（）A ．22B 6C ．2D 27．如图，在∠ABC 中，AC =8，BC =6，AB =10，P 为边AB 上一动点，PD ⊥AC 于D ，PE ⊥BC 于E ，则DE 的最小值为( )A ．3.6B ．4.8C ．5D ．5.28．如图，在矩形ABCD 中，AB=3，BC=5，在CD 上任取一点E ，连接BE ，将∠BCE沿BE 折叠，使点C 恰好落在AD 边上的点F 处，则CE 的长为（）A ．12 B ．13 C ．53 D ．14二、填空题9．一个凸边形的内角和为720°，则这个多边形的边数是__________________10．八边形内角和度数为_____．11．如图，平行四边形ABCD 的周长为20cm ，对角线交于点O ，点E 是边AB 的中点，已知6AB cm =，则OE =______cm ．12．如图，已知菱形ABCD 的面积为24，正方形AECF 的面积为18，则菱形的边长是__________．13．如图，在矩形ABCD 中，AB 4=，BC 6=，点E 为BC 的中点，将ABE V 沿AE 折叠，使点B 落在矩形内点F 处，连接CF ，则CF 的长为________．三、解答题14．已知n 边形的内角和等于1800°，试求出n 边形的边数．15．如图，在菱形ABCD 中，M ，N 分别为BC ，CD 的中点．求证：AM ＝AN ．16．（7分）如图，∠ABC 中，∠ACB=90°，D ．E 分别是BC 、BA 的中点，联结DE ，F 在DE 延长线上，且AF=AE ．（1）求证：四边形ACEF 是平行四边形；（2）若四边形ACEF 是菱形，求∠B 的度数．17．如图，菱形ABCD 的对角线AC 、BD 相交于点O ，DE AC P ，12DE AC =，连接AE 、CE ．（1）求证四边形ODEC 为矩形（2）若2AB =，60ABC ∠=︒，求AE 的长．18．如图，在四边形纸片 ABCD 中，∠B ＝∠D ＝90°，点 E ，F 分别在边 BC ，CD 上，将 AB ，AD 分别沿 AE ，AF 折叠，点 B ，D 恰好都和点 G 重合，∠EAF ＝45°．（1）求证：四边形 ABCD 是正方形；（2）若 EC ＝FC ＝1，求 AB 的长度．沪科版八年级数学下册19章四边形单元测试参考答案一、选择题1．C ，2．C ，3．C ，4．C ，5．B ，6．D ，7．B8．C二、填空题9．6，10．1080°．，11．2，12．5，13．185 三、解答题14．解：由题意得，（n ﹣2）•180°=1800°，解得：n=12．答：n 边形的边数是12．15．证明：∠四边形ABCD 是菱形，∠AB ＝BC ＝CD ＝AD ，∠B ＝∠D∠M ，N 分别是BC ，CD 的中点，∠BM ＝12BC ，DN ＝12CD ， ∠BM ＝DN ．在∠ABM 和∠ADN 中，AB AD B D BM DN =⎧⎪∠=∠⎨⎪=⎩∠∠ABM∠∠ADN（SAS）∠AM＝AN．16．解：（1）∠∠ACB=90°，E是BA的中点，∠CE=AE=BE，∠AF=AE，∠AF=CE，在∠BEC中，∠BE=CE 且D是BC的中点，∠ED是等腰∠BEC底边上的中线，∠ED也是等腰∠BEC的顶角平分线，∠∠1=∠2，∠AF=AE，∠∠F=∠3，∠∠1=∠3，∠∠2=∠F，∠CE∠AF，又∠CE=AF，∠四边形ACEF是平行四边形；（2）∠四边形ACEF是菱形，∠AC=CE，由（1）知，AE=CE，∠AC=CE=AE，∠∠AEC是等边三角形，∠∠CAE=60°，在Rt∠ABC中，∠B=90°﹣∠CAE=90°﹣60°=30°．17．解：（1）证明：在菱形ABCD中，AC∠BD，OC＝12 AC．又∠12 DE AC=∠DE＝OC．∠DE∠AC，∠四边形OCED是平行四边形．∠AC∠BD，∠平行四边形OCED是矩形．（2）在菱形ABCD中，BC＝AB，∠ABC＝60°，∠∠ABC为等边三角形，∠AC＝AB＝2．∠OA＝OC＝1．∠AC∠BD，∠在Rt∠AOD中，OD223AD AO-=∠在矩形OCED 中，CE ＝OD ．∠在Rt∠ACE 中，AE =．∠AE ．18．解：(1)由折叠性质知：∠BAE=∠EAG ，∠DAF=∠FAG ，∠∠EAF=45°,∠∠BAD=2∠EAF=2⨯45°=90°，又∠∠B=∠D=90°，∠四边形ABCD 是矩形，由折叠性质知：AB=AG ，AD=AG ，∠AB=AD ，∠四边形ABCD 是正方形；(2)∠EC=FC=1，∠BE=DF ，== ∠EF=EG+GF=BE+DF ，∠BE=DF=12EF=2，1．。

沪科版八年级下册《第19章四边形》单元测试(二)含答案

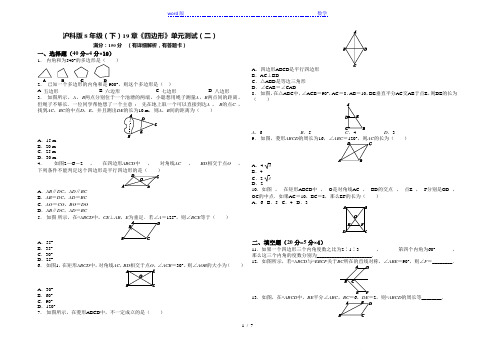
沪科版8年级（下）19章《四边形》单元测试（二）满分：150分（有详细解析，有答题卡）一、选择题（40分=4分×10）1．内角和为540°的多边形是（）2．已知一个多边形的内角和是900°，则这个多边形是（）A. 五边形B. 六边形C. 七边形D. 八边形3．如图所示，A，B两点分别位于一个池塘的两端，小聪想用绳子测量A，B两点间的距离，但绳子不够长．一位同学帮他想了一个主意：先在地上取一个可以直接到达A，B的点C，找到AC，BC的中点D，E，并且测出DE的长为10 m，则A，B间的距离为（）A．15 mB．20 mC．25 mD．30 m4．如图2－G－2，在四边形ABCD中，对角线AC，BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）A．AB∥DC，AD∥BCB．AB＝DC，AD＝BCC．AO＝CO，BO＝DOD．AB∥DC，AD＝BC5．如图所示，在▱ABCD中，CE⊥＝125°，则∠BCE等于（）A．55°B．35°C．30°D．25°6．如图1，在矩形ABCD中，对角线AC∠ACB＝30°，则∠AOB的大小为（）A．30°B．60°C．90°D．120°7．如图所示，在菱形ABCD中，不一定成立的是（）A．四边形ABCD是平行四边形B．AC⊥BDC．△ABD是等边三角形D．∠CAB＝∠CAD8．如图，在△ABC中，∠ACB＝90°，AC＝8，AB＝10，DE垂直平分AC交AB于点E，则DE的长为（）A．6 B．5 D．39．如图，菱形ABCD的周长为16，∠ABC＝120°，则AC的长为（）A．4 3B．4C．2 3D．210．如图，在矩形ABCD中，O是对角线AC，BD的交点，点E，F分别是OD，OC的中点．如果AC＝10，BC＝8，那么EF的长为（）A．6 B．5 C．4 D．3二、填空题（20分=5分×4）11．如果一个四边形三个内角度数之比为2∶1∶3，第四个内角为60°，那么这三个内角的度数分别为______________________．12．如图所示，若▱ABCD与▱EBCF关于ABE＝90°，则∠F＝________．13．如图，在▱ABCD中，BE平分∠ABC，BC＝6，DE＝2，则▱ABCD的周长等________．14．如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE＝DF.给出下列条件：①BE⊥EC；②BF∥CE；③AB＝AC.从中选择一个条件使四边形BECF是菱形，你认为这个条件是________(只填写序号)．三、解答题（90分）15．如图所示，已知四边形ABCD是菱形，对角线AC与BD相交于点O，AB＝5，AO＝4，求BD的长．16．如图，在△ABC中，AB＝AC＝5，BC＝6，AD是BC边上的中线，四边形ADBE是平行四边形．(1)求证：四边形ADBE是矩形；(2)求矩形ADBE的面积．17．如图，已知BD是△ABC的角平分线，点E，F分别在边AB，BC上，ED∥BC，EF∥AC.求证：BE＝CF.18．如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.猜想线段CD 与线段AE的位置关系和大小关系,并加以证明.19．如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF,相交于点D.(1)求证:BE=CF;(2)当四边形ACDE为菱形时,求BD的长.20．如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC的外角∠CAM的平分线,CE⊥AN,垂足为点E.(1)求证:四边形ADCE为矩形.(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.21．如图，在正方形ABCD中，AB=BC=CD=AD，∠BAD=∠B=∠C=∠D=90°，点E、F分别在正方形ABCD的边DC、BC上，AG⊥EF且AG=AB，垂足为G，则：（1）△ABF与△ AGF全等吗？说明理由；（2）求∠EAF的度数；（3）若AG=4，△AEF的面积是6，求△CEF的面积．22．已知：如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作平行四边形ABDE，连接AD，EC．（1）求证：△ADC≌△ECD；（2）当点D在什么位置时，四边形ADCE是矩形，请说明理由．23．ABCD中，E是CD边上一点，（1）将△ADE绕点A按顺时针方向旋转，使AD、AB重合，得到△ABF，如图1所示．观察可知：与DE相等的线段是________，∠AFB=∠ ________.（2）如图2，正方形ABCD中，P、Q分别是BC、CD边上的点，且∠PAQ=45°，试通过旋转的方式说明：DQ+BP=PQ.（3）在（2）题中，连接BD分别交AP、AQ于M、N，你还能用旋转的思想说明BM2+DN2=MN2．19章《四边形》单元测试（二）（参考答案）一、选择题1．【答案】C【解析】设多边形的边数是n，则(n－2)·180°＝540°，解得n＝5.故选C.2．【答案】C【解析】多边形内角与外角【解析】【解答】解：设这个多边形是n边形，则（n﹣2）•180°=900°，解得：n=7，即这个多边形为七边形．故本题选C．【分析】设这个多边形是n边形，内角和是（n﹣2）•180°，这样就得到一个关于n的方程组，从而求出边数n的值．3．【答案】B4．【答案】D【解析】A项，由“AB∥DC，AD∥BC”可知，四边形ABCD的两组对边互相平行，所以该四边形是平行四边形．故本选项不符合题意；B项，由“AB＝DC，AD＝BC”可知，四边形ABCD的两组对边分别相等，所以该四边形是平行四边形．故本选项不符合题意；C项，由“AO＝CO，BO＝DO”可知，四边形ABCD的两条对角线互相平分，所以该四边形是平行四边形．故本选项不符合题意；D项，由“AB∥DC，AD＝BC”可知，四边形ABCD的一组对边平行，另一组对边相等，据此不能判定该四边形是平行四边形．故本选项符合题意．故选D.5．【答案】B【解析】根据平行四边形的性质得∠B＝180°－∠A＝55°.在Rt△BCE中，∠BCE＝90°－∠B＝35°.故选B. 6．【答案】B7．【答案】C【解析】灵活掌握菱形的性质定理即可判断．8．【答案】D【解析】∵在Rt△ACB中，∠ACB＝90°，AC＝8，AB＝10，∴BC＝6.又∵DE垂直平分AC交AB于点E，∴DE是△ACB的中位线，∴DE＝12BC＝3.9．【答案】A【解析】设AC与BD交于点E，则∠ABE＝60°.根据菱形的周长求出AB＝16÷4＝4.在Rt△ABE中，求出BE ＝2，根据勾股定理求出AE＝42－22＝2 3，故可得AC＝2AE＝43. 10．【答案】D【解析】∵四边形ABCD是矩形，∴AB＝CD，∠ABC＝90°.∵AC＝10，BC＝8，由勾股定理得AB＝102－82＝6，∴CD＝AB＝6.∵点E，F分别是OD，OC的中点，∴EF＝12CD＝3.故选D.二、填空题11．【答案】100°，50°，150°【解析】设这三个内角的度数分别为2x，x，3x，则有2x＋x＋3x＝360°－60°，解得x＝50°，则2x＝100°，3x＝150°.12．【答案】45°【解析】根据轴对称的性质，得∠EBC＝∠ABC＝45°，因为平行四边形的对角相等，所以∠F＝∠EBC＝45°. 13．【答案】20【解析】∵四边形ABCD为平行四边形，∴AE∥BC，AD＝BC，AB＝CD，∴∠AEB＝∠EBC.∵BE平分∠ABC，∴∠ABE＝∠EBC，∴∠ABE＝∠AEB，∴AB＝AE，∴AE＋DE＝AD＝BC＝6，∴AE＝4，∴AB＝CD＝4，∴▱ABCD的周长＝4＋4＋6＋6＝20.14．【答案】③【解析】由题意得BD＝CD，ED＝FD，∴四边形EBFC是平行四边形．①BE⊥EC，根据这个条件只能得出四边形EBFC是矩形；②BF∥CE，根据EBFC是平行四边形已可以得出BF∥CE，因此不能根据此条件得出▱EBFC是菱形；③AB＝AC，∵⎩⎪⎨⎪⎧AB＝AC，DB＝DC，AD＝AD，∴△ADB≌△ADC(SSS)，∴∠BAD＝∠CAD，∴△AEB≌△AEC(SAS)，∴BE＝CE，∴四边形BECF是菱形．三、解答题15．【答案】解：∵四边形ABCD是菱形，∴AC⊥BD，DO＝BO.∵AB＝5，AO＝4，∴BO＝AB2－AO2＝52－42＝3，∴BD＝2BO＝6.16．【答案】解：(1)证明：∵AB＝AC，AD是BC边上的中线，∴AD⊥BC，∴∠ADB＝90°.∵四边形ADBE是平行四边形，∴▱ADBE是矩形．(2)∵AB＝AC＝5，BC＝6，AD是BC边上的中线，∴BD＝DC＝6×12＝3.在Rt△ACD中，AD＝AC2－DC2＝52－32＝4，∴S 矩形ADBE＝BD·AD ＝3×4＝12.17．【答案】证明：∵ED∥BC，EF∥AC，∴四边形EFCD是平行四边形，∴DE＝CF.∵BD平分∠ABC，∴∠EBD＝∠DBC.∵DE ∥BC ，∴∠EDB＝∠DBC ，∴∠EBD＝∠EDB，∴BE＝ED，∴BE ＝CF.18．【答案】解:线段CD与线段AE的位置关系和大小关系是平行且相等.证明:∵CE ∥AB,∴∠ADO=∠CEO,∠DAO=∠ECO.又∵OA=OC,∴△ADO≌△CEO,∴AD=CE,∴四边形ADCE是平行四边形,∴CD∥AE,CD=AE.19．【答案】(1)证明:由旋转可知,∠EAF=∠BAC,AF=AC,AE=AB.∴∠EAF+∠BAF=∠BAC+∠BAF,即∠BAE=∠CAF.又∵AB=AC,∴AE=AF.∴△ABE≌△ACF,∴BE=CF.(2)解:∵四边形ACDE 是菱形,AB=AC=1,∴AC∥DE,DE=AE=AB=1.又∵∠BAC=45°,∴∠AEB=∠ABE=∠BAC=45°.∵∠AEB+∠BAE+∠ABE=180°,∴∠BAE=90°,∴BE===.∴BD=BE-DE=-1.20．【答案】(1)证明:在△ABC中,AB=AC,AD⊥BC,∴∠BAD=∠DAC.∵AN是△ABC的外角∠CAM的平分线,∴∠MAE=∠CAE,∴∠DAE=∠DAC+∠CAE=×180°=90°.又∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形.(2)解:当∠BAC=90°时,四边形ADCE是正方形,证明如下:∵∠BAC=90°,AB=AC,AD⊥BC于D,∴∠ACD=∠DAC=45°,∴DC=AD.由(1)知四边形ADCE是矩形,∴四边形ADCE是正方形. 解：(2)题答案不唯一.21．【答案】（1）解：△ABF与△ AGF全等，理由如下：在Rt ABF和Rt AGF中，,∴△ABF△ AGF.（2）解：∵△ABF△ AGF，∴BAF=GAF，同理易得：△AGE△ ADE，有GAE=DAE，即EAF=EAD+FAG=BAD=45.（3）解：∵S AEF=EF AG，AG=4，∴6=EF AG，∴EF=3，∵BF=FG，EG=DE，AG=AB=BC=CD=4，设FC=x，EC=y，则BF=4-x，DE=4-y，∵BF+DE=FG+EG=EF=3，∴4-x+4-y=3，∴x+y=5 ①在Rt EFC中，∵EF2=EC2+FC2，∴x2+y2=32②①2-②得到，2xy=16，∴S CEF=xy=4.【解析】全等三角形的判定与性质，正方形的性质【解析】【分析】（1）根据HL可得出△ABF△ AGF；（2）只要证明BAF=GAF，GAE=DAE，即可求出EAF=45；（3）设FC=x，EC=y，则BF=4-x，DE=4-y，构建方程组，求出xy即可求出△CEF的面积．22．【答案】（1）证明：∵四边形ABDE为平行四边形，∴AB=DE，∠ABD=∠AED，AE∥BD，∴∠AED=∠CDE，又∵AB=AC，∴∠ABD=∠ACD，AC=DE，∴∠ACD=∠AED，∴∠ACD=∠CDE，在△ADC和△ECD中，∵，∴△ADC≌△ECD；（2）解：当点D在BC中点时，四边形ADCE是矩形；理由如下：∵D为BC中点，∴BD=CD，又∵四边形ABDE为平行四边形，∴AE∥BD，AE=BD，AB=DE，∴AE∥CD，AE=CD，∴四边形ADCE为平行四边形，又∵AB=AC，∴AC=DE，∴平行四边形ADCE为矩形.【解析】全等三角形的判定，等腰三角形的性质，平行四边形的判定与性质，矩形的判定【解析】【分析】（1）由平行四边形的性质得出AB=DE，∠ABD=∠AED，AE∥BD，再由平行线的性质得出∠AED=∠CDE，又由等腰三角形的性质得出∠ABD=∠ACD，根据等量代换得出AC=DE，∠ACD=∠AED=∠CDE，再由全等三角形的判定SAS得证.（2）当点D在BC中点时，四边形ADCE是矩形；理由如下：由D为BC中点得出BD=CD；由平行四边形的性质得出AE∥BD，AE=BD，AB=DE；由等量代换得出AE∥CD，AE=CD，根据平行四边形的判定得出四边形ADCE为平行四边形，再由对角线相等的平行四边形为矩形. 23．【答案】（1）BF.；AED.（2）解：将△ADQ绕点A按顺时针方向旋转90°，则AD与AB重合，得到△ABE，如图2，则∠D=∠ABE=90°，即点E、B、P共线，∠EAQ=∠BAD=90°，AE=AQ，BE=DQ，∵∠PAQ=45°，∴∠PAE=45°，∴∠PAQ=∠PAE，在△APE和△APQ中∵，∴△APE≌△APQ（SAS），∴PE=PQ，而PE=PB+BE=PB+DQ，∴DQ+BP=PQ.（3）解：四边形ABCD为正方形，∴∠ABD=∠ADB=45°，如图，将△ADN绕点A按顺时针方向旋转90°，则AD与AB重合，得到△ABK，则∠ABK=∠ADN=45°，BK=DN，AK=AN，与（2）一样可证明△AMN≌△AMK，得到MN=MK，∵∠MBA+∠KBA=45°+45°=90°，∴△BMK为直角三角形，∴BK2+BM2=MK2，∴BM2+DN2=MN2.【解析】全等三角形的判定与性质，正方形的性质，旋转的性质【解析】【解答】（1）如图1，∵△ADE绕点A按顺时针方向旋转，使AD、AB重合，得到△ABF，∵DE=BF，∠AFB=∠AED．故答案为：BF，AED.【分析】（1）如图1，直接根据旋转的性质得到DE=BF，∠AFB=∠AED．（2）将△ADQ绕点A按顺时针方向旋转90°，则AD与AB重合，得到△ABE，根据旋转的性质得∠EAQ=∠BAD=90°，AE=AQ，BE=DQ，而∠PAQ=45°，则∠PAE=45°，再根据全等三角形的判定方法得到△APE≌△APQ，则PE=PQ，于是PE=PB+BE=PB+DQ，即可得到DQ+BP=PQ.（3）根据正方形的性质有∠ABD=∠ADB=45°，将△ADN绕点A按顺时针方向旋转90°，则AD与AB重合，得到△ABK，根据旋转的性质得∠ABK=∠ADN=45°，BK=DN，AK=AN，与（2）一样可证△AMN≌△AMK，得到MN=MK，由于∠MBA+∠KBA=45°+45°=90°，得到△BMK 为直角三角形，根据勾股定理得BK2+BM2=MK2，然后利用等量代换即可得到BM2+DN2=MN2.答题卷班级__________ 座号_____ 姓名__________ 分数__________11．__________________________________12．__________________________________13．__________________________________14．__________________________________三、解答题15．16．17．18．19．20．21．22．23．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

四边形
（满分：150分时间：120分钟）
一、选择题（本大题共10小题，每小题4分，满分40分）
1.一个正多边形，它的每个内角都等于相邻外角的5倍，则这个正多边形是（）
A.正五边形
B.正十边形
C.正十二边形
D.不存在
2.下列条件中，能够判定四边形是平行四边形的是（）
A.一组对角相等
B.两条对角线互相平分
C.一组对边相等
D.两条对角线互相垂直
3.四边形的四条边长依次是a ，b ，c ，d ,其中a ，c 为对边，且满足222222a b c d ac bd +++=+，则这个四边形是（）
A.任意四边形
B.对角线相等的四边形
C.对角线垂直的四边形
D.平行四边形
4.平行四边形两条对角线把它分成的全等三角形的对数是（）
A.2对
B.4对
C.6对
D.8对
5.下列命题中正确的是（）
A.对角线相等的四边形是矩形
B.对角线垂直的四边形是矩形
C.对角线互相平分且相等的四边形是矩形
D.对角线相等且垂直的四边形是矩形
6.下列条件能判定四边形是菱形的是（）
A.对角线互相垂直
B.对角线互相垂直平分
C.对角线相等
D.对角线垂直相等
7.下列命题中是真命题的是（）
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线互相垂直的平行四边形是正方形
D.对角线相等的菱形是正方形
8.有下列命题：①两条对角线互相垂直，有一条对角线平分一组对角的四边形是菱形；②矩形是菱形；③矩形是正方形④正方形是矩形，下列说法正确的是（）
A.①、②、③、④都是假命题
B.只有②是假命题
C.只有④是真命题
D.只有②、③是假命题
9.如图，矩形ABCD 中，∠DAE ︰∠BAE =3︰1，AE ⊥BD ,则∠EAC 的度数是 ( )
A.60°
B.30°
C.120°
D.45°
10.如图，菱形ABCD 的对角线的长分别为2和5，P 是对角线AC 上任一点（点P 不与点A 、C 重合），且PE ∥BC 交AB 于点E ，PF ∥CD 交AD 于点F ，则阴影部分的面积为（） A.2.5 B.5 C.10 D.20
第9题E D C B
A
第10题F E 第13题D C B A
F E 第14题
O D C
B A
二、填空题（本大题共4小题，每小题5分，满分20分）
11.一个n 边形除去一个内角后其余内角和为500°，则n =________.
12.在四边形ABCD 中，AB =2，CD =1，∠A =60°，∠B =∠D =90°，则四边形ABCD 的面积为____________.
13.如图，矩形纸片长为8㎝，宽为6㎝，将纸片对折使相对顶点A ，C 重合，折痕EF 的长为__________㎝.
14.如图，E ，F 分别是正方形ABCD 的边CD ，AD 上的点，且CE =DF ，AE ，BF 相交于点O ，下列结论：①AE =BF ；②AE ⊥BF ；③AO =OE ；④S △AOB =S 四边形DEOF 中，正确的有________________（填序号）.
三、（本大题共两小题，每小题8分，满分16分）
15．一个多边形中的各个内角都相等，且每个内角与外角之差的绝对值为60°，求此多边形的边数.
16.如图，在△ABC 中，将∠C 沿DE 折叠，使顶点C 落在三角形内.已知∠A =75°， ∠B =65°，∠1=20°，求∠2的度数.
2
1C
'E D C B A
四、（本大题共两小题，每小题8分，满分16分）
17.如图，在□ABCD 中，点E 、F 在对角线AC 上，且AE =CF ，请你以F 为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等（只需证明一组线段相等即可）.
（1）连接：____________.
（2）猜想：__________=_________.
（3）请证明上述猜想.
18.已知：如图，□ABCD 中，E 、F 分别是AC 上两点，且BE ⊥AC 于点E ，DF ⊥AC 于点F . 求证：四边形BEDF 是平行四边形.
E
F D
C B A
五、（本大题共两小题，每小题10分，满分20分）
19.如图，矩形ABCD 中，CE ⊥BD 于点E ，∠DCE ︰∠BCE =3︰1，OM =MC .
求证：ME ⊥AC .
E M O D
C B A
20.如图，AD 是△ABC 中∠BAC 的平分线，EF 垂直平分AD ，分别交AB 于点E ，交AC 于点F . 求证：四边形AEDF 是菱形.
E F
D C B A
六、（本题满分12分）
21.如图是正方形ABCD 和CEFG ，连接DG ，BE 并延长DG 交BE 于点H .试问：DG 与B E 具有
怎样的关系？请证明你的结论.
H E F
G D C B A
七、（本题满分12分）
22.已知：如图，在正方形ABCD 中，E 是CD 上的点，BF 平分∠ABE ，F 在AD 上. 求证：BE =AF +CE .
E
F D
C B A
八、（本题满分14分）
23.已知四边形ABCD 中，AB =CD ，AC =BD ，试添加适当的条件使四边形ABCD 成为特殊的平行四边形，并说明理由.
参考答案
1. C
2. C
3. D
4. B
5. C
6. B
7. D
8. C
9. D 10. A
①②④ 15. 多边形的边数是3或6
16. 60
0 17. 答案不唯一，如（1）DF (2)DF=BE (3) 证DCF BAE ∆≅∆即可
18. 先证(AAS)ADF CBE ∆≅∆得DF=BE ，再证DF ∥BE 即可
19.先求出∠EOM =∠ECM =45°得OE =CE ，
再由OM =MC 得ME ⊥AC
20.设EF 与AD 交于点O ，
先证△AEO ≌△AFO （ASA ）得OE =OF ，
再由EF 垂直平分AD 得EF 与AD 互相垂直平分即可
21.DG =BE ，DG ⊥BE ；
先证△DCG ≌△BCE （SAS ）得DG =BE ，
再由∠CDG =∠CBE ,∠CBE +∠CEB =90°得∠CDG +∠CEB =90°即可
22.延长DC 至G 点，使CG =AF ，则△BCG ≌△BAF （SAS ），
∴∠G=∠AFB,∠CBG=∠ABF,
∴∠GBE=∠CBG+∠CBE
=∠ABF+∠CBE
=∠FBE+∠CBE
=∠FBC
=∠AFB
=∠G
∴BE=GE=GC+CE=AF+CE
23. 答案不唯一，如添加条件AC 垂直平分BD ，则这个四边形是正方形，理由：∵AC 垂直平分BD ，
∴AB=AD,BC=CD,
又∵AB=DC,
∴AB=AD=BC=DC,
∴四边形ABCD 是菱形，
又∵AC=BD,
∴四边形ABCD 是正方形.。