第九章 谐振电路 练习题答案
第9章振动之练习题及参考答案

1、 一质点沿x 轴作简谐振动,振动方程为 )312cos(1042π+π⨯=-t x (SI).从t = 0时刻起,到质点位置在x = -2 cm 处,且向x 轴正方向运动的最短时间间隔为(A)s 81(B)s 61 (C)s 41 (D)s 31 (E)s 21 [ ]2、一物体作简谐振动,振动方程为)41cos(π+=t A x ω.在 t = T /4(T 为周期)时刻,物体的加速度为 (A) 2221ωA -. (B)2221ωA .(C) 2321ωA -. (D) 2321ωA .3、一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为[ ]4、一弹簧振子作简谐振动,总能量为E 1,如果简谐振动振幅增加为原来的两倍,重物的质量增为原来的四倍,则它的总能量E 2变为(A) E 1/4. (B) E 1/2.(C) 2E 1. (D) 4 E 1 . [ ]5、一质点沿x 轴作简谐振动,振动范围的中心点为x 轴的原点.已知周期为T ,振幅为A .(1) 若t = 0时质点过x = 0处且朝x 轴正方向运动,则振动方程为x =_____________________________.(2) 若t = 0时质点处于A x 21=处且向x 轴负方向运动,则振动方程为x =_____________________________.(A (B ) (C )(D -x6、一简谐振动的旋转矢量图如图所示,振幅矢量长2 cm ,则该简谐振动的初相为____________.振动方程为____________________________.7、一质点在x 轴上作简谐振动,选取该质点向右运动通过A 点时作为计时起点( t = 0 ),经过2秒后质点第一次经过B 点,再经过2秒后质点第二次经过B 点,若已知该质点在A 、B 两点具有相同的速率,且AB = 10 cm 求:(1) 质点的振动方程;(2) 质点在A 点处的速率.8、一弹簧振子沿x 轴作简谐振动(弹簧为原长时振动物体的位置取作x 轴原点).已知振动物体最大位移为x m = 0.4 m 最大恢复力为F m = 0.8 N ,最大速度为v m = 0.8π m/s ,又知t = 0的初位移为+0.2 m ,且初速度与所选x 轴方向相反.(1) 求振动能量;(2) 求此振动的表达式.9、质量m = 10 g 的小球与轻弹簧组成的振动系统,按)318cos(5.0π+π=t x 的规律作自由振动,式中t 以秒作单位,x 以厘米为单位,求(1) 振动的角频率、周期、振幅和初相; (2) 振动的速度、加速度的数值表达式; (3) 振动的能量E ; (4) 平均动能和平均势能.10、一简谐振动的振动曲线如图所示.求振动方程.参考答案1、E2、B3、B4、Dt-5、)212cos(π-πTt A , )312c o s (π+πTt A6、 π/4 , )4/c o s (1022π+π⨯=-t x (SI)7、解:由旋转矢量图和 |v A | = |v B | 可知 T /2 = 4秒, ∴ T = 8 s , ν = (1/8) s -1,ω = 2πν = (π /4) s -1(1) 以AB 的中点为坐标原点,x 轴指向右方. t = 0时, 5-=x cm φcos A = t = 2 s 时, 5=x cm φφωsin )2cos(A A -=+=由上二式解得 tg φ = 1 因为在A 点质点的速度大于零,所以φ = -3π/4或5π/4(如图)25c o s /==φx A cm∴ 振动方程 )434c o s (10252π-π⨯=-t x (SI) (2) 速率)434s i n (41025d d 2π-π⨯π-==-t t xv (SI)当t = 0 时,质点在A 点221093.3)43sin(10425d d --⨯=π-⨯π-==tx v m/s 8、解:(1) 由题意 kA F m =,m x A =,m m x F k /=. 16.021212===m m m x F kx E J(2) π===2mm m x Av v ω rad /s由 t = 0, φc o s0A x ==0.2 m , 0sin 0<-=φωA v 可得 π=31φ则振动方程为)312c o s (4.0π+π=t x9、解:(1) A = 0.5 cm ;ω = 8π s -1;T = 2π/ω = (1/4) s ;φ = π/3(2) )318s i n (1042π+π⨯π-==-t xv (SI))318cos(103222π+π⨯π-==-t xa (SI)(3) 2222121Am kAE E E P K ω==+==7.90×10-5 J(4) 平均动能 ⎰=TK tm T E 02d 21)/1(v⎰π+π⨯π-=-Tt t m T 0222d )318(s i n )104(21)/1(= 3.95×10-5 J =E2110、解:(1) 设振动方程为 )c o s (φω+=t A x由曲线可知 A = 10 cm , t = 0,φcos 1050=-=x ,0sin 100<-=φωv 解上面两式,可得 φ = 2π/3由图可知质点由位移为 x 0 = -5 cm 和v 0 < 0的状态到x = 0和 v > 0的状态所需时间t = 2 s ,代入振动方程得 )3/22c o s (100π+=ω (SI) 则有2/33/22π=π+ω,∴ ω = 5 π/12 故所求振动方程为 )3/212/5cos(1.0π+π=t x (SI)。
电路理论基础课后答案(哈工大陈希有)第9章
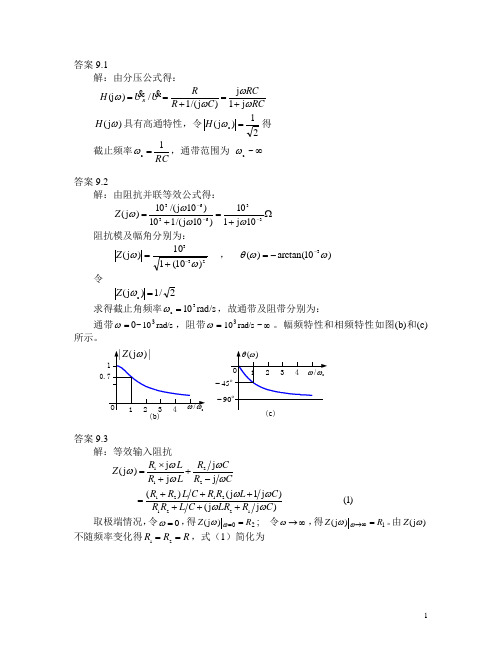
答案9.1解:由分压公式得:U U H R/)(j =ωRCRC C R R ωωωj 1j )j /(1+=+= )j (ωH 具有高通特性,令21)j (c =ωH 得截止频率RC1c =ω,通带范围为∞~c ω答案9.2解:由阻抗并联等效公式得:Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为:233)10(110)j (ωω-+=Z , )10arctan()(3ωωθ--= 令2/1)j (c =ωZ求得截止角频率rad/s 103c =ω,故通带及阻带分别为:通带=ω0~rad/s 103,阻带=ωrad/s 103~∞。
幅频特性和相频特性如图(b)和(c)所示。
(b)--答案9.3解:等效输入阻抗)1()j j ()j 1j ()(j j j j )j (122121212211C R LR C L R R C L R R C L R R CR CR L R L R Z ωωωωωωωωω++++++=-++⨯=取极端情况,令0=ω,得20)j (R Z ==ωω; 令∞→ω,得1)j (R Z =∞→ωω。
由)j (ωZ 不随频率变化得R R R ==21,式(1)简化为)j 1j ()j 1j (2)j 1j ()j 1j (2)j (22C L RC L R C L R CL RC L R C L R C L R C L R Z ωωωωωωωωω+++++=+++++= 由)j (ωZ 为实数得:CL R R C L R R C L =+=2,2 故当C L R R ==21时端口电流与端口电压的波形相似,此时C L Z =)j (ω。
答案9.4解: RC 并联的等效阻抗RCRC R C R Z RC ωωωj 1j /1j /+=+=RC RCZ L Z U U H +==ωωj /)j (12 RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时,1)j (=ωH ;当∞→ω时,0)j (=ωH所以它具有低通特性。
电路习题第九章.docx

第八、九章向量法、正弦稳态电路的分析习题一、填空题。
1. 某负载接电压为i/=10扼收(刃t+90。
)V 的电源,其电流为z =5V2cos (ft> t+30°) A, 有功功率p=二、选择题。
C.提高电源的输出功率D,减小电源输出电流A.f=50HzB.Um=100VC.U=70.7VD.cj) = -45°3. 图3所示电路中u (t) = 20 cos (伸t+75° )V, i (t)=扼cos (伸t + 30° )A, N°中无独立源, 则N 。
吸收的复功率为(D )。
A. (9+j8)V - A B. (10+jl0)V - A C. (8+j8)V • A D. (8 + j9) V • Ai(t)2mH +o —^-i —rww u(t)-o 4. 图 4 所示电路中 u (t) = 20 cos (103 1+ 75° )V , i (t) = 41 cos (103t+ 30° )A, N o 中无独立 源,则No 的输入阻抗乙0为(D )。
1.对于提高电路功率因数 (X )意义,以下说法正确的是(D )。
A.可以提高负载的功率B. 一般采用串联电容C 来提高电路的功率因数 2.电压 u= —100cos(314r — 45 )匕表述该电压错误的是(D )则负载Z= A. 20/45° Q B. 14.14/45° Q C. (9+j8) Q D. (8 + j9)Q2。
d CZ1~~-i(t) 1mH c -------------+ ----- r rm •u(t) 2。
d 广 No -o I I •—Zi ()5.图5中N为不含独立源的一端口,端口电压、电流分别为u=10cos(10t+45° )V, i=2cos(10t-90° )A,则端口的输入阻抗Z等于(B )。
RLC串联谐振电路及答案

RLC串联谐振电路及答案RLC 串联谐振电路⼀、知识要求:理解RLC 串联电路谐振的含义;理解谐振的条件、谐振⾓频率、频率;理解谐振电路的特点,会画⽮量图。
⼆、知识提要:在RLC 串联电路中,当总电压与总电流同相位时,电路呈阻性的状态称为串联谐振。
(1)、串联谐振的条件:C L C L X X U U ==即(2)、谐振⾓频率与频率:由LC f LC :C L πωωω21110===谐振频率得(3)、谐振时的相量图:(4)、串联谐振电路的特点:①.电路阻抗最⼩:Z=R②、电路中电流电⼤:I 0=U/R③、总电压与总电流同相位,电路呈阻性④、电阻两端电压等于总电压,电感与电容两端电压相等,相位相反,且为总电压的Q 倍,。
即:U L =U C =I 0X L =I 0X C =L X RU =U R X L =QU 式中:Q 叫做电路的品质因数,其值为:CRf R L f R X R X Q C L 00212ππ====>>1(由于⼀般串联谐振电路中的R 很⼩,所以Q 值总⼤于1,其数值约为⼏⼗,有的可达⼏百。
所以串联谐振时,电感和电容元件两端可能会产⽣⽐总电压⾼出Q 倍的⾼电压,⼜因为U L =U C ,所以串联谐振⼜叫电压谐振。
)(5)、串联谐振电路的应⽤:适⽤于信号源内阻较低的交流电路。
常被⽤来做选频电路。
三、例题解析:1、在RLC 串联回路中,电源电压为5mV ,试求回路谐振时的频率、谐振时元件L 和C 上的电压以及回路的品质因数。
解:RLC 串联回路的谐振频率为UcLC f π210=谐振回路的品质因数为RL f Q 02π= 谐振时元件L 和C 上的电压为mV 5mV 5C L CL R Q U U === 2、在RLC 串联电路中,已知L =100mH ,R =3.4Ω,电路在输⼊信号频率为400Hz 时发⽣谐振,求电容C 的电容量和回路的品质因数。
解:电容C 的电容量为F 58.14.6310141)2(120µπ≈==L f C 回路的品质因数为744.31.040028.620≈??==R L f Q π3、已知某收⾳机输⼊回路的电感L=260µH,当电容调到100PF 时发⽣串联谐振,求电路的谐振频率,若要收听频率为640KHz 的电台⼴播,电容C 应为多⼤。
大学电路习题第9章

哈尔滨理工大学电气学院 理论电工教研室 第九章(正弦稳态电路分析)习题解答 一、选择题 1. 在图9—1所示的电路中,如果其等效导纳的模为21YYYeq ,则 。 A. LYCY1j , j21; B. CYRYj , 121; C. LYRY1j , 121 ; D. 正为实数)kkYY( 21
2. 图9—2(a)所示的电路为不含独立电源的线性一端口电路。已知00 /100UV,045
/210I
A,则图9—2(b)、9—2(c)、9—2(d)、9—2(e)四个电路中不是图9—2
(a)的等效电路的为 。
A. 图9—2(b); B. 图9—2(c); C. 图9—2(d); D. 图9—2(e)
3. 电路如图9—3所示,Z是一段不含独立源的电路。开关断开时,瓦特表、电压表、电流表的读数分别是100W、220V 和1A;开关闭合时,瓦特表、电压表、电流表的读数分别是100W、220V和8.0A。那么Z是 电路。
A. 电阻性; B容性; C. 感性; 哈尔滨理工大学电气学院 理论电工教研室 4. 电路如图9—4所示,U固定不变。如果 ,则改变Z(Z不等于无限大)时,I不变。
A. 21ZZ; B. 21ZZ; C. 21ZZ;D. )Arg()Arg(21ZZ 5. 10R的电阻,F1C的电容与电感L串联,接到频率1000Hz的正弦电压源上。为使电阻两端的电压达到最高,电感应取 。
A. 1H; B. 21H; C. 21H; D. 241H 二、填空题
1. 若3R,6L,2011C ,2012C,则图9—5所示电路的输入阻抗为 j4)3(。 2. 在图9—11所示的电路中,010/5SUV,5.01Z,j0.6)2.0(2Z,j13Z,j2)1(2SUV。用回路电流法求1I,2I,3I。
电路第9章作业答案
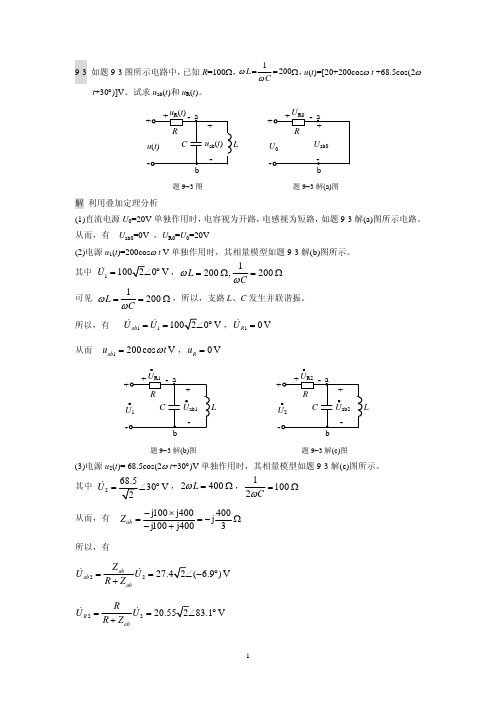
(3)交流电流表、电压表和功率表的读数分别为 电流表的读数为 电压表的读数为 功率表的读数为
I=
I 02 + I 32 = 4 2 + 1.412 = 4.24 A
2 U = U 02 + U 3 = 0 + 2.056 2 = 2.056 V
ωL= 9-3 如题 9-3 图所示电路中, 已知 R=100Ω,
t+30°)]V。试求 uab(t)和 uR(t)。
1 = 200Ω, u(t)=[20+200cosω t +68.5cos(2ω ωC
+ u(t)
+ uR(t) - a R C b
题 9−3 图
+ uab(t) L
+ U0
+ UR0 - a + R Uab0
P = P0 + P3 = 899.6 W
9-7 如题 9-7 图所示电路中, 已知 uS(t) =141cosωt + 14.1cos(3ωt+30°) V, 基波频率 f =500 Hz, C1=C2=3.18μF,R=10Ω。当基波电压单独作用时,电流表读数为 0;三次谐波电压单独 作用时,电压表的读数为 0。求电感 L1、L2 及电容 C2 两端的电压 uo。
Z = 50 +
− j15 × j(4 / 3) = 50 − j1.46 = 50.05∠( −1.67°) Ω j15 − j4 / 3
2
从而,有
& & = U S 3 = 1.41∠1.67° A I 3 Z
高二物理第九章机械振动知识点及习题练习+单元练习(含答案)

机械振动三、基础知识 1、简谐运动的概念①简谐运动的定义:____________________________________________________________。
②简谐运动的物体的位移x 、回复力F 、加速度a 、速度v 、动能E K 、势能E P 的变化规律: A .在研究简谐运动时位移的起点都必须在平衡位置处。
B .在平衡位置:位移最小、回复力最小、加速度最小;速度最大、动能最大。
C .在离开平衡位置最远时:_________________________________________。
D .振动中:注意以上各量的矢量性和对称性。
③简谐运动机械能守恒,但机械能守恒的振动不一定时简谐运动。
④注意:A .回复力是效果力。
B .物体运动到平衡位置不一定处于平衡状态。
C .简谐运动定义式F=-K x 中的K 不一定是弹簧的劲度系数。
2、总体上描述简谐运动的物理量①振幅A :______________________称为振幅。
它是描述振动______的物理量。
它是__量。
简谐运动的振幅不变,而位移在时刻变化。
②周期T 和频率f :_________________________________称为周期T,它是_____量,单位是秒;________________________________称为振动频率,单位是赫兹(Hz )。
周期和频率都是描述___________的物理量,它们的关系是:T=1/f 。
它们与______无关,由_________________决定,因而以叫_______周期,或______频率。
3、单摆①单摆的概念:在细线的一端拴一个小球,另一端固定在悬点上,________________可忽略,线长远大于球的直径,这样的装置叫单摆。
②单摆的特点:A .单摆是实际摆的理想化,是一个理想模型;B .单摆的等时性,在振幅很小的情况下,单摆的振动周期与___________________无关;动C.单摆的回复力由_______________________提供,当最大摆角α<100时,单摆的振动是简谐运动,其振动周期T=__________。
电工基础-RLC串联电路谐振练习题(含答案) 江苏省对口单招

PLC串联电路谐振练习题⼀、选择题1、RLC并联电路在f0时发⽣谐振,当频率增加到2f0时,电路性质呈()A、电阻性B、电感性C、电容性2、处于谐振状态的RLC串联电路,当电源频率升⾼时,电路将呈现出()A、电阻性B、电感性C、电容性3、下列说法中,()是正确的。
A、串谐时阻抗最⼩B、并谐时阻抗最⼩C、电路谐振时阻抗最⼩4、发⽣串联谐振的电路条件是()A 、B 、C 、5、在RLC串联正弦交流电路,已知XL=XC=20欧,R=20欧,总电压有效值为220V,电感上的电压为()V。
A、0B、220C、73.36、正弦交流电路如图所示,已知电源电压为220V,频率f=50HZ时,电路发⽣谐振。
现将电源的频率增加,电压有效值不变,这时灯泡的亮度()。
A、⽐原来亮B、⽐原来暗C、和原来⼀样亮HL L Cu7、正弦交流电路如图所示,已知开关S打开时,电路发⽣谐振。
当把开关合上时,电路呈现()。
A、阻性B、感性C、容性S C2R L C1~u⼆、计算题1、在RLC串联电路中,已知L=100mH,R=3.4Ω,电路在输⼊信号频率为400Hz时发⽣谐振,求电容C的电容量和回路的品质因数.2、⼀个串联谐振电路的特性阻抗为100Ω,品质因数为100,谐振时的⻆频率为1000rad/s,试求R,L和C的值.3、⼀个线圈与电容串联后加1V的正弦交流电压,当电容为100pF时,电容两端的电压为100V 且最⼤,此时信号源的频率为100kHz,求线圈的品质因数和电感量。
4、已知⼀串联谐振电路的参数,,,外加电压mV。
试求电路在谐振时的电流、品质因数及电感和电容上的电压。
5、已知串谐电路的线圈参数为“”,接在⻆频率的10V 电压源上,求电容C为何值时电路发⽣谐振?求谐振电流I0、电容两端电压U C、线圈两端电压U RL及品质因数Q。
6、如右图所示电路,其中V,调节电容C使电流i与电压u同相,此时测得电感两端电压为200V,电流I=2A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电工技术基础与技能
第九章 谐振电路 练习题
班别:高二( ) 姓名: 学号: 成绩:
一、是非题
1、在R-L-C串联电路中,若R = XL = XC =100Ω,则该电路处于谐振状态。 ( )
2、R-L-C串联谐振又称为电流谐振。 ( )
3、串联谐振时,感抗等于容抗,此时电路中的电流最大。 ( )
4、谐振电路的功率因数大于1。 ( )
5、谐振电路的选择性越好,那么频带宽度也就越宽。 ( )
二、选择题
1、在R-L-C串联电路发生谐振时,下列说法正确的是( )。
A.Q值越大,通频带越宽
B.端电压是电容两端电压的Q倍
C.电路的电抗为零,则感抗和容抗也为零
D.总阻抗最小,总电流最大
2、处于谐振状态的R-L-C串联电路,当电源频率升高时,电路呈( )。
A.电感性 B.电容性 C.电阻性 D.无法确定
3、R-L-C串联电路谐振的条件是( )。
A.ωL=ωC B.L=C C. CL1 D. L1C
4、在R-L-C串联电路中,当端电压与电流同相时,下列关系式正确的是( )。
A. ωL2C=1 B. ω2 LC=1 C. ωLC=1 D. ω=LC
5、电感线圈与电容器并联的电路中,当R、L不变,增大电容C时,谐振频率f0将
( )。
A.增大 B.减小 C.不变 D.不能确定
三、填充题
1、R-L-C串联电路的谐振频率仅由电路参数 L 和 C 决定,而与电阻
R的大小 无关 ,它反映了电路本身的固有特性。
2、串联谐振时,电阻上的电压等于 端电压 ,电感和电容上的电压 相等 并
为端电压的 Q 倍。因此串联谐振又称为 电压谐振 。
3、电路品质因数Q值的大小是电路品质优劣的重要指标。Q值越高,谐振曲线就
越 陡 ,电路选择性 越好 ,通频带 越窄 ,所以在广播通信中,
既要考虑 选择性 ,又要考虑 通频带宽度 ,因此品质因数要选择的适当。
4、R-L-C串联电路中,电路端电压U=20V,ω=100rad/s,R=10Ω,L=2H,调节电
容C使电路发生谐振,此时C= 50 μF,电容两端的电压为 400 V。
5、电感线圈与电容器并联的谐振电路中,线圈电阻越大,电路的品质因数
越 小 ,电路的选择性就越 差 。
四、问答与计算题
1、收音机的输入调谐回路为R-L-C串联谐振电路,当电容为160pF,电感为250
μH,电阻为20Ω时,求谐振频率和品质因数。
解: KHzXXLCf79610250*10160*14.3*21216120
6.622010250*798000*14.3*22600XRLfRLQ
2、在R-L-C串联谐振电路中,已知信号源电压为1V,频率为1MHz,现调节电容使回路达到
谐振 ,这时回路电流为100mA,电容两端电压为100V,求电路元件参数R、L、C和回路
的品质因数。
解: ①因为电路处于谐振状态,由I0=U/R有
Ω1010100130XIUR
②Ω10001.01000IUcXc
pFXc1591000*10*14.3*211C6
③因为电路处于谐振状态,有XL=Xc,则
HXCL15910159*)10*14.3*2(1112262
④6.621010159*10*14.3*226600XRLfRLQ
3、在电感线圈和电容器的并联谐振电路中,已知电阻为50Ω,电感为0.25mH,电容为10pF,
求电路的谐振频率、谐振时的阻抗和品质因数。
解: MHzXXLCf18.31010*1025.0*14.3*21211230
ΩKXXRCZ5001010*501025.0L1230
100501025.0*1018.3*14.3*223600XXRLfRLQ
4、在上题的并联谐振电路中,若已知谐振时阻抗是10KΩ,电感是0.02mH,电容是200pF,
求电阻和电路的品质因数?
解: RCZL0
Ω1010200*100001002.0L1230XXCZR
MHzXXLCf5.210200*1002.0*14.3*21211230
4.31101002.0*105.2*14.3*223600XXRLfRLQ
