线性系统理论
线性系统理论全课件
2/2,13/50
2.4 由系统输入输出描述导出状态空间描述
由输入输出描述导出状态空间描述
5/7,9/50
离散时间线性系统的状态空间描述 状态空间描述形式 离散时间线性时不变系统 X (k 1) Gx(k) Hu (k) Y (k) Cx(k) Du (k)
n n阵G : 系统矩阵 n p阵H : 输入矩阵 q n阵C : 输出矩阵 q p阵D : 传输矩阵
离散时间线性时变系统 X (k 1) G(k)x(k) H (k)u(k ) Y (k) C(k)x(k) D(k)u(k)
cM
J
ce La f
J
ia
1
La 0
e
0
1ia
上式可表为形如 X AX Bu Y CX Du
Ra
i f const
J,F
La
2/7,6/50
连续时间线性系统的状态空间描述 动态系统的结构
u1 u2
up
x1 x2
动力学部件
xn
输出部件
y1 y2
yq
连续时间线性系统的状态空间描述
u1
yq
外部描述常被称作为输出—输入描述
u2
x1, x2 , , xn
y2
up
yq
例如.对SISO线性定常系统:时间域的外部描述:
y(n) an1 y(n1) a1 y(1) a0 y bn1u(n1) b1u (1) b0u
复频率域描述即传递函数描述
线性系统理论3线性系统的运动分析

THANKS
伯德图判据
通过观察系统开环伯德图(对数幅频特性和相频特性曲线)来判断系统的稳定性。若开环伯 德图在穿越频率处的相位裕度大于0,则系统是稳定的。
不稳定系统的分析与处理
不稳定原因分析
不稳定系统可能由于系统内部参数摄动、外部扰动或控 制器设计不当等原因导致。需要对系统进行详细分析, 找出不稳定的原因。
不稳定系统处理
线性微分方程
01
描述线性系统动态行为的数学工具,通过求解微分方程可以得
到系统的输出响应。
传递函数
02
在频域中描述线性系统输入输出关系的数学表达式,常用于控
制系统的分析和设计。
状态空间方程
03
描述线性系统状态变量和输入输出关系的数学方程组,适用于
多输入多输出系统和时变系统。
线性系统的建模方法
1 2
机理建模
运动方程的物理意义
描述系统运动状态
运动方程描述了线性系统的运动状态,包括位置、速度和 加速度等物理量。通过求解运动方程,可以得到这些物理 量的时域解和频域解。
预测系统响应
根据已知输入和初始条件,通过求解运动方程可以预测线 性系统的响应。这对于控制系统的设计和分析具有重要意 义。
分析系统稳定性
通过分析运动方程的解的性质,可以判断线性系统的稳定 性。例如,如果解是收敛的,则系统是稳定的;如果解是 发散的,则系统是不稳定的。
对求解结果进行可视化展示和数据分 析,研究电路系统的动态响应特性, 如谐振频率、阻尼振荡等。
建立模型
运动方程
求解方法
结果分析
根据电路元件的连接方式和电气特性, 建立电路系统的数学模型,如RLC串 联或并联电路。
采用解析法或数值法求解运动方程, 得到电路中各元件的电压、电流等电 气参数。
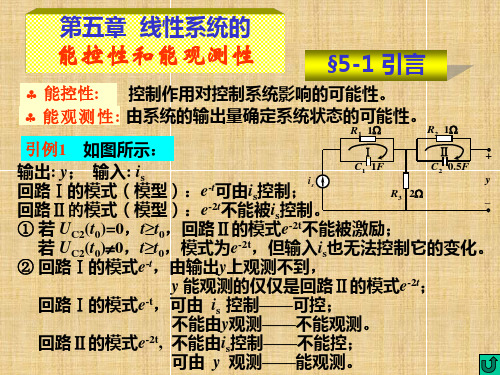
第5章 线性系统理论
2. 定理2 [秩判据]
线性定常系统状态完全能1 控的充要条件是: 能控性判别矩阵WC
W C [B, AB, A2 B, , An1 B]
为满秩。即 rankWC=n (A—nn,B—np,WC—nnp)
(该定理也适用于线性定常离散系统:
WC [H, GH, G2 H, , Gn1H] )
证明:a)充分性 已知rankWC = n 系统完全能控。
J1
J
J2
J
k
nn
J i1
Ji
Ji2
J i i
i i
B1
B
B2
Bk n p
Bi1
Bi
Bi
2
B
i
i
i p
i
J ij
1
1
i rijrij
Bij
B1ij
Байду номын сангаас
Brij rij p
i
rij i
j 1
则系统(A, B)完全能控的充要条件是:
证明:
Bii 0, (i 1,2,, k)
WCW [B , JB , J 2 B ,, J n1 B ]
T 1[B, AB, A2 B,, An1 B] T 1WCX
系 统[J , B] 完全能控
rankWCW = n rankWCX = n 系统(A, B)完全能控。
J
l 1
Jl
WC
[B AB A2 B]
1
1
2
2
4
4
1 1 2 2 4 4
2 1 3 2 5 4 行初等变换 1 1 2 2 4 4
0 0 0 0 0 0
rankWC = 2<3 (n=3) 系统不完全能控。 3.定理3 对状态变量x(t)进行非奇异线性变换, 即x(t) = PZ(t)(P为非奇异),不改变系统的能控性。 证明:已知 x(t) Ax(t) Bu(t)
线性系统理论和设计

线性系统理论和设计是控制工程中的重要内容,涉及到对线性系统的建模、分析和控制设计。
以下是关于线性系统理论和设计的基本内容:
1. 线性系统模型
-线性系统描述:线性系统是指具有线性性质的动态系统,其输出与输入之间满足线性关系。
-线性系统模型:通常用微分方程、差分方程或状态空间方程描述线性系统的动态特性。
2. 线性系统分析
-系统稳定性分析:通过研究系统的零点、极点等性质来判断系统的稳定性。
-频域分析:通过频率响应、波特图等方法分析系统在频域下的性能。
-时域分析:通过阶跃响应、脉冲响应等方法研究系统在时域下的响应特性。
3. 线性系统设计
-控制器设计:设计合适的控制器来实现系统的性能要求,常见的控制器包括比例积分微分(PID)控制器、根轨迹设计等。
-系统鲁棒性设计:设计具有鲁棒性的控制器,能够抵抗参数变化和外部干扰的影响。
-最优控制设计:利用最优控制理论设计最优的控制器,使系统性能
达到最佳。
4. 线性系统应用
-自动控制系统:将线性系统理论和设计方法应用于自动控制系统,实现对各种工程系统的自动控制和调节。
-信号处理系统:利用线性系统理论设计数字滤波器、信号处理算法等,对信号进行处理和提取。
-机电系统:应用线性系统理论设计机电系统的控制器,实现机电系统的精密控制和运动规划。
线性系统理论和设计在控制工程领域具有广泛的应用,能够帮助工程师分析和设计各种复杂系统的控制策略,提高系统的性能和稳定性。
线性系统理论总结ppt

线性系统理论总结ppt
一、线性系统简介
1.线性系统定义:
线性系统是指用线性微分方程、线性积分方程和线性算子(算子运算)来表示、描述和分析的一个系统。
这种系统的输入输出之间的关系可以表
示为线性函数的形式。
2.线性系统的实例:
线性系统的例子包括信号处理、控制系统、数字图像处理、模式识别
等等。
线性系统的应用也很广泛,可以应用在机器人、汽车、航空、通信、医疗和金融等行业中。
二、线性系统的演示
1.系统模型:
线性系统通常用状态空间模型来描述,该模型由一组线性微分方程以
及输入、输出和内部状态变量组成。
该模型的工作原理是:系统的输入到
达模型的输入,系统的内部状态变量发生改变,然后将内部状态变量产生
的输出发送到系统的输出端。
2.系统特性:
线性系统具有许多特性,包括平衡点、平稳性、稳定性、反馈和动力
学建模等等。
这些特性是线性系统能够更好地实现高效操作和有效控制的
基础。
三、线性系统的分析
1.状态变量分析:
状态变量是描述系统当前状态的量,它们通过系统的状态转移方程的变化反映系统的行为。
状态变量的分析包括:求出状态变量的收敛状态,判断系统的稳。
线性系统理论

系统:系统一词来源于英文system的音译,即若干部分相互联系、相互作用,形成的具有某些功能的整体。
中国著名学者钱学森认为:系统是由相互作用相互依赖的若干组成部分结合而成的,具有特定功能的有机整体,而且这个有机整体又是它从属的更大系统的组成部分。
线性系统:线性系统是一数学模型,是指用线性运算子组成的系统。
相较于非线性系统,线性系统的特性比较简单。
线性系统需满足线性的特性,若线性系统还满足非时变性(即系统的输入信号若延迟τ秒,那么得到的输出除了这τ秒延时以外是完全相同的),则称为线性时不变系统。
线性系统理论:系统控制的理论与实践被认为是20世纪中对人类生产和社会生活活动产生重大影响的科学领域之一。
其中,线性系统理论是系统控制理论的一个最为基本的与成熟发展的分支。
概述:线性系统科学技术是一门应用性很强的学科,面对着各种各样错综错杂的系统,控制对象可能是确定性的,也可能是随机性的,控制方法可能是常规控制,也可能需要最优化控制。
控制理论和社会生产及科学技术的发展密切相关,近代得到极为迅速的发展。
线性系统理论是现代控制理论中最基础、最成熟的分支,是控制科学重要课程之一。
线性系统理论内容丰富、思想深刻、方法多样、充满美感,不仅提供了对线性控制系统进行建模、分析、综合系统完整的理论,而且其中蕴涵着许多处理复杂问题的方法,这些方法使系统的建模、分析、综合得以简化,为系统控制理论的其它分支乃至其它学科提供了可借鉴的思路,它们是解决复杂问题的一条有效途径。
主要特点:与经典线性控制理论相比,现代线性系统理论的主要特点是:研究对象一般是多变量线性系统;除输入变量和输出变量外,还着重考虑描述系统内部状态的状态变量;在分析和综合方法方面以时域方法为主,兼而采用频域方法;使用更多的数学工具,除经典理论中使用的拉普拉斯变换外,现代线性系统理论大量使用线性代数、矩阵理论和微分方程理论等。
线性系统理论全

稳定性判据与判定方法
稳定性判据
在控制工程中,常用的稳定性判据有Routh判据、Nyquist判据、 Bode判据等。这些判据通过分析系统的特征方程或频率响应来判 断系统的稳定性。
判定方法
除了使用稳定性判据外,还可以通过时域仿真、频域分析、根轨 迹法等方法来判定系统的稳定性。这些方法各有优缺点,适用于 不同类型的线性系统和不同的问题背景。
100%
线性偏差分方程
处理离散空间和时间的问题,如 数字滤波器和图像处理等。
80%
初始条件与边界条件
在差分方程中,初始条件确定系 统的起始状态。
状态空间模型
状态变量与状态方程
表示系统内部状态的变化规律 ,揭示系统动态特性。
输出方程
描述系统输出与状态变量和输 入的关系,反映系统对外部激 励的响应。
状态空间表达式的建立
复频域分析法
拉普拉斯变换
将时域信号转换为复频域信号,便于分析系统的稳定性和动态性 能。
系统函数
描述Байду номын сангаас统传递函数的复频域表示,反映系统的固有特性和对输入信 号的响应能力。
极点、零点与稳定性
通过分析系统函数的极点和零点分布,可以判断系统的稳定性以及 动态性能。
04
线性系统稳定性分析
BIBO稳定性
01
线性系统理论全
目
CONTENCT
录
• 线性系统基本概念 • 线性系统数学模型 • 线性系统分析方法 • 线性系统稳定性分析 • 线性系统能控性与能观性分析 • 线性系统优化与综合设计
01
线性系统基本概念
线性系统定义与性质
线性系统定义
满足叠加性与均匀性的系统。
线性系统性质
《线性系统理论》课程教学探讨

《线性系统理论》课程教学探讨《线性系统理论》是控制理论中的基础课程之一,主要研究线性动态系统的建模、分析与控制。
在工程领域,线性系统理论被广泛应用于自动控制、信号处理、通信系统等各个方面。
对于控制理论专业的学生来说,学习《线性系统理论》课程是非常重要的。
在教学中,如何更好地教授《线性系统理论》课程,引导学生深入理解并掌握相关知识,是每位控制理论教师都面临的一个重要问题。
本文将探讨如何进行《线性系统理论》课程的教学,包括教学内容、教学方法、教学手段等方面,以期能够为相关教师提供一些启发与帮助。
一、教学内容《线性系统理论》课程的教学内容主要包括线性系统的基本概念、线性系统的数学描述、线性系统的时域分析、线性系统的频域分析、线性系统的稳定性分析、线性系统的控制器设计等方面。
时域分析包括状态空间描述、零输入响应、零状态响应、传递函数描述等内容;频域分析包括拉普拉斯变换、傅里叶变换、频率响应等内容;稳定性分析包括系统的内稳定性、外稳定性等内容;控制器设计包括状态反馈控制、输出反馈控制、最优控制等内容。
在教学内容的安排上,可以根据教学大纲和学生的实际需求进行适当的调整和补充。
可以结合具体的工程案例,引入一些实际的控制问题,让学生通过学习《线性系统理论》课程,能够更好地理解和应用所学知识。
二、教学方法针对《线性系统理论》课程的教学方法,可以采用多种方式,包括课堂讲授、案例分析、实验教学等。
在课堂讲授方面,可以通过引入生动的实例和案例,以及讲解一些与线性系统相关的最新研究成果,激发学生的学习兴趣,增强他们的学习动力。
在案例分析方面,可以选取一些实际的控制工程问题,进行详细的分析和讨论,让学生通过具体的案例了解线性系统理论的应用。
在实验教学方面,可以通过实验平台、仿真软件等工具,进行相应的实验操作和数据分析,让学生通过实际操作来加深对线性系统理论的理解。
还可以采用小组讨论、课外阅读、学术论文撰写等方式,培养学生的团队合作能力、独立思考能力和科研创新能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
系统控制的理论和实践被认为是对20世纪人类生产和社会活动产生重大影响的科学领域之一。
其中,线性系统理论是系统控制理论中最基础,最成熟的分支。
系统存在于自然界和人类社会的各个领域。
从系统控制理论的角度来看,它通常被定义为具有某些相关功能和受限制部分的特定功能的整体。
系统状态由描述系统行为的变量表示。
它具有完整性,抽象性和相对性的特征。
摘要
线性系统科学与技术是一门应用广泛的学科。
面对各种各样的复杂系统,控制对象可以是确定性的或随机的,并且控制方法可以是常规控制或最优控制。
控制理论与社会生产和科学技术的发展密切相关,并且在近代发展迅速。
线性系统理论是现代控制理论中最基础,最成熟的分支,是控制科学的重要课程之一。
线性系统理论内容丰富,思想深刻,方法多样,富有美感。
它不仅为线性控制系统的建模,分析和综合提供了完整的理论,而且还包含许多解决复杂问题的方法。
这些方法简化了系统的建模,分析和综合,为系统控制理论的其他分支和其他学科提供了参考。
它们是解决复杂问题的有效方法。
线性系统理论的发展经历了两个阶段:经典线性系统理论和现代线性系统理论。
古典理论形成于1930年代和1940年代。
奈奎斯特在1932年提出了反馈放大器的稳定性理论。
波特在1940年代初提出了波特图。
埃文斯在1948年提出了根轨迹理论。
这表明了经典线性控制理论的
形成。
古典理论在第二次世界大战中的应用取得了巨大的成功。
本文主要研究单输入单输出线性时不变系统。
1950年代后,随着航空技术的发展和控制理论的应用范围的扩大,经典线性控制理论的局限性日益明显。
这种情况促进了线性系统的研究,从1960年以后的古典阶段到现代阶段。
美国学者R.E.卡尔曼首先将状态空间方法应用于多元线性系统的研究,提出了可控性和可观测性两个基本概念,并提出了相应的标准。
1963年,例如吉尔伯特,他得到了揭示线性系统结构分解的重要结果,为现代线性系统理论的形成和发展做出了开创性的工作。
1965年后,现代线性系统理论又得到发展。
有许多研究多元系统的理论和方法,例如线性系统的几何理论,线性系统的代数理论和多变量频域方法。
随着计算机技术的发展,线性系统的计算方法和计算机辅助设计受到越来越多的关注。
