Z0014-多 面 体
第一章 硅的晶体结构

m3不为互质,那么这两个格点之间一定还包含有格点。对于 任何一个确定的晶格来说,x,y,z是确定的,实际上只用这 三个互质的整数m1、m2、m3来标记晶向,一般写作[m1、m2、 m3],称为晶向指数。
14
3. 硅晶体不同晶向上的原子分布情况
(或米勒指数)。
16
关于米勒指数的一些其他规定: ( h kl):代表在x轴上截距为负的平面,如 ( 1 00) {hkl} :代表相对称的平面群,如在立方对称平面中,可用 (00 1 )六个平面。 (0 1 0), ( 1 00), {100}表示(100),(010),(001), [hkl]:代表一晶体的方向,如 [100]方向定义为垂直于 (100) 平 面的方向,即表示 x 轴方向。而 [111] 则表示垂直于 (111) 平面的 方向。 <hkl> :代表等效方向的所有方向组,如 <100> 代表 [100] 、 [010]、[001]、 [ 1 00]、 [0 1 0]、 [00 1 ] 六个等效方向的族群。
间隙式杂质
替位式杂质
24
1.3.2 线缺陷
线缺陷,亦称位错-刃位错和螺位错: 晶体中的位错可以设想是由滑移所形成的,滑移以后两部分
晶体重新吻合。滑移的晶面中,在滑移部分和未滑移部分的 交界处形成位错; 当位错线与滑移矢量垂直时,这样的位错称为刃位错; 如果位错线与滑移矢量平行,称为螺位错。
3 4 r Si / 3 则空间利用率为: 34% 3 a /8
空隙为66%
12
1.2 晶向、晶面和堆积模型
1.2.1 晶向
一、晶列
晶体晶格中的原子被看作是处在一系列方向相同的平行 直线系上,这种直线系称为晶列。同一晶体中存在许多取向 不同的晶列,在不同取向的晶列上原子排列情况一般是不同 的。
第三章微波传输线教材

线单位长度分布电容为C1, 则
空气微带线传播相速: vp0 c
1 LC0
介质微带线传播相速:vp1
c
r
1 LC1
14:00
电子科技大学电子工程学院
微波技术与天线
第三章 微波传输线
引入微带线等效介电常数 c
2
c
vp0 vp1
C1 C0
设空气微带线特性阻抗为
Z
,则实际微带线特性阻抗为
00
Z0
Z00
cr
只要求得空气微带线的特性阻抗
Z
00
及有效介电常数
,
c
就
可求得介质微带线的特性阻抗。
14:00
电子科技大学电子工程学院
微波技术与天线
第三章 微波传输线
工程上常用的一组实用经验公式:
(1) 导带厚度为零时
59.952ln(8h w ) w 4h
( w 1) 4h
微波技术与天线
第三章 微波传输线
第三章 微波传输线
导波系统中的电磁波按纵向场分量的有无,可分为 以下三种波型(或模):
(1) 横磁波(TM波),又称电波(E波):Hz 0, Ez 0
(2) 横电波(TE波),又称磁波(H波):Ez 0, Hz 0
(3) 横电磁波(TEM波):
Ez 0, Hz 0
Z00
119.904
w 2.42 0.44 h (1 12h)2
h
w
w
( w 1) w:导带宽度 h h:基片厚度
e
r 1
2
r 1 (1
2
12
ICD-10疾病分类

E15-E16 E20-E35 E40-E46 E50-E64 E65-E68 E70-E90 F00-F99 F00-F09 F10-F19 F20-F29 F30-F39 F40-F48 F50-F59 F60-F69 F70-F79 F80-F89 F90-F98 F99-F99 G00-G99 G00-G09 G10-G14 G20-G26 G30-G32 G35-G37 G40-G47 G50-G59 G60-G64 G70-G73 G80-G83 G90-G99 H00-H59 H00-H06 H10-H13 H15-H22 H25-H28 H30-H36 H40-H42 H43-H45
R90-R94 R95-R99 S00-T98 S00-S09 S10-S19 S20-S29 S30-S39 S40-S49 S50-S59 S60-S69 S70-S79 S80-S89 S90-S99 T00-T07 T08-T14 T15-T19 T20-T32 T33-T35 T36-T50 T51-T65 T66-T78 T80-T88 T90-T98 V01-Y98 V01-V99 W00-X59 X60-X84 X85-Y09 Y10-Y34 Y35-Y36 Y40-Y84 Y85-Y89 Y90-Y98 Z00-Z99 Z00-Z13 Z20-Z29 Z30-Z39 Z40-Z54
分娩 主要与产褥期有关的并发症 其他产科情况,不可归类在他处者 起源于围生期的某些情况 胎儿和新生儿受母体因素及妊娠、产程和分娩并发症的影响 与妊娠期长短和胎儿生长有关的疾患 产伤 特发于围生期的呼吸和心血管疾患 特发于围生期的感染 胎儿和新生儿出血性和血液学疾患 特发于胎儿和新生儿的短暂性内分泌和代谢疾患 胎儿和新生儿的消化系统疾患 累及胎儿和新生儿体被和体温调节的情况 起源于围生期的其他疾患 先天性畸形、变形和染色体异常 神经系统先天性畸形 眼、耳、面和颈部先天性畸形 循环系统先天性畸形 呼吸系统先天性畸形 唇裂和腭裂 消化系统的其他先天性畸形 生殖器官先天性畸形 泌尿系统先天性畸形 肌肉骨骼系统先天性畸形和变形 其他先天性畸形 染色体异常,不可归类在他处者 症状、体征和临床与实验室异常所见,不可归类在他处者 累及循环和呼吸系统的症状和体征 累及消化系统和腹部的症状和体征 累及皮肤和皮下组织的症状和体征 累及神经和肌肉骨骼系统的症状和体征 累及泌尿系统的症状和体征 累及认知、感觉、情绪状态和行为的症状和体征 累及言语和语音的症状和体征 一般症状和体征 血液检查的异常所见,无诊断者 尿检查的异常所见,无诊断者 其他体液、体内物质和组织检查的异常所见,无诊断者
835-附件:泰安市教育科学十二五”规划课题
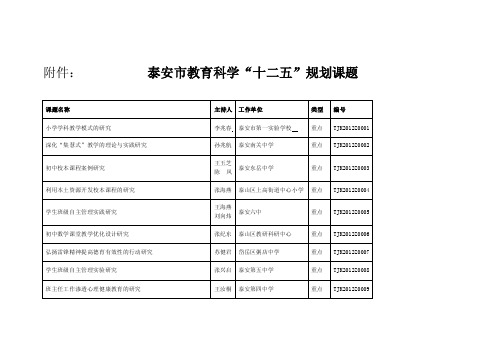
韩晓霞 泰山区白峪店子小学
规划
泰山区邱 家店镇 前光彩 小
徐方琴
规划
学
程 刚 泰山区财源学校
规划
TJK2012G0008 TJK2012G0009 TJK2012G0010
徐 莉 泰山区御碑楼小学
规划 TJK2012G0011
促进学生 主动参 与学习 活动的 策略研 究 小学语文 课堂教 学中的 设问技 巧研究 英语课堂 教学中 学生听 说读写 能力的 培养研 究 “合作学 习”的 课堂组 织形式 研究 “小纸条 反馈法 ”引领 英语教 学反馈 的尝试 研究 计算教学 中渗透 解决问 题教学 的方式 研究 小学估算 能力培 养研究 小学课堂 教学中 即时性 评价的 方法和 形式研 究 课堂练习 有效性 的研究 幼儿户外 活动器 材有效 性研究 小学《品 德与生 活(社 会)》 生活化 的表现 形式研 究 优化初中 语文作 业设计 研究
学生干部 的选拔 和培养 研究 多媒体技 术与初 中音乐 课堂教 学整合 研究 智障儿童 社会适 应能力 培养之 教学内 容研究 县域初中 语文高 效课堂 的实验 与研究 农村初中 留守儿 童教育 对策研 究 镇级教育 科研课 题建设 实践探 索与研 究 运用小组 合作学 习构建 小学高 效课堂 实践探 索与策 略研究 帮助小学 高年级 学生增 加古诗 词积累 的策略 小学口算 能力培 养研究 农村初中 学段留 守儿童 教育策 略研究 小学教学 中培养 学生良 好的学 习习惯 的研究 整体推进 县域教 育科研 大众化 常态化 的实践 应用研 究
提高课堂 教学有 效性的 案例研 究 初中理化 生家庭 小实验 与学生 创新能 力培养 的研究 小学数学 课堂训 练题设 计有效 性研究 幼儿园主 题性区 域活动 园本化 研究 书香班级 建设研 究 小学语文 综合实 践活动 课程资 源开发 深化研 究 班主任指 导下的 家校共 育实效 性研究 学生自主 管理, 健康和 谐发展 管理模 式研究 与实践
2024年辽宁省中考数学真题(学生版+解析版)

2024年辽宁省中考数学真题第一部分选择题(共30分)一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中;有一项是符合题目要求的)1.如图是由5个相同的小立方块搭成的几何体,这个几何体的俯视图是()2.亚洲、欧洲、非洲和南美洲的最低海拔如下表:大洲亚洲欧洲非洲南美洲最低海拔/m -415-28-156-40其中最低海拔最小的大洲是()A.亚洲B.欧洲C.非洲D.南美洲3.越山向海,一路花开.在5月24日举行的2024辽宁省高品质文体旅融合发展大型产业招商推介活动中,全省30个重大文体旅项目进行集中签约,总金额达532亿元.将53200000000用科学记数法表示为()A. 532xl08B. 53.2X109C. 5.32xlO 10D. 5.32X10114.如图,在矩形A8C 。
中,点E 在AQ 上,当一EBC 是等边三角形时,ZAEB 为()B. 45°5.下列计算正确的是()A. a 2 + a 3 = 2a 5 C. 60° D. 120°C.(疽)3=/D. = a 2 a B. q 2 .次二 /6. 一个不透明袋子中装有4个白球,3个红球,2个绿球,1个黑球,每个球除颜色外都相同.从中随机摸3出一个球,则下列事件发生的概率为一的是()10A.摸出白球B.摸出红球C.摸出绿球D.摸出黑球7.纹样是我国古代艺术中 瑰宝.下列四幅纹样图形既是轴对称图形又是中心对称图形的是()' " °^°C D 8.我国古代数学著作《孙子算经》中有“雉兔同笼”问题:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何? ”其大意:鸡兔同笼,共有35个头,94条腿,问鸡兔各多少只?设鸡有尤只,兔有》只,根据题意可列方程组为()x+y = 94A. <4% + 2y = 35x+y = 94B. <2x + 4y = 35x+ y = 35x+ y = 35D. <4x + 2y = 94 [2x + 4y = 949.如图,YABCD 的对角线 AC, BQ 相交于点。
2022高三高考数学知识点第7章 高考专题突破4 高考中的立体几何问题

跟踪训练3 (2020·宜昌一中模拟)如图,在四棱锥 P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC, AD=DC=AP=2,AB=1,点E为棱PC的中点. (1)证明:BE⊥PD;
解 依题意,以点A为原点,以AB,AD,AP为x轴、y轴、z轴建立空间 直角坐标系如图, 可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2). 由E为棱PC的中点,得E(1,1,1). 证明 向量B→E=(0,1,1),P→D=(0,2,-2), 故B→E·P→D=0,所以B→E⊥P→D,所以 BE⊥PD.
设直线AM与平面PBC所成的角为θ,
则
sin
θ=|cos〈m,A→M〉|=
→ |m·AM|
→
=
|m|·|AM|
23×1+12×0+
2×
7 4
23×1=
42 7.
∴直线 AM 与平面 PBC 所成角的正弦值为
42 7.
命题点3 二面角
例3 (2020·全国Ⅰ)如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为
设平面QCD的一个法向量为n=(x,y,z),
[5分] [6分]
则DD→→CQ··nn==00,, 即ym=x+0,z=0,
令x=1,则z=-m, 所以平面QCD的一个法向量为n=(1,0,-m),
则 cos〈n,P→B〉=|nn|·|PP→→BB|=
1+0+m 3· m2+1.
[9分] [10分]
当且仅当m=1时取等号,
所以直线PB与平面QCD所成角的正弦值的最大值为
6 3
.
[12分]
答题模板
第一步:根据线面位置关系的相关定理,证明线面垂直. 第二步:建立空间直角坐标系,确定点的坐标. 第三步:求直线的方向向量和平面的法向量. 第四步:计算向量夹角(或函数值),借助基本不等式确定最值. 第五步:反思解题思路,检查易错点.
高中数学第一章空间向量与立体几何1.4.2第2课时夹角问题课件新人教A版选择性必修第一册 (1)

【对点训练】❸ (2020·合肥市高三教学质量检测)在四棱锥 P- ABCD 中,BC=BD=DC=2 3,AD=AB=PD=PB=2.
(1)若点 E 为 PC 的中点,求证:BE∥平面 PAD; (2)当平面 PBD⊥平面 ABCD 时,求二面角 C-PD-B 的余弦值.
[解析] (1)取 CD 的中点为 M,连接 EM,BM. 由已知得,△BCD 为等边三角形,BM⊥CD. ∵AD=AB=2,BD=2 3, ∴∠ADB=∠ABD=30°, ∴∠ADC=90°, ∴BM∥AD. 又∵BM⊄平面 PAD,AD⊂平面 PAD, ∴BM∥平面 PAD.
2.求两条异面直线所成的角的两个关注点. (1)余弦值非负:两条异面直线所成角的余弦值一定为非负值,而对 应的方向向量的夹角可能为钝角. (2)范围:异面直线所成角的范围是0,2π,故两直线方向向量夹角的 余弦值为负时,应取其绝对值.
【对点训练】❶ 直三棱柱 ABC-A1B1C1 中,∠BCA=90°,M、N
第一章 空间向量与立体几何
1.4 空间向量的应用 1.4.2 用空间向量研究距离、夹角问题
第2课时 夹角问题
素养目标•定方向 必备知识•探新知 关键能力•攻重难 课堂检测•固双基 素养作业•提技能
素养目标•定方向
课程标准
学法解读
1.理解两异面直线所成角与它们的方向向量之间的关
1.会用向量法求
则 D(0,0,0)、A(0,0,2)、B(2,0,0)、C(0,2 3,0)、E(0, 3,1)、F(1, 3,0).
∵E为PC的中点,M为CD的中点, ∴EM∥PD. 又∵EM⊄平面PAD,PD⊂平面PAD, ∴EM∥平面PAD. ∵EM∩BM=M,EM,BM⊂平面BEM. ∴平面BEM∥平面PAD. ∵BE⊂平面BEM, ∴BE∥平面PAD.
材料微观分析作业题答案(一)

材料微观分析作业题答案(一)第一章1.衍射分析用的单色X射线采用的阳极靶材料的哪种标识X射线、滤波片材料的原子序数与阳极靶材料的原子序数关系如何?滤波片吸收限λk与阳极靶材料的标识X射线波长是什么关系?答:①采用Kα标识X射线。
②40Z<靶时,=-1Z Z片靶;40Z≥靶时,=-2Z Z片靶③kλ刚好位于辐射源的Kα和Kβ之间并尽可能靠近Kα2、X射线与物质相互作用时,产生哪两种散射?各有什么特点?哪种散射适用于X射线衍射分析?什么方向是晶体对X射线的衍射方向?答:相干散射、非相干散射。
相干散射:振动频率与入射X射线的相同,这些散射波之间符合振动方向相同、频率相同、位相差恒定的光的干涉条件。
适用于X射线衍射分析。
非相干散射:X射线波长增长并与原方向偏离2θ角,散布于空间各个方向的量子散射波与入射波的波长不相同,位相也不存在确定的关系。
入射波长越短,被照射物质元素越轻。
不能参与晶体对X射线的衍射。
3、X射线是怎么产生的?什么是标识X射线(特征X射线)谱?什么是连续X射线谱?两种谱的产生机理和特点。
答:①X射线的产生:X射线是由高速运动的带电粒子与某种物质相撞击后猝然减速,且与该物质中的内层电子相互作用产生的。
②若我们对X射线管施加不同的电压,在用适当的方法去测量由X射线管发出的X射线的波长和强度,便会得到X射线强度与波长的关系曲线,称之为X射线光谱。
·在管压很低,小于20kV时的曲线是连续变化的,故而称这种X射线谱为连续谱·当电压继续升高,大于某临界值时,突然在连续谱的某个波长处出现强度峰,峰窄而尖锐,改变管电流、管电压,这些谱线只改变强度而峰的位置所对应的波长不变,即波长只与原子序数有关,与电压无关,叫做特征X射线。
4、根据原子结构的模型,阐述封闭式热阴极X射线管中K系标识X射线的产生。
(画图说明)材料微观分析作业题答案(一)6、什么叫X射线光电效应?什么叫荧光X射线?俄歇电子?答:①X射线光电效应:入射X射线的光子与物质原子中电子相互碰撞时产生的物理效应,称为X射线的光电效应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
斜棱锥
三,四,五,...棱台
直棱柱——正棱台
斜棱台
性
(斜)
(1)侧棱相等,侧面是平行四边形
(2)底面与平行截面为全等多边形
(3)对角面为平行四边形
平行于底面的截面与底面相似
=
(1)侧面对角面为梯形
(2)两底及平行截面相似
质
(直)(1)侧棱=高
(2)侧面,对角面为矩形
(正)(3)侧面是全等矩形
对角线:
长方体:l2=a2+b2+c2(正方体=3a2)
(正)(1)侧棱等,斜高等;
侧面是全等的等腰三角形
(2)侧棱与底面成角等,
侧面与底面成角
(3)截面:2个重要Rt
(正)(1)同左,侧面是
全等的等腰梯形
(2)同右
(3)截面:2个重要
直角梯形
S
斜柱:S侧= C'L(直截面周长侧棱长)
直柱:S侧= C h(底面周长高)
柱:S中=S底
锥:
台: 中=
正四面体。(见P43)
l2= h2+ R2
h'2= h2+ r2
l2= h2+ (RR')2
h'2= h2+ (rr')2
= = = =
= = =
=
3组合体
(三)习题类型P46--46
立体几何问题的解题思想(1)立体几何问题截面,侧面展开平面几何问题
(2)计算题:公式建立方程
正锥:S侧=
(底面周长斜高2)
正台:S=
(两底面周长和斜高2)
V
斜柱:V=S’L(直截面面积侧棱长)
直柱:V=S h(底面面积高)
棱柱:V=
(底面面积高3)
棱台:V=
圆柱
圆锥
圆台
球
定义
以矩形一边(Rt直角边,直角梯形的直角腰)所在直线为轴
旋转成曲面围成几何体:圆柱,圆锥,圆台。
半圆:直径——轴
球面,球体
1有关角。距离的计算(见十二章)
2面积。体积的计算:柱:斜直;锥柱;台锥(比例)
3最值问题:点与点距离平面;球面点间距离截面;面积、体积建立函数
4组合体问题:利用截面;割补法;
轴截面
全等矩形
全等的等腰三角形
全等的等腰梯形
等圆
侧面展开图
]
=
=
侧面积
圆柱:圆锥:圆台: Nhomakorabea球面:
体积
圆柱:
圆锥:
圆台
球体:
(二)重要结论P46-45
1棱柱(台)对角面; 个,体对角线:2( )条
*三棱椎四面体特性:四种放置*球面上两点距离:球大圆上劣弧长
2截面:平行底面的截面.对角面
中截面.轴截面
中截面积
高三数学总复习(十四)第十三章多面体与旋转体P46-44
(一)知识内容
棱柱
棱锥
棱台
定
义
有两面平行,其它各面都是四边形
且相邻公共边都平行的几何体
有一个面为多边形,其他各面为有一公共顶点的三角形的几何体
用平行底面的平面截棱锥,截面与底面之间的几何体
分
类
三,四,五,...棱柱
斜棱柱
直棱柱——正棱柱
三,四,五,...棱锥
