第六章 章末能力提升
第六章 6.3等比数列及其前n项和

1.等比数列的定义一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母 q 表示(q ≠0). 2.等比数列的通项公式设等比数列{a n }的首项为a 1,公比为q ,则它的通项a n =a 1·q n -1. 3.等比中项如果三个数x ,G ,y 组成等比数列,则G 叫做x 和y 的等比中项. 4.等比数列的常用性质 (1)通项公式的推广:a n =a m ·q n-m(n ,m ∈N +).(2)若{a n }为等比数列,且k +l =m +n (k ,l ,m ,n ∈N +),则a k ·a l =a m ·a n .(3)若{a n },{b n }(项数相同)是等比数列,则{λa n }(λ≠0),⎩⎨⎧⎭⎬⎫1a n ,{a 2n },{a n ·b n },⎩⎨⎧⎭⎬⎫a n b n 仍是等比数列. 5.等比数列的前n 项和公式等比数列{a n }的公比为q (q ≠0),其前n 项和为S n , 当q =1时,S n =na 1;当q ≠1时,S n =a 1(1-q n )1-q =a 1-a n q 1-q .6.等比数列前n 项和的性质公比不为-1的等比数列{a n }的前n 项和为S n ,则S n ,S 2n -S n ,S 3n -S 2n 仍成等比数列,其公比为 q n . 【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)满足a n +1=qa n (n ∈N +,q 为常数)的数列{a n }为等比数列.( × ) (2)G 为a ,b 的等比中项⇔G 2=ab .( × )(3)如果数列{a n }为等比数列,b n =a 2n -1+a 2n ,则数列{b n }也是等比数列.( × )(4)如果数列{a n }为等比数列,则数列{ln a n }是等差数列.( × ) (5)数列{a n }的通项公式是a n =a n,则其前n 项和为S n =a (1-a n )1-a.( × )(6)数列{a n }为等比数列,则S 4,S 8-S 4,S 12-S 8成等比数列.( × )1.(2015·课标全国Ⅱ)已知等比数列{a n }满足a 1=3,a 1+a 3+a 5=21,则a 3+a 5+a 7等于( ) A.21 B.42 C.63 D.84 答案 B解析 设等比数列{a n }的公比为q ,则由a 1=3,a 1+a 3+a 5=21得3(1+q 2+q 4)=21,解得q 2=-3(舍去)或q 2=2,于是a 3+a 5+a 7=q 2(a 1+a 3+a 5)=2×21=42,故选B. 2.设等比数列{a n }的前n 项和为S n .若S 2=3,S 4=15,则S 6等于( ) A.31 B.32 C.63 D.64答案 C解析 根据题意知,等比数列{a n }的公比不是-1.由等比数列的性质,得(S 4-S 2)2=S 2·(S 6-S 4),即122=3×(S 6-15),解得S 6=63.故选C.3.等比数列{a n }中,a 4=2,a 5=5,则数列{lg a n }的前8项和等于( ) A.6 B.5 C.4 D.3 答案 C解析 数列{lg a n }的前8项和S 8=lg a 1+lg a 2+…+lg a 8=lg(a 1·a 2·…·a 8)=lg(a 1·a 8)4 =lg(a 4·a 5)4=lg(2×5)4=4.4.(2015·安徽)已知数列{a n }是递增的等比数列,a 1+a 4=9,a 2a 3=8,则数列{a n }的前n 项和等于 . 答案 2n -1解析 由等比数列性质知a 2a 3=a 1a 4,又a 2a 3=8,a 1+a 4=9,所以联立方程⎩⎪⎨⎪⎧a 1a 4=8,a 1+a 4=9,解得⎩⎪⎨⎪⎧ a 1=1,a 4=8或⎩⎪⎨⎪⎧a 1=8,a 4=1,又∵数列{a n }为递增数列, ∴a 1=1,a 4=8,从而a 1q 3=8,∴q =2. ∴数列{a n }的前n 项和为S n =1-2n 1-2=2n-1.5.(教材改编)在9与243中间插入两个数,使它们同这两个数成等比数列,则这两个数为 . 答案 27,81解析 设该数列的公比为q ,由题意知, 243=9×q 3,q 3=27,∴q =3.∴插入的两个数分别为9×3=27,27×3=81.题型一 等比数列基本量的运算例1 (1)设{a n }是由正数组成的等比数列,S n 为其前n 项和.已知a 2a 4=1,S 3=7,则S 5等于( ) A.152 B.314 C.334 D.172(2)在等比数列{a n }中,若a 4-a 2=6,a 5-a 1=15,则a 3= . 答案 (1)B (2)4或-4解析 (1)显然公比q ≠1,由题意得⎩⎪⎨⎪⎧a 1q ·a 1q 3=1,a 1(1-q 3)1-q =7,解得⎩⎪⎨⎪⎧ a 1=4,q =12,或⎩⎪⎨⎪⎧a 1=9,q =-13(舍去),∴S 5=a 1(1-q 5)1-q=4(1-125)1-12=314.(2)设等比数列{a n }的公比为q (q ≠0),则⎩⎪⎨⎪⎧a 1q 3-a 1q =6,a 1q 4-a 1=15,两式相除,得q 1+q 2=25,即2q 2-5q +2=0,解得q =2或q =12.所以⎩⎪⎨⎪⎧a 1=1,q =2,或⎩⎪⎨⎪⎧a 1=-16,q =12.故a 3=4或a 3=-4.思维升华 等比数列基本量的运算是等比数列中的一类基本问题,数列中有五个量a 1,n ,q ,a n ,S n ,一般可以“知三求二”,通过列方程(组)可迎刃而解.(1)在正项等比数列{a n }中,a n +1<a n ,a 2·a 8=6,a 4+a 6=5,则a 5a 7等于( )A.56B.65C.23D.32(2)(2015·湖南)设S n 为等比数列{a n }的前n 项和,若a 1=1,且3S 1,2S 2,S 3成等差数列,则a n = . 答案 (1)D (2)3n -1解析 (1)设公比为q ,则由题意知0<q <1,由⎩⎪⎨⎪⎧a 2·a 8=a 4·a 6=6,a 4+a 6=5,得a 4=3,a 6=2,所以a 5a 7=a 4a 6=32.(2)由3S 1,2S 2,S 3成等差数列知,4S 2=3S 1+S 3,可得a 3=3a 2,所以公比q =3,故等比数列通项a n =a 1q n -1=3n -1.题型二 等比数列的判定与证明例2 设数列{a n }的前n 项和为S n ,已知a 1=1,S n +1=4a n +2. (1)设b n =a n +1-2a n ,证明:数列{b n }是等比数列; (2)求数列{a n }的通项公式.(1)证明 由a 1=1及S n +1=4a n +2, 有a 1+a 2=S 2=4a 1+2. ∴a 2=5,∴b 1=a 2-2a 1=3.又⎩⎪⎨⎪⎧S n +1=4a n +2, ①S n =4a n -1+2 (n ≥2), ② ①-②,得a n +1=4a n -4a n -1 (n ≥2), ∴a n +1-2a n =2(a n -2a n -1) (n ≥2). ∵b n =a n +1-2a n ,∴b n =2b n -1 (n ≥2), 故{b n }是首项b 1=3,公比为2的等比数列. (2)解 由(1)知b n =a n +1-2a n =3·2n -1, ∴a n +12n +1-a n 2n =34, 故{a n 2n }是首项为12,公差为34的等差数列. ∴a n 2n =12+(n -1)·34=3n -14, 故a n =(3n -1)·2n -2. 引申探究例2中“S n +1=4a n +2”改为“S n +1=2S n +(n +1)”,其他不变探求数列{a n }的通项公式. 解 由已知得n ≥2时,S n =2S n -1+n . ∴S n +1-S n =2S n -2S n -1+1, ∴a n +1=2a n +1,∴a n +1+1=2(a n +1),又a 1=1,当n =1时上式也成立,故{a n +1}是以2为首项,以2为公比的等比数列, ∴a n +1=2·2n -1=2n ,∴a n =2n -1.思维升华 (1)证明一个数列为等比数列常用定义法与等比中项法,其他方法只用于选择题、填空题中的判定;若证明某数列不是等比数列,则只要证明存在连续三项不成等比数列即可.(2)利用递推关系时要注意对n =1时的情况进行验证.设数列{a n }的前n 项和为S n ,已知a 1+2a 2+3a 3+…+na n =(n -1)S n +2n (n ∈N +).(1)求a 2,a 3的值;(2)求证:数列{S n +2}是等比数列.(1)解 ∵a 1+2a 2+3a 3+…+na n =(n -1)S n +2n (n ∈N +), ∴当n =1时,a 1=2×1=2; 当n =2时,a 1+2a 2=(a 1+a 2)+4, ∴a 2=4;当n =3时,a 1+2a 2+3a 3=2(a 1+a 2+a 3)+6, ∴a 3=8.综上,a 2=4,a 3=8.(2)证明 a 1+2a 2+3a 3+…+na n =(n -1)S n +2n (n ∈N +),① ∴当n ≥2时,a 1+2a 2+3a 3+…+(n -1)a n -1 =(n -2)S n -1+2(n -1).②①-②得na n =(n -1)S n -(n -2)S n -1+2=n (S n -S n -1)-S n +2S n -1+2=na n -S n +2S n -1+2. ∴-S n +2S n -1+2=0,即S n =2S n -1+2, ∴S n +2=2(S n -1+2).∵S 1+2=4≠0,∴S n -1+2≠0, ∴S n +2S n -1+2=2,故{S n +2}是以4为首项,2为公比的等比数列. 题型三 等比数列的性质及应用例3 (1)在等比数列{a n }中,各项均为正值,且a 6a 10+a 3a 5=41,a 4a 8=5,则a 4+a 8= . (2)等比数列{a n }的首项a 1=-1,前n 项和为S n ,若S 10S 5=3132,则公比q = .答案 (1)51 (2)-12解析 (1)由a 6a 10+a 3a 5=41及a 6a 10=a 28,a 3a 5=a 24, 得a 24+a 28=41.因为a 4a 8=5,所以(a 4+a 8)2=a 24+2a 4a 8+a 28=41+2×5=51.又a n >0,所以a 4+a 8=51. (2)由S 10S 5=3132,a 1=-1知公比q ≠±1, 则可得S 10-S 5S 5=-132.由等比数列前n 项和的性质知S 5,S 10-S 5,S 15-S 10成等比数列,且公比为q 5, 故q 5=-132,q =-12.思维升华 (1)在等比数列的基本运算问题中,一般利用通项公式与前n 项和公式,建立方程组求解,但如果能灵活运用等比数列的性质“若m +n =p +q ,则有a m a n =a p a q ”,可以减少运算量.(2)等比数列的项经过适当的组合后构成的新数列也具有某种性质,例如等比数列S k ,S 2k -S k ,S 3k -S 2k ,…成等比数列,公比为q k (q ≠-1).(1)已知等比数列{a n }的公比为正数,且a 3a 9=2a 25,a 2=2,则a 1等于( )A.12 B.22C. 2D.2(2)等比数列{a n }共有奇数项,所有奇数项和S 奇=255,所有偶数项和S 偶=-126,末项是192,则首项a 1等于( ) A.1 B.2 C.3D.4答案 (1)C (2)C解析 (1)由等比数列的性质得a 3a 9=a 26=2a 25,∵q >0,∴a 6=2a 5,q =a 6a 5=2,a 1=a 2q=2,故选C.(2)设等比数列{a n }共有2k +1(k ∈N +)项,则a 2k +1=192,则S 奇=a 1+a 3+…+a 2k -1+a 2k +1=1q (a 2+a 4+…+a 2k )+a 2k +1=1q S 偶+a 2k +1=-126q +192=255,解得q =-2,而S 奇=a 1-a 2k +1q 21-q 2=a 1-192×(-2)21-(-2)2=255,解得a 1=3,故选C.12.分类讨论思想在等比数列中的应用典例 (12分)已知首项为32的等比数列{a n }的前n 项和为S n (n ∈N +),且-2S 2,S 3,4S 4成等差数列.(1)求数列{a n }的通项公式; (2)证明:S n +1S n ≤136(n ∈N +).思维点拨 (1)利用等差数列的性质求出等比数列的公比,写出通项公式; (2)求出前n 项和,根据函数的单调性证明. 规范解答(1)解 设等比数列{a n }的公比为q , 因为-2S 2,S 3,4S 4成等差数列,所以S 3+2S 2=4S 4-S 3,即S 4-S 3=S 2-S 4, 可得2a 4=-a 3,于是q =a 4a 3=-12.[2分]又a 1=32,所以等比数列{a n }的通项公式为a n =32×⎝⎛⎭⎫-12n -1=(-1)n -1·32n .[3分] (2)证明 由(1)知,S n =1-⎝⎛⎭⎫-12n , S n +1S n=1-⎝⎛⎭⎫-12n +11-⎝⎛⎭⎫-12n=⎩⎨⎧2+12n (2n+1),n 为奇数,2+12n(2n-1),n 为偶数.[6分]当n 为奇数时,S n +1S n 随n 的增大而减小,所以S n +1S n ≤S 1+1S 1=136.[8分]当n 为偶数时,S n +1S n 随n 的增大而减小,所以S n +1S n ≤S 2+1S 2=2512.[10分]故对于n ∈N +,有S n +1S n ≤136.[12分]温馨提醒 (1)分类讨论思想在等比数列中应用较多,常见的分类讨论有 ①已知S n 与a n 的关系,要分n =1,n ≥2两种情况. ②等比数列中遇到求和问题要分公比q =1,q ≠1讨论. ③项数的奇、偶数讨论.④等比数列的单调性的判断注意与a 1,q 的取值的讨论.(2)数列与函数有密切的联系,证明与数列有关的不等式,一般是求数列中的最大项或最小项,可以利用图象或者数列的增减性求解,同时注意数列的增减性与函数单调性的区别.[方法与技巧] 1.已知等比数列{a n }(1)数列{c ·a n }(c ≠0),{|a n |},{a 2n },{1a n }也是等比数列. (2)a 1a n =a 2a n -1=…=a m a n -m +1. 2.判断数列为等比数列的方法(1)定义法:a n +1a n =q (q 是不等于0的常数,n ∈N +)⇔数列{a n }是等比数列;也可用a n a n -1=q (q 是不等于0的常数,n ∈N +,n ≥2)⇔数列{a n }是等比数列.二者的本质是相同的,其区别只是n 的初始值不同.(2)等比中项法:a2n+1=a n a n+2(a n a n+1a n+2≠0,n∈N+)⇔数列{a n}是等比数列.[失误与防范]1.特别注意q=1时,S n=na1这一特殊情况.2.由a n+1=qa n,q≠0,并不能立即断言{a n}为等比数列,还要验证a1≠0.3.在运用等比数列的前n项和公式时,必须注意对q=1与q≠1分类讨论,防止因忽略q=1这一特殊情形而导致解题失误.4.等比数列性质中:S n,S2n-S n,S3n-S2n也成等比数列,不能忽略条件q≠-1.A组专项基础训练(时间:35分钟)1.已知等比数列{a n}中,a2+a3=1,a4+a5=2,则a6+a7等于()A.2B.2 2C.4D.4 2答案 C解析因为a2+a3,a4+a5,a6+a7成等比数列,a2+a3=1,a4+a5=2,所以(a4+a5)2=(a2+a3)(a6+a7),解得a6+a7=4.2.等比数列{a n}满足a n>0,n∈N+,且a3·a2n-3=22n(n≥2),则当n≥1时,log2a1+log2a2+…+log2a2n-1等于()A.n(2n-1)B.(n+1)2C.n2D.(n-1)2答案 A解析由等比数列的性质,得a3·a2n-3=a2n=22n,从而得a n=2n.方法一log2a1+log2a2+…+log2a2n-1=log2[(a1a2n-1)·(a2a2n-2)·…·(a n-1a n+1)a n]=log22n(2n-1)=n(2n-1).方法二取n=1,log2a1=log22=1,而(1+1)2=4,(1-1)2=0,排除B,D;取n=2,log2a1+log2a2+log2a3=log22+log24+log28=6,而22=4,排除C,选A.3.在正项等比数列{a n}中,已知a1a2a3=4,a4a5a6=12,a n-1a n a n+1=324,则n等于()A.12B.13C.14D.15答案 C解析设数列{a n}的公比为q,由a1a2a3=4=a31q3与a4a5a6=12=a31q12,可得q9=3,a n-1a n a n+1=a31q3n-3=324,因此q3n-6=81=34=q36,所以n =14,故选C.4.若正项数列{a n }满足lg a n +1=1+lg a n ,且a 2 001+a 2 002+…+a 2 010=2 016,则a 2 011+a 2 012+…+a 2 020的值为( ) A.2 015·1010 B.2 015·1011 C.2 016·1010 D.2 016·1011答案 C解析 ∵lg a n +1=1+lg a n ,∴lg a n +1a n=1, ∴a n +1a n=10,∴数列{a n }是等比数列, ∵a 2 001+a 2 002+…+a 2 010=2 016,∴a 2 011+a 2 012+…+a 2 020=1010(a 2 001+a 2 002+…+a 2 010)=2 016×1010.5.已知S n 是等比数列{a n }的前n 项和,若存在m ∈N +,满足S 2m S m =9,a 2m a m =5m +1m -1,则数列{a n }的公比为( )A.-2B.2C.-3D.3答案 B解析 设公比为q ,若q =1,则S 2mS m =2,与题中条件矛盾,故q ≠1.∵S 2mS m =a 1(1-q 2m )1-q a 1(1-q m )1-q =q m +1=9,∴q m =8. ∴a 2m a m =a 1q 2m -1a 1q m -1=q m =8=5m +1m -1, ∴m =3,∴q 3=8,∴q =2.6.等比数列{a n }中,S n 表示前n 项和,a 3=2S 2+1,a 4=2S 3+1,则公比q 为 . 答案 3解析 由a 3=2S 2+1,a 4=2S 3+1得 a 4-a 3=2(S 3-S 2)=2a 3, ∴a 4=3a 3,∴q =a 4a 3=3.7.等比数列{a n }的前n 项和为S n ,公比不为1.若a 1=1,则对任意的n ∈N +,都有a n +2+a n +1-2a n =0,则S 5= . 答案 11解析 由题意知a 3+a 2-2a 1=0,设公比为q , 则a 1(q 2+q -2)=0.由q 2+q -2=0解得q =-2或q =1(舍去),则S 5=a 1(1-q 5)1-q=1-(-2)53=11.8.已知数列{a n }的首项为1,数列{b n }为等比数列且b n =a n +1a n,若b 10·b 11=2,则a 21= . 答案 1 024解析 ∵b 1=a 2a 1=a 2,b 2=a 3a 2,∴a 3=b 2a 2=b 1b 2, ∵b 3=a 4a 3,∴a 4=b 1b 2b 3,…,a n =b 1b 2b 3·…·b n -1, ∴a 21=b 1b 2b 3·…·b 20=(b 10b 11)10=210=1 024.9.数列{b n }满足:b n +1=2b n +2,b n =a n +1-a n ,且a 1=2,a 2=4. (1)求数列{b n }的通项公式; (2)求数列{a n }的前n 项和S n .解 (1)由b n +1=2b n +2,得b n +1+2=2(b n +2), ∴b n +1+2b n +2=2,又b 1+2=a 2-a 1+2=4, ∴数列{b n +2}是首项为4,公比为2的等比数列. ∴b n +2=4·2n -1=2n +1,∴b n =2n +1-2. (2)由(1)知,a n -a n -1=b n -1=2n -2 (n ≥2), ∴a n -1-a n -2=2n -1-2 (n >2), …,a 2-a 1=22-2,∴a n -2=(22+23+…+2n )-2(n -1), ∴a n =(2+22+23+…+2n )-2n +2 =2(2n -1)2-1-2n +2=2n +1-2n .∴S n =4(1-2n )1-2-n (2+2n )2=2n +2-(n 2+n +4).10.已知数列{a n }和{b n }满足a 1=λ,a n +1=23a n +n -4,b n =(-1)n (a n -3n +21),其中λ为实数,n 为正整数.(1)证明:对任意实数λ,数列{a n }不是等比数列; (2)证明:当λ≠-18时,数列{b n }是等比数列. 证明 (1)假设存在一个实数λ,使{a n }是等比数列, 则有a 22=a 1a 3,即⎝⎛⎭⎫23λ-32=λ⎝⎛⎭⎫49λ-4 ⇔49λ2-4λ+9=49λ2-4λ⇔9=0,矛盾. 所以{a n }不是等比数列.(2)b n +1=(-1)n +1[a n +1-3(n +1)+21]=(-1)n +1⎝⎛⎭⎫23a n -2n +14 =-23(-1)n ·(a n -3n +21)=-23b n . 又λ≠-18,所以b 1=-(λ+18)≠0.由上式知b n ≠0,所以b n +1b n =-23(n ∈N +). 故当λ≠-18时,数列{b n }是以-(λ+18)为首项,-23为公比的等比数列. B 组 专项能力提升(时间:25分钟)11.设{a n }是各项为正数的无穷数列,A i 是边长为a i ,a i +1的矩形的面积(i =1,2,…),则{A n }为等比数列的充要条件是( )A.{a n }是等比数列B.a 1,a 3,…,a 2n -1,…或a 2,a 4,…,a 2n ,…是等比数列C.a 1,a 3,…,a 2n -1,…和a 2,a 4,…,a 2n ,…均是等比数列D.a 1,a 3,…,a 2n -1,…和a 2,a 4,…,a 2n ,…均是等比数列,且公比相同答案 D解析 ∵A i =a i a i +1,若{A n }为等比数列,则A n +1A n =a n +1a n +2a n a n +1=a n +2a n 为常数,即A 2A 1=a 3a 1,A 3A 2=a 4a 2,….∴a 1,a 3,a 5,…,a 2n -1,…和a 2,a 4,…,a 2n ,…成等比数列,且公比相等.反之,若奇数项和偶数项分别成等比数列,且公比相等,设为q ,则A n +1A n =a n +2a n=q ,从而{A n }为等比数列. 12.若等比数列{a n }的各项均为正数,且a 10a 11+a 9a 12=2e 5,则ln a 1+ln a 2+…+ln a 20= . 答案 50解析 因为a 10a 11+a 9a 12=2a 10a 11=2e 5,所以a 10a 11=e 5.所以ln a 1+ln a 2+…+ln a 20=ln(a 1a 2…a 20)=ln [(a 1a 20)·(a 2a 19)·…·(a 10a 11)]=ln(a 10a 11)10=10ln(a 10a 11)=10ln e 5=50.13.数列{a n }满足a 1=2且对任意的m ,n ∈N +,都有a n +m a m=a n ,则a 3= ;{a n }的前n 项和S n = . 答案 8 2n +1-2解析 ∵a n +m a m=a n , ∴a n +m =a n ·a m ,∴a 3=a 1+2=a 1·a 2=a 1·a 1·a 1=23=8;令m =1,则有a n +1=a n ·a 1=2a n ,∴数列{a n }是首项为a 1=2,公比为q =2的等比数列,∴S n =2(1-2n )1-2=2n +1-2. 14.定义在(-∞,0)∪(0,+∞)上的函数f (x ),如果对于任意给定的等比数列{a n },{f (a n )}仍是等比数列,则称f (x )为“保等比数列函数”.现有定义在(-∞,0)∪(0,+∞)上的如下函数: ①f (x )=x 2:②f (x )=2x ;③f (x )=|x |;④f (x )=ln |x |.则其中是“保等比数列函数”的f (x )的序号为 .答案 ①③解析 设{a n }的公比为q ,验证①f (a n +1)f (a n )=a 2n +1a 2n =q 2,③f (a n +1)f (a n )=|a n +1||a n |=|q |,故①③为“保等比数列函数”. 15.已知数列{a n }中,a 1=1,a n ·a n +1=⎝⎛⎭⎫12n ,记T 2n 为{a n }的前2n 项的和,b n =a 2n +a 2n -1,n ∈N +.(1)判断数列{b n }是否为等比数列,并求出b n ;(2)求T 2n .解 (1)∵a n ·a n +1=⎝⎛⎭⎫12n ,∴a n +1·a n +2=⎝⎛⎭⎫12n +1,∴a n +2a n =12,即a n +2=12a n . ∵b n =a 2n +a 2n -1,∴b n +1b n =a 2n +2+a 2n +1a 2n +a 2n -1=12a 2n +12a 2n -1a 2n +a 2n -1=12, ∵a 1=1,a 1·a 2=12, ∴a 2=12⇒b 1=a 1+a 2=32. ∴{b n }是首项为32,公比为12的等比数列. ∴b n =32×⎝⎛⎭⎫12n -1=32n . (2)由(1)可知,a n +2=12a n , ∴a 1,a 3,a 5,…是以a 1=1为首项,以12为公比的等比数列;a 2,a 4,a 6,…是以a 2=12为首项,以12为公比的等比数列,∴T 2n =(a 1+a 3+…+a 2n -1)+(a 2+a 4+…+a 2n )=1-⎝⎛⎭⎫12n1-12+12⎣⎡⎦⎤1-⎝⎛⎭⎫12n1-12=3-32n.。
第六章 人工智能及其应用 课件(共16张PPT).ppt

人工智能 Artificial Intelligence
人工智能是计算机科学的一个分支, 是研究计算机模拟人的某些感知能力、 思维过程和智能行为的学科。人工智能 是引领未来的战略性技术,将深刻改变 人类生产生活方式。人们要保持对人工 智能的控制能力,防范人工智能失控的 风险和对人类社会未来发展的潜在威胁。
揭阳市揭东区第二中学 许家乐 原创课件
《数据与计算》
初识人工智能
第六章导学课
6.1
认识人工智能
6.2
人工智能的应用
揭阳市揭东区第二中学 许家乐 原创课件
PEPORT ON WORK
01
人工智能
什么是人工智能? 人工智能的诞生和发展历程是怎样的?
揭阳市揭东区第二中学 许家乐 原创课件
揭阳市揭东区第二中学 许家乐 原创课件
1997年“深蓝”战胜卡斯帕罗夫 2006年深度学习的开始研究 2010年大数据时代到来 2016年3月AlphaGo以4比1战胜 世界围棋冠军李世石
揭阳市揭东区第二中学 许家乐 原创课件
人工智能的研究领域
图像识别
看
人脸识别
做 机器人 自动驾驶
语音识别 听
机器学习 学习
理解
机器翻译
思考
人机对弈
专家系统
在教育领域,人工智能成
为教师和学生的得力助手。
比如智能导师:主要通过 自然语言处理和语音识别技术,
Hi
由计算机模拟教师教学的经验
和方法,对学生实施一对一的
教学,并向具有不同需求和特
征的学习者传递知识。
揭阳市揭东区第二中学 许家乐 原创课件
4、智能交通 智能交通系统是通信、信息和控
制技术在交通系统中集成应用的产物, 它借助现代科技手段和设备,将各核 心交通元素联通,实现信息互通与共 享,建立安全、高效、便捷和低碳的 交通运输管理系统。
运用监督学的相关知识任选教材第四五六章末尾的其中一个案例进行详细分析

运用监督学的相关知识任选教材第四五六章末尾的其中一个案例进行详细分析在第四、五、六章末尾的案例中,我选择了第六章末尾的案例,即"Titanic: Machine Learning from Disaster"。
这个案例是一个典型的二分类问题,通过对Titanic号船上的乘客数据进行分析,预测乘客是否在事故中幸存。
首先,我会对案例进行简要介绍,然后详细分析问题背景、数据集特征、模型选择和评估,最后总结该案例的启示和提出改进方法。
"Titanic: Machine Learning from Disaster"案例是Kaggle平台上的一个竞赛项目。
通过建立机器学习模型,根据乘客的相关信息,预测乘客是否在Titanic号的沉船事故中幸存。
这个问题可以看作一个二分类问题,目标是预测乘客的幸存与否,即乘客在事故中的获救概率。
首先,对于数据集的预处理,我会进行数据清洗和特征工程。
数据清洗包括处理缺失值和异常值。
例如,可以使用均值、中位数或模型预测来填充缺失值;通过观察和分析特征值的分布,可以检测和处理异常值。
特征工程可以通过创建新的特征来提取原始特征的信息。
例如,从乘客的名字中提取出称呼,作为一个新的特征;将连续的数值特征离散化,使其更适合模型建模。
接下来,选择合适的模型进行训练和预测。
由于这是一个典型的分类问题,可以选择逻辑回归、决策树、支持向量机等多种分类模型。
在选择模型时,可以使用交叉验证来评估模型的性能,并选择性能最好的模型。
另外,可以通过调整模型的超参数来提高模型性能,如学习率、正则化参数等。
对于评估模型性能,可以使用准确率、精确率、召回率、F1分数等指标。
准确率评估模型的整体性能,精确率评估模型对正例的预测能力,召回率评估模型对正例的预测覆盖率,F1分数综合考虑了精确率和召回率。
此外,还可以使用混淆矩阵、ROC曲线等工具来了解模型的性能和预测结果。
最后,我从这个案例中得到了一些启示。
第六章几何图形初步章末小结课七年级上册数学人教版

重难剖析
8.如图,∠AOB=∠COD=90°,∠BOC=42°,则
∠AOD=( C )
A.48°
B.148°
C.138° D.128°
分析:由图可知∠AOB,∠BOC,∠COD,∠AOD组成一个周角, 所以∠AOD=360°-∠AOB-∠COD-∠BOC=138°. 故选C.
重难剖析 9.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的 摆放方式是( A )
111 11 32
从前面看
从上面看
最少摆法示意图(不唯一)
能力提升
2.用小立方块搭一个几何体,使得它从前面看和从上 面看得到的图,如图所示. 这样的几何体只有一种吗?它最少需要多少个小立方块? 最多需要多少个小立方块?
321 32 32
从前面看
从上面看
最多摆法示意图
能力提升 解:如图所示.
111 11 32 最少摆法(不唯一)所需小立 方块个数:3+2+1+1+1+1+1= 10(个).
并求出 CD的长;比较(1)(2)的结果,你发现了什么规律?
解:(1)因为C,D分别是线段OA,OB的中点, 所以OC=12AO,OD=12BO. 所以CD=OC+OD=12 (OA+OB)=12AB=12a.
能力提升
A
C BD O
解:(2)当点O在线段AB的延长线上时,如图所示. 因为C,D分别是线段OA,OB的中点,
能力提升 (3) 如图2的位置关系,探究∠AOC 与∠DOE 之间的数量关系.
解:(3)因为∠COD是直角, 所以∠COD=∠COE+∠DOE=90°, 所以2∠COE+2∠DOE=180°. 因为OE平分∠BOC,所以∠COE=∠BOE. 所以∠BOC+∠AOC=2∠COE+∠AOC=180°.
新教材高中地理章末复习3步方案第六章自然灾害学案新人教版必修第一册
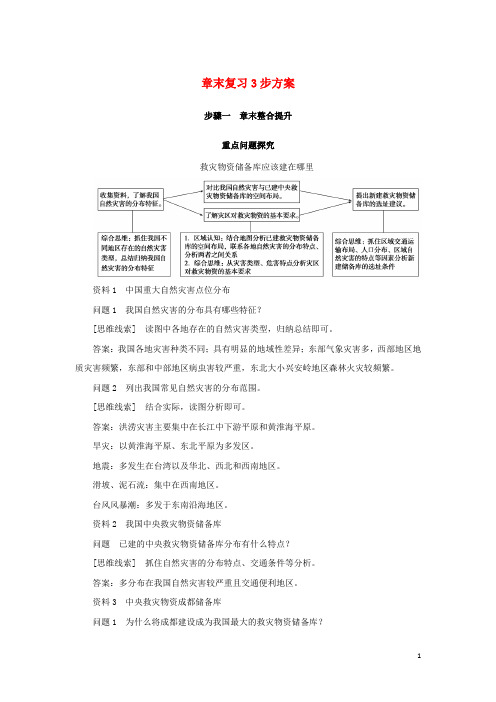
章末复习3步方案步骤一章末整合提升重点问题探究救灾物资储备库应该建在哪里资料1 中国重大自然灾害点位分布问题1 我国自然灾害的分布具有哪些特征?[思维线索] 读图中各地存在的自然灾害类型,归纳总结即可。
答案:我国各地灾害种类不同;具有明显的地域性差异;东部气象灾害多,西部地区地质灾害频繁,东部和中部地区病虫害较严重,东北大小兴安岭地区森林火灾较频繁。
问题2 列出我国常见自然灾害的分布范围。
[思维线索] 结合实际,读图分析即可。
答案:洪涝灾害主要集中在长江中下游平原和黄淮海平原。
旱灾:以黄淮海平原、东北平原为多发区。
地震:多发生在台湾以及华北、西北和西南地区。
滑坡、泥石流:集中在西南地区。
台风风暴潮:多发于东南沿海地区。
资料2 我国中央救灾物资储备库问题已建的中央救灾物资储备库分布有什么特点?[思维线索] 抓住自然灾害的分布特点、交通条件等分析。
答案:多分布在我国自然灾害较严重且交通便利地区。
资料3 中央救灾物资成都储备库问题1 为什么将成都建设成为我国最大的救灾物资储备库?[思维线索] 抓住成都所在地区的自然灾害分布、交通状况进行分析。
答案:我国西南地区地貌结构复杂,是我国地质灾害多发区,其他自然灾害也多有发生。
成都位于我国西南地区,交通便利,救灾的辐射范围广,且经济较为发达,救灾物资的生产供应能力强。
问题2 你所在的省级行政区域有没有救灾物资储备库?如果有,查找该储备库的地点,并了解其物资储备情况。
如果没有,请给出选址建议。
[思维线索] 主要通过调查,然后作答,可从灾害分布、交通状况方面分析选址条件。
答案:分析储备库的物资储备情况,应主要从所在区域的自然灾害种类方面分析灾害发生后所需的救灾物资种类及救灾物资数量。
分析储备库的选址条件时,可选择自然灾害频发,受灾人口众多,灾害损失严重且交通便利,物资供应能力较强的地区。
知识网络构建本章自我梳理:热点问题聚焦热点聚焦一堰塞湖的形成与危害【热点关注】堰塞湖是由火山熔岩流、冰碛物或由地震活动使山体岩石崩塌下来等原因引起山崩滑坡体等堵截山谷、河谷或河床后贮水而形成的湖泊。
新教材2023年高中地理 章末整合提升6 第6章 自然灾害课件 新人教版必修第一册

5.对该预警监测系统的描述,正确的是
①运用GPS采集雨量信息
②利用BDS(北斗系统)采集滑坡体位移数据
③运用RS模拟滑坡动态过程
④利用GIS进行数据分析与共享
A.①②
B.②④
C.①③
D.③④
(D ) (B )
[解析] 第4题,滑坡是在自然或者人为因素的作用下形成的,对人 类生命财产、环境造成破坏和损失的地质作用(现象),属于地质灾害。 第5题,GPS主要应用于定位、导航,雨量信息采集与之无关;BDS作 为定位导航系统可监测滑坡体位移数据;GIS是在计算机硬、软件系统 支持下,对有关地理分布数据进行采集、储存、管理、运算、分析、显 示和描述的技术系统,模拟滑坡动态过程需要GIS。
第(2)题,本题要求回答的是泥石流防御的工程措施。山区公路多沿等高 线修建,泥石流顺坡流下会导致道路冲毁,防御措施可构筑护坡工程, 用以抵御或消除泥石流对主体建筑物的冲刷、冲击、侧蚀和淤埋等的危 害。修建排导工程,建设排流、导流设施,以改善泥石流流势,增大桥 梁等建筑物的排泄能力,使泥石流按设计意图顺利排泄;修建拦水坝等 拦挡工程,用以控制泥石流的固体物质和暴雨、洪水径流,削弱泥石流 的流量、下泄量和能量,以减少泥石流对下游建筑工程的冲刷、撞击和 淤埋等危害的工程措施。
(1)图中甲、乙、丙、丁是四艘轮船的逃生路 线,比较合理的是哪条路线,请说明理由。
(2) 台 风 普 遍 带 来 暴 雨 和 大 风 。 但 是 在 不 同 地 区,还会形成其他自然灾害,请举例说明。
(3)试分析广东、福建等地多台风的原因,并列 举两项预防台风的措施。
[解析] 第(1)题,台风的危害主要由强风、暴雨和风暴潮组成,台 风的危害性极大。台风逃生应远离台风的控制区域,远离台风中心位 置,不能和台风的移动方向一致。图中台风移动的方向为自东南向西北 移动,丙沿着台风移动的方向,甲、丁向着风力最大的台风中心符近方 向,都极具危险;乙路线远离台风中心,比较合理。第(2)题,注意不同 灾害发生的关联性和具体条件。台风带来的灾害在沿海地区形成风暴 潮,在山区由于地势陡峻和暴雨的冲刷力强容易形成泥石流和滑坡,在 地势低洼处容易积水易形成内涝(涝灾)。第(3)题,广东、福建多台风的 原因,从广东和福建的位置进行分析。加强监测预报、及时远离台风区 可减轻台风灾害的损失。
2021版高考物理(基础版)一轮复习课件:第六章 1 第一节 动量 冲量 动量定理

2.应用动量定理解释的两类物理现象 (1)当物体的动量变化量一定时,力的作用时间Δt 越短,力 F 就越大,力的作用时间Δt 越长,力 F 就越小,如玻璃杯掉在水泥地上易碎,而掉在沙地上不易碎. (2)当作用力 F 一定时,力的作用时间Δt 越长,动量变化量Δp 越大,力的作用时间Δt 越短,动量变化量Δp 越小.
【自我诊断】 1.判一判 (1)动量越大的物体,其速度越大. (2)物体的动量越大,其惯性也越大. (3)物体所受合力不变,则动量也不变. (4)物体沿水平面运动时,重力不做功,其冲量为零. (5)物体所受合外力的冲量方向与物体末动量的方向相同. (6)物体所受合外力的冲量方向与物体动量变化的方向相同.
B.0.54 Pa
C.1.5 Pa
D.5.4 Pa
解析:选 A.设雨滴受到睡莲叶面的平均作用力为 F,在Δt 时间内有质量为Δm 的雨水 的速度由 v=12 m/s 减为零,以向上的方向为正方向,对这部分雨水应用动量定理:F Δt=0-(-Δmv)=Δmv,得到 F=ΔΔmt v.设水杯横截面积为 S,对水杯里的雨水,在 Δt 时间内水面上升Δh,则有Δm=ρSΔh,得 F=ρSvΔΔht ,压强 p=FS=ρvΔΔht =1×103 ×12×453×61000-3 Pa=0.15 Pa.
对动量和冲量的理解
【知识提炼】
1.动能、动量、动量变化量的比较 动能
动量
动量变化量
定义
物体由于运动而具有 物体的质量和速度的 物体末动量与初动量
的能量
乘积
的矢量差
定义式
Ek=12mv2
p=mv
Δp=p′-p
标矢性 特点状态量
动量 矢量 状态量
动量变化量 矢量 过程量
抽象代数应用

抽象代数应用一、课程目标知识目标:1. 让学生理解抽象代数的基本概念,如群、环、域等,并掌握其基本性质和运算规律。
2. 使学生掌握抽象代数在解决实际问题中的应用方法,如编码理论、密码学等。
3. 培养学生运用抽象代数知识分析和解决实际问题的能力。
技能目标:1. 培养学生运用抽象代数的思维方式进行问题求解,提高逻辑思维和抽象思维能力。
2. 培养学生通过合作与交流,运用所学知识解决复杂问题的能力。
情感态度价值观目标:1. 培养学生对抽象代数学科的兴趣和好奇心,激发他们主动探索未知领域的热情。
2. 培养学生面对困难时保持坚持不懈、勇于挑战的精神,增强自信心。
3. 使学生认识到数学在科学技术发展中的重要作用,提高他们的社会责任感和使命感。
课程性质分析:本课程为高中数学选修课程,旨在让学生在掌握基本代数知识的基础上,进一步提高抽象思维能力,培养运用数学知识解决实际问题的能力。
学生特点分析:高中学生具有一定的数学基础和抽象思维能力,但抽象代数知识较为抽象,学生可能存在理解困难。
因此,课程设计需注重启发式教学,引导学生主动参与,提高他们的学习兴趣。
教学要求:1. 教师应注重理论知识与实践应用相结合,提高课程的实用性和趣味性。
2. 针对学生特点,采用多样化的教学方法和评价手段,确保课程目标的实现。
3. 关注学生个体差异,实施差异化教学,使每个学生都能在课程中取得进步。
二、教学内容1. 抽象代数基本概念:群、环、域的定义及性质,相关定理和推论。
- 教材章节:第二章“群的初步概念”,第三章“环与域的基本理论”。
2. 抽象代数运算规律:群的运算规律,环与域的运算规律。
- 教材章节:第四章“群的运算规律”,第五章“环与域的运算规律”。
3. 抽象代数应用实例:编码理论、密码学、图论等领域的应用。
- 教材章节:第六章“抽象代数在实际中的应用”。
4. 抽象代数问题求解:运用抽象代数知识解决实际问题,提高学生解决问题的能力。
- 教材章节:第七章“抽象代数问题求解方法与实践”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章末能力提升
地理评价说明型
(2012·安徽文综)根据材料和下图,结合所学知识,回答下列问题。
云南苍山洱海地区山清水秀、林茂粮丰,大理古城宛如一颗明珠镶嵌在青山绿水之间,人与自然和谐统一。
如果在洱海西岸大规模建设住宅,可能对地理环境产生哪些不利影响?
地遭破坏,入湖污水增多,生物多样性减少,自然灾害增多,环境质量下降,不利于大理古城的保护,人地关系恶化。
评价说明类问题是用科学的观点和正确的地理思想对地理环境、措施、对策、布局进行评价或说明,多表述为“作用、意义、影响”等。
常见问题有评价大型工程(如水库建设、跨流域调水、能源跨区域调配等)带来的影响,分析区域发展条件的优劣,评价工农业、城市区位等。
评价说明类试题一般有两种情况:
1.要求直接评价某个地理事物或者现象,包括评价地理事象的影响、区位条件或发展条件等。
对此类设问进行分析时要注意:一要从有利和不利两个方面来辩证阐述,针对优势和不足进行全面论证;二要从多角度分析利弊。
影响类的问题可以从对社会、经济与生态环境等的影响加以分析;而区位问题或发展条件评价类问题,可以从自然条件和社会经济条件两个方面去分析。
2.给出限定条件,比如“与××相比,评价其优势或者不足”或“从××方面进行评
价”。
分析这类设问时,要注意审题,抓住限定词,是评价利还是弊,是对比分析还是没有限定,是从哪方面进行评价等,这样就缩小了答题范围。
“与××相比,评价其优势或者不足”,就要先注意前者的优势或者不足,然后对比分析要评价事物的优势或者不足。
而“从××方面进行评价”注意评价时限定了条件,只能从某一方面进行分析。
【思维模板】
1.阅读下列材料,回答问题。
新疆阿拉尔位于天山南麓塔克拉玛干沙漠北缘。
阿拉尔在维吾尔语里是“绿色岛屿”的意思。
阿拉尔借助得天独厚的自然优势,经过几代兵团人的努力,已经成为全国重要的细绒棉和最大的长绒棉生产基地,长绒棉出口占全国出口总量的65%。
(1)据图说明阿拉尔成为“绿色岛屿”的主要自然条件。
(2)简述阿拉尔地区棉花生产得以迅速发展的主要区位因素。
(3)阿拉尔地区大规模发展棉花生产,你认为是否合理?试简述理由。
(4)有人提出“海水西调引渤入新”的设想,引渤海海水经内蒙古自治区东南部进
入新疆盆地。
分析“海水西调引渤入新”对新疆受水区生态环境可能产生的影响。
答案(1)位于沙漠边缘,地处山麓冲积扇地区;位于多条河流交汇处,水源充足。
(2)政府政策支持;交通运输条件改善;农业技术的进步;消费市场区域的拓展;棉
纺织工业发展迅速。
(3)合理。
理由:耕地资源较为充足;接纳劳动力就业,增加农民收入;促进经济
发展。
不合理。
理由:气候干旱,生态环境脆弱;大规模发展棉花生产消耗大量水资源,水源枯竭导致荒漠化;不合理灌溉易导致土壤盐碱化。
(4)新疆气候干旱,蒸发旺盛,“海水西调”可能会增加受水区域的土层湿度及大气
湿度,减轻扬尘和沙尘暴,使地理环境有所改善;大量含盐海水可能提高受水区域地下水位,加剧盐碱化。
解析(1)注意从图中获取相关信息,从周边环境、地形、河流等方面分析“绿色岛屿”的形成条件。
(2)根据“迅速发展”锁定社会经济因素,如政策、交通、技术、市场等角度区位因素的优势条件。
(3)该题属于开放性问题,既可支持,又可反对。
支持要从对棉花生产有利的角度分析,反对从限制性因素及不利影响的方面阐释。
(4)抓住“干旱”特征,从有利与不利影响两个方面论证问题。
2.贵州省地处我国西南地区,是一个山川秀丽、气候宜人、民族众多、资源富集、发展潜力巨大的省份。
读图及相关材料,回答下列问题。
材料一石漠化是在亚热带湿润气候条件下的喀斯特地区,地表由于自然因素和人类活动的影响,植被严重破坏、土壤严重侵蚀、岩石大面积裸露,呈现类似荒漠化景观的过程。
贵州省目前是全国石漠化面积最大、程度最深、危害最严重的省份。
材料二瓮安县两个不同时期工矿业生产示意图
(1)分析回答石漠化对贵州省农业生产条件的不利影响。
(2)简要评价瓮安县工矿业生产转变的主要意义。
答案(1)水土流失加剧,耕地面积减少;部分地区气候恶化,旱涝灾害频发;土层变薄,土壤肥力下降;涵养水源能力降低,水资源不足。
(2)提高科技水平,实现产业升级;减少废弃物排放,提高资源利用率;延长产业链,提高经济效益。
解析(1)根据地理环境的整体性原理,从气候、土壤、水文等方面分析其不利影响,要注意前因后果的逻辑联系。
(2)结合图示信息比较早期与现在工矿生产的差异,从经济、社会、生态等方面评价其主要意义。
