石景山区2020届第一学期期末高三数学试题及答案
2023-2024学年北京市石景山区高三上学期期末数学试题+答案解析

2023-2024学年北京市石景山区高三上学期期末数学试题一、单选题:本题共10小题,每小题5分,共50分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则()A. B. C. D.2.已知复数,在复平面内的对应点关于虚轴对称,则()A.5B.C.D.3.展开式中含的项的系数为()A.8B.C.4D.4.已知向量,若,则()A. B.1 C.2 D.5.已知为等差数列的前n项和,若,则()A.24B.26C.28D.306.直线与圆有两个不同交点的一个充分不必要条件是()A. B. C. D.7.设函数,则()A.2B.5C.7D.108.在中,,则()A. B. C. D.9.设函数,则是()A.偶函数,且在区间单调递增B.奇函数,且在区间单调递减C.偶函数,且在区间单调递增D.奇函数,且在区间单调递减10.在正方体中,点P在正方形内不含边界,则在正方形内不含边界一定存在一点Q,使得()A. B.C.平面D.平面平面ABC二、填空题:本题共5小题,每小题5分,共25分。
11.函数的定义域为__________.12.已知双曲线的一条渐近线方程为,则该双曲线的离心率为__________.13.某学校从全校学生中随机抽取了50名学生作为样本进行数学知识测试,记录他们的成绩,测试卷满分100分,将数据分成6组:并整理得到如右频率分布直方图,则图中的t值为__________,若全校学生参加同样的测试,估计全校学生的平均成绩为__________每组成绩用中间值代替14.已知命题p:若,则能说明p为假命题的一组的值为__________,__________.15.在数列中,,给出下列四个结论:①若,则一定是递减数列;②若,则一定是递增数列;③若,,则对任意,都存在,使得;④若,,且对任意,都有,则k的最大值是其中所有正确结论的序号是__________.三、解答题:本题共6小题,共72分。
2019-2020年北京市石景山区高三上学期期末考试数学(理)试卷(有答案)【优质版】
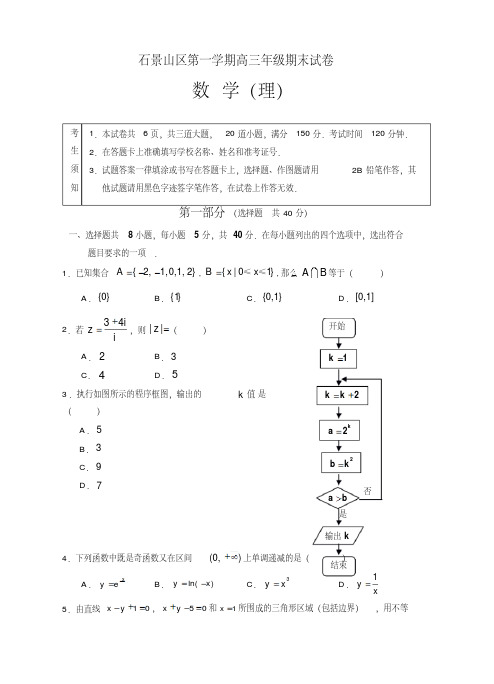
石景山区第一学期高三年级期末试卷数学(理)第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{2,1,0,1,2}A,{|01}Bx x ≤≤,那么AB 等于()A .{0}B .{1}C .{0,1}D .[0,1]2.若34i zi ,则||z ()A .2B .3C .4D .53.执行如图所示的程序框图,输出的k 值是()A .5B .3C .9D .74.下列函数中既是奇函数又在区间(0,)上单调递减的是()A .xy eB .ln()yx C .3yxD .1yx5.由直线10xy ,50x y和1x 所围成的三角形区域(包括边界),用不等考生须知1.本试卷共6页,共三道大题,20道小题,满分150分.考试时间120分钟.2.在答题卡上准确填写学校名称、姓名和准考证号.3.试题答案一律填涂或书写在答题卡上,选择题、作图题请用2B 铅笔作答,其他试题请用黑色字迹签字笔作答,在试卷上作答无效.1k a b 2kk2ka 2b k输出k是否开始结束式组可表示为()A .10,50,1xy xy x B .10,50,1xy xy x C .10,50,1xy xy xD .10,50,1xy xy x6.一个几何体的三视图如右图所示.已知这个几何体的体积为8,则h()A .1B .2C .3D .67.将函数2(3)yx图象上的点2(,(3))P t t向左平移m(m >0)个单位长度得到点Q .若Q 位于函数2y x 的图象上,则以下说法正确的是()A .当2t 时,m 的最小值为3B .当3t 时,m 一定为3C .当4t时,m 的最大值为3D .tR ,m 一定为38.六名同学A 、B 、C 、D 、E 、F 举行象棋比赛,采取单循环赛制,即参加比赛的每两个人之间仅赛一局.第一天,A 、B 各参加了3局比赛,C 、D 各参加了4局比赛,E参加了2局比赛,且A 与C 没有比赛过,B 与D 也没有比赛过,那么F 在第一天参加的比赛局数为()A .1B .2C .3D .4第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分.9.在7(3)x的展开式中,5x 的系数是(结果用数值表示).10.已知ABC △中,=3AB ,=1BC ,sin =3cos C C ,则ABC △的面积为.11.若双曲线2214xym的渐近线方程为32yx ,则双曲线的焦点坐标是.12.等差数列{}n a 中,12a ,公差不为零,且1a ,3a ,11a 恰好是某等比数列的前三项,那么该等比数列公比的值等于.侧视图正视图4h俯视图313.有以下4个条件:①a b ;②||||a b ;③a 与b 的方向相反;④a 与b 都是单位向量.其中a //b 的充分不必要条件有.(填正确的序号).14.已知函数11,1,()4ln ,1x x f x x x,①方程()f x x 有________个根;②若方程()f x ax 恰有两个不同实数根,则实数a 的取值范围是____________.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题共13分)已知函数π()2sin()sin 3cos22f x x x x .(Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在ππ[,]126上的最大值.16.(本小题共13分)2016年微信用户数量统计显示,微信注册用户数量已经突破9.27亿.微信用户平均年龄只有26岁,97.7%的用户在50岁以下,86.2%的用户在18-36岁之间.为调查大学生这个微信用户群体中每人拥有微信群的数量,现从北京市大学生中随机抽取100位同学进行了抽样调查,结果如下:微信群数量频数频率0至5个006至10个300.311至15个300.316至20个a c20个以上5b合计1001(Ⅰ)求a,b,c的值;(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过15个的概率;(Ⅲ)以这100个人的样本数据估计北京市的总体数据且以频率估计概率,若从全市..大.3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列学生..中随机抽取和数学期望EX.17.(本小题共14分)如图1,等腰梯形BCDP 中,BC ∥PD ,BAPD 于点A ,3PDBC ,且1ABBC.沿AB 把PAB △折起到P AB △的位置(如图2),使90P AD.(Ⅰ)求证:CD ⊥平面P AC ;(Ⅱ)求二面角AP DC 的余弦值;(Ⅲ)线段P A 上是否存在点M ,使得BM ∥平面P CD .若存在,指出点M 的位置并证明;若不存在,请说明理由.图1图218.(本小题共13分)已知椭圆2222:1(0)xy C a b ab的离心率为32,点(2,0)在椭圆C 上.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)过点(1,0)P 的直线(不与坐标轴垂直)与椭圆交于A B 、两点,设点B 关于轴的对称点为B .直线B A 与轴的交点Q 是否为定点?请说明理由.19.(本小题共14分)已知函数2()11x f x x,2()(0)a xg x x e a.(Ⅰ)求函数()f x 的单调区间;BCAPDB A CP ′ABCD(Ⅱ)若对任意12,[0,2]x x ,12()()f x g x 恒成立,求a 的取值范围.20.(本小题共13分)集合M 的若干个子集的集合称为集合M 的一个子集族.对于集合{1,2,3}n 的一个子集族D 满足如下条件:若,A D BA ,则BD ,则称子集族D 是“向下封闭”的.(Ⅰ)写出一个含有集合{1,2}的“向下封闭”的子集族D 并计算此时(1)AAD的值(其中A 表示集合A 中元素的个数,约定0;AD表示对子集族D 中所有成员A 求和);(Ⅱ)D 是集合{1,2,3}n 的任一“向下封闭的”子集族,对AD ,记max kA ,()max(1)AA Df k (其中ma 表示最大值),(ⅰ)求(2)f ;(ⅱ)若k 是偶数,求()f k .石景山区第一学期期末考试高三数学(理科)参考答案一、选择题共8小题,每小题5分,共40分.题号 12345678答案CDADABBD二、填空题共6小题,每小题5分,共30分.三、解答题共6小题,共80分.15.(本小题共13分)解:(Ⅰ)()2cos sin 3cos2f x x x x……1分sin 23cos2xx……2分π2sin(2)3x,……4分因此)(x f 的最小正周期为π.…………6分(Ⅱ)当ππ[,]126x 时,ππ2π2633x,………8分题号9 10 11 12 13 14答案18932(7,0)4①③1,11[,)4e当ππ232x,πsin(2)3x有最大值1.………10分即π12x时,()f x 的最大值为2.……………13分16.(本小题共13分)解:(Ⅰ)030305100a 解得35a ,5110020b,35710020c.…………………3分(Ⅱ)记“2人中恰有1人微信群个数超过15个”为事件A ,则114060210016()33C C P A C.所以,2人中恰有1人微信群个数超过15个的概率为1633.……………7分(Ⅲ)依题意可知,微信群个数超过15个的概率为25P.X 的所有可能取值0,1,2,3.……………8分则0033270()(1)2255125P XC ,1123541()(1)2255125P XC ,2213362()(1)2255125P XC ,33383()(22551)125P XC .其分布列如下:X123P2712554125361258125所以,2754368601231251251251255EX.……………13分17.(本小题共14分)解:(Ⅰ)因为90P AD ,所以P A ⊥AD .因为在等腰梯形中,AB ⊥AP ,所以在四棱锥中,AB ⊥AP .又ADAB A ,所以P A ⊥面ABCD .因为CD 面ABCD ,所以P A ⊥CD .……3分因为等腰梯形BCDE 中,ABBC ,3PDBC ,且1ABBC.所以2AC ,2CD ,2AD .所以222ACCDAD .所以AC ⊥CD .因为P A AC =A , 所以CD ⊥平面P AC .……5分(Ⅱ)由(Ⅰ)知,PA ⊥面ABCD ,AB ⊥AD ,如图,建立空间直角坐标系,A 0,0,0,B 1,0,0,C 1,1,0,D 0,2,0,P 0,0,1.…………5分所以(1,0,0)AB,(1,1,1)P C.由(Ⅰ)知,平面P AD 的法向量为(1,0,0)AB,设(,,)nx y z 为平面P CD 的一个法向量,则n CD n P C ,即00x y xyz,再令1y ,得(1,1,2)n .cos ,AB n =AB nAB n=66.所以二面角AP DC 的余弦值为66.…………9分(Ⅲ)若线段P A 上存在点M ,使得BM ∥平面P CD .依题意可设AM AP ,其中01.所以(0,0,)M ,(1,0,)BM.由(Ⅱ)知,平面P CD 的一个法向量(1,1,2)n.因为BM ∥平面P CD ,所以BMn ,所以120BM n ,解得12.所以,线段P A 上存在点M ,使得BM ∥平面P CD …………………14分18.(本小题共13分)解:(Ⅰ)因为点(2,0)在椭圆C 上,所以2a .又因为32c ea,所以3c ,221bac.所以椭圆C 的标准方程为:2214xy.……………………5P B A CP ’ABCD xyz分(Ⅱ)设112222(,),(,),(,),(,0)A x y B x y B x y Q n .设直线AB :(1)(0)y k x k.……………………6分联立22(1)440y k x x y和,得:2222(14)8440k x k xk.所以2122814kx x k,21224414kx x k.……………8分直线AB 的方程为121112()y y yy xx x x ,……………9分令0y,解得112122111212()y x x x y x y nx y y y y (11)分又1122(1),(1)y k x y k x ,所以121212()42x x x x nx x .所以直线B A 与轴的交点Q 是定点,坐标为(4,0)Q .………13分19.(本小题共14分)解:(Ⅰ)函数()f x 的定义域为R ,()()()()()()x x x f x x x 2222211111.……2分当x 变化时,()f x ,()f x 的变化情况如下表:x (,)1(,)11(,)1()f x ()f x 所以,函数()f x 的单调递增区间是(,)11,单调递减区间是(,)1,(,)1.…………5分(Ⅱ)依题意,“对于任意12,[0,2]x x ,12()()f x g x 恒成立”等价于“对于任意[0,2]x,minmax ()()f x g x 成立”.由(Ⅰ)知,函数()f x 在[0,1]上单调递增,在[1,2]上单调递减,因为(0)1f ,2(2)115m f ,所以函数()f x 的最小值为(0)1f .所以应满足max ()1g x .………………………………………………7分因为2()e axg x x ,所以2()(+2)e axg x ax x .………8分因为0a,令()0g x 得,10x ,22x a.(ⅰ)当22a,即10a 时,在[0,2]上()0g x ,所以函数()g x 在[0,2]上单调递增,所以函数2max ()(2)4e ag x g .由24e1a得,ln 2a,所以1ln 2a .……………11分(ⅱ)当202a ,即1a时,在2[0,)a上()0g x ,在2(,2]a上()0g x ,所以函数()g x 在2[0,)a 上单调递增,在2(,2]a上单调递减,所以max2224()()eg x g a a .由2241ea 得,2ea,所以1a .……………13分综上所述,a 的取值范围是(,ln 2].……………14分20.(本小题共13分)解:(Ⅰ)含有集合{1,2}的“向下封闭”的子集族{,{1},{2},{1,2}}D……2分此时112(1)(1)(1)(1)(1)0AA D…………4分(Ⅱ)设{1,2,3}n 的所有不超过k 个元素的子集族为kD (ⅰ)易知当2DD 时,(1)AA D达到最大值,所以21122(1)32(2)(1)(1)(1)122n n n n nn f C C n…6分(ⅱ)设D 是使得max kA 的任一个“向下封闭”的子集族,记'''DDD ,其中'D 为不超过2k元的子集族,''D 为1k 元或k 元的子集则(1)AA D='''''(1)(1)(2)(1)AAAA DA DA Df k ………8 分现设''D有l (kn l C )个{1,2,3}n 的k 元子集,由于一个1k 元子集至多出现在1n k个{1,2,3}n 的k 元子集中,而一个k 元子集中有1k kC个1k 元子集,故l 个k 元子集至少产生11k k lC nk个不同的1k 元子集.''11(1)(1)(1)111k Ak k k knnnA DlCkkl l C CCn k n k n k 1(1)(2)()Ak k nnA Df kCC f k 由(ⅰ)得11221()(1)(1)(1)(1)(1)kkk ii nnnni f k CCCC …13分【注:若有其它解法,请酌情给分.】。
2020~2021北京市石景山区高三上学期数学期末试卷及答案

石景山区2020—2021学年第一学期高三期末试卷数 学本试卷共8页,满分为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无效,考试结束后上交答题卡.第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.( 1 )已知集合{}1,2,3A =,{}1,0,2,3B =-,则A B =(A ){}0,1,2(B ){}0,2(C ){2,3}(D ){}1,0,1,2,3-( 2 )复数2(1i)-=(A )0(B )1(C )2i(D )2i -( 3 )5(1)x +的展开式中x 的系数为(A ) 1(B )5(C )10(D )15( 4 )某三棱锥的三视图如图所示, 则该三棱锥的体积为(A ) 16(B ) 13 (C )23(D ) 2( 5 )若抛物线24y x =上的点A 到焦点的距离为10,则点A 到y 轴的距离是 (A ) 6 (B )7 (C )8 (D )9侧(左)视图11( 6 )“πϕ=”是“函数sin()y x ϕ=+为奇函数”的 (A )充分而不必要条件 (B )必要而不充分条件(C )充分必要条件(D )既不充分也不必要条件( 7 )直线:1l y kx =+与圆22:(1)4C x y +-=的位置关系是(A ) 相切(B )相交(C )相离(D )不确定( 8 )等差数列{}n a 的首项为1,公差不为0,若124,,a a a 成等比数列,则{}n a 前5项的和为(A )10(B )15(C )21(D )28( 9 )已知函数2,0,(),0,x x f x x x ⎧=⎨-<⎩≥ 则函数||()2x y f x =-的零点个数是 (A ) 0 (B )1 (C )2 (D )3(10)斐波那契螺线又叫黄金螺线,广泛应用于绘画、建筑等,这种螺线可以按下列方法 画出:如图,在黄金矩形ABCD(AB BC =)中作正方形ABFE ,以F 为圆心, AB 长为半径作圆弧BE ;然后在矩形CDEF 中作正方形DEHG ,以H 为圆心,DE 长 为半径作圆弧EG ;……;如此继续下去,这些圆弧就连成了斐波那契螺线. 记圆弧BE ,EG ,GI 的长度分别为,,l m n ,对于以下四个命题:①l m n =+ ②2m l n =⋅ ③2m l n =+④211m l n =+ 其中正确的是(A ) ①②(B )①④(C )②③ (D )③④L J IKH GFE DC BA第二部分(非选择题 共110分)二、填空题共5小题,每小题5分,共25分.(11)函数()ln f x x =的定义域为__________.(12)已知平面向量(2,1)=a ,(4,)y =b ,且∥a b ,则实数y =__________.(13)已知双曲线C 的两个焦点为()()3,0,3,0-,一个顶点是),则C 的标准方程为__________;C 的焦点到其渐近线的距离是__________.(14)若函数π()sin()cos()3f x x x ωω=++的一个周期是π,则常数ω的一个取值可以为__________.(15)从4G 到5G 通信,网络速度提升了40倍.其中,香农公式2log (1)SC W N=+是 被广泛公认的通信理论基础和研究依据,它表示:在受噪声干扰的信道中,最 大信息传递率C 取决于信道带宽W 、信道内信号的平均功率S 、信道内部的高 斯噪声功率N 的大小,其中SN叫做信噪比. 根据香农公式,以下说法正确的是__________.(参考数据:lg50.6990≈) ①若不改变信噪比SN,而将信道带宽W 增加一倍,则C 增加一倍; ②若不改变信道带宽W 和信道内信号的平均功率S ,而将高斯噪声功率N 降低 为原来的一半,则C 增加一倍; ③若不改变带宽W ,而将信噪比SN从255提升至1023,C 增加了25%; ④若不改变带宽W ,而将信噪比SN从999提升至4999,C 大约增加了23.3%.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程. (16)(本小题13分)如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥平面ABCD ,,M N 分别为棱,PD BC 的中点,2PA AB ==.(Ⅰ)求证:MN ∥平面PAB ;(Ⅱ)求直线MN 与平面PCD 所成角的正弦值.(17)(本小题13分)在ABC △中,2c =,30C =︒.再从条件①、条件②、条件③这三个条件中选择一个作为已知,使其能够确定唯一的三角形,求: (Ⅰ)a 的值; (Ⅱ)ABC △的面积.条件①:2b ; 条件②:45A =︒;条件③:b =注:如果选择多个条件分别解答,按第一个解答计分.DB(18)(本小题14分)在学期末,为了解学生对食堂用餐满意度情况,某兴趣小组按性别采用分层抽样的方法,从全校学生中抽取容量为200的样本进行调查.被抽中的同学分别对食堂进行评分,满分为100分.调查结果显示:最低分为51分,最高分为100分.随后,兴趣小组将男、女生的评分结果按照相同的分组方式分别整理成了频数分布表和频率分布直方图,图表如下:为了便于研究,兴趣小组将学生对食堂的评分转换成了“满意度情况”,二者的对应关系如下:(Ⅰ)求a 的值;(Ⅱ)为进一步改善食堂状况,从评分在[50,70)的男生中随机抽取3人进行座谈,记这3人中对食堂“不满意”的人数为X ,求X 的分布列;(Ⅲ)以调查结果的频率估计概率,从该校所有学生中随机抽取一名学生,求其对食堂“比较满意”的概率.男生评分结果的频数分布表 a女生评分结果的频率分布直方图(19)(本小题15分)已知椭圆2222:1(0)x y C a b a b +=>>的离心率e (0,1)D .(Ⅰ)求椭圆C 的方程;(Ⅱ)已知点(1,0)A -和点(4,0)B -,过点B 的动直线l 交椭圆C 于,M N 两点(M 在N 左侧),试讨论BAM ∠与OAN ∠的大小关系,并说明理由.设函数1()ln ,f x a x a x=+∈R .(Ⅰ)设l 是()y f x =图象的一条切线,求证:当0a =时,l 与坐标轴围成的三角形的面积与切点无关;(Ⅱ)若函数()()g x f x x =-在定义域上单调递减,求a 的取值范围.对于数列{}n a ,若从第二项起的每一项均大于该项之前的所有项的和,则称{}n a 为P 数列.(Ⅰ)数列{}n a 为1,1,3,5,7-,数列{}n b 为1111,,,248--.判断数列{}n a ,{}n b 是否为P 数列,并说明理由;(Ⅱ)设数列{}n a 是首项为2的P 数列,其前n 项和为n S (*n ∈N ).求证:当2n ≥时,2nn S >;(Ⅲ)设无穷数列{}n a 是首项为a (a >0),公比为q 的等比数列,有穷数列{}n b ,{}n c 是从{}n a 中取出部分项按原来的顺序所组成的不同数列,其所有项和分别为1T ,2T . 若12T T =.判断{}n a 是否为P 数列,并说明理由.(考生务必将答案答在答题卡上,在试卷上作答无效)石景山区2020—2021学年第一学期高三期末数学试卷参考答案一、选择题:本大题共10个小题,每小题4分,共40分.二、填空题:本大题共5个小题,每小题5分,共25分.(11)(0,)+∞; (12)2; (13)22163x y -= (14)2;(答案不唯一) (15)①③④.三、解答题:本大题共6个小题,共85分.解答题应写出文字说明,证明过程或演算步骤.(16)(本小题13分)解:(Ⅰ)在四棱锥P ABCD -中,取PA 的中点E ,连接EB 、EM ,因为M 是PD 的中点,所以 EM ∥AD ,且12EM AD =.又因为 底面ABCD 是正方形,N 是BC 的中点, 所以 BN AD ∥,且12BN AD =. 所以 EM ∥•=BN . 所以 四边形MNBE 是平行四边形.所以 MN EB ∥. 由于 EB ⊂平面PAB ,MN ⊄平面PAB ,所以 MN ∥平面PAB .N DB C(II )因为 底面ABCD 是正方形,所以 AB ⊥AD .又因为 PA ⊥平面ABCD .所以以点A 为坐标原点,AB 、AD 、AP 分别为x 、y 、z 轴, 如图建立空间直角坐标系.(0,0,0)A ,(2,2,0)C ,(0,2,0)D ,(0,0,2)P ,(0,1,1)M ,(2,1,0)N .(2,2,2),(2,0,0),PC CD −−→−−→=-=-设平面PCD 的法向量为(,,)m x y z =.有:0,0,m PC m CD ⎧⋅=⎪⎨⋅=⎪⎩即0,0,x y z x +-=⎧⎨=⎩令1y =,则=1z , 所以(0,1,1)m =.(2,0,1)MN =-.设直线MN 与平面PCD 所成角为θ. 有:sin cos ,MN m θ==MN m MN m⋅⋅. 所以直线MN 与平面PCD .(17)(本小题13分) 选择条件①:2b 解:(Ⅰ)在ABC △中,因为2b=, 所以b =. 因为2c =,30C =︒.根据余弦定理:222cos 2a b cCab+-=,得22)4cos30a +-︒, 整理,得216a =, 由于0a >,所以 =4a .(Ⅱ)由(I)可知,b ==因为4a =,2c =, 所以222a b c =+. 所以=90A ︒.因此,ABC △是直角三角形.所以11222S bc ==⨯=.选择条件②:45A =︒. 解:(Ⅰ)在ABC △中,因为 45A =︒,30C =︒,=2c .根据正弦定理:sin sin a cA C= ,所以2sin 2sin 452=1sin sin 302c A a C ︒===︒(Ⅱ)在ABC △中,因为sin sin()B A C =+.所以sin sin(3045)=sin30cos45cos30sin 45B =︒+︒︒︒+︒︒所以1sin 2S ac B=1=22⨯.选择条件③:不给分(18)(本小题14分)解:(Ⅰ)因为0.005+0.0200.0400.020)101a +++⨯=(, 所以 0.015a =.(Ⅱ)依题意,随机变量X 的所有可能取值为0,1,2,3.0333361(0)20C C P X C ⋅=== ; 1233369(1)20C C P X C ⋅===; 2133369(2)20C C P X C ⋅===; 3033361(3)20C C P X C ⋅===. 所以随机变量X 的分布列为:(Ⅲ)设事件=A “随机抽取一名学生,对食堂‘比较满意’”.因为样本人数200人,其中男生共有80人, 所以样本中女生共有120人. 由频率分布直方图可知,女生对食堂“比较满意”的人数共有:1200.02010=24⨯⨯人.由频数分布表,可知男生对食堂“比较满意”的共有16人,241612005+=. 所以随机抽取一名学生,对食堂“比较满意”的概率为1()5P A =.(19)(本小题15分)解:(Ⅰ)由已知1b =,c e a ==, 又222a b c =+,解得2,1a b ==.所以椭圆C 的方程为2214x y +=.(Ⅱ)依题意设直线l 的方程为(4)y k x =+,设1122(,),(,)M x y N x y .联立224(4),1,y k x y x +=⎧⎪⎨⎪=+⎩消去y ,得2222(41)326440k x k x k +++-=,则216(112)0k ∆=->,解得k <<. (*) 则21223241k x x k -+=+,212264441k x x k -=+.若11x =-,则1y =k =与(*)式矛盾,所以11x ≠-.同理21x ≠-.所以直线AM 和AN 的斜率存在,分别设为AM k 和AN k .因为1212121212(4)(4)332111111AM ANy y k x k x k kk k k x x x x x x +++=+=+=++++++++1212121212222222223(2)3(2)22(1)(1)1323(2)3(242)142206443236311414k x x k x x k k x x x x x x k k k k k k k k k k k k ++++=+=++++++-+-++=+=+=---++++ 所以AM AN k k =-.所以BAM ∠=OAN ∠.(20)(本小题15分)解:(Ⅰ)当0a =时,1(),0f x x x =>,21()f x x'=-,设()f x 图象上任意一点001(,)P x x ,切线l 斜率为0201()k f x x '==-. 过点001(,)P x x 的切线方程为020011()y x x x x -=--. 令0x =,解得02y x =;令0y =,解得02x x =. 切线与坐标轴围成的三角形面积为0012|||2|22S x x =⋅=. 所以l 与坐标轴围成的三角形的面积与切点无关. (Ⅱ)由题意,函数()g x 的定义域为(0,)+∞.因为()g x 在(0,)+∞上单调递减,所以21()10a g x x x'=--≤在(0,)+∞上恒成立,即当(0,)x ∈+∞,1a x x+≤恒成立,所以min 1)a x x+≤(因为当(0,)x ∈+∞,12x x +≥,当且仅当1x =时取等号.所以当1x =时,min 1)2x x+=(所以2a ≤.所以a 的取值范围为(,2]-∞.(21)(本小题15分)解:(Ⅰ)数列{}n a 不是P 数列,数列{}n b 是P 数列. 对于数列{}n a ,11357-+++>,所以数列{}n a 不是P 数列;对于数列{}n b ,1111111,1,1224248-<-+<--+-<,所以数列{}n b 是P 数列.(Ⅱ)由题意知,1n n a S +>,即1n n n S S S +->,即12n n S S +>.又因为1120S a ==>, 所以 0n S >. 所以 当2n ≥时,1211212n n n n n n S S S S S S S S ---=⋅⋅⋅⋅> 命题得证.(Ⅲ)数列{}n a 不是P 数列.假设数列{}n a 是P 数列,则2a aq a =>得1q >, 所以数列{}n a 是单调递增数列,且0n a >,*n ∈N . ⑴若数列{}n b 中的元素都在数列{}n c 中,则12T T <; ⑵若数列{}n c 中的元素都在数列{}n b 中,则12T T >;⑶若数列{}n b 和数列{}n c 有部分公共元素,将数列{}n b 和{}n c 的公共元素去掉得到新的数列{'}n b 和{'}n c ,不妨设数列{'}n b 和{'}n c 中的最大元素m a 在数列{'}n c 中, 则数列{}n a 的前1m -项和1m m S a -<. 因为0n a >,*n ∈N ,所以数列{'}n b 中的所有项和小于等于1m S -. 所以数列{'}n b 中的所有项和小于m a . 所以12T T <.综上⑴⑵⑶知12T T ≠.与已知12T T =矛盾,所以数列{}n a 不是P 数列.【若有不同解法,请酌情给分】。
2019-2020学年北京石景山高三上学期期末数学试卷+参考答案+评分标准

石景山区2019—2020学年第一学期高三期末试卷数 学本试卷共5页,满分为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无效,考试结束后上交答题卡.第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合{}02A x x =≤≤,{}1,0,2,3B =-,则A B =I A. {}0,1,2 B. {}0,2C. {}1,3-D. {}1,0,1,2,3-2. 复数21iz =+的共轭复数在复平面内对应的点所在象限为 A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限3. 下列函数中既是奇函数,又在区间01(,)上单调递减的是 A. 3()f x x =B. ()lg ||f x x =C. ()f x x =-D. ()cos f x x =4. 已知向量()5,m =a ,()2,2=-b ,若()-⊥a b b ,则实数m = A. 1-B. 1C. 2D. 2-5. 我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为 A. 134石B. 169石C. 338石D. 1365石6. 已知3log 4a =,πlog 3b =,c =,则a ,b ,c 的大小关系是 A. a b c << B. a c b << C. b c a << D. b a c <<7. 艺术体操比赛共有7位评委分别给出某选手的原始评分,评定该选手的成绩时,从7个原始评分中去掉1个最高分、1个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,不变的数字特征是 A. 中位数B. 平均数C. 方差D. 极差8. 一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与原正方体体积的比值为 A. 81B. 71C. 61D.519. 在等差数列{}n a 中,设,,,k l p r *∈N ,则k l p r +>+是k l p r a a a a +>+的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充要必要条件D. 既不充分也不必要条件10. 关于曲线:C 224x xy y ++=.给出下列三个结论:① 曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ② 曲线C上任意一点到原点的距离都不大于 ③ 曲线C 上任意一点到原点的距离都不小于2. 其中,正确结论的个数是 A.0B. 1C. 2D. 3第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分.11. 在62()x x-的二项展开式中,常数项等于__________.(用数字作答) 12. 已知双曲线标准方程为2213x y -=,则其焦点到渐近线的距离为 .13. 已知数列{}*()n a n n +∈N 为等比数列,11a =,22a =,则3a =________.14. 已知平面,,αβγ.给出下列三个论断:①αβ⊥;②αγ⊥;③β∥γ.以其中 的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:____. 15. 在ABC △中,角,,A B C 所对的边分别是,,a b c .已知14b c a -=, 2sin 3sin B C =,则cos A 的值为_______.16. 已知向量1e u r ,2e u u r是平面α内的一组基向量,O 为α内的定点,对于α内任意一点P ,当12OP xe ye =+u u u r u r u u r时,则称有序实数对(,)x y 为点P 的广义坐标,若点A 、B 的广义坐标分别为11(,)x y 、22(,)x y ,对于下列命题:① 线段AB 的中点的广义坐标为1212(,)22x x y y ++; ② 向量OA u u u r 平行于向量OB u u u r的充要条件是1221x y x y =;③ 向量OA u u u r 垂直于向量OB u u u r的充要条件是12120x x y y +=.其中,真命题是 .(请写出所有真命题的序号)三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 17. (本小题13分)已知函数1()cos (sin cos )2f x x x x =+-. (Ⅰ)若2π0<<α,且53sin =α,求()f α的值; (Ⅱ)求函数()f x 的最小正周期,及函数()f x 的单调递减区间.18.(本小题13分)一款小游戏的规则如下:每盘游戏都需抛掷骰子三次,出现一次或两次“6点”获得15分,出现三次“6点”获得120分,没有出现“6点”则扣除12分(即获得-12分). (Ⅰ)设每盘游戏中出现“6点”的次数为X ,求X 的分布列; (Ⅱ)玩两盘游戏,求两盘中至少有一盘获得15分的概率;(Ⅲ)玩过这款游戏的许多人发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析解释上述现象.19.(本小题14分)已知在四棱锥ABCD P -中,底面ABCD 是边长为4的正方形,PAD △是正三角形,CD ⊥平面PAD ,O G F E 、、、分别是AD BC PD PC 、、、 的中点.(Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求平面EFG 与平面ABCD 所成锐二面角的大小;(Ⅲ)线段PA 上是否存在点M ,使得直线GM与平面EFG 所成角为π6,若存在,求线段PM的长度;若不存在,说明理由.20.(本小题14分)已知函数()e x f x ax =-.(a ∈R ) (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若3a =,()f x 的图象与y 轴交于点A ,求()y f x =在点A 处的切线方程; (Ⅲ)在(Ⅱ)的条件下,证明:当0x >时,2()31f x x x >-+恒成立.21. (本小题13分)已知椭圆222:12x y C a +=过点(2,1)P . (Ⅰ)求椭圆C 的方程,并求其离心率;(Ⅱ)过点P 作x 轴的垂线l ,设点A 为第四象限内一点且在椭圆C 上(点A 不在直线l上),直线PA 关于l 的对称直线PB 与椭圆交于另一点B .设O 为坐标原点,判断直线AB 与直线OP 的位置关系,并说明理由.22.(本小题13分)已知由*()n n ∈N 个正整数构成的集合1212{,,,}(,3)n n A a a a a a a n =<<<L L ≥, 记12A n S a a a =+++L ,对于任意不大于A S 的正整数m ,均存在集合A 的一个子集,使得该子集的所有元素之和等于m . (Ⅰ)求21,a a 的值;(Ⅱ)求证:“n a a a ,,,21Λ成等差数列”的充要条件是“2)1(+=n n S A ”; (Ⅲ)若2020=A S ,求n 的最小值,并指出n 取最小值时n a 的最大值.石景山区2019-2020学年第一学期高三期末数学试卷答案及评分参考一、选择题:本大题共10个小题,每小题4分,共40分.二、填空题:本大题共6个小题,每小题5分,共30分. 11.160-; 12.1; 13. 5;14.①③⇒② 或②③⇒①; 15. 14-; 16. ①② .三、解答题:本大题共6个小题,共80分.解答题应写出文字说明,证明过程或演算步骤.17.(本小题13分) 解:(Ⅰ)因为 20πα<<,且53sin =α, 所以 4cos 5α==. ……………2分 所以 ()434128131=555225250f α⎛⎫=+-=- ⎪⎝⎭. ……………5分 (Ⅱ)()()21cos sin cos 21cos sin cos 2-+⋅=-+=x x x x x x x f ……………8分 所以函数()x f 的最小正周期2ππ2T ==. ……………9分 由ππ3π2π22π+242k x k ,k +≤+≤∈Z , 解得π5πππ+88k x k ,k +≤≤∈Z . ……………11分 所以函数()x f 的单调递减区间π5πππ+88k ,k ,k ⎡⎤+∈⎢⎥⎣⎦Z . ……………13分 )42sin(22)2cos 2(sin 212122cos 12sin 21π+=+=-++=x x x x x )42sin(22)2cos 2(sin 212122cos 12sin 21π+=+=-++=x x x x x解:(Ⅰ)X 可能的取值为0,1,2,3. ……………1分每次抛掷骰子,出现“6点”的概率为16p =. 0331125(0)(1)6216P X C ==-=, 1231175(1)(1)66216P X C ==⋅-=, 2231115(2)()(1)66216P X C ==⋅-=,33311(3)()6216P X C ===,……………5分所以X 的分布列为:……………6分(Ⅱ)设“第i 盘游戏获得15分”为事件A i (i =1,2),则12905()()(1)(2)21612P A P A P X P X ===+===. ……………8分 所以“两盘游戏中至少有一次获得15分”的概率为12951()()144P A P A -= 因此,玩两盘游戏至少有一次获得15分的概率为95144. ……………10分 (Ⅲ)设每盘游戏得分为Y .由(ⅠY 的数学期望为1512151202161221636EY =-⨯+⨯+⨯=-. ……12分 这表明,获得分数Y 的期望为负.因此,多次游戏之后分数减少的可能性更大. ……………13分(Ⅰ)证明:因为△PAD 是正三角形,O 是AD 的中点,所以 ⊥PO AD . 又因为⊥CD 平面PAD ,⊂PO 平面PAD ,所以⊥PO CD . D CD AD =⋂,⊂CD AD ,平面ABCD ,所以⊥PO 面ABCD . ……………4分 (Ⅱ)如图,以O 点为原点分别以OA 、OG 、OP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系.则)32,0,0(),0,4,0(),0,0,2(),0,4,2(),0,4,2(),0,0,2(),0,0,0(P G D C B A O --, )3,0,1(),3,2,1(--F E ,)3,2,1(),0,2,0(-=-=,设平面EFG 的法向量为),,,(z y x m =⎪⎩⎪⎨⎧=-+=-,032,02z y x y令1=z ,则 )10,3(,=,又平面ABCD 的法向量)1,0,0(=,设平面EFG 与平面ABCD 所成锐二面角为θ所以21cos ==θ. 所以平面EFG 与平面ABCD 所成锐二面角为3π. ……………9分(Ⅲ)假设线段PA 上存在点M ,使得直线GM 与平面EFG 所成角为π6, 设]1,0[,∈=λλ,PA GP PM GP GM λ+=+=,所以))1(32,4,2(λλ--=. ……………11分所以76423,cos |6πsin2+->=<=λλ, …………13分整理得02322=+-λλ,无解,所以,不存在这样的点M . ………14分20.(本小题14分)解:(Ⅰ)()x f x e a '=-, ……………1分当0a ≤时,()0f x '≥恒成立,所以()f x 在R 上单调递增, ……………3分 当0a >时,令()0f x '=,解得ln x a =. 当x 变化时,(),()f x f x '的变化情况如下表:所以0a >时,()f x 在(,ln )a -∞上单调递减,在(ln ,)a +∞上单调递增. …5分 (Ⅱ)令0x =,得1y =,则()0,1A , …………6分因为()e 3x f x '=-,所以()0132f '=-=-, …………7分 所以在A 点处的切线方程为12(0)y x -=--,即21y x =-+. ………9分 (Ⅲ)证明:令()22()(3+1)=e 1x g x f x x x x =----,则()e 2x g x x '=-.令()e 2x h x x =-,则()e 2x h x '=-, 当0ln2x <<时,()0h x '<,()h x 单调递减,当ln2x >时,()0h x '>,()h x 单调递增; …………11分 所以()()ln2ln2e 2ln222ln20h x h ≥=-=->,即()0g x '>恒成立.所以()g x 在(),-∞+∞上单调递增,所以()()01010g x g >=--=,………13分所以2e 10x x -->,即当0x >时,()231f x x x >-+恒成立. …………14分21.(本小题13分)解:(Ⅰ)由椭圆222:12x y C a +=过点(2,1)P , 可得24112a +=,解得28a =. …………2分 所以222826c ab =-=-=, …………3分所以椭圆C 的方程为22182x y +=,离心率e == …………5分(Ⅱ)直线AB 与直线OP 平行. …………6分证明如下:由题意,设直线:1(2)PA y k x -=-,:1(2)PB y k x -=--,设点A11,)x y (,B 22,)x y (, 由2218221x y y kx k ⎧+=⎪⎨⎪=-+⎩得 22241)8(12)161640k x k k x k k ++-+--=(, …………8分 所以128(21)2+41k k x k -=+,所以21288241k k x k --=+,同理2228+8241k k x k -=+, 所以1221641k x x k -=-+, …………10分 由1121y kx k =-+,2221y kx k =-++, 有121228()441k y y k x x k k -=+-=-+, 因为A 在第四象限,所以0k ≠,且A 不在直线OP 上,所以121212AB y y k x x -==-, 又12OP k =,故AB OP k k =,所以直线AB 与直线OP 平行. …………13分22. (本题13分)解:(Ⅰ)由条件知A S ≤1,必有A ∈1,又n a a a <<<Λ21均为整数,11=a . ……2分A S ≤2,由A S 的定义及n a a a <<<Λ21均为整数,必有A ∈2,22=a .……………4分(Ⅱ)必要性:由“n a a a ,,,21Λ成等差数列”及11=a ,22=a得),,2,1(n i i a i Λ==此时},,3,2,1{n A Λ=满足题目要求 从而)1(21321+=++++=n n n S A Λ. ……………6分 充分性:由条件知,21n a a a <<<Λ且均为正整数,可得),,,3,2,1(n i i a i Λ=≥ 故)1(21321+=++++≥n n n S A Λ,当且仅当),,3,2,1(n i i a i Λ==时,上式等号成立. 于是当)1(21+=n n S A 时,),,3,2,1(n i i a i Λ==,从而n a a a ,,,21Λ成等差数列. 所以“n a a a ,,,21Λ成等差数列”的充要条件是“)1(21+=n n S A ”. ……8分 (Ⅲ)由于含有n 个元素的非空子集个数有12-n ,故当10=n 时,10231210=-, 此时A 的非空子集的元素之和最多表示1023个不同的整数m ,不符合要求. 而用11个元素的集合}1024,512,256,128,64,32,16,8,4,2,1{=A 的非空子集的元素之和可以表示2047,2046,,3,2,1Λ共2047个正整数.因此当2020=A S 时,n 的最小值为11. ……………10分 当2020=A S 时,n 的最小值为11.记102110a a a S +++=Λ则20201110=+a S 并且11101a S ≥+.事实上若11101a S <+,11111022020a a S <+=,则101011>a ,10101110<<a S , 所以1010=m 时无法用集合A 的非空子集的元素之和表示,与题意不符. 于是122020111110-≥+=a a S ,得2202111≤a ,*11N a ∈,所以101011≤a . 当101011=a 时}1010,499,256,128,64,32,16,8,4,2,1{=A 满足题意所以当2020=A S 时,n 的最小值为11,此时n a 的最大值1010. ……13分【若有不同解法,请酌情给分】。
北京市石景山区2019-2020学年第一学期期末高三数学试题及答案

北京市石景山区2020届第一学期高三期末数 学本试卷共5页,满分为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无效,考试结束后上交答题卡.第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合{}02A x x =≤≤,{}1,0,2,3B =-,则A B =A. {}0,1,2B. {}0,2C. {}1,3-D. {}1,0,1,2,3-2. 复数21iz =+的共轭复数在复平面内对应的点所在象限为 A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 下列函数中既是奇函数,又在区间01(,)上单调递减的是 A. 3()f x x = B. ()lg ||f x x = C. ()f x x =- D. ()cos f x x =4. 已知向量()5,m =a ,()2,2=-b ,若()-⊥a b b ,则实数m = A. 1-B. 1C. 2D. 2-5. 我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为 A. 134石B. 169石C. 338石D. 1365石6. 已知3log 4a =,πlog 3b =,c =a ,b ,c 的大小关系是A. a b c <<B. a c b <<C. b c a <<D. b a c <<7. 艺术体操比赛共有7位评委分别给出某选手的原始评分,评定该选手的成绩时,从7个原始评分中去掉1个最高分、1个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,不变的数字特征是 A. 中位数B. 平均数C. 方差D. 极差8. 一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与原正方体体积的比值为 A. 81B. 71C. 61D.519. 在等差数列{}n a 中,设,,,k l p r *∈N ,则k l p r +>+是k l p r a a a a +>+的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充要必要条件D. 既不充分也不必要条件10. 关于曲线:C 224x xy y ++=.给出下列三个结论:① 曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ② 曲线C上任意一点到原点的距离都不大于; ③ 曲线C 上任意一点到原点的距离都不小于2. 其中,正确结论的个数是 A.0B. 1C. 2D. 3第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分.11. 在62()x x-的二项展开式中,常数项等于__________.(用数字作答) 12. 已知双曲线标准方程为2213x y -=,则其焦点到渐近线的距离为 .13. 已知数列{}*()n a n n +∈N 为等比数列,11a =,22a =,则3a =________.14. 已知平面,,αβγ.给出下列三个论断:①αβ⊥;②αγ⊥;③β∥γ.以其中 的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:____. 15. 在ABC △中,角,,A B C 所对的边分别是,,a b c .已知14b ca , 2sin 3sin BC ,则cos A 的值为_______.16. 已知向量1e ,2e 是平面α内的一组基向量,O 为α内的定点,对于α内任意一点P ,当12OP xe ye =+时,则称有序实数对(,)x y 为点P 的广义坐标,若点A 、B 的广义坐标分别为11(,)x y 、22(,)x y ,对于下列命题:① 线段AB 的中点的广义坐标为1212(,)22x x y y ++; ② 向量OA 平行于向量OB 的充要条件是1221x y x y =;③ 向量OA 垂直于向量OB 的充要条件是12120x x y y +=. 其中,真命题是 .(请写出所有真命题的序号)三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 17. (本小题13分)已知函数1()cos (sin cos )2f x x x x =+-. (Ⅰ)若2π0<<α,且53sin =α,求()f α的值; (Ⅱ)求函数()f x 的最小正周期,及函数()f x 的单调递减区间.18.(本小题13分)一款小游戏的规则如下:每盘游戏都需抛掷骰子三次,出现一次或两次“6点”获得15分,出现三次“6点”获得120分,没有出现“6点”则扣除12分(即获得-12分). (Ⅰ)设每盘游戏中出现“6点”的次数为X ,求X 的分布列; (Ⅱ)玩两盘游戏,求两盘中至少有一盘获得15分的概率;(Ⅲ)玩过这款游戏的许多人发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析解释上述现象.19.(本小题14分)已知在四棱锥ABCD P -中,底面ABCD 是边长为4的正方形,PAD △是正三角形,CD ⊥平面PAD ,O G F E 、、、分别是AD BC PD PC 、、、 的中点.(Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求平面EFG 与平面ABCD 所成锐二面角的大小;(Ⅲ)线段PA 上是否存在点M ,使得直线GM与平面EFG 所成角为π6,若存在,求线段PM的长度;若不存在,说明理由.C20.(本小题14分)已知函数()e x f x ax =-.(a ∈R ) (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若3a =,()f x 的图象与y 轴交于点A ,求()y f x =在点A 处的切线方程; (Ⅲ)在(Ⅱ)的条件下,证明:当0x >时,2()31f x x x >-+恒成立.21. (本小题13分)已知椭圆222:12x y C a +=过点(2,1)P . (Ⅰ)求椭圆C 的方程,并求其离心率;(Ⅱ)过点P 作x 轴的垂线l ,设点A 为第四象限内一点且在椭圆C 上(点A 不在直线l上),直线PA 关于l 的对称直线PB 与椭圆交于另一点B .设O 为坐标原点,判断直线AB 与直线OP 的位置关系,并说明理由.22.(本小题13分)已知由*()n n ∈N 个正整数构成的集合1212{,,,}(,3)n n A a a a a a a n =<<<≥,记12A n S a a a =+++,对于任意不大于A S 的正整数m ,均存在集合A 的一个子集,使得该子集的所有元素之和等于m . (Ⅰ)求21,a a 的值;(Ⅱ)求证:“n a a a ,,,21 成等差数列”的充要条件是“2)1(+=n n S A ”; (Ⅲ)若2020=A S ,求n 的最小值,并指出n 取最小值时n a 的最大值.石景山区2020届第一学期高三期末数学试卷答案及评分参考一、选择题:本大题共10个小题,每小题4分,共40分.二、填空题:本大题共6个小题,每小题5分,共30分. 11.160-; 12.1; 13. 5;14.①③⇒② 或②③⇒①; 15. 14-; 16. ①② .三、解答题:本大题共6个小题,共80分.解答题应写出文字说明,证明过程或演算步骤.17.(本小题13分) 解:(Ⅰ)因为 20πα<<,且53sin =α, 所以 4cos 5α==. ……………2分 所以 ()434128131=555225250f α⎛⎫=+-=- ⎪⎝⎭. ……………5分 (Ⅱ)()()21cos sin cos 21cos sin cos 2-+⋅=-+=x x x x x x x f ……………8分 所以函数()x f 的最小正周期2ππ2T ==. ……………9分 由ππ3π2π22π+242k x k ,k +≤+≤∈Z , 解得π5πππ+88k x k ,k +≤≤∈Z . ……………11分 所以函数()x f 的单调递减区间π5πππ+88k ,k ,k ⎡⎤+∈⎢⎥⎣⎦Z . ……………13分 )42sin(22)2cos 2(sin 212122cos 12sin 21π+=+=-++=x x x x x )42sin(22)2cos 2(sin 212122cos 12sin 21π+=+=-++=x x x x x解:(Ⅰ)X 可能的取值为0,1,2,3. ……………1分每次抛掷骰子,出现“6点”的概率为16p =. 0331125(0)(1)6216P X C ==-=, 1231175(1)(1)66216P X C ==⋅-=, 2231115(2)()(1)66216P X C ==⋅-=,33311(3)()6216P X C ===, ……………5分所以X 的分布列为:……………6分(Ⅱ)设“第i 盘游戏获得15分”为事件A i (i =1,2),则12905()()(1)(2)21612P A P A P X P X ===+===. ……………8分 所以“两盘游戏中至少有一次获得15分”的概率为12951()()144P A P A -= 因此,玩两盘游戏至少有一次获得15分的概率为95144. ……………10分 (Ⅲ)设每盘游戏得分为Y .由(Ⅰ)知,的分布列为:Y 的数学期望为12551512151202161221636EY =-⨯+⨯+⨯=-. ……12分 这表明,获得分数Y 的期望为负.因此,多次游戏之后分数减少的可能性更大. ……………13分(Ⅰ)证明:因为△PAD 是正三角形,O 是AD 的中点,所以 ⊥PO AD . 又因为⊥CD 平面PAD ,⊂PO 平面PAD ,所以⊥PO CD . D CD AD =⋂,⊂CD AD ,平面ABCD ,所以⊥PO 面ABCD . ……………4分 (Ⅱ)如图,以O 点为原点分别以OA 、OG 、OP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系.则)32,0,0(),0,4,0(),0,0,2(),0,4,2(),0,4,2(),0,0,2(),0,0,0(P G D C B A O --,)3,0,1(),3,2,1(--F E ,)3,2,1(),0,2,0(-=-=EG EF ,设平面EFG 的法向量为),,,(z y x m =⎪⎩⎪⎨⎧=-+=-,032,02z y x y令1=z ,则 )10,3(,=m ,又平面ABCD 的法向量)1,0,0(=n ,设平面EFG 与平面ABCD 所成锐二面角为θ所以21||||cos ==n m n m θ. 所以平面EFG 与平面ABCD 所成锐二面角为3π. ……………9分(Ⅲ)假设线段PA 上存在点M ,使得直线GM 与平面EFG 所成角为π6, 设]1,0[,∈=λλPA PM ,PA GP PM GP GM λ+=+=,所以))1(32,4,2(λλ--=GM . ……………11分所以76423,cos |6πsin2+->=<=λλm GM , …………13分整理得02322=+-λλ,无解,所以,不存在这样的点M . ………14分20.(本小题14分)解:(Ⅰ)()xf x e a '=-, (1)分当0a ≤时,()0f x '≥恒成立,所以()f x 在R 上单调递增, ……………3分 当0a >时,令()0f x '=,解得ln x a =. 当x 变化时,(),()f x f x '的变化情况如下表:所以0a >时,()f x 在(,ln )a -∞上单调递减,在(ln ,)a +∞上单调递增. …5分 (Ⅱ)令0x =,得1y =,则()0,1A , …………6分因为()e 3x f x '=-,所以()0132f '=-=-, …………7分 所以在A 点处的切线方程为12(0)y x -=--,即21y x =-+. ………9分 (Ⅲ)证明:令()22()(3+1)=e 1x g x f x x x x =----,则()e 2x g x x '=-.令()e 2x h x x =-,则()e 2x h x '=-, 当0ln2x <<时,()0h x '<,()h x 单调递减,当ln2x >时,()0h x '>,()h x 单调递增; …………11分 所以()()ln2ln2e 2ln222ln20h x h ≥=-=->,即()0g x '>恒成立.所以()g x 在(),-∞+∞上单调递增,所以()()01010g x g >=--=,………13分所以2e 10x x -->,即当0x >时,()231f x x x >-+恒成立. …………14分21.(本小题13分)解:(Ⅰ)由椭圆222:12x y C a +=过点(2,1)P ,可得24112a +=,解得28a =. …………2分 所以222826c ab =-=-=, …………3分所以椭圆C 的方程为22182x y +=,离心率e ==. …………5分(Ⅱ)直线AB 与直线OP 平行. …………6分证明如下:由题意,设直线:1(2)PA y k x -=-,:1(2)PB y k x -=--,设点A11,)x y (,B 22,)x y (, 由2218221x y y kx k ⎧+=⎪⎨⎪=-+⎩得 22241)8(12)161640k x k k x k k ++-+--=(, …………8分所以128(21)2+41k k x k -=+,所以21288241k k x k --=+,同理2228+8241k k x k -=+, 所以1221641kx x k -=-+, …………10分由1121y kx k =-+,2221y kx k =-++, 有121228()441ky y k x x k k -=+-=-+,因为A 在第四象限,所以0k ≠,且A 不在直线OP 上,所以121212AB y y k x x -==-,又12OP k =,故AB OP k k =,所以直线AB 与直线OP 平行. …………13分22. (本题13分)解:(Ⅰ)由条件知A S ≤1,必有A ∈1,又n a a a <<< 21均为整数,11=a . ……2分A S ≤2,由A S 的定义及n a a a <<< 21均为整数,必有A ∈2,22=a .……………4分(Ⅱ)必要性:由“n a a a ,,,21 成等差数列”及11=a ,22=a得),,2,1(n i i a i ==此时},,3,2,1{n A =满足题目要求 从而)1(21321+=++++=n n n S A . ……………6分 充分性:由条件知,21n a a a <<< 且均为正整数,可得),,,3,2,1(n i i a i =≥ 故)1(21321+=++++≥n n n S A ,当且仅当),,3,2,1(n i i a i ==时,上式等号成立. 于是当)1(21+=n n S A 时,),,3,2,1(n i i a i ==,从而n a a a ,,,21 成等差数列. 所以“n a a a ,,,21 成等差数列”的充要条件是“)1(21+=n n S A ”. ……8分 (Ⅲ)由于含有n 个元素的非空子集个数有12-n ,故当10=n 时,10231210=-, 此时A 的非空子集的元素之和最多表示1023个不同的整数m ,不符合要求. 而用11个元素的集合}1024,512,256,128,64,32,16,8,4,2,1{=A 的非空子集的元素之和可以表示2047,2046,,3,2,1 共2047个正整数.因此当2020=A S 时,n 的最小值为11. ……………10分 当2020=A S 时,n 的最小值为11.记102110a a a S +++=则20201110=+a S 并且11101a S ≥+.事实上若11101a S <+,11111022020a a S <+=,则101011>a ,10101110<<a S , 所以1010=m 时无法用集合A 的非空子集的元素之和表示,与题意不符. 于是122020111110-≥+=a a S ,得2202111≤a ,*11N a ∈,所以101011≤a .当101011=a 时}1010,499,256,128,64,32,16,8,4,2,1{=A 满足题意 所以当2020=A S 时,n 的最小值为11,此时n a 的最大值1010. ……13分【若有不同解法,请酌情给分】。
2020届北京市石景山区高三上学期期末考试数学试题(含答案)

石景山区2020届高三第一学期期末考试试题数学本试卷共5页,满分为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无 效,考试结束后上交答题卡.第一部分(选择题共40分)、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项 已知集合 A x0WxW2,B 1,0,2,3 ,则 AI B复数z 上-的共轲复数在复平面内对应的点所在象限为 1 i卜列函数中既是奇函数,又在区间 (0,1)上单调递减的是夹谷约为7 .艺术体操比赛共有7位评委分别给出某选手的原始评分,评定该选手的成绩时,从7个原始评分中去掉1个最高分、1个最低分,得到5个有效评分.5个有效 评分与7个原始评分相比,不变的数字特征是 A.中位数B.平均数C.方差D.极差8 . 一个正方体被一个平面截去一部分后,A. 0,1,2B. 0,2C. 1,3D. 1,0,1,2,31.2.A.第一象限B.第二象限C.第三象限D. 第四象限4.5.一3A. f(x) xB. f(x) lg|x|C. f (x) xD. f(x) cosx已知向量a 5, m , b 2, 2 ,若a A. 1B. 1C.D.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮, 有人送来米 1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷 28粒,则这批米内3.6.A. 134 石B. 169石C. 338石D. 1365 石已知 a log 3 4 , b log 3c 的大小关系是A. a b cB. a cC.D. b a c42一 ... ............. ............ . 」 1 在△ ABC 中,角A,B,C 所对的边分别是a,b,c.已知b- c= — a,剩余部分的三视图如右图,则截去部分 体积与原正方体体积的比值为 A. B.C. D.9.在等差数列{a n }中,设k,l, p,r N ,则kA.充分而不必要条件B.C.充要必要条件D. l p r 是 a k a l a p a 「的必要而不充分条件 既不充分也不必要条件10.关于曲线C : x 2 xy y 2 4 .给出下列三个结论:① 曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ② 曲线C 上任意一点到原点的距离都不大于 ③曲线C 上任意一点到原点的距离都不小于 2.其中,正确结论的个数是 A. 0B. 1C.D. 3二、填空题共 11.在(X 12.13. 14.第二部分(非选择题共6小题,每小题5分,共30分. 2、6八 । ……-)的二项展开式中,常数项等于x110 分)2x 2已知双曲线标准万程为 一 y 2 1 ,则其焦点到渐近线的距离为3一,.、“一, , …*、已知数列a n n (n N )为等比数歹U, 已知平面,.给出下列三个论断:①a 1.以其中的两个论断作为条件,余下的一个论断作为结论, 写出一个正确的命题: 15.2sinB = 3sinC ,则 cosA 的值为16 .已知向量er, e 2是平面内的一组基向量,。
2019-2020年北京市石景山区高三上学期期末数学

石景山区2019—2020学年第一学期高三期末试卷数 学本试卷共5页,满分为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无效,考试结束后上交答题卡.第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合{}02A x x =≤≤,{}1,0,2,3B =-,则A B =A. {}0,1,2B. {}0,2C. {}1,3-D. {}1,0,1,2,3-2. 复数21iz =+的共轭复数在复平面内对应的点所在象限为 A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 下列函数中既是奇函数,又在区间01(,)上单调递减的是 A. 3()f x x = B. ()lg ||f x x = C. ()f x x =- D. ()cos f x x =4. 已知向量()5,m =a ,()2,2=-b ,若()-⊥a b b ,则实数m = A. 1-B. 1C. 2D. 2-5. 我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为 A. 134石B. 169石C. 338石D. 1365石6. 已知3log 4a =,πlog 3b =,c =a ,b ,c 的大小关系是A. a b c <<B. a c b <<C. b c a <<D. b a c <<7. 艺术体操比赛共有7位评委分别给出某选手的原始评分,评定该选手的成绩时,从7个原始评分中去掉1个最高分、1个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,不变的数字特征是 A. 中位数B. 平均数C. 方差D. 极差8. 一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与原正方体体积的比值为 A. 81B. 71C. 61D.519. 在等差数列{}n a 中,设,,,k l p r *∈N ,则k l p r +>+是k l p r a a a a +>+的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充要必要条件D. 既不充分也不必要条件10. 关于曲线:C 224x xy y ++=.给出下列三个结论:① 曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ② 曲线C上任意一点到原点的距离都不大于; ③ 曲线C 上任意一点到原点的距离都不小于2. 其中,正确结论的个数是 A.0B. 1C. 2D. 3第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分.11. 在62()x x-的二项展开式中,常数项等于__________.(用数字作答) 12. 已知双曲线标准方程为2213x y -=,则其焦点到渐近线的距离为 .13. 已知数列{}*()n a n n +∈N 为等比数列,11a =,22a =,则3a =________.14. 已知平面,,αβγ.给出下列三个论断:①αβ⊥;②αγ⊥;③β∥γ.以其中 的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:____. 15. 在ABC △中,角,,A B C 所对的边分别是,,a b c .已知14b c a -=, 2sin 3sin B C =,则cos A 的值为_______.16. 已知向量1e ,2e 是平面α内的一组基向量,O 为α内的定点,对于α内任意一点P ,当12OP xe ye =+时,则称有序实数对(,)x y 为点P 的广义坐标,若点A 、B 的广义坐标分别为11(,)x y 、22(,)x y ,对于下列命题:① 线段AB 的中点的广义坐标为1212(,)22x x y y ++; ② 向量OA 平行于向量OB 的充要条件是1221x y x y =;③ 向量OA 垂直于向量OB 的充要条件是12120x x y y +=. 其中,真命题是 .(请写出所有真命题的序号)三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 17. (本小题13分)已知函数1()cos (sin cos )2f x x x x =+-. (Ⅰ)若2π0<<α,且53sin =α,求()f α的值; (Ⅱ)求函数()f x 的最小正周期,及函数()f x 的单调递减区间.18.(本小题13分)一款小游戏的规则如下:每盘游戏都需抛掷骰子三次,出现一次或两次“6点”获得15分,出现三次“6点”获得120分,没有出现“6点”则扣除12分(即获得-12分). (Ⅰ)设每盘游戏中出现“6点”的次数为X ,求X 的分布列; (Ⅱ)玩两盘游戏,求两盘中至少有一盘获得15分的概率;(Ⅲ)玩过这款游戏的许多人发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析解释上述现象.19.(本小题14分)已知在四棱锥ABCD P -中,底面ABCD 是边长为4的正方形,PAD △是正三角形,CD ⊥平面PAD ,O G F E 、、、分别是AD BC PD PC 、、、 的中点.(Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求平面EFG 与平面ABCD 所成锐二面角的大小;(Ⅲ)线段PA 上是否存在点M ,使得直线GM与平面EFG 所成角为π6,若存在,求线段PM的长度;若不存在,说明理由.C20.(本小题14分)已知函数()e x f x ax =-.(a ∈R ) (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若3a =,()f x 的图象与y 轴交于点A ,求()y f x =在点A 处的切线方程; (Ⅲ)在(Ⅱ)的条件下,证明:当0x >时,2()31f x x x >-+恒成立.21. (本小题13分)已知椭圆222:12x y C a +=过点(2,1)P . (Ⅰ)求椭圆C 的方程,并求其离心率;(Ⅱ)过点P 作x 轴的垂线l ,设点A 为第四象限内一点且在椭圆C 上(点A 不在直线l上),直线PA 关于l 的对称直线PB 与椭圆交于另一点B .设O 为坐标原点,判断直线AB 与直线OP 的位置关系,并说明理由.22.(本小题13分)已知由*()n n ∈N 个正整数构成的集合1212{,,,}(,3)n n A a a a a a a n =<<<≥,记12A n S a a a =+++,对于任意不大于A S 的正整数m ,均存在集合A 的一个子集,使得该子集的所有元素之和等于m . (Ⅰ)求21,a a 的值;(Ⅱ)求证:“n a a a ,,,21 成等差数列”的充要条件是“2)1(+=n n S A ”; (Ⅲ)若2020=A S ,求n 的最小值,并指出n 取最小值时n a 的最大值.。
北京市石景山区普通高中2020届高三毕业班上学期期末考试数学答案

解得 ,符合题意,
所以当 为线段 中点时,直线 与平面 所成角的大小为 .
………………14分
18.(本小题13分)
解:(Ⅰ)由题可知, 的所有可能取值为 , , .
; ; .
所以 的分布列为
………………6分
(Ⅱ)由(Ⅰ)知, .
若小明先回答 问题,记 为小明的累计得分,则 的所有可能取值为 , , .
选条件②: .
(Ⅰ)
,
所以 最小正周期是 .………………7分
(Ⅱ)因为 ,
所以 ≤ ≤ ,
所以 ≤ ≤ ,
当 ,即 时, 有最小值 .………………13分
17.(本小题14分)
解:(Ⅰ)因为四棱锥 中, ,
所以 ,
因为 , ,
所以 .………………4分
(Ⅱ)因为 , ,所以 ,
又因为 ,所以 ,
因为 , ,
14. (答案不唯一);15.①③.
三、解答题:本大题共6个小题,共80分.解答题应写出文字说明,证明过程或演算步骤.
16.(本小题13分)
解:选条件①: ;
(Ⅰ)
,
所以 的最小正周期是 .………………7分
(Ⅱ)因为 ,
所以 ≤ ≤ ,
所以 ≤ ≤ ,
所以 ≤ ≤ ,
当 ,即 时, 有最小值 .……………13分
因为 , 为正实数,且 所以 ≥ ,故 ≥ ,
则数列 从 开始以后的各项为 ,
当 ≥ 时 , 与 为“趋势递减数列”矛盾,故假设不成立, 的项中没有 .
再证明充分性:
得 ,
因为 的项中没有 ,所以对于任意正整数 , ,于是 ,
所以 .
当 时, ,
当 时, ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
石景山区2020届第一学期高三期末数 学本试卷共5页,满分为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无效,考试结束后上交答题卡.第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合{}02A x x =≤≤,{}1,0,2,3B =-,则A B =A. {}0,1,2B. {}0,2C. {}1,3-D. {}1,0,1,2,3-2. 复数21iz =+的共轭复数在复平面内对应的点所在象限为 A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 下列函数中既是奇函数,又在区间01(,)上单调递减的是 A. 3()f x x = B. ()lg ||f x x = C. ()f x x =- D. ()cos f x x =4. 已知向量()5,m =a ,()2,2=-b ,若()-⊥a b b ,则实数m = A. 1-B. 1C. 2D. 2-5. 我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为 A. 134石B. 169石C. 338石D. 1365石6. 已知3log 4a =,πlog 3b =,c =a ,b ,c 的大小关系是A. a b c <<B. a c b <<C. b c a <<D. b a c <<7. 艺术体操比赛共有7位评委分别给出某选手的原始评分,评定该选手的成绩时,从7个原始评分中去掉1个最高分、1个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,不变的数字特征是 A. 中位数B. 平均数C. 方差D. 极差8. 一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与原正方体体积的比值为 A. 81B. 71C. 61D.519. 在等差数列{}n a 中,设,,,k l p r *∈N ,则k l p r +>+是k l p r a a a a +>+的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充要必要条件D. 既不充分也不必要条件10. 关于曲线:C 224x xy y ++=.给出下列三个结论:① 曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ② 曲线C上任意一点到原点的距离都不大于; ③ 曲线C 上任意一点到原点的距离都不小于2. 其中,正确结论的个数是 A.0B. 1C. 2D. 3第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分.11. 在62()x x-的二项展开式中,常数项等于__________.(用数字作答) 12. 已知双曲线标准方程为2213x y -=,则其焦点到渐近线的距离为 .13. 已知数列{}*()n a n n +∈N 为等比数列,11a =,22a =,则3a =________.14. 已知平面,,αβγ.给出下列三个论断:①αβ⊥;②αγ⊥;③β∥γ.以其中 的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:____. 15. 在ABC △中,角,,A B C 所对的边分别是,,a b c .已知14b c a -=, 2sin 3sin B C =,则cos A 的值为_______.16. 已知向量1e ,2e 是平面α内的一组基向量,O 为α内的定点,对于α内任意一点P ,当12OP xe ye =+时,则称有序实数对(,)x y 为点P 的广义坐标,若点A 、B 的广义坐标分别为11(,)x y 、22(,)x y ,对于下列命题:① 线段AB 的中点的广义坐标为1212(,)22x x y y ++; ② 向量OA 平行于向量OB 的充要条件是1221x y x y =;③ 向量OA 垂直于向量OB 的充要条件是12120x x y y +=. 其中,真命题是 .(请写出所有真命题的序号)三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 17. (本小题13分)已知函数1()cos (sin cos )2f x x x x =+-. (Ⅰ)若2π0<<α,且53sin =α,求()f α的值; (Ⅱ)求函数()f x 的最小正周期,及函数()f x 的单调递减区间.18.(本小题13分)一款小游戏的规则如下:每盘游戏都需抛掷骰子三次,出现一次或两次“6点”获得15分,出现三次“6点”获得120分,没有出现“6点”则扣除12分(即获得-12分). (Ⅰ)设每盘游戏中出现“6点”的次数为X ,求X 的分布列; (Ⅱ)玩两盘游戏,求两盘中至少有一盘获得15分的概率;(Ⅲ)玩过这款游戏的许多人发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析解释上述现象.19.(本小题14分)已知在四棱锥ABCD P -中,底面ABCD 是边长为4的正方形,PAD △是正三角形,CD ⊥平面PAD ,O G F E 、、、分别是AD BC PD PC 、、、 的中点.(Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求平面EFG 与平面ABCD 所成锐二面角的大小;(Ⅲ)线段PA 上是否存在点M ,使得直线GM与平面EFG 所成角为π6,若存在,求线段PM的长度;若不存在,说明理由.C20.(本小题14分)已知函数()e x f x ax =-.(a ∈R ) (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若3a =,()f x 的图象与y 轴交于点A ,求()y f x =在点A 处的切线方程; (Ⅲ)在(Ⅱ)的条件下,证明:当0x >时,2()31f x x x >-+恒成立.21. (本小题13分)已知椭圆222:12x y C a +=过点(2,1)P . (Ⅰ)求椭圆C 的方程,并求其离心率;(Ⅱ)过点P 作x 轴的垂线l ,设点A 为第四象限内一点且在椭圆C 上(点A 不在直线l上),直线PA 关于l 的对称直线PB 与椭圆交于另一点B .设O 为坐标原点,判断直线AB 与直线OP 的位置关系,并说明理由.22.(本小题13分)已知由*()n n ∈N 个正整数构成的集合1212{,,,}(,3)n n A a a a a a a n =<<<≥,记12A n S a a a =+++,对于任意不大于A S 的正整数m ,均存在集合A 的一个子集,使得该子集的所有元素之和等于m . (Ⅰ)求21,a a 的值;(Ⅱ)求证:“n a a a ,,,21 成等差数列”的充要条件是“2)1(+=n n S A ”; (Ⅲ)若2020=A S ,求n 的最小值,并指出n 取最小值时n a 的最大值.石景山区2020届第一学期高三期末数学试卷答案及评分参考一、选择题:本大题共10个小题,每小题4分,共40分.二、填空题:本大题共6个小题,每小题5分,共30分. 11.160-; 12.1; 13. 5;14.①③⇒② 或②③⇒①; 15. 14-; 16. ①② .三、解答题:本大题共6个小题,共80分.解答题应写出文字说明,证明过程或演算步骤.17.(本小题13分) 解:(Ⅰ)因为 20πα<<,且53sin =α, 所以 4cos 5α==. ……………2分 所以 ()434128131=555225250f α⎛⎫=+-=- ⎪⎝⎭. ……………5分 (Ⅱ)()()21cos sin cos 21cos sin cos 2-+⋅=-+=x x x x x x x f ……………8分 所以函数()x f 的最小正周期2ππ2T ==. ……………9分 由ππ3π2π22π+242k x k ,k +≤+≤∈Z , 解得π5πππ+88k x k ,k +≤≤∈Z . ……………11分 所以函数()x f 的单调递减区间π5πππ+88k ,k ,k ⎡⎤+∈⎢⎥⎣⎦Z . ……………13分 )42sin(22)2cos 2(sin 212122cos 12sin 21π+=+=-++=x x x x x )42sin(22)2cos 2(sin 212122cos 12sin 21π+=+=-++=x x x x x解:(Ⅰ)X 可能的取值为0,1,2,3. ……………1分每次抛掷骰子,出现“6点”的概率为16p =. 0331125(0)(1)6216P X C ==-=, 1231175(1)(1)66216P X C ==⋅-=, 2231115(2)()(1)66216P X C ==⋅-=,33311(3)()6216P X C ===,……………5分所以X 的分布列为:……………6分(Ⅱ)设“第i 盘游戏获得15分”为事件A i (i =1,2),则12905()()(1)(2)21612P A P A P X P X ===+===. ……………8分 所以“两盘游戏中至少有一次获得15分”的概率为12951()()144P A P A -= 因此,玩两盘游戏至少有一次获得15分的概率为95144. ……………10分 (Ⅲ)设每盘游戏得分为Y .由(ⅠY 的数学期望为12551512151202161221636EY =-⨯+⨯+⨯=-. ……12分 这表明,获得分数Y 的期望为负.因此,多次游戏之后分数减少的可能性更大. ……………13分(Ⅰ)证明:因为△PAD 是正三角形,O 是AD 的中点,所以 ⊥PO AD . 又因为⊥CD 平面PAD ,⊂PO 平面PAD ,所以⊥PO CD . D CD AD =⋂,⊂CD AD ,平面ABCD ,所以⊥PO 面ABCD . ……………4分 (Ⅱ)如图,以O 点为原点分别以OA 、OG 、OP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系.则)32,0,0(),0,4,0(),0,0,2(),0,4,2(),0,4,2(),0,0,2(),0,0,0(P G D C B A O --,)3,0,1(),3,2,1(--F E ,)3,2,1(),0,2,0(-=-=,设平面EFG 的法向量为),,,(z y x m =⎪⎩⎪⎨⎧=-+=-,032,02z y x y令1=z ,则 )10,3(,=,又平面ABCD 的法向量)1,0,0(=n ,设平面EFG 与平面ABCD 所成锐二面角为θ所以21||||cos ==n m θ. 所以平面EFG 与平面ABCD 所成锐二面角为3π. ……………9分(Ⅲ)假设线段PA 上存在点M ,使得直线GM 与平面EFG 所成角为π6, 设]1,0[,∈=λλPM ,PA GP PM GP GM λ+=+=,所以))1(32,4,2(λλ--=. ……………11分所以76423,cos |6πsin2+->=<=λλ, …………13分整理得02322=+-λλ,无解,所以,不存在这样的点M . ………14分20.(本小题14分)解:(Ⅰ)()xf x e a '=-, (1)分当0a ≤时,()0f x '≥恒成立,所以()f x 在R 上单调递增, ……………3分 当0a >时,令()0f x '=,解得ln x a =. 当x 变化时,(),()f x f x '的变化情况如下表:所以0a >时,()f x 在(,ln )a -∞上单调递减,在(ln ,)a +∞上单调递增. …5分 (Ⅱ)令0x =,得1y =,则()0,1A , …………6分因为()e 3x f x '=-,所以()0132f '=-=-, …………7分 所以在A 点处的切线方程为12(0)y x -=--,即21y x =-+. ………9分 (Ⅲ)证明:令()22()(3+1)=e 1x g x f x x x x =----,则()e 2x g x x '=-.令()e 2x h x x =-,则()e 2x h x '=-, 当0ln2x <<时,()0h x '<,()h x 单调递减,当ln2x >时,()0h x '>,()h x 单调递增; …………11分 所以()()ln2ln2e 2ln222ln20h x h ≥=-=->,即()0g x '>恒成立.所以()g x 在(),-∞+∞上单调递增,所以()()01010g x g >=--=,………13分所以2e 10x x -->,即当0x >时,()231f x x x >-+恒成立. …………14分21.(本小题13分)解:(Ⅰ)由椭圆222:12x y C a +=过点(2,1)P ,可得24112a +=,解得28a =. …………2分 所以222826c ab =-=-=, …………3分所以椭圆C 的方程为22182x y +=,离心率e ==. …………5分(Ⅱ)直线AB 与直线OP 平行. …………6分证明如下:由题意,设直线:1(2)PA y k x -=-,:1(2)PB y k x -=--,设点A11,)x y (,B 22,)x y (, 由2218221x y y kx k ⎧+=⎪⎨⎪=-+⎩得 22241)8(12)161640k x k k x k k ++-+--=(, …………8分所以128(21)2+41k k x k -=+,所以21288241k k x k --=+,同理2228+8241k k x k -=+, 所以1221641kx x k -=-+, …………10分由1121y kx k =-+,2221y kx k =-++, 有121228()441ky y k x x k k -=+-=-+,因为A 在第四象限,所以0k ≠,且A 不在直线OP 上,所以121212AB y y k x x -==-,又12OP k =,故A B O P k k =,所以直线AB 与直线OP 平行. …………13分22. (本题13分)解:(Ⅰ)由条件知A S ≤1,必有A ∈1,又n a a a <<< 21均为整数,11=a . ……2分A S ≤2,由A S 的定义及n a a a <<< 21均为整数,必有A ∈2,22=a .……………4分(Ⅱ)必要性:由“n a a a ,,,21 成等差数列”及11=a ,22=a得),,2,1(n i i a i ==此时},,3,2,1{n A =满足题目要求 从而)1(21321+=++++=n n n S A . ……………6分 充分性:由条件知,21n a a a <<< 且均为正整数,可得),,,3,2,1(n i i a i =≥ 故)1(21321+=++++≥n n n S A ,当且仅当),,3,2,1(n i i a i ==时,上式等号成立. 于是当)1(21+=n n S A 时,),,3,2,1(n i i a i ==,从而n a a a ,,,21 成等差数列. 所以“n a a a ,,,21 成等差数列”的充要条件是“)1(21+=n n S A ”. ……8分 (Ⅲ)由于含有n 个元素的非空子集个数有12-n ,故当10=n 时,10231210=-, 此时A 的非空子集的元素之和最多表示1023个不同的整数m ,不符合要求. 而用11个元素的集合}1024,512,256,128,64,32,16,8,4,2,1{=A 的非空子集的元素之和可以表示2047,2046,,3,2,1 共2047个正整数.因此当2020=A S 时,n 的最小值为11. ……………10分 当2020=A S 时,n 的最小值为11.记102110a a a S +++=则20201110=+a S 并且11101a S ≥+.事实上若11101a S <+,11111022020a a S <+=,则1011>a ,10101110<<a S , 所以1010=m 时无法用集合A 的非空子集的元素之和表示,与题意不符. 于是122020111110-≥+=a a S ,得2202111≤a ,*11N a ∈,所以101011≤a .当101011=a 时}1010,499,256,128,64,32,16,8,4,2,1{=A 满足题意 所以当2020=A S 时,n 的最小值为11,此时n a 的最大值1010. ……13分【若有不同解法,请酌情给分】。
