2018—2019上学期创新班入学考试数学试卷
精选2018-2019学年高二数学上学期入学考试试题(扫描版)
又平面 平面 ，平面 平面 ， 平面
平面 ， 为三棱柱 的高
为等边三角形， ，所以
，
12分
21．（I） ；（II） .
详解：（I）由已知
因为 经过点 ，所以 ， 解得 .6分
（II）由（I）知 ，因为 ，所以 ，
当 ，即 时， ，
因为 恒成立，即 ，所以
因此的取值范围为： 12分
22．（I） ；（II）不存在直线
所以该函数的对称轴是
因此 ，解得
所以的取值范围是 5分
（II）因为 恒成立，
所以 ，整理得
解得 ,
因此的取值范围是 .10分
18．（I） ， ；（II） .
详解：（I）设 的公差为，则由已知得
即 ，解得： 或 （舍）
所以
因为 ，所以 的公比
所以 6分
（II）由（I）可知
所以 ①
②
-②式得：
所以 12分
解:（I）由已知，线段 的中点 ，
故线段 的中垂线方程为： ，即
因为圆经过 两点，故圆心在线段 的中垂线上
又因为直线： 平分圆，所以直线经过圆心
由 ，解得 ，即圆心的坐标为
而圆的半径
所以圆的方程为：6分
（II）设 ，
将 代入方程 ，得：
即 ①
由 ，得
所以 ， .
又因为
所以
即 ，解得 或
此时①式中 ，没有实根，直线与交于 两点相矛盾，
贵州省凯里市第一中学2018-2019学年高二数学上学期入学考试试题（扫描版）
凯里一中2020届高二上入学考试参考答案
数学
1、选择题（每小题5分，共60分）
题号
1
2
2019年试验初中创新班招生考试数学试卷及答案
2019年试验初中创新班招生考试试卷（数学）一、选择题（每小题1分，共5分）1．甲数比乙数少25％，甲数比乙数的最简整数比是（）A、1：4B、4：1C、3：4D、4：32．把底面积是18平方厘米，高是2厘米的圆柱形零件削成最大的圆锥，削成的面积是（）立方厘米。
A、12B、18C、24D、363．一列数1，2，2，3，3，3，4，4，4，4，……中的第34个数为（）A 、6 B、7 C、8 D、94．一件衣服打“七五折”出售，售价600元，这件西服原价是（）元A、150B、450C、800D、24005、如图，一个三角形的三个顶点分别为三个半径为3厘米的圆的圆心，则图中阴影部分的面积是（）A、π平方厘米B、9π平方厘米C、4.5π平方厘米D、3π平方厘米二、填空题（每题2分，共20分）1. ＝15÷（）＝七五折2．甲数的等于乙数的，乙数比甲数小（）。
3. 停车场有四轮车和两轮摩托车共13辆，轮子共有36个，摩托车共有（）辆。
4. 在101克水中放进4克盐，然后义加进20克浓度5％的盐水，搅匀后盐水浓度为（）％。
5．学校运来两捆苗，共240棵，准备分给四、五、六年级植树，六年载总棵树的，四五年级载的棵数比是3：4，四年级应栽树（）棵。
6. 做一个圆柱形的笔筒，底面半径是4厘米，高是10厘米，做这个笔简至少需要（）平方米的铁皮（保留整数）。
7. 将一个绳子对折后在对折，然后在对折一次，最后从对折的中间剪断，绳子被剪成（）段。
8．甲乙二人完成同样的工作，甲耗的时间是乙的8P则甲的工效比乙的工效高（）％9．一张等腰三角形纸片，底和高的比是8：3，把它沿底边上的高剪开，可以拼成一个长方形，拼成的长方形的周长是28厘米，原来三角形面积（）平方厘米。
10．一根长方体的木料，正好可以截成两个同样的正方体，这是表面积增加了24平方厘米，这根长方体原来的表面积是（）平方厘米。
三．判断题（每题1分，共5分）1．圆的周长一定，圆的直径和圆周率成反比。
18—19学年上学期七年级开学考试数学试题(附答案)
七年级数学入学考试试题考试时间：60分钟，试卷满分100分一、选择题（共30分，每题3分） 1、把98的分子上加32，要使分数的大小不变，分母应该加上（ ） A ．27B ．36C ．32D ．452、一张长方形纸长12厘米，宽8厘米，在这张长方形的纸中剪一个最大的圆，这个圆的面积是（ ）平方厘米． A ．113.04B ．50.24C ．96D ．45.763、某商品按原来的8折出售，仍可获利10%，此商品的原价是2200元，此商品的进货价是（ ）A ．1584元B ．1540元C ．1600元D ．1760元5、一种代号为Hc 的细菌在培养过程中，每半小时分裂一次（由一个分裂成两个）。
若这种细菌由1个分裂成16个，这个过程要经过（ ）。
A ．1小时 B.2小时 C.3小时 D.4小时 6、一个三角形，三个内角度数的比为2︰5︰3，则此三角形为（ ） （A ）锐角三角形 （B ）直角三角形 (C)锐角三角形 (D) 无法确定 7、一个长方形长5厘米，宽3厘米，535 表示（ ）几分之几。
A ．长比宽多 B ．长比宽少 C ．宽比长少 D ．宽比长多 8、一个分数的分子缩小3倍，分母扩大3倍，分数值就缩小（ ）倍。
A.3 B.6 C.9 D.不变9、把一个平行四边形任意分割成两个梯形，这两个梯形，这两个梯形中（ ） 总是相等。
A ．高 B.上下两底的和 C.周长 D. 面积10、两根同样长的绳子，第一根剪去35，第二根剪去35米，剩下的绳子相比（）（A）第一根长（B）第二根长(C)同样长(D) 三种情况都有可能二、填空：（共40分每空2分）1、种50棵果树，其中有2棵没有成活，成活率是( )﹪；2、344时=（）时（）分；3、爸爸今年a岁，洋洋比爸爸小b岁，爷爷比洋洋大c岁爷．爷今年( )岁；4、a=2×3×5,b=2×3×7,a和b的最大公约数是( )，最小公倍数是( )；5、某班六年级男生人数是女生人数的911，则这个班女生人数占全班人数的( ) ；6、一件衣服降价50元后，售200元，降价前是( ) 元，降幅（）﹪；7、一本故事书共135页，第一天和第二天共看了全书的25，若第三天接着看，应从第( )页看起；8、70305880改写成用“万”作单位的数是（），省略万位后面的尾数约是（）。
2018年衡阳县创新实验班招生数学试卷及答案
2018年衡阳县创新实验班招生数学试卷及答案满分:120分 时量:100分钟姓名：___________准考证号：____________________一、选择题（本大题共6道小题，每题5分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的.）1、在平面直角坐标系中，若一点的横坐标与纵坐标互为相反数，则该点一定不在A .直线x y =上B .抛物线2x y =上C .直线x y -=上D .双曲线1=xy 上2、若01<<-a ，将aa a a 1,,,33这四个数按从小到大的顺序排列，则从左数起第2个数应为a A . 3.a B 3.a C aD 1.3、如图是一个无盖正方体盒子的表面展开图，A ，B ，C 为图上三点，则在正方体盒子中，∠ABC 的度数为 A. 150°B ．120°C ．90°D ．60°4、已知b a ,是一元二次方程0732=-+x x 的两个根，则=-+b a a 2210.A 11.B 12.C 13.D 5、若一直角三角形的斜边长为c ，内切圆半径是r ，则内切圆的面积与三角形面积之比是rc r A 2.+πrc r B +π.rc r C +2.π22.r c rD +π6、反比例函数)0(>=x xky 的图象过面积等于1的长方形OABC 的顶点B ，P 为函数图象上任意一点，则OP 的最小值为1.A2.B3.C 2.D二、填空题（本大题共7道小题，每题5分，满分35分） 7、化简144)2(|2|22+---+-x x x x 所得的结果为__________.8、同时抛掷两枚质地均匀的色子，（色子为六个面分别标有1，2，3，4，5，6点的正方体），朝上的两个面的点数之和能被3整除的概率为_________.9、若抛物线122+-+=p px x y 中p 不管取何值时，它的图象都通过定点，则该定点的坐标为__________.10、如图， 边长为2的正方形ABCD 绕点A 逆时针旋转300到正方形AB ’C ’D ’，则图中阴影部分的面积为_________.11、已知x 为正实数，且2)2(2322=+-+x x xx ，则x 的值为__________.12、已知不等式63<x 的解都能使不等式5)1(->-a x a 成立，则a 的取值范围是_________.13、有一张矩形纸片ABCD ，5,12==AD AB ,将纸片折叠使C A ,两点重合，那么折痕长是________.三、解答题（本大题共6道小题，满分55分，解答应写出文字说明、证明过程或演算步骤.） 14、（本小题满分8分） 已知关于x 的一元二次方程)0(0122≠=+-a x ax 的两个不相等的实数根都在0和2之间（不包括0和2），求实数a 的取值范围.15、（本小题满分9分）某企业近期决定购买6台机器用于生产一种零件，现有甲、乙两种机器供选择，其中每种机器的价格和每台机器日生产零件数如下表所示。
2018_2019学年高二数学上学期入学考试试题
2020届高二年级入学考试数学试题时量：120分钟 总分：150分班级： 姓名：一、选择题（本大题共12小题，每题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求） 1、sincos1212ππ的值是 ( )A ．1B ．C ．14 D ．182、直线210ax y +-=与直线2310x y --=垂直，则a 的值为（ ）A ．3-B ．43-C ．2D ．3 3、△ABC 中，36a =，50c =，30B =︒，则△ABC 的面积为（ ）A.450B. 900C.4、已知等比数列{}n a 中，32a =，4616a a =，则91157a a a a -=-（ ）A ． 2B ． 4C ．8D ．165、在△ABC 中，如果()()3a b c b c a bc +++-=，那么A 等于（ ）A ． 60︒B ． 30︒C ．120︒D ．150︒ 6、设a ＝0.50.5，b ＝0.30.5，c ＝log 0.30.2，则a ，b ，c 的大小关系是( )A ．c ＜a ＜bB ．b ＜a ＜cC ．c ＜b ＜aD ．a ＜b ＜c7、设等差数列{}n a 的前项和为()*n S n ∈N，若48a=，420S =，则8a =（ ）A. 12B. 14C. 16D. 188、变量,x y 满足约束条件20,20,1,x y x y y +-≥⎧⎪--≤⎨⎪≥⎩，则目标函数2z x y =+的最小值为（ ）A ． 3B ． 4C ． 1D ． 29、等差数列{}n a 的前项和为n S ，若64711a a =，则117SS =（ ）A ．1-B ． 2C ． 1D ．1210、若直线)0,0(1:>>=+b a bya x l 过点(1,2)A ，则8ab +的最小值为（ ） A ．34 B ．27 C ．16 D ．25 11、不等式111x ≥--的解集为（ ） A ．(][),01,-∞+∞ B ．[)0,+∞C ．(](),01,-∞+∞ D ．[)()0,11,+∞12、在△ABC 中，,,a b c 分别为角,,A B C 的对边，21cos222A bc=+，则△ABC 的形状为( ) A ．等边三角形 B ．直角三角形 C ．等腰直角三角形 D ．等腰三角形 二、填空题(本题共4小题，每小题5分，共20分)13、若14a <<，24b -<<，则2a b -的取值范围是_____________． 14、等差数列{}n a 的前项和为n S ，若37116a a a ++=，则13S 等于_________． 15、函数()4sin 3cos 1f x x x =+-的最大值为____________．16、在△ABC中，已知sin :sin :sin 1:A B C =，则最大角等于 ． 三、解答题(本题共6大题计70分．解答应写出必要的文字说明、证明过程或演算步骤） 17、（10分）已知等差数列{}n a 中，2614a a +=，n S 为其前项和，525S =. （1）求{}n a 的通项公式； （2）设12n n n b a a +=⋅，求数列{}n b 的前项和n T.18、（12分）如图，在直三棱柱111ABC A B C -中，AC BC ⊥，点D 是AB 的中点．求证：（1）1AC BC ⊥； （2）1//AC 平面1B CD ．19、（12分）△ABC 的内角,,A B C 的对边分别是,,a b c ，已知222a b c ab+- cos cos 1ab B Ac c ⎛⎫⋅+= ⎪⎝⎭．（1）求角C ；（2）若c =ABC 的周长为5+，求△ABC 的面积S ．20、（12分）设n S 为数列{}n a 的前n 项和，对任意n *∈N ，都有21n n S a =-.（1）求数列{}n a 的通项公式； （2）若数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n T ，求使得12500nT -<成立的的最小值.21、（12分）已知函数()4cos sin 6f x x x a π⎛⎫=⋅-+ ⎪⎝⎭的最大值为3. （1）求a 的值及()f x 的单调递减区间； （2）若0,2πα⎛⎫∈ ⎪⎝⎭，1125f α⎛⎫=⎪⎝⎭，求cos α的值.22、（12分）解关于x 的不等式2(1)10ax a x -++>.高二年级入学考试数学试题时量：120分钟 总分：150分班级： 姓名：一、选择题（本大题共12小题，每题5分，共60分。
2018-2019年度升八年级数学入学分班检测卷(含答案)
2018-2019年度升八年级数学入学分班检测卷一、选择题（每题3分，共24分）1．的平方根是（）A．±9 B．±3 C．﹣3 D．32．下列各数中：+3、+（﹣2.1）、﹣、﹣π、0、﹣|﹣9|、﹣0.1010010001中，负有理数有（）A．2个 B．3个 C．4个 D．5个3．对于实数a，b，如果a＞0，b＜0且|a|＜|b|，那么下列等式成立的是（）A．a+b=|a|+|b| B．a+b=﹣（|a|+|b|）C．a+b=﹣（|a|﹣|b|） D．a+b=﹣（|b|﹣|a|）4．如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30°，那么这两个角是（）A．42°、138° B．都是10°C．42°、138°或42°、10° D．以上都不对5．若ab＞0，则++的值为（）A．3 B．﹣1 C．±1或±3 D．3或﹣16．如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（）A．2 B．3 C．4 D．57．如图，AB ∥CD ，用含∠1，∠2，∠3的式子表示∠4，则∠4的值为（ ）A ．∠1+∠2﹣∠3B ．∠1+∠3﹣∠2C ．180°+∠3﹣∠1﹣∠2D ．∠2+∠3﹣∠1﹣180°8．如图，一个粒子在第一象限和x ，y 轴的正半轴上运动，在第一秒内，它从原点运动到（0，1），接着它按图所示在x 轴、y 轴的平行方向来回运动，（即（0，0）→（0，1）→（1，1）→（1，0）→（2，0）→…）且每秒运动一个单位长度，那么2010秒时，这个粒子所处位置为（ ） A ．（14，44）B ．（15，44）C ．（44，14）D ．（44，15）二、填空题（每题3分，共21分）9．若关于x 、y 的代数式y xy x nxy mx +-+-232323中不含三次项，则2019)3(n m -= ． 10．已知：04)(222=-+y x ，则22y x += ．11．为了估算湖里有多少条鱼，从湖里捕上100条做上标记，然后放回湖里，经过一段时间待标记的鱼全混合于鱼群中后，第二次捕得200条，发现其中带标记的鱼25条，我们可以估算湖里有鱼 条． 12．已知a ，b 为实数，且﹣（b ﹣1）=0，则20182017b a-的值为 .13．若不等式组恰有两个整数解．则实数a 的取值范围是 ．14．已知数a ，b ，c 的大小关系如图所示：则下列各式：①b+a+（﹣c ）＞0；②（﹣a ）﹣b+c ＞0；③；④bc ﹣a ＞0；⑤|a ﹣b|﹣|c+b|+|a ﹣c|=﹣2b ．其中正确的有 （请填写编号）．15．在数学兴趣小组活动中，小明为了求…+的值，在边长为1的正方形中，设计了如图所示的几何图形．则…+的值为（结果用n 表示）．三、解方程（每小题5分，共10分）16、（1）（2）四、解答题（一）（每题6分，共18分）17．某校七年级社会实践小组去商场调查商品销售情况，了解到该商场以每件80元的价格购进了某品牌衬衫500件，并以每件120元的价格销售了400件，商场准备采取促销措施，将剩下的衬衫降价销售．请你帮商场计算一下，每件衬衫降价多少元时，销售完这批衬衫正好达到盈利45%的预期目标？18．已知：如图所示，∠ABD和∠BDC的平分线交于E，BE交CD于点F，∠1+∠2=90°．（1）求证：AB∥CD；（2）试探究∠2与∠3的数量关系．19．如图，直线AB、CD相交于点O，OE平分∠BOD．（1）若∠AOC=70°，∠DOF=90°，求∠EOF的度数；（2）若OF平分∠COE，∠BOF=15°，求∠AOC的度数．五、解答题（二）（每题9分，共27分）20．为了抓住惠州市文化艺术节的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．（1）求购进A、B两种纪念品每件各需多少元？（2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，但不超过7650元，那么该商店共有几种进货方案？（3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？21．如图，已知两条射线OM∥CN，动线段AB的两个端点A、B分别在射线OM、CN上，且∠C=∠OAB=108°，F在线段CB上，OB平分∠AOF，OE平分∠COF．（1）请在图中找出与∠AOC相等的角，并说明理由；（2）若平行移动AB，那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化？若变化，找出变化规律；若不变，求出这个比值；（3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=2∠OBA？若存在，请求出∠OBA 度数；若不存在，说明理由．32．如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC=120°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．（1）将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC．问：此时直线ON是否平分∠AOC？请说明理由．（2）将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，求t的值．（3）将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，试探索：在旋转过程中，∠AOM与∠NOC的差是否发生变化？若不变，请求出这个差值；若变化，请求出差的变化范围．2018-2019年度升八年级数学入学分班检测卷答案1. B2.C3.D4.D5.D6.A7.D8.A9.-1 10.2 11.800 12.-2 13.121≤x 14. （2）（3）（5） 15.n 211- 16.（1）解：原方程组化为：，即，将（1）×2﹣（2）×3得： ﹣x=﹣4， x=4， 代入（1），得 y=2．所以方程组的解为．（2）解：①+②得：4x +y=16④， ②×2+③得：3x +5y=29⑤， ④⑤组成方程组解得将x=3，y=4代入③得：z=5， 则方程组的解为．17.解：设每件衬衫降价x 元，依题意有120×400+（120﹣x ）×100=80×500×（1+45%）， 解得x=20．答：每件衬衫降价20元时，销售完这批衬衫正好达到盈利45%的预期目标．18.证明：（1）∵BE、DE平分∠ABD、∠BDC，∴∠1=∠ABD，∠2=∠BDC；∵∠1+∠2=90°，∴∠ABD+∠BDC=180°；∴AB∥CD；（同旁内角互补，两直线平行）解：（2）∵DE平分∠BDC，∴∠2=∠FDE；∵∠1+∠2=90°，∴∠BED=∠DEF=90°；∴∠3+∠FDE=90°；∴∠2+∠3=90°．19.解：（1）∠DOB=∠AOC=70°∵OE平分∠BOD∴∴∠EOF=∠DOF﹣∠DOE=55°；（2）设∠AOC=x，则∠DOB=∠AOC=x∵OE平分∠BOD∴∴∵∠EOF=∠EOB+∠BOF∴∠EOF=∵OF平分∠COE∴∠EOC=2∠EOF∴=解得：x=100°即∠AOC=100°．20.解：（1）设该商店购进一件A种纪念品需要a元，购进一件B种纪念品需要b元，根据题意得方程组得：，解方程组得：，∴购进一件A种纪念品需要100元，购进一件B种纪念品需要50元；（2）设该商店购进A种纪念品x个，则购进B种纪念品有（100﹣x）个，∴，解得：50≤x≤53，∵x 为正整数，x=50，51，52，53∴共有4种进货方案，分别为：方案1：商店购进A种纪念品50个，则购进B种纪念品有50个；方案2：商店购进A种纪念品51个，则购进B种纪念品有49个；方案3：商店购进A种纪念品52个，则购进B种纪念品有48个；方案4：商店购进A种纪念品53个，则购进B种纪念品有47个．（3）因为B种纪念品利润较高，故B种数量越多总利润越高，设利润为W，则W=20x+30（100﹣x）=﹣10x+3000．∵k=﹣10＜0，∴W随x大而小，∴选择购A种50件，B种50件．总利润=50×20+50×30=2500（元）∴当购进A种纪念品50件，B种纪念品50件时，可获最大利润，最大利润是2500元．22.解：（1）直线ON平分∠AOC．理由：如图：所示设ON的反向延长线为OD．∵OM平分∠BOC，∴∠MOC=∠MOB．又∵OM⊥ON，∴∠MOD=∠MON=90°．∴∠COD=∠BON．又∵∠AOD=∠BON（对顶角相等），∴∠COD=∠AOD．∴OD平分∠AOC，即直线ON平分∠AOC．（2）∵∠BOC=120°，∴∠AOC=60°．∴∠BON=∠COD=30°．即旋转60°或240°时直线ON平分∠AOC．由题意得，6t=60°或240°．解得：t=10或40；（3）∠AOM-∠NOC的差不变．∵∠MON=90°，∠AOC=60°，∴∠AOM=90°-∠AON、∠NOC=60°-∠AON．∴∠AOM-∠NOC=（90°-∠AON）-（60°-∠AON）=30°．。
2018年创新班六年级数学
学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题2018年学而思数学创新班入学诊断试卷 六年级考生须知1．本试卷共4页，21题2．本试卷满分150分，考试时间90分钟3．在试卷密封线内填写学校、班级、姓名、联系电话一、 填空题（将答案填在答题纸对应处）1.2220182017=-________．2.22018除以7的余数是________．3. 下图中有________个平行四边形．4. 下图是由9个等边三角形拼成的六边形．已知中间最小的等边三角形的边长是1，问：这个六边形的周长是________．5. 少年宫春季书法班、美术班、器乐班招生．书法班招收了29名学员，在这些学员中，既报书法又报美术的有13名，既报书法又报器乐的有12人，三个科目都报的有5名．那么，只参加书法学习的学员有________名．6. 数值小于10且分母为36的最简分数共有________个．7. 有一个自然数，它乘以2后是完全平方数，乘以3后是完全立方数，乘以5后是5次方数，这个自然数最小是________.（结果用分解质因数的形式写出来）8. 从4个整数中任意选出3个，求出它们的平均值，然后再求这个平均值和余下1个数的和，这样可以得到4个数：4、6、153和243，则原来给定的4个整数的和为________． 9. 如图所示的除法算式中，每个□各代表一个数字，则被除数是________．367410. 一次考试有三道题，四个好朋友考完后互相交流了成绩. 发现四人各对了3、2、1、0题. 这时一个路人问：你们考的怎么样啊？甲：“我对了两道题，而且比乙对的多，丙考的不如丁.” 乙：“我全对了，丙全错了，甲考的不如丁.”丙：“我对了一道，丁对了两道，乙考的不如甲.” 丁：“我全对了，丙考的不如我，甲考的不如乙.”已知大家都是对了几道题就说几句真话，那么对了2题的人是________．11. 一位少年短跑选手，顺风跑90米用了10秒，在同样的风速下逆风跑70米，也用了10秒，则在无风时他跑100米要用________秒．12. 联欢会上有一则数字谜语，谜底是一个八位数．现已猜出：□54□7□39，主持人提示：“这个无重复数字的八位数中，最小的数是2．”要猜出这个谜语，最多还要猜________次．13. 有2个大小不同的正方形A 和B．如下左图所示的那样，在将B 正方形的对角线的交点与A 正方形的一个顶点相重叠时，相重叠部分的面积为A 正方形面积的19．求A 与B的边长之比________,如果当按下右图那样，将A 和B 反向重叠的话，所重叠部分的面积是B 的________．左图右图14. 如图的三角形ABC 中，G 是BC 边的中线AD 上一点，满足：:2:1AG GD =．又3AG =，4BG =，5CG =，ABC △的面积等于________．15. 甲、乙两人分别从A 、B 两地出发，相向而行(不一定同时出发)，甲骑自行车，乙步行．两人在距A 地500米处第一次相遇．甲继续走到C 地后发现忘带东西，于是将速度提高一倍，立即返回A 地，并在距A 地400米处追上乙．到达A 地后不作停留立即前往B 地，在距A 地300米处与乙第二次相遇，最后两人同时到达目的地．那么B 、C 两地相距________米．16. 如图，一个有底无盖圆柱体容器，从里面量直径为10厘米，高为15厘米．在侧面距离底面9厘米的地方有个洞．请你设计一种方案，使得容器装水最多，这个容器最多能装________毫升水（ 取3.14）二、 简答题（将答案填在答题纸对应处，写出详细过程）17. 如图所示，小华用15张不同的直角三角形纸片拼成一个海螺的图形．直角的位置、长为1的线段都己经标出．则这海螺图形的周长为多少？(备注：考试时是16)18. 11223 1.919.54 3.542323156210.160.51 4.17520⨯+÷++÷=⎛⎫-⨯+ ⎪⎝⎭________.（在答题卡中写出具体计算过程）19. 如图，小明家和小强家相距10千米，小强家与公园相距25千米．小明9：20从家骑车出发去公园，l0：40小强从家出发，步行去公园．当小明到达学校时，他立即弃车步行；又过了一会 儿，当小强到达学校时，他立即开始骑车．两人同时于下午2：00到达公园．如果两人步行速度相同，骑车速度也相同，那么学校与公园相距多少千米？公园学校小强家小明家20. 有2、3、4、5、6、7、8、9、10和11共10个自然数，（1）从这10个数中选出7个数，使这7个数中的任何3个数都不会两两互质； （2）说明从这10个数中最多可以选出多少个数，这些数两两互质．21. 右图是Master Chan 为国际海豚保护组织设计的LOGO ，该图案是依托于三个相邻的长方形设计而成，已知表示海豚左右鱼鳍部分的阴影面积分别为63平方厘米和25平方厘米，表示下方尾鳍部分的阴影部分面积为18平方厘米，那么上方表示海豚头部的三角形A 的面积为多少平方厘米？。
2018--2019学年度第一学期八年级上教版入学考试数学试卷
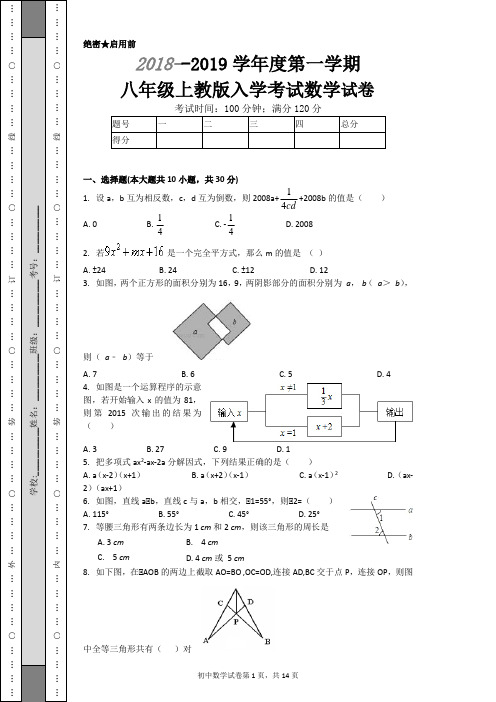
……○…………外……○…………内绝密★启用前2018--2019学年度第一学期八年级上教版入学考试数学试卷一、选择题(本大题共10小题，共30分)1. 设a ，b 互为相反数，c ，d 互为倒数，则2008a+cd41+2008b 的值是（ ） A. 0 B. 41 C. -41D. 2008 2. 若是一个完全平方式，那么m 的值是 （ ）A. ±24B. 24C. ±12D. 123. 如图，两个正方形的面积分别为16，9，两阴影部分的面积分别为 a ， b （ a ＞ b ），则（ a ﹣ b ）等于A. 7B. 6C. 5D. 4 4. 如图是一个运算程序的示意图，若开始输入x 的值为81，则第2015次输出的结果为（ ）A. 3B. 27C. 9D. 15. 把多项式ax 2-ax-2a 分解因式，下列结果正确的是（ ）A. a （x-2）（x+1）B. a （x+2）（x-1）C. a （x-1）2D. （ax-2）（ax+1）6. 如图，直线a ∥b ，直线c 与a ，b 相交，∠1=55°，则∠2=（ ） A. 115° B. 55° C. 45° D. 25°7. 等腰三角形有两条边长为1 cm 和2 cm ，则该三角形的周长是 A. 3 cm B. 4 cm C. 5 cmD. 4 cm 或 5 cm8. 如下图，在∠AOB 的两边上截取AO=BO ,OC=OD,连接AD,BC 交于点P ，连接OP ，则图中全等三角形共有（ ）对初中数学试卷第2页，共14页A. 2B. 3C. 4D.5ba 9. 在△ABC 中，∠A 、∠B 、∠C 的度数之比为3：4：5，那么△ABC 是（ ）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形 10. 如图，数轴上A 、B 两点表示的数分别为1和3，点B 关于点A 的对称点为点C ，则点C 所表示的数是（ ） A. 3-1 B. 1-3 C. 2- 3 D. 3-2二、填空题(本大题共8小题，共24分)11. 如图，是一个数值转换机．若输入数为3，则输出数是____________．12. 已知x 为整数，且分式的值为整数，则x 可取的所有值为 ______ ．13. 已知2+32=22×32，3+83=32×83，4+154=42×154，…，若10+ba =102×（a ，b 为正整数），则a+b= ______ ．14. 如图，P 是正方形ABCD 内的一点，连结BP 、CP ，将△PBC 绕点B 逆时针旋转到△P′BA 的位置，则它旋转了 ______ 度． 15. 已知△ABC 的三个内角分别是∠A 、∠B 、∠C ，若∠A=30°，∠C=2∠B ，则∠C= ______ ．．16. 如图，已知AB ∥DE ，∠ABC=75°，∠CDE=125°，则∠BCD 的度数为 ______ ．17. 一个角的度数是40°，那么它的余角的补角的大小是 .18. 如图所示：B 、D 、E 在一条直线上，AB=AC ，AD=AE ，∠BAC=∠DAE ，∠1=25°，∠2=30°，则∠3=____________．三、计算题(本大题共4小题，共24分)19. 先化简，再求值．5( 3 a 2 b － a b 2)－( 5 a 2 b ＋ a b 2)，其中 a ＝－1， b ＝2.21. 因式分解：①②22. 计算：|-2|-8+38-(3)2+(-1)2012初中数学试卷第4页，共14页四、解答题(本大题共5小题，共42分)23. 作图题，用直尺和圆规按下列要求作图． （1）根据对称轴l ，画出如图的轴对称图形；（2）根据轴对称图形的性质，结合（1）中所作图形，写出一条关于轴对称图形的结论．24. 在平面直角坐标系中，点A 的坐标是（0，3），点B 在x 轴上，将△AOB 绕点A 逆时针旋转90°得到△AEF ，点O 、B 的对应点分别是点E 、F ．（1）若点B 的坐标是（-4，0），请在图中画出△AEF ，并写出点E 、F 的坐标．（2）当点F 落在x 轴的上方时，试写出一个符合条件的点B 的坐标．25. 已知A=x 3-5x 2，B=x 2-11x+6，求（1）A+2B ；（2）当x=-1时，求A+5B 的值． 26. 如图，CD ⊥AB 于D ，点F 是BC 上任意一点，FE ⊥AB 于E ，且∠1=∠2，∠3=80°． （1）试证明∠B=∠ADG ； （2）求∠BCA 的度数．27. 如图1，将一个长为4a，宽为2b的长方形，沿图中虚线均匀分成4个小长方形，然后按图2形状拼成一个正方形．（1）图2的空白部分的边长是多少？（用含a，b的式子表示）（2）若2a-b=7，求图2中的空白正方形的面积．（3）观察图2，用等式表示出（2a-b）2，ab和（2a+b）2的数量关系．初中数学试卷第6页，共14页○…………………装※※不※※要○…………………装2018-2019学年度第一学期八年级上教版入学考试数学试卷【答案】1. B2. A3. A4. A5. A6. B7. C8. C9. A 10. C11. 60 12. 0，2 3 13. 109 14. 90 15. 100° 16. 20° 17. 130°. 18. 55°19.解：原式＝15a 2b －5ab 2－5a 2b －ab 2＝10a 2b －6ab 2当a ＝－1，b ＝2时，原式＝10×(－1)2×2－6(－1)×22＝20 +24 ＝44. 20. 解：（1）将方程两边乘以（x-2）得，2x=x-2+1， 解这个方程得，x=-1， 检验：当x=-1时，x-2≠0， ∴原分式方程的解为x=-1； （2）将方程两边同时×（x+1）（x-1）得，x+1-2（x-1）=4，…………装…………○…………订…………○…………线……学校:___________姓名：___________班级：___________考号：___________…………装…………○…………订…………○…………线……解这个方程得，x=-1，检验：当x=-1时，（x+1）（x-1）=0, ∴原分式方程无解. 21. ①②22. 解：23. 解：（1）如图所示：△A′B′C′即为所求；（2）例如：△ABC≌△A′B′C′．直线l 垂直平分AA′等． 24. 解：（1）∵△AOB 绕点A 逆时针旋转90°后得到△AEF， ∴AO⊥AE，AB⊥AF，BO⊥EF，AO=AE ，AB=AF ，BO=EF ， ∴△AEF 在图中表示为：∵AO⊥AE，AO=AE ， ∴点E 的坐标是（3，3）， ∵EF=OB=4，∴点F 的坐标是（3，-1）．（2）∵点F 落在x 轴的上方， ∴EF＜AO ， 又∵EF=OB，∴OB＜AO ，AO=3， ∴OB＜3，∴一个符合条件的点B 的坐标是（-2，0）．25. 解：（1）原式=x 3-5x 2+2（x 2-11x+6） =x 3-3x 2-22x+12；初中数学试卷第8页，共14页………装…………请※※不※※要※※在※※装※………装…………（2）A+5B=x 3-5x 2+5（x 2-11x+6） =x 3-55x+30； 当x=-1时，原式=-1+55+30=84．26. （1）证明：∵CD⊥AB，FE⊥AB， ∴CD∥EF， ∴∠2=∠BCD， ∵∠1=∠2， ∴∠1=∠BCD， ∴BC∥DG， ∴∠B=∠ADG；（2）解：∵DG∥BC， ∴∠3=∠BCG， ∵∠3=80°，∴∠BCA=80°． 27. 解：（1）图2的空白部分的边长是2a-b（2）由(1)知，小正方形的面积=（2a-b ）2=72=49．（3）由图2可以看出，大正方形面积=空白部分的正方形的面积+四个小长方形的面积即：（2a+b ）2-（2a-b ）2=8ab ．【解析】 1.解：由题意得：a+b=0，cd=1，把a+b=0，cd=1以整体形式代入2008a++2008b=2008（a+b ）+=．故选B ．根据相反数、倒数的定义，求出a+b=0，cd=1，从而求出代数式的值．主要考查相反数、倒数的概念．相反数的定义：若两个数的和是1，我们就称这两个数互为相反数；倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数． 2.此题主要考查了完全平方公式的应用.两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式.注意积的2倍的符号，避免漏解.这里首末两项是3x 和4这两个数的平方，那么中间一项为加上或减去4x 和4积的2倍.解：∵9x 2=(3x)2，16=42， ∴mx=2×(±12x)=±24x， ∴m=±24． 故选A ．3.解：设重叠部分面积为c ， a-b=(a+c)-(b+c)=16-9=7， 故选A ． 4.………○…………线…………○……：___________………○…………线…………○……解：把x=81代入得：×81=27， 把x=27代入得：×27=9， 把x=9代入得：×9=3， 把x=3代入得：×3=1， 把x=1代入得：1+2=3， 把x=3代入得：×3=1，依此类推，∵（2015-2）÷2=1006…1， ∴第2015次输出的结果为3， 故选A把x=81代入运算程序中计算即可得到结果．此题考查了代数式，熟练掌握运算法则是解本题的关键．5.解：ax 2-ax-2a ，=a （x 2-x-2）， =a （x-2）（x+1）． 故选A ．先提取公因式a ，再根据十字相乘法的分解方法分解即可．本题主要考查十字相乘法分解因式，其实质是对公式（x+p ）（x+q ）=x 2+（p+q ）x+pq 的逆用．6.解：∵直线a∥b，直线c 与a ，b 相交，∠1=55°， ∴∠2=∠1=55°． 故选B ．直接根据平行线的性质即可得出结论．本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等． 7.当等腰三角形的腰长为1cm ，底边长为2cm 时，∵1+1=2，∴不能构成三角形；当等腰三角形的腰长为2cm ，底边长为1cm 时，∵1+2＞2，∴能构成三角形，初中数学试卷第10页，共14页……外…………○…………装※※请※※不※※要……内…………○…………装∴三角形的周长=1+2+2=5cm ；∴该三角形的周长是5cm.故选C 。
江苏省海安高级中学2018-2019学年高一上学期第一次月考数学试题(创新班) 含解析
高一年级阶段检测一数学（创新班）试卷一、填空题：本大题共14小题，每小题5分，共计70分．1.已知集合，则＝______．【答案】【解析】，填．2.已知数列的一个通项公式为______．【答案】【解析】【分析】将化为，然后探究分母、分子的规律，然后还有正负的交替出现【详解】由已知可以得到，则有故通项公式为【点睛】本题主要考查了通过观察分析猜想归纳求数列的通项公式的方法，属于基础题。
3.在中，，，，则此三角形的最大边长为______．【答案】【解析】试题分析：首先根据最大角分析出最大边，然后根据内角和定理求出另外一个角，最后用正弦定理求出最大边．因为B=135°为最大角，所以最大边为b，根据三角形内角和定理：A=180°-（B+C）=30°，在△ABC中有正弦定理有：考点：正弦定理4.已知角的终边经过点，则的值等于______．【答案】【解析】，所以，，故，填．5.已知向量，，，则的值为______．【答案】8【解析】，所以，所以，故，填．6.已知函数则的值为______．【答案】2【解析】【分析】先求出的值，然后代入求解【详解】由函数的表达式可知：当时，当时，故答案为2【点睛】本题主要考查了求函数的值，只需代入分段函数中即可得到结果，较为简单。
7.《九章算术》是中国古代数学名著，其对扇形田面积给出“以径乘周四而一”的算法与现代数学的算法一致，根据这一算法解决下列问题：现有一扇形田，下周长（弧长）为20米，径长（两段半径的和）为24米，则该扇形田的面积为______平方米．【答案】120【解析】扇形的半径为，故面积为（平方米），填．8.若关于的不等式的解集，则的值为______．【答案】-3【解析】试题分析：显然t<0，且是方程的两根，由韦达定理得，解得．考点：不等式的解法．9.已知函数在区间上的最大值等于8，则函数的值域为______．【答案】【解析】二次函数的对称轴为，故，所以且，对称轴为，故所求值域为，填．10.已知函数是定义在R 上的偶函数，则实数的值等于____．【答案】-1 【解析】因为为偶函数，故，所以，整理得到，即，又当时，有，，故，为偶函数，故填．11.如图，在梯形ABCD 中，，P 为线段CD 上一点，且，E 为BC 的中点，若，则的值为______．【答案】 【解析】，整理得到，又，所以，也就是，，填．12.在锐角△ABC 中，若，则边长的取值范围是_________。
2018-2019学年高一3月月考数学试卷(创新班)(附答案)
2019级创新实验班阶段检测（一）数学试卷一、选择题（本大题共10小题，共50.0分）1．设集合U =R ，A ={x |0<x <2}，B ={x |x <1}，则图中阴影部分表示的集合为（）．A. {x |x ≥1}B. {x |x ≤1}C. {x |0<x ≤1} D. {x |1≤x <2}2．已知函数2()4f x x，则函数的值域为（）．A. (0，+∞)B. [0，+∞)C. (2，+∞) D. [2，+∞)3．函数123yxx的定义域为（）．A. (2，3)∪(3，+∞)B. [2，3)∪(3，+∞)C. [2，+∞)D. (3，+∞)4．函数,0,2,0,1)(2xx xx x f 则f (f (-2018))= （）．A. 1B. -1C. 2018D. -2018 5．若关于x 的一元二次方程x 2- 4x + m =0没有实数根，则m 的取值范围为（）．A. m <2 B.m>4 C. m>16 D. m<8 6．函数y =|x 2-1|与y =a 的图象有4个交点，则实数a 的取值范围是（）．A．(0，) B．(-1，1) C．(0，1) D．(1，)7．已知函数22()21f x xax a，若关于x 的不等式0ff x的解集为空集，则实数a 的取值范围是（）．A ．(-3，-2)B ．(-∞，-1)C ．(-∞，-2)D ．(-∞，-2]8．函数f (x )定义域为R ，且对任意x ，y ∈R ，()()()f xy f x f y 恒成立.则下列选项中不恒成立．．．．的是（）．A ．(0)0f B ．(2)2(1)f f C．11()(1)22f f D．()()0f x f x 9．已知函数f (x )=|1- |x -1||，若关于x 的方程 [f (x )]2+af (x )=0(a ∈R)有n 个不同实数根，则n 的值不可能为（）．A ．3B ．4C ．5D ．610．设f (x )与g (x )是定义在同一区间[a ，b ]上的两个函数，若函数y =f (x )- g (x )在x ∈[a ，b ]上有两个不同的解，则称f (x )和g (x )在[a ，b ]上是“关联函数”，区间[a ，b ]称为“关联区间”．若f (x )=x 2-3x +4与g (x )=2x +m 在[0，3]上是“关联函数”，则m 的取值范围为（）．A. 9(2]4， B. [-1，0] C. (-∞，-2)D.9()4，二、填空题（本大题共6小题，共30.0分）11．函数,03,82,10,11)(2xx xx x x f 的值域是▲ ．12．已知函数()y f x 的定义域为(22)，，函数()(1)(32)g x f x f x ．则函数()g x 的定义域▲ ．13．不等式11x的解集是▲ ．14．已知函数f (x )=x 2-2x 在区间[-1，t ]上的最大值为3，则实数t 的取值范围是▲ ．15．已知关于x 的不等式20ax bx c的解集是(21)，，则不等式20cxbx a的解集是▲ ．16．定义：符合()f x x 的x 称为f x 的一阶不动点，符合(())f f x x 的x 称为()f x 的二阶不动点．设函数2f xxbx c ，若函数()f x 没有一阶不动点，则函数()f x 二阶不动点的个数为▲ ．三、解答题：本大题共6小题，计80分．请在答题卡指定的区域内作答，解答时应写出文字说明，证明过程或演算步骤．17．（本题满分12分）已知集合2+230A x x x ≤，22240Bx xmx mx m R R ≤，，．（1）若]1,0[B A ，求实数m 的值；（2）若B A RC ，求实数m 的取值范围．18．（本题满分12分）已知二次函数2()f x axbx c 最小值为1，且(2)(2)()f x f f x ．（1）求()f x 的解析式；（2）若()f x 在区间2,1m m 上单调，求m 的取值范围．。
2018-2019江苏省海安高一数学试题（创新班）
（第11题）D2018-2019学年江苏省海安高级中学高一上学期第一次月考数学试题（创新班）一、填空题：本大题共14小题，每小题5分，共计70分． 1．已知集合{0,1,2},{0,2,4}A B ==，则A B ＝ ▲ ．2．已知数列1157,,,221220--的一个通项公式为 ▲ ． 3．在ABC ∆中，135B =︒，15C =︒，5a =，则此三角形的最大边长为 ▲ ． 4．已知角α的终边经过点(2,4)P -，则sin cos αα-的值等于 ▲ ． 5．已知向量(,5)AB m =，(4,)AC n =，(7,6)BC =，则m n +的值为 ▲ ．6．已知函数1232e ,2,()log (1),2,x x f x x x -⎧<⎪=⎨-⎪⎩≥ 则))2((f f 的值为 ▲ ． 7．《九章算术》是中国古代数学名著，其对扇形田面积给出“以径乘周四而一”的算法与现代数学的算法一致，根据这一算法解决下列问题：现有一扇形田，下周长（弧长）为20米，径长（两段半径的和）为24米，则该扇形田的面积为 ▲ 平方米． 8．若关于x 的不等式2260tx x t -+<的解集(,)(1,)a -∞+∞，则a 的值为 ▲ ．9．已知函数2() 2 (0)f x x ax a =++>在区间[0,2]上的最大值等于8，则函数() ([2,1])y f x x =∈-的值域为 ▲ ．10．已知函数2()22x x f x x m -=+-⋅是定义在R 上的偶函数，则实数m 的值等于 ▲ ． 11．如图，在梯形ABCD 中，2DC AB =，P 为线段CD 上一点，且3DC PC =，E 为BC的中点，若1212 (,)EP AB AD λλλλ=+∈R ，则12λλ+的值为 ▲ ． 12．在锐角△ABC 中，若a =2，b =3，则边长c 的取值范围是 ▲ ． 13．将函数sin y x =的图象向左平移3π个单位长度，再将图象上每个点的横坐标变为原来的1(0)ωω>倍（纵坐标不变），得到函数()y f x =的图象，若函数()y f x =在区间π(0,)2上有且仅有一个零点，则ω的取值范围为 ▲ ． 14．已知,x y 为非零实数，()ππ,42θ∈，且同时满足：①sin cos y xθθ=，② 22103x y xy =+，则cos θ的值等于 ▲ ．（第17题）二、解答题：本大题共6小题，共计90分． 15．（本小题满分14分）已知函数1()41x f x a =++的图象过点3(1,)10-．（1）判断函数()f x 的奇偶性，并说明理由； （2）若1()6f x -≤≤0，求实数x 的取值范围．16．（本小题满分14分）如图，在四边形ABCD 中，4,2AD AB ==．（1）若△ABC 为等边三角形，且AD BC ∥，E 是CD 的中点，求AE BD ⋅； （2）若AC AB =，3cos 5CAB ∠=，45AC BD ⋅=，求||DC ．17．（本小题满分14分）如图，在海岸A处，发现南偏东45°方向距A为(23－2)海里的B处有一艘走私船，在A处正北方向，距A为22海里的C处的缉私船立即奉命以103海里/时的速度追截走私船．（1）刚发现走私船时，求两船的距离；（2）若走私船正以102海里/时的速度从B处向南偏东75°方向逃窜，问缉私船沿什么方向能最快追上走私船？并求出所需要的时间(精确到分钟，参考数据：2≈1.4，6≈2.5)．18．（本小题满分16分）已知sinα+cosβ=35，cosα+sinβ=45，求：（1）sin(α+β)的值；（2）cosα sinβ的值．19．（本小题满分16分）已知(2cos ,1),cos ,1)x x x ==+-a b ，函数()f x =⋅a b ．（1）求()f x 在区间π[0,]4上的最大值和最小值； （2）若06()5f x =，0[,]42x ππ∈，求0cos2x 的值； （3）若函数()y f x ω=在区间(,)33π2π上是单调递增函数，求正数ω的取值范围．20．（本小题满分16分）设a 为实数，设函数()5f x a =+，设t =（1）求t 的取值范围，并把()f x 表示为t 的函数()g t ； （2）若()0g t ≥恒成立，求实数a 的取值范围； （3）若存在t 使得()g t t <成立，求实数a 的取值范围．一、填空题：1.{}0,22. 121(1)(1)n n n n ---⋅+3. 524.355.86.27.1208.-39.7[,4]410.1-11.1312. 13.410(,]3310 二、解答题：15．解：（1）因为()f x 的图象过点3(1,)10-， 所以13510a +=-，解得12a =-，所以11(),412x f x =-+ ……………………2分 ()f x 的定义域为R ． ……………………4分因为114141()()4124122(41)x x xx x f x f x ---=-=-==-+++， ……………………7分 所以()f x 是奇函数． …………………………………………8分（2）因为1()06f x -≤≤， 所以11106412x--+≤≤， 所以1113412x +≤≤， …………………………………………10分 所以2413x ≤+≤，所以142x ≤≤， ……………………………………12分 解得102x ≤≤． ……………………………………14分 16．（1）法一：因为△ABC 为等边△，且,AD BC ∥所以120DAB ∠=︒．…2分又2,AD AB =所以2AD BC =，因为E 是CD 中点，所以1()2AE AD AC =+1()2AD AB BC =++11()22AD AB AD =++3142AD AB =+． ……………………………………4分 又BD AD AB =-，所以AE BD ⋅31()()42AD AB AD AB =+⋅- 22311424AD AB AD AB =--⋅ ……………………………………6分311116442()4242=⨯-⨯-⨯⨯⨯-=11. ……………………………………8分 法二：如图，以A 为原点，AB 所在直线为x 轴，建立平面直角坐标系，则(00)(2,0)A B ，，， 因为△ABC 为等边△，且,AD BC ∥所以120DAB ∠=︒． ………2分又24,AD AB ==所以2AB AC ==，所以(C D -，因为E 是CD 中点， 所以1(22E -，………………4分 所以1(22AE =-，,(4BD =- ……6 分所以1((42AE BD ⋅=-⋅-，1()(4)22=-⨯-+=11． ………………………………8分（2）因为2AB AC AB ==，，所以2AC =,因为4,5AC BD ⋅=所以4(),5AC AD AB ⋅-=所以4.5AC AD AC AB ⋅-⋅= ………………………………10分 又312cos 4.55AC AB AC AB CAB ⋅=∠=⨯=所以41655AC AD AC AB ⋅=+⋅=．……12分22222DC AC AD AC AD AC AD=-=+-⋅1641625=+-⨯685=．所以285DC =14分 17．解：（1）在△ABC 中，∵AB ＝(23－2)海里，AC ＝22海里，∠BAC ＝135°，由余弦定理，得 BC ＝(23－2)2＋(22)2－2×22×(23－2)cos 135°＝4(海里)． ……….4分 （2）根据正弦定理，可得sin ∠ABC ＝AC sin 135°BC ＝22.∴∠ABC ＝45°，易知∠ACB ＝15°，…2分设缉私船应沿CD 方向行驶t 小时，才能最快截获(在D 点)走私船，则有CD ＝103t (海里)，BD ＝10t (海里)．而∠CBD ＝120°，在△BCD 中，根据正弦定理，可得 sin ∠BCD ＝BD sin ∠CBD CD ＝102t ·sin 120°103t＝22，∴∠BCD ＝45°，∠BDC ＝15°， ………..2分 ∴根据正弦定理，得233104264t=-，解得分钟小时4778.0526≈≈+=t ．………..2分 故缉私船沿南偏东60°方向，需47分钟才能追上走私船．19．（1）()2cos cos )12cos2f x x x x x x =⋅=+-+a b π2sin(2)6x =+， …2分因为π[0,]4x ∈，所以ππ2π2663x +≤≤，所以1πsin(2)126x +≤≤， 所以max min ()2,()1f x f x ==． …………………………………………4分 （2）因为06()5f x =，所以0π62sin(2)65x +=，所以0π3sin(2)65x +=， 因为0ππ[,]42x ∈，所以02ππ7π2366x +≤≤，所以0π4cos(2)65x +==-， ………………………………6分所以0000πππ1πcos2cos[(2)])sin(2)662626x x x x =+-=+++4133()252510-=-+⨯=． ………………………………………8分 （3）()n 26πsi f x x ωω⎛⎫=+ ⎪⎝⎭令222,,26πππππ2k x k k ω-++∈Z ≤≤ 得ππ6ππ3k k x ωωωω+-≤≤， ……10分 因为函数()f x 在(π2,3π)3上是单调递增函数，所以存在0k ∈Z ，使得002(,)(ππππππ,)3336k k ωωωω⊆-+所以有00ππππ,33π2.63πk k ωωωω⎧-⎪⎪⎨⎪+⎪⎩≤≥ 即0031,614.k k ωω+⎧⎨+⎩≤≥ …………………………12分因为0,ω>所以01,6k >-又因为212332πππ2ω-⋅≤， 所以302ω<≤, 所以05.6k ≤ 14分从而有01566k -<≤，所以00k =，所以10.4ω<≤ …16分（另解：由212332πππ2ω-⋅≤，得302ω<≤. 因为2(,)33x ππ∈，所以242(,)63636x ωωωπππππ+∈++，所以4362ωπππ+≤或23362ωπππ+≥，解得104ω<≤或2ω≥.又302ω<≤，所以10.4ω<≤） 20．解：1）t =要使t 有意义，必须10x +≥且10x -≥，即11x -≤≤，∴22t =+0t ≥① ∴t的取值范围是2⎤⎦2112t =-， ∴2()3g t t at =++2t ≤≤；（2）由0g t ≥（）恒成立，即有min 0g t ≤（），注意到直线2a t =-是抛物线2()3g t t at =++的对称轴， 分以下几种情况讨论：①当2a-≤a ≥-时，()g t在2⎤⎦上为递增函数，即有t =时，取得最小值，且为5；22a<-<即4a -<<-()g t 的最小值为2()324a a g -=-；③当22a-≥即4a ≤-时，()g t在2⎤⎦上为递减函数， 即有2t =时，取得最小值，且为72a +．则50a ⎧≥-⎪⎨+≥⎪⎩或24304a a -<⎧-≥<-⎪⎨⎪⎩或4720a a ≤-⎧⎨+≥⎩，解得：a ≥-或a -≤-或a ∈∅，则有a ≥-。
2018-2019学年高二数学上学期入学考试试题(扫描版)
cn 3 31 5 32
2n 1 3n ①
3Sn 3 32 5 33
1 -②式得： ○
2n 1 3n1 ②
2 Sn 2 32 33 2 3 32 1 3n 1
3n 9 2n 1 3n 1 9 2n 1 3n 1
PO 平面 ABCD ， PO 为三棱柱 P ABC 的高
PAD 为等边三角形， AD 2 ，所以 PO 3
CD 3, OD 1 ，OC AB 2
Байду номын сангаасSABC 1 1 2 AB BC 2 1 2 2 2
1 1 2 6 ··········· 12 分 VB PAC VP ABC SABC PO 3 3 3 2 6
2 详解： （I）设 an 的公差为，则由已知得 a1a13 a4
10 分
即 3 3 12d 3 3d ，解得： d 2 或 d 0 （舍）
2
所以 an 3 2 n 1 2n 1 因为 b2 a4 9 ，所以 bn 的公比 q 3 所以 bn 3n ······························ 6 分 （II）由（I）可知 cn anbn 2n 1 3 所以 Sn c1 c2
2
2 所以 m 1 16 0 ，整理得 m 2m 15 0
2
1
2
3
4
5
6
7
8
9
10
11
12
14、 2
x
x
15、
2 2
16、
XXX2018-2019学年九年级上入学考试数学试题
XXX2018-2019学年九年级上入学考试数学试题XXX2018-201年度第一学期入学考试试卷九年级数学时量:120分钟总分:120分一、选择题(每小题3分,共36分)1.2017年中秋小长假长沙县的旅游收入约为1900万,将1900万用科学记数法表示应为（）A.19×10^4B.1.9×10^4C.1.9×10^7D.19×10^82.下列标志中不是中心对称图形的是（）3.下列计算正确的是（）A.a^6-a^2=a^4B.-a^6/(2^2)=a^12C.a^6/a^2=a^3D.a^6×a^2=a^124.已知在平面直角坐标系中,点P在第二象限且点P到x轴和y轴的距离分别6和5,那么点P的坐标为（）A.(-5,-6)B.(-6,-5)C.(-5,6)D.(-6,5)5.如图,直线y=-x+4与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO' B',则点B'的坐标是（）A.(5,4)B.(5,3)C.(7,4)D.(7,3)6.若方程ax^2+bx+c=0的两个根是-3和1,那么二次函数y=ax^2+bx+c的图象的对称轴是（）A.直线x=-1B.直线x=-2C.直线x=-3D.直线x=17.如图,已知直线a∥b∥c,直线m、n与直线a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=6,BD=3,则BF=（）A.7B.7.5C.8D.8.58.在函数y=(x+1)/(2x-1)中,自变量x的取值范围是（）A.x≥-1B.x>-1且x≠1/2C.x≥-1且x≠1/2D.x>-19.抛物线y=x^2+bx+c的图象向右平移2个单位长度再向下平移3个单位长度，所得图象的解析式为y=x^2-2x-3,则b、c的值为（）A.b=2，c=2B.b=2，c=-1C.b=-2，c=-1D.b=-3，c=210.《九章算术》是中国传统数学的重要著作,方程术是它的最高成就,其中记载:今有共买物,人出八,盈三；人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱；每人出7钱,又会差4钱,问人数、物价各是多少?设合伙人数为x人,物价为y钱,以下列出的方程组正确的是（）11.如图，AB是半圆的直径，点D是弧AC的中点，∠ABC=50°，则∠DAB等于（）答案：C。
创新学校2018-2019年八年级上第二次月考数学试卷含答案解析
2018-2019学年江苏省盐城市东台市创新学校八年级（上）第二次月考数学试卷一、选择题（每小题3分，共24分）1．我国重要银行的商标设计都融入了中国古代钱币的图案，下列我国四大银行的商标图案不是轴对称图形的是( )A．B．C．D．2．下列点中，位于直角坐标系第二象限的点是( )A．（2，1）B．（﹣2，﹣1）C．（﹣2，1）D．（2，﹣1）3．到△ABC三个顶点距离相等的点是△ABC的( )A．三条角平分线的交点B．三条中线的交点C．三条高的交点 D．三条垂直平分线的交点4．在平面直角坐标系中，已知A（2，2），在x轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P有( )A．2个B．3个C．4个D．5个5．如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是( )A．△ABC绕点C顺时针旋转90°，再向下平移3B．△ABC绕点C顺时针旋转90°，再向下平移1C．△ABC绕点C逆时针旋转90°，再向下平移1D．△ABC绕点C逆时针旋转90°，再向下平移36．如图，是象棋盘的一部分．若“帅”位于点（1，﹣2）上，“相”位于点（3，﹣2）上，则“炮”位于点( )上．A．（﹣1，1）B．（﹣1，2）C．（﹣2，1）D．（﹣2，2）7．在平面直角坐标系中，P点关于原点的对称点为P1（﹣3，﹣），P点关于x轴的对称点为P2（a，b），则=( )A．﹣2 B．2 C．4 D．﹣48．在直角坐标系中，我们把横、纵坐标都是整数的点叫做整点，且规定，正方形的内部不包含边界上的点．观察如图所示的中心在原点、一边平行于x轴的正方形：边长为1的正方形内部有1个整点，边长为2的正方形内部有1个整点，边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )A．64个B．49个C．36个D．25个二、填空题（每空2分，共22分）9．一个等腰三角形的两边长分别为3和7，这个三角形的周长是__________．10．4.6048（保留三个有效数字）__________，0.3060精确到__________位．11．若点A（x，0）与B（2，0）的距离为5，则x=__________．12．已知点A（a，﹣2）与点B（3，﹣2）关于y轴对称，则a=__________．13．在平面直角坐标系中，以原点为中心，把点A（4，5）逆时针旋转90°，得到的点A′的坐标为__________．14．如图，已知：AD平分∠BAC，AC=AB+BD，∠B=56°，则∠C=__________．15．如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC=__________°．16．如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线交AB于点D，交AC于点E，连接BE，则∠CBE的度数为__________．17．已知点P（a，2a+3）点在第二、四象限的角平分线上，则a=__________．18．如图，一圆柱高8cm，底面圆周长为12cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是__________cm．三、解答题（每小题12分共54分）19．计算题（1）（﹣2）3×+（﹣1）2003﹣；（2）|﹣1|+（﹣2）2+（7﹣π）0﹣（）﹣1．20．利用网格线画图：如图，点A、B、C都在正方形网格的格点上．（1）在BC上找一点P，使PA=PB；（2）在BC上找一点Q，使点Q到AB和AC的距离相等．21．如图，已知∠AOB=30°，P为其内部一点，OP=3，M、N分别为OA、OB边上的一点，要使△PMN的周长最小，请给出确定点M、N位置的方法，并求出最小周长．22．在同一直角坐标系中分别描出点A（﹣3，0）、B（2，0）、C（1，3），再用线段将这三点首尾顺次连接起来，求△ABC的面积与周长．23．如图，已知：在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD．图中的CE、BD有怎样的大小和位置关系？试证明你的结论．24．如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD 翻折，使点O落在BC边上的点E处，求D、E两点的坐标．25．如图，在直角坐标系中，B点的坐标为（a，b），且a、b满足．（1）求B点的坐标；（2）点A为y轴上一动点，过B点作BC⊥AB交x轴正半轴于点C，求证：BA=BC．26．如图，在平面直角坐标系中，OA=OB=OC=8，过点A的直线AD交BC于点D，交y 轴与点G，△ABD的面积为△ABC面积的．（1）求点D的坐标；（2）过点C作CE⊥AD，交AB交于F，垂足为E．求证：OF=OG；（3）若点F的坐标为（，0），在第一象限内是否存在点P，使△CFP是以CF为腰长的等腰直角三角形？若存在，请求出点P坐标；若不存在，请说明理由．2018-2019学年江苏省盐城市东台市创新学校八年级（上）第二次月考数学试卷一、选择题（每小题3分，共24分）1．我国重要银行的商标设计都融入了中国古代钱币的图案，下列我国四大银行的商标图案不是轴对称图形的是( )A．B．C．D．【考点】轴对称图形．【分析】根据轴对称图形和的概念结合各图形特点解答即可．【解答】解：A、是轴对称图形，故本选项错误；B、不是轴对称图形，故本选项正确；C、是轴对称图形，故本选项错误；D、是轴对称图形，故本选项错误；故选B．【点评】本题考查了轴对称图形的特点，判断轴对称图形的关键是寻找对称轴，图象沿对称轴折叠后可重合．2．下列点中，位于直角坐标系第二象限的点是( )A．（2，1）B．（﹣2，﹣1）C．（﹣2，1）D．（2，﹣1）【考点】点的坐标．【专题】应用题．【分析】根据点在第二象限的符号特点横坐标是负数，纵坐标是正数作答．【解答】解：∵点在第二象限的符号特点是横坐标是负数，纵坐标是正数，∴符合题意的只有选项C，故选C．【点评】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣），比较简单．3．到△ABC三个顶点距离相等的点是△ABC的( )A．三条角平分线的交点B．三条中线的交点C．三条高的交点 D．三条垂直平分线的交点【考点】线段垂直平分线的性质．【分析】根据线段垂直平分线的性质（三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等）可得到△ABC的三个顶点距离相等的点是三边垂直平分线的交点．【解答】解：△ABC的三个顶点距离相等的点是三边垂直平分线的交点．故选：D．【点评】本题考查的是线段垂直平分线的性质（三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等）．4．在平面直角坐标系中，已知A（2，2），在x轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P有( )A．2个B．3个C．4个D．5个【考点】等腰三角形的判定；坐标与图形性质．【分析】此题应该分情况讨论．以OA为腰或底分别讨论，进而得出答案．【解答】解：（1）若AO作为腰时，有两种情况，①当A是顶角顶点时，P是以A为圆心，以OA为半径的圆与x轴的交点，共有1个，若OA是底边时，P是OA的中垂线与x轴的交点，有1个，②当O是顶角顶点时，P是以O为圆心，以OA为半径的圆与x轴的交点，有2个；（2）若OA是底边时，P是OA的中垂线与x轴的交点，有1个，以上4个交点没有重合的．故符合条件的点有4个．故选：C．【点评】此题主要考查了坐标与图形的性质及等腰三角形的判定；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．5．如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是( )A．△ABC绕点C顺时针旋转90°，再向下平移3B．△ABC绕点C顺时针旋转90°，再向下平移1C．△ABC绕点C逆时针旋转90°，再向下平移1D．△ABC绕点C逆时针旋转90°，再向下平移3【考点】坐标与图形变化-旋转；坐标与图形变化-平移．【分析】观察图形可以看出，Rt△ABC通过变换得到Rt△ODE，应先旋转然后平移即可．【解答】解：根据图形可以看出，△ABC绕点C顺时针旋转90°，再向下平移3个单位可以得到△ODE．故选：A．【点评】本题考查的是坐标与图形变化旋转和平移的知识，掌握旋转和平移的概念和性质是解题的关键．6．如图，是象棋盘的一部分．若“帅”位于点（1，﹣2）上，“相”位于点（3，﹣2）上，则“炮”位于点( )上．A．（﹣1，1）B．（﹣1，2）C．（﹣2，1）D．（﹣2，2）【考点】坐标确定位置．【专题】压轴题；网格型．【分析】根据已知两点的坐标可确定平面直角坐标系，再判断其它各点的坐标．【解答】解：依题意，坐标系的原点是从下数第3行与从左数第4列的交点，故炮的坐标为（﹣2，1）．故选：C．【点评】考查类比点的坐标及学生解决实际问题和阅读理解的能力．解决此类问题需要先确定原点的位置，再求未知点的位置，或者直接利用坐标系中的移动法则“右加左减，上加下减”来确定坐标．7．在平面直角坐标系中，P点关于原点的对称点为P1（﹣3，﹣），P点关于x轴的对称点为P2（a，b），则=( )A．﹣2 B．2 C．4 D．﹣4【考点】关于原点对称的点的坐标；立方根；关于x轴、y轴对称的点的坐标．【专题】计算题．【分析】利用关于原点对称点的坐标性质得出P点坐标，进而利用关于x轴对称点的坐标性质得出P2坐标，进而得出答案．【解答】解：∵P点关于原点的对称点为P1（﹣3，﹣），∴P（3，），∵P点关于x轴的对称点为P2（a，b），∴P2（3，﹣），∴==﹣2．故选：A．【点评】此题主要考查了关于原点对称点的性质以及关于x轴对称点的性质，得出P点坐标是解题关键．8．在直角坐标系中，我们把横、纵坐标都是整数的点叫做整点，且规定，正方形的内部不包含边界上的点．观察如图所示的中心在原点、一边平行于x轴的正方形：边长为1的正方形内部有1个整点，边长为2的正方形内部有1个整点，边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )A．64个B．49个C．36个D．25个【考点】规律型：点的坐标．【分析】求出边长为1、2、3、4、5、6、7的正方形的整点的个数，得到边长为1和2的正方形内部有1个整点，边长为3和4的正方形内部有9个整点，边长为5和6的正方形内部有25个整点，推出边长为7和8的正方形内部有49个整点，即可得出答案．【解答】解：设边长为8的正方形内部的整点的坐标为（x，y），x，y都为整数．则﹣4＜x＜4，﹣4＜y＜4，故x只可取﹣3，﹣2，﹣1，0，1，2，3共7个，y只可取﹣3，﹣2，﹣1，0，1，2，3共7个，它们共可组成点（x，y）的数目为7×7=49（个）．故选：B．【点评】本题主要考查点的坐标与正方形的性质，根据已知总结出规律是解此题的关键．二、填空题（每空2分，共22分）9．一个等腰三角形的两边长分别为3和7，这个三角形的周长是17．【考点】等腰三角形的性质；三角形三边关系．【专题】计算题．【分析】求等腰三角形的周长，即是确定等腰三角形的腰与底的长求周长；题目给出等腰三角形有两条边长为3和7，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【解答】解：（1）若3为腰长，7为底边长，由于3+3＜7，则三角形不存在；（2）若7为腰长，则符合三角形的两边之和大于第三边．所以这个三角形的周长为7+7+3=17．故答案为：17．【点评】本题考查了等腰三角形的性质和三角形的三边关系；题目从边的方面考查三角形，涉及分类讨论的思想方法．求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否组成三角形的好习惯，把不符合题意的舍去．10．4.6048（保留三个有效数字）4.60，0.3060精确到万分位．【考点】近似数和有效数字．【分析】根据有效数字的定义把4.6048中千分位上的数字4进行四舍五入即可；利用近似数的精确度可判断0.3060精确到哪位．【解答】解：4.6048≈4.60（保留三个有效数字），0.3060精确到万分位．故答案为4.60；万分．【点评】本题考查了近似数和有效数字：经过四舍五入得到的数为近似数；从一个数的左边第一个不是0的数字起到末位数字止，所有的数字都是这个数的有效数字．近似数与精确数的接近程度，可以用精确度表示．一般有，精确到哪一位，保留几个有效数字等说法．11．若点A（x，0）与B（2，0）的距离为5，则x=﹣3或7．【考点】两点间的距离公式．【分析】根据两点间的距离公式便可直接解答．【解答】解：∵点A（x，0）与B（2，0）的距离为5，∴AB==5，解得x=﹣3或x=7．故答案填：﹣3或7．【点评】解答此题的关键是熟知两点间的距离公式．12．已知点A（a，﹣2）与点B（3，﹣2）关于y轴对称，则a=﹣3．【考点】关于x轴、y轴对称的点的坐标．【分析】根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”求出a的值即可．【解答】解：∵点A（a，﹣2）与点B（3，﹣2）关于y轴对称，∴a+3=0，∴a=﹣3，故答案为：﹣3．【点评】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．13．在平面直角坐标系中，以原点为中心，把点A（4，5）逆时针旋转90°，得到的点A′的坐标为（﹣5，4）．【考点】坐标与图形变化-旋转．【分析】首先根据点A的坐标求出OA的长度，然后根据旋转变换只改变图形的位置，不改变图形的形状与大小，可得OA′=OA，据此求出点A′的坐标即可．【解答】解：如图，过点A作AC⊥y轴于点C，作AB⊥x轴于点B，过A′作A′E⊥y轴于点E，作A′D⊥x轴于点D，，∵点A（4，5），∴AC=4，AB=5，∵点A（4，5）绕原点逆时针旋转90°得到点A′，∴A′E=AB=5，A′D=AC=4，∴点A′的坐标是（﹣5，4）．故答案为：（﹣5，4）．【点评】此题主要考查了坐标与图形变换﹣旋转，要熟练掌握，解答此题的关键是要明确：旋转变换只改变图形的位置，不改变图形的形状与大小．14．如图，已知：AD平分∠BAC，AC=AB+BD，∠B=56°，则∠C=28°．【考点】全等三角形的判定与性质；等腰三角形的性质．【分析】在AC上取一点E，使AE=AB，连接DE，由条件就可以得出△ADB≌△ADE，就可以得出BD=DE，就可以得出DE=CE，由三角形的外角与内角的关系就可以得出∠C的值．【解答】解：在AC上取一点E，使AE=AB，连接DE，∵AD平分∠BAC，在△ADB和△ADE中．∴△ADB≌△ADE（SAS），∴BD=ED．∠B=∠AED=56°．∵AC=AB+BD，AC=AE+EC∴AB+BD=AE+CE，∴BD=CE，∴DE=CE．∴∠CDE=∠C．∵∠C+∠CDE=∠AED，∴2∠C=56°，∴∠C=28°．故答案为：28°．【点评】本题考查了角平方形的性质的运用，全等三角形的判定及性质的运用，三角形的外角与内角的关系的运用．解答时证明三角形全等是关键．15．如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC=66.5°．【考点】三角形内角和定理．【分析】根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠CAE+∠ACE，再根据三角形的内角和等于180°列式计算即可得解．【解答】解：∵三角形的外角∠DAC和∠ACF的平分线交于点E，∴∠CAE+∠ACE=（∠B+∠ACB）+（∠B+∠BAC），=（∠BAC+∠B+∠ACB+∠B），=（180°+47°），=113.5°，在△ACE中，∠AEC=180°﹣（∠CAE+∠ACE），=180°﹣113.5°，=66.5°．故答案为：66.5．【点评】本题考查了三角形的内角和定理，角平分线的定义，三角形的一个外角等于与它不相邻的两个内角的和的性质，整体思想的利用是解题的关键．16．如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线交AB于点D，交AC于点E，连接BE，则∠CBE的度数为30°．【考点】线段垂直平分线的性质；等腰三角形的性质．【分析】根据等腰三角形的性质求出∠ABC=∠C=70°，根据线段的垂直平分线的性质得到EA=EB，计算即可．【解答】解：∵AB=AC，∠A=40°，∴∠ABC=∠C=70°，∵DE是AB的垂直平分线，∴EA=EB，∴∠EBA=∠A=40°，∴∠CBE=∠ABC﹣∠EBA=30°，故答案为：30°．【点评】本题考查的是线段的垂直平分线的性质，线段的垂直平分线上的点到线段的两个端点的距离相等．17．已知点P（a，2a+3）点在第二、四象限的角平分线上，则a=﹣1．【考点】点的坐标．【分析】根据二四象限角平分线上的点的横坐标与纵坐标互为相反数，可得答案．【解答】解：由点P（a，2a+3）点在第二、四象限的角平分线上，得a+2a+3=0，解得a=﹣1，故答案为：﹣1．【点评】本题考查了点的坐标，二四象限角平分线上的点的横坐标与纵坐标互为相反数，一三象限角平分线上的点的横坐标与纵坐标相等．18．如图，一圆柱高8cm，底面圆周长为12cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是10cm．【考点】平面展开-最短路径问题．【分析】先把圆柱的侧面展开，连接AB，利用勾股定理求出AB的长即可．【解答】解：如图所示：连接AB，∵圆柱高8cm，底面圆周长为12cm，∴AC=×12=6cm，在Rt△ABC中，AB==10cm．故答案为：10【点评】本题考查的是平面展开﹣最短路径问题，解答此类问题的关键是画出圆柱的侧面展开图，利用勾股定理进行解答．三、解答题（每小题12分共54分）19．计算题（1）（﹣2）3×+（﹣1）2003﹣；（2）|﹣1|+（﹣2）2+（7﹣π）0﹣（）﹣1．【考点】实数的运算；零指数幂；负整数指数幂．【专题】计算题；实数．【分析】（1）原式利用乘方的意义，二次根式性质，以及立方根定义计算即可得到结果；（2）原式利用绝对值的代数意义，乘方的意义，以及零指数幂、负整数指数幂法则计算即可得到结果．【解答】解：（1）原式=﹣8×﹣1﹣3=﹣44﹣1﹣3=﹣48；（2）原式=1+4+1﹣3=2．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．20．利用网格线画图：如图，点A、B、C都在正方形网格的格点上．（1）在BC上找一点P，使PA=PB；（2）在BC上找一点Q，使点Q到AB和AC的距离相等．【考点】作图—复杂作图；角平分线的性质；线段垂直平分线的性质．【分析】（1）直接利用线段垂直平分线的性质结合网格得出答案；（2）直接利用角平分线的性质结合网格得出答案．【解答】解：（1）如图所示：点P即为所求；（2）如图所示：点Q即为所求．【点评】此题主要考查了角平分线的性质以及线段垂直平分线的性质，正确借助网格作图是解题关键．21．如图，已知∠AOB=30°，P为其内部一点，OP=3，M、N分别为OA、OB边上的一点，要使△PMN的周长最小，请给出确定点M、N位置的方法，并求出最小周长．【考点】轴对称-最短路线问题．【分析】作点P关于OA的对称点P1，点P关于OB的对称点P2，连结P1P2，与OA的交点即为点M，与OB的交点即为点N，则此时M、N符合题意，求出线段P1P2的长即可．【解答】解：作点P关于OA的对称点P1，点P关于OB的对称点P2，连结P1P2，与OA的交点即为点M，与OB的交点即为点N，△PMN的最小周长为PM+MN+PN=P1M+MN+P2N=P1P2，即为线段P1P2的长，连结OP1、OP2，则OP1=OP2=3，又∵∠P1OP2=2∠AOB=60°，∴△OP1P2是等边三角形，∴P1P2=OP1=3，即△PMN的周长的最小值是3．【点评】本题考查了等边三角形的性质和判定，轴对称﹣最短路线问题的应用，关键是确定M、N的位置．22．在同一直角坐标系中分别描出点A（﹣3，0）、B（2，0）、C（1，3），再用线段将这三点首尾顺次连接起来，求△ABC的面积与周长．【考点】勾股定理的应用；点的坐标；三角形的面积．【专题】应用题．【分析】建立平面直角坐标系将三个点描出来，利用勾股定理求得三边的长后即可计算周长及面积．【解答】解：利用勾股定理得：AC==5，BC==，AB=2﹣（﹣3）=5，∴周长为AC+BC+AB=5+5+=10+；面积=3×5﹣×3×4﹣×1×3=．【点评】本题考查了勾股定理的知识，根据点的坐标画图形，一定要明确点所在的象限及坐标，求不规则三角形的面积，一般用“割补法”．23．如图，已知：在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD．图中的CE、BD有怎样的大小和位置关系？试证明你的结论．【考点】全等三角形的判定与性质．【分析】根据全等三角形的判定得出△BAD≌△CAE，进而得出∠ABD=∠ACE，求出∠DBC+∠DCB=∠DBC+∠ACE+∠ACB即可得出答案．【解答】解：BD=CE，BD⊥CE；理由：∵∠BAC=∠DAE=90°，∴∠BAC+∠CAD=∠DAE+∠CAD，即∠BAD=∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS），∴BD=CE；∵△BAD≌△CAE，∴∠ABD=∠ACE，∵∠ABD+∠DBC=45°，∴∠ACE+∠DBC=45°，∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°，则BD⊥CE．【点评】此题主要考查了全等三角形的判定与性质和三角形内角和定理等知识，根据已知得出△BAD≌△CAE是解题关键．24．如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD 翻折，使点O落在BC边上的点E处，求D、E两点的坐标．【考点】翻折变换（折叠问题）；坐标与图形性质．【分析】先根据勾股定理求出BE的长，进而可得出CE的长，求出E点坐标，在Rt△DCE 中，由DE=OD及勾股定理可求出OD的长，进而得出D点坐标．【解答】解：依题意可知，折痕AD是四边形OAED的对称轴，∴在Rt△ABE中，AE=AO=10，AB=8，BE===6，∴CE=4，∴E（4，8）．在Rt△DCE中，DC2+CE2=DE2，又∵DE=OD，∴（8﹣OD）2+42=OD2，∴OD=5，∴D（0，5），综上D点坐标为（0，5）、E点坐标为（4，8）．【点评】本题主要考查了翻折变换、勾股定理等知识点，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解答此题的关键．25．如图，在直角坐标系中，B点的坐标为（a，b），且a、b满足．（1）求B点的坐标；（2）点A为y轴上一动点，过B点作BC⊥AB交x轴正半轴于点C，求证：BA=BC．【考点】坐标与图形性质；非负数的性质：偶次方；非负数的性质：算术平方根．【专题】动点型．【分析】（1）由于所给的等式是两个非负数的和是0，根据非负数的性质得到每一个非负数都等于0，从而得到一个关于a，b的二元一次方程组，解之即可．（2）作BM⊥y轴于M，BN⊥x轴于N点，很容易知道△ABM≌△CBN．而B点坐标是（2，2），那么就有一组对应边相等，故全等，可得BA=BC．【解答】解：（1）∵，（a﹣b）2≥0，而∴，（a﹣b）2=0∴．解得．∴B点坐标为（2，2）；（2）作BM⊥y轴于M，BN⊥x轴于N点，如图：∴∠MBN=90°．∵BC⊥AB，∴∠ABC=90°．∴∠ABM=∠CBN．∵B点坐标是（2，2），∴BM=BN，在△ABM和△CBN中，，∴△ABM≌△CBN（AAS）．∴BA=BC．【点评】本题主要考查了非负数的性质，主要利用了两个非负数的和是0，则每一个非负数都等于0，也利用了全等三角形的判定（ASA）和性质．26．如图，在平面直角坐标系中，OA=OB=OC=8，过点A的直线AD交BC于点D，交y 轴与点G，△ABD的面积为△ABC面积的．（1）求点D的坐标；（2）过点C作CE⊥AD，交AB交于F，垂足为E．求证：OF=OG；（3）若点F的坐标为（，0），在第一象限内是否存在点P，使△CFP是以CF为腰长的等腰直角三角形？若存在，请求出点P坐标；若不存在，请说明理由．【考点】一次函数综合题．【分析】（1）过点D作DH⊥AB．利用面积法求得：DH=2，设直线CB的解析式为y=kx+b，将点B、C的坐标代入可求得直线BC的解析式为y=﹣x+8，将y=2代入得；﹣x+8=2，解得x=6．从而得到点D的坐标为（6，2）；（2）证明∠AOG=∠CEG，∠GAO=∠OCF，从而可得到Rt△AGO≌Rt△CFO，故此可得到OG=OF；（3）如图2所示，过点P作PH⊥y轴，垂足为H．依据AAS证明Rt△HPC≌Rt△OFC，于是得到HC=OF=，PH=OC=8，从而可求得点P的坐标为（8，9）；如图3所示：过点P作PH⊥x轴，垂足为H．依据AAS证明Rt△HPF≌Rt△OFC，于是得到OC=FH=8，PH=OF=，从而求得点P的坐标为（9，）．【解答】解：（1）如图1，过点D作DH⊥AB．∵，∴．∴DH=2．设直线CB的解析式为y=kx+b，将点B、C的坐标代入得：，解得：k=﹣1，b=8．∴直线BC的解析式为y=﹣x+8．将y=2代入得；﹣x+8=2．解得x=6．∴点D的坐标为（6，2）．（2）∵CE⊥AD，CO⊥AO，∴∠AOG=∠CEG．又∵∠AGO=∠CGO，∴∠GAO=∠OCF．在Rt△AGO和Rt△CFO中，，∴Rt△AGO≌Rt△CFO．∴OG=OF．（3）如图2，过点P作PH⊥y轴，垂足为H．∵△PCF为等腰直角三角形，∴PC=CF，∠PCF=90°．∴∠HCP+∠FCO=90°．又∵∠OCF+∠OFC=90°，∴∠HCP=∠COF．在Rt△HPC和Rt△OFC中，，∴Rt△HPC≌Rt△OFC．∴HC=OF=，PH=OC=8．∴点P的纵坐标=8+=．∴点P的坐标为（8，9）．如图3所示：过点P作PH⊥x轴，垂足为H．∵△PCF为等腰直角三角形，∴PC=CF，∠CFP=90°．∴∠PFH+∠OFC=90°．又∵∠HFP+∠FPH=90°，∴∠OHC=∠FPH．在Rt△HPF和Rt△OFC中，，∴Rt△HPF≌Rt△OFC．∴OC=FH=8，PH=OF=．∴点P的横坐标=8+=9．∴点P的坐标为（9，）．【点评】本题主要考查的是一次函数的综合应用，解答本题主要应用了全等三角形的性质和判定、等腰直角三角形的性质、待定系数法求一次函数的解析式，掌握本题的辅助线的作法是解题的关键．。
2018_2019学年高二数学上学期入学考试试题
双峰一中2018年下学期高二入学考试数学试题总分值：150分 时量：120分钟一、选择题（每题5分，共60分，每题只有一个正确选项）1．设集合}{3,2,1,0=A ，{}032<-=x x x B ，那么=B A （ ）A.}0{B.C.}{30<<x x D.}2,1{2.已知a =(),3x ，b =()3,1，且a ⊥b ，那么x 等于（ ） A 、-1 B 、 -9 C 、9 D 、13.圆2286160x y x y +-++=与圆2216x y +=的位置关系是（ ）A 、相交B 、相离C 、内切D 、外切 4.以下函数中，以π为周期且在区间0,2π⎛⎫⎪⎝⎭上为增函数的是( ) A. sin2xy = B.sin y x = C. tan y x =- D .cos 2y x =- 5.已知等差数列{}n a 知足56a a +=28，那么其前10项之和为 （ ） A 140 B 280 C 168 D 566.βα,都是锐角，且5sin 13α=，()4cos 5αβ+=-，那么βsin 的值是（ ） A 、3365 B 、1665 C 、5665 D 、63657. 用秦九韶算法计算65432()3456781f x x x x x x x =++++++，当0.4x =时需要做加法和乘法的次数别离为（ ）A ．5，6B ．6，6C ．5，5D ．6，58.点P(4,-2)与圆224x y +=上任一点连线的中点的轨迹方程是（ ） A 、()()22211x y -++= B 、()()22214x y -++= C 、()()22421x y ++-= D 、()()22211x y ++-= 9.要取得函数2sin 2y x =的图像，只需将x x y 2cos 2sin 3-=的图像（ ）A 、向右平移6π个单位B 、向右平移12π个单位C 、向左平移6π个单位D 、向左平移12π个单位10. 从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是( )A. 至少有1个白球,都是白球B. 至少有1个白球,至少有1个红球C. 恰有1个白球,恰有2个白球D. 至少有1个白球,都是红球 11.已知O是平面内必然点，A,B,C是平面上不共线的三个点，动点P知足)(0,)AB AC OP OA AB AC λλ⎛⎫⎪=++∈+∞⎡⎣ ⎪⎝⎭,那么点P 的轨迹必然通过△ABC 的（ ） A ． 外心 B.内心 C.重心 D.垂心12.函数()f x 在区间D 上是凸函数，那么关于区间D 上的任意实数1x ，2x ，…，n x 都有()()()12...n f x f x f x n +++≤12...nx x x f n +++⎛⎫⎪⎝⎭，现已知()sin f x x =在[]0,π上是 凸函数，那么在△ABC 中，sin in sin A s B C ++的最大值是（ ） A 、12B 、3C 、3D 、33二、填空题（每题5分，共20分）13.cos43°cos77°+sin 43°cos167°的值为14.过两直线23100x y -+=和3420x y +-=的交点，且垂直于直线240x y -+=的直线方程为________ 15设ABC ∆的内角,,A B C 的对边别离为,,a b c ，且12,cos ,3sin 2sin ,4a C A B ==-=则c =16．如图，在棱长为1的正方体ABCD －A 1B 1C 1D 1中，已知E 、F 别离是棱AB 、AD 的中点．假设P 为棱CC 1上一点，且平面A 1EF ⊥平面EFP ，那么CP ＝.三、解答题(第17题10分，其余每题12分，共70分)17.已知等差数列｛a n ｝中，a 1＝29，S 10＝S 20，问那个数列的前多少项和最大?并求此最大值18.已知向量a ,b 的夹角为60°，且a =2,b =1,假设c =a -4b ，d =a +2b ，求： ⑴a ·b⑵c +d19.如图，在四棱锥P ABCD -中，底面ABCD 是正方形，PA ⊥底面ABCD ,且PA =AB =1⑴求证：BD ⊥平面ACP ⑵求异面直线BC 与PD 所成的角⑶求直线PB 与平面PAC 所成的角20.已知向量()3,1,cos ,sin 33x x a b ⎛⎫==- ⎪⎝⎭，记()2sin 3x f x a b =⋅⑴若[]0,x π∈，求函数()f x 的值域；⑵在△ABC 中，假设()1f C =，求sin sin A B +的最大值21.已知关于x 的一次函数y mx n =+.（1）设集合{2,1,1,2,3}P =--和{2,3}Q =-，别离从集合P 和Q 中随机取一个数作为m 和n ，求函数y mx n =+是增函数的概率；（2）实数,m n 知足条件101111m n m n +-≤⎧⎪-≤≤⎨⎪-≤≤⎩，求函数y mx n =+的图象通过第一、二、三象限的概率.22. 已知函数()cos 2(),(0,0,0)222A A f x x A πωϕωϕ=-+>><<的图象过点(1,2)，相邻两条对称轴间的距离为2，且()f x 的最大值为2. (1)求ϕ；(2)计算(1)(2)(2010)f f f +++；(3)假设函数()()1g x f x m =--在区间[1，4]上恰有一个零点，求m 的范围.入学考试（数学）参考答案一、DAADA CBADC BD 二、13.12-14、220x y ++= 1五、4 1六、38三、17（10分）设数列｛a n ｝的公差为d ∵S 10＝S 20，∴10×29＋2910⨯d ＝20×29＋21920⨯d 解得d ＝－2 ∴a n ＝－2n ＋31设那个数列的前n 项和最大，a n ≥0 －2n ＋31≥0那么需： 即a n ＋1≤0 －2(n ＋1)＋31≤0∴14.5≤n ≤15.5∵n ∈N ，∴n ＝15 ∴当n ＝15时，S n 最大，最大值为S 15＝15×29＋21415⨯ (－2)＝225.1八、（12分）（1）cos 1a b a b θ⋅=⋅⋅=（5分）（2）()()22242c d c da b a b+=+=-++=()224212a b a b +-⋅= 因此23c d +=（12分）1九、（12分）证明：∵PA ⊥平面ABCD ， BD ⊂平面ABCD ，PA BD ∴⊥又ABCD 为正方形，BD AC ∴⊥而,PA AC 是平面PAC 内的两条相交直线，BD ∴⊥平面PAC （4分）(2)解： ∵ABCD 为正方形，BC ∴∥AD ，PDA ∴∠为异面直线BC 与AD 所成的角， （6分） 由已知可知，PDA ∆为直角三角形，又PA AB =，∵PA AD =， 45PDA ∴∠=︒，异面直线BC 与PD 所成的角为45º. （8分）（3）设AC 与BD 交于点O ，连接PO ，因为BD ⊥平面ACP 因此∠BPO 或其补角为直线PB 与平面PAC 所成角（10分） 因为BO=22，PB=2，因此sin ∠BPO=12，因此∠BPO=30° 因此所成角为30°（12分） 20.()22sin2sin 1336x f x a b x π⎛⎫=⋅=+- ⎪⎝⎭（3分）y m=（1）∵[]250,,,3666x x ππππ⎡⎤∈∴+∈⎢⎥⎣⎦因此函数()f x 的值域为[]0,1（6分） （2）()()22sin 11,0,36f C C C ππ⎛⎫=+-=∈⎪⎝⎭因此C=2π2A B π∴+=则2B A π=-且0,2A π⎛⎫∈ ⎪⎝⎭sin sin sin sin 2A B A A π⎛⎫∴+=+- ⎪⎝⎭=sin cos A A +=2sin 4A π⎛⎫+ ⎪⎝⎭∴当4A π=时有最大值2（12分）2一、解：（1）由已知，抽取的全数结果表示为（m ，n ），那么大体事件有：（-2，-2），（-2，3），（-1，-2），（-1，3），（1，-2），（1，3），（2，-2），（2，3），（3，-2），（3，3），共10个大体事件，设使函数为增函数的事件为A ，m 〉0，那么A 包括的大体事件有：（1，-2），（1，3），（2，-2），（2，3），（3，-2），（3，3）共6个大体事件，由古典概型公式，P （A ）=63105=．…（6分） （2）m 、n 知足条件的区域如下图：故使函数图象过一、二、三象限的（m ，n ）的区域为第一象限的阴影部份， 由几何概型的概率公式得所求事件的概率为17P =．…（12分） 22.解：（1）22,4,02224T T T πππωωω==>∴==∴=，由于()f x 的最大值为2且A>0， 因此222A A +=即A=2得()1cos 2()4f x x πϕ=-+，又函数()f x 的图象过点(1,2)则cos 2()1sin 2122,042424k k πππππϕϕϕπϕπϕϕ+=-∴=∴=+=+<<∴=……3分（2）由(1)知()1cos 2()44f x x ππ=-+且周期为4，2020=4×502+2故()()()(){}()()502123412f f f f f f +++++=502432011⨯+=……………7分(3) 由()()1cos()sin222g x f x m x m x m πππ=--=-+-=-在区间[1,4]上恰有一个零点知：函数sin2y x π=的图象与直线恰有一个交点。
2018-2019学年高二上学期开学考试数学试题
2018—2019 学年高二上学期开学考试数学试题一．选择题（每个题 5 分，共 60 分）1．若集合M = {x | x 2 - x - 2 > 0} ，N = { y | 1 < y ≤ 3} ，则(C R M ) ⋂ N = （）A ．{x | -1 ≤ x ≤ 3}B ．{x | -1 ≤ x ≤ 2}C ．{x | 1 < x ≤ 2}D ．φ2.命题“22sin cos 1αα+=恒成立”的否定是（ ）A. R α∃∈ ，使得22sin cos 1αα+=B. R α∀∈ ，使得22sin cos 1αα+≠C. R α∀∈，使得22sin cos 1αα+=D. R α∃∈，使得22sin cos 1αα+≠3.方程3 x + x = 3 的解所在的区间为 （ ） A ．（0,1） B ．（1,2） C ．（2,3） D ．（3,4） 4．若 a , b ∈ R ,则下列恒成立的不等式是( )A. 2a b ab + B ．2b a a b+ C ．222()22a b a b ++≥ D ．11()()4()a b a b a b ++≥+ 5.要得到 y = sin(2 x -23π) 图像, 需要将函数 y = sin 2 x 的图像（ ） A.向左平移23π个单位 B.向右平移23π个单位 C.向左平移3π个单位 D.向右平移3π个单位6.已知直线 l 1 ： ax - y + 2a = 0 ，l 2 ： (2a - 1) x + ay + a = 0 互相垂直，则 a 的值是 （ ）A ．0B ．1C ．0 或 1D ．0 或﹣17.已知 tan(α+ β) =25 tan(β-4π) =14, 则 tan(α+4π) = A. 16 B ．2213 C ．322 D ．1318 8．在△ABC 中，若 sin B sin C = cos 22A ，则下面等式一定成立的是() A ．A ＝B B ．A ＝C C ．B ＝CD ．A ＝B ＝C9．已知变量 x , y 满足约束条件20170x y x x y -+≤⎧⎪≥⎨⎪+-≤⎩则y x 的取值范围是 A. 9[,6]5 B ．9(,][6,)5-∞+∞ C ．(,3][6,)-∞+∞ D ．[3,6] 10．如图，在四面体 ABCD 中，E ，F 分别是 AC 与 BD 的中点，若 CD ＝2AB ＝4，EF⊥BA，则 EF 与 CD 所成的角为( )A ．90°B ．45°C ．60°D ．30°11．定义12...nn p p p +++为 n 个正数 p 1 , p 2 , , p n 的“均倒数”，若已知数列{a n } 的前n 项的“均倒数”为15,又5n n a b =,则121b b +231b b +10111...b b += A. 817 B ．919 C ．1021 D ．1123 12.分别以直角三角形的斜边和两直角边所在直线为轴，将三角形旋转一周所得旋转体的体积 依次为 V 1、V 2、V 3，则( )A. V 1 = V 2 + V 3 B ．222123V V V =+ C ．211V 221V =231V + D ．11V 21V =31V +二．填空题（每个题 5 分，共 20 分）13.已知一个三棱锥的正视图和俯视图如图所示，其中俯视图是顶角为120°的等腰三角形，则该三棱锥的侧视图面积为 ．14.某同学在借助计算器求“方程 lg x = 2 - x 的近似解（精确到 0.1）”时，设 f ( x ) = lg x + x - 2 ，算得 f (1) < 0, f (2) > 0；在以下过程中，他用“二分法”又取了 4个x 的值，计算了其函数值的正负，并得出判断：方程的近似解是 x = 1.8 ．那么他所取的 x 的4 个值中最后一个值是 ．15．若a = (-2, -1),b = (λ,1) ，若 a 与b 的夹角为钝角，则λ的取值范围是 16．α、β是两个不同的平面，m 、n 是平面α及β之外的两条不同直线，给出四个结论：①m⊥n；②α⊥β；③n⊥β；④m⊥α，以其中三个论断作为条件，余下一个作为结论，写出你认为正确的一个命题是 ．三．解答题（共 6 道题，70 分）17.（10 分）在平面直角坐标系 xOy 中，点 A(0,3)，直线l ： y = 2 x - 4 .设圆 C 的半径为 1， 圆心在 l 上.(1)若圆心 C 也在直线 y = x - 1 上，过点 A 作圆 C 的切线，求切线的方程；(2)若圆 C 上存在点 M ，使 MA = 2 MO ，求圆心 C 的横坐标 a 的取值范围.18. (12 分)如图所示，在四边形 ABCD 中，∠D = 2∠B ，且 AD = 1 ，CD = 3 ， cos B（Ⅰ）求△ ACD 的面积；（Ⅱ）若 BC =，求AB 的长．19．(12 分)如图，正方形 ABCD 和四边形 ACEF 所在的平面互相垂直，EF∥AC，ABCE ＝EF ＝1.(1)求证：AF∥平面 BDE ；(2)求证：CF⊥平面 BDE.20．(12 分)在△ABC 中，a ，b ，c 分别是角 A ，B ，C 的对边，设 f ( x ) = a 2 x 2 - (a 2 - b 2 ) x - 4c 2(1)若 f (1) = 0 ，且 B - C = 3π ，求角 C 的大小； (2)若 f (2) = 0 ，求角 C 的取值范围．21. (12 分)函数 f ( x ) = (a - 1)4 x + 2 x + 3（1）当 a =12 时，求函数 f ( x ) 在[-1,3]的最值 （2）当 x ∈ (-1,3) ， f ( x ) > 0 恒成立，求实数 a 的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
安义中学2018-2019学年上学期高一创新班阶段测试
数 学 试 题
一、选择题（本大题共有12个小题，每小题5分，共60分，在每小题给出的四选项中只有
一项是符合题目要求的。
）
1、已知集合{}
,30≤<∈=x Z x A 则集合A 的非空子集个数为（ ）个. A. 15 B. 16 C. 7 D. 8 2、设f (x )的定义域是(0,1),则函数y =f (x 2
)的定义域是( ) A.(0,1)
B.(−1,1)
C.(−1,0)
D.(−1,0)∪(0,1)
3、设a 、b ∈R ，集合｛1，a+b,a ｝={0, b
a ,b}，则b-a 等于（ ）
A.1
B.-1
C.2
D.-2
4、设集合M={x|x=k 2 +14 ,k ∈Z},N={x|x=k 4 +1
2 ,k ∈Z},则正确的是( )
A.M=N
B.M ⊂≠N
C.N ⊂≠
M D.M ⋂N=∅ 5、已知A={0,1} ,B={-1,0,1},f 是从A 到B 的映射，则满足f(0)>f(1)的映射有( ) A.3个 B.4个 C.5个 D.6个 6、若f(1x )=x
1-x ,则当x ≠0且x ≠1时，f(x)等于( )
A. 1x
B. 1x-1
C. 11-x
D. 1
x
-1 7、已知函数f(x)= 3
3x-1ax 2+ax-3 的定义域是R ，则实数a 的取值范围是( )
A.a>13
B.-12<a<0
C.-12<a ≤0
D.a ≤13
8.若f （x ）满足关系式f （x ）+2f （1
x ）=3x ，则f （2）的值为（ ）
A ．1
B ．﹣1
C ．﹣32
D ．3
2
9.设全集U ={(x ,y )|x ,y ∈R },集合M ={(x ,y )|y −3
x −2
=1},N ={(x ,y )|y ≠x +1},那么∁U (M ∪N )等于( )
A .∅
B .{(2,3)}
C .(2,3)
D .{(x ,y )|y =x +1}
10.A={y|y=x 2
+1,x ∈N},B={x|x=a 2
+2a+2,a ∈N}，则A 与B 的关系是（ ）
A.A=B
B.A ⊂≠B
C.B ⊆A
D.B ⊂≠
A 11. 已知b ax y x f
B y A x R B A +=→∈∈==:,,,是从A 到B 的映射，若1和8的原象分别是3和10，则5在f 下的象是（ ）
A .3
B .4
C .5
D .6
12.设函数=≠=-+-)(,,2)23()32()(2
2
x f b a x x bf x af x f 则且满足 （ ） A ．
b a x - B.b a b a x ++-3 C.b a b a x ++-13 D.b
a x
b a ++-3 二、填空题：（本题共4小题，每小题5分，共20分.）
13.已知集合A ＝｛－1，3，2m －1},集合B ＝｛3，m 2
｝，若B ⊆A ，则实数m ＝ .
14.集合P ={(x ,y )|x 2
−y 2
=0},Q ={(x ,y )|y =1−|x |},则P ∩Q 的子集个数是________.
15. 如果集合{
}
0122
=++=x ax x A 中只有一个元素，则a 的值是________. 16．设1
()1f x x
=
-,则(){}
f f f x ⎡⎤⎣⎦的解析式为________. 三、解答题（本大题6小题，共70分.解答时应写出文字说明、证明过程或演算步骤）.
17．(本题满分10分）若3232c ++-=和集合｝｛R b a b a x x ∈+==,,6|M 试
判断c 与集合M 的关系。
18、(本题满分12分)已知集合{}22310A x x x =++=，{}
22(2)10B x m x m x =+++=，若
A B A =，求实数m 的取值范围.
19、(本题满分12分)已知集合A ＝｛x| 73<≤x ｝, B={x| 2<x<10}, C={x|x<a}
（1）求;B A ⋃ （2）求
B A R ）（
C ; （3）若A C ⊆,求a 的取值范围．
20、(本题满分12分)已知函数3()1
x
f x x ，猜想单调性并用单调性的定义证明，且求()f x 在区间[2,5]上的最大值和最小值
21.(本题满分12分)已知定义在[]3,2-的一次函数()f x 为单调增函数，且值域为[]2,7，
（I ）求()f x 的解析式；
（II ）求函数[]()f f x 的解析式并确定其定义域。
22.(本题满分12分)通过研究学生的学习行为，心理学家发现，学生的接受能力依赖于老师引入概念和描述问题所用的时间：讲座开始时，学生兴趣激增；中间有一段不太长的时间，学生的兴趣保持较理想的状态；随后学生的注意力开始分散。
分析结果和实验表明，用()f x 表示学生接受概念的能力（()f x 的值愈大，表示接受的能力愈强），x 表示提出和讲授概念的时间（单位：分钟），可有以下的公式：
()20.1 2.643,(010)59,(1016)3107,(1630)x x x f x x x x ⎧-++<≤⎪⎪=<≤⎨⎪
-+<≤⎪⎩
，
(1)开讲后多少分钟，学生的接受能力最强？能维持多长时间？ (2)开讲后5分钟与开讲后20分钟比较，学生的接受能力何时强一些？
（3）一个数学难题需要55的接受能力及13分钟时间，老师能否在学生一直达到所需接受能力的状态下讲完这个难题？。