浙江省瑞安中学八年级数学下册《2.2一元二次方程的解法2》课件
合集下载
新浙教版八年级下册初中数学 2-2 一元二次方程的解法(2) 教学课件

典例精讲
例1 解下列方程:
(1)3x2-48=0
(2)(2x-3)2=7
解: 移项,得
3x2 48 x2 16
x 4
解:2x 3 7,
或2x 3 - 7
x1
7 3, 2
x2
7 3 2
第十页,共二十八页。
探究2 你能用开平方法解下列方程吗?
x2-10x=-16
不能
变 形 为
归纳
配方法解二次项系数为1的一元二次方程的基本步骤:
(1)移项:把常数项移到方程的右边; (2)配方:方程两边同时加上一次项系数一半的平方; (3)开方:根据平方根的意义,方程两边开平方; (4)求解:解一元一次方程; (5)定解:写出原方程的解.
第十三页,共二十八页。
典例精讲
例2 用配方法解下列一元二次方程
二次项系数不是1,把它变成1.
第十六页,共二十八页。
解答 2x2 4x 3 0
解:方程两边同除以
得
x2 2x - 3 0 2
移项, 得
x2 2x 3 2
2,
. .
方程两边同加上 1 , 得
x2 2x 1 3 1 2
.
5
即( x 1 )2
2
.
x 1 1 2
10或
. x 1 - 1 10 2
常数n的值.
第十九页,共二十八页。
典例精讲
用配方法求2x2 7x 2的最小值
2x2 7x 2 2 x2 7 x 2
2 2 x 7 2 33 33,
4 8 8 2x2 7x 2的最小值为 33
8
第二十页,共二十八页。
练一练
用配方法解下列方程:
(1)0.2x2 0.4x 1
一元二次方程的解法课件浙教版数学八年级下册2

将方程的左边分解因式得:
(5x+4)(5x-4)=0
则5x+4=0或5x-4=0
∴x1= 4 , x2=- 4
5
5
例2 解下列一元二次方程: (1)(x-5) (3x-2)=10; 解: 化简方程,得 3x2-17x=0.
这一步利用什么 方法分解因式?
将方程的左边分解因式,得 x(3x-17)=0,
1.方程(x-3)2=0的根是 (
)
A.x=-3 B.x=3 C.x=±3 D.x= 3
1.选B
2.解方程:(1)x2=3x;(2)3(x-1)2=x(x-1).
解:(1)移项,得x2-3x=0, 分解因式,得x(x-3)=0, 则x=0或x-3=0, 解得x1=0,x2=3; (2)移项,得3(x-1)2-x(x-1)=0, 分解因式,得(x-1)[3(x-1)-x]=0, 即(x-1)(2x-3)=0,则x-1=0或2x-3=0, 解得 x1=1,x2=32.
2.你能用上面的结论解方程(2x+3)(2x-3)=0吗? 2x+3=0,或2x-3=0.
解得x1=- ,x2=
【思考】前面解方程时利用了什么方法呢?
因式分解 把一个多项式化成几个整式的积的形式. 像上面这种利用因式分解解一元二次方程的方法叫做因式分解法.
它的基本步骤是: 1.若方程的右边不是零,则先移项,使方程的右边为零; 2、将方程的左边分解因式; 3、根据若A·B=0,则A=0或B=0,将解方程转化为解两个一元一次方程.
3.解下列方程:
(1)x(x-1)=0;(2)x(x-1)=2-2x; (3)9m2-(2m+1)2=0;(4)x2+7=2 7x.
解:(1)x=0或x-1=0, 解得x1=0,x2=1; (2)移项,得x(x-1)-(2-2x)=0, 分解因式,得(x+2)(x-1)=0, 则x+2=0或x-1=0, 解得x1=-2,x2=1;
新浙教版八年级数学下册同步课件:2.2一元二次方程的解法

2.用配方法解下列方程:
(1) n(n 1) 3n 1 2
(2) 3 x16n 是一个
关于x的完全平方式,求常数n的值。
已知 9x2 18n 1x 18n 是一个关于x
的完全平方式,求常数n的值。
---------------------------------- 赠予 ----------------------------------
★一除、二移、三配、四开、五解.
用配方法解 2x2 x 1 0 时,配方结果正确的是( D )
( A) ( x 1 )2 3 24
(B) ( x 1)2 3 44
(C ) ( x 1)2 17 4 16
(D) ( x 1)2 9 4 16
1.用配方法解下列方程: (1)2x2+6x+3=0 (2)2x2-7x+5=0
新浙教版八年级数学 下册同步课件
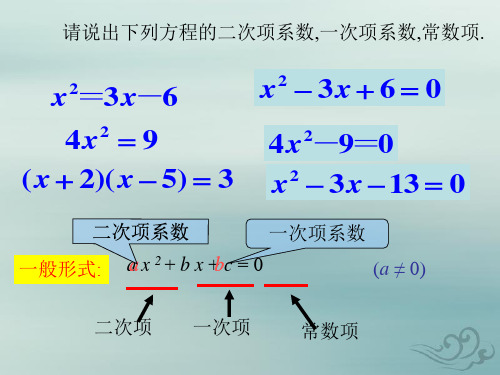
1、一元二次方程的一般形式:
ax 2 bx c 0 (a 0)
ax 2 二次项, a 二次项系数
c 常数项
bx 一次项, b 一次项系数
2、一元二次方程的解法: (1)因式分解法 (2)开平方法 (3)配方法
开平方法解一元二次方程:
一般地,对于形如:① x 2 a 2
② m x n b 其中 a,b 是非负数,
这样的一元二次方程,可用开平方法 直接得 出它的两个解或者将它转化为两个一元一次 方程进行求解.
配方法解一元二次方程的基本步骤:
移项:把常数项移到方程的右边; 配方:方程两边都加上一次项系数一半的平方; 开方:根据平方根意义,方程两边开平方; 求解:解一元一次方程;
晨起凭栏眺 但见云卷云舒 风月乍起 春寒已淡忘 如今秋凉甚好 几度眼迷离
浙教版数学八下课件2.2一元二次方程解法

练习1、用直接开平方法解下列方程 (1)3x2-75=0(2)x2+4=0
(3) x2 1(a 0) a
例3、解方程:16(x-3)2=25 分析:用换元法,(x-3)看成一个整体。 练习1、解方程9(2x+3)2=(x-3)2
2、方程ax2=c有实根的条件是————
配方法 先把方程的常数项移到方程的右边,再把左边 配成一个完全平方式,如果右边是非负数,就 可以进一步通过直接开平方法来求出它的解.
(1)当每辆车的月租金定3600元时,能租出多少辆?
100-(3600-3000)÷50=88(辆)
(2)当每辆车的月租金定为多少元时,租赁公司的月收益
(租金收入扣除维护费)可达到306600元?
设月租金定为x元,得:
(x 150)(100 x 3000) 306600 (3)3x2=4
x1+x2=3;x1·x2=0 x1+x2=0;x1·x2=-4/3
例3 已知方程x2-(k+1)x+3k=0的一个根是2,求 它的另一个根和k的值.
解:设方程的另一个根为x1 把x=2代入方程,得 4-2(k+1)+3k=0, 解这个方程,得 k=-2,
9.某种药品原价为36元/盒,经过连续两次降价后售价
为25元/盒。设平均每次降价的百分率为x,根据题意所
列方程正确的是() C
A.36(1-x)2=36-25 B.36(1-2x)=25
C.36(1-x)2=25
D.36(1-x2)=25
12.如果关于x的一元二次方程kx2-x+1=0有两个不相 等的实数根,那么k的取值范围是() D
怎样解形如与ax 2 0
ax2 c 0
的一元二次方程呢?
(3) x2 1(a 0) a
例3、解方程:16(x-3)2=25 分析:用换元法,(x-3)看成一个整体。 练习1、解方程9(2x+3)2=(x-3)2
2、方程ax2=c有实根的条件是————
配方法 先把方程的常数项移到方程的右边,再把左边 配成一个完全平方式,如果右边是非负数,就 可以进一步通过直接开平方法来求出它的解.
(1)当每辆车的月租金定3600元时,能租出多少辆?
100-(3600-3000)÷50=88(辆)
(2)当每辆车的月租金定为多少元时,租赁公司的月收益
(租金收入扣除维护费)可达到306600元?
设月租金定为x元,得:
(x 150)(100 x 3000) 306600 (3)3x2=4
x1+x2=3;x1·x2=0 x1+x2=0;x1·x2=-4/3
例3 已知方程x2-(k+1)x+3k=0的一个根是2,求 它的另一个根和k的值.
解:设方程的另一个根为x1 把x=2代入方程,得 4-2(k+1)+3k=0, 解这个方程,得 k=-2,
9.某种药品原价为36元/盒,经过连续两次降价后售价
为25元/盒。设平均每次降价的百分率为x,根据题意所
列方程正确的是() C
A.36(1-x)2=36-25 B.36(1-2x)=25
C.36(1-x)2=25
D.36(1-x2)=25
12.如果关于x的一元二次方程kx2-x+1=0有两个不相 等的实数根,那么k的取值范围是() D
怎样解形如与ax 2 0
ax2 c 0
的一元二次方程呢?
新浙教版数学八年级下课件:2.2 一元二次方程的解法(2)(9张幻灯片)课件

解:方程两边同除以2,得
x2+2x-3/2=0 移项,得 x2+2x=3/2 方程两边都加上1,得 x2+2x+1=5/2 即:(x+1)2=5/2
∴x+1=
x2-8/3x-1=0 移项,得 x2-8/3x=1 方程两边都加上16/9,得 x2-8/3x+16/9=25/9 即:(x-4/3)2=25/9 5
∴x- 4/3= 5/3 或x- 4/3=- 5/3
5 或x+1=-
∴x1= -1+
5 或x2= -1-
5 ∴ x 1= 3
或x2= -1/3
一级达标重点名校: ax2+bx+c=0
1.方程两边同时除以a,得 x2+ b x+ c =0 a a 2.移项,得 x 2+ b x= - c a a
一级达标重点名校中学课件
试一试
解方程 5x2=10x+1
遇到二次项系数不是1的一元二次方程,只要将方程的 两边都除以二次项系数,转化为我们能用配方法解二 次项系数是1的一元二次方法。
一级达标重点名校中学课件
例3 用配方法解下列一元二次方程 (2) 3x2-8x-3=0
解:方程两边同除以3,得
(1) 2x2+4x-3=0
2-4ac b b 2 b ) 2= 3.方程两边都加上( 2a ) ,得 x2+ b x+( 2 a 4a 2a
4.用开平方法,解得答案。
一级达标重点名校中学课件
练一练
1.用配方法解下列方程: (1) 2x2+6x+3=0 (2) 2x2-7x+5=0
一级达标重点名校中学课件
x2+2x-3/2=0 移项,得 x2+2x=3/2 方程两边都加上1,得 x2+2x+1=5/2 即:(x+1)2=5/2
∴x+1=
x2-8/3x-1=0 移项,得 x2-8/3x=1 方程两边都加上16/9,得 x2-8/3x+16/9=25/9 即:(x-4/3)2=25/9 5
∴x- 4/3= 5/3 或x- 4/3=- 5/3
5 或x+1=-
∴x1= -1+
5 或x2= -1-
5 ∴ x 1= 3
或x2= -1/3
一级达标重点名校: ax2+bx+c=0
1.方程两边同时除以a,得 x2+ b x+ c =0 a a 2.移项,得 x 2+ b x= - c a a
一级达标重点名校中学课件
试一试
解方程 5x2=10x+1
遇到二次项系数不是1的一元二次方程,只要将方程的 两边都除以二次项系数,转化为我们能用配方法解二 次项系数是1的一元二次方法。
一级达标重点名校中学课件
例3 用配方法解下列一元二次方程 (2) 3x2-8x-3=0
解:方程两边同除以3,得
(1) 2x2+4x-3=0
2-4ac b b 2 b ) 2= 3.方程两边都加上( 2a ) ,得 x2+ b x+( 2 a 4a 2a
4.用开平方法,解得答案。
一级达标重点名校中学课件
练一练
1.用配方法解下列方程: (1) 2x2+6x+3=0 (2) 2x2-7x+5=0
一级达标重点名校中学课件
2020年浙教版八年级数学下册第二章《一元二次方程的解法》精品课件 (2)

即:(x+1)2=5/2
时 学
∴x+1=
5 或x+1=-
5
练∴x1= -1+ 5 或x2= -1-
解:方程两边同除以2,得
x2-8/3x-1=0 移项,得 x2-8/3x=1 方程两边都加上16/9,得
x2-8/3x+16/9=25/9 即:(x-4/3)2=25/9
∴x- 4/3= 5/3 或x- 4/3=- 5/3
b a
x+
c a
=0
2.移项,得 x2+
倍
b a
x= -
c a
速 课
3.方程两边都加上(
b 2a
)2 ,得
时
x2+
b a
x+(2ba
)2=
b2-4ac 4a2
学 练
4.用开平方法,解得答案。
(1) n (n - 1) - 3n = 1
2
倍 速
(2) 3 x 2 - 1 x - 1 = 0
课
4
28
时
学
练
比一比:看谁做得快
用配方法解下列方程:
(1) 2x 2 - 5x + 2 = 0
倍 (2) 2 - 1 x 2 = 5 x
速 课
3
3
时
学
练
小结
ax2+bx+c=0
1.方程两边同时除以a,得 x2+
速 课 时 学 练
开平方法解一元二次方程
• 一般地,对于形如: ① x 2 = a
( ) ②
m
2
x+n =b
其中 a,b 是非负数,
这样的一元二次方程,可用开平方法 直接得
浙教版初中数学八年级下册2.2一元二次方程的解法(2)-配方法(一)课件

这样的方程,
• 【归纳结论】一般地,如果一个一元二次方程通过 配方转化成
• (x+n)2=p
(Ⅱ)
• 的形式,那么就有:
• (1)当p>0时,方程(Ⅱ)有两个不等的实数根
• (2)当p=0时,方程(Ⅱ)有两个相等的实数根
• x1=x2=-n; • (3)当p<0时,因为对任意实数x,都有(x+n)2≥0, 所以方程(Ⅱ)无实数根.
永远不要埋怨你已经发生的事情, 要么就改变它,要么就安静的接受它。
探讨怎样解方程x2-10x=―16
• x2+8x―9=0 • 分析:先把它变成 (x+m) 2 =n ( n≥0 )的形式 直接开平方法求解. • 解:移项,得:x2-10x=-16配方,得:x2-10x+52=16+52(两边同时加上一次项系数一半的平方) • 即:(x-5)2=9 • 开平方,得:x-5=±3 • 即:x-5=3,或x-5=-3 • 所以:x1=8,x2=2
• 例5用配方法解下列一元二次方程
• (1)x2+6x=1Βιβλιοθήκη (2) x2+5x-6=0
3.请认真阅读小 马的解题过程, 并思考下列问题:
(1)验证求解是否正确;
(2)两边为什么同时加上
?
(3)能否将
写成
?
(4)从③到④用到什么方法?
4.填空:
5.请用配方法解下列一元二次方程:
对于形如 在什么条件下才有实数根?
义务教育教科书(浙教)八年级数学下册
第2章 一元二次方程
填一填
1
4
• 我们知道,形如 • 的方程,可变形为 • 再根据平方根的意义,用直接开平方法求解.
八年级数学下册 2.2一元二次方程的解法 课件(新版)浙教版
例2 . 解方程 x2 2 2x 2
解:移项,得x2 2 2x 2 0 即 x2 2 2x ( 2)2 0 即 (x 2)2 0 解得 x1 x2 2
辨一辨:下列解一元二次方程的方法对吗?
解方程: ( x 2)2 2x( x 2) 解:方程两边都除以 ( x 2得) : x 2 2x
回顾复习:
12、、你你能能对用下因列式各分式解因法式解分下解列方程吗?
吗?
(1)
2y2 - 6y
=0
(2) 4x2 - 9 =0
(3) (3m - 4)2 - (4m - 3)2 =0
(4) x2 +12x + 36 =0
(5) 2x2-7x + 6 =0
例1:用因式分解法解下列一元二次方程。
(1) (x 5)(3x 2) 10 (2) 9y2 ( y 1)2 (3) t2 18t 17 (4) 20t2 70t-30
2.2 一元二次方程的解 法(1)
试一试:你能说出下列方程的解吗?
( x 2)( x 5) 0 x1 2,x2 5
若A·B=0, 则 (D )
(A)A=0; (B)B=0; (C)A=0且B=0;(D)A=0或B=0
你能说出下列方程的解吗?
( x 1)( x 4) 0 x1 1,x2 4
x( x2 x33x) 0
x1 0,x2 3
(xx2- +39)(x0- 3) = 0 x1 3,x2 3
x(x2-- 36x)2==-09
x1 3,x2 3
因式分解法的基本步骤:
(1)将方程变形,使方程的右边为零; (2)将方程的左边因式分解; (3)根据若A·B=0,则A=0或B=0,将解一元二次方 程转化为解两个一元一次方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) 2x22x20
x1
4622,x2
2 6 24
用配方法解一元二次方程的基本步骤:
ax2+bx+c=0
1.方程两边同时除以a,得 x2+
b a
x+
c a
=0
2.移项,得
x2+
b a
x=
-
c a
3.方程两边都加上(
b 2a
)2 ,得
x2+
b a
x+(2ba
)2=
b2-4ac 4a2
4.用开平方法,解得答案。
1.方程两边同时除以a,得 x2+
b a
x+
c a
=0
2.移项,得 x2+
b a
x= -
c a
3.方程两边都加上(
b 2a
)2 ,得
x2+
b a
x+(2ba
)2=
b2-4ac 4a2
4.用开平方法,解得答案。
一次聚会,出席的每位代表都和 其他代表各握一次手,统计结果 表明,一共握手45次。问参加聚 会的代表有多少人?
解:设参加聚会的代表有x人
由题意得 x (x 1) 45 2
解得 x1 10
x 2 9 (不合题意,舍去)
答:参加聚会的代表有10人
小结
用配方法解一元二次方程的基本步骤:
ax2+bx+c=0
2
即:பைடு நூலகம்(x+
b 2
)2=
b2-4c 4
③当 b2-4c≥0 时,就可以通过开平方法求
出方程的根.
解一元二次方程: x2- 8x- 4=0
解: 移项,得 x2- 8x = 4 方程两边同加上16得 x2- 8x+16 = 4+16 即 (x-4)2 = 20 ∴ x-4 = 2 5 或 x-4 = 2 5 解得 x1 = 2 5 +4,x2= 2 5 +4
试一试
解方程 5x2-10x-1=0
遇到二次项系数不是1的一元二次方 程,只要将方程的两边都除以二次项 系数,转化为我们能用配方法解二次 项系数是1的一元二次方法。
例3 用配方法解下列一元二次方程
(1)2x2x30
3
x1
1,
x2
2
(2)3x21x10 4 28
10 1
10 1
x1
6
3,x2
6
3
2.2一元二次方程的解法(2)
x2bxc0
复习回顾
一元二次方程开平方法和配方法(a=1)解法的 区别与联系.
开平方法:形如x2=b(b≥0);(x-a)2=b(b≥0)。
配方法:①先把方程x2+bx+c=0移项得x2+bx=-c.
②方程两边同时加一次项系数一半的平方,得
x2+bx+
(
b 2
)2
= -c + ( b )2
