课标通用甘肃省2019年中考数学总复习优化设计第8讲一元一次不等式组及其应用课件PPT
中考数学第一轮考点系统复习第二章方程(组)与不等式(组)第8讲一元一次不等式(组)及其应用(练本)课

4、享受阅读快乐,提高生活质量。下午12时36分6秒下午12时36分12:36:0622.3.11
谢谢观独具赏方为先
匠心可成锋 Y o u m a d e m y d a y !
我们,还在路上……
场最多能购买50个甲种奖品.
(2)学校计划购买甲、乙两种奖品共100个,且此次购买奖品的费用不超过2 000元.正逢商场促销,所有商品一律八折销售,求学校在商场最多能购买 多少个甲种奖品.
解:设学校在商场购买m个甲种奖品,则购买(100-m)个乙种奖品. 根据题意,得30×0.8m+20×0.8(100-m)≤2 000, 解得m≤50. 答:学校在商场最多能购买50个甲种奖品.
解:设购进电视机x台,则购进洗衣机(100-x)台.
根据题意,得
x
1 (100 x), 2
1800x 1500(100 x) 161800,
解得 33 1 x 39 1 .
3
3
∵x为整数,
∴x可以取34,35,36,37,38,39,
∴商店共有6种进货方案.
11.学校准备为“趣味数学”比赛购买奖品.已知在商场购买3个甲种奖品和2 个乙种奖品共需130元,购买6个甲种奖品和5个乙种奖品共需280元.
3倍,购进A,B两种风扇的总金额不超过1 170元.根据以上信息,小丹共
有哪些进货方案? 解:设购进A型风扇m台,则购进B型风扇(100-m)台.
根据题意,得
m 3(100 m),
10m
16(100
m)
解得71 2
1170,
3
m 75.
∵m为正整数,∴m可以取72,73,74,75,∴小丹共有4种进货方案:
12.(2020·德州)若关于x的不等式组
课标通用安徽2019中考数学总复习第一篇第二单元第8讲一元一次不等式(组)及其应用课件

考点必备梳理
考题初做诊断
考法必研突破
考点一
考点二
考点三
考点四
4.解集表示
类型 (a>b) x>a x>b ������ < ������ ������ < ������ ������ < ������ ������ > ������ ������ > ������ ������ < ������
解 x>a x<b
第8讲 一元一次不等式(组)及其 应用
考点必备梳理
考题初做诊断
考法必研突破
考点一
考点二
考点三
考点四
考点一不等式及其基本性质 1.定义 用不等号连接而成的式子. 2.性质
性 质 内 容 性质 不等式的两边都加上(或减去)同一 1 个数(或式子),不等号的方向不变 性质 不等式的两边都乘(或除以)同一个 2 正数,不等号的方向不变 性质 不等式的两边都乘(或除以)同一个 3 负数,不等号的方向改变
解析:首先解不等式组求得不等式组的解集,然后根据不等式组 ������-1 1 的整数解的个数从而确定a的范围.解不等式 3 − x<2 1得:x>4,解不 等式4(x-1)≤2(x-a)得:x≤2-a.则不等式组的解集是4<x≤2-a. ∵不等式组有3个整数解,∴7≤2-a<8, 解得:-6<a≤-5,故选B.
考点必备梳理
考题初做诊断
考法必研突破
考法1
考法2
考法3
考法4
考法3不等式(组)中字母的取值
������-1 1 - ������ < -1, 例3(2018· 山东泰安)不等式组 3 2 有3个整数解,则 4(������-1) ≤ 2(������-������) a的取值范围是( ) A.-6≤a<-5 B.-6<a≤-5 C.-6<a<-5 D.-6≤a≤-5 答案:B
备战 中考数学基础复习 第8课 一元一次不等式(组)及其应用课件(35张ppt)

3.性质3:不等式两边乘(或除以)同一个负数,不等号的方向___改__变____. 即如果a>b,c<0,那么ac___<___bc(或 a _<___ b ).
cc
二、不等式解集在数轴上的表示方法
三、一元一次不等式组的解集的四种类型(设a<b)
不等式组 (1) (2)
数轴表示
解集 _x_>_b_ _x_<_a_
【解析】(1)设购买篮球x个,则足球(60-x)个.由题意得70x+80(60-x)=4 600, 解得x=20,则60-x=40. 答:篮球买了20个,足球买了40个. (2)设购买了篮球y个.由题意得70y≤80(60-y),解得y≤32. 答:最多可购买篮球32个.
变式2.(2020·抚顺)某校计划为教师购买甲、乙两种词典.已知购买1本甲种 词典和2本乙种词典共需170元,购买2本甲种词典和3本乙种词典共需290元. (1)求每本甲种词典和每本乙种词典的价格分别为多少元? (2)学校计划购买甲种词典和乙种词典共30本,总费用不超过1 600元,那么最 多可购买甲种词典多少本?
2
2
y
4
3
y 1 3
13,① 12
2(y a) 0,②
解不等式①,得y≤0.
解不等式②,得y<a.
∵关于y的不等式组的解集为y≤0, ∴a>0.∴0<a≤5且a≠3. 又a为整数,则a的值为1,2,4,5. 符合条件的所有整数a的积为1×2×4×5=40.
6.寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小 组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中 国象棋需用158元; (1)求每副围棋和每副中国象棋各多少元; (2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅 中学最多可以购买多少副围棋?
中考数学复习课件:第1轮第2章第8讲 不等式(组)及应用

答:最多购买 5 千克苹果.
A.夯实基础
1.(2018·北海)若 m>n,则下列不等式正确的
是( B )
A.m-2<n-2
B.m4 >n4
C.6m<6n
D.-8m>-8n
2.(2019·宿迁)不等式 x-1≤2 的非负整数解有
2.解不等式:y-6 1-y+3 1>1. 解:不等式的解集为y<-9.
3.解一元一次不等式组的一般步骤: (1)求出这个不等式组中各个一元一次不等式的解 集; (2)利用数轴确定每个解集的公共部分,即求出了这 个一元一次不等式组的解集.
3(x-1)+2<5x+3,
3.解不等式组:x-2 1+x≥3x-4,
考点 解一元一次不等式(5 年 2 考) 2.(2019·常德)不等式 3x+1>2(x+4)的解集为 __x_>__7___.
3.(2020·泰安)解不等式:x+3 1-1<x-4 1. 解:不等式两边同时乘以 12 得 4(x+1)-12<3(x-1),解得 x<5. 所以不等式的解集为 x<5.
采购方案及最大利润. 解:由题意得
1 600x+2 500(20-x)≤39 200, 400x+500(20-x)≥8 500,
解得12≤x≤15, ∵x为正整数,∴x=12、13、14、15,
共有四种采购方案: ①甲型电脑12台,乙型电脑8台; ②甲型电脑13台,乙型电脑7台; ③甲型电脑14台,乙型电脑6台; ④甲型电脑15台,乙型电脑5台;
(1)设该商店购进甲型平板电脑 x 台,请写出全 部售出后该商店获利 y 与 x 之间函数表达式;
中考数学复习讲义课件 第2单元 第8讲 一元一次不等式(组)及其应用

14.(2021·成都)为改善城市人居环境,《成都市生活垃圾管理条例》(以下简 称《条例》)于 2021 年 3 月 1 日起正式施行.某区域原来每天需要处理生活 垃圾 920 吨,刚好被 12 个 A 型和 10 个 B 型预处置点位进行初筛、压缩等 处理.已知一个 A 型点位比一个 B 型点位每天多处理 7 吨生活垃圾. (1)求每个 B 型点位每天处理生活垃圾的吨数;
解:设需要增设 y 个 A 型点位才能当日处理完所有生活垃圾.由(1)可知, 《条例》施行后,每个 A 型点位每天处理生活垃圾 38+7-8=37(吨), 每个 B 型点位每天处理生活垃圾 38-8=30(吨). 根据题意,得 37(12+y)+30(10+5-y)≥920-10. 解得 y≥176. ∵y 是正整数,∴符合条件的 y 的最小值为 3. 答:至少需要增设 3 个 A 型点位才能当日处理完所有生活垃圾.
.
11.(2021·凉山州)解不等式1-3 x-x<3-x+4 2. 解:去分母,得 4(1-x)-12x<36-3(x+2). 去括号,得 4-4x-12x<36-3x-6. 移项,得-4x-12x+3x<36-6-4. 合并同类项,得-13x<26. 系数化为 1,得 x>-2.
5x-2>3(x+1), ① 12.(2021·成都)解不等式组:21x-1≤7-32x. ② 解:解不等式①,得 x>2.5. 解不等式②,得 x≤4. 则不等式组的解集为 2.5<x≤4.
一元一次不等式(组)的应用(10 年 3 考) ☞例 为响应政府“绿色发展”的号召,某商场从厂家购进 A,B 两种型号 的节能灯共 160 盏,A 型号节能灯的进价是 150 元/盏,B 型号节能灯的进 价是 350 元/盏,购进两种型号的节能灯共用去 36000 元. (1)求 A,B 两种型号节能灯各购进了多少盏; [分析] 设 A 型号节能灯购进了 x 盏,B 型号节能灯购进了 y 盏,根据“购 进了 A,B 两种型号节能灯共 160 盏,购进两种型号的节能灯共用去 36000 元”,列出方程组解答即可;
2019年中考数学全国通用复习讲义§2.4 一元一次不等式(组)(讲解部分)

(5 分)
(4 分)
(Hale Waihona Puke 分)㊀ ㊀ 用转化思想将实际问题中的不等关系抽象出来, 用不等式 ( 组) 的知识解答应用题和方案设计型问题. 例 2㊀ ( 2017 四川绵阳,21,11 分) 江南农场收割小麦, 已知
方法二㊀ 一元一次不等式( 组) 的应用
(4)1ɤxɤ3.
1 台大型收割机和 3 台小型收割机 1 小时可以收割小麦 1. 4 公
是大于等于或小于等于,那么这个点一定是实心点; 如果是大于 ㊀ ㊀ 变式训练 1㊀ 3x -5<-2x,① 组: 3x +2 ȡ1. ㊀ ② 2 由②得 xȡ0, 或小于,那么这个点应用空心圈表示. ( 2017 湖 北 黄 冈, 15, 5 分 ) 解 不 等 式
易错警示㊀ 在数轴上表示不等式的解集时, 要注意如果
考点三㊀ 一元一次不等式( 组) 的应用
的两边乘( 或除以) 同一个负数时,不等号的方向改变.
(1) 审:认真审题,分清已知量, 未知量及其关系, 找出题中 小于
不大
㊀ ㊀ 1. 定义:类似于方程组,把几个含有相同未知数的 ⑨㊀ 一元一 次不等式㊀ 合起来,就组成了一个一元一次不等式组. 这几个不等式所组成的不等式组的解集.
11 ㊀
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
4. 由两个一元一次不等式组成的不等式组的解集的四种情
课标通用甘肃省2019年中考数学总复习优化设计考点强化练7分式方程及其应用

考点强化练7 分式方程及其应用基础达标一、选择题1.解分式方程1x -1-2=31-x ,去分母得( )A.1-2(x-1)=-3B.1-2(x-1)=3C.1-2x-2=-3D.1-2x+2=3 答案A 2.关于x 的分式方程2x +3x -a =0的解为x=4,则常数a 的值为( )A.a=1B.a=2C.a=4D.a=10 答案D 解析把x=4代入方程2x+3x -a =0,得24+34-a =0,解得a=10.故选D . 3.分式方程x x -1-1=3(x -1)(x+2)的解为( )A.x=1B.x=-1C.无解D.x=-2 答案C解析方程两边同乘以(x-1)(x+2)得,x (x+2)-(x-1)(x+2)=3,解得x=1,经检验,x=1不是原方程的根,原分式方程无解,故选C .4.分式方程3x (x+1)=1-3x+1的根为( ) A.-1或3B.-1C.3D.1或-3 答案C解析去分母得:3=x 2+x-3x ,解得:x=-1或x=3,经检验x=-1是增根,分式方程的根为x=3,故选C .5.(2018山东淄博)“绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x 万平方米,则下面所列方程中正确的是( )A.60x −60(1+25%)x =30B.60(1+25%)x −60x =30C.60×(1+25%)x −60x=30D.60x −60×(1+25%)x=30答案C解析设实际工作时每天绿化的面积为x万平方米,则原来每天绿化的面积为x1+25%万平方米,依题意得:60x1+25%−60x=30,即60×(1+25%)x −60x=30.故选C.二、填空题6.(2017江苏宿迁)若关于x的分式方程mx-2=1-x2-x-3有增根,则实数m的值是.答案1解析方程两边同乘以x-2,可得m=x-1-3(x-2),解得m=-2x+5,因分式方程mx-2=1-x2-x-3有增根,可得x=2,所以m=1.三、解答题7.解方程:3x-1−2x=0.解两边乘x(x-1),得3x-2(x-1)=0, 解得x=-2,经检验:x=-2是原分式方程的解.8.(易错题)解方程:1+3xx-2=6x-2.解方程两边同乘以(x-2)得,(x-2)+3x=6, 解得:x=2,检验:当x=2时,x-2=0,∴x=2不是原分式方程的解,∴原分式方程无解.9.解方程:x+1x-1+4x2-1=1.解方程两边乘以(x+1)(x-1)得:(x+1)2+4=(x+1)(x-1), 解这个方程得:x=-3,检验:当x=-3时,(x+1)(x-1)≠0,x=-3是原方程的解;∴原方程的解是:x=-3.10.(2018湖南岳阳)为落实党中央“长江大保护”新发展理念,我市持续推进长江岸线保护,还洞庭湖和长江水清岸绿的自然生态原貌.某工程队负责对一面积为33 000平方米的非法砂石码头进行拆除,回填土方和复绿施工,为了缩短工期,该工程队增加了人力和设备,实际工作效率比原计划每天提高了20%,结果提前11天完成任务,求实际平均每天施工多少平方米?解设原计划平均每天施工x平方米,则实际平均每天施工1.2x平方米,根据题意得:33000x −330001.2x=11,解得:x=500,经检验,x=500是原方程的解,∴1.2x=600.答:实际平均每天施工600平方米.〚导学号13814034〛能力提升一、选择题1.(2018黑龙江)已知关于x的分式方程m-2x+1=1的解是负数,则m的取值范围是()A.m≤3B.m≤3且m≠2C.m<3D.m<3且m≠2答案D解析m-2x+1=1,解得x=m-3,∵关于x的分式方程m-2x+1=1的解是负数,∴m-3<0,解得m<3,当x=m-3=-1时,方程无解,则m≠2,故m的取值范围是:m<3且m≠2.故选D.2.关于x的分式方程5x =ax-2有解,则字母a的取值范围是()A.a=5或a=0B.a≠0C.a≠5D.a≠5且a≠0 答案D解析5x =ax-2,去分母得:5(x-2)=ax,去括号得:5x-10=ax,移项,合并同类项得:(5-a)x=10,∵关于x的分式方程5x =ax-2有解,∴5-a ≠0,x ≠0且x ≠2,即a ≠5,系数化为1得:x=105-a , ∴105-a ≠0且105-a ≠2,即a ≠5且a ≠0,综上所述关于x 的分式方程5x=a x -2有解,则字母a 的取值范围是a ≠5且a ≠0. 3.关于x 的方程3x -2x+1=2+m x+1无解,则m 的值为 ( )A.-5B.-8C.-2D.5 答案A 解析去分母得:3x-2=2x+2+m ,由分式方程无解,得到x+1=0,即x=-1,代入整式方程得-5=-2+2+m ,解得m=-5,故选A .二、填空题4.若关于x 的分式方程x+m x -2+2m 2-x =3的解为正实数,则实数m 的取值范围是 .答案m<6且m ≠2解析x+m x -2+2m 2-x =3,方程两边同乘(x-2)得,x+m-2m=3x-6,解得x=6-m2,由题意得,6-m2>0,解得m<6,∵6-m2≠2,∴m ≠2,∴m<6且m ≠2三、解答题5.(2017江苏盐城)某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3 500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2 400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.(1)2014年这种礼盒的进价是多少元/盒?(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?解(1)设2014年这种礼盒的进价为x 元/盒,则2016年这种礼盒的进价为(x-11)元/盒,根据题意得:3500x =2400x -11, 解得:x=35,经检验,x=35是原方程的解.答:2014年这种礼盒的进价是35元/盒.(2)设年增长率为m,2014年的销售数量为3500÷35=100(盒).根据题意得:(60-35)×100(1+a)2=(60-35+11)×100,解得:a=0.2=20%或a=-2.2(不合题意,舍去).答:年增长率为20%.6.(2018江苏扬州)京沪铁路是我国东部沿海地区纵贯南北的交通大动脉,全长1 462 km,是我国最繁忙的铁路干线之一.如果从北京到上海的客车速度是货车速度的2倍,客车比货车少用6 h,那么货车的速度是多少?(精确到0.1 km/h)解设货车的速度是x千米/小时,则客车的速度是2x千米/小时,根据题意得:1462x −14622x=6,解得:x=12156≈121.8.经检验,x=121.8为此分式方程的解.答:货车的速度约是121.8千米/小时.〚导学号13814035〛7.(预测)某校为了增强学生对中华优秀传统文化的理解,决定购买一批相关的书籍.据了解,经典著作的单价比传说故事的单价多8元,用12 000元购买经典著作与用8 000元购买传说故事的本数相同,这两类书籍的单价各是多少元?解设传说故事的单价为x元,则经典著作的单价为(x+8)元.由题意,得8000x =12000x+8,解得x=16,经检验x=16是原方程的解,x+8=24,答:传说故事的单价为16元,经典著作的单价为24元.。
【人教版】2019年春九年级数学下册:全册中考知识点梳理第8讲 一元一次不等式(组)
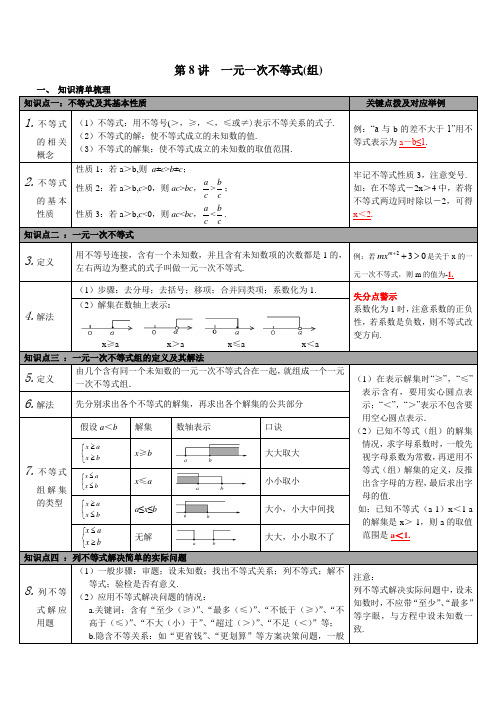
a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;
b.隐含不等关系:如“更省钱”、“更划算”等方案决策问题,一般还需根据整数解,得出最佳方案
注意:
列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.
第8讲一元一次不等式(组)
一、知识清单梳理
知识点一:不等式及其基本性质
关键点拨及对应举例
1.不等式的相关概念
(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子.
(2)不等式的解:使不等式成立的未知数的值.
(3)不等式的解集:使不等式成立的未知数的取值范围.
例:“a与b的差不大于1”用不等式表示为a-b≤1.
2.不等式的基本性质
性质1:若a>b,则a±c>b±c;
性质2:若a>b,c>0,则ac>bc, > ;
性质3:若a>b,c<0,则ac<bc, < .
牢记不等式性质3,注意变号.
如:在不等式-2x>4中,若将不等式两边同时除以-2,可得x<2.
知识点二:一元一次不等式
3.定义
用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式.
6.解法
先分别求出各个不等式的解集,再求出各个解集的公共部分
7.不等式组解集的类型
假设a<b
解集
数轴表示
口诀
x≥b
大大取大
x≤a
小小取小
a≤x≤b
大小,小大中间找
无解
大大,小小ห้องสมุดไป่ตู้不了
