2020-2021学年广西陆川中学高一下周测5理科数学试卷
广西陆川县中学2020-2021学年高三下学期第二次质量检测数学试卷含解析〖附16套高考模拟卷〗
广西陆川县中学2020-2021学年高三下学期第二次质量检测数学试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.台球是一项国际上广泛流行的高雅室内体育运动,也叫桌球(中国粤港澳地区的叫法)、撞球(中国台湾地区的叫法)控制撞球点、球的旋转等控制母球走位是击球的一项重要技术,一次台球技术表演节目中,在台球桌上,画出如图正方形ABCD ,在点E ,F 处各放一个目标球,表演者先将母球放在点A 处,通过击打母球,使其依次撞击点E ,F 处的目标球,最后停在点C 处,若AE=50cm .EF=40cm .FC=30cm ,∠AEF=∠CFE=60°,则该正方形的边长为( )A .2cmB .2cmC .50cmD .6cm2.已知点()2,0A 、()0,2B -.若点P 在函数y x =PAB △的面积为2的点P 的个数为( ) A .1B .2C .3D .43.从集合{}3,2,1,1,2,3,4---中随机选取一个数记为m ,从集合{}2,1,2,3,4--中随机选取一个数记为n ,则在方程221x y m n +=表示双曲线的条件下,方程221x y m n+=表示焦点在y 轴上的双曲线的概率为( ) A .917B .817C .1735D .9354.执行下面的程序框图,如果输入1995m =,228n =,则计算机输出的数是( )A .58B .57C .56D .555.设函数()210100x x x f x lgx x ⎧++≤⎪=⎨>⎪⎩,,若关于x 的方程()()f x a a R =∈有四个实数解()1234i x i =,,,,其中1234x x x x <<<,则()()1234x x x x +-的取值范围是( )A .(]0101, B .(]099,C .(]0100,D .()0+∞,6.设复数z 满足z ii z i-=+,则z =( ) A .1B .-1C .1i -D .1i +7.阅读如图的程序框图,运行相应的程序,则输出的a 的值为( )A .2-3B .3-2C .52D .258.在ABC 中,AD 为BC 边上的中线,E 为AD 的中点,且||1,||2AB AC ==,120BAC ∠=︒,则||EB =( )A 19B .114C 3D .749.如图,2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为43π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为( )A .22B .3 C .212+ D .312+ 10.已知随机变量X 的分布列如下表: X1-0 1P ab c其中a ,b ,0c >.若X 的方差()13D X ≤对所有()0,1a b ∈-都成立,则( ) A .13b ≤B .23b ≤C .13b ≥D .23b ≥11.已知函数()[]f x x x =-,其中[]x 表示不超过x 的最大正整数,则下列结论正确的是( ) A .()f x 的值域是[]0,1 B .()f x 是奇函数 C .()f x 是周期函数D .()f x 是增函数12.设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A ⋃B ,则集合中的元素共有( ) A .3个B .4个C .5个D .6个二、填空题:本题共4小题,每小题5分,共20分。
2020-2021学年广西陆川县中学秋季期高一9月考试题数学答题卡

18、解:(1)由题意得y 3x 2 2 3 2
…………..3 分
x2
x2
x2 0
2 0 x2
3 2 3 …….4 分 x2
y 3
…………..5 分
综上所述: y 3x 8的值域是y | y 3, y R ……..6 分
x2
(2) 设 x 2 t,则x t 2 2 t 0, ……………..2 分
f
1 2
1
f
2
1
…………….3 分
(2) 令0
x1
x2时,则
x2 x1
1
……………4 分
当x
0时,f
x
0
f
x2 x1
0
又 f mn f m f n
…………..5 分
f
x2
f x1
f
x1
x2 x1
f
x1
f
x1
f
x2 x1
f
x1
f
x2 x1
当 B 时,m 1 2m 1 m 2
………………..7 分
m 1 2m 1 当 B 时,m 1 2
2m 1 5
m 2 m 3
m 3
………………10 分
2 m 3 综上所述实数 m 的取值范围:m 3
……………………11 分 ……………………12 分
20、解: f x x2 2x 1 x 12 2
又 f x在区间0,+上是增函数
………………9 分
x
12 x4
x 0
12
0
x4
x 6
2 x 4或x 6
x 0
……………..11 分
x
广西陆川县中学2020-2021学年高一下学期开学考试(理)数学试题 答案和解析

广西陆川县中学【最新】高一下学期开学考试(理)数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{}{}10,1,2,3,2,k A B n n k A -===∈,则A B =A .{}1,2,3B .{}1,2C .{}1D .{}32.已知()224f x x x -=-,那么()f x = ( ) A .284x x -- B .24x x --C .28x x +D .24x -3.22sin10sin 80cos 35sin 35⋅-的值为( ) A .12-B .12C .1D .1-4.已知ABC ∆的三边,,a b c 满足222a b c ab +=+,则ABC ∆的内角C 为( ) A .150︒B .120︒C .60︒D .305.设函数2log ,0()2,0x x x f x x ->⎧=⎨≤⎩,则2(2)(log 3)f f +-的值为( )A .4B .43C .5D .66.若sin 63πα⎛⎫-=⎪⎝⎭,则sin 26πα⎛⎫+ ⎪⎝⎭的值为( ) A .59 B .59-C .79D .79-7.已知2()sin 2cos f x x x =+,则()f x 的最大值为( ) A .1-B .0C .1D .28.已知函数()21cos 2f x x =-,则下列说法正确的是( ) A .()f x 是周期为2π的奇函数 B .()f x 是周期为2π的偶函数 C .()f x 是周期为π的奇函数 D .()f x 是周期为π的偶函数9.已知()f x 是定义在R 上的偶函数,且满足(6)()f x f x +=,当(0,3)x ∈时,2()f x x =,则(64)f =( )A .4-B .4C .98-D .2r10.函数()()sin (0,0,)2f x A x A πωφωφ=+>><的图象如图所示,为了得到()5sin 34g x x π⎛⎫=+⎪⎝⎭的图象,只需将()f x 的图象( )A .向右平移π个单位长度B .向左平移π个单位长度C .向右平移3π个单位长度 D .向左平移3π个单位长度 11.奇函数()f x 在(0)+∞,上为增函数,且(1)0f =,则不等式[()()]0x f x f x -->的解集为( ) A .(1,0)(0,1)-B .(,1)(0,1)-∞-C .(,1)(1,)-∞-+∞D .(1,0)(1,)12.将函数()()2sin 2()2f x x πφφ=+<的图象向左平移2π个单位长度之后,所得图象关于直线4x π=对称,且()00f >,则φ=( )A .8π B .38π C .8π-D .38π-二、填空题 13.如果1cos 3α=,且α是第四象限的角,那么cos 2πα⎛⎫+ ⎪⎝⎭=______________.14.函数()21f x x mx =+-在[]1,3-上是单调函数,则实数m 的取值范围是____.15.化简:(4010sin tan ︒︒= ________.16.函数22()sin 2sin )f x x x x =-的图象为C ,如下结论: ①图象C 关于直线1112x π=对称; ②图象C 关于点(23π,0)对称;③函数()f x 在区间(5(,)1212ππ-内是增函数;④由2sin 2y x =的图角向右平移3π个单位长度可以得到图象C .其中正确结论的序号是_________.三、解答题17.已知圆22:8120C x y y +-+=,直线:20l ax y a ++=.(1)当a 为何值时,直线与圆C 相切.(2)当直线与圆C 相交于A 、B 两点,且AB =时,求直线的方程.18.如图,在三棱锥V C -AB 中,平面V AB ⊥平面C AB ,V ∆AB 为等边三角形,C C A ⊥B 且C C A =B =O ,M 分别为AB ,V A 的中点.(1)求证:V //B 平面C MO ; (2)求证:平面C MO ⊥平面V AB ; (3)求三棱锥V C -AB 的体积.19.已知直线l 过点P(-1,2)且与两坐标轴的正半轴所围成的三角形面积等于12. (1)求直线l 的方程.(2)求圆心在直线l 上且经过点(2,1)M ,(4,1)N -的圆的方程.20.如图,直四棱柱ABCD –A 1B 1C 1D 1中,AB //CD ,AD ⊥AB ,AB =2,AD ,AA 1=3,E 为CD 上一点,DE =1,EC =3. (1)证明:BE ⊥平面BB 1C 1C ; (2)求点B 1到平面EA 1C 1的距离.21.如图,在平面直角坐标系内,已知点A(1,0,B(-1,0),圆C 的方程为2268210x y x y +--+=,点P 为圆上的动点.(1)求过点A 的圆C 的切线方程.(2)求22||||AP BP +的最大值及此时对应的点P 的坐标.22.三棱锥被平行于底面ABC 的平面所截得的几何体如图所示,截面为A 1B 1C 1,∠BAC =90°,A 1A ⊥平面ABC ,A 1A AB ,AC =2,A 1C 1=1,12BD DC =. (1)证明:BC ⊥A 1D ;(2)求二面角A -CC 1-B 的余弦值.参考答案1.B 【解析】集合{}{}10,1,2,3,2,k A B n n k A -===∈= 1,1,2,42⎧⎫⎨⎬⎩⎭,则A B ⋂={}1,2,故选B.点睛: 1.用描述法表示集合,首先要弄清集合中代表元素的含义,再看元素的限制条件,明确集合类型,是数集、点集还是其他的集合.2.求集合的交、并、补时,一般先化简集合,再由交、并、补的定义求解.3.在进行集合的运算时要尽可能地借助Venn 图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn 图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍. 2.D 【解析】因为()224f x x x -=-=()224x --,则()24f x x =-,故选D.点睛: 本题考查函数的表示方法,属于基础题目.求函数解析式的一般方法主要有:待定系数法,配凑法,换元法,构造方程组法,赋值法等.已知函数类型时,比如一次函数,二次函数,反比例函数以及指数函数或者对数函数时,往往使用待定系数法设出函数的表达式,再利用已知条件带入求出参数的值. 3.B 【解析】原式=1sin 20sin10cos1012cos70sin 202︒︒︒==︒︒,故选B. 4.C 【解析】原式可化为2221cos 22a b c C ab +-==,又()0,C π∈,则C=60︒,故选C.5.A 【解析】()()2log 3221,log 323f f =-==,则()()22log 3f f +-的值为4,故选A.6.A【解析】 【分析】 把26πα+表示为226ππα⎛⎫-- ⎪⎝⎭,再利用诱导公式和二倍角公式计算sin 26πα⎛⎫+ ⎪⎝⎭的值. 【详解】因为sin 2sin 2cos 26266ππππααα⎡⎤⎛⎫⎛⎫⎛⎫+=--=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,所以25sin 212sin 669ππαα⎛⎫⎛⎫+=--= ⎪ ⎪⎝⎭⎝⎭,故选A .【点睛】三角函数的化简求值中,注意角与角的关系,有时他们的和或差是特殊角,有时要求的角可以用已知的角来表示,有时他们之间有倍数关系等,找到它们的关系后再用三角变换求值. 7.D 【解析】函数()2sin 2cos f x x x =+=21cos 2cos x x -+,令cosx=t ∈[-1,1],则221y t t =-++,二次函数开口向下,对称轴为1t =,则当1t =时, max 2y =,即()f x 的最大值为2,故选D. 8.D 【解析】函数()21cos 2f x x =-= 12cos2x,则()f x 是周期为π的偶函数,故选D. 9.B 【解析】由()()6f x f x +=知,()f x 周期为6,且()f x 是定义在R 上的偶函数,则()64f =()()()261122224f f f ⨯-=-===,故选B.10.D 【解析】 【分析】先由题设中的图像求出函数的解析式为()sin 34f x x π⎛⎫=+ ⎪⎝⎭,再把()5sin 34g x x π⎛⎫=+ ⎪⎝⎭变形为()sin 334g x x ππ⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦,从而可得平移的方向和平移的长度. 【详解】由图像可以得到1A =,且46T π=,故3ω=,所以()()sin 3f x x φ=+. 又5112f π⎛⎫=-⎪⎝⎭,所以53242k ππφπ+=+即2,4k k Z πφπ=+∈, 根据2πφ<得到4πφ=,所以()sin 34f x x π⎛⎫=+⎪⎝⎭. 而()5sin 3sin 3434g x x x πππ⎡⎤⎛⎫⎛⎫=+=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故只需将()f x 的图象向左平移3π个单位长度可得()g x 的图像,故选D . 【点睛】已知()sin y A x ωφ=+的图像,求其解析式时可遵循“两看一算”,“两看”指从图像上看出振幅和周期,“一算”指利用最高点或最低点的坐标计算φ. 11.C 【解析】由奇函数()f x , 不等式()()0x f x f x ⎡⎤-->⎣⎦可化简为()2?0xf x >,即()00x f x >⎧⎨>⎩或()0x f x <⎧⎨<⎩,又()f x 在()0+∞,上为增函数,且()()101f f ==-,则x∈()(),11,-∞-⋃+∞,故选C.12.B 【分析】先根据题设条件得到()f x 的图像关于34x π=对称,从而得到,28k k Z ππφ=-∈,再根据()00f >及2πφ<得到φ的值.【详解】()f x 的图像关于34x π=对称,所以3242k ππφπ+=+即,28k k Z ππφ=-∈,因2πφ<,故8πφ=-或者38πφ=,因()00f >,故sin 0φ>,故38πφ=,选B . 【点睛】形如()()sin f x A x =+ωϕ的函数,如果其图像的对称轴为0x x =,则有()0f x A =±,如果其图像的对称中心为()0,0x ,则()00f x =.13.3【解析】解:因为1cos 5α=且α是第四象限的角,那么cos()sin 2παα+=-= 14.(][),62,-∞-+∞【解析】 【分析】就对称轴的位置分1,322m m-≤--≥两种情况讨论即可. 【详解】因为()f x 在[]1,3-是单调函数,故12m -≤-或32m-≥,所以6m ≤-或者2m ≥,故填(][),62,-∞-+∞.【点睛】本题考察二次函数的单调性,是基础题. 15.-1 【解析】原式sin10sin?40?(cos10=︒︒︒()sin402sin40 sin1?0?0cos10cos10︒︒︒︒︒︒==(1sin1?0?0)2︒︒ 2sin40sin80cos?401cos10cos10-︒-︒︒︒︒===-.故答案为1-【点睛】本题的关键点有: 先切化弦,再通分; 利用辅助角公式化简;16.①②③ 【解析】函数())22sin2cos sin sin222sin 23f x x x x x x x π⎛⎫=-==-⎪⎝⎭. ①∵111132222121232f sin sin ππππ⎛⎫⎛⎫=⨯-==- ⎪ ⎪⎝⎭⎝⎭, 因此图象C 关于直线1112x π=对称,正确; ②∵2420333f sin πππ⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭, 因此图象C 关于点(23π,0)对称对称,正确; ③由x ∈5,1212ππ⎛⎫-⎪⎝⎭,得到2,322x πππ⎛⎫⎛⎫-∈- ⎪ ⎪⎝⎭⎝⎭,因此函数f (x )在区间5,1212ππ⎛⎫- ⎪⎝⎭内是增函数,正确;④由y =2sin2x 的图角向右平移3π个单位长度得到图象2222222333y sin x sin x sin x πππ⎛⎫⎛⎫⎛⎫=-=-≠- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,因此不正确.综上可知:只有①②③正确. 故答案为①②③.点睛:函数y =A sin(ωx +φ)(A >0,ω>0)的性质: (1)对称性:求对称轴只需令π2,2x k k Z ωϕπ+=+∈,求解即可,求对称中心只需令,x k k Z ωϕπ+=∈.(2)周期性:y =A sin(ωx +φ)存在周期性,其最小正周期为T =2πω.(3)单调性:由-2π+2k π≤ωx +φ≤2π+2k π(k ∈Z)得单调增区间;由2π+2k π≤ωx +φ≤32π+2k π(k ∈Z)得单调减区间. 17.(1)34a =-;(2)20x y -+=或7140x y -+=.(1)将圆C 的方程化为标准形式,得出圆C 的圆心坐标和半径长,利用圆心到直线的距离等于半径,可计算出实数a 的值;(2)利用弦长的一半、半径长和弦心距满足勾股定理可求得弦心距,利用点到直线的距离公式可求得实数a 的值,进而可得出直线l 的方程. 【详解】(1)圆C 的标准方程为()2244x y +-=,圆心C 的坐标为()0,4,半径长为2,当直线l 与圆C2=,解得34a =-;(2)由题意知,圆心C 到直线l的距离为d ==由点到直线的距离公式可得d ==整理得2870a a ++=,解得1a =-或7-.因此,直线l 的方程为20x y -+=或7140x y -+=. 【点睛】本题考查直线与圆的位置关系,考查利用直线与圆相切求参数以及根据弦长求直线方程,解答的核心就是圆心到直线的距离的计算,考查计算能力,属于中等题. 18.(1)见解析;(2)见解析;(3)3. 【解析】试题分析:(Ⅰ)利用三角形的中位线得出OM ∥VB ,利用线面平行的判定定理证明VB ∥平面MOC ;(Ⅱ)证明OC ⊥平面V AB ,即可证明平面MOC ⊥平面V AB ;(Ⅲ)利用等体积法求三棱锥A-MOC 的体积即可试题解析:(Ⅰ)证明:∵O ,M 分别为AB ,V A 的中点, ∴OM ∥VB ,∵VB ⊄平面MOC ,OM ⊂平面MOC , ∴VB ∥平面MOC ;(Ⅱ)证明:∵AC=BC ,O 为AB 的中点, ∴OC ⊥AB ,又∵平面V AB ⊥平面ABC ,平面ABC∩平面V AB=AB ,且OC ⊂平面ABC ,∴OC ⊥平面VAB ,∵OC ⊂平面MOC ,∴平面MOC ⊥平面V AB(Ⅲ)在等腰直角三角形ACB中,AC BC ==所以2,1AB OC ==.所以等边三角形V AB的面积VAB S ∆=又因为OC ⊥平面V AB ,所以三棱锥C V -AB的体积等于13VAB OC S ∆⨯⨯=. 又因为三棱锥V C -AB 的体积与三棱锥C V -AB 的体积相等,所以三棱锥V C -AB的体积为3. 考点:平面与平面垂直的判定;直线与平面平行的判定;用向量证明平行19.(1)10x y +-=;(2)22(2)(1)4x y -++=【解析】【详解】试题分析: (1)设所求的直线方程为:1x y a b+=,(0,0)a b >>,将P 点坐标带入,再根据图象写出三角形面积,得到关于a,b 的方程组,解出即可;(2) 设圆心坐标(),1a a -+,又圆经过()2,1M ,()4,1N -,则M,N 到圆心的距离相等,列出方程求出a 值,进而求出圆心和半径,写出圆的方程.试题解析:(1)设所求的直线方程为:1x y a b+=,(0,0)a b >>, ∵过点()1,2P -且与两坐标轴的正半轴所围成的三角形面积等于12,∴1211122a b ab -⎧+=⎪⎪⎨⎪=⎪⎩,解得1a b ==,故所求的直线方程为:x+y-1=0.(2)设圆心坐标(),1a a -+,则∵圆经过()2,1M ,()4,1N -,∴()()()()2222211411a a a a -+-+-=-+-++, ∴2a =,圆心()2,1-,圆半径2r ,∴()()22214x y -++=.20.(1)详见解析;(2)5. 【分析】(1)过B 作CD 的垂线交CD 于F ,则1,2BF AD EF AB DE FC ===-==,在Rt BFE ∆中和Rt BFC ∆中利用勾股定理证明BE BC ⊥,再证明1BE BB ⊥,即可证明11BE BB C C ⊥平面;(2)先求得11A C E S ∆的面积,设点B 1到平面11EA C 的距离为d,用d 表示111B EAC -三棱锥的体积,列式计算即可.【详解】(1)过B 作CD 的垂线交CD 于F,则1,2BF AD EF AB DE FC ===-==在Rt BFE BE Rt BFC BC ∆∆中,中,在2229BCE BE BC EC ∆+中,因为==,故BE BC ⊥由1111BB ABCD BE BB BE BB C C ⊥⊥⊥平面,得,所以平面(2)111111113A B C E A B C V AA S ∆-⋅三棱锥的体积=11111Rt A D C AC ∆=在中, 同理,1EC =1EA =因此11A C E S ∆=.设点B 1到平面11EA C 的距离为d,则111B EAC -三棱锥的体积1113A EC V d S ∆⋅⋅=,5d == 21.(1)3x-4y-3=0或x=1;(2)详见解析.【解析】试题分析: (1)当k 存在时,设过点A 切线的方程为()1y k x =-,由圆心到直线的距离等于半径列出方程,求出k 值,即可得到切线方程; 当k 不存在时方程1x =也满足;(2) 设点(),P x y ,则由两点之间的距离公式知()22222||222||2AP BP x y OP +=++=+,即所求的最大值可转化为2||OP 最大值, 又P 为圆上点,所以()max OP OC r =+,再联立此时的直线OC 与圆方程求出对应的P 点坐标.试题解析:(1) 当k 存在时,设过点A 切线的方程为()1y k x =-,∵圆心坐标为()3,4,半径2r =,∴2=,计算得出34k =, ∴所求的切线方程为340x y -=; 当k 不存在时方程1x =也满足,综上所述,所求的直线方程为3430x y --=或1x =.(2)设点(),P x y ,则由两点之间的距离公式知()22222||222||2AP BP x y OP +=++=+, 要22||AP BP +取得最大值只要使2||OP 最大即可, 又P 为圆上点,所以()max 27OPOC r =+==, ∴()222max ||272100AP BP +=⨯+=,此时直线4:3OC y x =,由224368210y x x y x y ⎧=⎪⎨⎪+--+=⎩,计算得出95125x y ⎧=⎪⎪⎨⎪=⎪⎩(舍去)或215285x y ⎧=⎪⎪⎨⎪=⎪⎩,∴点P 的坐标为.22.(1)详见解析;(2). 【详解】 试题分析: (1)由线面垂直的性质定理可得1A A BC ⊥,在Rt ABC △中,根据长度比例可得DBA ABC ∽,可推出AD BC ⊥,再由线面垂直的判定定理推出BC ⊥平面1A AD ,根据定义得出结论成立;(2) 作1AE C C ⊥交1C C 于E 点,连接BE ,由线面垂直得到线线垂直,找到二面角的平面角, 过1C 作1C F AC ⊥交AC 于F 点,在三角形中求出1C CF ∠,再从Rt AEC △和Rt BAE △中分别求出AE 和BE,代入公式即可.试题解析:(1) 1A A ⊥平面ABC BC ,⊂平面ABC ,∴ 1A A BC ⊥.在Rt ABC △中,2AB AC BC ==∴=, :1:2BD DC =,3BD ∴=,又3BD AB AB BC==, DBA ABC ∴∽,90ADB BAC ∴∠=∠=,即AD BC ⊥.又1A A AD A =,BC ∴⊥平面1A AD , 又A 1D ⊂平面1A AD .BC ∴⊥A1D.(2)如图,作1AE C C ⊥交1C C 于E 点,连接BE ,由已知得AB ⊥平面11ACC A .∴AB┴CC1,又CC 1AE=E,∴CC 1┴平面AEB, ∴CC 1┴BE,AEB ∴∠为二面角1A CC B --的平面角.过1C 作1C F AC ⊥交AC 于F 点,则1CF AC AF =-=,11C F A A =, 160C CF ∴∠=.在Rt AEC △中,sin6022AE AC ==⨯= 在Rt BAE △中,AB=, AE=, ∴BE=.即二面角1A CC B --的余弦值为.。
广西陆川县中学2024届高一数学第二学期期末达标测试试题含解析

广西陆川县中学2024届高一数学第二学期期末达标测试试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的1.已知向量(),2m a =,()1,1n a =+,若//m n ,则实数a 的值为( ) A .23-B .2或1-C .2-或1D .2-2.若(3,4)AB =,A 点的坐标为()2,1--,则B 点的坐标为( ) A .()1,3B .()5,5C .()1,5D .()5,43.设0x >,0y >,24x y +=,则()()121x y xy++的最小值为( )A .2B .4C .72D .924.在空间直角坐标系中,点P (3,4,5)关于yOz 平面的对称点的坐标为( ) A .(−3,4,5) B .(−3,−4,5) C .(3,−4,−5) D .(−3,4,−5)5.函数()cos 3f x x πω⎛⎫=+ ⎪⎝⎭的最小正周期为π,则()f x 的图象的一条对称轴方程是( ) A .12x π=-B .6x π=-C .6x π=D .3x π=6.某林区改变植树计划,第一年植树增长率,以后每年的植树增长率都是前一年植树增长率的,若成活率为,经过年后,林区的树木量是原来的树木量的多少倍?( ) A .B .C .D .7.函数()cos f x x x x =+在[],ππ-上的图像大致为( )A .B .C .D .8.已知实数满足250x y ++=,22x y +的最小值为( )A 5B .5C .25D .559.为了得到函数sin(2)3y x π=-的图像,只需把函数sin(2)6y x π=+的图像A .向左平移4π个长度单位 B .向右平移4π个长度单位C .向左平移2π个长度单位D .向右平移2π个长度单位10.角α的终边经过点321⎛⎫ ⎪ ⎪⎝⎭,那么tan α的值为( ) A .12B .3C .3D .3二、填空题:本大题共6小题,每小题5分,共30分。
广西省陆川县中学高一数学下学期周测 新人教A版必修3
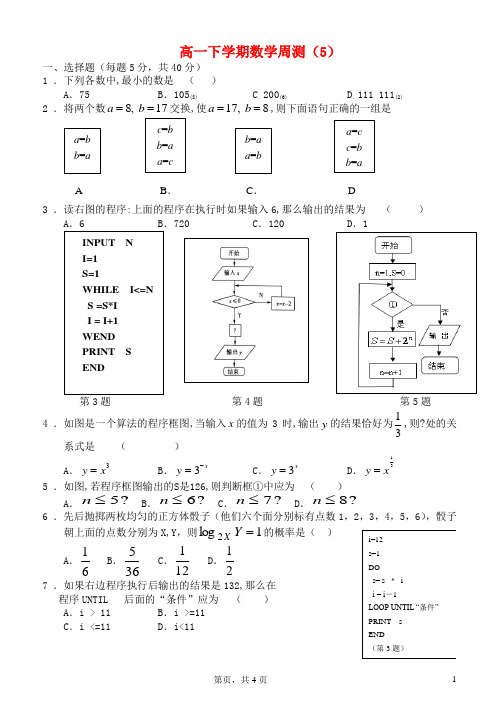
高一下学期数学周测(5)一、选择题(每题5分,共40分) 1 .下列各数中,最小的数是 ( )A .75B .105(8)C .200(6)D .111 111(2) 2 .将两个数8, 17a b ==交换,使17, 8a b ==,则下面语句正确的一组是3 .读右图的程序:上面的程序在执行时如果输入6,那么输出的结果为 ( )720 C .120 D .1第4题 第5题 4 .如图是一个算法的程序框图,当输入x 的值为3时,输出y 的结果恰好为13,则?处的关系式是 ( )A .3y x = B .3xy -= C .3xy = D .13y x = 5 .如图,若程序框图输出的S 是126,则判断框①中应为 ( )A .?5≤nB .?6≤nC .?7≤nD .?8≤n6 .先后抛掷两枚均匀的正方体骰子(他们六个面分别标有点数1,2,3,4,5,6),骰子朝上面的点数分别为X,Y ,则1log 2=Y X 的概率是( )A .61 B .365 C .121 D .217 .如果右边程序执行后输出的结果是132,那么在程序UNTIL 后面的“条件”应为 ( ) A .i > 11 B .i >=11 C .i <=11 D .i<11INPUT NI=1 S=1WHILE I<=N S =S*I I = I+1 WEND PRINT S ENDa =b b =ac =b b =a a =c b =aa =b a =cc =b b =a AB .C .Di=12 s=1 DO s= s ﹡ i i = i -1LOOP UNTIL “条件” PRINT s END (第3题)Read xIf x >0 Then1y x ←+Else1y x ←-End If Print y8 .甲、乙两人相约在某地见面,没有安排确定的时间,但都要在晚上7点到8点之间到达,先到的人等待10分钟,若没有见到另一人则离开,那么他们能见面的概率是(A .23B .1136C .13D .169 .如图,汉诺塔问题是指有3根杆子A .B .C ,B 杆上有若干碟子,把所有碟子从B 杆移到C 杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面。
人教版数学高一-广西陆川县中学高一下学期周测(6)数学(理)试题

陆川中学2015级高一(下)数学(理)周测(6)2016年4月17日一、选择题(请将选择题的答案填写在后面答题卡的对应题号的表格内)1 .直线2y=与正切曲线tan 3y x =相交的相邻两点间的距离是( )A .πB .23πC .3π D .6π 2 .已知1sin 123πα⎛⎫+= ⎪⎝⎭,则7cos 12πα⎛⎫+ ⎪⎝⎭的值等于 ( )A .13 B.3 C .13-D.3-3 .函数y =的定义域是 ( )A .2,2()33k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦B .2,2()66k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦C .22,2()33k k k Z ππππ++∈⎡⎤⎢⎥⎣⎦D .222,2()33k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦4 .将函数()sin()6f x x πω=+的图象关于6x π=对称,则ω的值可能是( )A .12B .32C .5D .25 .已知7sin cos (0)13αααπ+=<<,则tan α=( )A .125-B .512-C .512D .125-或512-6=( )其中,2πθπ⎛⎫∈ ⎪⎝⎭( )A .sin θ-cos θB .cos θ-sin θC .±(sin θ-cos θ)D .sin θ+cos θ7 .已知αsin 是方程06752=--x x 的根,且α是第三象限角,则()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛--⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛--απαπαπαππα2sin 2co tan 23co 23sin 2s s = ( ) A .169 B .169-C .43 D .43-8 .在ABC ∆中,角,A B 均为锐角,且cos sin A B >,则ABC ∆的形状是( )A .锐角三角形B .直角三角形C .等腰三角形D .钝角三角形9 .已知sin sin αβ>,那么下列命题成立的是( )A .若,αβ是第一象限角,则cos cos αβ>;B .若,αβ是第二象限角,则tan tan αβ>;C .若,αβ是第三象限角,则cos cos αβ>;D .若,αβ是第四象限角,则tan tan αβ>10.关于)42sin(3)(π+=x x f 有以下命题,其中正确的个数①若0)()(21==x f x f ,则)(21Z k k x x ∈=-π;②)(x f 图象与)42cos(3)(π-=x x g 图象相同;③)(x f 在区间]83,87[ππ--上是减函数;④)(x f 图象关于点)0,8(π-对称.( )A .0B .1C .2D .311.定义在R 上的偶函数)(x f 在(,0]-∞上是减函数,βα,是钝角三角形的两个锐角,则下列不等式关系中正确的是 ( )A .(sin )(cos )f f αβ>B .(cos )(cos )f f αβ<C .(cos )(cos )f f αβ>D .(sin )(cos )f f αβ<二、填空题(请将填空题的答案填写在答题卡对应题号的横线上)12.函数sin(2)6y x π=-的单调减区间是__________________13.若函数()2sin (0)3f x x πωω⎛⎫=-> ⎪⎝⎭的图象两相邻对称轴之间的距离为3,则(0)(1)(2)(2016)f f f f ++++= .14.函数1cos 21cos 2-+=x x y的值域为 .15.已知函数()cos(3)3f x x π=+,其中[,]6x m π∈,若()f x 的值域是[1,2--,则m 的取值范围是 .陆川中学2015级高一(下)数学(理)周测(6)答题卡姓名__________ 班级_________ 座号_________ 分数_________一、选择题(每小题5分,满分55分)题号 1 2 3 4 5 6 7 8 9 10 11 答案二、填写题(每小题5分,满分20分)12. 13. 14. ;15. . 三、解答题(每小题12分)16.设(0,4),(0,4)x y ∈∈.(1)若,x N +∈y N +∈以,x y 作为矩形的边长,记矩形的面积为S ,求4S <的概率; (2)若,,x R y R ∈∈求这两数之差不大于2的概率.17.已知函数()2sin 23f x x π⎛⎫=+⎪⎝⎭(1)求函数()f x 的最小正周期和单调增区间; (2)当[,]33x ππ∈-时,求()f x 的最值,并指明相应x 的值. (3)在给出的直角坐标系中,画出函数()y f x =在区间[0,]π上的图象.陆川中学2015级高一(下)数学(理)周测(6)参考答案一、选择题1. C 解析:直线2y =与正切曲线tan 3y x =相交的相邻两点间的距离就是函数tan 3y x =的最小正周期3π,故选C. 2. C 提示:71cos cos sin 12122123ππππααα⎛⎫⎛⎫⎛⎫+=++=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故选择C. 3. D 提示:由01cos 2≥+x 得21cos -≥x ,∴222233k x k πππ-≤≤π+,Z k ∈. 4. D 解析:试题分析:根据正弦型函数的性质及已知条件,有()662k k Z ωππππ+=+∈,取0k =,得2ω=满足条件,选D5. A分析:由7sin cos 13αα+=可得2249sin 2sin cos cos 169αααα++=即4912sin cos 169αα+=,也就是1202sin cos 169αα=-,因为0απ<<,所以sin 0,cos 0αα><,且222120289(sin cos )sin 2sin cos cos 1169169αααααα-=-+=+=,所以17sin cos 13αα-==,联立方程7sin cos 1317sin cos 13αααα⎧+=⎪⎪⎨⎪-=⎪⎩,解得12sin 135cos 13αα⎧=⎪⎪⎨⎪=-⎪⎩,所以sin 12tan cos 5ααα==-,故选A. 6. A 提示:=== sin cos θθ=-又,2πθπ⎛⎫∈ ⎪⎝⎭,∴sin 0,cos 0θθ><= sin θ-cos θ,故选A7. B 提示:因为根据诱导公式可知原式化简为22cos (sin )tan tan sin cos α-αα=-ααα,343sin cos tan 554α=-∴α=-∴α=,因此选B8. D.提示:cos sin ,sin sin ,2A B A B π⎛⎫>∴-> ⎪⎝⎭又角,A B 均为锐角,则0,0,222B A A B πππ<<-<∴<+<且ABC ∆中,,2A B C C πππ++=∴<<,故选D.9. D 提示:A 错误,例如060,30,cos cos ;αβαβ==<B 错误,例如00120,145,tan tan ;a βαβ==< C 错误,例如0210,240,cos cos ;αααβ==< D 正确,,(2,2)(),2k k k Z παβππ∈-∈正弦函数sin y x =在(2,2)2k k πππ-上是增函数,22,2k k ππβαπ∴-<<<又正切函数tan y x =在(2,2)2k k πππ-上是增函数,所以tan tan .αβ>故选D10. D. 分析:①:∵)42sin(3)(π+=x x f ,0)()(21==x f x f ,∴)(221Z k k x x ∈=-π,∴①错误; ②:∵)42sin(]2)42sin[()42cos(ππππ+=+-=-x x x ,∴②正确;③:当]83,87[ππ--∈x 时,]2,23[42πππ--∈+x ,∴)(x f 在区间]83,87[ππ--上是减函数,③正确;④:当8π-=x 时, 042=+πx ,∴0)8(=-πf ,∴④正确.11. D 提示:因为,αβ是钝角三角形的两个锐角,所以090αβ︒<+<︒,即090αβ︒<<︒-,所以0sin sin(90)cos 1αββ<<︒-=<,因为定义在R 上的偶函数)(x f 在(,0]-∞上是减函数,所以)(x f 在()∞+,0上单调递增.所以(sin )(cos )f f αβ< 二、填空题 12. ,63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦提示:因为,sin(2)6y x π=-=sin(2)6x π--,所以,由222,262k x k k z πππππ-≤-≤+∈,得,,63k x k k z ππππ-≤≤+∈,故函数sin(2)6y x π=-的单调减区间是,63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦.13.6T=,所以263ππωω=⇒=,所以()2sin 33f x x ππ⎛⎫=-⎪⎝⎭所以(0)(1)(2)(2016)336((0)(1)(2)(3)(4)(5))(0)f f f f f f f f f f f ++++=⨯++++++3362002sin 3π⎛⎛⎫⨯⨯+-+-= ⎪ ⎝⎭⎝⎭ 14.此为dx c bx a y-+=cos cos 型的三角函数求最值问题,分子、分母的三角函数同名、同角,这类三角函数一般先化为部分分式,再利用三角函数的有界性去解.或者也可先用反解法,再用三角函数的有界性去解.解法一:原函数变形为1cos ,1cos 221≤-+=x x y ,可直接得到:3≥y 或.31≤y解法一:原函数变形为()()∴≤-+∴≤-+=,1121,1cos ,121cos y y x y y x 3≥y 或.31≤y15.解析:因为[,]6x m π∈,所以533633x m πππ≤+≤+,当5336x ππ+=即6x π=时,()62f π=-而()f x 的值域是[1,2--,故可得72525333636918m m m πππππππ≤+≤⇒≤≤⇒≤≤,故m 的取值范围是25[,]918ππ. 三、解答题16. (1)59.(2)222423()44P II -==提示:(1)x=1,2,3.y=1,2,3.所以把所有的结果表示出来.然后再从这些结果当中找出事件发生的结果.再利用古典概型概率计算公式计算即可. (2) 所有的结果的区域为{}(,)|04,04,x y x y Ω=<<<<两个之差不大于2的所有结果的区域为{}(,)|04,04,||2,II x y x y x y =<<<<-≤分别求出对应区域的面积,然后求面积比即可.(1)若,x N +∈则(,)x y 所有的结果为(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共9个,满足4S <的(,)x y 所有的结果为1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),共5个,故4S <的概率为59. (2)所有的结果的区域为{}(,)|04,04,x y x y Ω=<<<<两个之差不大于2的所有结果的区域为{}(,)|04,04,||2,II x y x y x y =<<<<-≤则222423()44P II -== 17. 分析:(1)先利用三角恒等变换公式对函数的解析式进行化简,用二倍角公式和两个角的和的正弦公式,再根据化简后的解析式求三角函数的周期;(2)在所给的区间上找出函数值域的几个特殊点:最大值和最小值点,再列出表格,在坐标系中描出点画出函数图像. 解析: (1) ()2sin 23f x x π⎛⎫=+ ⎪⎝⎭所以f(x)的最小正周期T=ππ=22. 由2k π-2π<2x+3π<2kπ+2π得125ππ-k <2x+3π<12ππ+k所以f(x)的单调增区间为]12,125[ππππ+-k k (k ∈Z).(2)由23333x x πππππ-≤≤⇒≤+≤所以当23x ππ+=即3x π=时,()f x 取得最小值()2sin 03f ππ==当232x ππ+=即12x π=时,()f x 取得最大值()2sin2122f ππ==.(3)列表:x 012π 3π 127π 65π π2x+3π 3π 2π π 23π 2π 37π f(x)32-23描点连线得图象,如图所示.。
【数学】广西陆川县2020学年高一下学期期末考试理科数学试题版含答案
【关键字】数学广西陆川县中学2017年春季期高一期末考试卷理科数学一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合M={-1,1},N={x|{x<0或x>},则下列结论正确的是()A.N⊆MB.N∩M=∅C.M⊆ND.M∪N=R2.设=(2,-1),=(-3,4),则2+等于()A.(3,4)B.(1,2)C.-7D.33.若cos>0,sin <0,则角的终边在( ).A.第一象限B.第二象限C.第三象限D.第四象限4.sin 20°cos 40°+cos 20°sin 40°的值等于( ).A.B.C.D.5. 已知0<A<,且cos A=,那么sin 等于( ).A.B.C.D.6. 若,则()A.-3 B.C.-D.7. 已知,则()A.B.C.D.8. 函数的周期,振幅,初相分别是()A.,,B. ,,C. ,,D. ,,9.要得到函数y=sin(2x-)的图象,只要将函数y=sin2x的图象( )A.向左平行移动个单位B.向左平行移动个单位C.向右平行移动个单位D.向右平行移动个单位10.函数是()A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数11.已知是定义在R上的偶函数,且,当时,,则()A .0B .C .-D .3.512. 函数y=Asin(ωx+φ)(A >0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )12题图A.2B.C.D.二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13. 半径为的半圆卷成一个圆锥,则圆锥的体积为 .14. 设,若,则的最小值为 .15. 在正四面体中,分别是和的中点,则异面直线和所成角为__________.16. 数列是正数列,且,则= .三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17、(本小题满分10分,(1)小问5分,(2)小问5分)已知全集,函数的定义域为集合,集合(1)求; (2)求.18、(本小题满分12分,(1)小问6分,(2)小问6分)在平面直角坐标系中,若角的始边为轴的非负半轴,其终边经过点.(1)求的值; (2)求的值.19、(本小题满分12分,(1)小问6分,(2)小问6分)已知二次函数,且满足.(1)求函数的解析式;(2)若函数的定义域为,求的值域.20、(本小题满分12分,(1)小问6分,(2)小问6分)已知函数 ,且的最小正周期为.(1)求的值; (2)求函数在区间上的单调增区间.21、(本小题满分12分,(1)小问7分,(2)小问5分)已知函数 是奇函数.(1)判断函数在上的单调性,并用定义法证明你的结论;(2)若对于区间[]5,2上的任意x 值,使得不等式n x f x+≤2)(恒成立,求实数n 的取 值范围.22、(本小题满分12分,(1)小问4分,(2)小问8分) 已知函数12sin 94)cos sin ()(--+=x x x a x f ,若9132)4(-=πf (1)求a 的值,并写出函数)(x f 的最小正周期(不需证明);(2)是否存在正整数k ,使得函数)(x f 在区间[]πk ,0内恰有2017个零点? 若存在,求出k 的值,若不存在,请说明理由.理科数学答案1-6CBDBD D 7-12ACDBBC13. 3R 14. 4 15. 4π 16. 226n n + 17解:(1)由题意可得:⎩⎨⎧>-≥-01003x x ,则 {}103|<≤=x x A .........….5分(2){}75|≥<=x x x B C U 或........….8分{}10753|)(<≤<≤=x x x A B C U 或 ........…10分18解:(1)由任意角三角函数的定义可得:224tan ==α........….6分 (2)ααααcos sin cos sin 2++=原式.....…8分 1tan 1tan 2++=αα.....…10分 351214=++=.....…12分 19解:(1))3()1(f f =-由可得该二次函数的对称轴为1=x .....…2分即124=-m从而得2-=m ....…4分 所以该二次函数的解析式为142)(2++-=x x x f ....…6分(2)由(1)可得()312)(2+--=x x f ....…9分 所以(](]3,15-2,2)(上的值域为在-x f ....…12分20解:(1)x x x x f ωωω2cos 212sin 322cos 1)(-+-=....…3分2162sin 2+⎪⎭⎫ ⎝⎛-=πωx ....…5分 由题意得πωπ=22 即可得1=ω....…6分 (2)由(1)知2162sin 2)(+⎪⎭⎫ ⎝⎛-=πx x f 则由函数单调递增性可知:Z k k x k ∈+≤-≤-,226222πππππ 整理得Z k k x k ∈+≤≤-,36ππππ........9分所以()π,0)(在x f 上的增区间为⎥⎦⎤ ⎝⎛3,0π,⎪⎭⎫⎢⎣⎡ππ,65...........12分 21解:(1)由条件可得0)()(=+-x f x f ,即 0121log 121log 22=⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛---x mx x mx 化简得222411x x m -=-,从而得2±=m ;由题意2-=m 舍去,所以 2=m 即x x x x f -⎪⎭⎫ ⎝⎛-+=1221log )(2...........2分 ⎪⎭⎫ ⎝⎛+∞∈,21)(x x f 在上为单调减函数...........3分 证明如下:设+∞<<<2121x x ,则 22221112211221log 1221log )()(x x x x x x x f x f +⎪⎪⎭⎫ ⎝⎛-+--⎪⎪⎭⎫ ⎝⎛-+=- 因为+∞<<<2121x x ,所以012>-x x ,012,01221>->-x x ;所以可得1211212212211>+-⋅-+x x x x ,所以0)()(21>-x f x f ,即)()(21x f x f >;所以函数)(x f 在⎪⎭⎫ ⎝⎛+∞∈,21x 上为单调减函数...........7分 (2)设x x f x g 2)()(-= ,由(1)得)(x f 在⎪⎭⎫ ⎝⎛+∞∈,21x 上为单调减函数, 所以x x f x g 2)()(-=在[]5,2上单调递减;所以x x f x g 2)()(-=在[]5,2上的最大值为()6log 2352-=g ...........10分由题意知()x g n ≥在[]5,2上的最大值,所以6log 352-≥n ...........12分22解:(1) π==T a ,1……………4分(2)存在n =504,满足题意……5分理由如下:当⎥⎦⎤⎢⎣⎡∈2,0πx 时,12sin 94)cos (sin )(--+=x x x x f ,设x x t cos sin +=,则 []2,1∈t ,12sin 2-=t x ,则9594)(2-+-=t t t g ,095942=-+-t t 可得 1=t 或45=t ,由x x t cos sin +=图像可知, x 在⎥⎦⎤⎢⎣⎡2,0π上有4个零点满足题意…8分 当),2(ππ∈x 时,12sin 94)cos (sin )(---=x x x x f ,x x t cos sin -=,则 (]2,1∈t ,212sin t x -=,91394)(2-+=t t t h ,0913942=-+t t ,1=t 或413-=t ,因为(]2,1∈t ,所以x 在⎪⎭⎫ ⎝⎛ππ,2上不存在零点。
广西壮族自治区玉林市陆川实验中学2021-2022学年高一数学理月考试题含解析
广西壮族自治区玉林市陆川实验中学2021-2022学年高一数学理月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知点(3,m)到直线x+y﹣4=0的距离等于,则m=()A.3 B.2 C.3或﹣1 D.2或﹣1参考答案:C【考点】点到直线的距离公式.【分析】由题意可得=,解之可得.【解答】解:由题意可得=,即|m﹣1|=2,解得m=3,或m=﹣1故选C【点评】本题考查点到直线的距离公式,属基础题.2. 已知直线l:x+ay﹣1=0(a∈R)是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A(﹣4,a)作圆C 的一条切线,切点为B,则|AB|=()A.2 B.4C.2D.6参考答案:D【考点】圆的切线方程.【分析】求出圆的标准方程可得圆心和半径,由直线l:x+ay﹣1=0经过圆C的圆心(2,1),求得a 的值,可得点A的坐标,再利用直线和圆相切的性质求得|AB|的值.【解答】解:∵圆C:x2+y2﹣4x﹣2y+1=0,即(x﹣2)2+(y﹣1)2 =4,表示以C(2,1)为圆心、半径等于2的圆.由题意可得,直线l:x+ay﹣1=0经过圆C的圆心(2,1),故有2+a﹣1=0,∴a=﹣1,点A(﹣4,﹣1).∵AC==2,CB=R=2,∴切线的长|AB|==6.故选:D.3. 在中,若=1,C=, =则A的值为 ( )A. B. C. D.参考答案:A略4. 设,若对任意的时,不等式恒成立,则的取值范围是()A. B. C. D.参考答案:B略5. 函数的图象大致是()A B CD参考答案:A6. 已知等比数列{a n}中,各项都是正数,且成等差数列,则等于()A. B. C. D.参考答案:C【分析】由条件可得a3=a1+2a2 ,即a1q2=a1+2a1q,解得q=1.代入所求运算求得结果.【详解】∵等比数列{a n}中,各项都是正数,且a1,a3,2a2成等差数列,故公比q不等于1.∴a3=a1+2a2 ,即a1q2=a1+2a1q,解得q=1.∴3+2,故选:C.【点睛】本题主要考查等差中项的性质,等比数列的通项公式,考查了整体化的运算技巧,属于基础题.7. 已知数列是等差数列,若,,且数列的前项和有最大值,那么取得最小正值时等于A. B. C. D.参考答案:c试题分析:由等差数列的性质和求和公式可得又可得:而,进而可得取得最小正值时.考点:等差数列的性质8. 若实数a、b满足条件a>b,则下列不等式一定成立的是A. B. a2>b2 C. ab>b2 D. a3>b3参考答案:D【分析】根据题意,由不等式的性质依次分析选项,综合即可得答案.【详解】根据题意,依次分析选项:对于A、,时,有成立,故A错误;对于B、,时,有成立,故B错误;对于C、,时,有成立,故C错误;对于D、由不等式的性质分析可得若,必有成立,则D正确;故选:D.【点睛】本题考查不等式的性质,对于错误的结论举出反例即可.9. 化简的结果为( )A.5 B.C.﹣D.﹣5参考答案:B【考点】方根与根式及根式的化简运算.【专题】计算题.【分析】利用根式直接化简即可确定结果.【解答】解:===故选B【点评】本题考查根式的化简运算,考查计算能力,是基础题.10. 已知中,角的对边分别为,,则()A. B. C. D.参考答案:B略二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数f(x)=,其中m>0,若存在实数b,使得关于x的方程f(x)=b 有三个不同的根,则m 的取值范围是.参考答案:(3,+∞)【考点】根的存在性及根的个数判断.【分析】作出函数f(x)=的图象,依题意,可得4m﹣m2<m(m>0),解之即可.【解答】解:当m>0时,函数f(x)=的图象如下:∵x>m时,f(x)=x2﹣2mx+4m=(x﹣m)2+4m﹣m2>4m﹣m2,∴y要使得关于x的方程f(x)=b有三个不同的根,必须4m﹣m2<m(m>0),即m2>3m(m>0),解得m>3,∴m的取值范围是(3,+∞),故答案为:(3,+∞).12. 已知函数,若对任意都有()成立,则的最小值为__________.参考答案:4π【分析】根据和的取值特点,判断出两个值都是最值,然后根据图象去确定最小值.【详解】因为对任意成立,所以取最小值,取最大值;取最小值时,与必为同一周期内的最小值和最大值的对应的,则,且,故. 【点睛】任何一个函数,若有对任何定义域成立,此时必有:,.13. 若函数的零点为,则满足且k为整数,则k= ▲.参考答案:214. 将正偶数排列如下表,其中第行第个数表示为,例如,若,则▲ .参考答案:6115. 给出函数,若对一切成立,则________。
广西陆川县中学2020学年高一数学5月月考试题 理
广西陆川县中学2020学年下学期高一5月考试卷理科数学一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.算法的三种基本结构是()A. 顺序结构、模块结构、条件结构B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构2.如图,阅读程序框图,则输出的S=()D403.“双色球”彩票中有33个红色球,每个球的编号分别为01,02,…,33.一位彩民用随机数表法选取6个号码作为6个红色球的编号,选取方法是从下面的随机数表中第1行第5列和第6列的数字开始,从左向右读数,则依次选出来的第5个红色球的编号为( )7816 6572 0802 6314 0214 4319 9714 0198 3204 9234 4936 8200 3623 4869 6938 7181 A. 01B. 02C. 14D. 194.下列函数的最小值为2的是( )A. 1lg lg y x x =+B. y =C. 22xxy -=+ D. 1sin (0)sin 2y x x x π=+<< 5.第二次数学周练题比较难,姚老师对本班学生的12道选 择题答题情况进行了统计分析,出错的人数用茎叶图表示, 如下图所示,则该组数据的中位数、众数、极差分别是( ) A. 18,12,29B. 19,22,29 第5题图C. 18,22,29D. 19,12,6.执行如图所示的程序语句,输出的结果为( ) A. 3025- B. 1009- C. 10097.从装有大小材质完全相同的1个白球,2个黑球和3个红球的 不透明口袋中,随机摸出两个小球,则两个小球同色的概率 是( ) A. 15B.415C.25D.138.若(0,)απ∈,且,则cos 2α=( ).A D 0 1 31 2 2 8 6 2 0 2 3 2 2 3 0xyO 1 2 2-A B9. 要得到函数y sin(2x 4π)的图象,只需将函数y cos2x 的图象( ).A .向左平移8π个单位 B .向右平移8π个单位长度C .向左平移4π个单位长度 D .向右平移4π个单位长度 10.如图所示,为函数()()2sin f x x ωϕ=+(0,2πωϕπ>≤≤)的部分图象,其中,A B 两点之间的距离为5,则()=1f ( ). A .3 B .3- C .1 D .1-11. 已知函数21xy -=m x --有两个零点,则实数m 的取值范围是( )A .(-2,2)B .(-1,1)C . 2)D .]22[,-12. 过点(3,1)作圆(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则直线AB 的方程为( ) A .2x +y -3=0 B .2x -y -3=0 C .4x -y -3=0 D .4x +y -3=0二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上) 13.=(2,3),=(-3,5)a b ,则在a b 方向上的投影为_________.14.已知正方形ABCD 的边长为2,E 为CD 的中点,则AE →·BD →=________.15.若直线3450x y -+=与圆222(0)x y r r +=>相交于,A B 两点,且0120AOB ∠=()O 为坐标原点,则r =_________.16.已知函数1tan sin )(++=x b x a x f ,满足(5)7f =,则)5(-f =_________.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17. (10分)若2cos 3α=,α是第四象限角,求sin(2)sin(3)cos(3)cos()cos()cos(4)απαπαππαπααπ-+--------的值.18. (12分)用“五点法”画出函数3sin(2)3y x π=-在 7,66x ππ⎡⎤∈⎢⎥⎣⎦的简图.19.(12分)全世界越来越关注环境保护问题,某监测站点于2020年8月某日起连续n 天监测空气质量指数(AQI ),数据统计如下:(1)根据所给统计表和频率分布直方图中的信息求出n ,m 的值,并完成频率分布直方图. (2)由频率分布直方图,求该组数据的平均数与中位数.20.(12分) 已知角的终边经过点,且α为第二象限角.(1)求实数m 和的值;空气质量指数(μg/m 3)0﹣50 51﹣100 101﹣150 151﹣200 201﹣250 空气质量等级空气优 空气良 轻度污染中度污染 重度污染天数2040m105(2)若,求βαβαπβαπβαsin sin 3)cos()cos(sin )2cos(3cos sin --+-+的值.21.(12分)已知函数22()44f x x ax b =-+,{|13}A x x =≤≤,{|14}B x x =≤≤. (1)若a ,b 都是从集合A 中任取的整数,求函数()y f x =有零点的概率.(2)若a ,b 都是从集合B 中任取的实数,求函数()y f x =在区间[2,4]上为单调函数的概率.22.(12分)在平面直角坐标系xOy 中,点A (0,3),直线l :y =2x -4.设圆C 的半径为1,圆心在l 上.(1)若圆心C 也在直线y =x -1上,过点A 作圆C 的切线,求切线的方程; (2)若圆C 上存在点M ,使MA =2MO ,求圆心C 的横坐标a 的取值范围.理科数学答案1 C2 D3 A4 C5 B6 B7B 8 A 9 B 10D 11. C 12. A13.9343414.2 15. 2 16.-5 17、25. 18.略。
【满足】广西陆川县2020学年高一数学下学期期中试题理
【关键字】满足广西陆川县2016-2017学年高一数学下学期期中试题理一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知五个数成等比数列,则的值为()A.3 B.C.D.2.已知,则()A.B.C.D.3.已知向量,且,则()A.B.C.D.4.在数列中,,则()A.B.C.D.5.在下列区间中,函数的零点所在大致区间为()A. B.C.()D()6、若函数对于任意实数恒有,则等于()A、 B、 C、 D、7、函数是定义在上为增函数,且,则实数的取值范围是()A、 B、 C、 D、8、函数的零点所在的大致区间是()A、 B、 C、 D、9、下列四种说法:①函数在R上单调递加;②若函数在上单调递减,则;③若,则;④若是定义在R上的奇函数,则,其中正确的序号是()A、① ②B、②③C、③ ④D、②④资*源%库10、函数,其中,若动直线与函数的图象有三个不同的交点,它们的横坐标分别为,则的取值范围是()A、B、C、D、11.设等差数列满足,公差,当且仅当时,数列的前项和取得最大值,求该数列首项的取值范围( )A.B.C.D.12.在锐角三角形中,,,分别是角,,的对边,=,则的取值范围为( )A .B .C .D .二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13. 函数的图像关于 对称.14.已知是奇函数,,且则 .15. 若函数的值域是 .16.对于函数,定义域为,以下命题正确的是 (只要求写出命题的序号) ①若,则是上的偶函数;②若对于任意,都有,则是上的奇函数;③若函数在上具有单调性且,则是上的递减函数;④若,则是上的递加函数。
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17. (本小题满分10分.)已知等差数列中,.等比数列的通项公式.(I )求数列的通项公式;(II )求数列的前项和.18、(12分)设(1)求的值及的定义域;(2)求在区间上的最大值19.(本题满分12分)已知函数(1)求函数的最小正周期和函数的单调递加区间; (2)已知中,角的对边分别为,若,求.20. (本小题满分12分.)已知(1)若;(2)若函数)(x f 在区间()1,+∞上是增函数,求实数的取值范围.21.(本小题满分12分.)如图,,A B 是海面上位于东西方向相距5(33)+海里的两个观测点,现位于A 点北偏东045,B 点北偏西060的D 点有一艘轮船发出求救信号,位于B 点南偏西060且与B 点相距3C 点的救援船立即前往营救,其航行速度为30海里/小时,则该救援船达到D 点需要多长时间?22. (本小题满分12分.)已知函数()()2lg 12++++=a x a x x f ,()2-≠a (1)若()x f 能表示成一个奇函数()x g 和一个偶函数()x h 的和,求()x g 和()x h 的解析式;(2)若()x f 和()x g 在区间()()21,+∞-a 上都是减函数,求a 的取值范围; (3)在(2)的条件下,比较()1f 和61的大小. 理科数学答案1-5.BAACB 6-10ABADA 11.C 12.B 13.y 轴14.6 15. ()(),22,-∞+∞16. ②③17.解(I )由题知517149613=+=⎧⎨=+=⎩a a d a a d , 解得112a d =⎧⎨=⎩, 所以21,n a n n N *=-∈.(II )由(I )知,()1212n n n a b n -+=-+,…………….6分所以()()()()0121123252212n n s n -⎡⎤=+++++++-+⎣⎦ ()()112121212n n n ⨯-+-⎡⎤⎣⎦=+-,从而221n n S n =+-.18、(1)()2,22log 2log )1(,21=∴=+=∴=a f f a a -----2分题21图若函数有意义需满足31,0301<<-∴⎩⎨⎧>->+x x x ------3分所以函数的定义域为()3,1------(2)()()⎥⎦⎤⎢⎣⎡∈-+=32,0,31log )(2x x x x f ,设()()()4131)(2+--=-+=x x x x g 当32=x 时,9354132)(2max =+⎪⎭⎫ ⎝⎛--=x g --------10分 所以)(x f 在⎥⎦⎤⎢⎣⎡∈32,0x 的最大值为935log 2-----12分 19.(本题满分12分)解:(1)()sin(2)sin(2)cos 2166f x x x x ππ=++-++3sin 2cos21x x =++ …………………………………………1分=2sin(2)16x π++…………………………………………3分 )(x f ∴的最小正周期ππ==22T ……………………………4分 要使()f x 函数的单调递增-()36k x k k Z ππππ∴≤≤+∈ ………………………………………5分故函数()f x 的单调递增区间[,]()36k k k Z ππππ-+∈ ………………6分(2)()2sin(2)1,()36f x x f A π=++=sin(2)16A π+= ………………………………………………7分132666A πππ<+<又 ……………………………………………8分2,626A A πππ∴+=∴= ………………………………………………9分在ABC ∆中,由正弦定理得:c sin sin a A C =,即12=…………………………………………11分2b =,即=2AC b = ………………………………12分 20. 解析:(1)(1)21,f a ==由得(2)()1212,1,,,x x x x ∈+∞<任取且1<因为函数)(x f 在区间()1,+∞上是增函数所以()1212120x x a x x x x --•< 由12,x x <1<得120x x -<,120x x >所以120x x a ->在()1,+∞上恒成立,即12a x x <在()1,+∞上恒成立,又因为121x x >,所以1a ≤所以实数a 的取值范围为(],1-∞21.解:在ABD ∆中,0006045105ADB ∠=+=,由正弦定理可得:0sin sin 45AB BD ADB =∠,sin 45BD BD =⇒= ...................5分 在BCD ∆中,060CBD ∠=,由余弦定理可知:2222cos CD BD CB BD CB CBD =+-⋅⋅⋅∠,即22202cos60900CD =+-⋅=,故30CD =....................10分所以130CD t ==(小时),救援船到达D 点需要1小时时间. ...........12分 22.(1)()(),1x a x g += ()2lg 2++=a x x h(2)a 的取值范围⎪⎭⎫⎢⎣⎡--1,23 (3)()2lg 21+++=a a f ,∈a ⎪⎭⎫⎢⎣⎡--1,23 函数2lg 2+++=a a y 在∈a ⎪⎭⎫⎢⎣⎡--1,23为增函数,此文档是由网络收集并进行重新排版整理.word 可编辑版本!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【最新】广西陆川中学高一下周测5理科数学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知A={第一象限角},B={锐角},C={小于90°的角},那么A 、B 、C 关系是( ) A .B=A∩CB .B ∪C=CC .A ⫋CD .A=B=C2.已知α角与0120角的终边相同,那么3α的终边不可能落在( )A .第一象限B .第二象限C .第三象限D .第四象限 3.已知α是第三象限角,且cos cos22αα=-,则2α是( ) A .第一象限角 B .第二象限角 C .第三象限角D .第四象限角4.已知tan 3α=,则222sin 4sin cos 9cos αααα+-的值为( )A .130B .13C .2110D .35.已知一扇形的周长为20 cm ,当这个扇形的面积最大时,半径R 的值为( )A .4cmB .5cmC .6cmD .7cm6.设0tan 35,cos55,sin 23a b c ===,则( )A .a b c >>B .b c a >>C .c b a >>D .c a b >> 7)A .sin 2cos2+B .cos2sin 2-C .sin 2cos2--D .sin 2cos2-8.若角α∈(−π,−π2),则√1+sinα1−sinα−√1−sinα1+sinα=( )A .−2tanαB .2tanαC .−tanαD .tanα 9.已知01cos(60)3α+=,且0018090α-<<-,则0cos(30)α-的值为( ) A. BC. D10.已知角α的终边上有一点(1,3)P ,则sin()sin()22cos(2)ππαααπ--+-的值为( )A .1B .45-C .-1D .-4 11.已知角α的终边上一点坐标为77(sin ,cos )1111ππ,则角α的最小正值为( )A .711πB .1511πC .4122πD .1811π二、填空题12.已知扇形的周长等于它所在圆的周长的一半,则这个扇形的圆心角是 . 13.已知θ是第三象限角,且2sin 2cos 5θθ-=-,则sin cos θθ+=________. 14.(cos )cos5f x x =,则(sin )f x =_________. 15.设函数23()()4f x x mx m R =++∈,对任意的0x R ∈,0()f x 和0(1)f x +至少有一个为非负值,则实数m 的取值范围是_________.三、解答题16.(1)若2cos θ=,求sin(5)cos()cos(8)23sin()sin(4)2πθπθπθπθθπ------的值.(2)求函数2()lg(2cos 1)49f x x x =-+-的定义域.17.在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,060BAD ∠=,PA ⊥面ABCD , 3PA =,,E F 分别为,BC PA 的中点.(1)求证://BF 面PDE ;(2)求二面角D PE A --的大小的正弦值; (3)求点C 到面PDE 的距离.参考答案1.B 【解析】 【分析】由集合A ,B ,C ,求出B 与C 的并集,判断A 与C 的包含关系,以及A ,B ,C 三者之间的关系即可. 【详解】 由题B ⊆A ,∵A ={第一象限角},B ={锐角},C ={小于90°的角}, ∴B ∪C ={小于90°的角}=C ,即B ⊆C ,则B 不一定等于A ∩C ,A 不一定是C 的真子集,三集合不一定相等, 故选B . 【点睛】此题考查了集合间的基本关系及运算,熟练掌握象限角,锐角,以及小于90°的角表示的意义是解本题的关键,是易错题 2.C 【解析】试题分析:因为α角与0120角的终边相同,所以360120,k k Z α=⋅+∈,从而12040,3k k Z α=⋅+∈,所以3α可能落在第一、二、三象限,故选择C.考点:终边相同的角、象限角. 3.B 【分析】由α是第三象限角,知2α在第二象限或在第四象限,再由cos cos 22αα=-,知cos 02α≤,由此能判断出2α所在象限. 【详解】α是第三象限角,()180360270360k k k Z α∴+⋅<<+⋅∈, ()901801351802k k k Z α∴+⋅<<+⋅∈.当k 是偶数时,设()2k n n =∈Z ,则()903601353602n n n Z α+⋅<<+⋅∈,此时2α为第二象限角; 当k 是奇数时,设()21k n n Z =+∈,则()2703603153602n n n Z α+⋅<<+⋅∈,此时2α为第四象限角. 综上所述,2α为第二象限角或第四象限角,coscos22αα=-,cos02α∴≤,2α∴为第二象限角.故选:B . 【点睛】本题考查角所在象限的判断,属于基础题,关键在于由所在的象限,得出关于α的不等式,再求出2α的范围. 4.C 【解析】 【分析】利用同角三角函数的基本关系把原式的分母“1”变为sin 2α+cos 2α,然后给分子分母求除以cos 2α,把原式化为关于tanα的关系式,把tanα的值代入即可求出值. 【详解】 因为tanα=3,所以222222249249sin sin cos cos sin sin cos cos sin cos αααααααααα+-+-=+ 2224921110tan tan tan ααα+-==+. 故选C . 【点睛】本题是一道基础题,考查学生灵活运用同角三角函数间的基本关系化简求值的能力,做题的突破点是“1”的灵活变形.5.B 【解析】试题分析:设扇形的圆心角为α,由题意可得:220r r α+=202rrα-⇒=,所以扇形的面积:22221120210(5)2522r S r r r r r rα-==⨯⨯=-=--+,所以当5r =时,扇形的面积最大,故选择B.考点:扇形的弧长公式、面积公式. 6.A 【解析】试题分析:由题可知,00cos55sin 35b ==,00sin 35sin 23>,有b c >,利用三角函数线比较0tan 35,sin 35,如图,单位圆中35AOB ∠=,AB 是35的正切线,CD 是正弦线,通过比较三角函数可知,00tan35sin35>,则有a b >,综上,a b c >>.故选A.x考点:1、三角函数大小比较;2、三角函数线. 7.D 【解析】试题分析:本题可先利用三角函数诱导公式对原式进行等价变形,再结合sin 2,cos 2的大小关系,即可得出所需结果.因为==24ππ<<,所以原式sin 2cos2=-.故选D. 考点:三角函数诱导公式. 8.A【解析】试题分析:√1+sinα1−sinα−√1−sinα1+sinα= √(1+sinα)21−sin 2α−√(1−sinα)21−sin 2α =|1+sinα|−|1−sinα||cosα|,因为α∈(−π,−π2),所以cosα<0,1±sinα≥0,所以原式=(1+sinα)−(1−sinα)−cosα=2sinα−cosα=−2tanα,故选A.考点:三角函数恒等变形与化简. 9.A 【解析】试题分析:因为0018090α-<<-,所以()60120,30α+∈--,再由01cos(60)3α+=,可得()sin 60α+=,从而0cos(30)α-()()2cos 9060sin 60αα⎡⎤=-+=+=-⎣⎦,故选A. 考点:诱导公式、三角变换. 10.A 【解析】试题分析:根据三角函数的定义可知tan 3α=,根据诱导公式和同角三角函数关系式可知:sin()sin()22cos(2)ππαααπ--+-sin cos 1131tan 12cos 222αααα--==-==,故选A.考点:1、三角函数的定义;2、诱导公式和同角三角函数关系.【方法点晴】本题是一个三角函数的定义、三角函数诱导公式及同角三角函数关系式方面的综合性问题,属于中档题.解决本题的基本思路及其切入点是,首先根据三角函数的诱导公式将被求式进行整理与化简,再由点(1,3)P 的坐标,根据三角函数的定义求出角α的有关三角函数值,进而可得到所求结果. 11.C 【解析】试题分析:由于角α的终边上一点坐标为77(sin ,cos )1111ππ,且7sin 011π>,7cos 011π<,因此点77(sin,cos )1111ππ位于第四象限,而7cos7734111tan cot tan()tan()tan()7112112222sin 11ππππππαπ===-=-=,所以角α的最小正值为4122π,故选C.考点:坐标法求三角函数值.【思路点晴】本题是一个已知角的终边上一点的坐标,用坐标法求三角函数值方面的问题,属于中档题.解决本题的基本思路是:首先应根据角α的终边上一点的坐标确定角α所在的象限,再利用坐标法定义的三角函数的计算方法求出角α的一个三角函数值,进而在[)0,2π内得到角α的唯一的一个角,也求是角α的最小正值,从而使问题得到解决. 12.2π- 【解析】试题分析:设扇形的半径R ,弧长l ,根据题意2R l R π+=,解得2lRπ=-,而圆心角2lR απ==-.故答案填2π-. 考点:扇形的弧长、圆心角. 13.3125-【分析】由题意,联立两个方程2sin 2cos 5θθ-=-和22sin cos 1θθ+=,解得cos θ,进而求出sin θ,由此能求出结果. 本题应注意θ是第三象限角.【详解】∵θ是第三象限角,且2sin 2cos 5θθ-=-代入22sin cos 1θθ+=,解得7cos 25θ=-或3cos 5θ=(舍),∴24sin 25θ=-,∴31sin cos 25θθ+=-,故答案为3125-. 【点睛】本题主要考查三角函数得化简求值,掌握同角三角函数间的关系是解题的关键. 14.sin5x 【解析】试题分析:因为sin cos 2x x π⎛⎫=- ⎪⎝⎭,而(cos )cos5f x x =,所以5(sin )(cos())cos5()cos(5)sin 5222f x f x x x x πππ=-=-=-=.考点:同角三角函数间的关系及诱导公式.【方法点晴】本题是一个同角三角函数间的关系及诱导公式方面的问题,属于中当题.解决本题的基本思路及切入点是,紧紧围绕着“结构式”(cos )cos5f x x =,因此要求(sin )f x 的值,首先要将其化为形如“()cos f θ”的结构,结合诱导公式sin cos 2x x π⎛⎫=- ⎪⎝⎭,转化不难实现,问题得以解决. 15.[2,2]- 【解析】试题分析:因为关于x 的二次函数23()()4f x x mx m R =++∈的判别式为223434m m ∆=-⨯=-,①当0∆≤即230m m -≤⇔≤≤()0f x ≥恒成立,满足:对任意的00,()x R f x ∈和0(1)f x +至少有一个为非负值;②当0∆>即230m m ->⇔2304x mx ++=的两个根分别为12,x x ,则有1212{34x x m x x +=-=,此外由对任意的0x R ∈,0()f x 和0(1)f x +至少有一个为非负值可知211x x -≤,故22212121()1()41x x x x x x -≤⇔+-≤2231422m m m ⇔-≤⇔≤⇔-≤≤,结合前提条件m <或m >2m -≤<2m <≤,综上可知所求实数m 的取值范围为[2,2]-.考点:二次函数的三个“二次”之间的关系.【思路点晴】本题是一个关于二次函数的图象、一元二次不等式的解、一元二次方程的根,三个“二次”方面的综合性问题,属于中档题.解决本题的基本思路是:首先考察二次函数的图象与x 轴之间的关系,也就是对二次方程的判别式进行讨论,然后再将问题“对任意的0x R ∈,0()f x 和0(1)f x +至少有一个为非负值”进行转化,从而可求出实数m 的取值范围.16.(1)3±;(2)55{|77}3333x x x x ππππ-≤<--<<<≤或或. 【解析】试题分析:对于问题(1)先根据诱导公式将被求式进行化简,再由cos 3θ=,即可求出结论;对于问题(2和()lg 2cos 1x -各自有意义的x 的取值集合,再求其交集即可得到函数()f x 的定义域. 试题解析:(1)因为sin(5)cos()cos(8)(sin )sin cos 2sin 3cos (sin )3sin()sin(4)2πθπθπθθθθθπθθθθπ----===±----. (2)由题意可知:21cos 2490x x ⎧>⎪⎨⎪-≥⎩,解得:22,3377k x k k Zx ππππ⎧-<<+∈⎪⎨⎪-≤≤⎩, 得:573x π-≤<-或33x ππ-<<或573x π<≤. 故函数的定义域为55{|77}3333x x x x ππππ-≤<--<<<≤或或.考点:1、三角函数式化简及诱导公式;2、函数的定义域.【思路点晴】本题是一个关于三角函数诱导公式、三角恒等变换与化简,以及函数定义域、二次不等式、三角不等式方面的综合性问题,属于中档题.解决本题的基本思路是:对于问题(1)先根据诱导公式将被求式进行化简,再由cos 3θ=,即可求出结论;对于问题(2)和()lg 2cos 1x -各自有意义的x 的取值集合,再求其交集即可得到函数()f x 的定义域.17.(1)证明见解析;(2)7;(3)7. 【解析】试题分析:(1)要证明线面平行,可以通过构造平行四边形先证明线线平行,进而证明线面平行;(2)根据二面角的定义,先作出二面角D PE A --的平面角,再进行论证,最后进行计算,从而求得其正弦值;(3)可根据等体积法由P CDE C PDEV V--=即可求得点C到面PDE的距离.试题解析:(1)如图所示,取PD中点G,连结,GF GE,因为,E F分别为,BC PA的中点,所以可证得//FG BE,FG BE=,所以四边形BFGE是平行四边形,所以//BF EG,又因为EG⊂平面PDE,BF⊄平面PDE,所以//BF平面PDE;(2)作DH AE⊥于H点,作HI PE⊥于I点,连结DI,易证DH⊥平面PAE,所以DH PE⊥,又因为PE HI⊥,HI DH H=,所以PE⊥平面DIH,所以PE DI⊥,所以DIH∠即为二面角D PE A--的平面角,在Rt DIH∆中,23102sin107721DHDIHDI∠==⋅=;(3)因为P CDE C PDEV V--=,所以1133CDE PDES PA S h∆∆⨯=⨯3321217372CDEPDES PAhS∆∆⨯⇒===考点:1、线面平行;2、二面角;3、点到平面的距离.【思路点晴】本题是一个关于线面平行、二面角、点到平面的距离方面的综合性问题,属于难题.解决本题的基本思路是:对于问题(1)要证明线面平行,可以通过构造平行四边形先证明线线平行,进而证明线面平行;对于问题(2)根据二面角的定义,先作出二面角D PE A--的平面角,再进行论证,最后进行计算,从而求得其正弦值;对于问题(3)可本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
