中学保送生考试数学试卷
2023年重庆市渝中区巴蜀中学保送生数学试卷

一、填空题(8'×7=56分)1.(8分)如图是某建筑物的侧面图形.已知AB建筑物坡度为3:1总长为米.斜坡AC和平台CD形成∠ACD为135°,从E点看D点的仰角为30°,AC斜坡长15米.求DE长度为米.(结果保留根号)2.(8分)如图,点Q为正六边形对角线的交点,机器人置于该正六边形的某顶点处.柱柱同学操控机器人以每秒1个单位长度的速度在图1中给出的线段路径上运行,柱柱同学将机器人运行时间设为t秒,机器人到点A距离设为y,得到函数图象如图2.通过观察函数图象,可以得到下列推断:①该正六边形的边长为1;②当t=3时,机器人一定位于点Q;③机器人一定经过点D;④机器人一定经过点E;其中正确的有.3.(8分)已知如图,矩形纸片ABCD,CD=3,AD=8,点E、F分别在AD和BC上,将纸片按照如图所示的方式沿EF折叠,点C、D的对应点是C'和D',连接CC'并延长交线段AB于G,G点恰好是AB的三等分点(BG<AG),则线段EF长为.4.(8分)若关于y的不等式组有且仅有三个非负整数解,且关于x的分式方程有非负整数解,则满足条件的所有整数m的和为.5.(8分)将一枚六个面编号分别为1、2、3、4、5、6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a,第二次掷出的点数为b,则使关于x、y的方程组只有正数解的概率为.6.(8分)若a、b、c均为整数,且满足(a﹣b)2+(a﹣c)2=1,则|a﹣b|+|b﹣c|+|a﹣c|=.7.(8分)已知有数列:a1,a2,…,a n,和c1,c2,…,c n且满足:a n+a n+1=n,c n=a n a n+1,b n=c2n﹣1,已知a1=1,则下列说法正确的有:.①a5=a8②a10=5③b2023=2022×2023④b1+b2+…+b100=33300二、解答题:(16'+18'+20'+20'+20'=94')8.(16分)先化简再求值:,其中x是方程x2+x﹣6=0的解.9.(18分)广阳岛原称广阳坝、广阳洲,位于重庆市南岸区明月山、铜锣山之间,距离市中心11公里,面积6.44平方公里,是长江上游最大的江心绿岛,市政府邀请国内一流的智库力量和设计团队,开展各项规划和城市设计,着力将广阳岛建设成“回归五百年前的生态,引领五十年后的生活”的智创生态城.2022年8月经历重新打造的广阳岛景区重新面对游客开放.游客可以选择从朝天门码头乘轮渡登岛游览或者在岛外乘坐摆渡车进入岛内游玩.据了解,9月试营业期间轮渡票价和摆渡车票价之比为5:2,预计试营业期间一个月登岛观光人数达到18000人,摆渡车票销售总额20万元,轮渡票销售总额是摆渡车票销售总额的两倍.(1)求轮渡票价格和摆渡车票价格每张多少元?(2)为了庆祝国庆佳节,提升市民生活品质,景区管理处决定,十月份降低轮渡票价和摆渡车票价.轮渡票价在试运行单价的基础上降低0.2a%(a>0),摆渡车票价比试运行单价降低元,这样轮渡票销售量和九月一样,摆渡车票的销售量比九月减少了a%,轮渡船票和摆渡车票的销售总额比预计减少了4550a元.求a的值.10.(20分)若一个各位数字都不为0的三位正整数满足:十位数字与个位数字之和减去百.位数字的差为4,则称这个三位数为“顺利数”,例如:123,因为2+3﹣1=4,所以123是“顺利数”;同时定义任何一个顺利数t=(1≤a≤9,0≤b≤9,0≤c≤9且a、b、c均为整数)的F(t)=.(1)判断326与875是否为“顺利数”,并说明理由;(2)已知数S=100m+20n+p(1≤m≤6,1≤n≤4,1≤p≤9)是“顺利数”,且3F(S)﹣10p能被11整除,求所有符合题意的S的值.11.(20分)如图1,抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,∠BAC的平分线与y轴交于点D,与抛物线交于点Q,点P是线段AB上一点,过点P作x轴的垂线,分别交AD,AC于点E、F,连接OE,OF.(1)当△OEF面积最大时,求P点的坐标.(2)在(1)的条件下,在直线PF上取点M,在y轴上取点N,当BN+MN+MQ最小时,求出N的坐标.(3)如图2,将抛物线y沿着射线AC方向平移得到y',y'的图象恰好经过点C,在抛物线y'的对称轴上取点G,在抛物线y'上取点K,在(2)的条件下,是否存在以P、N、K、G为顶点的平行四边形,如果存在直接写出k点坐标,如果不存在请说明理由.12.(20分)如图,已知四边形ABCD,AB∥CD,且BC⊥CD,过C点作CF⊥AD交AD于F,点E在AF上且EF=CF,点H在BA延长线上且BC=BH,连接EH.(1)如图1,若∠HAE=60°,AH=10,S△AEH=5,CD=2,求BC的长度.(2)如图2,取EH中点G,连接BG、FG,求证:BG=FG.(3)如图3,在(2)条件下,连接HF,若∠AHE=30°,BH=4,将△GEF绕着G点旋转,GF所在直线与直线BC交于Q,N是△BHQ内部一点,当HF最大时,直接写出HN+4NQ+3NB的最小值.。
初三保送生选拔数学试卷及答案
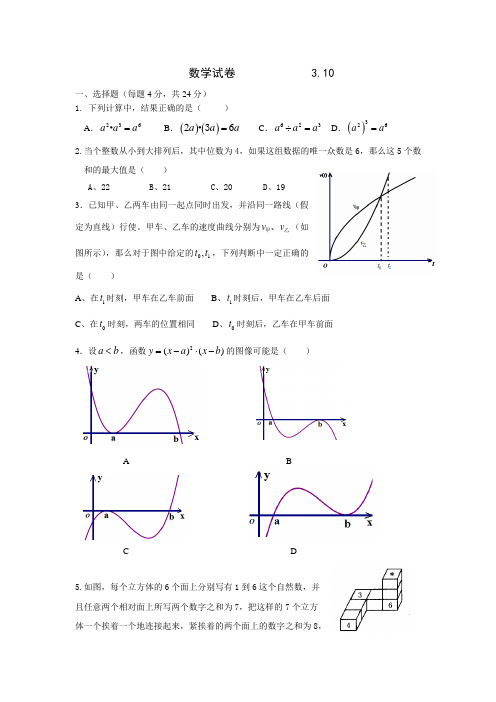
数学试卷 3.10 一、选择题(每题4分,共24分) 1. 下列计算中,结果正确的是( )A .236a a a =· B .()()26a a a =·3 C .623a a a ÷= D .()326aa =2.当个整数从小到大排列后,其中位数为4,如果这组数据的唯一众数是6,那么这5个数和的最大值是( )A 、22B 、21C 、20D 、19 3.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行使。
甲车、乙车的速度曲线分别为v v 甲乙、(如图所示),那么对于图中给定的01,t t ,下列判断中一定正确的是( )A 、在1t 时刻,甲车在乙车前面B 、1t 时刻后,甲车在乙车后面C 、在0t 时刻,两车的位置相同D 、0t 时刻后,乙车在甲车前面 4.设a b <,函数2()()y x a x b =-⋅-的图像可能是( )A BC D5.如图,每个立方体的6个面上分别写有1到6这个自然数,并 且任意两个相对面上所写两个数字之和为7,把这样的7个立方 体一个挨着一个地连接起来,紧挨着的两个面上的数字之和为8,则图中“*”所在面上的数字是( ) (第6题) A 、4 B 、3 C 、2 D 、1 6. 一个三角形的边长分别为,,a a b ,另一个三角形的边长分别为,,b b a ,其中a b >,若两个三角形的最小内角相等,则ab的值等于( ) AB二、填空题(每题4分,共20分)7、有一个多项式为a 8-a 7b +a 6b 2-a 5b 3+…,按照此规律写下去,这个多项式的第八项是8、有三条绳子穿过一片木板,姊妹两人分别站在木板 的左、右两边,各选该边的一条绳子,若每边每条绳子被选中的机会相等,则两人选到同一条绳子的概率为9.△ABC 中,a ,b ,c 分别是∠A 、∠B 、∠C 的对边.已知a =10,b =23+,c =23-,则b sin B +c sin C 的值等于 。
中学保送生考试数学试卷

保送生考试数学试卷一、 选择题(每题只有一个答案是正确的。
每题4分,共16分。
)1、若有m 个数的平均数是x , 另有n 个数的平均数是y ,则这m n +个数的平均数是( ) (A )2x y + (B )x y m n ++ (C )mx nym n++ (D )mx ny x y ++2、如图是一个正方体包装盒的表面展开图,若在其中的三个正方形A 、B 、C 内分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,相对面上的两数互为相反数,则填在A 、B 、C 内的三个数依次是( ) (A )1,0,-2 (B ) 0,1,-2 (C )0,-2,1 (D )-2,0,1 3、函数y ax a =-+与ay x-=(a ≠0)在同一个坐标系中的图像可能是( )4、已知梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于O ,△AOD 的面积为4,△BOC 的面积为9,则梯形ABCD 的面积为( )(A )21 (B )22 (C )25 (D )26二、填空题(每题4分,共16分。
)5、在某一时刻,一个身高1.6米的同学影长2米,同时学校旗杆的影子有一部分落在12米外的墙上,墙上影高1米,则旗杆高为_______.6、一个幻方中,每一行,每一列,及每一对角线上的三个数之和有相同的值,如图所示已知一个幻方中的三个数,则x 的值是 .7、观察下列等式: (第1条)222543=+(第2条)222221413121110+=++(第3条)222222227262524232221++=+++写出(第4条)8、老李到办公室后,他总要完成以下事情:烧开水10分钟,洗茶杯1分钟,准备茶叶和冲茶1分钟,打扫办公室9分钟,收听新闻10分钟,问老李做好以上事情至少需要 分钟时间。
三、解答题9、如图所示,AB 为⊙O 的直径,P 为AB 延长线上一点,PD 切⊙O 于C ,BC 和AD 的延长线相交于点E ,且AB =AE 。
初中数学保送生数学试卷

一、选择题(每题3分,共30分)1. 已知函数f(x) = x^2 - 4x + 3,其图像的对称轴是:A. x = 1B. x = 2C. x = 3D. x = 42. 在直角三角形ABC中,∠C = 90°,AC = 3,BC = 4,则AB的长度为:A. 5B. 6C. 7D. 83. 已知等差数列{an},a1 = 3,公差d = 2,则a10的值为:A. 21B. 22C. 23D. 244. 已知方程x^2 - 5x + 6 = 0的两个根为a和b,则a^2 + b^2的值为:A. 25B. 30C. 35D. 405. 在等腰三角形ABC中,AB = AC,∠BAC = 40°,则∠B的度数为:A. 40°C. 60°D. 70°6. 已知函数f(x) = |x - 2| + |x + 3|,则f(x)的最小值为:A. 5B. 6C. 7D. 87. 已知方程组:$$\begin{cases}x + 2y = 5 \\3x - y = 7\end{cases}$$的解为:A. x = 1,y = 2B. x = 2,y = 1C. x = 3,y = 0D. x = 4,y = -18. 已知等比数列{an},a1 = 2,公比q = 3,则a6的值为:A. 54B. 162D. 14589. 在等边三角形ABC中,AB = BC = AC,则∠ABC的度数为:A. 30°B. 45°C. 60°D. 90°10. 已知方程x^2 - 6x + 9 = 0的两个根为a和b,则a^3 + b^3的值为:A. 36B. 48C. 60D. 72二、填空题(每题5分,共20分)11. 已知函数f(x) = 2x - 3,若f(x)的值域为[1, 5],则x的取值范围为______。
12. 在等腰三角形ABC中,AB = AC,∠BAC = 50°,则∠ABC的度数为______。
重点高中招收保送生考试数学试题及答案

B CFE 重点高中招收保送生考试数学试题一、选择题(每小题3分,共30分) 1. 下列计算正确的是 ( ) A .633x y x= B. 532)(m m =C. 22212x x=- D. 336)()(a a a -=-÷-2. 已知20082010+=x a ,20092010+=x b ,20102010+=x c ,则多项式ac bc ab c b a ---++222的值为 ( )A. -3B. 3C. 2D. 13. 甲、乙、丙、丁四位同学参加校田径运动会4×100米接力跑比赛,如果任意安排四位同学的跑步顺序,那么恰好由甲将接力棒交给乙的概率是( ) A.41 B.61 C. 81D. 1214. 某工厂第二季度的产值比第一季度的产值增长了%x ,第三季度的产值又比第二季度的产值增长了%x ,则第三季度的产值比第一季度增长了 ( ) A .%2x B .%21x + C .%%)1(x x ⋅+ D .%%)2(x x ⋅+ 5. 在平面直角坐标系中,A(0,3)、B(4,1)、C(m,0).当△ABC 的周长最小时,m 的值为( )A. -3B. 3C. 2D. 1 6. 计算机是将信息转换顾二进制数进行处理的,二进制即“逢2进1”,如(1101)2表二进制数,将它换成十进制形式是132********123=⨯+⨯+⨯+⨯。
那么将二进制2)1111(转换成十进制形式是数( )A. 8B. 15C. 20D. 30 7. 如图,矩形ABCD 的周长是20cm ,以AB 、AD 为边向 外作正方开ABEF 和正方形ADGH 。
若正方形ABEF 和 正方形ADGH 的面积之和是682cm ,那么矩形ABCD 的面积是( )A. 221cmB. 162cmC. 224cmD. 92cm8. 如果一元二次方程)0(02≠=++a c bx ax 满足0=++c b a ,那么称这种方程为“凤凰方程”。
初中数学 2024年重庆市渝中区保送生数学试卷

2024年重庆市渝中区巴蜀中学保送生数学试卷一、选择题(共12小题)A .3152B .173C .112D .321.如图,已知四边形ABCD 内接于⊙O ,直径AC =6,对角线AC 、BD 交于E 点,且AB =BD ,EC =1,则AD 的长为( )√√A .2:3B .2:5C .4:9D .2:32.如图,梯形ABCD 中,AD ∥BC ,∠B =∠ACD =90°,AB =2,DC =3,则△ABC 与△DCA 的面积比为( )√√A .1:2B .2:3C .1:3D .1:43.如图,△ABC 中,AD 、BE 是两条中线,则S △EDC :S △ABC =( )A .1:4B .2:3C .1:3D .1:24.如图,在△ABC 中,两条中线BE 、CD 相交于点O ,则S △DOE :S △COB =( )A .7.5B .10C .15D .205.如图,在△ABC 中,点D 在边AB 上,BD =2AD ,DE ∥BC 交AC 于点E ,若线段DE =5,则线段BC 的长为( )6.如图,△ABC 中,AE 交BC 于点D ,∠C =∠E ,AD :DE =3:5,AE =8,BD =4,则DC 的长等于( )A .154B .125C .203D.174A .3B .4C .5D .67.如图,在△ABC 中,点D ,E 分别在AB ,AC 上,DE ∥BC ,AD =CE .若AB :AC =3:2,BC =10,则DE 的长为( )A .4个B .3个C .2个D .1个8.如图,四边形ABCD 、CEFG 都是正方形,点G 在线段CD 上,连接BG 、DE ,DE 和FG 相交于点O ,设AB =a ,CG =b (a >b ).下列结论:①△BCG ≌△DCE ;②BG ⊥DE ;③DG GC=GO CE;④(a -b )2•S△EFO =b 2•S △DGO .其中结论正确的个数是( )A .158B .113C .103D .1659.如图,四边形ABCD 是矩形,点E 和点F 是矩形ABCD 外两点,AE ⊥CF 于点H ,AD =3,DC =4,DE =52,∠EDF =90°,则DF 长是( )A .1B .2C .3D .410.如图,已知△ABC 和△ADE 均为等边三角形,D 在BC 上,DE 与AC 相交于点F ,AB =9,BD =3,则CF 等于( )11.如图,在△ABC 中,D 、E 分别是AB 、BC 上的点,且DE ∥AC ,若S △BDE :S △CDE =1:4,则S △BDE :S △ACD =( )二、填空题(共6小题)A .1:16B .1:18C .1:20D .1:24A .1B .2C .122-6D .62-612.如图,△ABC 中,AB =AC =18,BC =12,正方形DEFG 的顶点E ,F 在△ABC 内,顶点D ,G 分别在AB ,AC 上,AD =AG ,DG =6,则点F 到BC 的距离为( )√√13.如图,在△ABC 中,点D 、E 分别在AB 、AC 上,DE ∥BC .若AD =4,DB =2,则DE BC的值为 .14.如图,△ABC 中,D 、E 分别为AB 、AC 的中点,则△ADE 与△ABC 的面积比为 .15.如图,AD 是△ABC 的高,AE 是△ABC 的外接圆⊙O 的直径,且AB =42,AC =5,AD =4,则⊙O 的直径AE =.√16.如图,平行于BC 的直线DE 把△ABC 分成的两部分面积相等,则AD AB= .17.如图,在△ABC 中,DE ∥BC ,DE BC=23,△ADE 的面积是8,则△ABC 的面积为.18.将(n +1)个边长为1的正方形按如图所示的方式排列,点A 、A 1、A 2、A 3、…A n +1和点M 、M 1、M 2、M 3,…M n 是正方形的顶点,连接AM 1,AM 2,AM 3,…AM n ,分别交正方形的边A 1M ,A 2M 1,A 3M 2,…A n M n -1于点N 1,N 2,N 3,…,N n ,四边形M 1N三、解答题(共12小题)1A 1A 2的面积为S 1,四边形M 2N 2A 2A 3的面积是S 2,…四边形M n N n A n A n +1的面积是S n ,则S n =.19.如图,已知AB ∥CD ,AD 与BC 相交于点E ,BF 平分∠ABC 交AD 于F .(1)当CE =12BE 时,线段CD 与AB 之间有怎样的数量关系?请写出你的结论并给予证明;(2)当AF =12AD 时,线段AB 、BC 、CD 之间有怎样的数量关系?请写出你的结论并给予证明.20.如图,已知△ABC 中,点D 在AC 上且∠ABD =∠C ,求证:AB 2=AD •AC .21.如图,在△ABC 中,点D ,E 分别在边AB ,AC 上,若DE ∥BC ,DE =2,BC =3,求AE AC的值.22.如图,D 是△ABC 的边AC 上的一点,连接BD ,已知∠ABD =∠C ,AB =6,AD =4,求线段CD 的长.23.如图,AB 是⊙O 的直径,弦CD ⊥AB 于点G ,点F 是CD 上一点,且满足CF FD=13,连接AF 并延长交⊙O 于点E ,连接AD 、DE ,若CF =2,AF =3.(1)求证:△ADF ∽△AED ;(2)求FG 的长;(3)求证:tan ∠E =54.√24.等边三角形ABC 的边长为6,在AC ,BC 边上各取一点E ,F ,连接AF ,BE 相交于点P .(1)若AE =CF ;①求证:AF =BE ,并求∠APB 的度数;②若AE =2,试求AP •AF 的值;(2)若AF =BE ,当点E 从点A 运动到点C 时,试求点P 经过的路径长.25.如图,AB 是⊙O 的直径,C ,P 是AB 上两点,AB =13,AC =5.(1)如图(1),若点P 是AB 的中点,求PA 的长;(2)如图(2),若点P 是BC 的中点,求PA 的长.⌢⌢⌢26.如图,在△ABC 中,∠BAC 的角平分线AD 交BC 于E ,交△ABC 的外接圆⊙O 于D .(1)求证:△ABE ∽△ADC ;(2)请连接BD ,OB ,OC ,OD ,且OD 交BC 于点F ,若点F 恰好是OD 的中点.求证:四边形OBDC 是菱形.27.如图,在四边形ABCD 中,AB =AD ,AC 与BD 交于点E ,∠ADB =∠ACB .(1)求证:AB AE=AC AD;(2)若AB ⊥AC ,AE :EC =1:2,F 是BC 中点,求证:四边形ABFD 是菱形.28.如图,AB 是⊙O 的直径,延长AB 至P ,使BP =OB ,BD 垂直于弦BC ,垂足为点B ,点D 在PC 上.设∠PCB =α,∠POC =β.求证:tanα•tan β2=13.29.已知:如图,梯形ABCD 中,AD ∥BC ,AB =DC ,对角线AC 、BD 相交于点F ,点E 是边BC 延长线上一点,且∠CDE =∠ABD .(1)求证:四边形ACED 是平行四边形;(2)连接AE ,交BD 于点G ,求证:DG GB=DF DB.30.如图,四边形ABCD 内接于⊙O ,AB 是⊙O 的直径,AC 和BD 相交于点E ,且DC 2=CE •C A .(1)求证:BC =CD ;(2)分别延长AB ,DC 交于点P ,过点A 作AF ⊥CD 交CD 的延长线于点F ,若PB =OB ,CD =22,求DF 的长.√。
保送生初中数学试卷

一、选择题(每题5分,共50分)1. 下列各数中,不是有理数的是()A. 2.5B. -3C. √4D. 0.101010...2. 已知a、b是实数,且a+b=0,则下列等式中正确的是()A. a^2 = b^2B. a^2 = -b^2C. a^2 = 2b^2D. a^2 = b^2 + 23. 下列各式中,能被3整除的是()A. 15 + 24B. 27 - 18C. 36 + 9D. 48 - 124. 已知一个长方体的长、宽、高分别为a、b、c,则它的体积V=()A. abcB. ab + bc + acC. a^2b + b^2c + c^2aD. a^2b^2c^25. 在直角坐标系中,点P的坐标为(-2,3),则点P关于x轴的对称点坐标是()A. (-2,-3)B. (2,3)C. (2,-3)D. (-2,3)6. 下列各式中,能表示反比例函数的是()A. y = 2x + 1B. y = 3/xC. y = x^2D. y = x^37. 下列各式中,正确的是()A. 3^2 = 9^1B. 4^3 = 64C. 5^2 = 10^1D. 6^3 = 36^18. 已知a、b、c是三角形的三边,且a+b+c=10,若a=3,b=4,则c的取值范围是()A. 3 < c < 7B. 2 < c < 8C. 3 < c < 9D. 2 < c < 109. 下列各图中,能表示y=2x+1的是()A.B.C.D.10. 下列各数中,不是整数的是()A. -1/2B. 3/4C. -2/3D. 5/6二、填空题(每题5分,共50分)11. 计算:-3 + 5 - 2 + 4 = _______12. 若a=2,b=-3,则a^2 - 2ab + b^2 = _______13. 已知长方形的周长为20,长为6,则宽为 _______14. 在直角坐标系中,点A的坐标为(3,4),则点A关于y轴的对称点坐标是_______15. 下列函数中,反比例函数的图象是 _______16. 下列各数中,能被5整除的是 _______17. 若x^2 - 5x + 6 = 0,则x的值为 _______18. 下列各式中,能表示一次函数的是 _______19. 下列各数中,不是有理数的是 _______20. 若a、b、c是等差数列,且a=2,b=5,则c的值为 _______三、解答题(每题20分,共60分)21. 已知一元二次方程x^2 - 4x + 3 = 0,求它的解。
初中升学保送生选拔考试(一中拔尖考试)数学试卷

xx 年初三数学试卷时量:120分钟 总分:120分一、填空题(每小题3分,共24分)1、-|21-|的倒数= ;1-x ≥02、不等式组 的整数解为 ; 2x-1>-33、当x= 时,分式6322---x x xx 的值为0;4、若方程2112=-+-+x xx k x 有一增根x=1,则k= ; 5、袋中有同样大小的4个小球,其中3个红色,1个白色,从袋中任意地同时摸出2个球,这两个球颜色相同的概率是 ;6、在平面直角坐标系中,将抛物线y=x 2+4x+4沿着直线y=0向右平移2个单位,然后绕顶点旋转180°,所得抛物线的解析式为 。
7、如图,在矩形ABCD 中,AB=6cm ,将矩形ABCD 折叠,使点B 与点D 重 合,点C 落在C ′处,若AE :BE=1:2, 则折痕EF 的长为 ;8、如图,将一副三角板叠放, 则△AOB 与△DOC 的面积之比为 。
二、选择题(每小题的3分,共24分) 9、温家宝总理有一句名言:“多么小的问题乘以13亿,都会变得很大,多么大的经济总量除以13亿,都会变得很小。
”如果每人每天浪费0.5升水,我国13亿人每天就浪费水( )A 、6.5×108升B 、6.5×109升C 、2.6×108升D 、2.6×109升10、两圆半径分别为5和3,圆心距为8,则两圆的位置关系是( )A 、内切B 、相交C 、外切D 、外离 11、下列命题是假命题的是( )A 、若a=b,则a 2=b 2B 、xxx 是中华人民共和国的首都C 、垂直于同一直线的两直线平行D 、平移不改变图形的形状与大小 12、如图,一次函数的图象过点A , 且与正比例函数y=-x 的图象交于点B , 则该一次函数的表达式为( ) A 、y=-x+2 B 、y=x+2 C 、y=x-2 D 、y=-x-2 13、如图,已知MB=ND , ∠MBA=∠NDC ,加上下列哪个 条件不能用来判定△ABM ≌△CDN ( ) A 、∠M=∠N B 、AB=CD C 、AM=CN D 、AM ∥CN14、如图,∠1+∠2+∠3+∠4+∠5+∠6 的度数为( ) A 、180° B 、360° C 、540° D 、无法确定 15、为执行“两免一补”政策,某地区2006年投入教育经费2500万元,由于加大投入力度,2008年投入3600万元,设两年中投入教育经费的平均增长率为x ,则下列方程正确的是( )A 、2500x 2=3600B 、2500(1+x )2=3600C 、2500(1+x%)=3600D 、2500(1+x )+2500(1+x)2=3600 16、小明从正面观察一个圆柱体邮筒和一个正方体箱子,看到的应该是( )密封线内 不得 作答…………………………密……………………封…………………………装…………………………订……………………线…………………………三、解答题(每小题7分,共28分)17、计算:()︒--+--⎪⎭⎫⎝⎛-+︒-2009273145sin 2183118、先化简,再求值:2,1·11112=-⎪⎭⎫ ⎝⎛+--a a a a a 其中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
保送生考试数学试卷
一、 选择题(每题只有一个答案是正确的。
每题4分,共16分。
)
1、若有m 个数的平均数是x , 另有n 个数的平均数是y ,则这m n +个数的平均数是( ) (A )
2x y + (B )x y m n ++ (C )mx ny m n ++ (D )mx ny
x y
++ 2、如图是一个正方体包装盒的表面展开图,若在其中的三个正方形A 、B 、
C 内分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,相对面上的两数互为相反数,则填在A 、B 、C 内的三个数依次是( ) (A )1,0,-2 (B ) 0,1,-2 (C )0,-2,1 (
D )-2,0,1 3、函数y ax a =-+与a
y x
-=
(a ≠0)在同一个坐标系中的图像可能是( )
4、已知梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于O ,△AOD 的面积为4,△BOC 的面积为9,则梯形ABCD 的面积为( )
(A )21 (B )22 (C )25 (D )26
二、填空题(每题4分,共16分。
)
5、在某一时刻,一个身高1.6米的同学影长2米,同时学校旗杆的影子有一部分落在12米外的墙上,墙上影高1米,则旗杆高为_______.
6、一个幻方中,每一行,每一列,及每一对角线上的三个数之和有相同的值,如图所示已知一个幻方中的三个数,则x 的值是 .
7、观察下列等式: (第1条)2
2
2
543=+
(第2条)2
2
2
2
2
1413121110+=++
(第3条)2
2
2
2
2
2
2
27262524232221++=+++
写出(第4条)
8、老李到办公室后,他总要完成以下事情:烧开水10分钟,洗茶杯1分钟,准备茶叶和冲茶1分钟,
打扫办公室9分钟,收听新闻10分钟,问老李做好以上事情至少需要 分钟时间。
三、解答题
9、如图所示,AB 为⊙O 的直径,P 为AB 延长线上一点,PD 切⊙O 于C ,BC 和AD 的延长线相交于点E ,且AB =AE 。
(1)求证:AD PD ⊥
(2)若圆的半径为 ,BP=1。
求证:ABE ∆是等边三角形。
(题中横线上的数字被墨迹污染了,请你填上半径的值,并证明这个题目)(本题10分)
10、1960年,数学家证明存在一个正整数n ,使得5
5
5
5
5
1331108427n +++=,推翻了数学家欧拉的一个猜想。
请你求出n 的值。
(简要说明理由,本题10分)
11、某一天的不同时刻老板把信交给秘书打字,每次都将信放在秘书信堆的最上面,秘书有时间就将信堆最上面的那封信取来打。
(1)假定共有5封信,且老板以1、2、3、4、5的顺序交来,在下列各顺序中,哪一顺序不可能是秘书打字的顺序?
A 、12345
B 、54321
C 、23541
D 、23514
(2)假定共有3封信,且老板以1、2、3的顺序交来,则秘书打字的顺序有多少种可能? (简要说明理由,本题8分)
【数学】
二、 选择题(每题只有一个答案是正确的。
每题4分,共16分。
)
1、若有m 个数的平均数是x , 另有n 个数的平均数是y ,则这m n +个数的平均数是( ) (A )
2x y + (B )x y m n ++ (C )mx ny m n ++ (D )mx ny
x y
++ 2、如图是一个正方体包装盒的表面展开图,若在其中的三个正方形A 、B 、C 内分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,相对面上的两数互为相反数,则填在A 、B 、C 内的三个数依次是( )
(A )1,0,-2 (B ) 0,1,-2 (C )0,-2,1 (D )-2,0,1
3、函数y ax a =-+与a
y x
-=
(a ≠0)在同一个坐标系中的图像可能是( ) 4、已知梯形ABCD 中,AD
∥BC ,对角线AC 、BD 交于O ,△AOD 的面积为4,△BOC 的面积为9,则梯形ABCD 的面积为( )
(A )21 (B )22 (C )25 (D )26
二、填空题(每题4分,共16分。
)
5、在某一时刻,一个身高1.6米的同学影长2米,同时学校旗杆的影子有一部分落在12米外的墙上,墙上影高1米,则旗杆高为_______.
6、一个幻方中,每一行,每一列,及每一对角线上的三个数之和有相同的值,如图所示已知一个幻方中的三个数,则x 的值是 .
7、观察下列等式:
(第1条)2
22543=+
(第2条)2
22221413121110+=++
(第3条)2
22222227262524232221++=+++
写出(第4条)
8、老李到办公室后,他总要完成以下事情:烧开水10分钟,洗茶杯1分钟,准备茶叶和冲茶1分钟,打扫办公室9分钟,收听新闻10分钟,问老李做好以上事情至少需要 分钟时间。
三、解答题
9、如图所示,AB 为⊙O 的直径,P 为AB 延长线上一点,PD 切⊙O 于C ,BC 和AD 的延长线相交于点E ,且AB =AE 。
(1)求证:AD PD ⊥
(2)若圆的半径为 ,BP=1。
求证:ABE ∆是等边三角形。
(题中横线上的数字被墨迹污染了,请你填上半径的值,并证明这个题目)(本题10分)
10、1960年,数学家证明存在一个正整数n ,使得55555
1331108427n +++=,推翻了数学家欧拉的一个猜想。
请你求出n 的值。
(简要说明理由,本题10分)
11、某一天的不同时刻老板把信交给秘书打字,每次都将信放在秘书信堆的最上面,秘书有时间就将信堆最上面的那封信取来打。
(1)假定共有5封信,且老板以1、2、3、4、5的顺序交来,在下列各顺序中,哪一顺序不可能是秘书打字的顺序?
A 、12345
B 、54321
C 、23541
D 、23514
(2)假定共有3封信,且老板以1、2、3的顺序交来,则秘书打字的顺序有多少种可能? (简要说明理由,本题8分)
1、答案:C.
2、答案:C.
3、答案:A.
4、答案:CD.
5、答案:10.6米.
6、答案:26.
7、答案:
2
2
2
2
2
2
2
2
244
43
42
41
40
39
38
37
36+
+
+
=
+
+
+
+
8、答案:11
9、答案:(1)连接OC,AE∥OC (2)半径为1
10、答案:144
11、答案:(1)D(2)5。
