第九章第2节
合集下载
第9章 第2节 二项式定理

5-r=3, r=2,
解得 r=2.所以 x3y2 的系数是 C25123×(-2)2=5.故选 A.]
第二节 二项式定理
1
2
3
走进教材·夯实基础 细研考点·突破题型 课时分层作业
3.若x+1xn展开式的二项式系数之和为 64,则展开式的常数项 为( )
A.10
B.20
C.30
D.120
B [二项式系数之和 2n=64,所以 n=6,Tr+1=Cr6·x6-r·1xr=Cr6x6 -2r,当 6-2r=0,即当 r=3 时为常数项,T4=C36=20.]
(2)偶数项的二项式系数的和等于奇数项的二项式系数的和,即 C0n+C2n+C4n+…=C1n+C3n+C5n+…= 2n-1 .
提醒:二项式系数与项的系数是完全不同的两个概念.二项式系
数是指 C0n,C1n,…,Cnn,它只与各项的项数有关,而与 a,b 的值无 关;而项的系数是指该项中除变量外的常数部分,它不仅与各项的项
第二节 二项式定理
1
2
3
走进教材·夯实基础 细研考点·突破题型 课时分层作业
(3)法一:(1+2x-3x2)5=(1-x)5(1+3x)5,所以 x5 的系数为 C05C55 35+C15(-1)C4534+C25(-1)2C3533+C35(-1)3C2532+C45(-1)4C1531+C55(- 1)5C0530=92.
1
2
3
走进教材·夯实基础 细研考点·突破题型 课时分层作业
形如(a+b+c)n 的展开式问题 [典例 1-3] (1)将x+4x-43展开后,常数项是________. (2)x2-2x+y6的展开式中,x3y3 的系数是________.(用数字作答)
第九章第2节 法拉第电磁感应定律

第2节
法拉第电磁感应定律
结束
第 2 节 法拉第电磁感应定律
栏目索引
课前基础· 简要回顾
课堂释疑· 一站突破
课后演练· 对点设计
第2节
法拉第电磁感应定律
结束
(1)线圈中磁通量越大,产生的感应电动势越大。 (2)线圈中磁通量变化越大,产生的感应电动势越大。 (3)线圈中磁通量变化越快,产生的感应电动势越大。 (4)线圈匝数 n 越多,磁通量越大,产生的感应电动势也越大。 (5)磁场相对于导体棒运动时,导体棒中也可能产生感应电动势。
栏目索引
课前基础· 简要回顾 课堂释疑· 一站突破 课后演练· 对点设计
第2节
法拉第电磁感应定律
结束
[针对训练] 1.(2014· 江苏高考)如图 922 所示,一正方 形线圈的匝数为 n,边长为 a,线圈平面 与匀强磁场垂直, 且一半处在磁场中。 在 Δt 时间内,磁感应强度的方向不变,大 小由 B 均匀地增大到 2B。在此过程中, 线圈中产生的感应电动势为 Ba2 A. 2Δ t nBa2 C. Δt
栏目索引
课前基础· 简要回顾
课堂释疑· 一站突破
课后演练· 对点设计
第2节
法拉第电磁感应定律
结束
2.应用法拉第电磁感应定律的三种情况 (1)磁通量的变化是由面积变化引起时, ΔΦ= B·ΔS,则 E BΔS =n ; Δt (2)磁通量的变化是由磁场变化引起时, ΔΦ= ΔB· S,则 E ΔB· S =n ; Δt (3)磁通量的变化是由面积和磁场变化共同引起时, 则根据 B2S2- B1S1 ΔBΔS 定义求, ΔΦ= Φ 末 - Φ 初, E= n ≠n 。 Δt Δt
栏目索引
课前基础· 简要回顾
法拉第电磁感应定律
结束
第 2 节 法拉第电磁感应定律
栏目索引
课前基础· 简要回顾
课堂释疑· 一站突破
课后演练· 对点设计
第2节
法拉第电磁感应定律
结束
(1)线圈中磁通量越大,产生的感应电动势越大。 (2)线圈中磁通量变化越大,产生的感应电动势越大。 (3)线圈中磁通量变化越快,产生的感应电动势越大。 (4)线圈匝数 n 越多,磁通量越大,产生的感应电动势也越大。 (5)磁场相对于导体棒运动时,导体棒中也可能产生感应电动势。
栏目索引
课前基础· 简要回顾 课堂释疑· 一站突破 课后演练· 对点设计
第2节
法拉第电磁感应定律
结束
[针对训练] 1.(2014· 江苏高考)如图 922 所示,一正方 形线圈的匝数为 n,边长为 a,线圈平面 与匀强磁场垂直, 且一半处在磁场中。 在 Δt 时间内,磁感应强度的方向不变,大 小由 B 均匀地增大到 2B。在此过程中, 线圈中产生的感应电动势为 Ba2 A. 2Δ t nBa2 C. Δt
栏目索引
课前基础· 简要回顾
课堂释疑· 一站突破
课后演练· 对点设计
第2节
法拉第电磁感应定律
结束
2.应用法拉第电磁感应定律的三种情况 (1)磁通量的变化是由面积变化引起时, ΔΦ= B·ΔS,则 E BΔS =n ; Δt (2)磁通量的变化是由磁场变化引起时, ΔΦ= ΔB· S,则 E ΔB· S =n ; Δt (3)磁通量的变化是由面积和磁场变化共同引起时, 则根据 B2S2- B1S1 ΔBΔS 定义求, ΔΦ= Φ 末 - Φ 初, E= n ≠n 。 Δt Δt
栏目索引
课前基础· 简要回顾
红星照耀中国批注第九章第二节

《红星照耀中国》第九章第二节的批注,可以从以下几个方面进行:
1.红军骑兵的英勇:描述了红军骑兵在战争中的勇敢和决心,他们为了民族和国家的独立,奋勇向前,不畏艰难险阻。
2.红军小战士的成长:强调了红军小战士在艰苦的环境中,逐渐成长为勇敢、坚定的战士,他们的精神状态积极向上,充满了对革命的热情。
3.少先队员的精神风貌:描述了少先队员的精神状态,他们充满了生机和活力,对红军有着强烈的向往和敬仰,展现了他们的爱国情怀和革命精神。
4.红军领导人的亲和力和忙碌:展现了红军领导人的亲和力和忙碌状态,他们不仅关心战士,还积极为革命事业付出,体现了他们的敬业精神和无私奉献。
第九章第二节 人体的消化与吸收(第2课时)七年级生物下册课件(苏教版 )

泌
,能促进
的乳化.
(2)消化食物和吸收营养物质的主要场所是
.
(3)淀粉开始消化的部位是[ ]
,
其最终被分解为
。
(4)蛋白质开始消化的部位是[ ]
,
其最终被分解为
。
(5)脂肪开始消化的部位是[ ] ,
其最终被分解为
.
参考答案:(1) 8 肝脏 胆汁 脂肪 (2)小肠 (3)1 口腔 葡萄糖 (4)3 胃 氨基酸 (5)4 小肠 甘油和脂肪酸
• 蛋白质 蛋白酶 初步消化形成多肽 肽酶 • ③脂肪的消化:
氨基酸
• 脂肪 胆汁 脂肪微粒 脂肪酶 甘油 + 脂肪酸
参考教材33页图片,小组合作,总结:
1、口腔中的物理性消化? 化学性消化? • 胃中的物理性消化? 化学性消化? • 小肠中的物理性消化? 化学性消化? • 2、蛋白质、脂肪、淀粉的最终消化产物分别是什么? • 3、消化的主要器官是?为什么?
• 2、食物中的哪些营养物质必须经过消化?不消化行吗?
食物中的蛋白质、淀粉、脂肪等大分子物质必须经过消化,转 变成小分子物质,才能被消化道吸收。
• 3、请按照消化方式进行分类。
消化分为物理性消化和化学性消化。
六大营养物质的消化
有机物 无机物
蛋白质 糖类 脂肪 维生素 水 无机盐
大分子物质
必须经过消化,由大分子物 质分解成小分子物质,才能 被消化道吸收。
消化道各段的吸收情况
小肠是吸收营养物质 的主要器官。 为什么?这与小肠的结 构有关。
小肠内除大部分的甘油、 脂肪酸被毛细淋巴管吸 收外,其余的各种营养 物质都被毛细血管直接 吸收进入血液。
观察小肠结构
• 目的:说明小肠结构特点。 • 器材:放大镜、培养皿、镊子、剪刀、鸭小肠等。 • 指导: 1、剪开一段鸭小肠,用水洗净。把小肠放入盛有清水的培养皿中,内表面向上。 2、由于水的浮力作用,小肠内表面绒毛彼此松散、伸展开来。用放大镜仔细观
第九章 第二节 磁场
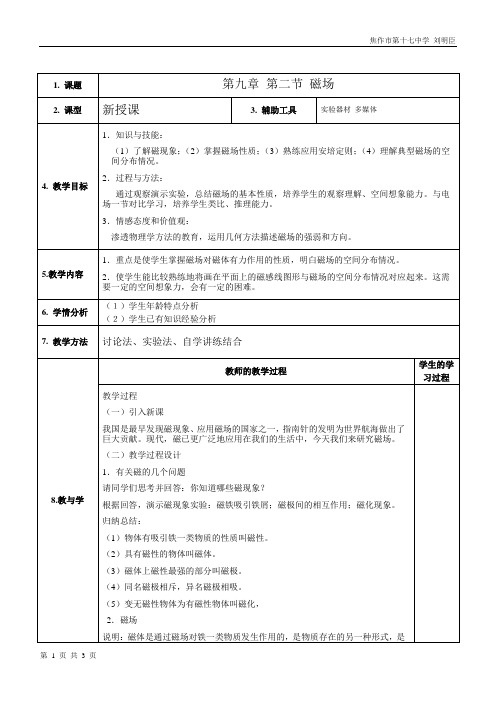
3.磁场的方向
复习:在电学中,电流方向是人们规定的,同理,人们也规定了磁场的方向。
(1)规定:在磁场中的任意一点,静止时小磁针北极所指(受力)的方向就是那一点的磁场方向。
确定磁场方向的方法是:将一小磁ቤተ መጻሕፍቲ ባይዱ放入磁场中需测定的位置,当小磁针在该位置静止时,小磁针N级的指向即为该点的磁场方向。
(2)磁场方向的判定
(2)学生已有知识经验分析
7.教学方法
讨论法、实验法、自学讲练结合
8.教与学
教师的教学过程
学生的学习过程
教学过程
(一)引入新课
我国是最早发现磁现象、应用磁场的国家之一,指南针的发明为世界航海做出了巨大贡献。现代,磁已更广泛地应用在我们的生活中,今天我们来研究磁场。
(二)教学过程设计
1.有关磁的几个问题
磁场是一种物质存在,存在于何处?
(1)磁体周围空间存在磁场;
演示实验:磁体对小磁针的作用;电流对小磁针的作用。
推理分析:电流周围空间存在磁场,电流是大量运动电荷形成的,所以运动电荷周围空间也有磁场。静止电荷周围空间没有磁场。
小结:磁场存在于磁体周围的空间。
(3)磁场是物质存在的一种形式
设问:怎样知道磁场的存在?
(2)磁感线特点
磁感线从N极指向S极(内部从S指向N);
磁感线是闭合曲线,且任意两条磁感线不相交;
磁感线的疏密表示磁场强弱。
9.反馈
1.磁场是物质存在的一种形式,磁场的性质是对放入其中的磁体有力的作用。
2.磁感线是形象描述磁场的方法(模型法)。
3.会用磁感线画出各种磁场的分布情况。
10.板书设计
1.课题
第九章第二节磁场
2.课型
新授课
3.辅助工具
复习:在电学中,电流方向是人们规定的,同理,人们也规定了磁场的方向。
(1)规定:在磁场中的任意一点,静止时小磁针北极所指(受力)的方向就是那一点的磁场方向。
确定磁场方向的方法是:将一小磁ቤተ መጻሕፍቲ ባይዱ放入磁场中需测定的位置,当小磁针在该位置静止时,小磁针N级的指向即为该点的磁场方向。
(2)磁场方向的判定
(2)学生已有知识经验分析
7.教学方法
讨论法、实验法、自学讲练结合
8.教与学
教师的教学过程
学生的学习过程
教学过程
(一)引入新课
我国是最早发现磁现象、应用磁场的国家之一,指南针的发明为世界航海做出了巨大贡献。现代,磁已更广泛地应用在我们的生活中,今天我们来研究磁场。
(二)教学过程设计
1.有关磁的几个问题
磁场是一种物质存在,存在于何处?
(1)磁体周围空间存在磁场;
演示实验:磁体对小磁针的作用;电流对小磁针的作用。
推理分析:电流周围空间存在磁场,电流是大量运动电荷形成的,所以运动电荷周围空间也有磁场。静止电荷周围空间没有磁场。
小结:磁场存在于磁体周围的空间。
(3)磁场是物质存在的一种形式
设问:怎样知道磁场的存在?
(2)磁感线特点
磁感线从N极指向S极(内部从S指向N);
磁感线是闭合曲线,且任意两条磁感线不相交;
磁感线的疏密表示磁场强弱。
9.反馈
1.磁场是物质存在的一种形式,磁场的性质是对放入其中的磁体有力的作用。
2.磁感线是形象描述磁场的方法(模型法)。
3.会用磁感线画出各种磁场的分布情况。
10.板书设计
1.课题
第九章第二节磁场
2.课型
新授课
3.辅助工具
第九章浮力与升力第2节阿基米德原理第2课时教学课件--粤沪版初中物理八年级下

B.5 N
C.8 N
解析:F浮=G-F示=8 N-3 N=5 N。
D.11 N
跟踪训练
某实验小组在探究“浮力大小跟排开液体所受重力的关系”时,做了
如图所示的四次测量,弹簧测力计的示数分别为F1、F2、F3和F4,则( C )
A.F浮=F1-F2
B.F浮=F4-F3
C.F浮=F2-F3
D.F浮=F2-F4
的压力差产生的,所以F浮=pS=2 000 Pa×0.03 m2=60 N。
跟踪训练
(多选)同一物体分别按如图所示两种方式置于同种液体中,则
下列说法中正确的是( BC )
A.物体上下表面第一次受到的压力差大于第二次受到的压力差
B.物体上下表面第一次受到的压力差等于第二次受到的压力差
C.物体上下表面第一次受到的压强差大于第二次受到的压强差
铝块的重力G=mg=0.27 kg×10 N/kg=2.7 N
铝块所受的浮力F浮=G-F示=2.7 N-1.5 N=1.2 N
物体浸没在液体中,则V排=V=1×10-4 m3,由F浮=ρ液gV排可得
1.2 N
浮
液体的密度液= = 10 N/kg×1×10−4 m3 =1.2 × 103 kg/m3
F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×0.6×10-3 m3=6 N。
物体受竖直向下的重力、细线的拉力和竖直向上的浮力,所以拉力
F=F浮-G=6 N-4 N=2 N。
2.求物体的体积和密度。
在物体全部浸入或知道浸入比例的情况下,根据变情势排=
浮
液
,可以得到V排,
继而求得物体的体积V物,物体完全浸入时,V物=V排;知道了物体浸入的比例,也可
第九章第二节液体的压强

3.同种液体内部压强,深度越深,压强越大。
h:研究点到 自由液面的 竖直距离。
增大探头在水中的深度,看看液体内部的压强与 深度有什么关系。
ቤተ መጻሕፍቲ ባይዱ
4.深度相同时,液体密度越大,液体内部压强越大。
换用不同液体,看看在深度相同时,液体内部的 压强是否与液体的密度有关。
二、液体压强的大小
S平面上方的液柱对平面的压力
带鱼生活在深海中。为什么 我们在鱼市上看不到活带鱼?
三、连通器
1.上端开口、下端连通的容器叫做连通器。 实验3
2.连通器的特点:连通器里装同种液体,当液体不 流动时,连通器个部分中的液面总是相平的。
假设容器底部有一竖直膜 片,分析下图中p1与p2的大 小。
如果p1、p2大小不相等,会 发生什么现象? 右侧液面下降,最后当 液体静止时,两侧液面 相平。
2
假设脚背所受压力的大小相当于n个成年人所受重力
9.1 105 N n 1500 2 6 10 N
利用公式 p gh 计算的时候,密度单位必须 用kg/m3,深度的单位要用m。
帕斯卡裂桶实验
帕斯卡在1648年表演了一个著名的实验: 他用一个密闭的装满水的桶,在桶盖上插入一 根细长的管子,从楼房的阳台上向细管子里灌 水。结果只用了几杯水,就把桶压裂了,桶里 的水就从裂缝中流了出来。 原来由于细管子的容积较小,几杯水灌进 去,其深度h是很大了,能对水桶产生很大的 压强。这个很大的压强就在各个方向产生很大 的压力,把桶压裂了。
甲
乙
3.三个底面积相同的形状不同的容器装有等高 的同种液体。哪个容器底受到的压强大。 甲 S h 乙 S
丙 S
4.(1)一个装满水的烧杯,放入一木块,烧杯 底受到的压强有何变化? (2)一个未装满水的烧杯,放入一物体水未 溢出,烧杯底受到的压强有何变化?
第九章第2节黑格尔政治哲学

人,才不会掉进第九坑章第里2节黑。格尔”政治哲学
二、黑格尔的法哲学体系
• 黑格尔的法哲学分为三个环节: • 1、法或抽象法(抽象权利):它是自由意志
借外物以实现自身(这里将的外物就是私 有财产。黑格尔指出,财产是自由的最初 定在,它本身是本质的目的); • 2、道德:是自由意志在内心的实现,主要 阐明的是个人的行为规范和道德评价标准。 • 3、伦理:是自由意志既通过外物、又通过 内心得到充分的实现性。
• 司法不应该受到第九其章第他2节黑权格尔力政治哲的学 影响和限制。
• (二)黑格尔法治思想的局限性 • 首先,他否定习惯法和判例法的地位。 • 其次,黑格尔关于法的概念的阐述,尤其
• 3、立法要与时俱进。
• “要求一部完备的法典,即看来绝对完整 而勿须作进一步规定的法典——这种要求 主要是德国人犯的毛病,——以及借法典 不可能修订的那么完整为理由,就主张不 该让所谓不完整的东西产生,即不该让它 达到现实,以上两种情况都是基因于对象 私法那样的、有限对象的本性的一种误解, 其实,所谓私法的完整性只是永久不断地 对完整性的接近第九而章第已2节黑。格尔”政治哲学
得它的普遍性的形式,而且必须获得它的 真实的规定性。” • 黑格尔区分法和法律,法是“应有”领域, 法律是“现有”概念。
第九章第2节黑格尔政治哲学
• 黑格尔反对用习惯代替法律,他说,“习 惯法所不同于法律的仅仅在于,它们是主 观地和偶然地被制定的,因而它们本身是 比较不确定的,思想的普遍性也比较模 糊。”他极力主张一个文明民族应当自己 编纂法典,建立自己的法律体系。
• 黑格尔晚年对普鲁士王国表现出忠顺 态度,但对法国革命始终持有好评, 对德国保守派——历史法学派持反对 态度。
第九章第2节黑格尔政治哲学
二、黑格尔的法哲学体系
• 黑格尔的法哲学分为三个环节: • 1、法或抽象法(抽象权利):它是自由意志
借外物以实现自身(这里将的外物就是私 有财产。黑格尔指出,财产是自由的最初 定在,它本身是本质的目的); • 2、道德:是自由意志在内心的实现,主要 阐明的是个人的行为规范和道德评价标准。 • 3、伦理:是自由意志既通过外物、又通过 内心得到充分的实现性。
• 司法不应该受到第九其章第他2节黑权格尔力政治哲的学 影响和限制。
• (二)黑格尔法治思想的局限性 • 首先,他否定习惯法和判例法的地位。 • 其次,黑格尔关于法的概念的阐述,尤其
• 3、立法要与时俱进。
• “要求一部完备的法典,即看来绝对完整 而勿须作进一步规定的法典——这种要求 主要是德国人犯的毛病,——以及借法典 不可能修订的那么完整为理由,就主张不 该让所谓不完整的东西产生,即不该让它 达到现实,以上两种情况都是基因于对象 私法那样的、有限对象的本性的一种误解, 其实,所谓私法的完整性只是永久不断地 对完整性的接近第九而章第已2节黑。格尔”政治哲学
得它的普遍性的形式,而且必须获得它的 真实的规定性。” • 黑格尔区分法和法律,法是“应有”领域, 法律是“现有”概念。
第九章第2节黑格尔政治哲学
• 黑格尔反对用习惯代替法律,他说,“习 惯法所不同于法律的仅仅在于,它们是主 观地和偶然地被制定的,因而它们本身是 比较不确定的,思想的普遍性也比较模 糊。”他极力主张一个文明民族应当自己 编纂法典,建立自己的法律体系。
• 黑格尔晚年对普鲁士王国表现出忠顺 态度,但对法国革命始终持有好评, 对德国保守派——历史法学派持反对 态度。
第九章第2节黑格尔政治哲学
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L
AO : y x , x : 1 0 OB : y x , x : 0 1 x yd x AO x yd x OB x yd x
y
B(1,1)
y x
解法2 取 y 为参数, 则
1
2 x d x 4 0 5
1
3 2
o
y x A(1, 1)
2 x y d x y y 2 y d y L x 1
4. 两类曲线积分的联系
L P d x Q d y P d x Q d y R d z
18
作业 122页习题9—2
2,3,4,5,6 6.
19
处受 力F 的作用, 备用.设一个质点在 F 的大小与M 到原点 O 的距离成正比, F 的方向与OM 垂直且与 y 轴夹锐角,此质点由点 沿椭圆
2
(2)
的参数方程为
B
R
0
y
AB
2
14
A
kt kdt
0
每一点 上, 123页B6 设在 椭圆 都作用力 其大小 等于 从 到椭圆中心的距离 方向 指向 椭圆 中心, 今有一质量为 的质点 在椭圆 沿逆时针移动,求 (1) 经过 第一象限的椭圆弧段时, 所作的功 (2) 走遍 全椭圆时, 所作的功 解 (1 )
4
性质 (1)若 L= L1+L2 则
P ( x , y ) d x Q( x , y ) d y L P ( x , y ) d x Q( x , y ) d y L
1 2
L
P ( x , y ) d x Q( x , y ) d y
(2) 用L- 表示 L 的反向曲线 , 则
{ P [ x , ( x )] Q [ x , ( x )] ( x )}d x a x (t ) y ( t ) t : ,类似有 对空间曲线 : z (t )
b
( t ) Q [ ( t ) , ( t ) , ( t )] ( t ) ( t ) ( t ) P [ , , ] ( t )
P ( x , y )d x Q( x , y )d y
P ( x , y )d x Q( x , y )d y
L
5
三、对坐标的曲线积分的计算法
定理: 设 在有向曲线 L 上
连续,
L 的参数方程为 y (t )
x (t )
t : ,
( t ) dt ( t ) dt
y
x
2 0
o
?
/2
0
15
(2 )
内容小结 1. 定义 2. 性质
(1)若 L=L1+L2 则
L
P ( x , y )d x Q( x , y )d y
1 2
P ( x , y )d x Q( x , y )d y P ( x , y )d x Q( x , y )d y L L
1
y
x y
o
2
(1,1) (3) 原式 [ x x 3 ( x 3 x ) 3 x 2 ]d x 0
3
1
yx
( x 3 x 3 x 3 )d x
4 5
0
1
x
11
例3. 求
z
其中
2
从 z 轴正向看 为顺时针方向. 解: 取 的参数方程
1 y
o
x
x cos t t: 0 y sin t , z cos t sin t 2
7
R[ ( t ) , ( t ) , ( t ) ] ( t ) }d t
• 定积分是第二类曲线积分的特例.
设L为xoy面内 x 轴上 从点(a, 0) 到点(b, 0) 例如,
的一段直线,计算
相当于一元函数 P(x,0)
从 a 到 b的定积分。
8
例1.计算 L x y d x 其中L 为沿抛物线 y 2 x 从点 A(1, 1) 到B(1, 1) 的一段. 解法1 取 x 为参数, 则 L : AO OB
y
B(0, b)
按逆时针方向移动到 求力F 所作的功W. 解: OM ( x , y ),F k ( y , x )
F M ( x, y)
A(a ,0)x
o
x a cos t AB : y b sin t t :0 2
2 2 F k x y 且OM F 则
W F ds k y dx xd y AB AB
2
( 2 2cos t sin t ) cos t
2 0
(2sin t 2cos t 1 2cos 2t )dt 2
13
例4.设在力场 沿移动到
质点由 作用下, 其中为
试求力场 对质点 所作的功. 解:(1)
z
( R 2 k 2 t )d t 0
(2) 用L- 表示 L 的反向弧 ,则
P ( x , y )d x Q( x , y )d y P ( x , y )d x Q( x , y )d y
L
•对坐标的曲线积分必须注意积分弧段的方向 !
16
3. 计算
x (t ) t : • 对有向光滑弧 L : y (t )
第二节 对坐标的曲线积分
一、基本概念
第九章
二、对坐标的曲线积分的概念与性质 三、对坐标 的曲线积分 的计算法
1
一、基本概念
曲线
弧微分
t : , ds 2 (t ) 2 (t ) 2 ( t ) d t
( ( t ), ( t ),
规定了 方向 的曲线叫有向曲线,
则曲线积分 存在, 且有
{ P [ ( t ) , ( t ) ] ( t ) Q [ ( t ) , ( t )] ( t ) dt
6
特别是, 如果 L 的方程为 y ( x ), x : a b, 则
d y ( x )d x ,
{ P [ ( t ), ( t )] ( t ) Q [ ( t ), ( t )] ( t ) dt
• 对有向光滑弧 L : y ( x ) ,
x :a b
P [ x , ( x )] Q [ x , ( x )] ( x ) d x a
平面 变力 F F ( x , y ) (P ( x , y ) , Q( x , y ) ) 将质点 从点 A 沿曲线 移动到 点 B 所作的功.
W F d r
P ( x , y ) d x Q ( x , y )d y
对坐标的曲线积分 或第二类曲线积分
B A
F d r W lim 0 F i r i
n
Fi
M i 1
Mi
B
P d x Q d y R dz 对坐标的曲线积分 或第二类曲线积分 (P
i 1
ห้องสมุดไป่ตู้
A
F Q
R
)ds
对弧长的曲线积分 r i ) 或第一类曲线积分 A( xi , yi , ziB 3
切向量:
( t ))
单位 切向量:
同样
d x ( t ) d t d y (t ) d t d z (t ) d t
ds ds ds
2 ds ( t ) ( t )
2
若记 d r (d x ,d y ,d (t ) z) 其中 2 则 dr (t ) 2
b
17
3.对空间光滑曲线弧 :
x (t ) y (t ) t : , 有 z (t )
P [ ( t ), ( t ) , ( t )] ( t )
Q [ ( t ), ( t ) , ( t )] ( t ) R [ ( t ), ( t ) , ( t )] ( t ) }d t
二、对坐标的曲线积分的概念与性质
空间 变力 F F( x , y , z ) (P ( x , y , z ) , Q( x , y , z ) , R( x , y , z ) ) 将质点 从点 A 沿曲线 移动到 点 B 所作的功. 特别 常力 沿直线 所作的功 W F AB ―取极限” 解决办法: ―大化小”―常代变” ―近似和”
kab (sin t cos t )dt
2 0 2 2
2
kab 20
9
例2.计算 L y d x ,其中 L 为 (1) 半径为 a 圆心在原点的 上半圆周, 方向为逆时针方向 (2) 从点 A ( a , 0 ) 沿 x 轴 到点 B (– a , 0 ). 解: (1) 取L的 参数方程为
2
2 2 a sin t ( a sin t )dt 则 L 0 4 3 3 2 2a 1 a 3 3 y (2) 取 L 的方程为 y 0, x : a a ,
y dx
2
B a
o
A a x
则 L y d x
2
10
122页1
计算
其中L为
(1) 直线 L : y x ,
(2) 抛物线 到 那一段
(3) 立方抛物线 L : y x 3 上从 解: (1) 原式
2 2 )d y 2 y y y ( y y (2) 原式 0
