理想气体的内能、热容和焓
物理学24-理想气体的内能

张宏浩
1
பைடு நூலகம்
三、理想气体的内能
分子间相互作用 可以忽略不计 分子间相互作用的势能=0
理想气体的内能=所有分子的热运动动能之总和
i i 1mol理想气体的内能为 E 0 N A ( kT ) RT 2 2
M i 一定质量理想气体的内能为 E RT M mol 2
温度改变,内能改变量为 E M
当温度极低时,转动自由度 r 也被“冻结”, 任何分子都可视为只有平动自由度。
4
刚性分子理想气体内能:
f E kT N 2 f R T N A 2 NA f RT 2
:气体系统的摩尔(mol)数
5
根据
求等体热容
小结:
练习 就质量而言,空气是由76%的N2,23%的O2 和1%的Ar三种气体组成,它们的分子量分别为28、 32、40。空气的摩尔质量为28.910-3kg,试计算1mol 空气在标准状态下的内能。
3
3
3 3 M 28 . 9 10 1 % 0 . 289 10 kg Ar质量 3
M3 0.289 摩尔数 n3 0.007 M mol 3 40 1mol空气在标准状态下的内能
i3 i1 i2 E n1 RT n2 RT n3 RT 2 2 2 1 ( i1 n1 i2 n2 i3 n3 )RT 2
内能: E N( k p) p ij
i j
E (T ,V )
(i>j)
由 T 决定
由 V 决定
3
对理想气体: p ij 0 , E E (T ) ;
对刚性分子(rigid molecule):v 0 ,i t r
热力学第一定律

热力学第一定律功:δW =δW e +δW f(1)膨胀功 δW e =p 外dV 膨胀功为正,压缩功为负。
(2)非膨胀功δW f =xdy非膨胀功为广义力乘以广义位移。
如δW (机械功)=fdL ,δW (电功)=EdQ ,δW (表面功)=rdA 。
热 Q :体系吸热为正,放热为负。
热力学第一定律: △U =Q —W 焓 H =U +pV 理想气体的内能和焓只是温度的单值函数。
热容 C =δQ/dT(1)等压热容:C p =δQ p /dT = (∂H/∂T )p (2)等容热容:C v =δQ v /dT = (∂U/∂T )v 常温下单原子分子:C v ,m =C v ,m t =3R/2常温下双原子分子:C v ,m =C v ,m t +C v ,m r =5R/2 等压热容与等容热容之差:(1)任意体系 C p —C v =[p +(∂U/∂V )T ](∂V/∂T )p (2)理想气体 C p —C v =nR 理想气体绝热可逆过程方程:pV γ=常数 TV γ-1=常数 p 1-γT γ=常数 γ=C p / C v 理想气体绝热功:W =C v (T 1—T 2)=11-γ(p 1V 1—p 2V 2) 理想气体多方可逆过程:W =1nR-δ(T 1—T 2) 热机效率:η=212T T T - 冷冻系数:β=-Q 1/W 可逆制冷机冷冻系数:β=121T T T -焦汤系数: μJ -T =H p T ⎪⎪⎭⎫⎝⎛∂∂=-()pT C p H ∂∂ 实际气体的ΔH 和ΔU :ΔU =dT T U V ⎪⎭⎫ ⎝⎛∂∂+dV V U T ⎪⎭⎫ ⎝⎛∂∂ ΔH =dT T H P ⎪⎭⎫ ⎝⎛∂∂+dp p H T⎪⎪⎭⎫ ⎝⎛∂∂ 化学反应的等压热效应与等容热效应的关系:Q p =Q V +ΔnRT 当反应进度 ξ=1mol 时, Δr H m =Δr U m +∑BB γRT化学反应热效应与温度的关系:()()()dT B C T H T H 21T T m p B1m r 2m r ⎰∑∆∆,+=γ热力学第二定律Clausius 不等式:0TQS BAB A ≥∆∑→δ—熵函数的定义:dS =δQ R /T Boltzman 熵定理:S =kln Ω Helmbolz 自由能定义:F =U —TS Gibbs 自由能定义:G =H -TS 热力学基本公式:(1)组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU =TdS -pdV dH =TdS +Vdp dF =-SdT -pdV dG =-SdT +Vdp (2)Maxwell 关系:T V S ⎪⎭⎫⎝⎛∂∂=V T p ⎪⎭⎫ ⎝⎛∂∂Tp S ⎪⎪⎭⎫ ⎝⎛∂∂=-p T V ⎪⎭⎫ ⎝⎛∂∂ (3)热容与T 、S 、p 、V 的关系:C V =T VT S ⎪⎭⎫⎝⎛∂∂ C p =T p T S ⎪⎭⎫ ⎝⎛∂∂Gibbs 自由能与温度的关系:Gibbs -Helmholtz 公式 ()pT /G ⎥⎦⎤⎢⎣⎡∂∆∂T =-2T H ∆ 单组分体系的两相平衡: (1)Clapeyron 方程式:dT dp=mX m X V T H ∆∆ 式中x 代表vap ,fus ,sub 。
rg气体常数

rg气体常数rg气体常数是一个在物理学和化学中常用的重要常数。
它代表了单位质量的理想气体在恒定压力下的体积与温度之间的关系。
这个常数的值是一个非常关键的参数,可以帮助我们理解气体的行为以及在许多实际问题中的应用。
在研究理想气体时,rg气体常数起着至关重要的作用。
它的值通常用符号R表示,而具体数值取决于所选择的单位制。
在国际单位制中,rg气体常数的数值约为8.314焦耳/(摩尔·开)。
而在厘米-克-秒单位制中,它的数值约为1.987卡/(摩尔·开)。
理想气体状态方程可以用rg气体常数来表示,即PV = nRT。
在这个方程中,P代表气体的压力,V代表气体的体积,n代表气体的摩尔数,T代表气体的温度。
通过这个方程,我们可以推导出很多有关气体的性质和行为的重要信息。
rg气体常数也可以用来计算理想气体的内能和焓的变化。
内能的变化可以表示为ΔU = nCvΔT,其中Cv代表摩尔定容热容量。
而焓的变化可以表示为ΔH = nCpΔT,其中Cp代表摩尔定压热容量。
这些公式在热力学和热力学过程的研究中起着至关重要的作用。
除了在理想气体的研究中,rg气体常数在化学反应和热力学过程中也有着广泛的应用。
在计算化学反应的热效应时,我们经常会用到rg气体常数来计算反应的焓变。
而在工业生产中,rg气体常数也被广泛用于设计和优化化工过程。
总的来说,rg气体常数在物理学和化学中扮演着非常重要的角色。
它不仅帮助我们理解气体的行为和性质,还在实际问题的解决中发挥着关键作用。
因此,对rg气体常数的深入理解和熟练运用对于科学研究和工程实践都至关重要。
希望通过本文的介绍,读者能对rg 气体常数有更深入的了解,并在相关领域的学习和工作中有所裨益。
热力学第二章 理想气体性质

t2
t2
t1
(3)定值比热
CV ,m i R 2 C P ,m i 1 R 2
i 取值:单原子:3; 双原子: 5; 多原 子:7
一.比热力学能
d u=cvdt
1. cv const
理想气体、任何过程
u cv t
2. cv 为真实比热
3. cv 为平均比热
h是状态量,
h f (T , p )
h h dh ( ) p dT ( )T dp T p
h h q ( ) p dT [( )T v ]dp T p
定压状态下,dq=u,
由定义知:
h q p ( ) p dT T q p h Cp ( ) ( )v dT T
dT p2 s s2 s1 1 c p Rg ln T p1
2
s 1
2
2 dv dp cp 1 cv v p
s s2 s1 c p ln
T2 p Rg ln 2 T1 p1
v2 p2 s c p ln cv ln v1 p1
t2
1
u cv dt
T1
T2
u cv t (T2 T1 ) cv 0 t2 cv 0 t1
4. 查T-u表, 附表4 (零点规定: 0K, u=0, h=0 )
t2
t2
u u2 u1
二. 比焓
dh c p dT
利息气体、任何过程
1. c p const
1kg 工质温度
物理意义:表示在 p 一定时, 升高 1K ,焓的增加量 所以当作状态量 ;
说明: 1、对于cv、cp因为过程定容、定压,
热工基础-3-(1)-第三章 理想气体

∆T
若比热容取定值或平均值,有: ∆ h = c p ∆ T
∆h = c p
T2 T1
∆T
3. 理想气体熵变化量的计算:
δ q du + pdv cv dT p ds = = = + dv T T T T cv dT p v cv dT dv = + dv = + Rg T T v T v
同理:
δ q dh − vdp c p dT v ds = = = − dp T T T T c p dT p v c p dT dp = − dp = − Rg T T p T p
Rg ,eq = ∑ wi Rg ,i
i
作业:P103-104
3-10 3-15
思考题: P102
10
五. 理想气体的基本热力过程 热力过程被关注的对象:
1) 参数 ( p, T, v, u, h, s ) 变化 2) 能量转换关系, q , w, wt 。
思路:
1) 抽象分类:
p
v T
s
n
基本过程 2) 简化为可逆过程 (不可逆再修正)
R = 8.314 J/(mol ⋅ K)
R 是一个与气体的种类
无关,与气体的状态也 无关的常数,称为通用 (摩尔)气体常数。
R = M ⋅ Rg
例题3.1: 已知体积为0.03m3的钢瓶内装有氧气,初 始压力p1=7×105Pa,温度t1=20℃。因泄漏,后 压力降至p2=4.9×105Pa ,温度未变。问漏去多少 氧气? 解:取钢瓶的容积为系统(控制容积),泄漏过 程看成是一个缓慢的过程。初终态均已知。假定 瓶内氧气为理想气体。根据状态方程:
V
0 m
= 22 . 414 m
理想气体的性质

第二章理想气体的性质第一章一开始,我们就讲了工质是实现热能与机械能相互转化的媒介物,热能与机械能的相互转化是靠工质在设备中吸热膨胀作功等状态变化过程实现的。
因此必须熟悉常用工质的热力性质。
此外,我们也了解到,热能与机械能的转化是通过工质的膨胀实现的,所以,作为这样的工质必须具有可胀缩性和流动性,而在气固液三态中,只有气态具有这种性质,所以,在这一章我们就专门研究的气态的这种性质,研究工质在一定的状态下三个基本状态参数的关系—状态方程式。
比热容和内能、焓、熵的计算方法,其中状态方程的建立和比热容的计算是主要的只有知道了工质的状态方程和比热容其他参数,Δu、Δh、Δs才能推算出来。
2-1 理想气体与实际气体在普通物理学中,已经介绍过理想气体的概念,所谓的理想气体是一种实际并不存在的假想的气体,那么我们为什么还需要研究它呢?一、何为理想气体定义:1、气体分子是些弹性的,不占体积的质点。
2、分子相互间没有作用力。
二、为什么要研究它1、为了研究方便如果考虑了气体分子之间有相互作用力和分子本身的体积,那么气体的性质就变得很复杂,状态参数之间的函数关系,也会变得很复杂,要用较长的关系式来表达,这样的关系式对我们分析问题带来极大的困难,引入理想气体后,使得气体分子的运动规律大大简化了,这样,不但可以定性地分析气体的热力学现象,还可以定量地得出状态参数之间简单的函数关系,简化了分析计算,然后根据具体情况,加以修正,就可以接近实际气体的计算这种方法在科学研究和生产实践中常用的一种处理问题的方法。
2、工程技术上具有实际的意义经过简化之后,能否符合实际情况,偏差有多大,这要看具体条件。
当T很高、P很低→气体V很大→离液态很远,因为V很大→分子间距离很大→分子间作用力越小→可以忽略→分子本身的体积相对空间少→忽略作用力,本身的体积→误差不会很大,所以理想气体实质上是实际气体P→0、V→∞时的理想极限状态。
工程上,一定状态下的实际气体,都可以处理想气体,例如:H2、O2、N2、CO2及组成的气体,烟气,他们的液化温度较低(1标准大气压-183℃才能液化)离液液态较远,在通常P、T下,可处理为理想气体,误差不大,都在工程所需要的范围。
热力学第一定律应用

3 2 V1(
pa
pc )
450R
300
c
b
循环过程中系统吸热
O
1
2 V(10-3m3)
Q1 Qab Qca 600R ln 2 450R 866R
循环过程中系统放热
此循环效率
Q2 Qbc 750R
1
Q2 Q1
1
750R 866R
13.4 00
29
例 逆向斯特林致冷循环的热力学循环原理如图所示
当高温热源的温度T1一定时,理想气体卡诺循环的致 冷系数只取决于T2 。 T2 越低,则致冷系数越小。
26
三、 卡诺定理
1. 在温度分别为T1 与T2 的两个给定热源之间工作的一切可 逆热机,其效率 相同,都等于理想气体可逆卡诺热机的
效率,即
1 Q2 1 T2
Q1
T1
2. 在相同的高、低温热源之间工作的一切不可逆热机,其
曲线起始于同一点. n可取任意值,不同n对应不同的过程曲线。
16
3种多方过程方程:
理想气体多方过程的定义 :
pV n C
再根据理想气体的状态方程:
PV RT
以T、V或T、p为独立变量,还可有如下多方过程方程 :
TV n1 C
p n1 Tn
C
17
二、多方过程摩尔热容
设多方过程的摩尔热容为Cn.m ,则:
dQ Cn,mdT
根据理想气体的热一律,可得:
Cn,m dT CV ,m dT pdV
在两边分别除以 dT
Cn,m
CV ,m
p( dVm dT
)n
CV ,m
p( Vm T
)n
式中的下标n 表示是沿多方指数为n 的路径变化。
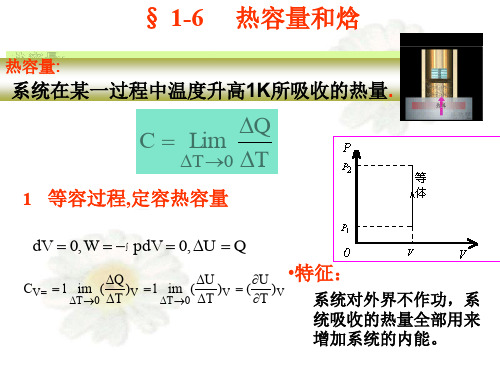
热容量和焓
•热力学第二定律的开尔文表述( 1851): 不可能从单一热源吸热使之完全变成有用功而不引 起其它变化。
开氏表述指明功变热的过程是不可逆的。
开尔文(W. Thomson,1824-1907),原名汤姆 孙,英国物理学家,热力学的奠基人之一。1851 年表述了热力学第二定律。他在热力学、电磁学、 波动和涡流等方面卓有贡献,1892年被授予开尔 文爵士称号。他在1848年引入并在1854年修改的 温标称为开尔文温标。为了纪念他,国际单位制 中的温度的单位用“开尔文”命名。
ln V4 V3
Q2
m M
RT2
ln V3 V4
p1
A
DA:绝热压缩绝热压缩过程:体
积由V4变到V1,系统不吸收热量,
Q1
外界对系统所作的功等于系统增加 的内能。
p2
B
在一次循环中, 系统对外界所作
T1
的净功为
p4 p3
D
T1
C
|W|= Q1-Q2
T2
0
Q2
V1
V4 V2
V3
V
Q1
W
Q2
T2
卡诺热机效率
Q1
制冷机经历一个逆循环后,由于外界对它作 功,可以把热量由低温热源传递到高温热源。
Q2
W
在一个循环中,外界作功W,从低温热源吸
收热量Q2,向高温热源放出热量Q1。并且工 质回到初态,内能不变。
低温热源 T2
制冷系数:
表示制冷机的效能
e Q2 Q2 W Q1 Q2
三、卡诺循环
法国工程师、热力学的创始人之一。 他创造性地
CV
dU ,U dT
CV dT U 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
(2)由图可以看出:
PaVa = PcVc ∴Ta = Tc ⇒ ΔU = 0
P (atm )
a 3
2
b
1
c
o 1 2 3 V(10−3m3)
(3)由热力学第一定律得:
Q = ΔU + A = 405.2J
5
二、理想气体的热容
1. 热容、比热容、摩尔热容
设系统温度升高 dT ,所吸收的热量为dQ
在等压过程中,dp=0,故 pdVm = RdT 将其代入 Cp,mdT = CV ,mdT + pdVm 得:
Cp,mdT = CV ,mdT + RdT 等式两边约去dT得:
迈耶公式 C p,m = Cv,m + R
表明:理想气体定压摩尔热容等于定体摩尔热容与普适
气体常量R之和。
C p,m > CV ,m
质量之比。
c
=
C m
=
1 m
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠
M:摩尔质量
摩尔热容Cm:物质的量为v的该物质的热容C与v之比。
Cm
=
C
ν
=1
ν
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠
=
cm
ν
=
Mc
或: c = Cm
M
单位: J·mol-1·K-1
(1)定体摩尔热容CV, m:
CV ,m
=1
ν
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠V
(2)定压摩尔热容Cp, m:
热容:
C = lim ΔQ = dQ ΔT →0 ΔT dT
单位:J/K
(1)定体热容:
CV
=
⎛ ⎜⎝
dQ ⎞ dT ⎟⎠V
(体积不变)
(2)定压热容:
Cp
=
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠ p
(压强不变)
脚标V和p分别表示过程中的体积和压强保持不变。 6
比热容c(简称比热):质量为m的该物质的热容C与
(1) 严格满足 pV = ν RT 关系;
(2) 满足道耳顿分压定律;
(3) 满足阿伏伽德罗定律;
(4) 满足焦耳定律:即U = U (T )。
注意:对于一般的气体(即非理想气体),因为
U = U ( T,V ),
内能还是V 的函数,所以气体向真空自由膨胀时温度是
要变化的。
3
例 : 一定质量的理想气体,由状态a经b到达c,如
般
ΔQV = ΔU
气 体
CV ,m
=
⎜⎛ ⎝
∂U m ∂T
⎟⎞ ⎠V
(ΔQ )p = ΔH
C p,m
=
理 U = U (T )
H = H (T )
想 气
CV ,m
=
dU m dT
C p,m
=
dH m dT
C p,m = CV ,m + R
体
dU = νCV ,m dT
在等体过程中,dV=0,由热力学第一定律得: (dQ)V = dU m
Um表示1mol气体的内能,而U则表示任意质量气体的内能。
根据Cv,m的定义,可知1mol气体在等体过程中的热量为: (dQ)V = CV ,mdT
故 dU m = CV ,mdT 若Cv,m为常量,则:ΔU m = CV ,mΔT
图所示,abc为一直线,求此过程中。
(1)气体对外做的功; P(atm)
(2)气体内能的增加; (3)气体吸收的热量; 3
(1atm=1.013×105Pa). 2 1
a b c
解:气体对外做的功为: o 1 2 3 V(10−3m3)
A
=
1 2
(Vc
−Va
)(Pa
−
Pc
)
+
(Vc
−Va
)Pc
= 405.2J
对于一个微元过程:
( d Q) p = dH
上式表明:在等压过程中,系统所吸收的热量 等于系统态函数焓的增量。
定压热容:
Cp
=
( dQ)p dT
=
⎛ ⎜⎝
∂H ∂T
⎞ ⎟⎠ p
为什么采用偏导数? 因为H是多元函数 11
气体公式小结
一 U = U (T,V )
H = U + pV = H (T,p )
精确的实验表明:实际气体的内能与温度和体积都 有关系。但当气体的压强越小时,气体的内能随体积的 变化也越小,而在压强趋于0的情形下,气体的内能只 是温度的函数。
故:
•理想气体内能仅是温度的函数,与体积无关。 •这一结论称为焦耳定律,这是理想气体的又一重
要性质。
2
理想气体宏观特性:
到现在为止,可把理想气体宏观特性总结为:
注意:计算内能增量的公式对一摩尔理想气体的任意过
程都适用。
在等压过程中,热力学第一定律为:
(dQ) p = dU m + pdVm 又因为: (dQ) p = Cp,mdT dU m = CV ,mdT
故热力学第一定律变为: Cp,mdT = CV ,mdT + pdVm
8
由1mol理想气体的物态方程pVm=RT两边同时取微分得: pdVm + Vmdp = RdT
(U1 + pV1),(U 2 + pV2 ) 是系统初、末的态函数
上式表明:系统在等压过程中从外界吸收的热量只
由系统的这个态函数之差决定,因而引进一个新的态
函数:
H = U + pV
H称为焓,它等于系统的内能和压强与体积之积的和。10
利用焓,可将系统在等压过程吸收的热量表 示为:
Qp = H2 − H1
dH = vC p,m dT
∫ ∫ U 2 − U 1 =
T2 T1
vC V
,m dT
H 2 − H1 =
ν C d T T 2
T1
p , m 12
§2-5 理想气体内能、热容和焓
一、理想气体的内能 焦耳实验 焦耳实验 (1845年)
焦耳在气体的绝热自由 膨胀实验中发现膨胀前后 温度没有改变,Q=0, A=0,由热力学第一定律得 出U2=U1,因此气体的内能 仅是温度的函数而与体积 无关。 这也说明:绝热自由膨胀过程是一个内能不变的过程。1
焦耳实验是比较粗糙的,汽缸内气体膨胀所产生微 小的温度变化而引起的汽缸周围水温的变化是很难精确 测定的。当时的温度计是测不出温度的微小变化。
9
三、焓
为了便于计算等压过程中传递的热量,引入热力学函 数——焓
在等压过程中,系统对外所作的功为:
∫ A =
V2 V1
pdV
=
p(V2
− V1)
根据热力学第一定律,系统从外界吸收的热量为:
Qp = (U 2 − U1) + p(V2 − V1) = (U 2 + pV2 ) − (U1 + pV1)
显然有:
C p,m
=1
ν
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠ p
(dQ)V = ν CV ,mdT
(dQ) p = ν C p,mdT
若在温度变化为 ΔT 的有限过程中,CV,m和Cp,m为常量,
则:
QV = ν CV ,mΔT
Qp =ν C p,mΔT
ΔT = T2 − T1 可用于热量的计算
7
2. 理想气体的Cv,m与Cp,m的关系(迈耶公式)
