数学专项复习--平行四边形的存在性问题(1)
【常考压轴题】平行四边形存在性问题—2023-2024学年八年级数学下册(浙教版) (解析版)

平行四边形存在性问题【知识储备】①平行四边形是中心对称图形②中心对称图形的性质:对称中心平分中心对称图形内通过该点的任意线段,且使中心对称图形的面积被平分③中点公式: 类型一 几何背景下的平行四边形存在性问题【典题练习】1.(2023•河北二模)如图,在四边形ABCD 中,∠A =∠B =90°,AD =8cm ,BC =6cm ,点P 从点D 出发,以1cm /s 的速度向点A 运动,点M 从点B 同时出发,以相同的速度向点C 运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P 的运动时间为t (单位:s ),下列结论正确的是( )A .当t =3s 时,四边形ABMP 为矩形B .当t =4s 时,四边形CDPM 为平行四边形C .当CD =PM 时,t =3sD .当CD =PM 时,t =3s 或5s【分析】根据题意,表示出DP ,BM ,AP 和CM 的长,当四边形ABMP 为矩形时,根据AP =BM ,列方程求解即可;当四边形CDPM 为平行四边形,根据DP =CM ,列方程求解即可;当CD =PM 时,分两种情况:①四边形CDPM 是平行四边形,②四边形CDPM 是等腰梯形,分别列方程求解即可.【解答】解:根据题意,可得DP =t cm ,BM =t cm ,∵AD =8cm ,BC =6cm ,∴AP =(8﹣t )cm ,CM =(6﹣t )cm ,当四边形ABMP 为矩形时,AP =BM ,即8﹣t =t ,解得t =4,故A 选项不符合题意;当四边形CDPM 为平行四边形,DP =CM ,)2,2),(),,(21212211y y x x P y x B y x A ++坐标为(,则其中点若即t=6﹣t,解得t=3,故B选项不符合题意;当CD=PM时,分两种情况:①四边形CDPM是平行四边形,此时CM=PD,即6﹣t=t,解得t=3,②四边形CDPM是等腰梯形,过点M作MG⊥AD于点G,过点C作CH⊥AD于点H,如图所示:则∠MGP=∠CHD=90°,∵PM=CD,GM=HC,∴△MGP≌△CHD(HL),∴GP=HD,∵AG=AP+GP=8﹣t+,又∵BM=t,∴8﹣t+=t,解得t=5,综上,当CD=PM时,t=3s或5s,故C选项不符合题意,D选项符合题意,故选:D.2.(2023春•盱眙县期末)如图,在▱ABCD中,AB=6cm,AD=10cm,点P在AD边上以每秒1cm的速度从点A向点D运动.点Q在BC边上以每秒4cm的速度从点C出发,在CB之间往返运动.两个点同时出发,当点P到达点D时停止(同时点Q也停止运动),设运动时间为t秒.当5<t<10时,运动时间t为何值时,以P、D、Q、B为顶点的四边形是平行四边形()A.B.8C.4或D.或8【分析】根据P的速度为每秒1cm,可得AP=t cm,从而得到PD=(10﹣t)cm,由四边形ABCD为平行四边形可得出PD∥BQ,结合平行四边形的判定定理可得出当PD=BQ时以P、D、Q、B四点组成的四边形为平行四边形,当5<t<10时,分两种情况考虑,在每种情况中由PD=BQ即可列出关于t的一元一次方程,解之即可得出结论.【解答】解:∵四边形ABCD为平行四边形,∴PD∥BQ.若要以P、D、Q、B四点组成的四边形为平行四边形,则PD=BQ.当5<t≤时,AP=t cm,PD=(10﹣t)cm,CQ=(4t﹣20)cm,BQ=(30﹣4t)cm,∴10﹣t=30﹣4t,解得:t=;当<t≤10时,AP=t cm,PD=(10﹣t)cm,BQ=(4t﹣30)cm,∴10﹣t=4t﹣30,解得:t=8综上所述:当运动时间为秒或8秒时,以P、D、Q、B四点组成的四边形为平行四边形.故选:D.3.(2022春•曹县期中)如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F 运动:点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q 也同时停止运动,当点P运动()秒时,以点P、Q、E、F为顶点的四边形是平行四边形.A.2B.3C.3或5D.4或5【分析】由平行四边形的性质可得AD∥BC,AD=BC,由平行线的性质可得BF=DF=12cm,可得AD =AF+DF=18cm=BC,由平行四边形的性质可得PF=EQ,列出方程可求解.【解答】解:∵四边形ABCD是平行四边形∴AD∥BC,AD=BC∴∠ADB=∠MBC,且∠FBM=∠MBC∠ADB=∠FBM∴BF=DF=12cm∴AD=AF+DF=18cm=BC,∵点E是BC的中点∴EC=BC=9cm,∵以点P、Q、E、F为顶点的四边形是平行四边形∴PF=EQ∴6﹣t=9﹣2t,或6﹣t=2t﹣9∴t=3或5故选:C.4.(2023春•大竹县校级期末)如图,平行四边形ABCD的对角线AC,BD相交于点O,BD=12cm,AC=6cm,点E在线段BO上从点B以1cm/s的速度运动,点F在线段OD上从点O以2cm/s的速度运动.若点E,F同时运动,设运动时间为t秒,当t=时,四边形AECF是平行四边形.【分析】先根据平行四边形的性质求出OB的长,从而得到OE的长,再由平行四边形的性质得到OE=OF进而得到关于t的方程,解方程即可.【解答】解:由题意得OE=OB﹣BE=OB﹣t,OF=2t,∵四边形ABCD是平行四边形,BD=12cm,∴OB=OD=6cm,∴OE=6﹣t,∵四边形AECF是平行四边形,∴OE=OF,∴6﹣t=2t,∴t=2,∴当t=2时,四边形AECF是平行四边形,故答案为:2.5.(2023秋•红山区校级月考)如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度向点C运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点P运动到点C时,点Q随之停止运动,设运动的时间t(秒).(1)求DQ、PC的代数表达式;(2)当t为何值时,四边形PQDC是平行四边形;(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.【分析】(1)根据题意,写出代数表达式即可;(2)根据平行四边形的性质知DQ=CP,分当P从B运动到C时,当P从C运动到B时,两种情况进行求解即可;(3)分PQ=QD、PQ=PD、QD=PD三种情况讨论求出t值即可.【解答】解:(1)根据题意,DQ=(16﹣t)cm,PC=(21﹣2t)cm;(2)∵四边形PQDC是平行四边形,∴DQ=CP,当P从B运动到C时,∵DQ=AD﹣AQ=16﹣t,CP=21﹣2t,∴16﹣t=21﹣2t,解得:t=5,∴当t=5秒时,四边形PQDC是平行四边形;(3)当PQ=PD时,作PH⊥AD于H,则HQ=HD,∵cm,AH=BP,∴,∴.当PQ=QD时,QH=AH﹣AQ=BP﹣AQ=2t﹣t=t cm,QD=(16﹣t)cm,∵QD2=PQ2=t2+122,∴(16﹣t)2=122+t2,解得.当QD=PD时,DH=AD﹣AH=AD﹣BP=16﹣2t,∵QD2=PD2=PH2+HD2=122+16﹣2t)2,∴(16﹣t)2=122+(16﹣2t)2,即3t2﹣32t+144=0,∵Δ=(﹣32)2﹣4×3×144=﹣704<0,∴方程无实根,综上可知,当秒或秒时,△PQD是等腰三角形.6.(2023春•和平区校级月考)已知▱ABCD中,一动点P在AD边上,以每秒1cm的速度从点A向点D 运动.(1)如图1,运动过程中,若BP平分∠ABC,且满足AB=BP,求∠ABC的度数.(2)如图2,在(1)的条件下,连结CP并延长,与AB的延长线交于点F,连结DF,若CD=2cm,直接写出:△DPF的面积为cm2.(3)如图3,另一动点Q在BC边上,以每秒4cm的速度从点C出发,在BC间往返运动,两个点同时出发,当点P停止运动时Q点也停止,设运动时间为t(t>0),若AD=12cm,则t=秒时,以P、D、Q、B为顶点的四边形是平行四边形.【分析】(1)可证AB=AP,从而可证AB=BP=AP,即可求解;(2)设边CD上的高为h1,边BC上的高为h2,,可得S△DPF=S△P AB,即可求解;(3)当PD=BQ时,四边形PDBQ是平行四边形,进行分类讨论:①当12﹣t=12﹣4t时,②当12﹣t =24﹣4t时,③当12﹣t=4t﹣12时,④当12﹣t=4t﹣24时,⑤当12﹣t=36﹣4t时,⑥当12﹣t=4t﹣36时,即可求解.【解答】解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠APB=∠CBP,∵BP平分∠ABC,∴∠ABP=∠CBP,∴∠ABP=∠APB,∴AB=AP,∵AB=BP,∴AB=BP=AP,∴△ABP是等边三角形,∴∠ABP=60°,∴∠ABC=120°.(2)如图,设边CD上的高为h1,边BC上的高为h2,,∵四边形ABCD是平行四边形,∴S△CDF=•CD=S▱ABCD,S△PBC=h2•BC=S▱ABCD,∴S△PBC=S△CDF=S▱ABCD,∴S△PCD+S△DPF=S▱ABCD,∴S△P AB+S△PCD=S▱ABCD,∴S△PCD+S△DPF=S△P AB+S△PCD,∴S△DPF=S△P AB,∵△ABP是等边三角形,∴S△DPF=S△P AB==3,故答案为:;(3)∵PD∥BQ,∴当PD=BQ时,四边形PDBQ是平行四边形,∵(s),∴0≤t<12,①当12﹣t=12﹣4t时,解得:t=0(不合题意,舍去);此时当P与A重合,Q与C重合;②当12﹣t=24﹣4t时,解得:t=4;③当12﹣t=4t﹣12时,解得:t=4.8;④当12﹣t=4t﹣24时,解得:t=7.2;⑤当12﹣t=36﹣4t时,解得:t=8;⑥当12﹣t=4t﹣36时,解得:t=9.6;综上所述:t为4秒或4.8秒或7.2秒或8秒或9.6秒.类型二“三定一动”求平行四边形的顶点坐标当平面直角坐标系中有3个定点,找第4个点形成平行四边形时:①设第4个点的坐标②以3个定点组成的3条线段为对角线分类讨论③以中心对称图形的性质为等量关系列式求解例,如图所示,平面直角坐标系内有A、B、C三点,在平面内找第4个点,构成平行四边形;【典题练习】7.(2022春•西双版纳期末)在平面直角坐标系中,点A、B、C的坐标分别是A(0,1),B(1,0),C(3,1),若以A,B,C,D为顶点的四边形是平行四边形,那么点D的坐标是.【分析】分三种情况:①BC为对角线时,②AB为对角线时,③AC为对角线时;由平行四边形的性质容易得出点D的坐标.【解答】解:分三种情况:①BC为对角线时,点D的坐标为(4,0);②AB为对角线时,点D的坐标为(﹣2,0)③AC为对角线时,点D的坐标为(2,2)综上所述,点D的坐标是(﹣2,0)或(4,0)或(2,2);故答案为:(4,0)或(﹣2,0)或(2,2).8.(2018春•大邑县期末)如图,在平面直角坐标系中,A(﹣2,3),B(﹣5,1),C(﹣1,0).(1)在图中作出△ABC关于x轴的对称图形△A1B1C1;(2)在图中作出△ABC关于y轴的对称图形△A2B2C2;(3)若以点A,B,C,D为顶点的四边形为平行四边形时,请直接写出满足条件的点D的坐标.【分析】(1)根据关于x轴对称的点的坐标特征写出A1、B1、C1的坐标,然后描点即可得到△A1B1C1;(2)根据关于y轴对称的点的坐标特征写出A2、B2、C2的坐标,然后描点即可得到△A2B2C2;(3)分别以AB、BC、AC为对角线画平行四边形可得到D点坐标.【解答】解:(1)如图,△A11C1为所作;(2如图,△A2B2C2为所作;(3)满足条件的点D的坐标为(2,2)或(﹣4,﹣2)或(﹣6,4).9.(2023春•凤山县期末)如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,且OA,OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C,过点C作AB的垂线,垂足为点D,交y轴于点E.(1)求直线AB的解析式;(2)若△ABC的面积为15,求点C的坐标;(3)在(2)的条件下,在坐标平面内是否存在点P,使以O,C,E,P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.【分析】(1)根据绝对值和完全平方式的非负性得出OA和OB的值,然后确定A点和B点的坐标,用待定系数法求出直线AB的解析式即可;(2)根据△ABC的面积为15,得出AC的长,确定C点的坐标即可;(3)分情况根据平行四边形的性质分别求出P点的坐标即可.【解答】解:(1)∵|OA﹣8|+(OB﹣6)2=0,∴OA=8,OB=6,∴A(﹣8,0),B(0,6),设直线AB的解析式为y=kx+b,代入A点和B点的坐标得,解得,∴直线AB的解析式为y=;(2)∵△ABC的面积为15,∴AC•OB=15,即AC×6=15,∴AC=5,∵OA=8,∴OC=OA﹣AC=8﹣5=3,即C(﹣3,0);(3)存在,∵D点在直线AB上,设D(a,a+6),∵BC平分∠ABO,∴CD=OC,即=3,解得a=﹣,∴D(﹣,),设直线DE的解析式为y=sx+t,∴,解得,∴直线DE的解析式为y=﹣x﹣4,∴E(0,﹣4),设点P的坐标为(m,n),①以CE为对角线时,此时以O,C,E,P为顶点的四边形是矩形,∵O(0,0),C(﹣3,0),E(0,﹣4),∴P(﹣3,﹣4);②以OE为对角线时,由平行四边形对角线互相平分可知,,解得,即P'(3,﹣4);③以OC为对角线时,由平行四边形对角线互相平分可知,,解得,即P''(﹣3,4);综上所述,符合条件的P点坐标为(﹣3,﹣4)或(3,﹣4)或(﹣3,4).类型三“两定两动”求平行四边形的顶点坐标当坐标系中有2个定点,且另外两个动点均在特殊的位置上时,方法策略同类型二。
专题课平行四边形的存在性问题

专题课平行四边形的存在性问题
在运动变化过程中,四点构成平行四边形求点的坐标或者求运动的时间是平行四边形存在性问题的主要类型。
数形结合
例1 如图,直线y=x+2分别与x轴交于点A(-2,0),C(4,0),B(0,5),点P是直线y=x+2上的一个动点.
(1). 在平面内存在一点D,使得以A,B,C,D为顶点的平行四边形,求出此时点D的坐标;
(2). 点P是直线y=x+2上一个动点,在x轴上是否存在点E,使得
B,C,P,E为顶点的四边形是平行四边形,若存在求出点E的坐标,若不存在,说明理由.
【解析】:(1)属于“三定一动”的问题,对于这种类型的题目则需分类讨论,分别以AB,AC,AD为对角线,画出符合题意的示意图.
【解析】:(2)属于“两定两动”的问题,对于这种类型的题目则需分类讨论,①以AB为边,②以AB为对角线。
定点所连线段为分类标准。
例2 如图,在平面直角坐标系内,A(0,4),B(3,0).
(1). 点Q在平面直角坐标系内,则在x轴上是否存在点P,使得A,B,P,Q为顶点的四边形是菱形,若存在求出点P的坐标,若不存在,说明理由.
【解析】:题目属于“两定两动”的菱形的存在性问题,对于这种类型的题目(四点构成菱形)则需分类讨论,①以AB为边,②以AB为对角线。
定点所连线段为分类标准。
例3 如图,▱ABCD中,AD=20cm,点F在AD上,且AF=8cm,点E是BC的中点.若点P以1cm/s的速度由点A向点F运动,点Q以2cm/s 的速度由点C向点B运动,点P运动到点F时停止运动,点Q也停止运动.点P,Q分别从点A,C同时出发,当P运动到多少秒时,以点P,Q,E,F为顶点的四边形是平行四边形.。
中考数学专题复习 二次函数背景下的平行四边形的存在性问题

专题二二次函数背景下的平行四边形的存在性问题知识梳理平行四边形的存在性问题是分类讨论中的一大难点。
此类题目多在直角坐标平面内,辅以二次函数为背景.一般会根据两个或者三个定点,在某个特定的位置上找另两个顶点或者第四个顶点,这样的顶点往往不止一个,需要仔细考虑解题策略,如:若已知两点构成的线段是平行四边形的一边或者对角线.如何利用平行四边形的性质确定出其他的顶点的位置,否则在分类时就容易漏解.【典型例题】【例1】如图.抛物线y= ax2 +bx+c与y轴正半轴交于点C,与x轴交于点A(1,0)、B (4,0),∠OCA=∠OBC.(1)求抛物线的解析式;(2)在直角坐标平面内确定点M,使得以点M、A、B、C为顶点的四边形是平行四边形,请直接写出点M的坐标.[思路分析]本题在平行四边形分类讨论中已经有三个点是定点,则第四个顶点可利用平行四边形两组对边分别平行的方法去找,AC,AB,BC中任意两边可作为平行四边形的邻边,分别作这两邻边的平行线,它们的交点就是所求的平行四边形的第四个顶点.解:当CA和CB为平行四边形的邻边时,M在第四象限,BH=AO=1,M,=−2所以M3(5, −2)综上所述:M点的坐标为M1(3,2)或M2(−3,2)或M3(5, −2).[点评]M1,M2的坐标相对易求得,而M3的坐标利用平行四边形的性质:对角顶点到对角线距离相等或者三角形全等求得M3的坐标.【例2】如图,抛物线y=ax2+ 2ax+3与y轴交于点C,与x轴交于A、B两点(点A和点B分别在x轴的正、负半轴上),cot∠OCA = 3.(1)求抛物线的解析式;(2)平行于x轴的直线l与抛物线交于点E, F(点F在点E的左边),如果四边形OBFE是平行四边形,求点E的坐标.[思路分析]由题意得BO不可能是平行四边形的对角线,所以只可能OB = EF =3,又因为EF被对称轴平分,根据对称轴的方程便能求得点E的坐标[点评]本题借助于抛物线的一条重要性质:抛物线关于对称轴对称.因为EF // AB,所以E,F关于对称轴对称,同时线段EF被对称轴垂直平分.【例3】如图,抛物线y= ax2+ bx +3与y轴交于点C,与x轴交于A, B两点,tan∠OCA =1 3S△ABC = 6.(1)求点B的坐标;解:(2)求抛物线的解析式及顶点坐标;(3)若E 点在x 轴上,F 点在抛物线上,如果A, C, E, F 构成平行四边形,写出点E 的坐标。
专题训练四 平行四边形的存在性问题

专题训练四 平行四边形的存在性问题解平行四边形的存在性问题一般分为三个步骤:第一步寻找分类标准,第二步画图,第三步计算.难点在与寻找分类标准,寻找恰当的分类标准,可以使得解的个数不重复不遗漏,也可以使计算又准又快.如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点如果已知两定点,一般是把确定的一条线段按照边或对角线分为两种情况.灵活运用向量和中心对称的性质,可以使得解题简便.1.如图,已知抛物线223y x x =--+与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为P.若以A 、C 、P 、M 为顶点的四边形是平行四边形,求点M 的坐标.2.如图,在平面直角坐标系xOy 中,已知抛物线223y x x =-++与x 轴交于A 、B 两点,点M 在这条抛物线上,点P 在y 轴上,如果以点P 、M 、A 、B 为顶点的四边形是平行四边形,求点M 的坐标.3.将抛物线21:c y =x 轴翻折,得到抛物线2c ,如图示.现将抛物线1c 向左平移m 个单位长度,平移后得到新抛物线的顶点为M ,与x 轴的交点从左到右依次为A 、B ;将抛物线2c 向右平移m 个单位长度,平移后得到新的抛物线的顶点为N ,与x 轴的交点从左到右依次为D 、E.在平移过程中,是否存在以点A 、N 、E 、M 为顶点的四边形为矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理由.4.如图抛物线254y x bx c =-++与y 轴交于点A(0,1),过点A 的直线与抛物线交于另一点B(3, 52),过点B 作BC ⊥x 轴,垂足为C. (1)求抛物线的表达式;(2)点P 是x 轴正半轴上一动点,过点P 作PN ⊥x 轴,交直线AB 与点M ,交抛物线与点N ,设OP 的长度为m.连接CM 、BN ,当m 为何值时,四边形BCMN 为平行四边形?5.如图,已知二次函数的图象M 经过A(-1,0)、B(4,0)、C(2,-6)三点.(1)求该二次函数的解析式;(2)点G 是线段AC 上的动点(点G 与线段AC 的端点不重合),若△ABG 与△ABC 相似,求点G 的坐标;(3)设图象M 的对称轴为L ,点D(m,n)(-<m<2)是图象M 上一动点,当△ACD 的面积为278时,点D 关于L 的对称点为E ,能否在图象M 和L 上分别找到点P 、Q 使得以点D 、E 、P 、Q 为顶点的四边形为平行四边形?若能,请求出点P 的坐标;若不能,请说明理由..6.已知直线(0)y kx b k =+≠过点F(0,1),与抛物线214y x =相交于B 、C 两点. (1)如图1,当点C 的横坐标为1时,求直线BC 的解析式;(2)在(1)的条件下,点M 是直线BC 上的动点,过点M 作y 轴的平行线,与抛物线交于点D ,是否存在这样的点M ,使得以M 、D 、O 、F 为顶点的四边形为平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由;(3)如图2,设B(m,n)(m<0),过点E(0,-1)的直线L//x 轴,BR ⊥L 于R ,CS ⊥L 于S ,连接FR 、FS.试判断△RFS 的形状,并说明理由.7.在平面直角坐标系xOy 中,抛物线2211()44y x m m m =--+的顶点为A ,与y 轴的交点为B.连接AB ,AC ⊥AB ,交y 轴于点C ,延长CA 到点D ,使得AD=AC ,连接BD.作AE//x 轴,DE//y 轴.(1)当m=2时,求点B 的坐标;(2)求DE 的长;(3)①设点D 的坐标为(x ,y),求y 关于x 的函数关系式;②过点D 作AB 的平行线,与第(3)①题确定的函数图象的另一个交点为P ,当m 为何值时,以A 、B 、D 、P 为顶点的四边形是平行四边形?8.如图,二次函数2y ax bx c =++的图象经过点(-1,4),且与直线112y x =-+交于A 、B 两点,点A 在y 轴上,过点B 作BC ⊥x 轴,垂足为点C(-3,0).(1)求二次函数的表达式;(2)点N 是二次函数图象上的一点(点N 在AB 上方),过N 作NP ⊥x 轴,垂足为P ,交AB 于点M ,求MN 的最大值;(3)在(2)的条件下,点N 在何位置时,BM 与NC 互相垂直平分?并求出所有满足条件的点N 的坐标.9.如图,顶点为(1,4)的抛物线2y ax bx c =++与直线12y x n =+交于点A(2,2),直线12y x n =+与y 轴交于点B ,与x 轴交于点C. (1)求n 的值及抛物线的解析式;(2)点P 为抛物线上的点,点P 关于直线AB 的对称点在x 轴上,求点P 的坐标;(3)点D 为x 轴上方抛物线上的一点,点E 为x 轴上的一点,当以A 、B 、E 、D 为顶点的四边形为平行四边形时,直接写出点E 的坐标.10.如图,已知抛物线23y ax ax c =++与y 轴交于点C ,与x 轴交于点A 、B 两点(点A 在点B 的左侧),点B 的坐标为(1,0),tan OBC ∠=3.(1)求抛物线的解析式.(2)点E 在x 轴上,点P 在抛物线上,是否存在以A 、C 、E 、P 为顶点且以AC 为一边的平行四边形?若存在,写出点P 的坐标;若不存在,请说明理由(3)抛物线的对称轴与AC 交于点Q ,请说明以Q 为圆心,以OQ 为半径的圆与直线BC 的关系.=60°,F、H分别是AB、CD的中点,E、G分别11.如图,菱形ABCD的边长为4,B在AD、BC上,且AE=CG.(1)求证四边形EFGH是平行四边形;(2)当四边形EFGH是矩形时,求AE的长;(3)当四边形EFGH是菱形时,求AE的长.。
2024年九年级中考数学专题复习训练平行四边形的存在性问题
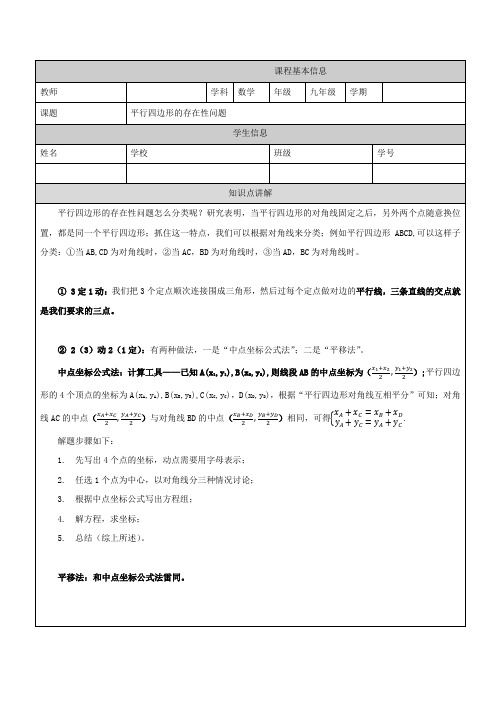
1.如图,已知抛物线y=x22x+3与x轴交于A、B两点(点A在点B的左侧),与 y轴交于点C,顶点为P.若以A、
C、P、M为顶点的四边形是平行四边形,求点M的坐标.
2.在平面直角坐标系中,已知抛物线y=x2+2x+3与x轴交于A、B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.
4.如图,抛物线y= 54x 2+bx+c 与y 轴交于点A(0,1),过点A 的直线与抛物线交于另一点B (3,5
2),过点B 作BC ⊥x 轴,垂足为C.
(1)求抛物线的表达式.
(2)点P 是x 轴正半轴上的一动点,过点P 作PN ⊥x 轴,交直线AB 于点M ,交抛 物线于点N ,设OP 的长度为m.连接CM 、BN,当m 为何值时,四边形BCMN 为平行四边形?
9.如图所示,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),与y轴交于点C(0,3),顶点D的坐标为(1,4).
(1)求抛物线的解析式.
(2)在y轴上找一点E,使得△EAC为等腰三角形,请直接写出点E的坐标
(3)点P是x轴上的动点,点Q是抛物线上的动点,是否存在点P、Q,使得以点P、Q、B、D为顶点,BD为一边的四边形是平行四边形?若存在,请求出点P、Q 的坐标;若不存在,请说明理由.。
高四边形专题复习1平行四边形存在性问题

专题复习课1:平行四边形存在性问题引例:已知三点A、B、C(不在同一直线上),平面中是否存在一点使得这四点构成平行四边形?存在请画出图形,不存在,请说明理由。
B例1、在直角坐标系中,已知A(1,0)、B(-1,-2)、C(2,-2)三点坐标,若以A、B、C、练习1、己知△ABC三个坐标分别A(-2,3)、B(-6,0)、C(-1,0).(1)将△ABC绕坐标原点O逆时针旋转90°,请画出旋转后的图形;(2)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D坐标,并画出图形。
练习2、△ABC的顶点坐标分别为A(-3,0),B(-1,-2),C(-2,2).(1)请在图中画出△ABC绕O点顺时针旋转180°后的图形;(2)请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标,并画出图形。
例2、如图,在平面直角坐标系中,点A(1,0)、B(4,0),点C在y轴的正半轴上,且OB = 2 OC.(1)求直线BC的解析式;(2)在直角坐标平面内确定点M,使得以点M、A、B、C为顶点的四边形是平行四边形,请写出点M的坐标.课后练习:1. 如图,一次函数 y = 13 x + 43 图像经过两个点,其中A (─ 1,m ),B (n ,n ).(1)求点A 、B 的坐标;(2)坐标平面内是否存在点C ,使以A 、O 、B 、C 为顶点的四边形是平行四边形,若存在,请求出点C 的坐标;若不存在,请说明理由.2. 如图,点A (1,m )和点B (─ 3,23 )在反比例函数y = kx (k ≠ 0)的图像上,直线y = 2 x + b经过点A 且与x 轴交予点C.(1)求反比例函数的解析式及点A 、点C 的坐标;(2)在坐标平面内是否存在点D ,使O 、A 、C 、D 为顶点的四边形是平行四边形.①这样的点D 有几个,请直接写出点D 的坐标;②写出一条直线DC 的解析式.3. 如图,点A (m ,m +1),B (m +3,m -1)都在反比例函数xky的图象上. (1)求m ,k 的值; (2)如果M 为x 轴上一点,N 为y 轴上一点,以点A ,B ,M ,N 为顶点的四边形是平行四边形,试求直线MN 的函数表达式. (第1题)(第2题)。
中考数学总复习《二次函数中的平行四边形存在性问题》专题训练-附答案

中考数学总复习《二次函数中的平行四边形存在性问题》专题训练-附答案学校:___________班级:___________姓名:___________考号:___________1.如图,三角形ABC 是以BC 为底边的等腰三角形,点A 、C 分别是一次函数334y x =-+的图象与y 轴、x 轴的交点,点B 在二次函数218y x bx c =++的图象上,且该二次函数图象上存在一点D 使四边形ABCD 能构成平行四边形.(1)求B 、D 坐标,并写出该二次函数表达式;(2)动点P 从A 到D ,同时动点Q 从C 到A 都以每秒1个单位的速度运动,问: ①当P 运动到何处时,有PQ AC ⊥?②当P 运动到何处时,四边形PDCQ 的面积最小?此时四边形PDCQ 的面积是多少?2.如图,二次函数()24y x =+的图象与x 轴交于点A ,与y 轴交于点B .(1)求抛物线的对称轴;(2)在平面直角坐标系内是否存在一点P ,使以P 、A 、O 、B 为顶点的四边形为平行四边形?若存在,求出点P 的坐标;若不存在,请说明理由.3.如图,二次函数()24y x =+的图象与x 轴交于点A ,与y 轴交于点B .(1)求点A B 、的坐标; (2)求抛物线的对称轴;(3)平面内是否存在一点P ,使以P A O B 、、、为顶点的四边形为平行四边形?若存在,求出点P 的坐标;若不存在,请说明理由.4.如图,已知二次函数2y x bx c =-++的图像交x 轴于点()10A -,和()50B ,,交y 轴于点C .(1)求这个二次函数的表达式;(2)如图1,点M 从点B 出发,以每秒2个单位长度的速度沿线段BC 向点C 运动,点N 从点O 出发,以每秒1个单位长度的速度沿线段OB 向点B 运动,点M ,N 同时出发.设运动时间为t 秒()05t <<.当t 为何值时,BMN 的面积最大?最大面积是多少?(3)已知P 是抛物线上一点,在直线BC 上是否存在点Q ,使以A ,C ,P ,Q 为顶点的四边形是平行四边形?若存在,求点Q 坐标;若不存在,请说明理由. 5.已知二次函数213442y x x =--与x 数轴交于点A 、B (A 在B 的左侧),与y 轴交于点C ,连接BC . 发现:点A 的坐标为__________,求出直线BC 的解析式;拓展:如图1,点P 是直线BC 下方抛物线上一点,连接PB 、PC ,当PBC 面积最大时,求出P 点的坐标; 探究:如图2,抛物线顶点为D ,抛物线对称轴交BC 于点E ,M 是线段BC 上一动点(M 不与B 、C 两点重合),连接PM ,设M 点的横坐标为()08<<m m ,当m 为何值时,四边形PMED 为平行四边形?6.解答题如图,在平面直角坐标系中,二次函数24y ax bx =+-的图像交坐标轴于()1,0A -、()4,0B 两点,点P 是抛物线上的一个动点.(1)求这个二次函数的解析式;(2)若点P 在直线BC 下方,P 运动到什么位置时,四边形PBOC 面积最大?求出此时点P 的坐标和四边形PBOC 的最大面积;(3)直线BC 上是否存在一点Q ,使得以点A B P Q 、、、组成的四边形是平行四边形?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.7.如图,二次函数23y ax bx =++的图象与x 轴交于点()30A -,和()4,0B ,点A 在点B 的左侧,与y 轴交于点C .(1)求二次函数的函数解析式;(2)如图,点P 在直线BC 上方的抛物线上运动,过点P 作PD AC ∥交BC 于点D ,作PE x ⊥轴交BC 于点E ,求724PD PE +的最大值及此时点P 的坐标;(3)在(2)中724PD PE +取最大值的条件下,将抛物线沿水平方向向右平移4个单位,再沿竖直方向向上平移3个单位,点Q 为点P 的对应点,平移后的抛物线与y 轴交于点G ,M 为平移后的抛物线的对称轴上一点,在平移后的抛物线上确定一点N ,使得以点Q 、G 、M 、N 为顶点的叫边形是平行四边形,写出所有符合条件的点N 的坐标,并写出求解点N 的坐标的其中一种情况的过程. 8.如图,二次函数234y x bx c =++的图象与x 轴交于点A 和B ,点B 的坐标是(4,0),与y 轴交于点C (0,-3),点D 在抛物线上运动.(1)求抛物线的表达式;(2)当点E 在x 轴上运动时,探究以点B ,C ,D ,E 为顶点的四边形是平行四边形,并直接写出点E 的坐标. 9.在平面直角坐标系中,二次函数22y ax bx =++的图象与x 轴交于(30)A -,,()1,0B 两点,与y 轴交于点C .(1)求这个二次函数的解析式;(2)点M 为抛物线上一动点,在x 轴上是否存在点Q ,使以A 、C 、M 、Q ,为顶点的四边形是平行四边形?若存在,直接写出M 的坐标;若不存在,说明理由. 10.如图,直线122y x =+分别与x 轴、y 轴交于C ,D 两点,二次函数2y x bx c =-++的图像经过点D ,与直线相交于点E ,且:4:3CD DE =.(1)求点E 的坐标和二次函数表达式. (2)过点D 的直线交x 轴于点M .①当DM 与x 轴的夹角等于2DCO ∠时,请直接写出点M 的坐标;①当DM CD ⊥时,过抛物线上一动点P (不与点D ,E 重合),作DM 的平行线交直线CD 于点Q ,若以D ,M ,P ,Q 为顶点的四边形是平行四边形,求点P 的横坐标.11.如图,在平面直角坐标系中,二次函数的图像交坐标轴于()()1,04,0A B C -、、三点,且OB OC =,点P 是抛物线上的一个动点.(1)求这个二次函数的解析式;(2)若点P 在直线BC 下方,P 运动到什么位置时,四边形PBOC 面积最大?求出此时点P 的坐标和四边形PBOC 的最大面积;(3)直线BC 上是否存在一点Q ,使得以点A B P Q 、、、组成的四边形是平行四边形?若存在,求出点Q 的坐标;若不存在,请说明理由.12.已知二次函数220y ax x c a =++≠()的图像与x 轴交于10()A B 、,两点,与y 轴交于点(03)C -,.(1)求二次函数的表达式;(2)D 是二次函数图像上位于第三象限内的点,求ACD 的面积最大时点D 的坐标;(3)M 是二次函数图像对称轴上的点,在二次函数图像上是否存在点N ,使以M N B O 、、、为顶点的四边形是平行四边形?若有,请写出点N 的坐标.(不写求解过程)13.在平面直角坐标系中,二次函数22y ax bx =++的图像与x 轴交于()()3,0,1,0A B -两点,与y 轴交于点C . (1)求二次函数的解析式;(2)点P 是直线AC 上方的抛物线上一动点,当ACP △面积最大时,求出点P 的坐标;(3)点M 为抛物线上一动点,在x 轴上是否存在点Q ,使以A C M Q 、、、为顶点的四边形是平行四边形?若存在,直接写出点Q 的坐标;若不存在,说明理由.14.如图1,二次函数2y ax bx =+的图像过点A (-1,3),顶点B 的横坐标为1.(1)求二次函数的解析式;(2)点P 为二次函数第一象限图象上一点,点Q 在x 轴上,若以A 、B 、P 、Q 为顶点的四边形是平行四边形,求点P 的坐标;(3)如图3,一次函数y kx =(k >0)的图象与该二次函数的图像交于O 、C 两点,点T 为该二次函数图像上位于直线OC 下方的动点,过点T 作直线1:l y x b k=-+交线段OC 于点M (不与O 、C 重合),过点T 作直线TN //y 轴交OC 于点N ,若在点T 运动的过程中,2ON OM =常数m ,求m 、k 的值. 15.如图,在平面直角坐标系中,二次函数214y x bx c =-++的图象与坐标轴交于、、A B C 三点,其中点A的坐标为()0,8,点B 的坐标为()4,0-.(1)求该二次函数的表达式及点C 的坐标;(2)点D 为该二次函数在第一象限内图象上的动点,连接AC CD 、,以AC CD 、为邻边作平行四边形ACDE ,设平行四边形ACDE 的面积为.S ①求S 的最大值;①当S 取最大值时,Р为该二次函数对称轴上--点,当点D 关于直线CP 的对称点E 落在y 轴上时,求点Р的坐标.参考答案1.【答案】(1)()4,0B - ()8,3D 211384y x x =--(2)当点P 运动到距离点52A 个单位处时,四边形PDCQ 面积最小,最小值为8182.【答案】(1)4x =-(2)()4,16或()4,16--或()4,16-3.【答案】(1)()4,0A - ()0,16B (2)4x =-(3)()4,16或()4,16-或()4,16--. 4.【答案】(1)245y x x =-++(2)当52t =时,BMN 的面积最大,最大面积是258(3)存在,Q 的坐标为()712-,或()72-,或()14,或()23, 5.【答案】发现:()2,0-,直线BC 的解析式为1y x 42=-;拓展:()4,6P -;探究:当5m =时,四边形PMED 为平行四边形6.【答案】(1)234y x x =--(2)当P 点坐标为(2,6)-时,16(3)Q 的坐标为(2,6)--或(10,6)7.【答案】(1)211344y x x =-++(2)724PD PE +的最大值为12,此时522⎛⎫ ⎪⎝⎭,(3)1611632N ⎛⎫ ⎪⎝⎭, 2471632N ⎛⎫-- ⎪⎝⎭,32147216N ⎛⎫- ⎪⎝⎭,.8.【答案】(1)239344y x x =--(2)(1,0)或(7,0)或41502⎛⎫+- ⎪ ⎪⎝⎭,或41502⎛⎫- ⎪ ⎪⎝⎭, 9.【答案】(1)224233y x x =--+(2)存在,点M 的坐标为(2,2)-或---,(172)或(17,2)-+-10.【答案】(1)2722y x x =-++(2)①302⎛⎫- ⎪⎝⎭,或302⎛⎫⎪⎝⎭,;①3192-或3192+ 11.【答案】(1)234y x x =--(2)(2,6)P -,四边形PBOC 的最大面积为16(3)存在,Q 的坐标为(2,6)--或(10,6) 12.【答案】(1)223y x x =+-(2)315(,)24D --(3)存在,点N 的坐标为(2,5)或(0,3)-或(2,3)--13.【答案】(1)224233y x x =--+;(2)35(,)22P -(3)存在 12(1,0),(5,0)Q Q -- 34(27,0),(27,0)+-Q Q .14.【答案】(1)22y x x =-;(2)点P 的坐标(15,4)+或(13,2)+;(3)554m =12k =.15.【答案】(1)y =-14x 2+x +8,C 点坐标为(8,0);(2)①32;①P (2,2)或(2,6)。
平行四边形的存在性问题的处理方法
平行四边形的存在性问题的处理一、问题说明关于此类问题,其实已经不是考试的主流了,但是作业及期末考试偶有出现,同学们又不会进行处理,所以简单将解题思路讲解一下,同学们可以自己看看。
二、解题方法总结平行四边形的存在性问题中,已知两点,求双动点的存在性问题是比较经典的。
以这个问题为切入点,讲讲解决这类问题需要克服的两个难点:(1)分类的处理(如何找到所有存在的可能性)(2)计算技巧的处理(平移法)三、问题的演绎例1,(已知三点求一点)如图在坐标平面内再找一点D,使得点A,点B,点C,点D组成平行四边形。
(一)分类处理任意连接两个已知点,例如选择连接AC,对线段AC进行分类讨论(1)若AC是平行四边形的边,则BD一定会和AC平行,且长度等于AC,所以点D在点B的右上方或左下方(如下图)(3,0)(1,1)C1C2(3,0)C(2)若AC是平行四边形的对角线,则BD和AC相互平分,则点D位置如图综上所述存在3个点D满足要求(二)计算技巧的处理平行四边形的计算方法很多,从平移的角度去处理是非常简单的以D1为例:如红色箭头标注方向为例:∵点C(0,-1)往右平移1个单位往上平移2个单位得点A(1,1)∴点D1的坐标是点B以同样的方式平移得到,点D坐标为(4,2)同样类似的方法得到点D2的坐标为(2,-2)D3的坐标为(-2,0)D 3(3,0)2D 31例2,已知二次函数322--=x x y 上两点A(-1,0),C(2,-3),点M在X轴上运动,点N在抛物线上运动,求出所有的点M的坐标。
使得点A ,C,M,N组成平行四边形。
、解题分析:已知点A,点C,所以只需要对AC进行分类讨论,点M在X轴上运动,所以设成(a,0),点N通过点M平移得到,然后代入二次函数解析式求解即可。
设点M的坐标为(a,0)(1)若AC是边,则点N在M的左上方或者右下方当点N在左上方时,点N的坐标(a-3,3)将点N(a-3,3)代入322--=x x y 中解得724±=a 当点N在右上方时,点N的坐标(a+3,-3)将点N(a+3,-3)代入322--=x x y 中解得3-=a 或1-=a (舍)(2)若AC是对角线时,则点N的坐标为(1-a,-3)将点N(1-a,-3)代入322--=x x y 中解得1=a 或1-=a (舍)四、问题的拓展双动点的载体,可以是坐标轴,二次函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1.1
平行四边形的存在性问题(1)例2014年上海市静安区初二下学期期末第26题
如图1,如图,在平面直角坐标系中,一次函数
y =kx -3的图像与x 轴的负半轴相交于点A ,与y 轴
相交于点B ,△AOB 的面积为3,点C 、D 在反比例函数12
y x =的图像上,四边形ABCD 是平行四边形.
(1)求这个一次函数的解析式;
(2)求点C 、D 的坐标.
图1
例2013年黄浦区初二下学期期末第25题
如图1,在平面直角坐标系中,点A的坐标为A(3,0),点B的坐标为A(0,4).
(1)求直线AB的解析式;
(2)点C是线段AB上一点,点O为坐标原点,点D在第二象限,且四边形BCOD为菱形,求点D坐标;
(3)在(2)的条件下,点E在x轴上,点P在直线AB上,且以B、D、E、P为顶点的四边形是平行四边形,请写出所有满足条件的点P的坐标.
图1
例2013年上海市青浦区初二下学期期末第25题
如图1,已知点A(m,6)和点B(6,2)(点B在点A的右侧)在反比例函数的图像上,直线BC//x轴,与y轴交于点C.
(1)求m的值及直线AC的解析式;
(2)如果点D在x轴的正半轴上,点E在反比例函数的图像上,当四边形ACDE是平行四边形时,求CD的长.
图1
例2012年浦东新区初二下学期期末第25题
如图1,在平面直角坐标系中,函数y=2x+12的图像分别交x轴、y轴于A、B两点.过点A的直线交y轴正半轴于点C,且点C为线段OB的中点.
(1)求直线AC的表达式;
(2)如果四边形ACPB是平行四边形,求点P的坐标.
【拓展】如果以A、C、P、B为顶点的四边形是平行四边形,求点P的坐标.
图1
如图1,在平面直角坐标系中,一次函数
的图像与反比例函数的图像相交于A、B两点,
点A的坐标为(2,3),点B的横坐标为6.
(1)求反比例函数与一次函数的解析式;
(2)如果点C、D分别在x轴、y轴上,
四边形ABCD是平行四边形,求直线CD的表
达式.图1
定义[p,q]为一次函数y=px+q的特征数.
(1)若特征数为[3,k-1]的一次函数为正比例函数,求k的值;
(2)一次函数y=kx+b的图像与x轴交于点A(3-,0),与y轴交于点B,且与正比例
函数
4
3
y x
=的图像的交点为C(m,4).求过A、B两点的一
次函数的特征数;
(3)在(2)的条件下,若点D与A、O、C构成的
四边形为平行四边形,直接
..写出所有符合条件的点D的坐
标.
图1。
