流体的压力体积温度关系共27页
合集下载
流体的体积与温度的关系
流体的体积与温度的关系引言流体是物质的一种状态，在自然界和人类生活中无处不在。
流体的体积与温度之间存在着密切的关系，不同温度下的流体体积会发生变化。
本文将探讨流体体积与温度的关系，阐述其原理和应用。
流体体积的定义流体的体积是指在一定条件下，所占据的空间大小。
常用的单位有立方米、立方厘米等。
流体的体积与其温度相关，当温度发生变化时，流体的体积也会相应变化。
流体热胀冷缩的原理流体的体积与温度的关系可以归结为流体的热胀冷缩现象。
在一般情况下，物质在受热时，分子振动会增强，分子间距离变大，从而导致物质体积的增大，称为热胀。
相反，在受冷时，分子振动减弱，分子间距离减小，物质体积减小，称为冷缩。
流体的热胀冷缩现象可以用理想气体状态方程来描述。
理想气体状态方程表明，理想气体的体积与温度成正比。
PV = nRT其中，P为压强，V为体积，n为摩尔数，R为气体常数，T为绝对温度。
流体体积与温度的变化规律根据理想气体状态方程，可以得出流体体积与温度变化的规律。
1. 等温过程在等温条件下，流体的温度保持不变，根据理想气体状态方程，可以得出流体体积与压强成反比。
PV = 常数由此可见，当流体的温度不变时，其体积和压强呈现反比关系。
2. 等压过程在等压条件下，流体的压强保持不变，根据理想气体状态方程，可以得出流体体积与温度成正比。
V/T = 常数由此可见，当流体的压强不变时，其体积和温度呈现正比关系。
3. 等体过程在等体条件下，流体的体积保持不变，根据理想气体状态方程，可以得出流体温度与压强成正比。
P/T = 常数由此可见，当流体的体积不变时，其温度和压强呈现正比关系。
流体体积与温度的应用流体体积与温度的关系在实际生活和工程中有着广泛的应用。
1. 温度计温度计利用了流体体积与温度的关系。
常见的温度计有水银温度计和酒精温度计。
温度计将流体放入一个细长的玻璃管中，根据流体的体积变化来测量温度。
温度的读数是根据不同温度下流体的体积变化来确定的。
化工热力学第二章 流体的p-V-T关系和状态方程
第二章 内 容
§2.1 纯流体的p-V-T相图 §2.2 气体状态方程（EOS） §2.3 对应态原理和普遍化关联式 §2.4 液体的p-V-T性质 §2.5 真实气体混合物p-V-T关系
§2.6 状态方程的比较和选用
§2.1 纯流体的p-V-T相图
§2.1.1 T –V 图 §2.1.2 p-V 图 §2.1.3 p-T 图 §2.1.4 p-V-T 立体相图 §2.1.5 纯流体p-V-T关系的应用及思考
§2.1.4 P-V-T立体相图
P-V-T立体相图
§2.1.4 P-V-T立体相图
水的P-V-T立体相图
【例2-1】 将下列纯物质经历的过程表 示在p-V图上：
1）过热蒸汽等温冷凝为过冷液体； 2）过冷液体等压加热成过热蒸汽； 3）饱和液体恒容加热； 4）在临界点进行的恒温膨胀
P
C
1）过热蒸汽等温冷凝为过冷液体； 2）过冷液体等压加热成过热蒸汽； 3）饱和蒸汽可逆绝热膨胀； 4）饱和液体恒容加热； 5）在临界点进行的恒温膨胀
• 1）由于刚性容器体积保持不变， 因此加热过程在等容线上变化，到 达B1时，汽液共存相变为液相单相； 继续加热，当T>Tc，则最终单相为 超临界流体，即C1点。
• 2）当水慢慢加热后，则状态从位 于汽液共存区的A2，变为汽相单相 B2，继续加热，当T>Tc，则最终单 相为临界流体C2。
§2.1 纯流体的P-V-T相图
P-T图
液相区
8atm下变成液体
气相区
1atm下变成气体
液化气的p-T 图
-82.62 ℃
室温10~40℃
乙烯、丙烯、 丁烯能做液化 气吗？
96.59℃
TC = 196.46 Tb =36.05 ℃
化工原理ppt-第一章流体流动
其单位为J/kg。
2022/8/11
34
二、流体系统的质量守恒与能量守恒
2. 柏努利方程
(1) 总能量衡算
4）外加能量 流体输送机械（如泵或风机）向流体作功。单位质量流体所获得
的机械能。用We表示，单位J/kg。 5）能量损失
液体流动克服自身粘度而产生摩擦阻力，同时由于管路局部装置 引起的流动干扰、突然变化而产生的阻力。流体流动时必然要消耗 部分机械能来克服这些阻力。单位质量流体克服各种阻力消耗的机 械能称为能量损失。用Σhf ，单位J/kg。
2022/8/11
27
知识运用
【1-3】某自来水厂要求安装一根输水量为30m3/h的管道，试选择一合 适的管子。
解：水的密度：1000kg/m3， 体积流量：Vs=30000/（3600×1000）=0.0083（m3/s）
查表水流速范围，取u=1.8m3/s
根据d 4Vs
u
d 4Vs 4 30 / 3600 0.077 m 77mm
22
一、流体流量和流速
2.流速
单位时间内流体质点在流动方向上所流经的距离。
（1）平均流速：u=Vs/A （m/s）
关系:G =u
（2）质量流速：G=Ws/A (kg/(m2·s))
2022/8/11
23
一、流体流量和流速
3.圆形管道直径的选定
2022/8/11
24
一、流体流量和流速
3.圆形管道直径的选定
2022/8/11
8
二、流体压力
2.表压与真空度
表压和真空度
p 当地大气压，
表压强=绝对压强-大气压强
p 当地大气压，
真空度=大气压强-绝对压强
化工热力学讲义-1-第二章-流体的p-V-T关系36页PPT文档
②研究化工过程中各种能量的相互转化及其有效利用的规律。
二、研究方法 热力学研究方法：分为宏观、微观两种。本书就工程应用而言， 主要介绍的是宏观研究方法。
宏观研究方法特点： ①研究对象：将大量分子组成的体系视为一个整体，研究大量 分子中发生的平均变化，用宏观物理量来描述体系的状态；
②研究方法：采取对大量宏观现象的直接观察与实验，总结出 具有普遍性的规律。
2a
VC3
而：V2p2 T
2RT
Vb3
6a V4
V 2p2TTC V2CRbC T3 V 6C a4 0
2RTC VC b
3
6a
VC4
上两式相除，得：
VC b VC 23
1
b 3 VC
则： a
VC3 2
②图3中高于临界温度Tc的等温线T1、T2，曲线平滑且不与相界线相交， 近似于双曲线，即：PV=常数； 小于临界温度Tc的等温线T3、T4，由三个部分组成，中间水平线表示 汽液平衡共存，压力为常数，等于饱和蒸汽压。
③从图3还可知道：临界等温线（蓝线所示）在临界点处的斜率和 曲率等于零，即：
p 0 V TTC
第二章 流体的P-V-T关系
①P、V、T的可测量性：流体压力P、摩尔体积V和温度T是可以 直接测量的，这是一切研究的前提；
②研究的目的与意义：利用P、V、T数据和热力学基本关系式可 计算不能直接测量的其他性质，如焓H、内能U、熵S和自由能G。
一、p-V-T图
2.1纯物质的P-V-T关系
说明：①曲面以上或以下的空间为不平衡区； ②三维曲面上“固”、“液”和“气（汽）”表示单相区 ； ③“固-液”、“固-汽”和“液-汽”表示两相区；
③超临界流体的特殊性：它的密度接近于液体，但同时具有气体的 “体积可变性”和“传递性质”。所以和气体、液体之间的关系是： 既同又不同，
二、研究方法 热力学研究方法：分为宏观、微观两种。本书就工程应用而言， 主要介绍的是宏观研究方法。
宏观研究方法特点： ①研究对象：将大量分子组成的体系视为一个整体，研究大量 分子中发生的平均变化，用宏观物理量来描述体系的状态；
②研究方法：采取对大量宏观现象的直接观察与实验，总结出 具有普遍性的规律。
2a
VC3
而：V2p2 T
2RT
Vb3
6a V4
V 2p2TTC V2CRbC T3 V 6C a4 0
2RTC VC b
3
6a
VC4
上两式相除，得：
VC b VC 23
1
b 3 VC
则： a
VC3 2
②图3中高于临界温度Tc的等温线T1、T2，曲线平滑且不与相界线相交， 近似于双曲线，即：PV=常数； 小于临界温度Tc的等温线T3、T4，由三个部分组成，中间水平线表示 汽液平衡共存，压力为常数，等于饱和蒸汽压。
③从图3还可知道：临界等温线（蓝线所示）在临界点处的斜率和 曲率等于零，即：
p 0 V TTC
第二章 流体的P-V-T关系
①P、V、T的可测量性：流体压力P、摩尔体积V和温度T是可以 直接测量的，这是一切研究的前提；
②研究的目的与意义：利用P、V、T数据和热力学基本关系式可 计算不能直接测量的其他性质，如焓H、内能U、熵S和自由能G。
一、p-V-T图
2.1纯物质的P-V-T关系
说明：①曲面以上或以下的空间为不平衡区； ②三维曲面上“固”、“液”和“气（汽）”表示单相区 ； ③“固-液”、“固-汽”和“液-汽”表示两相区；
③超临界流体的特殊性：它的密度接近于液体，但同时具有气体的 “体积可变性”和“传递性质”。所以和气体、液体之间的关系是： 既同又不同，
流体的压力、体积、温度关系：状态方程式
程式
2.2.2 维里(Virial)方程
• Virial方程的几种形式
Z
pV RT
1
B V
C V2
压力小于 1.5 MPa 时
Z pV1B RT V
Z pV1 Bp RT RT
V B RT p
压力为数 个MPa时
ZR pV T1V BVC2
流体的压力、体积、温度关系：状 态方程式
2.2.2 维里(Virial)方程
流体的压力、体积、温度关系：状 态方程式
2.2.3 立方型状态方程
二、 Redlich - Kwong ( RK )方程（1949年）
• 1 在较低压力和较高温度下可用理想气体 方程进行计算。
• 2 为真实气体状态方程计算提供初始值。
• 3 判断真实气体状态方程的极限情况的正 确程度，当 P 0 或者 V 时，任何的状 态方程都还原为理想气体方程。
通常几百千帕压力下，理想气体状态方程能满足一 般工程技术需要。 流体的压力、体积、温度关系：状态方
(3)临界点C的斜率和曲率都 为零。
B
纯物质的P-V图
流体的压力、体积、温度关系：状 态方程式
•
在临界点 C ：
P V
Tc
0
ห้องสมุดไป่ตู้
2P V2
Tc
0
2-1式 2-2式
流体的压力、体积、温度关系：状态方 程式
2.2 流体的状态方程式
• 纯流体的状态方程(EOS) 是描述流体P-VT性质的关系式。
• 目前采用维里方程计算气体PVT性质时，一般最多采取 三项。这是由于多于三项的维里方程中的常数奇缺，所 以多于三项的维里方程一般不大采用。高压下，气体 PVT性质的计算一般采用其它状态方程。
2.2.2 维里(Virial)方程
• Virial方程的几种形式
Z
pV RT
1
B V
C V2
压力小于 1.5 MPa 时
Z pV1B RT V
Z pV1 Bp RT RT
V B RT p
压力为数 个MPa时
ZR pV T1V BVC2
流体的压力、体积、温度关系：状 态方程式
2.2.2 维里(Virial)方程
流体的压力、体积、温度关系：状 态方程式
2.2.3 立方型状态方程
二、 Redlich - Kwong ( RK )方程（1949年）
• 1 在较低压力和较高温度下可用理想气体 方程进行计算。
• 2 为真实气体状态方程计算提供初始值。
• 3 判断真实气体状态方程的极限情况的正 确程度，当 P 0 或者 V 时，任何的状 态方程都还原为理想气体方程。
通常几百千帕压力下，理想气体状态方程能满足一 般工程技术需要。 流体的压力、体积、温度关系：状态方
(3)临界点C的斜率和曲率都 为零。
B
纯物质的P-V图
流体的压力、体积、温度关系：状 态方程式
•
在临界点 C ：
P V
Tc
0
ห้องสมุดไป่ตู้
2P V2
Tc
0
2-1式 2-2式
流体的压力、体积、温度关系：状态方 程式
2.2 流体的状态方程式
• 纯流体的状态方程(EOS) 是描述流体P-VT性质的关系式。
• 目前采用维里方程计算气体PVT性质时，一般最多采取 三项。这是由于多于三项的维里方程中的常数奇缺，所 以多于三项的维里方程一般不大采用。高压下，气体 PVT性质的计算一般采用其它状态方程。
第2章流体的压力、体积、温度关系：状态方程式
化工热力学
2.3.3 偏心因子与三参数压缩因子图
化工热力学
2.3.3 偏心因子与三参数压缩因子图
化工热力学
2.3.4 普遍化第二维里系数关联式
VanNess和Abbott通过对14种非极性流体的研究和计算，得 出了最简单的表达式，也是许多专著和教材中引用的方程，其 具体表达如下：
化工热力学
2.3.4 普遍化第二维里系数关联式
化工热力学
2.3.5 立方型状态方程的对比形式
RK方程的对比形式为
vdW方程的对比形式为
鉴于临界体积不易测准，而且数据也相对较少，故拟用 代替 ，则RK和vdW方程的改良对比形式状态方程相应可表达 为 RK方程 vdW方程
化工热力学
2.3.6 临界参数和偏心因子的估算
2.3.6.1 临界参数 （１）Magoulas和Tassios法
2.4 液体的p-V-T关系
1 Rackett方程式 2 Yen-Woods关系式 3 Lydersen,Greenkorn和Hougen
对应态法 4 基团贡献法
化工热力学
2.4.1 Rackett方程式
用立方型状态方程计算液体的摩尔体积，其精确度并不 高。饱和液体的摩尔体积 可用普遍化方程计算，常用的 是Rackett方程
当压力达到数个MPa时，第三维里系数渐显重要。其近似 的截断式为
化工热力学
2.2.3 立方型方程式
2.2.3.1 范德瓦耳斯方程式
化工热力学
2.2.3 立方型方程式
拟考察当压力趋近于零，温度趋近于无穷大时， 方程 式的极限情况。将式（2-9）展开，可写成 2.2.3.2 Redlich Kwong方程（RK方程） （１）求蒸气相摩尔体积 （２）求液相摩尔体积
2.3.3 偏心因子与三参数压缩因子图
化工热力学
2.3.3 偏心因子与三参数压缩因子图
化工热力学
2.3.4 普遍化第二维里系数关联式
VanNess和Abbott通过对14种非极性流体的研究和计算，得 出了最简单的表达式，也是许多专著和教材中引用的方程，其 具体表达如下：
化工热力学
2.3.4 普遍化第二维里系数关联式
化工热力学
2.3.5 立方型状态方程的对比形式
RK方程的对比形式为
vdW方程的对比形式为
鉴于临界体积不易测准，而且数据也相对较少，故拟用 代替 ，则RK和vdW方程的改良对比形式状态方程相应可表达 为 RK方程 vdW方程
化工热力学
2.3.6 临界参数和偏心因子的估算
2.3.6.1 临界参数 （１）Magoulas和Tassios法
2.4 液体的p-V-T关系
1 Rackett方程式 2 Yen-Woods关系式 3 Lydersen,Greenkorn和Hougen
对应态法 4 基团贡献法
化工热力学
2.4.1 Rackett方程式
用立方型状态方程计算液体的摩尔体积，其精确度并不 高。饱和液体的摩尔体积 可用普遍化方程计算，常用的 是Rackett方程
当压力达到数个MPa时，第三维里系数渐显重要。其近似 的截断式为
化工热力学
2.2.3 立方型方程式
2.2.3.1 范德瓦耳斯方程式
化工热力学
2.2.3 立方型方程式
拟考察当压力趋近于零，温度趋近于无穷大时， 方程 式的极限情况。将式（2-9）展开，可写成 2.2.3.2 Redlich Kwong方程（RK方程） （１）求蒸气相摩尔体积 （２）求液相摩尔体积
化工热力学第2章流体的PVT关系
时，这种流体就处于对比状态。
例如：H2 和N2这两种流体
对于H2
状态点记为1，P1 V1 T1
Tr1 =T1/TcH2
Pr1=P1/PcH2
对于N2
状态点记为2，P2 V2 T2
Tr2 =T2/TcN2
Pr2=P2/PcN2
当Tr1=Tr2 ，Pr1=Pr2 时，此时就称这两种流体处
一.P-T图
P
Pc
3液
相
固
相
2
1
密 流 区 C
气相
Tc T
1-2线 汽固平衡线（升华线）
2-c线 汽液平衡线（汽化线） 2-3线 液固平衡线（熔化线） C点临界点，2点三相点 P<Pc,T<Tc的区域，属汽体 P<Pc,T>Tc的区域，属气体 P＝Pc,T＝Tc的区域，两相 性质相同
P>Pc,T>Tc的区域，密流区
压缩因 子，方 程的计 算值和 实测值 的符合 程度是 判断方 程的优 劣标志 之一。
2. R-K Equation (1949年，Redlich and Kwong)
(1) R-K Eq的一般形式：
P
RT V-b
-
a T0.5V(V
b)
(2-11)
① R-K Equation中常数值不同于范德华方程中的a、b值， 不能将二者混淆。 在范德华方程中，修正项为a/V2，没有考虑温度的影响 在R-K方程中，修正项为，考虑了温度的影响。 ② R-K Equation中常数a、b值是物性常数，具有单位。
为表征物质分子的偏心度，既非球型分子偏离球对称的 程度，简单流体为0
R-K Eq经过修改后，应用范围扩宽。 SRK Eq：可用于两相PVT性质的计算，对烃类计算，其 精确度很高。
例如：H2 和N2这两种流体
对于H2
状态点记为1，P1 V1 T1
Tr1 =T1/TcH2
Pr1=P1/PcH2
对于N2
状态点记为2，P2 V2 T2
Tr2 =T2/TcN2
Pr2=P2/PcN2
当Tr1=Tr2 ，Pr1=Pr2 时，此时就称这两种流体处
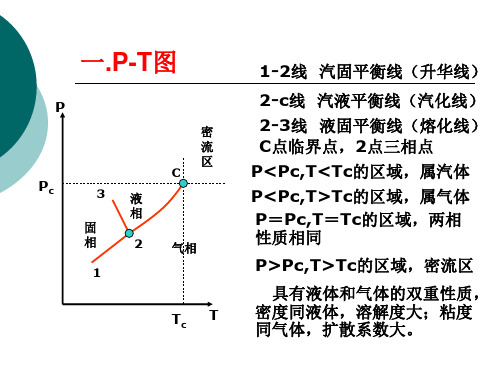
一.P-T图
P
Pc
3液
相
固
相
2
1
密 流 区 C
气相
Tc T
1-2线 汽固平衡线（升华线）
2-c线 汽液平衡线（汽化线） 2-3线 液固平衡线（熔化线） C点临界点，2点三相点 P<Pc,T<Tc的区域，属汽体 P<Pc,T>Tc的区域，属气体 P＝Pc,T＝Tc的区域，两相 性质相同
P>Pc,T>Tc的区域，密流区
压缩因 子，方 程的计 算值和 实测值 的符合 程度是 判断方 程的优 劣标志 之一。
2. R-K Equation (1949年，Redlich and Kwong)
(1) R-K Eq的一般形式：
P
RT V-b
-
a T0.5V(V
b)
(2-11)
① R-K Equation中常数值不同于范德华方程中的a、b值， 不能将二者混淆。 在范德华方程中，修正项为a/V2，没有考虑温度的影响 在R-K方程中，修正项为，考虑了温度的影响。 ② R-K Equation中常数a、b值是物性常数，具有单位。
为表征物质分子的偏心度，既非球型分子偏离球对称的 程度，简单流体为0
R-K Eq经过修改后，应用范围扩宽。 SRK Eq：可用于两相PVT性质的计算，对烃类计算，其 精确度很高。
第2章流体的PVT关系
R-K Eq中 a＝f (Tc，pc) SRK Eq中 a( T )＝f (Tc，pc，T, ω)
Soave-Redlish-Kwang 方程（简称RKS方程)
使用情况和意义 (1） RKS方程提高了对极性物质及含有氢键物质的p –V –T
计算精度。 （2） 可以用于液体p V T 性质计算。如在饱和液体密度的计
算中更准确。
Peng－Robinson方程（简称PR方程）
方程形式：
p
RT V b
V
V
aT b b
V
b
方程参数：
aT a T 0.45724R2Tc2 / pc T
b 0.07780RTc / pc
(T
)
1
k(1
a/V2 — 分子引力修正项。
由于分子相互吸引力存在，分子撞击器壁的力减小，造成压力减小。
b —分子本身体积的校正项。
分子本身占有体积，分子自由活动空间减小，由V变成V-b。分子 自由活动空间的减小造成分子撞击器壁的力增大。造成压力增大
• 参数a和b获得途径：
（1）从流体的p-V-T实验数据拟合得到
中间根无意义。
ps
•当p≠ps时，只有一个根有意义，
其他两个实根无意义。
Vsl
T>Tc T=Tc
T<Tc
Vsv
V
Redlich-Kwong方程
方程形式：
RT
a
p V b T 0.5V (V b)
vDW方程的引力项没有考虑温度的影响，而RK方程的引力
项加入了温度项。
方程参数：