2008年普通高等学校招生全国统一考试理数试题及答案-山东卷
2008年普通高等学校招生全国统一考试数学理试题(山东卷)(含解析)

2008年普通高等学校招生全国统一考试(山东卷)理科数学全解全析(1)满足M ⊆{}1234,,,a a a a 且{}{}12312,,,M a a a a a ⋂=的集合M 的个数是().1A ().2B ().3C ().4D2.设z 的共轭复数是z ,若4z z +=,8z z ⋅=,则zz等于 ().A i ().B i - ().1C ± ().D i ±【标准答案】:D 。
【试题分析】 可设2z b i =+,由8z z ⋅=得248, 2.b b +==±()2222.88i z z i z ±===±【高考考点】: 共轭复数的概念、复数的运算。
【易错提醒】: 可能在以下两个方面出错:一是不能依据共轭复数条件设2z bi =+简化运算;二是由248b +=只求得 2.b =【学科网备考提示】: 理解复数基本概念并进行复数代数形式的四则运算是复数内容的基本要求,另外待定系数法、分母实数化等解题技巧也要引起足够重视。
3、函数ln cos ()22y x x ππ=-<<的图象是5.已知4cos()sin 365παα-+=,则7sin()6πα+的值是 23().5A -23().5B 4().5C - 4().5D 【标准答案】:C 。
【试题分析】:334cos()sin cos sin 36225παααα-+=+=,134cos sin 225αα+=, 7314sin()sin()sin cos .66225ππαααα⎛⎫+=-+=-+=- ⎪ ⎪⎝⎭【高考考点】: 三角函数变换与求值。
【易错提醒】: 不能由334cos()sin cos sin 36225παααα-+=+=得到134c o s s i n 225αα+=是思考受阻的重要体现。
【学科网备考提示】:三角变换与求值主要考查诱导公式、和差公式的熟练应用,其间会涉及一些计算技巧,如本题中的为需而变。
2008年普通高等学校招生全国统一考试数学卷山东文含详解

2008年普通高等学校招生全国统一考试(山东文科数学及答案第I 卷(共60分)参考公式:1锥体的体积公式: V Sh ,其中S 是锥体的底面积,h 是锥体的高.32球的表面积公式: S =4 T R ,其中R 是球的半径. 如果事件 A , B 互斥,那么P (A BHP (A ) P (B ).一、选择题:本大题共 12小题,每小题5分,共 有一项是符合题目要求的.C . 3函数y =1 ncosxi n::: x ::: n的图象是I 2 2丿6.右图是一个几何体的三视图,根据图中数据, 可得该几何体的表面积是( ) A . 9 n B . 10 n60分.在每小题给出的四个选项中,只 1.满足 M 三问,a 2, O J , a 4?,且 M Pp. a ,a ,乱:-〔a a 2的集合M 的个数是2. 设z 的共轭复数是Z.z=8 , 则-等于(zC . -1D . _i3. y 二f (x )是幕函数,则函数 f (x )的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中, A . 35.设函数 f(x)C . 1D 011 -x 2, x < f 1 ]< 2则fx +x -2,X A1,lf(2)丿15 A .1627 16D . 18俯视图 o L 2 V o丿I 3 v4 .给出命题:若函数真命题的个数是( B . 2的值为(2侧(左)视图2正(主)视图C . 11nD . 12 nx 亠57•不等式 ------- 2》2的解集是()(X-1)2准方程是( )2 2B . (x -2)2 (y -1)2 hx12.已知函数f (x )=log a (2 ,b-1)(a 0, a=1)的图象如图所示,贝U a, b 满足的关系A.(x —3)2 y_7” (n4L rt f rf 10.已知 cos 1sin :- =—\ 3,则 sin l165 I2怎2.34A .B .c .55511•若圆C 的半径为1,圆心在第一象限,且与直线¥的值是2 2C . (x -1) (y -3) =1D . 2(y-1)2 =1B .,3C .D .三,18 .已知a ,△ ABC 的三个内角A, BC 勺对边,向的大小分别为 A ,m L n ,且 acosB bcosA =csin C ,则角 An n A. -6 39.从某项综合能力测试中抽取B .2 n n ~3,6亠 n n … n n C . 一,一D . -3 63 3分数5 4 3 2 1 人数2010303010A . ,3B .4x-3y=0和x 轴相切,则该圆的标是( )A . 0 :: a ' ::b :: 14_1B. 0 < b a :: 1-14D . 0 :: a ::C . 3D .100人的成绩,统计如表,则这100人成绩的标准差为(第H卷(共90分)二、填空题:本大题共 4小题,每小题4分,共16分.2 213.已知圆C: x y -6x -4y • 8 = 0 •以圆C 与坐标轴的交点分别作为双曲线的一个焦则z = 2x y 的最大值为 ______________ . 三、解答题:本大题共 6小题,共74分. 17. (本小题满分12分)已知函数 f (x) = . 3sin(• ■ x ?丨)- cos( x " ■ ) ( 0 ::: • ::: n ,> 0 )为偶函数,且函数ny = f (x)图象的两相邻对称轴间的距离为-.(I)求f I n 的值;8n(n)将函数y = f(x)的图象向右平移个单位后,得到函数y = g(x)的图象,求g(x)的6单调递减区间.18. (本小题满分12分)现有8名奥运会志愿者,其中志愿者 A , A ,, A 3通晓日语,B 1, B 2, B 3通晓俄语,C 1, C 2 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各(I)求A 被选中的概率;点和顶点,则适合上述条件的双曲线的标准方程为 14•执行右边的程序框图,若 p =0.8, 则输出的n 二 ____________ . x15.已知 f (3 ) =4xlog 2 3 233 , 则 f (2) f(4) f (8) ||( f (28)的值等于16.设x , y 满足约束条件x - y +2》0, 』5x-y-10 < 0, x 》0,n = n +1__________ J结束1名,组成一个小组.否.输出n(n)求B1和G不全被选中的概率.19. (本小题满分12分)如图,在四棱锥 P _ ABCD 中,平面PAD _平面ABCD , AB // DC , △ PAD 是等边三 角形,已知 BD=2AD=8,AB=2DC=4.,5 .(I)设M 是PC 上的一点,证明:平面 MBD _平面PAD ; (n)求四棱锥 P - ABCD 的体积.20. (本小题满分12 分) 将数列'a n 』中的所有项按每一行比上一行多一项的规则排成如下数表:a 1a 2 a 3a 4 a5a6a 7 a 8a9a10记表中的第一列数 6, a 2, 34, 37,构成的数列为 Z , ^=^=1. S n 为数列 g 的前n 项和,且满足b S2b:S 2"(n > 2).b n SnSn(I)证明数列1 .... ...................... . •、成等差数列,并求数列bn f 的通项公式;(n)上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为4同一个正数•当a 8i时,求上表中第k(k > 3)行所有项的和.9121. (本小题满分12分)设函数f (x)二x 2e x4 ' ax 3 bx 2,已知x ~ -2和x = 1为f (x)的极值点.(I)求a 和b 的值; (n)讨论f (x)的单调性;2 3 2(川)设g(x^-x -x,试比较f (x)与g(x)的大小.322. (本小题满分14分)已知曲线C i:凶+国=1(a Ab >0)所围成的封闭图形的面积为4亦,曲线C i的内切圆半径a b2 5为•记C2为以曲线C i与坐标轴的交点为顶点的椭圆.3(I)求椭圆C2的标准方程;(n)设AB是过椭圆C2中心的任意弦,I是线段AB的垂直平分线. M是I上异于椭圆中心的点.(1)若MO| =》OA ( O为坐标原点),当点A在椭圆C2上运动时,求点M的轨迹方程;(2)若M是I与椭圆C2的交点,求△AMB的面积的最小值.2008年普通高等学校招生全国统一考试(山东卷)文科数学(答案)一、选择题1. B2. D3. A4. C5. A6. D9. B 10. C 11. B 12. A7. D 8. C二、填空题2 2x y ’14. 4 15.2008 16. 1113. 14 121.满足M —0, a2, a s, a/,且M 门”©, a?, a?』的集合M的个数是(B )A . 1B . 2 C. 3 D . 4解析:本小题主要考查集合子集的概念及交集运算。
山东2008年全国各地高考理科数学试题及参考答案及参考答案
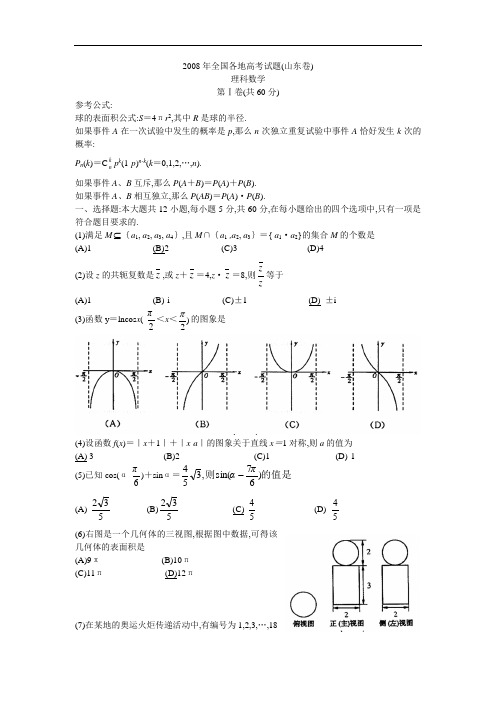
2008年全国各地高考试题(山东卷)理科数学 第Ⅰ卷(共60分)参考公式:球的表面积公式:S =4πr 2,其中R 是球的半径.如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好发生k 次的概率:P n (k )=C k n p k (1-p )n-k(k =0,1,2,…,n ).如果事件A 、B 互斥,那么P (A +B )=P (A )+P (B ). 如果事件A 、B 相互独立,那么P (AB )=P (A )·P (B ).一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)满足M ⊆{a 1, a 2, a 3, a 4},且M ∩{a 1 ,a 2, a 3}={ a 1·a 2}的集合M 的个数是 (A)1 (B)2 (C)3 (D)4 (2)设z 的共轭复数是z ,或z +z =4,z ·z =8,则zz等于 (A)1 (B)-i (C)±1 (D) ±i (3)函数y =lncos x (-2π<x <)2π的图象是(4)设函数f (x )=|x +1|+|x -a |的图象关于直线x =1对称,则a 的值为(A) 3 (B)2 (C)1 (D)-1 (5)已知cos(α-6π)+sin α=的值是则)67sin(,354πα- (A)-532 (B)532 (C)-54 (D) 54(6)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是(A)9π (B)10π (C)11π (D)12π(7)在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为(A)511 (B)681 (C)3061 (D)4081(8)右图是根据《山东统计年整2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为(A)304.6 (B)303.6 (C)302.6 (D)301.6 (9)(X -31x)12展开式中的常数项为(A)-1320 (B)1320 (C)-220 (D)220 (10)设椭圆C 1的离心率为135,焦点在X 轴上且长轴长为26.若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为(A)1342222=-y x (B)15132222=-y x(C)1432222=-y x (D)112132222=-y x(11)已知圆的方程为X 2+Y 2-6X -8Y =0.设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为(A)106 (B)206 (C)306 (D)406(12)设二元一次不等式组⎪⎩⎪⎨⎧≤-+≥+-≥-+0142,080192y x y x y x ,所表示的平面区域为M ,使函数y =a x (a >0,a ≠1)的图象过区域M 的a 的取值范围是(A)[1,3] (B)[2,10] (C)[2,9] (D)[10,9]第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分.(13)执行右边的程序框图,若p =0.8,则输出的n = 4 . (14)设函数f (x )=ax 2+c (a ≠0).若)()(010x f dx x f =⎰,0≤x 0≤1,则x 0的值为33. (15)已知a ,b ,c 为△ABC 的三个内角A ,B ,C 的对边,向量m =(1,3-),n =(cos A ,sin A ).若m ⊥n ,且a cos B +b cos A =c sin C ,则角B =6π. (16)若不等式|3x -b |<4的解集中的整数有且仅有1,2,3,则b 的取值范围为(5,7).三、解答题:本大题共6小题,共74分. (17)(本小题满分12分)已知函数f (x )=)0,0)(cos()sin(3><<+-+ωϕϕωϕωπx x 为偶函数,且函数y =f (x )图象的两相邻对称轴间的距离为.2π (Ⅰ)美洲f (8π)的值; (Ⅱ)将函数y =f (x )的图象向右平移6π个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )的单调递减区间. 解:(Ⅰ)f (x )=)cos()sin(3ϕωϕω+-+x x=⎥⎦⎤⎢⎣⎡+-+)cos(21)sin(232ϕωϕωx x=2sin(ϕω+x -6π) 因为 f (x )为偶函数,所以 对x ∈R ,f (-x )=f (x )恒成立,因此 sin(-ϕω+x -6π)=sin(ϕω+x -6π). 即-sin x ωcos(ϕ-6π)+cos x ωsin(ϕ-6π)=sin x ωcos(ϕ-6π)+cos x ωsin(ϕ-6π),整理得 sin x ωcos(ϕ-6π)=0.因为 ω>0,且x ∈R ,所以 cos(ϕ-6π)=0.又因为 0<ϕ<π,故 ϕ-6π=2π.所以 f (x )=2sin(x ω+2π)=2cos x ω.由题意得 .2,222 = 所以 ωπωπ⋅=故 f (x )=2cos2x . 因为 .24cos2)8(==ππf(Ⅱ)将f (x )的图象向右平移个6π个单位后,得到)6(π-x f 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到)64(ππ-f 的图象.).32(cos 2)64(2cos 2)64()(ππππππ-=⎥⎦⎤⎢⎣⎡-=-=f f x g 所以 当 2k π≤32ππ-≤2 k π+ π (k ∈Z),即 4k π+≤32π≤x ≤4k π+38π(k ∈Z)时,g (x )单调递减.因此g (x )的单调递减区间为 ⎥⎦⎤⎢⎣⎡++384,324ππππk k (k ∈Z)(18)(本小题满分12分)甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分。
……2008年普通高等学校招生全国统一考试理科数学试题及答案-全国卷1

2008年普通高等学校招生全国统一考试理科数学(必修+选修Ⅰ)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第I 卷1至2页,第II 卷3至9页.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷考生注意: 1.答题前,考生在答题卡上务必用0.5毫米黑色墨水签字笔将自己的姓名、准考证号、填写清楚 ,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目. 2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效..........3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 参考公式: 如果事件A B ,互斥,那么 球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ,相互独立,那么 其中R 表示球的半径()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是P ,那么 34π3V R =n 次独立重复试验中恰好发生k 次的概率其中R 表示球的半径()(1)(01,2)k k n kn n P k C P P k n -=-=,,,一、选择题1.函数y =)A .{}|0x x ≥ B .{}|1x x ≥ C .{}{}|10x x ≥D .{}|01x x ≤≤2.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图像可能是( )3.在ABC △中,AB =c ,AC =b .若点D 满足2BD DC =,则AD =( ) A .2133+b cB .5233-c b C .2133-b cD .1233+b c 4.设a ∈R ,且2()a i i +为正实数,则a =( ) A .2B .1C .0D .1-5.已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( ) A .138B .135C .95D .236.若函数(1)y f x =-的图像与函数1y =的图像关于直线y x =对称,则()f x =( )A .e 2x-1B .e 2xC .e 2x+1D . e 2x+27.设曲线11x y x +=-在点(32),处的切线与直线10ax y ++=垂直,则a =( ) A .2B .12C .12- D .2-8.为得到函数πcos 23y x ⎛⎫=+⎪⎝⎭的图像,只需将函数sin 2y x =的图像( ) A .向左平移5π12个长度单位 B .向右平移5π12个长度单位 C .向左平移5π6个长度单位D .向右平移5π6个长度单位9.设奇函数()f x 在(0)+∞,上为增函数,且(1)0f =,则不等式()()0f x f x x--<的解集为( )A .(10)(1)-+∞,,B .(1)(01)-∞-,,C .(1)(1)-∞-+∞,, D .(10)(01)-,,10.若直线1x ya b+=通过点(cos sin )M αα,,则( ) A .221a b +≤ B .221a b +≥ C .22111a b+≤D .22111a b+≥ 11.已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为A .B .C .D .ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( )A .13BCD .2312.如图,一环形花坛分成A B C D ,,,四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为( ) A .96 B .84 C .60 D .482008年普通高等学校招生全国统一考试理科数学(必修+选修Ⅰ)第Ⅱ卷注意事项:1.答题前,考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,然后贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.第Ⅱ卷共7页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效.......... 3.本卷共10小题,共90分.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.(注意:在试题卷上作答无效.........) 13.13.若x y ,满足约束条件03003x y x y x ⎧+⎪-+⎨⎪⎩,,,≥≥≤≤则2z x y =-的最大值为 .14.已知抛物线21y ax =-的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 .15.在ABC △中,AB BC =,7cos 18B =-.若以A B ,为焦点的椭圆经过点C ,则该椭圆的离心率e = .16.等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角C AB D --的余弦值为,M 、N 分别是AC 、BC 的中点,则EM 、AN 所成角的余弦值等于 . 三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分) (注意:在试题卷上作答无效.........) 设ABC △的内角A B C ,,所对的边长分别为a 、b 、c ,且3cos cos 5a Bb Ac -=. (Ⅰ)求tan cot A B 的值; (Ⅱ)求tan()A B -的最大值. 18.(本小题满分12分) (注意:在试题卷上作答无效.........) 四棱锥A BCDE -中,底面BCDE 为矩形,侧面ABC ⊥底面BCDE ,2BC =,CD =AB AC =.(Ⅰ)证明:AD CE ⊥;(Ⅱ)设CE 与平面ABE 所成的角为45,求二面角C AD E --的大小.19.(本小题满分12分)(注意:在试题卷上作答无效.........) 已知函数32()1f x x ax x =+++,a ∈R . (Ⅰ)讨论函数()f x 的单调区间;(Ⅱ)设函数()f x 在区间2133⎛⎫-- ⎪⎝⎭,内是减函数,求a 的取值范围. 20.(本小题满分12分)CDE AB(注意:在试题卷上作答无效.........) 已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方法:方案甲:逐个化验,直到能确定患病动物为止.方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;(Ⅱ)ξ表示依方案乙所需化验次数,求ξ的期望. 21.(本小题满分12分)(注意:在试题卷上作答无效.........) 双曲线的中心为原点O ,焦点在x 轴上,两条渐近线分别为12l l ,,经过右焦点F 垂直于1l 的直线分别交12l l ,于A B ,两点.已知OA AB OB 、、成等差数列,且BF 与FA 同向. (Ⅰ)求双曲线的离心率;(Ⅱ)设AB 被双曲线所截得的线段的长为4,求双曲线的方程. 22.(本小题满分12分)(注意:在试题卷上作答无效.........) 设函数()ln f x x x x =-.数列{}n a 满足101a <<,1()n n a f a +=.(Ⅰ)证明:函数()f x 在区间(01),是增函数; (Ⅱ)证明:11n n a a +<<; (Ⅲ)设1(1)b a ∈,,整数11ln a bk a b-≥.证明:1k a b +>.参考答案一、选择题 1、C 2、A 3、A 4、D 5、C 6、B 7、D 8、A 9.D 10.D . 11.B . 12.B. 二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上. 13.答案:9.14. 答案:2.15.答案:38. 16.答案:16. 三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.解析:(Ⅰ)由正弦定理得a=CBc b C A c sin sin ,sin sin = acosB-bcosA=(A CBB C A cos sin sin cos sin sin ⋅-⋅)c =c B A AB B A ⋅+-)sin(cos sin cos sin=c B A B A BA B A ⋅+-sin cos cos sin sin cos cos sin=1cot tan )1cot (tan +-B A cB A依题设得c B A c B A 531cot tan )1cot (tan =+- 解得tanAcotB=4(II)由(I )得tanA=4tanB ,故A 、B 都是锐角,于是tanB>0 tan(A-B)=B A BA tan tan 1tan tan +-=B B 2tan 41tan 3+ ≤43, 且当tanB=21时,上式取等号,因此tan(A-B)的最大值为4318.解:(I)作AO ⊥BC ,垂足为O ,连接OD ,由题设知,AO ⊥底面BCDE ,且O 为BC 中点, 由21==DE CD CD OC 知,Rt △OCD ∽Rt △CDE , 从而∠ODC=∠CED ,于是CE ⊥OD ,由三垂线定理知,AD ⊥CE(II )由题意,BE ⊥BC ,所以BE ⊥侧面ABC ,又BE ⊂侧面ABE ,所以侧面ABE ⊥侧面ABC 。
2008年普通高等学校招生全国统一考试理科数学试题及答案-全国卷1

2008年普通高等学校招生全国统一考试理科数学(必修+选修Ⅰ)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第I 卷1至2页,第II 卷3至9页.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷考生注意: 1.答题前,考生在答题卡上务必用0.5毫米黑色墨水签字笔将自己的姓名.准考证号.填写清楚 ,并贴好条形码.请认真核准条形码上的准考证号.姓名和科目. 2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效..........3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 参考公式: 如果事件A B ,互斥,那么 球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ,相互独立,那么 其中R 表示球的半径()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是P ,那么 34π3V R =n 次独立重复试验中恰好发生k 次的概率其中R 表示球的半径()(1)(01,2)k k n kn n P k C P P k n -=-=,,,一.选择题1.函数y =)A .{}|0x x ≥ B .{}|1x x ≥ C .{}{}|10x x ≥D .{}|01x x ≤≤2.汽车经过启动.加速行驶.匀速行驶.减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图像可能是( )3.在ABC △中,AB =c ,AC =b .若点D 满足2BD DC =,则AD =( ) A .2133+b cB .5233-c b C .2133-b cD .1233+b c 4.设a ∈R ,且2()a i i +为正实数,则a =( ) A .2B .1C .0D .1-5.已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( ) A .138B .135C .95D .236.若函数(1)y f x =-的图像与函数1y =的图像关于直线y x =对称,则()f x =( )A .e 2x-1B .e 2xC .e 2x+1D . e 2x+27.设曲线11x y x +=-在点(32),处的切线与直线10ax y ++=垂直,则a =( ) A .2B .12C .12- D .2-8.为得到函数πcos 23y x ⎛⎫=+⎪⎝⎭的图像,只需将函数sin 2y x =的图像( ) A .向左平移5π12个长度单位 B .向右平移5π12个长度单位 C .向左平移5π6个长度单位D .向右平移5π6个长度单位9.设奇函数()f x 在(0)+∞,上为增函数,且(1)0f =,则不等式()()0f x f x x--<的解集为( )A .(10)(1)-+∞,,B .(1)(01)-∞-,,C .(1)(1)-∞-+∞,, D .(10)(01)-,,10.若直线1x ya b+=通过点(cos sin )M αα,,则( ) A .221a b +≤ B .221a b +≥ C .22111a b+≤D .22111a b +≥ 11.已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为A .B .C .D .ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( )A .13BCD .2312.如图,一环形花坛分成A B C D ,,,四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为( ) A .96 B .84 C .60 D .482008年普通高等学校招生全国统一考试理科数学(必修+选修Ⅰ)第Ⅱ卷注意事项:1.答题前,考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名.准考证号填写清楚,然后贴好条形码.请认真核准条形码上的准考证号.姓名和科目.2.第Ⅱ卷共7页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效.......... 3.本卷共10小题,共90分.二.填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.(注意:在试题卷上作答无效.........) 13.13.若x y ,满足约束条件03003x y x y x ⎧+⎪-+⎨⎪⎩,,,≥≥≤≤则2z x y =-的最大值为 .14.已知抛物线21y ax =-的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 .15.在ABC △中,AB BC =,7cos 18B =-.若以A B ,为焦点的椭圆经过点C ,则该椭圆的离心率e = .16.等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角C AB D --的余弦值为3,M.N 分别是AC.BC 的中点,则EM.AN 所成角的余弦值等于 .三.解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分) (注意:在试题卷上作答无效.........) 设ABC △的内角A B C ,,所对的边长分别为a.b.c ,且3cos cos 5a Bb Ac -=. (Ⅰ)求tan cot A B 的值; (Ⅱ)求tan()A B -的最大值. 18.(本小题满分12分) (注意:在试题卷上作答无效.........) 四棱锥A BCDE -中,底面BCDE 为矩形,侧面ABC ⊥底面BCDE ,2BC =,CD =AB AC =.(Ⅰ)证明:AD CE ⊥;(Ⅱ)设CE 与平面ABE 所成的角为45,求二面角C AD E --的大小.19.(本小题满分12分)(注意:在试题卷上作答无效.........) 已知函数32()1f x x ax x =+++,a ∈R . (Ⅰ)讨论函数()f x 的单调区间;(Ⅱ)设函数()f x 在区间2133⎛⎫-- ⎪⎝⎭,内是减函数,求a 的取值范围. 20.(本小题满分12分)(注意:在试题卷上作答无效.........) 已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方法:方案甲:逐个化验,直到能确定患病动物为止.CDE AB方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;(Ⅱ)ξ表示依方案乙所需化验次数,求ξ的期望. 21.(本小题满分12分)(注意:在试题卷上作答无效.........) 双曲线的中心为原点O ,焦点在x 轴上,两条渐近线分别为12l l ,,经过右焦点F 垂直于1l 的直线分别交12l l ,于A B ,两点.已知OA AB OB 、、成等差数列,且BF 与FA 同向. (Ⅰ)求双曲线的离心率;(Ⅱ)设AB 被双曲线所截得的线段的长为4,求双曲线的方程. 22.(本小题满分12分)(注意:在试题卷上作答无效.........) 设函数()ln f x x x x =-.数列{}n a 满足101a <<,1()n n a f a +=.(Ⅰ)证明:函数()f x 在区间(01),是增函数; (Ⅱ)证明:11n n a a +<<; (Ⅲ)设1(1)b a ∈,,整数11ln a bk a b-≥.证明:1k a b +>.参考答案一.选择题 1.C 2.A 3.A 4.D 5.C 6.B 7.D 8.A 9.D 10.D . 11.B . 12.B. 二.填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上. 13.答案:9.14. 答案:2.15.答案:38. 16.答案:16. 三.解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.解析:(Ⅰ)由正弦定理得a=CBc b C A c sin sin ,sin sin = acosB-bcosA=(A CBB C A cos sin sin cos sin sin ⋅-⋅)c =c B A AB B A ⋅+-)sin(cos sin cos sin=c B A B A BA B A ⋅+-sin cos cos sin sin cos cos sin=1cot tan )1cot (tan +-B A cB A依题设得c B A c B A 531cot tan )1cot (tan =+- 解得tanAcotB=4(II)由(I )得tanA=4tanB ,故A.B 都是锐角,于是tanB>0 tan(A-B)=B A BA tan tan 1tan tan +-=B B 2tan 41tan 3+ ≤43, 且当tanB=21时,上式取等号,因此tan(A-B)的最大值为4318.解:(I)作AO ⊥BC ,垂足为O ,连接OD ,由题设知,AO ⊥底面BCDE ,且O 为BC 中点, 由21==DE CD CD OC 知,Rt △OCD ∽Rt △CDE , 从而∠ODC=∠CED ,于是CE ⊥OD , 由三垂线定理知,AD ⊥CE(II )由题意,BE ⊥BC ,所以BE ⊥侧面ABC ,又BE ⊂侧面ABE ,所以侧面ABE ⊥侧面ABC 。
2008年普通高等学校招生全国统一考试(全国 I卷)理数数学试题及详解

2008年普通高等学校招生全国统一考试理科数学(必修+选修Ⅰ)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第I 卷1至2页,第II 卷3至9页.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷考生注意: 1.答题前,考生在答题卡上务必用0.5毫米黑色墨水签字笔将自己的姓名、准考证号、填写清楚 ,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目. 2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效..........3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 参考公式: 如果事件A B ,互斥,那么 球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ,相互独立,那么 其中R 表示球的半径()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是P ,那么 34π3V R =n 次独立重复试验中恰好发生k 次的概率其中R 表示球的半径()(1)(01,2)k kn k n n P k C P P k n -=-=,,,一、选择题 1.函数y =)A .{}|0x x ≥ B .{}|1x x ≥ C .{}{}|10x x ≥D .{}|01x x ≤≤2.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图像可能是( )A .B .C .D .3.在ABC △中,AB =c ,AC =b .若点D 满足2BD DC =,则AD =( ) A .2133+b cB .5233-c b C .2133-b cD .1233+b c 4.设a ∈R ,且2()a i i +为正实数,则a =( ) A .2B .1C .0D .1-5.已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( ) A .138B .135C .95D .236.若函数(1)y f x =-的图像与函数1y =的图像关于直线y x =对称,则()f x =( ) A .21x e-B .2xeC .21x e+D .22x e+7.设曲线11x y x +=-在点(32),处的切线与直线10ax y ++=垂直,则a =( ) A .2B .12C .12- D .2-8.为得到函数πcos 23y x ⎛⎫=+⎪⎝⎭的图像,只需将函数sin 2y x =的图像( ) A .向左平移5π12个长度单位B .向右平移5π12个长度单位 C .向左平移5π6个长度单位D .向右平移5π6个长度单位 9.设奇函数()f x 在(0)+∞,上为增函数,且(1)0f =,则不等式()()0f x f x x--<的解集为( )A .(10)(1)-+∞,,B .(1)(01)-∞-,,C .(1)(1)-∞-+∞,,D .(10)(01)-,,10.若直线1x ya b+=通过点(cos sin )M αα,,则( ) A .221a b +≤ B .221a b +≥ C .22111a b+≤D .22111a b+≥11.已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( )A .13B .3C D .2312.如图,一环形花坛分成A B C D ,,,四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为( ) A .96 B .84 C .60 D .482008年普通高等学校招生全国统一考试理科数学(必修+选修Ⅰ)第Ⅱ卷注意事项:1.答题前,考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,然后贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.第Ⅱ卷共7页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效.......... 3.本卷共10小题,共90分.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.(注意:在试题卷上作答无效.........) 13.13.若x y ,满足约束条件03003x y x y x ⎧+⎪-+⎨⎪⎩,,,≥≥≤≤则2z x y =-的最大值为 .14.已知抛物线21y ax =-的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 .15.在ABC △中,AB BC =,7cos 18B =-.若以A B ,为焦点的椭圆经过点C ,则该椭圆的离心率e = .16.等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角C AB D --的余弦值为3,M N ,分别是AC BC ,的中点,则EM AN ,所成角的余弦值等于 . 三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分) (注意:在试题卷上作答无效.........) 设ABC △的内角A B C ,,所对的边长分别为a b c ,,,且3cos cos 5a Bb Ac -=.(Ⅰ)求tan cot A B 的值; (Ⅱ)求tan()A B -的最大值. 18.(本小题满分12分) (注意:在试题卷上作答无效.........) 四棱锥A BCDE -中,底面BCDE 为矩形,侧面ABC ⊥底面BCDE ,2BC =,CD =AB AC =.(Ⅰ)证明:AD CE ⊥;(Ⅱ)设CE 与平面ABE 所成的角为45,求二面角C AD E --的大小.19.(本小题满分12分)(注意:在试题卷上作答无效.........) 已知函数32()1f x x ax x =+++,a ∈R . (Ⅰ)讨论函数()f x 的单调区间;(Ⅱ)设函数()f x 在区间2133⎛⎫-- ⎪⎝⎭,内是减函数,求a 的取值范围. 20.(本小题满分12分)(注意:在试题卷上作答无效.........) 已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方法: 方案甲:逐个化验,直到能确定患病动物为止.方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;CDE AB(Ⅱ)ξ表示依方案乙所需化验次数,求ξ的期望. 21.(本小题满分12分)(注意:在试题卷上作答无效.........) 双曲线的中心为原点O ,焦点在x 轴上,两条渐近线分别为12l l ,,经过右焦点F 垂直于1l 的直线分别交12l l ,于A B ,两点.已知OA AB OB 、、成等差数列,且BF 与FA 同向. (Ⅰ)求双曲线的离心率;(Ⅱ)设AB 被双曲线所截得的线段的长为4,求双曲线的方程. 22.(本小题满分12分)(注意:在试题卷上作答无效.........) 设函数()ln f x x x x =-.数列{}n a 满足101a <<,1()n n a f a +=. (Ⅰ)证明:函数()f x 在区间(01),是增函数; (Ⅱ)证明:11n n a a +<<;(Ⅲ)设1(1)b a ∈,,整数11ln a bk a b-≥.证明:1k a b +>.参考答案1、C 由x(x-1)≥0,x ≥0得x ≥1或x=0;2、A 根据汽车加速行驶S=221at ,匀速行驶s=vt ,减速行驶s=221at -结合函数图象可知。
2008年普通高等学校招生全国统一考试数学(山东卷·理科)
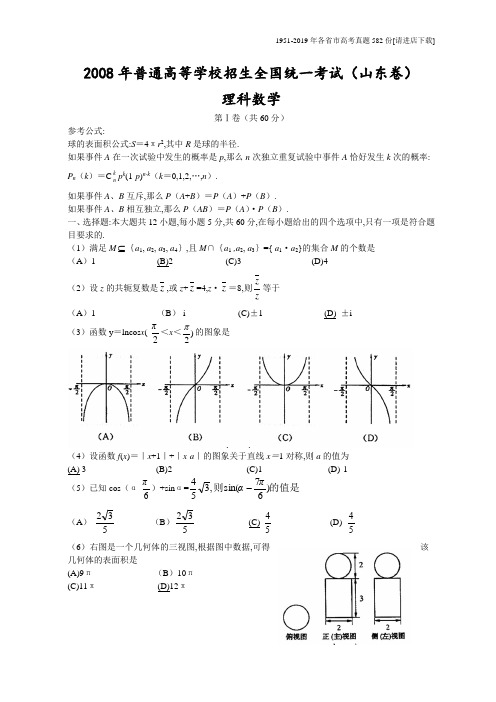
2008年普通高等学校招生全国统一考试(山东卷)理科数学第Ⅰ卷(共60分)参考公式:球的表面积公式:S =4πr 2,其中R 是球的半径.如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好发生k 次的概率: P n (k )=C kn p k (1-p )n-k (k =0,1,2,…,n ).如果事件A 、B 互斥,那么P (A +B )=P (A )+P (B ). 如果事件A 、B 相互独立,那么P (AB )=P (A )·P (B ). 一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)满足M ⊆{a 1, a 2, a 3, a 4},且M ∩{a 1 ,a 2, a 3}={ a 1·a 2}的集合M 的个数是 (A )1 (B)2 (C)3 (D)4 (2)设z 的共轭复数是z ,或z +z =4,z ·z =8,则zz等于 (A )1 (B )-i (C)±1 (D) ±i (3)函数y =lncos x (-2π<x <)2π的图象是(4)设函数f (x )=|x +1|+|x -a |的图象关于直线x =1对称,则a 的值为(A) 3 (B)2 (C)1 (D)-1 (5)已知cos (α-6π)+sin α=的值是则)67sin(,354πα- (A )-532 (B )532 (C)-54 (D) 54 (6)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是(A)9π (B )10π (C)11π (D)12π(7)在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为(A )511 (B )681 (C )3061 (D )4081(8)右图是根据《山东统计年整2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为(A )304.6 (B )303.6 (C)302.6 (D)301.6 (9)(X -31x)12展开式中的常数项为(A )-1320 (B )1320 (C )-220 (D)220 (10)设椭圆C 1的离心率为135,焦点在X 轴上且长轴长为26.若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为(A )1342222=-y x (B)15132222=-y x(C)1432222=-y x (D)112132222=-y x(11)已知圆的方程为X 2+Y 2-6X -8Y =0.设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为(A )106 (B )206 (C )306 (D )406(12)设二元一次不等式组⎪⎩⎪⎨⎧≤-+≥+-≥-+0142,080192y x y x y x ,所表示的平面区域为M ,使函数y =a x (a >0,a ≠1)的图象过区域M 的a 的取值范围是(A )[1,3] (B)[2,10] (C)[2,9] (D)[10,9]第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分.(13)执行右边的程序框图,若p =0.8,则输出的n = 4 . (14)设函数f (x )=ax 2+c (a ≠0).若)()(010x f dx x f =⎰,0≤x 0≤1,则x 0的值为33. (15)已知a ,b ,c 为△ABC 的三个内角A ,B ,C 的对边,向量m =(1,3-),n =(cos A ,sin A ).若m ⊥n ,且a cos B +b cos A =c sin C ,则角B =6π. (16)若不等式|3x -b |<4的解集中的整数有且仅有1,2,3,则b 的取值范围为(5,7).三、解答题:本大题共6小题,共74分. (17)(本小题满分12分)已知函数f (x )=)0,0)(cos()sin(3><<+-+ωϕϕωϕωπx x 为偶函数,且函数y =f (x )图象的两相邻对称轴间的距离为.2π(Ⅰ)求f (8π)的值; (Ⅱ)将函数y =f (x )的图象向右平移6π个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )的单调递减区间. 解:(Ⅰ)f (x )=)cos()sin(3ϕωϕω+-+x x=⎥⎦⎤⎢⎣⎡+-+)cos(21)sin(232ϕωϕωx x =2sin(ϕω+x -6π) 因为 f (x )为偶函数,所以 对x ∈R ,f (-x )=f (x )恒成立,因此 sin (-ϕω+x -6π)=sin(ϕω+x -6π). 即-sin x ωcos(ϕ-6π)+cos x ωsin(ϕ-6π)=sin x ωcos(ϕ-6π)+cos x ωsin(ϕ-6π),整理得 sin x ωcos(ϕ-6π)=0.因为 ω>0,且x ∈R ,所以 cos (ϕ-6π)=0. 又因为 0<ϕ<π,故 ϕ-6π=2π.所以 f (x )=2sin(x ω+2π)=2cos x ω.由题意得 .2,222 = 所以 ωπωπ⋅=故 f (x )=2cos2x . 因为 .24cos2)8(==ππf(Ⅱ)将f (x )的图象向右平移个6π个单位后,得到)6(π-x f 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到)64(ππ-f 的图象.).32(cos 2)64(2cos 2)64()(ππππππ-=⎥⎦⎤⎢⎣⎡-=-=f f x g 所以 当 2k π≤32ππ-≤2 k π+ π (k ∈Z),即 4k π+≤32π≤x ≤4k π+38π(k ∈Z)时,g (x )单调递减. 因此g (x )的单调递减区间为 ⎥⎦⎤⎢⎣⎡++384,324ππππk k (k ∈Z) (18)(本小题满分12分)甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分。
2008年普通高等学校招生全国统一考试山东卷

2008年普通高等学校招生全国统一考试(山东卷)数学(理) 第Ⅰ卷(共60分)参考公式:球的表面积公式:S =4πr 2,其中R 是球的半径. 如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好发生k 次的概率:P n (k )=C kn p k (1-p )n-k (k =0,1,2,…,n ).如果事件A 、B 互斥,那么P (A +B )=P (A )+P (B ). 如果事件A 、B 相互独立,那么P (AB )=P (A )·P (B ).一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)满足M ⊆{}1234,,,a a a a 且{}{}12312,,,M a a a a a ⋂=的集合M 的个数是 (A )1 (B)2 (C)3 (D)4 解析:本题考查集合子集的概念及交集运算。
集合M 中必含有12,a a 则{}{}12124,,,M a a M a a a ==或 (2)设z 的共轭复数是z ,或z +z =4,z ·z =8,则zz等于 (A )1 (B )-i (C)±1 (D) ±i 解析:本题考查共轭复数的概念、复数的运算。
可设2z bi =+,由8z z ⋅=得248, 2.b b +==±()2222.88i z z i z ±===±(3)函数ln cos ()22y x x ππ=-<<的图象是解析:本题考查复合函数的图象。
l n c o s 22y x x ππ⎛⎫=-<< ⎪⎝⎭是偶函数,可排除B,D;由cos x 的值域可以确定。
(4)设函数()1f x x x a =++-的图象关于直线x =1对称,则a 的值为 (A) 3 (B)2 (C)1 (D)-1解析:本题考查分段函数的图象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国校长网资源频道
中国校长网
第Ⅱ卷(共 90 分)
二、填空题:本大题共 4 小题,每小题 4 分,共 16 分.
(13) 执行右边的程序框图, 若 p=0.8, 则输出的 n= (14)设函数 f(x)=ax2+c(a≠0),若 4 .
P
3
1 27
2 9
4 9
8 27
中国校长网资源频道
中国校长网
ε 的数学期望为 Eε = 0
1 2 4 8 1 2 3 2. 27 9 9 27 2 3
解法二:根据题设可知 ~B (3, ) 因此ε 的分布列为
x2 y2 (A) 2 2 1 4 3
(C)
x2 y2 1 (B) 2 13 52
(D)
x2 y2 1 32 4 2
x2 y2 1 132 122
(11)已知圆的方程为 X2+Y2-6X-8Y=0.设该圆过点(3,5)的最长弦和最短弦分别为 AC 和 BD,则四边形 ABCD 的面积为 (A)10 6 (B)20 6 (C)30 6 (D)40 6
(16)若不等式|3x-b|<4 的解集中的整数有且仅有 1,2,3,则 b 的取值范围为(5,7).
三、解答题:本大题共 6 小题,共 74 分.
(17) (本小题满分 12 分) 已知函数 f(x)= 3 sin(x ) cos(x )(0 π , 0) 为偶函数,且函数 y=f(x) 图象的两相邻对称轴间的距离为 (Ⅰ)求 f(
2 1 2 2 2 P ( 0) C 03 (1 )3 , P( 1) C13 (1 ) 2 , 3 27 3 3 9 2 2 4 2 8 P ( 2) C 23 ( ) 2 (1 ) , P( 3) C 33 ( )3 . 3 3 9 3 27 所以ε 的分布列为 0 1 2 ε
x 2 y 19 0, (12)设二元一次不等式组 x y 8 0, 所表示的平面区域为 M,使函数 y=ax(a>0, 2 x y 14 0
a≠1)的图象过区域 M 的 a 的取值范围是 (A) [1,3] (B)[2, 10 ] (C)[2,9] (D)[ 10 ,9]
故 因此
f(x)=2cos2x.
个单位后,得到 f ( x ) 的图象,再将所得图象横坐标 6 6 x 伸长到原来的 4 倍,纵坐标不变,得到 f ( ) 的图象. 4 6
(Ⅱ)将 f(x)的图象向右平移个
f ( ) 2 cos 2 . 8 4
x x x 所以 g ( x) f ( ) 2cos 2( ) 2cos f ( ). 4 6 2 3 4 6
π . 2
π )的值; 8 π 个单位后,再将得到的图象上各点的横坐标伸长到 6
(Ⅱ)将函数 y=f(x)的图象向右平移
原来的 4 倍,纵坐标不变,得到函数 y=g(x)的图象,求 g(x)的单调递减区间. 解: (Ⅰ)f(x)= 3 sin(x ) cos(x ) = 2
2 ,乙队中 3 人答对的概率分别为 3
2 2 1 , , ,且各人回答正确与否相互之间没有影响。用ε 表示甲队的总得分。 3 3 2
(Ⅰ)求随机变量ε 分布列和数学期望; (Ⅱ)用 A 表示“甲、乙两个队总得分之和等于 3”这一事件,用 B 表示“甲队总得分大于 乙队总得分”这一事件,求 P(AB). (Ⅰ)解法一:由题意知,ε 的可能取值为 0,1,2,3,且
2k 2 2 k P( k ) C3 ( ) k (1 ) 2 k C k 3 3 , k 0,1,2,3. 3 3 3 2 2 因为~B(3, ), 所以E 3 2 3 3
(Ⅱ)解法一:用 C 表示“甲得 2 分乙得 1 分”这一事件,用 D 表示“甲得 3 分乙得 0 分” 这一事件,所以 AB=C∪D,且 C、D 互斥,又
因此 sin(- x -
中国校长网资源频道
中国校长网
又因为 0< <π ,故
π π π - = .所以 f(x)=2sin( x + )=2cos x . 6 2 2
2
由题意得
2
2
, 所以 =2.
所以 当n 2时,bn S n S n 1
中国校长网资源频道
29 30 31
1158 26 0247
(D)301.6
1
3
x
)12 展开式中的常数项为 (B)1320 (C)-220 (D)220
(A)-1320 (10)设椭圆 C1 的离心率为
5 , 焦点在 X 轴上且长轴长为 26.若曲线 C2 上的点到椭圆 C1 的两 13
个焦点的距离的差的绝对值等于 8,则曲线 C2 的标准方程为
π 4 7π 3, 则 sin(α )的值是 )+sinα = 6 5 6
(A)-
2 3 5
(B)
2 3 5
(C)-
4 5
(D)
4 5
(6)右图是一个几何体的三视图,根据图中数据,可得该几 何体的表面积是 (A)9π (B)10π (C)11π (D) 12π
中国校长网资源频道
3 1 sin(x ) cos(x ) 2 2
π ) 6
=2sin( x -
因为 f(x)为偶函数, 所以 对 x∈R, f(-x)=f(x)恒成立,
π π )=sin( x - ). 6 6 π π π π 即-sin x cos( - )+cos x sin( - )=sin x cos( - )+cos x sin( - ), 6 6 6 6 π π 整理得 sin x cos( - )=0.因为 >0,且 x∈R,所以 cos( - )=0. 6 6
中国校长网
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表: a1 a2 a3 a4 a5 a6 a7 a8 a9 a10
„„
记表中的第一列数 a1,a2,a4,a7,„构成的数列为{bn},b1=a1=1. Sn 为数列{bn}的前 n 项 和,且满足
2bn =1(n≥2). bn S N S 2 n
1 }成等差数列,并求数列{bn}的通项公式; Sn
4 时,求上表中第 k(k≥3)行所有项的和. 91
(Ⅰ)证明数列{
(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公 比为同一个正数.当 a81
(Ⅰ)证明:由已知,当 n≥2 时
2bn 1, bn S n S n 2 又 S n b1 b2 bn , ( 2 S n S n 1) 所以 1, ( S n S n 1 ) S n S 2 n ( 2 S S n 1) 即 n 1, S n 1S n 1 1 1 所以 , S n S n 1 2 又S1 b1 a1 1. 1 1 所以数列 是首项为1,公差为 的等差数列. 2 Sn 1 1 n 1 由上可知 = 1+ (n 1 ) , Sn 2 2 即 S n 2 . n 1 2 2 2 n 1 n n(n 1).
如果事件 A、B 互斥,那么 P(A+B)=P(A)+P(B). 如果事件 A、B 相互独立,那么 P(AB)=P(A) ²P(B).
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个 选项中,只有一项是符合题目要求的. (1)满足 M {a1, a2, a3, a4},且 M∩{a1 ,a2, a3}={ a1,a2}的集合 M 的个数是
(A)1 (B)2 (C)3 (D)4
(2)设 z 的共轭复数是 z ,若 z+ z =4, z² z =8,则 (A)i (3)函数 y=lncosx((B)-i (C)±1
z 等于 z
(D) ±i )
π π <x< =的图象是 ( A 2 2
(4)设函数 f(x)=|x+1|+|x-a|的图象关于直线 x=1 对称,则 a 的值为 (A) 3 (B)2 (C)1 (D)-1 (5)已知 cos(α -
中国校长网
(7)在某地的奥运火炬传递活动中,有编号为 1,2,3,„,18 的 号能组成以 3 为公差的等差数列的概率为
1 51 1 (C) 306
(A)
1 68 1 (D) 408
(B)
(8)右图是根据《山东统计年鉴 2007》中的资料作成的 1997 年至 2006 年我省城镇居民百户家庭人口数的茎 叶图,图中左边的数字从左到右分别表示城镇居民百 户家庭人口数的百位数字和十位数字,右边的数字表 示城镇居民百户家庭人口数的个位数字,从图中可以 得到 1997 年至 2006 年我省城镇居民百户家庭人口数 的平均数为 (A)304.6 (B)303.6 (C)302.6 (9) (X-
x ≤2 kπ + π (k∈Z), 2 3 2 8 4kπ + ≤x≤4kπ + (k∈Z)时,g(x)单调递减. 3 3
2kπ ≤
当 即
因此 g(x)的单调递减区间为
2 8 4 k , 4 k 3 3
(k∈Z)
(18) (本小题满分 12 分) 甲乙两队参加奥运知识竞赛,每队 3 人,每人回答一个问题,答对者为本队赢得一分, 答错得零分。假设甲队中每人答对的概率均为
2 1 1 22 1 1 1 2 ( ) 3 ( 2 ) C 2 3 3 ( 2 C 12 2 ) 3 2 3 2 3 2 3 3 34 . 243
