全等三角形判定的练习题

合集下载

(完整版)全等三角形判定综合练习题

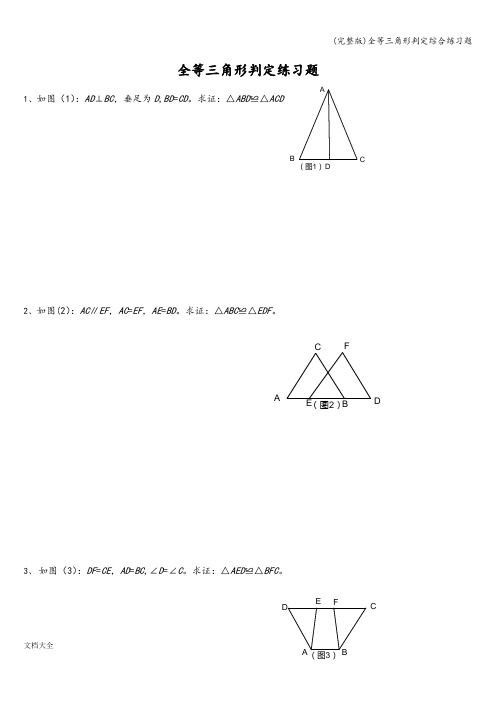
全等三角形判定练习题1、如图（1）：AD ⊥BC ，垂足为D ,BD =CD 。

求证：△ABD ≌△ACD2、如图(2）：AC ∥EF ，AC =EF ，AE =BD 。

求证：△ABC ≌△EDF 。

3、如图（3）：DF =CE ，AD =BC ,∠D =∠C 。

求证：△AED ≌△BFC 。

FE （图2）DCBAFEDC（图1）DCBA4、如图（4):AB =AC ，AD =AE ,AB ⊥AC ，AD ⊥AE .求证：（1）∠B =∠C ,（2）BD =CE5、如图（5）：AB ⊥BD ，ED ⊥BD ，AB =CD ，BC =DE 。

求证：AC ⊥CE 。

E（图4）DCBAE（图5）DCBA6、如图（6）：CG =CF ，BC =DC ，AB =ED ，点A 、B 、C 、D 、E 在同一直线上。

求证：（1）AF =EG ,（2）BF ∥DG .7、如图（7）：AC ⊥BC ,BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN =BC 。

求证：（1）MN 平分∠AMB ，（2)∠A =∠CBM 。

GFE（图6）DC BANM（图7）CBA8、如图（8）:A 、B 、C 、D 四点在同一直线上，AC =DB ，BE ∥CF ，AE ∥DF 。

求证：△ABE ≌△DCF 。

9、如图（9）AE 、BC 交于点M ,F 点在AM 上，BE ∥CF ，BE =CF 。

求证：AM 是△ABC 的中线。

FE（图8）DC B AMFE（图9）CBA10、如图（10）∠BAC =∠DAE ,∠ABD =∠ACE ,BD =CE . 求证:AB =AC 。

11、如图（11)在△ABC 和△DBC 中，∠1=∠2，∠3=∠4，P 是BC 上任一点。

求证：PA =PD .12、如图(12）AB ∥CD ，OA =OD ，点F 、D 、O 、A 、E 在同一直线上，AE =DF . 求证：EB ∥CF 。

《全等三角形的判定》练习(含答案)

全等三角形的判定一、选择题1.小明不小心把一块三角形形状的玻璃打碎成了三块，如图①②③，他想要到玻璃店去配一块大小形状完全一样的玻璃，你认为应带（）A ．①B ．②C ．③D ．①和②【答案】C ．【解析】解带③去可以利用“角边角”得到全等的三角形．故选C ．2.如图，已知：∠A=∠D ，∠1=∠2，下列条件中能使△ABC ≌△DEF 的是（）A ．∠E=∠B B ．ED=BC C ．AB=EFD ．AF=CD【答案】D ．【解析】添加AF=CD ，∵AF=CD ，∴AF+FC=CD+FC ，∴AC=FD ，在△ABC 和△DEF 中12A DAC DF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABC ≌△DEF （ASA ），故选D ．3.下列关于两个三角形全等的说法：①三个角对应相等的两个三角形全等；②三条边对应相等的两个三角形全等；③有两角和其中一个角的对边对应相等的两个三角形全等；④有两边和一个角对应相等的两个三角形全等．正确的说法个数是（）A ．1个B ．2个C ．3个D ．4个【答案】B ．【解析】①不正确，因为判定三角形全等必须有边的参与；②正确，符合判定方法SSS ；③正确，符合判定方法AAS ；④不正确，此角应该为两边的夹角才能符合SAS ．所以正确的说法有两个．故选B ．4.在△ABC 和△A ˊB ′C ′中，已知∠A=∠A ′，AB=A ′B ′，在下面判断中错误的是（）A ．若添加条件AC=A ′C ′，则△ABC ≌△A ′B ′C ′B ．若添加条件BC=B ′C ′，则△ABC ≌△A ′B ′C ′C ．若添加条件∠B=∠B ′，则△ABC ≌△A ′B ′C ′D ．若添加条件∠C=∠C ′，则△ABC ≌△A ′B ′C ′【答案】B.【解析】A ，正确，符合SAS 判定；B ，不正确，因为边BC 与B ′C ′不是∠A 与∠A ′的一边，所以不能推出两三角形全等；C ，正确，符合AAS 判定；D ，正确，符合ASA 判定；故选B ．5.如图，在等腰△ABC 中，AB=AC ，∠A=20°，AB 上一点D 使AD=BC ，过点D 作DE ∥BC 且DE=AB ，连接EC ，则∠DCE 的度数为（）A ．80°B ．70°C ．60°D ．45°【答案】B.【解析】如图所示，连接AE ．∵AE=DE，∴∠ADE=∠DAE，∵DE∥BC，∴∠DAE=∠ADE=∠B，∵AB=AC，∠BAC=20°，∴∠DAE=∠ADE=∠B=∠ACB=80°，在△ADE 与△CBA 中，DAE ACB AD BCADE B ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴AE=AC，∠AED=∠BAC=20°，∵∠CAE=∠DAE﹣∠BAC=80°﹣20°=60°，∴△ACE 是等边三角形，∴CE=AC=AE=DE，∠AEC=∠ACE=60°，∴△DCE 是等腰三角形，∴∠CDE=∠DCE，∴∠DEC=∠AEC﹣∠AED=40°，∴∠DCE=∠CDE=（180﹣40°）÷2=70°．故选B ．6.如图：AB=AC ，∠B=∠C，且AB=5，AE=2，则EC 的长为（）A ．2B ．3C ．5D ．2.5【答案】B.【解析】在△ABE 与△ACF 中，∵A AAB AC B C∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABE≌△ACF（ASA ），∴AC=AB=5∴EC=AC﹣AE=5﹣2=3，故选B.二、填空题.7.如图，AB=AC ，要使△ABE≌△ACD，依据ASA ，应添加的一个条件是．【答案】∠C=∠B ．【解析】添加∠C=∠B，在△ACD 和△ABE 中，A AAB AC C B∠=∠⎧⎪=⎨⎪∠=∠⎩，8.如图，AB∥CF，E 为DF 中点，AB=20，CF=15，则BD= 5 ．【答案】5.【解析】∵AB∥FC，∴∠ADE=∠EFC，∵E 是DF 的中点，∴DE=EF，在△ADE 与△CFE 中，ADE EFC DE EFAED CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ADE≌△CFE，∴AD=CF，∵AB=20，CF=15，∴BD=AB﹣AD=20﹣15=5．9.如图，∠1=∠2，∠3=∠4，BC=5，则BD= ．【答案】5. 【解析】∵∠ABD+∠3=180°∠ABC+∠4=180°，且∠3=∠4，∴∠ABD=∠ABC在△ADB 和△ACB 中，1=2AB ABABD ABC ∠∠⎧⎪=⎨⎪∠=∠⎩， ∴△ADB≌△ACB（ASA ），∴BD=BC=5．10.如图，要测量一条小河的宽度AB 的长，可以在小河的岸边作AB 的垂线 MN ，然后在MN 上取两点C ，D ，使BC=CD ，再画出MN 的垂线DE ，并使点E 与点A ，C 在一条直线上，这时测得DE 的长就是AB 的长，其中用到的数学原理是： .【答案】ASA ，全等三角形对应边相等．【解析】∵AB⊥MN，DE⊥MN，∴∠ABC=∠EDC=90°，在△ABC 和△EDC 中，ABC EDC BC DCACB ECD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABC≌△EDC（ASA ），∴DE=AB．11.如图，在四边形ABCD 中，AB∥DC，AD∥BC，对角线AC 、BD 相交于点O ，则图中的一对全等三角形为．（写出一对即可）【答案】△ABC ≌△ADC.【解析】△ABC≌△ADC，理由如下：∵AB∥DC，AD∥BC，∴∠BAC=∠DCA，∠DAC=∠BCA，在△ABC 与△ADC 中，BAC DCA AC CADAC BCA ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABC≌△ADC（ASA ），∴AB=DC，BC=DA ，在△ABO 与△CDO 中，BAO DCO AOB COD AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABO≌△CDO（AAS ），同理可得：△BCO≌△DAO，三、解答题12.如图，点A ，B ，C ，D 在同一条直线上，AB=FC ，∠A=∠F，∠EBC=∠FCB．求证：BE=CD ．【答案】证明见解析．【解析】∵∠EBC=∠FCB，∠EBC+∠ABE=180°，∠FCB+∠FCD=180°，∴∠ABE=∠FCD，在△ABE 与△FCD 中，A F AB FCABE FCD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABE≌△FCD（ASA ），∴BE=CD．13.如图，点D 在AB 上，DF 交AC 于点E ，CF∥AB，AE=EC ．求证：AD=CF ．【答案】答案见解析.【解析】∵CF∥AB，∴∠A=∠ACF，∠ADE=∠CFE．在△ADE 和△CFE 中，A ACF ADE CFE AE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADE≌△CFE（AAS ）．∴AD=CF．14. 如图，锐角△ABC 中，∠BAC=60°，O 是BC 边上的一点，连接AO ，以AO 为边向两侧作等边△AOD 和等边△AOE，分别与边AB ，AC 交于点F ，G ．求证：AF=AG ．【答案】答案见解析.【解析】∵△AOD 和△AOE 是等边三角形，∴∠E=∠AOF=60°，AE=AO ，∠OAE=60°，∵∠BAC=60°，∴∠FAO=∠EAG=60°﹣∠CAO，在△AFO 和△AGE 中， FAO EAG AO AEAOF E ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△AFO≌△AGE（ASA ）， ∴AF=AG．。

全等三角形的判定练习题

全等三角形的判定练习题一、选择题1. 下列哪组条件可以判定两个三角形全等？A. 两边和其中一边的对角相等B. 两角和其中一角的对边相等C. 两边和它们的夹角相等D. 两角和其中一边相等A. ∠A=∠DB. ∠B=∠EC. ∠C=∠FA. SAS（边角边）B. ASA（角边角）C. AAS（角角边）D. SSS（三边）二、填空题1. 若两个三角形的______相等，且它们的夹角相等，则这两个三角形全等。

2. 在全等三角形中，对应边______相等，对应角______相等。

3. 要判定两个三角形全等，至少需要知道它们的______个元素相等。

三、判断题1. 若两个三角形的两边和它们的夹角分别相等，则这两个三角形一定全等。

（）2. 两个等腰三角形的底角相等，则这两个三角形全等。

（）3. 两个等边三角形的边长相等，则这两个三角形全等。

（）四、解答题1. 在△ABC中，AB=AC，∠B=∠C，求证：△ABC是等腰三角形。

2. 已知△ABC和△DEF，AB=DE，BC=EF，∠B=∠E，求证：△ABC≌△DEF。

3. 在△ABC中，AB=AC，∠A=40°，∠B=70°，求∠C的度数。

4. 已知△ABC和△DEF，AB=DE，BC=EF，AC=DF，求证：△ABC≌△DEF。

5. 在△ABC中，AB=8cm，AC=10cm，∠A=60°，求BC的长度。

五、作图题1. 请作出一个三角形，使其与给定三角形全等，已知条件是两边及其夹角。

2. 请作出一个三角形，使其与给定三角形全等，已知条件是两角及其夹边。

3. 请作出一个三角形，使其与给定三角形全等，已知条件是三边。

六、综合题1. 在平面直角坐标系中，点A(2, 3)，点B(6, 3)，点C和点D在x轴上，且△ABC≌△ABD，求点C和点D的坐标。

2. 在四边形ABCD中，AB=CD，AD=BC，且∠ABC=∠CDA=90°，证明：△ABC≌△CDA。

三角形全等判定专题训练题

三角形全等判定专题训练题1.给定三角形ABC，AD垂直于BC，垂足为D，且BD=CD。

证明△ABD≌△ACD。

2.给定平行四边形ABCD，AC=EF，AC平行于EF，且F在AD上。

证明△ABC≌△EDF。

3.给定三角形ABC和DEF，DF=CE，AD=BC，∠D=∠C。

证明△AED≌△BFC，其中AE=BD。

4.给定等腰直角三角形ABC，AB=AC，AD=AE，AB垂直于AC，AD垂直于AE。

证明∠B=∠C且BD=CE。

6.给定四边形ABCDE，CG=CF，BC=DC，AB=ED，且A、B、C、D、E在同一直线上。

证明AF=EG且BF平行于DG。

7.给定三角形ABC，AC垂直于BC，___平分∠ABC，且交AC于点M，N是AB的中点，且BN=BC。

证明___平分∠AMB且∠A=∠___。

8.给定四边形ABCD，AC=DB，BE平行于CF，AE平行于DF。

证明△ABE≌△DCF。

9.给定三角形ABC，AE和BC相交于点M，F在AM上，BE平行于CF，且BE=CF。

证明AM是△ABC的中线。

10.给定四边形ABCD，且∠BAC=∠DAE，∠ABD=∠ACE，BD=CE。

证明AB=AC。

11.给定三角形ABC和△DBC，且∠1=∠2，∠3=∠4，P是BC上的任意一点。

证明PA=PD。

12.给定四边形ABCD，AB平行于CD，OA=OD，且F、D、O、A、E在同一直线上，AE=DF。

证明EB平行于CF。

13.给定三角形ABC和△EDC，且△ABC≌△EDC。

证明BE=AD。

14.给定等腰直角三角形ABC，AC=BC，AE是BC的中线，CF⊥AE于F，BD⊥CB交CF的延长线于点D。

证明AB=BD。

15、证明：由图可知，∠BAC=90°，且AB=2AC，因此由勾股定理可得BC=√5AC，而DE=AC，BF=2AC，EF=BC-AC=√5AC-AC=(√5-1)AC，因此AE=AC+EF=2AC+(√5-1)AC=(1+√5)AC，所以△ABC≌△AED。

全等三角形的判定精选练习题(分SSS、SAS、AAS、ASA、HL分专题)

全等三角形的判定〔SSS〕1、如图1，AB=AD，CB=CD，∠B=30°，∠BAD=46°，那么∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2，线段AD与BC交于点O，且AC=BD，AD=BC，•那么下面的结论中不正确的选项是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中，AB=A1B1，BC=B1C1，那么补充条件____________，可得到△ABC≌△A1B1C1．4、如图3，AB=CD，BF=DE，E、F是AC上两点，且AE=CF．欲证∠B=∠D，可先运用等式的性质证明AF=________，再用“SSS〞证明______≌_______得到结论．5、如图，AB=CD，AC=BD，求证：∠A=∠D．6、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导以下结论：⑴∠D=∠B；⑵AE∥CF．7、如图，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的根底上，求证：DE∥BF.D C BA 全等三角形的判定(SAS)1、如图1，AB ∥CD ，AB=CD ，BE=DF ，那么图中有多少对全等三角形( )A.3B.4C.5D.62、如图2，AB=AC ，AD=AE ，欲证△ABD ≌△ACE ，可补充条件( ) A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD3、如图3，AD=BC ，要得到△ABD 和△CDB 全等，可以添加的条件是( ) A.AB ∥CD B.AD ∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4，AB 与CD 交于点O ，OA=OC ，OD=OB ，∠AOD=________，•根据_________可得到△AOD ≌△COB ，从而可以得到AD=_________．5、如图5，△ABC 中，AB=AC ，AD 平分∠BAC ，请补充完整过程说明△ABD ≌△ACD 的理由． ∵AD 平分∠BAC ， ∴∠________=∠_________(角平分线的定义). 在△ABD 和△ACD 中，∵____________________________， ∴△ABD ≌△ACD 〔〕 6、如图6，AB=AD ，AC=AE ，∠1=∠2，求证∠ADE=∠B.7、如图，AB=AD ，假设AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？8、如图，在△ABC 和△DEF 中，B 、E 、F 、C ，在同一直线上，下面有4个条件，请你在其中选3个作为题设，余下的一个作为结论，写一个真命题，并加以证明. ①AB=DE ； ②AC=DF ； ③∠ABC=∠DEF ； ④BE=CF.9、如图⑴，AB ⊥BD ，DE ⊥BD ，点C 是BD 上一点，且BC=DE ，CD=AB ．⑴试判断AC 与CE 的位置关系，并说明理由．⑵如图⑵，假设把△CDE 沿直线BD 向左平移，使△CDE 的顶点C 与B 重合，此时第⑴问中AC与-.BE 的位置关系还成立吗？(注意字母的变化)全等三角形〔三〕AAS 和ASA【知识要点】1．角边角定理〔ASA 〕：有两角及其夹边对应相等的两个三角形全等. 2．角角边定理〔AAS 〕：有两角和其中一角的对边对应相等的两个三角形全等. 【典型例题】例1．如图，AB ∥CD ，AE=CF ，求证：AB=CD例2．如图，：AD=AE ，ABE ACD ∠=∠，求证：BD=CE.例3．如图，：ABD BAC D C ∠=∠∠=∠.，求证：OC=OD.例4．如图：AB=CD ，AD=BC ，O 是BD 中点，过O 点的直线分别交DA 和BC 的延长线于E ，F.求证：AE=CF.A-.例5．如图，321∠=∠=∠，AB=AD.求证：BC=DE.例6．如图，四边形ABCD 中，AB=DC ，AD=BC ，点F 在AD 上，点E 在BC 上，AF=CE ，EF 的对角线BD 交于O ，请问O 点有何特征？【经典练习】1.△ABC 和△C B A '''中，C B C B A A ''='∠=∠,'，C C '∠=∠那么△ABC 与△C B A ''' .2．如图，点C ，F 在BE 上，,,21EF BC =∠=∠请补充一个条件，使△ABC ≌DFE,补充的条件是 .3．在△ABC 和△C B A '''中，以下条件能判断△ABC 和△C B A '''全等的个数有〔〕 ①A A '∠=∠ B B '∠=∠，C B BC ''= ②A A '∠=∠，B B '∠=∠，C A C A ''=' ③A A '∠=∠ B B '∠=∠，C B AC ''= ④A A '∠=∠，B B '∠=∠，C A B A ''=' A ． 1个 B. 2个 C. 3个 D. 4个4．如图，MB=ND ，NDC MBA ∠=∠，以下条件不能判定是△ABM ≌△CDN 的是〔〕A ． N M ∠=∠ B. AB=CD C ． AM=CN D. AM ∥CN 5．如图2所示， ∠E =∠F =90°，∠B =∠C ，AE =AF ，给出以下结论：ABD C EO12 3AFDOB EC①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是_________ _________。

(完整版)全等三角形判定测试题(含答案)

全等三角形判定测试题班级_________ 学号 __________ 姓名______________ 分数_______一、选一选，看完四个选项后再做决定呀！ (每小题3分，共30分)1已知等腰三角形的一个内角为50°，则这个等腰三角形的顶角为【】(A)50°(B)80°( C) 50°或80°(D)40°或65°D , E, F分别是BC, AD , CE的中点，且S^ABC =4 5 6 7 84 工人师傅常用角尺平分一个任意角•做法如下：如图2所示，/ AOB是一个任意角，在边OA, OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M ,N重合.过角尺顶点C的射线OC即是/ AOB的平分线•这种做法的道理是【】.(A) HL ( B) SSS ( C) SAS( D) ASA5 利用三角形全等所测距离叙述正确的是( )A. 绝对准确B. 误差很大，不可信C. 可能有误差，但误差不大，结果可信D. 如果有误差的话就想办法直接测量，不能用三角形全等的方法测距离6 在图3所示的3 X3正方形网格中，/ 1 + Z 2+Z 3+Z 4+/5等于【】.2.如图1所示，在△ ABC中，已知点9(A) 145°( B) 180°(C) 225°( D) 270°7•根据下列条件，能判定厶ABC^A A'B'C'的是【】.(A)AB=A'B‘，BC=B'C； / A=Z A'(B)Z A= / A', / B= / B AC= B C '(C)Z A= / A', / B= / B； / C= / C'(D)AB=A'B‘，BC=B'C ；△ ABC 的周长等于△A'B'C'的周长8 如图 4 所示，△ ABC 中，/ C=90 °,点 D 在AB 上，BC=BD , DE 丄AB 交AC 于点E. △ ABC的周长为12,A ADE的周长为6•则BC的长为【】.(A) 3 ( B) 4 ( C) 5 (D) 69 将一副直角三角尺如图5所示放置，已知AE // BC ,则/ AFD的度数是【平方厘米，则S A BEF 的值为【】(A) 5厘米 (B ) 7厘米(C ) 9厘米 (D ) 11厘米】.(A ) 45°(B ) 50°(C )60°( D ) 75°(B ) 1平方厘米(C ) 1平方厘米2(D )-平方厘米4(A ) 2平方厘米图1则第三边长为【3.已知一个三角形的两边长分别是2厘米和9厘米，且第三边为奇数,、填一填，要相信自己的能力！（每小题3分，共30分）1 11•在ABC 中，若A= 2 B3 C，则ABC 是 -------------------- 三角形.2. 如图7所示，BD 是 ABC 的中线， AD 2 , AB BC 5，贝U ABC 的周长是 _________________ .3. 如图8所示所示，在 ABC 中，BD , CE 分别是AC 、AB 边上的高，且BD 与CE 相交于点0，如果 BOC 135，那么 A 的度数为 ________________ .4. 有5条线段，长度分别为 1厘米、2厘米、3厘米、4厘米、5厘米，以其中三条线段为边长，共可以组成 ________________ 个形状不同的三角形.的大小等于 _____ 度.方向的长度 DF 相等，则△ ABC ^A DEF ，理由是 ________ 7. 如图11所示，AD // BC , AB // DC ,点O 为线段AC 的中点，过点 O 作一条直线分别与AB 、CD 交于点M 、N .点E 、F 在直线MN 上，且OE=OF .图中全等的三角形共有 __________ 对.8. 如图12所示，要测量河两岸相对的两点 A 、B 的距离，在AB 的垂线BF 上取两点C 、D , 使BC=CD ，过D 作BF 的垂线 DE ,与AC 的延长线交于点 E ,则/ ABC= / CDE=90° , BC=DC ,Z 1= _______ , △ ABC 也 _________ ，若测得 DE 的长为25米，则河宽 AB 长为 9. 如图13所示，有一底角为35。

八年级数学-全等三角形的判定练习(含答案)

八年级数学-全等三角形的判定练习（含答案）一、选择题1.如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是（）A．AD∥BC B．DF∥BE C．∠D=∠B D．∠A=∠C 【答案】C．【解析】∠D=∠B,理由是：∵在△ADF和△CBE中AD BCD BDF BE=⎧⎪∠=∠⎨⎪=⎩∴△ADF≌△CBE（SAS）,即选项C正确；具备选项A、选项B,选项D的条件都不能推出两三角形全等,故选C．2.如图,若已知AE=AC,用“SAS”说明△ABC≌△ADE,还需要的一个条件是（）A．BC=DE B．AB=AD C．BO=DO D．EO=CO【答案】B.【解析】在△ABC与△ADE中AE ACA AAB AD=⎧⎪∠=∠⎨⎪=⎩,∴△ABC≌△ADE（SAS）,故选B.3.如图,AB=CD,AB∥CD,判定△ABC≌△CDA的依据是（）A．SSS B．SAS C．ASA D．HL 【答案】B.【解析】∵AB∥CD,∴∠BAC=∠DCA,在△ABC与△CDA中,AB CDBAC DCAAC CA=⎧⎪∠=∠⎨⎪=⎩∴△ABC≌△CDA（SAS）．故选B．4.如图所示,AB=BD,BC=BE,要使△ABE≌△DBC,需添加条件（）A．∠A=∠D B．∠C=∠E C．∠D=∠ED．∠ABD=∠CB E【答案】D.【解析】∵AB=BD,BC=BE,∴要使△ABE≌△DBC,需添加的条件为∠ABE=∠DBC,又∠ABE﹣∠DBE=∠DBC﹣∠DBE,即∠ABD=∠CBE,∴可添加的条件为∠ABE=∠DBC或∠ABD=∠CBE．综合各选项,D选项符合．故选D．5．如图在△ABD和△ACE都是等边三角形,则△ADC≌△ABE的根据是（）A．SSS B．SAS C．ASA D．AAS【答案】B.【解析】∵△ABD和△A CE都是等边三角形,∴AD=AB,AC=AE,又∵∠DAB+∠BAC=∠EAC+∠BAC,∴∠DAC=∠BAE,∴△ADC≌△ABE（SAS）．故选B．6.如图,在△ABC中,AB=AC,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD,则∠ECA的度数为（）A．30° B．35° C．40° D．45°【答案】C.【解析】在BC上截取BF=AB,连DF,则有△ABD≌△FBD（SAS）,∴DF=DA=DE,又∵∠ACB=∠ABC=40°,∠DFC=180°﹣∠A=80°,∴∠FDC=60°,∵∠EDC=∠ADB=180°﹣∠ABD﹣∠A=180°﹣20°﹣100°=60°,∴△DCE≌△DCF（SAS）,故∠ECA=∠DCB=40°．故选C．7.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=40°,则∠DEF的度数是（）A．75° B．70° C．65° D．60°【答案】B.【解析】∵AB=AC,∴∠B=∠C=12（180°﹣∠A）=70°,在△BDE和△CEF中,BD CEB CBE CF=⎧⎪∠=∠⎨⎪=⎩,∴△BDE≌△CEF（SAS）,∴∠BDE=∠CEF,∵∠CED=∠B+∠BDE,即∠CEF+∠DEF=∠B+∠BDE,∴∠DEF=∠B=70°；故选B．8.如图,AD∥BC,AD=CB,要使△ADF≌△CBE,需要添加的下列选项中的一个条件是（）A．AE=CF B．DF=BE C．∠A=∠C D．AE=EF 【答案】A.【解析】只有选项A正确,理由是：∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,∵AD∥BC,∴∠A=∠C,在△ADF和△CBE中,AD BCA CAF CE=⎧⎪∠=∠⎨⎪=⎩,∴△ADF≌△CBE（SAS）,故选A．二、填空题9.如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,AD=EC,AE=10,AC=6,则CD 的长为．【答案】2.【解析】∵AB∥EF,∴∠A=∠E,∵AD=EC,∴AD+DC=EC+DC,即AC=ED,在△ABC和△EFD中AB EFA EAC ED=⎧⎪∠=∠⎨⎪=⎩,∴△ABC≌△EFD（SAS）,∴AC=ED=6,∴CD=AC+ED﹣AE=6+6﹣10=2,10.如图,点F、C在线段BE上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还须补充一个条件．（只要填一个）【答案】AC=DF．【解析】补充AC=DF．∵∠1=∠2,BC=EF,AC=DF∴△ABC≌△DEF,11.如图,△ABC中,AB=AC,点D,E在BC边上,当时,△ABD≌△ACE．（添加一个适当的条件即可）【答案】BD=CE.【解析】BD=CE,理由是：∵AB=AC,∴∠B=∠C,在△ABD和△ACE中AB ACB CBD CE=⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△ACE（SAS）.12.如图,已知AC=AE,∠1=∠2,要使△ABC≌△ADE,还需添加的条件是（只需填一个）．【答案】AB=AD.【解析】AB=AD,理由是：∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,∴∠BAC=∠DAE,在△ABC和△ADE中,AB ADBAC DAEAC AE=⎧⎪∠=∠⎨⎪=⎩,∴△ABC≌△ADE（SAS）,13.如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D,下列结论：①∠EAB=∠FAC；②∠C=∠EFA；③AD=AC；④AF=AC．其中正确的结论是（填写所有正确结论的序号）．【答案】①②④.【解析】在△ABC与△AEF中,AB AEB EBC EF=⎧⎪∠=∠⎨⎪=⎩,∴△ABC≌△AEF（SAS）,∴∠EAB=∠FAC,∠C=∠EFA,AF=AC,∴①②④正确；由已知条件不能得出AD=AC,③不正确．三、解答题14.如图所示,CD=CA,∠1=∠2,EC=BC,求证：△ABC≌△DEC．【答案】证明见解析.【解析】∵∠1=∠2,∴∠ACB=∠DCE,在△ABC和△DE C中,CA CDACB DCEBC EC=⎧⎪∠=∠⎨⎪=⎩,∴△ABC≌△DEC（SAS）．15.如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E．求证：∠ADB=∠FCE．【答案】证明见解析.【解答】证明：∵BC=DE,∴BC+CD=DE+CD,即BD=CE,在△ABD与△FEC中,AB EFB EBD EC=⎧⎪∠=∠⎨⎪=⎩,∴△ABD≌△FEC（SAS）,∴∠ADB=∠FCE．16.已知：如图,在△ABC、△AD E中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E 三点在同一直线上,连接BD．求证：（1）△BAD≌△CAE；（2）试猜想BD、CE有何特殊位置关系,并证明．【答案】（1）证明见解析；（2）BD⊥CE．【解析】（1）∵∠BAC=∠DAE=90°∴∠BAC+∠CAD=∠DAE+CAD即∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△BAD≌△CAE（SAS）．（2）BD、CE特殊位置关系为BD⊥CE．证明如下：由（1）知△BAD≌△CAE∴∠ADB=∠E．∵∠DAE=90°,∴∠E+∠ADE=90°．∴∠ADB+∠ADE=90°．即∠BDE=90°．∴BD、CE特殊位置关系为BD⊥CE．。

全等三角形的判定方法50道经典题

全等三角形的判定方法50道经典题以下是全等三角形判定的50道经典题：1. 给定两个三角形的三边长，判断它们是否全等。

2. 给定两个三角形的一个角和两个侧边，判断它们是否全等。

3. 给定两个三角形的两个角和一个侧边，判断它们是否全等。

4. 给定两个三角形的一个角和两个高，判断它们是否全等。

5. 给定两个三角形的两个角和一个高，判断它们是否全等。

6. 给定两个三角形的两个角和一个中线，判断它们是否全等。

7. 给定两个三角形的一个角和两个角平分线，判断它们是否全等。

8. 给定两个三角形的两个角和一个外接圆半径，判断它们是否全等。

9. 给定两个三角形的一个角和一个内切圆半径，判断它们是否全等。

10. 给定两个三角形的一个角和一个内心到边的距离，判断它们是否全等。

11. 给定两个三角形的两个角和一个重心到边的距离，判断它们是否全等。

12. 给定两个三角形的两个角和一个垂心到边的距离，判断它们是否全等。

13. 给定两个三角形的一个角和一个外心到边的距离，判断它们是否全等。

14. 给定两个三角形的两个角和一个外心到边的距离，判断它们是否全等。

15. 给定两个三角形的两个角和一个垂足到边的距离，判断它们是否全等。

16. 给定两个三角形的两个角和一个内心到边的角平分线的距离，判断它们是否全等。

17. 给定两个三角形的一个角和一个外心到边的角平分线的距离，判断它们是否全等。

18. 给定两个三角形的两个角和一个内角平分线的夹角，判断它们是否全等。

19. 给定两个三角形的一个角和两个角平分线的夹角，判断它们是否全等。

20. 给定两个三角形的两个角和一个内心到边的角平分线的夹角，判断它们是否全等。

21. 给定两个三角形的两个角和一个内心到边的角平分线的夹角，判断它们是否全等。

22. 给定两个三角形的一个角和两个角平分线的夹角之和，判断它们是否全等。

23. 给定两个三角形的两个角和一个内心到边的角平分线的夹角之和，判断它们是否全等。

全等三角形判定测试题

全等三角形判定测试题一、选择题（每题3分，共15分）1. 以下哪组条件不能判定两个三角形全等？A. 边角边（SAS）B. 角边角（ASA）A. 角角边（AAS）D. 边边角（SSA）2. 如果两个三角形的对应边长分别为5、6和7，且对应角分别为30°、60°和90°，这两个三角形是否全等？A. 是B. 不是3. 三角形ABC与三角形DEF全等，且AB = DE，AC = DF，那么下列哪个条件是多余的？A. ∠A = ∠DB. ∠B = ∠EC. ∠C = ∠FD. 所有条件都是必要的4. 两个三角形的对应角相等，且有一组对应边相等，但另一组对应边不相等，这两个三角形：A. 一定全等B. 可能全等C. 不全等5. 如果两个三角形的对应角都相等，但没有任何一组对应边相等，这两个三角形：A. 一定全等B. 可能全等C. 不全等二、填空题（每题2分，共10分）6. 根据______判定，如果两个三角形的三边对应相等，那么这两个三角形全等。

7. 当两个三角形的对应角都相等时，我们可以使用______判定来确定这两个三角形是否全等。

8. 如果两个三角形的两边和夹角对应相等，我们可以使用______判定来确定这两个三角形是否全等。

9. 当两个三角形的两角和非夹边对应相等时，我们可以使用______判定来确定这两个三角形是否全等。

10. SSA判定条件通常不适用于______三角形。

三、简答题（每题5分，共20分）11. 解释为什么SSA判定条件不能证明两个三角形全等。

12. 给出一个例子，说明即使两个三角形的三边对应相等，但它们可能不是全等三角形。

13. 描述在实际问题中如何使用AAS判定来证明两个三角形全等。

14. 讨论在哪些情况下，SAS判定比ASA判定更适用。

四、计算题（每题10分，共20分）15. 已知三角形ABC和三角形DEF，其中AB = 10，AC = 8，∠BAC = 50°，DE = 10，DF = 8，∠EDF = 50°。

全等三角形的判定精选练习题(分SSS、SAS、AAS、ASA、HL分专题)

D CB A 全等三角形的判定（一）（SSS ）1、如图1，AB=AD ，CB=CD ，∠B=30°，∠BAD=46°，则∠ACD 的度数是( )A.120°B.125°C.127°D.104°2、如图2，线段AD 与BC 交于点O ，且AC=BD ，AD=BC ，•则下面的结论中不正确的是( ) A.△ABC ≌△BAD B.∠CAB=∠DBA C.OB=OC D.∠C=∠D3、在△ABC 和△A 1B 1C 1中，已知AB=A 1B 1，BC=B 1C 1，则补充条件____________，可得到△ABC ≌△A 1B 1C 1．4、如图3，AB=CD ，BF=DE ，E 、F 是AC 上两点，且AE=CF ．欲证∠B=∠D ，可先运用等式的性质证明AF=________，再用“SSS ”证明______≌_______得到结论．5、如图，已知AB=CD ，AC=BD ，求证：∠A=∠D ．6、如图，AC 与BD 交于点O ，AD=CB ，E 、F 是BD 上两点，且AE=CF ，DE=BF.请推导下列结论：⑴∠D=∠B ；⑵AE ∥CF ．7、已知如图，A 、E 、F 、C 四点共线，BF=DE ，AB=CD.⑴请你添加一个条件，使△DEC ≌△BFA ； ⑵在⑴的基础上，求证：DE ∥BF.全等三角形的判定(SAS)1、如图1，AB ∥CD ，AB=CD ，BE=DF ，则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2，AB=AC ，AD=AE ，欲证△ABD ≌△ACE ，可补充条件( ) A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD3、如图3，AD=BC ，要得到△ABD 和△CDB 全等，可以添加的条件是( ) A.AB ∥CD B.AD ∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4，AB 与CD 交于点O ，OA=OC ，OD=OB ，∠AOD=________，•根据_________可得到△AOD ≌△COB ，从而可以得到AD=_________．5、如图5，已知△ABC 中，AB=AC ，AD 平分∠BAC ，请补充完整过程说明△ABD ≌△ACD 的理由． ∵AD 平分∠BAC ， ∴∠________=∠_________(角平分线的定义). 在△ABD 和△ACD 中，∵____________________________， ∴△ABD ≌△ACD （） 6、如图6，已知AB=AD ，AC=AE ，∠1=∠2，求证∠ADE=∠B.7、如图，已知AB=AD ，若AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？8、如图，在△ABC 和△DEF 中，B 、E 、F 、C ，在同一直线上，下面有4个条件，请你在其中选3个作为题设，余下的一个作为结论，写一个真命题，并加以证明. ①AB=DE ；②AC=DF ；③∠ABC=∠DEF ；④BE=CF.9、如图⑴，AB ⊥BD ，DE ⊥BD ，点C 是BD 上一点，且BC=DE ，CD=AB ．⑴试判断AC 与CE 的位置关系，并说明理由．⑵如图⑵，若把△CDE 沿直线BD 向左平移，使△CDE 的顶点C 与B 重合，此时第⑴问中AC 与BE 的位置关系还成立吗？(注意字母的变化)全等三角形（三）AAS 和ASA【知识要点】1．角边角定理（ASA ）：有两角及其夹边对应相等的两个三角形全等.2．角角边定理（AAS ）：有两角和其中一角的对边对应相等的两个三角形全等. 【典型例题】例1．如图，AB ∥CD ，AE=CF ，求证：AB=CD例2．如图，已知：AD=AE ，ABE ACD ∠=∠，求证：BD=CE.例3．如图，已知：ABD BAC D C ∠=∠∠=∠.，求证：例4．如图已知：AB=CD ，AD=BC ，O 是BD 中点，过O AE=CF.例5．如图，已知321∠=∠=∠，AB=AD.求证：BC=DE.例6．如图，已知四边形ABCD 中，AB=DC ，AD=BC ，点F 在AD 交于O ，请问O 点有何特征？【经典练习】 1.△ABC 和△C B A '''中，C B C B A A ''='∠=∠,'，C C '∠=∠2．如图，点C ，F 在BE 上，,,21EF BC =∠=∠3．在△ABC 和△C B A ''' ） ①A A '∠=∠B B '∠=∠，BC =C A C A ''='③A A '∠=∠B B '∠=∠，AC =C A B A ''=' A ． 1个B. 2个C. 3个D. 4个4．如图，已知MB=ND ，NDC MBA ∠=∠，下列条件不能判定是△ABM ≌△CDN 的是（）A ． N M ∠=∠ B. AB=CD C ． AM=CN D. AM ∥CN 5．如图2所示， ∠E =∠F =90°，∠B =∠C ，AE =AF ，给出下列结论：①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是__________________。

全等三角形判定基础练习(有答案)

全等三角形判定基础练习（有答案）一．选择题（共3小题）1．如图，已知AD=AE，添加下列条件仍无法证明△ABE≌△ACD的是（）A．AB=AC B．∠ADC=∠AEB C．∠B=∠C D．BE=CD2．判定两个三角形全等，给出如下四组条件：①两边和一角对应相等；②两角和一边对应相等；③两个直角三角形中斜边和一条直角边对应相等；④三个角对应相等；其中能判定这两个三角形全等的条件是（）A．①和②B．①和④C．②和③D．③和④3．如图，下列各组条件中，不能得到△ABC≌△BAD的是（）A．BC=AD，∠ABC=∠BAD B．BC=AD，AC=BDC．AC=BD，∠CAB=∠DBA D．BC=AD，∠CAB=∠DBA二．解答题（共6小题）4．如图，AB=CB，BE=BF，∠1=∠2，证明：△ABE≌△CBF．5．如图所示，有两个直角三角形△ABC和△QPA按如图位置摆放C，P，A在同一条直线上，并且BC=PA．当QP与AB垂直时，△ABC能和△QPA全等吗，请说明理由．6．如图，BE⊥AC于E，CF⊥AB于F，CF、BE相交于点D，且BD=CD．求证：AD平分∠BAC．7．如图，在直角三角形ABC中，∠ABC=90°，点D在BC的延长线上，且BD=AB，过B作BE⊥AC，与BD的垂线DE交于点E．求证：△ABC≌△BDE．8．如图，在△ABC中，AB=AC，点D、E在BC上，且BD=CE．求证：△ABE≌△ACD．9．如图，已知点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C．求证：△ABE≌△ACD．全等三角形判定（孙雨欣）初中数学组卷参考答案与试题解析一．选择题（共3小题）1．如图，已知AD=AE，添加下列条件仍无法证明△ABE≌△ACD的是（）A．AB=AC B．∠ADC=∠AEB C．∠B=∠C D．BE=CD【分析】全等三角形的判定定理有SAS，ASA，AAS，SSS，看看条件是否符合判定定理即可．【解答】解：A、∵在△ABE和△ACD中，，∴△ABE≌△ACD（SAS），正确，故本选项错误；B、∵在△ABE和△ACD中，，∴△ABE≌△ACD（ASA），正确，故本选项错误；C、∵在△ABE和△ACD中，，∴△ABE≌△ACD（AAS），正确，故本选项错误；D、根据AE=AD，BE=CD和∠A=∠A不能推出△ABE和△ACD全等，错误，故本选项正确；故选D．【点评】本题考查了对全等三角形的判定定理的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．2．判定两个三角形全等，给出如下四组条件：①两边和一角对应相等；②两角和一边对应相等；③两个直角三角形中斜边和一条直角边对应相等；④三个角对应相等；其中能判定这两个三角形全等的条件是（）A．①和②B．①和④C．②和③D．③和④【分析】认真分析各选项提供的已知条件，结合全等三角形判定方法对选项提供的已知条件逐一判断．【解答】解：①两边和一角对应相等不正确，应该是两边的夹角，故本选项错误，②两角和一边对应相等，符合AAS，故本选项正确，③两个直角三角形中斜边和一条直角边对应相等，符合SAS，故本选项正确，④三个角对应相等，可以相似不全等，故本选项错误，故选C．【点评】本题主要考查了对全等三角形的判定方法的理解及运用．常用的判定方法有AAS，SSS，SAS 等，难度适中．3．如图，下列各组条件中，不能得到△ABC≌△BAD的是（）A．BC=AD，∠ABC=∠BAD B．BC=AD，AC=BDC．AC=BD，∠CAB=∠DBA D．BC=AD，∠CAB=∠DBA【分析】根据图形可得公共边AB=AB，再加上选项所给条件，利用判定定理SSS、SAS、ASA、AAS分别进行分析即可．【解答】解：根据图形可得公共边：AB=AB，A、BC=AD，∠ABC=∠BAD可利用SAS证明△ABC≌△BAD，故此选项不合题意；B、BC=AD，AC=BD可利用SSS证明△ABC≌△BAD，故此选项不合题意；C、AC=BD，∠CAB=∠DBA可利用SAS证明△ABC≌△BAD，故此选项不合题意；D、BC=AD，∠CAB=∠DBA不能证明△ABC≌△BAD，故此选项符合题意；故选：D．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．二．解答题（共7小题）4．如图，AB=CB，BE=BF，∠1=∠2，证明：△ABE≌△CBF．【分析】利用∠1=∠2，即可得出∠ABE=∠CBF，再利用全等三角形的判定SAS得出即可．【解答】证明：∵∠1=∠2，∴∠1+∠FBE=∠2+∠FBE，即∠ABE=∠CBF，在△ABE与△CBF中，，∴△ABE≌△CBF（SAS）．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．5．如图所示，有两个直角三角形△ABC和△QPA按如图位置摆放C，P，A在同一条直线上，并且BC=PA．当QP与AB垂直时，△ABC能和△QPA全等吗，请说明理由．【分析】首先根据∠QAP=90°，AB⊥PQ可证出∠PQA=∠BAC，在加上条件BC=AP，∠C=∠QAP=90°，可利用AAS定理证明△ABC和△QPA全等．【解答】△ABC能和△QPA全等；证明：∵∠QAP=90°，∴∠PQA+∠QPA=90°，∵QP⊥AB，∴∠BAC+∠APQ=90°，∴∠PQA=∠BAC，在△ABC和△QPA中，，∴△ABC≌△QPA（AAS）．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．6．如图，BE⊥AC于E，CF⊥AB于F，CF、BE相交于点D，且BD=CD．求证：AD平分∠BAC．【分析】要证AD平分∠BAC，只需证DF=DE．可通过证△BDF≌△CDE（AAS）来实现．根据已知条件，利用AAS可直接证明△BDF≌△CDE，从而可得出AD平分∠BAC．【解答】证明：∵BE⊥AC，CF⊥AB，∴∠BFD=∠CED=90°．在△BDF与△CDE中，，∴Rt△BDF≌Rt△CDE（AAS）．∴DF=DE，∴AD是∠BAC的平分线．【点评】本题考查了全等三角形的判定和性质，以及到角两边距离相等的点在角平分线上等知识．发现并利用△BDF≌△CDE是正确解答本题的关键．7．如图AB，CD相交于点O，AD=CB，AB⊥DA，CD⊥CB，求证：△ABD≌△CDB．【分析】首先根据AB⊥DA，CD⊥CB，可得∠A=∠C=90°，再利用HL定理证明Rt△ABD≌Rt△CBD即可．【解答】证明：∵AB⊥DA，CD⊥CB，∴∠A=∠C=90°，在Rt△ABD和Rt△CBD中，∴Rt△ABD≌Rt△CBD（HL）．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．8．如图，在△ABC中，AB=AC，点D、E在BC上，且BD=CE．求证：△ABE≌△ACD．【分析】由AB=AC可得∠B=∠C，然后根据BD=CE可证BE=CD，根据SAS即可判定三角形的全等．【解答】证明∵AB=AC，∴∠B=∠C，∵BD=EC，∴BE=CD，在△ABE与△ACD中，，∴△ABE≌△ACD（SAS）．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．9．如图，已知点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C．求证：△ABE≌△ACD．【分析】根据全等三角形的判定定理ASA推出即可．【解答】证明：∵在△ABE和△ACD中，∴△ABE≌△ACD（ASA）．【点评】本题考查了全等三角形的判定定理的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．10．如图，在直角三角形ABC中，∠ABC=90°，点D在BC的延长线上，且BD=AB，过B作BE⊥AC，与BD的垂线DE交于点E．求证：△ABC≌△BDE．【分析】利用已知得出∠A=∠DBE，进而利用ASA得出△ABC≌△BDE即可．【解答】证明：在Rt△ABC中，∵∠ABC=90°，∴∠ABE+∠DBE=90°，∵BE⊥AC，∴∠ABE+∠A=90°，∴∠A=∠DBE，∵DE是BD的垂线，∴∠D=90°，在△ABC和△BDE中，∵，∴△ABC≌△BDE（ASA）．【点评】此题主要考查了全等三角形的判定，三角形内角和定理的应用，正确发现图形中等量关系∠A=∠DBE是解题关键．。

全等三角形性质与判定练习50道含详细答案

第1页（共52页）那么下列结论错误的是AC =CA5.如图，已知• 1 =/2 ,全等三角形性质与判定练习50道.选择题（共24小题） 1.下列判断正确的个数是（）全等三角形对应边相等.C. 3个2.如图，AB^ . CDA ，并且 AB =CD ,D . AC = BC那么添加以下哪一个条件仍不能判断 .'ABC =「ADC 的是（）(1) 能够完全重合的两个图形全等; (2) 两边和一角对应相等的两个三角形全等; (3)两角和一边对应相等的两个三角形全等; 3EA . AE 二 AC 3.已知：如图，AB =AD , .1-/2，以下条件中，不能推出. ABC 三ADE 的是（）C. BC 二 DE4.如图，已知点A 、D 、C 、F 在同一条直线上， AB 二 DE , BC =EF,要使.：ABC = . ：DEF ,A .B = E 还需要添加一个条件是 B. BC//EFC.三 BCA Z FD. A= EDF2第2页（共52页）A •三角形的稳定性B .两点之间线段最短D •垂线段最短，下列所给条件不能证明 AABC 三UDCB 的是（B. AB 二 DCC.三ACB ZDBCD. AC =BD7.如图，一扇窗户打开后，用窗钩AB 可将其固定，这里所运用的几何原理是（）9•下列几种说法： ①全等三角形的对应边相等； ②面积相等的两个三角形全等；③周长相等的两个三角形全等； ④全等的两个三角形一定重合.其中正确的是（）A .①②B .②③C.③④D .①④10.如图，AD 是「ABC 的中线，E , F 分别是AD 和AD 延长线上的点，且 DE 二DF ,连接BF , CE 、下列说法： ①CE =BF ;②^ABD 和■ ACD 面积相等； ③BF //CE ;④BD^ CDE .其中正确的有（）A . BC =DC 6.如图, B. . BAC 二.DACF 、C 四点在同一条直线上,.：ABC 三.：DEF 的是（一个条件不能判断 DF //ACC. E B Z D EB =CF ，厶DEFC. AC =DFD. AB = AD-/ABC ，添加以下哪D. AB 二 DEC .两点确定一条直线A . Z AZ DA . 1个B . 2个 C. 3个 D . 4个11.如图，已知.1 =/2，要说明：AB^ . ACD，还需从下列条件中选一个，错误的选法是（）A . . ADB =/ADC B. . B =/C C. DB =DC D. AB =AC 12•下列条件能判断两个三角形全等的是（）①三边对应相等；②两边及其夹角对应相等；③两角及其夹边对应相等；④两角及其一角的对边对应相等.A .①②B .①②③ C.①②④ D .①②③④13 .如图，点E、F在AC上，AE=CF, • A=/C，添加下列条件后仍不能使第3页（共52页）2第4页（共52页）C. AD 二 CB D . . AFD - CEB添加一以下错误的是（）C . AC 二BD D. CB = DA15 .如图，已知AB =AD , - BAD =/CAE，则增加以下哪个条件仍不能判断= BAC =.：DAE的是（）)A . DF =BEA . /CBA - . DAB B . CB. BE =CFC. AC//DF17•王师傅用4根木条钉成一个四边形木架,如图，要使这个木架不变形，他至少还要再钉C. 2根18.如图，工人师傅砌门时，常用木条EF 固定长方形门框 ABCD ，使其不变形，这样做的A.两点之间，线段最短 C .三角形三个内角和等于 180 19•如图，使 AB^ ：ADC 成立的条件是B.直角三角形的两个锐A . AB =AD ，乙B Z D C. BC =DC , ■ BAC = DACA . AC =AE B. BC =DE C. .B =/D D. .C =/E16•如图，在「ABC 和 DEF 中，已知.B= DEF , AB 二ED ，加上该条件后仍无法证明B. AB 二 AD , - ACB 二.ACD. ABC 三. DEF 的是（） A DB EC FA . AC =DF(根据是（）D . AB = AD，/ BAC =^DAC第4页(共52页)第7页（共52页）C • Z A Z DD • ■ ABD DCA 20•如图所示，已知 AB//CD , AD//BC ，那么图中共有全等三角形（）A • 8对B • 4对 C. 2对D • 1对21 •两组邻边分别相等的四边形叫做 “筝形”，如图，四边形ABCD 是一个筝形，其中AD =CD ,AB =CB ，在探究筝形的性质时，得到如下结论：①：AB^ . ：CBD ；②AC _ BD ；③1四边形ABCD 的面积=-ACJBD ，其中正确的结论有（）A • 0个B • 1个 C. 2个 D • 3个22•如图，点A 、D 在线段BC 的同侧，连接AB 、AC 、DB 、DC ,已知.ABC =. DCB ,老师要求同学们补充一个条件使.\ABC =ADCB •以下是四个同学补充的条件，其中错误23 •下列语句：① 形状相同的三角形是全等三角形； ② 任意两边对应相等的两个直角三角形全等; ③ 两个等边三角形一定全等；④ 有两角一边对应相等的两个三角形全等其中错误的说法个数有（）A • AC = DB B • AB = DC个，不添加辅助线）第6页（共52页）A • 4个B • 3个24 •下面说法正确的是（）A •有两边和一角对应相等的两个三角形全等B .有两角和它们的夹边对应相等的两个三角形全等C •两个等边三角形一定全等D •两个等腰直角三角形一定全等二.填空题（共9小题）25.如图，在3 3的正方形网格中，贝U . 2 • . 3 • . 4 • . 5等于 ____________26•如图，把厶ABC的中线CD延长到E，使DE二CD，连接AE，若AC =4且.汨CD的周长比.：ACD的周长大1,则AE二 .27.如图，已知/DCE /A =90 , BE _ AC 于B，且DC 二EC , BE = 8cm，则AD AB =cm.28.如图，已知AB =AC , AD =AE , ■ BAC = DAE =50 , B、D、E 在同一直线上,则.BEC的度数为29.如图，AB//DE , BF二EC .要使AC二DF，还需添加一个条件：________________________ （只需要写第9页（共52页）个，不添加辅助线）第6页（共52页）（不添加30.在ABC中，D是BC的中点，E，F分别是线段AD及其延长线上的点，连接CE , BF .要使得：BD^ CDE，只需添加一个条件:辅助线）E是AC上的一点，BE交AD于F，已知AC = BF，=40 ，则/ C =的角平分线，G是BC中点，FG//AD，交AB于E，交CA的延ENDAC =35 0,厶EBC______ .（将你认为正确的结论的序号都填上）32 .如图，AD是ABC①—2 :② BE =CF ；③. ACN = ：ABM ;④ CD = DN .其中正确的结论是三•解答题（共16小题）34.如图，已知「ABC中，AB二AC =10cm , BC =8cm，点D为AB的中点.如果点P在线段BC上以3cm /s的速度由点B向C点运动，同时，点 Q在线段CA上由点C向A点运动.（1）若点Q的运动速度与点P的运动速度相等，经过 1秒后，BPD与CQP是否全等，请说明理由. （2）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使BPD与CQP全等?35.填空：把下面的推理过程补充完整，并在括号内注明理由，如图，已知 ABC中，E、F分别是AB、AC上的两点，且EF //BC , D为EF 上一点，且 BD=CD，ED =FD，请说明 BE =CF .解：：BD =CD （已知）. DBC "DCB（ ___________ ）:EF//BC （已知）.EDB = DBCFDC = ____ （ ____ ）EDB - FDC （等量代换）在EBD和FCD中，ED =FDEDB "FDCBD =CD..■: EBD = ：FCD( ______ ).BE 二CF( _______ )36.如图，BA=BE , Z A Z E，三ABE Z CBD , ED交BC 于点F，且乙FBD Z D . 求证：AC / / BD . 证明：：.ABE =. CBD (已知)..ABE . EBC CBD . EBC( ______________________ )即.ABC =/EBD在.ABC 和.：EBD 中，:ZABC=ZEBD：ZA=ZE..：ABC 二.：EBD( ______ ).■ C =/D( _________ )FBD = D■ - C二_ (等量代换).AC / /BD ( ________ )37.如图，已知：点B、E、F、C在同一直线上，• A - D，BE = CF，且AB//CD .求证：AF //ED证明：：BE=FCBE EF -FC EF(______________ )即： ____ :AB//CD=BC ,延长AB 至点D ，使DB WB ,连接CD ,CDE ，其中 ZDCE =90，连接 BE •在：ABF 和 DCE 中，有BF =CE.：ABF 三：DCE( ) ..AFB =/DEC( )(1) 求证：. ：ACD 二. ：BCE ; (2) 若 AB =3cm ，贝U BE = ________ cm .(3) BE 与AD 有何位置关系？请说明理由.E39.如图，点 B , D 在线段 AE 上, BC //EF , AD = BE , BC 二 EF ，将说明• C =/F ,AC //DF 的过程填写完整.因为AD =B E ,所以 AD DB 二 DB BE ，即 AB 二 DE .因为 BC //EF ,所以• ABC( ____ ).又因为BC =EF .所以.ABC = ：DEF( _________ )..AF//ED( )以CD 为，求.B 的度数. ，AD是中线，BE _ EC 且BE 二AD ，连接DE 、CE .若所以.C =/F , . _____________ =. FDE ( _______ ).所以 AC//DF( ).40.如图，AC 二BC , CAB =/CBA = 45 , D 为边 AB 上一动点，CD 二 CE , CDE = CED =45 .(1) 说明厶ACD 三厶BCE ;41•如图，在 SBC 中，D 为边BC 上一点，且 AD =AC , E 为■ ：ABC 外一点，连接 AE ,43.如图 CD _ AB 于 D ， BE _ AC 于 E ，OD =0E ，求证：OB =0C证明：TCD _ AB ， BE _ AC=36 AC =5，BE = .5，求 CE 的长."DB = ____________ =90 ( ________ )丁在BOD和COE中r_____________ (已证)J OD=OE (已知)[Z EOD=Z COE (..：BOD 三.COE( _________ )44.已知：ZACB =90 , AC 二BC , AD _CM , BE _ CM,垂足分别为D , E,①线段CD和BE的数量关系是：CD =BE ;②请写出线段AD , BE , DE之间的数量关系并证明.解：①结论：CD -BE .理由：T AD _CM , BE _CM ,-Z ACB Z BEC Z ADC =90 ,，•必ACD +N BCE =90 °，厶BCE +N CBE =90 :Z ACD = _________在.ACD 和.CBE 中，( ______________ )二也ACD M&BE , ( ___________ ).CD 二BE .②结论：AD =BE DE .理由：.IACD 三ACBE ,："CE =CD DE =BE DE ,.AD = BE DE .（2）如图2,上述结论②还成立吗？如果不成立，请写出线段AD , BE , DE之间的数量关系•并说明理由.45•填空：把下面的推理过程补充完整，并在括号内注明理由.已知：如图，.SBC中，D、E分别为AB、AC的中点，过点C作CF//AB交DE的延长线于F，求证：AB =2CF . 证明：；CF //AB （已知）.■ ADE =. F（ _________ ）:E为AC的中点（已知）.AE =CE （中点的定义）在ADE与■CFE中ZADE Z F , _____________ = _______, AE =CD..：ADE 二.CFE（_________ ）.AD =CF （ ________）:D为AB的中点.AB =2AD （中点的定义）.AB =2CF （等量代换）46 .如图，4=2，乙3 = . 4 .求证:(1) ABC LADC ;BC(2) BE =DE .47•如图，已知， BD 与CE 相交于点0 , AD =AE , . B =/C ，请解答下列问题:（1） ABD 与.：ACE 全等吗？为什么？（2） B0与CO 相等吗？为什么？48•把下列第（1 ）和（2）问题中的解题过程补充完成，并解答第（ 3）中问题.（1）如图1, A 、B 、C 三点在同一条直线上， Z A ZDBE E C =90 , BE =DB .求证:ABE =.CDB证明：；A 、B 、C 三点在同一条直线上ZDBE =90■ . 2 =180 -90 =90 （平角等于 180 ）在ABE 中.A =90-Z E J =90 （ __________ ）又 T • 1 • . 2 =90 （已证）.■ E -■ 2（ _______ ）在「ABE 和「CDB 中W A —CE 二2BE=DB.ABE 二 CDB( __________ )（2）如图2, A、B、C三点在同一条直线上，.A=/DBE二/C =60 , BE = DB .求证:. ABE 三. CDB （3 分）证明：：A、B、C三点在同一条直线上，.DBE =60..2 =180 _60「/1=120'-/1 （平角等于 180 ）在ABE中T . A =60二N E=______ 匕三角形内角和为180》.E^（等量代换）在ABE和.CDB中W A =/C.E 二/2BE 二DB..：ABE 三.CDB（ ______ ）（3）如图3，A、B、C三点在同一条直线上，Z A ZDBE Z C，BE = DB .判断ABE(1)与CDB全等吗？为什么？49.已知：如图，AB、CD相交于点O , AC//DB , AO二BO , E、F分别是OC、OD中点.（1）求证：DF 二 CE ；（2）若DB—BE，垂足为B , BD=6 , BE =8，求四边形AFBE的面积.第21页（共52页）。

全等三角形的判定提高练习题

1．如图，AB=AC，AD=AE，AB，DC相交于点M，AC，BE相交于点N，∠DAB=∠EAC．求证：∠ADM∠∠AEN．
2．如图，AB∠DE，AC∠DF，BE=CF．求证：∠ABC∠∠DEF．
3．如图，己知∠1=∠2，∠ABC=∠DCB，那么∠ABC与∠DCB全等吗？为什么？
4．如图，B，F，E，D在一条直线上，AB=CD，∠B=∠D，BF=DE．试证明：
∠AFE∠∠CEF．
5．如图：在∠ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．
（1）求证：∠ABD∠∠GCA；
（2）请你确定∠ADG的形状，并证明你的结论．
6．如图，点E在∠ABC外部，点D在BC边上，DE交AC于点F，若∠1=∠2=∠3，AC=AE．试说明下列结论正确的理由：
（1）∠C=∠E；
（2）∠ABC∠∠ADE
7．如图所示，在∠MNP中，H是高MQ与NE的交点，且QN=QM，猜想PM与HN有什么关系？试说明理由．
8．如图，在∠ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE∠GF，交AB于点E，连接EG．
（1）求证：BG=CF；
（2）请你判断BE+CF与EF的大小关系，并证明你的结论．。

全等三角形的判定精选练习题(分专题)

全等三角形的判定(SSS)针对性训练题1、如图1，AB=AD，CB=CD，∠B=30°，∠BAD=46°，则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2，线段AD与BC交于点O，且AC=BD，AD=BC，•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中，已知AB=A1B1，BC=B1C1，则补充条件____________，可得到△ABC≌△A1B1C1．4、如图3，AB=CD，BF=DE，E、F是AC上两点，且AE=CF．欲证∠B=∠D，可先运用等式的性质证明AF=________，再用“SSS”证明______≌_______得到结论．5、如图，AB=AC，BD=CD，求证：∠1=∠2．6、如图，已知AB=CD，AC=BD，求证：∠A=∠D．7、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．8、已知如图，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的基础上，求证：DE∥BF.全等三角形的判定(SAS)针对性训练题1、如图1，AB∥CD，AB=CD，BE=DF，则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2，AB=AC，AD=AE，欲证△ABD≌△ACE，可补充条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD3、如图3，AD=BC，要得到△ABD和△CDB全等，可以添加的条件是( )A.AB∥CDB.AD∥BCC.∠A=∠CD.∠ABC=∠CDA4、如图4，AB与CD交于点O，OA=OC，OD=OB，∠AOD=________，•根据_________可得到△AOD≌△COB，从而可以得到AD=_________．5、如图5，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程说明△ABD≌△ACD的理由．∵AD平分∠BAC，∴∠________=∠_________(角平分线的定义).在△ABD和△ACD中，∵____________________________，∴△ABD≌△ACD（）DC BA 6、如图6，已知AB=AD ，AC=AE ，∠1=∠2，求证∠ADE=∠B.7、如图，已知AB=AD ，若AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？8、如图，在△ABC 和△DEF 中，B 、E 、F 、C ，在同一直线上，下面有4个条件，请你在其中选3个作为题设，余下的一个作为结论，写一个真命题，并加以证明.①AB=DE ； ②AC=DF ； ③∠ABC=∠DEF ； ④BE=CF.9、如图⑴，AB ⊥BD ，DE ⊥BD ，点C 是BD 上一点，且BC=DE ，CD=AB ．⑴试判断AC 与CE 的位置关系，并说明理由． ⑵如图⑵，若把△CDE 沿直线BD 向左平移，使△CDE 的顶点C 与B 重合，此时第⑴问中AC 与BE 的位置关系还成立吗？(注意字母的变化)全等三角形的判定(AAS)和(ASA)针对性训练题【典型例题】例1．如图，AB ∥CD ，AE=CF ，求证：AB=CD例2．如图，已知：AD=AE ，ABE ACD ∠=∠，求证：BD=CE.例3．如图，已知：ABD BAC D C ∠=∠∠=∠.，求证：OC=OD.例4．如图已知：AB=CD ，AD=BC ，O 是BD 中点，过O 点的直线分别交DA和BC 的延长线于E ，F.求证：AE=CF. 例5．如图，已知321∠=∠=∠，AB=AD.求证：BC=DE.例6．如图，已知四边形ABCD 中，AB=DC ，AD=BC ，点F 在AD 上，点E 在BC 上，AF=CE ，EF 的对角线BD 交于O ，请问O 点有何特征？AEABDC EO12 3 AFDOBECABCDO【经典练习】1.△ABC 和△C B A '''中，C B C B A A ''='∠=∠,'，C C '∠=∠则△ABC 与△C B A ''' .2．如图，点C ，F 在BE 上，,,21EF BC =∠=∠请补充一个条件，使△ABC ≌DFE,补充的条件是 .3．在△ABC 和△C B A '''中，下列条件能判断△ABC 和△C B A '''全等的个数有（） ①A A '∠=∠ B B '∠=∠，C B BC ''= ②A A '∠=∠，B B '∠=∠，C A C A ''=' ③A A '∠=∠ B B '∠=∠，C B AC ''= ④A A '∠=∠，B B '∠=∠，C A B A ''='A ． 1个B. 2个C. 3个D. 4个4．如图，已知MB=ND ，NDC MBA ∠=∠，下列条件不能判定是△ABM ≌△CDN 的是（）A ．N M ∠=∠ B. AB=CDC ． AM=CND. AM ∥CN5．如图所示， ∠E =∠F =90°，∠B =∠C ，AE =AF ，给出下列结论①∠1=∠2 ②BE=CF ③△ACN ≌△ABM④CD=DN ，其中正确的结论是_________。

全等三角形的判定方法50道经典题

全等三角形的判定方法50道经典题全等三角形的判定方法是初中数学中重要的一部分，主要包括以下50道经典题目。

1. 如何通过边长判断两个三角形是否全等？答：如果两个三角形的三条边对应相等，则它们全等。

2. 如果通过角度判断两个三角形是否全等？答：如果两个三角形的三个角度对应相等，则它们全等。

3. 如何通过边角判断两个三角形是否全等？答：如果两个三角形中有一个角相等，并且两边对应相等，则它们全等。

4. 如果两个三角形的底边相等，底边上的高相等，判断它们是否全等。

答：根据边角对应的原理，如果底边和高都相等，则这两个三角形全等。

5. 给定两个相等的边和它们之间的夹角，判断它们所在的两个三角形是否全等。

答：根据边角对应的原理，如果两个相等的边和它们之间的夹角都相等，则这两个三角形全等。

6. 如果两个三角形的一个角相等，并且这个角的两边分别等于另一个三角形的两个角的两边，判断它们是否全等。

答：根据边角边的原理，如果两个三角形的一个角相等，并且这个角的两边分别等于另一个三角形的两个角的两边，则这两个三角形全等。

7. 如何通过勾股定理判断两个三角形是否全等？答：如果两个三角形的两条边的平方和相等，则它们全等。

8. 如果两个三角形的一个角相等，并且两边的比例相等，判断它们是否全等。

答：根据角边角的原理，如果两个三角形的一个角相等，并且两边的比例相等，则这两个三角形全等。

9. 如果两个三角形的两个角相等，并且两边的比例相等，判断它们是否全等。

答：根据角角边的原理，如果两个三角形的两个角相等，并且两边的比例相等，则这两个三角形全等。

10. 给定两个相等的边和它们夹角的正弦值，判断它们所在的两个三角形是否全等。

答：根据正弦定理，如果两个相等的边和它们夹角的正弦值都相等，则这两个三角形全等。

11. 给定两个相等的边和它们夹角的余弦值，判断它们所在的两个三角形是否全等。

答：根据余弦定理，如果两个相等的边和它们夹角的余弦值都相等，则这两个三角形全等。

全等三角形的判定精选练习题(分SSS、SAS、AAS、ASA、HL分专题)

全等三角形的判定（SSS）1、如图1，AB=AD，CB=CD，∠B=30°，∠BAD=46°，则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2，线段AD与BC交于点O，且AC=BD，AD=BC，•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中，已知AB=A1B1，BC=B1C1，则补充条件____________，可得到△ABC≌△A1B1C1．4、如图3，AB=CD，BF=DE，E、F是AC上两点，且AE=CF．欲证∠B=∠D，可先运用等式的性质证明AF=________，再用“SSS”证明______≌_______得到结论．5、如图，已知AB=CD，AC=BD，求证：∠A=∠D．6、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．7、已知如图，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的基础上，求证：DE∥BF.全等三角形的判定(SAS)1、如图1，AB∥CD，AB=CD，BE=DF，则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2，AB=AC，AD=AE，欲证△ABD≌△ACE，可补充条件( )D CBA A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD3、如图3，AD=BC ，要得到△ABD 和△CDB 全等，可以添加的条件是( ) A.AB ∥CD B.AD ∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4，AB 与CD 交于点O ，OA=OC ，OD=OB ，∠AOD=________，•根据_________可得到△AOD ≌△COB ，从而可以得到AD=_________．5、如图5，已知△ABC 中，AB=AC ，AD 平分∠BAC ，请补充完整过程说明△ABD ≌△ACD 的理由． ∵AD 平分∠BAC ， ∴∠________=∠_________(角平分线的定义). 在△ABD 和△ACD 中，∵____________________________， ∴△ABD ≌△ACD （） 6、如图6，已知AB=AD ，AC=AE ，∠1=∠2，求证∠ADE=∠B.7、如图，已知AB=AD ，若AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？8、如图，在△ABC 和△DEF 中，B 、E 、F 、C ，在同一直线上，下面有4个条件，请你在其中选3个作为题设，余下的一个作为结论，写一个真命题，并加以证明. ①AB=DE ； ②AC=DF ； ③∠ABC=∠DEF ； ④BE=CF.9、如图⑴，AB ⊥BD ，DE ⊥BD ，点C 是BD 上一点，且BC=DE ，CD=AB ．⑴试判断AC 与CE 的位置关系，并说明理由．⑵如图⑵，若把△CDE 沿直线BD 向左平移，使△CDE 的顶点C 与B 重合，此时第⑴问中AC 与BE 的位置关系还成立吗？(注意字母的变化)全等三角形（三）AAS 和ASA【知识要点】1．角边角定理（ASA ）：有两角及其夹边对应相等的两个三角形全等.2．角角边定理（AAS ）：有两角和其中一角的对边对应相等的两个三角形全等.【典型例题】例1．如图，AB ∥CD ，AE=CF ，求证：AB=CD例2．如图，已知：AD=AE ，ABE ACD ∠=∠，求证：BD=CE.例3．如图，已知：ABD BAC D C ∠=∠∠=∠.，求证：OC=OD. 例4．如图已知：AB=CD ，AD=BC ，O 是BD 中点，过O 点的直线分别交DA 和BC 的延长线于E ，F.求证：AE=CF.例5．如图，已知321∠=∠=∠，AB=AD.求证：BC=DE.例6．如图，已知四边形ABCD 中，AB=DC ，AD=BC ，点F 在AD 上，点E 在BC 上，AF=CE ，EF 的对角线BD 交于O ，请问O 点有何特征？AABD C O12 3AFDOBEC【经典练习】1.△ABC 和△C B A '''中，C B C B A A ''='∠=∠,'，C C '∠=∠则△ABC 与△C B A ''' .2．如图，点C ，F 在BE 上，,,21EF BC =∠=∠请补充一个条件，使△ABC ≌DFE,补充的条件是 .3．在△ABC 和△C B A '''中，下列条件能判断△ABC 和△C B A '''全等的个数有（） ①A A '∠=∠ B B '∠=∠，C B BC ''= ②A A '∠=∠，B B '∠=∠，C A C A ''=' ③A A '∠=∠ B B '∠=∠，C B AC ''= ④A A '∠=∠，B B '∠=∠，C A B A ''=' A ． 1个 B. 2个 C. 3个 D. 4个4．如图，已知MB=ND ，NDC MBA ∠=∠，下列条件不能判定是△ABM ≌△CDN 的是（）A ． N M ∠=∠ B. AB=CD C ． AM=CN D. AM ∥CN 5．如图2所示， ∠E =∠F =90°，∠B =∠C ，AE =AF ，给出下列结论：①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是_________ _________。

全等三角形的判定练习题及答案

全等三角形的判定练习题及答案一、1. 如果D是△ABC中BC边上一点，并且△ADB≌△ADC，则△ABC是Ａ．锐角三角形Ｂ．钝角三角形Ｃ．直角三角形Ｄ．等腰三角形2．如图，AO = BO，CO = DO，AD与BC交于E，∠O =0o，∠B =5o，则∠BED的度数是 A．60o B．90o C．75o D．85o 3．如图，已知△ABD和△ACE中，AB = AC，AD = AE，欲证△ABD≌△ACE，须补充的条件是第题第题A．∠B =∠CB．∠D =∠EC．∠DAE =∠BAC D．∠CAD =∠DAC4．在△ABC和△DEF中，下列各组条件中，不能判定两个三角形全等的是A．AB = DE，∠B =∠E，∠C =∠FB．AC = DF，BC = DE，∠C =∠DC．AB = EF，∠A =∠E，∠B =∠FD．∠A =∠F，∠B =∠E，AC = DE5．如图，已知△ABC的六个元素，则下面甲、乙、丙三个三角形中和△ABC全等的图形是A．都全等 B．乙和丙C．只有乙D．只有丙6．下列判断正确的是A．有两边和其中一边的对角对应相等的两个三角形全等B．有两边对应相等,且有一角为30°的两个等腰三角形全等C．有一角和一边对应相等的两个直角三角形全等D．有两角和一角的对边对应相等的两个三角形全等7．如图4所示，已知△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则三个结论：①A S=AR；②QP∥AR；③△BRP≌△QSP中A．全部正确 B、仅①和②正确C．仅①正确D．仅①和③正确8．如图1所示，△ABC与△BDE都是等边三角形，AB A．AE=CD B．AE>CD C．AE 9．如图2所示,在等边△ABC 中,D、E、F,分别为AB、BC、CA上一点，且AD=BE=CF，图中全等的三角形组数为A．3组 B．4组 C．5组 D．6组10. 已知△ABC≌△MNP，?A?48?，?N?62?，则?B? 度数分别为，，．，?C，?M和?P的二、1、已知：如图12，AB＝CD，DE⊥AC，BF⊥AC，E，F是垂足，DE?BF,AE=CF．求证：AF?CE；AB∥CD．A B C2．如图，已知AD = CB，AE = CF，DE = BF；求证：AB//CD 图．123．如图，已知AB = CD，AC = DB；求证：∠A =∠D．全等三角形的判定姓名1、已知AB=CD，BE=DF，AF=CE，则AB与CD有怎样的位置关系？2、已知O是AB中点，OC=OD，?AOD??BOC，求证：AC?BD3、已知：如图，?CAB??DBA，AC?BD。