广东海洋大学10-11第一学期高数考试B卷 (1)
广东海洋大学10-11第一学期高数考试A卷

、广东海洋大学 2010—2011学年第 一 学期《 高 等 数 学 》课程试题课程号: 19221101x1错考试 错误A卷 错误闭卷 □考查 □ B 卷 □ 开卷一 . 填空(3×6=18分)1. 函数 xxe x f -=)(的拐点是 .2. =⎰dx x e x212/1 . 3. 设 )1( )ln (2>='x x x f ,则 )(x f = .4. 曲线⎩⎨⎧=+=321ty t x 在2=t 处的切线方程为 . 5. 设⎰=Φxtdt x 0sin )(,则=Φ)4('π.6. 设 xx x f 1)1()(+=,则 )1(f '等于 . 二 .计算题(7×6=42分)1. 求3sin 22sin limxxx x -→.班级:姓名:学号:试题共 5 页加白纸3张密封线GDOU-B-11-3022. 求不定积分dx xx ⎰cos sin 13.3. 已知xxsin 是)(x f 的原函数,求dx x xf ⎰)('.4. 设方程05232=-+-+y x e y x 确定函数)(x y y =,求dxdy .5. 求x e x f x cos )(=的三阶麦克劳林公式.6. 求由曲线Inx y =与直线Ina y =及Inb y =所围成图形的面积0>>a b .三. 应用及证明题(10×4=40分)1. 证明:当0>x 时, x x +>+1211.2. 若函数)(x f 在),(b a 内具有二阶导函数,且)()()(321x f x f x f == )(321b x x x a <<<<,证明:在),(31x x 内至少有一点ξ,使得0)(''=ξf .3. 当x 为何值时,函数dt te x I xt ⎰-=02)(有极值.4. 试确定a 的值,使函数⎩⎨⎧≥+<=0,0,)(x x a x e x f x 在),(+∞-∞内连续.。
广东海洋大学(B卷)--高数1试题
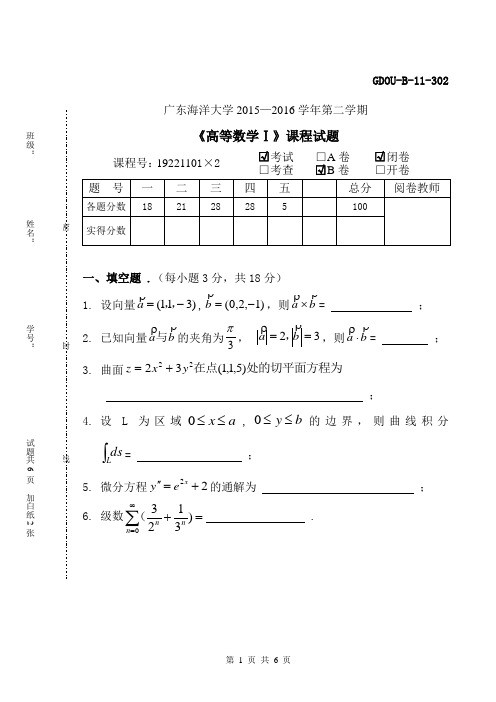
广东海洋大学2015—2016学年第二学期《高等数学Ⅰ》课程试题课程号: 19221101×2□√ 考试□ A 卷□√ 闭卷□ 考查 □√ B 卷 □ 开卷一、填空题 .(每小题3分,共18分)1. 设向量)311(-=,,a ,)1,2,0(-=b ,则b a⨯= ; 2. 已知向量b a 与的夹角为3π, 32==b a ,,则b a⋅= ; 3. 曲面处的切平面方程为在点)5,1,1(3222y x z +=;4. 设L 为区域a x ≤≤0,b y ≤≤0的边界,则曲线积分⎰Lds = ;5. 微分方程22+=''xe y 的通解为 ;6. 级数=+∑∞=)31230n n n (.班级:姓名:学号:试题共6页加白纸2张密封线GDOU-B-11-302二、计算下列各题.(每小题7分,共21分)1.求函数3-22y x y x e z xy ++++=的全微分.2.已知 0)2sin(=+--++z y x z y x ,求yzx z ∂∂∂∂和 .3.求函数3)(4),(22+---=y x y x y x f 的极值 .三、求下列积分. (每小题7分,共28分)1.求 σd y x D⎰⎰+)6(2,其中D 是由22y ===x x x y 及,直线围成的区域.2. 验证曲线积分dy xy y x dx y xy )36()622220032-+-⎰),(),((与路程无关,并计算积分值.3.求⎰⎰∑-+-++=dxdy ze z dzdx y ye dydz e x I xx x )25()2()3(,其中∑是平面22230a y x z z =+==及圆柱面和围成的圆柱体表面的外侧.4.求⎰⎰⎰Ωzdv 2,其中围成的区域和平面是由圆锥面222=+=Ωz y x z .四、解答下列问题.(每小题7分,共28分).1. 判定级数∑∞=-+-13411)1(n n n 的敛散性,若收敛,是条件收敛还是绝对收敛?2. 把函数31)(+=x x f 展开成1+x 的幂级数,并指出收敛域.3.求微分方程xe y y y 234=+'+''的通解.4.求微分方程25)3(32+=+-'x x yy 满足初值条件352=-=x y 的特解.五、设级数)0(1>∑∞=n n n a a 收敛.证明:级数∑∞=+11n n n a a 收敛.(5分)。
06-07第一学期高数B

广东海洋大学2006GD0U-B-11-3022007学年第一学期班级:《高等数学》课程试题(B)课程号:1921006x1J 考试 DA 卷J 闭卷姓名:、填空(21分,每题3分)学号..--封•…试题共页加白纸2张….或1. 假设函数f(x)=心在”0点连续,贝\\a=_L_a + X. x>02. 函数y = 6zsin^ + -sin3jc 在x = 处取得极值,贝。
=23 3 3. 假设广(0)存在,且门0) = 0,那么临冬=广(0)i° x --------------- 4.曲线y ="在点(0,1)处的法线方程为 ___________________5. 函数 y^x 2lnx 的二阶导数 y"= 21nx+36. 设/⑴具有原函数为F(x),贝叮"(工)办=xf(x)-F(x)+C7.+J1 -Jr?)2必;=2二、计算题(每题5分,共25分)1 > lim(l-3x)xx->0解:原式=lim[l + (-3x)]_3x ( 3x )x= e~3x->()2 lim ffx + 2 H x -x -x^\解:原式啊〜啊AH3 设 y = A : arc sin — +』4 一 x?,求 dy2-2x . x , + —/ = arcsin — J1-(必)2 2丁4_[ 2 2故 dy 二 arcsin —dx24.求由方程尤-y + Liny = 0所确定的隐函数y 的二阶导数么2 dx^解:两边对x 求导1-+ — cos y*y z= 0 ----- > y = -----------2 l-|cos,1 . ,--sm y ・y >”= \ (l--cos y)25.求曲线y = ln(l + /)的凸凹区间与拐点.解:y =马,y 〃= 2(1")«E = 2(1 W (),得二± 1工)~ (1 +解:y = arcsin- + ^.1/22(1 +打三.求以下积分(每题6分,共30分)1.二专JC牝所二C2 arctanxir倒二才林二R”C化r xJ时“《万二X。
广东海洋大学高等数学往年试卷

广东海洋大学2006 ——2007学年第一学期《高等数学》课程试题课程号: 1920008□ 考试□ A 卷□ 闭卷□ 考查□ B 卷□ 开卷一. 计算(20分,各4分).1.x x x x sin 2cos 1lim0-→. 2.⎰+x dx2cos 1.3.⎰-++1121sin 1dx xx . 4.x x x x )1232(lim ++∞→. 5.⎰262cos ππxdx .二.计算(20分,各5分). 1.求)arcsin(tan x y =的导数。
2.求由方程0=-+e xy e y所确定的隐函数y 的二阶导数22dxyd 。
3.已知⎩⎨⎧==te y t e x tt cos sin ,求当3π=t 时dx dy的值。
4.设x y y x z 33-=,求xy zx z ∂∂∂∂∂2,.三.计算.(25分,各5分).1. dx x x ⎰+9232.dx e x ⎰班级:计科1141 姓名: 阿稻学号:2014xx试题共2页加白纸4张密封线GDOU-B-11-3023.dttedt e xt xt x ⎰⎰→020222)(lim .4.求]1)1ln(1[lim 0xx x -+→. 5.dx x ⎰-202sin 1π.四.解答(14分,各7分).1.问12+=x xy ()0≥x 在何处取得最小值?最小值为多少? 2.证明x x xx<+<+)1ln(1.五.解答(21分,各7分).1.求由2x y =与x y 2=围成图形的面积。
2.求由x x x y ),0(,sin π≤≤=轴围成的图形绕x 轴所产生的旋转体的体积。
3.计算σd y x D⎰⎰+)(22,其中D 是矩形闭区域:1,1≤≤y x .《高等数学》课程试题A 卷答案一. 计算 (20分 各4分)1.原式=2sin sin 220lim =→x x x x 2.原式=c x xdx +=⎰tan 21sec 212 3. 原式=201arctan 211112π⎰-==+x dx x 4. 原式=e x x x =++∞→)1221(lim 5. 原式=83622cos 126-=+⎰πππdx x 二、计算 (20分 各5分) 1.x xy 22sec tan 11'-=2.两边对x 求导,得:0''=++xy y y e y yex yy +-=' 2)()'1()('''y y y e x y e y e x y y ++-+-= 32)(22y yy e x e y ye xy +-+= 3.tt tt t e t e t e t e dx dy tt t t sin cos sin cos cos sin sin cos +-=+-=2331313-=+-==πt dx dy 4.323y y x xz -=∂∂222233y x y x z x y z -=∂∂∂=∂∂∂三、计算 (20分 各5分)1.原式=c x x dx x x x x ++-=+-+⎰)9ln(29219992223 2. 原式=c e e x c e te dt te x xt t t +-=+-=⎰)(2)(223. 原式=2222220lim=⎰→x xt xx xedte e4. 原式=212111)1ln(lim lim20=+-=+-→→x x x x x x x 5. 原式=222)cos (sin )sin (cos cos sin 244020-=-+-=-⎰⎰⎰ππππdx x x dx x x dx x x四、解答 (14分 各7分)1.解:0)x (1x 1'y 222=+-= 1x ±= 1x -=(舍)又 00x y 211x y ==== 故:函数在1x =取到最大值,最大值为21。
海大大一上学期(第一学期)高数期末考试题

大一上学期高数期末考试一、单项选择题 (本大题有4小题, 每小题4分, 共16分)1. )(0),sin (cos )( 处有则在设=+=x x x x x f .(A )(0)2f '= (B )(0)1f '=(C )(0)0f '= (D )()f x 不可导.2. )时( ,则当,设133)(11)(3→-=+-=x x x x xx βα.(A )()()x x αβ与是同阶无穷小,但不是等价无穷小; (B )()()x x αβ与是等价无穷小;(C )()x α是比()x β高阶的无穷小; (D )()x β是比()x α高阶的无穷小.3.若()()()02xF x t x f t dt=-⎰,其中()f x 在区间上(1,1)-二阶可导且'>()0f x ,则( ).(A )函数()F x 必在0x =处取得极大值; (B )函数()F x 必在0x =处取得极小值;(C )函数()F x 在0x =处没有极值,但点(0,(0))F 为曲线()y F x =的拐点; (D )函数()F x 在0x =处没有极值,点(0,(0))F 也不是曲线()y F x =的拐点。
4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数,且设(A )22x (B )222x +(C )1x - (D )2x +.二、 填空题(本大题有4小题,每小题4分,共16分)5.=+→xx x sin 2)31(lim e 的 六次方 .6.,)(cos 的一个原函数是已知x f xx=⋅⎰x xxx f d cos )(则cos 方x/2x 方 .7.lim(cos cos cos )→∞-+++=22221n n nnnn ππππ -π/2 .8.=-+⎰21212211arcsin -dx xx x π/3 .三、解答题(本大题有5小题,每小题8分,共40分)9. 设函数=()y y x 由方程sin()1x ye xy ++=确定,求'()y x 以及'(0)y .10. .d )1(177x x x x ⎰+-求11. . 求,, 设⎰--⎪⎩⎪⎨⎧≤<-≤=1 32)(1020)(dx x f x x x x xe x f x12.设函数)(x f 连续,=⎰1()()g x f xt dt,且→=0()lim x f x A x ,A 为常数. 求'()g x 并讨论'()g x 在=0x 处的连续性.13. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、 解答题(本大题10分)14. 已知上半平面内一曲线)0()(≥=x x y y ,过点(,)01,且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和,求此曲线方程.五、解答题(本大题10分)15. 过坐标原点作曲线x y ln =的切线,该切线与曲线x y ln =及x 轴围成平面图形D.(1)求D 的面积A ;(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V .六、证明题(本大题有2小题,每小题4分,共8分)16. 设函数)(x f 在[]0,1上连续且单调递减,证明对任意的[,]∈01q ,1()()≥⎰⎰qf x d x q f x dx.17. 设函数)(x f 在[]π,0上连续,且0)(0=⎰πx d x f ,cos )(0=⎰πdx x x f .证明:在()π,0内至少存在两个不同的点21,ξξ,使.0)()(21==ξξf f (提示:设⎰=xdxx f x F 0)()()解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题(本大题有4小题,每小题4分,共16分)5.6e . 6.cx x +2)cos (21 .7. 2π. 8.3π.三、解答题(本大题有5小题,每小题8分,共40分) 9. 解:方程两边求导 (1)cos()()0x yey xy xy y +''+++=cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==,(0)1y '=-10. 解:767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11.解:10330()xf x dx xe dx ---=+⎰⎰⎰3()x xd e --=-+⎰⎰232cos (1sin )x x xe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰ 令3214e π=--12. 解:由(0)0f =,知(0)0g =。
广东海洋大学大一高数下学期考试试卷

广东海洋大学 2016—2017学年第 二 学期 《 高 等 数 学 》课程试题 课程号: x 2 考试 A 卷 闭卷开卷 一 . 填空(3×8=24分) 1. 设,{}{}1,0,2,0,3,2a b =-=,则a b •= 2. 与{}1,2,2同方向的单位向量为 3. 曲面22z x y =-在()1,1,0处的切平面方程为 4. 曲线23313x t y t z t =+⎧⎪=+⎨⎪=⎩在1t = 处的切线方程为 5. 幂级数12n n n x ∞=∑的收敛半径为 6. 设级数b b a a n n n n ==∑∑∞=∞=11,,则级数=+∑∞=)21n n n b a ( 7. 微分方程1y ''=的通解为 8. 函数()()22312z x y =---- 的极值点为 二 .计算题(7×2=14分) 1. 设()ln 1z x y =++,求dz .2.设),(y x f z =是由方程210xyz z e -+=所确定的具有连续偏导数的函数,求,zzx y ∂∂∂∂.班级:姓名: 学号: 试题共6页加白纸3张密封线GDOU-B-11-302三 .计算下列积分(7×4=28分) 1.()2Dx y d σ+⎰⎰其中D 是由x 轴y 轴以及直线1x y +=所围成的闭区域。
2.证明曲线积分(1,1)(0,0)(2)(2)x y dx x y dy +++⎰在整个xoy 平面内与路径无关,并计算积分值。
3. 计算()22sin D x y d σ+⎰⎰,其中D 是由224x y +≤围成的闭区域。
4. 计算32xdydz ydzdx zdxdy ∑++⎰⎰,其中∑是某半径为2的球面的整个边界曲面的外侧。
四 .计算题(7×4=28分)1. 判别级数 212nn n ∞=∑ 是否收敛。
2. 将函数3()x f x e -= 展开为x 的幂级数。
广东海洋大学寸金学院《信号与系统》课程考查试卷B(含答案)
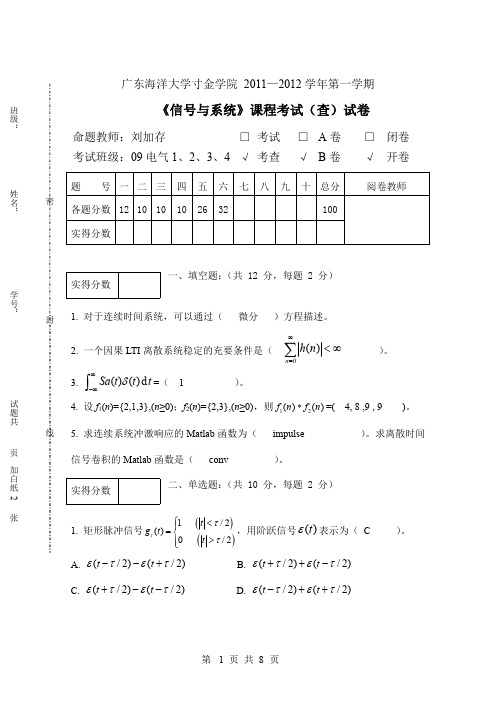
解:
第 5 页 共 8 页
RC电 路 的 频 率 响 应 为 H ( ) 而响应 由卷积定理得 已知 2 j 2 u 2 ( t ) u1 ( t ) h ( t ) U 2 ( ) U 1 ( ) H ( ) 1 e j e j , 故 j 1 2 1 1 j j e j e j e e j 2 j j 2 j U 1 ( ) U 2 ( ) 反变换得
各题分数 12 10 10 实得分数
实得分数
封 线
一、填空题: (共 12 分,每题 2 分)
1. 对于连续时间系统,可以通过(
微分
)方程描述。
2. 一个因果 LTI 离散系统稳定的充要条件是( 3.
h(n )
n 0
) 。
Sa(t ) (t ) d t =( 1
) 。 )。
4. 设 f1(n)={2,1,3},(n≥0);f2(n)={2,3},(n≥0),则 f1 (n ) f 2 (n ) =( 4, 8 ,9 , 9 5. 求连续系统冲激响应的 Matlab 函数为( 信号卷积的 Matlab 函数是( 实得分数 conv impulse ) 。
) 。求离散时间
) 。
z z 1
B.
z z 1
1 z 1
D.
1 z 1
实得分数
三、 判断题: (共 10 分, 每题 2 分; 正确的打√, 错误的打
)
1. 系统的阶跃响应属于零状态响应。 (
√
)
2. 信号的无失真传输是指输入信号经过系统后,输出信号与输入信号相比,只有 波形形状不同,而幅度大小和出现时间先后却不变。(
专业导论!
广东海洋大学2010——2011学年第一学期 《专业导论》课程试题 课程号: 23281101 □ 考试 □ A 卷 □ 闭卷 ■ 考查 □ B 卷 ■ 开卷的是对对外交流频繁、国际交流密切的外语专业的影响。
加入WTO 以后,我国外语类院校将面临哪些挑战和冲击,如何坚持外语类院校的办学特色,已经十分严峻地摆在了外语类院校的面前,直接关系到外语类院校学生在21世纪的生存和发展。
而外语类专业的人才的宗旨是服务于社会,服务于企业。
但在21世纪这个就业形势严峻的时代,英语专业的学生并不如往日那样受社会的青睐,出现了竞争激烈、人才过剩的局面。
因为目前学校给我们修的课程并不能完全符合社会所需,因此不能顺利进入岗位。
在如此复杂的情况下,培养复合型的英语人才是应对问题的首要解决方法。
一、复合型人才的短缺及其原因: 在懂得自己自身的专业前提下又懂得外语的人才确实难以寻找。
外语作为沟通的桥梁应用范围广泛。
但由于受长期以来重文史、轻科技的外语教育的影响,外语人才难以满足当前经济科技等各项事业的迅猛发展。
因此,英语专业人才缺乏相应专业知识或技能背景,难以胜任工作。
有关部门进行过的一次问卷调查显示,目前市场对纯外语人才的需求在逐年下降,希望外语人才具有较广博的知识的比例则上升至66%。
一位猎头公司老板说,现在,我国懂外语的人很多,但能熟练使用外语的工程技术人才却不多。
机械、化学、工艺、软件等专业的技术工程师,本身就十分紧缺,懂外语的就更稀有了,想找到符合企业要求的人很难。
金融、IT 、电子、通讯等行业也同样存在专业外语人才紧缺的状况。
据了解,当前绝大多数IT 行业实行软件外包,外语成为项目开发过程中的关键性因素之一,从事这些项目的技术人员仅靠三五百个计算机应用词汇是不足以读懂计算机科技类文章的。
因此,外语水平的高低成为从业人员发展的决定因素。
单一的外语人才已经不再“走俏”,精通国际经济贸易、公司管理等专业知识的复合型外语人才在就业市场上颇受青睐。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东海洋大学2010—2011学年第一学期《高等数学》课程试题课程号:19221101x1□√考试□A 卷□√闭卷□考查□√B 卷□开卷题号一二三四五六七八九十总分阅卷教师各题分数184240100实得分数一.填空(3×6=18分)1.函数x xe x f -=)(的拐点是.2.=-⎰dx x )sin 1(3.3.设)1( )ln (2>='x x x f ,则)(x f =.4.函数x e x y +=上点)1,0(处的切线方程是.5.设⎰=Φx tdt x 0sin )(,则=Φ4('π.6.设x x f arctan )(=,则)1(f '等于.二.计算题(7×6=42分)1.x x x x sin 1cos lim 20→.
班级
:
姓名:
学号
:试题
共6页
加白
纸
3
张密
封
线
GDOU-B-11-302
2.求定积分dx
x x ⎰+312211
.
3.已知x e x f x
=)(,求dx x xf ⎰)(''.
4.设参数方程⎩⎨⎧=+=t y
t x arctan )
1ln(2确定函数)(x y y =,求
dy .
5.求Inx x f =)(按)2(-x 的幂展开的四阶泰勒公式.
6.计算曲线)3(3
1x x y -=上相应于31≤≤x 的一段弧的弧长.三.应用及证明题(10×4=40分)
1.证明:当4>x 时,22x x >.
2.设)(x f 在]1,0[上连续,在)1,0(内可导,且0)1(=f ,求证:存在)1,0(∈ξ,使得ξξξ)
()('f f -=.
3.求函数⎰-=x
dt t t x F 0)4()(在]5,1[-上的最大值与最小值.
4.试确定a 的值,使函数⎪⎩
⎪⎨⎧>≤+=0,1sin 0,)(2x x x x a x x f 在),(+∞-∞内连续.。
