2016全国2卷高考文科数学试卷及答案
2016年高考文科数学全国卷2(含详细答案)
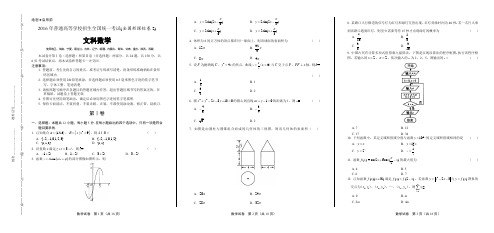
数学试卷 第1页(共18页) 数学试卷 第2页(共18页) 数学试卷 第3页(共18页)绝密★启用前2016年普通高等学校招生全国统一考试(全国新课标卷2)文科数学使用地区:海南、宁夏、黑龙江、吉林、辽宁、新疆、内蒙古、青海、甘肃、重庆、陕西、西藏本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共24题,共150分,共6页.考试结束后,将本试卷和答题卡一并交回. 注意事项:1. 答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内.2. 选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.3. 请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.4. 作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑.5. 保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀.第Ⅰ卷一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知集合{}123A =,,,{}2|9B x x =<,则A B =( ) A. {2,1,0,1,2,3}--B. {2,1,0,1,2}--C. {1,2,3}D. {1,2}2. 设复数z 满足3z i i +=-,则=z ( )A. 12i -+B. 12i -C. 32i +D. 32i -3. 函数()sin y A x ωϕ=+的部分图像如图所示,则A. 2sin(2)6y x π=-B. 2sin(2)3y x π=-C. 2sin()6y x π=+D. 2sin()3y x π=+4. 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )A. 12πB. 323πC. 8πD. 4π5. 设F 为抛物线C :24y x =的焦点,曲线0ky k x =>()与C 交于点P ,PF x ⊥轴,则=k( )A.12 B. 1 C. 32D. 26. 圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则=a( )A. 43-B. 34-C.D. 27. 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积( )A. 20πB. 24πC. 28πD. 32π8. 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为 ( )A. 710B. 58C. 38D. 3109. 中国古代有计算多项式值得秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的2x =,2n =,依次输入的a 为2,2,5,则输出的s = ( )A. 7B. 12C. 17D. 3410. 下列函数中,其定义域和值域分别与函数lg 10x y =的定义域和值域相同的是 ( )A. y x =B. lg y x =C. 2x y =D. 1y x=11. 函数() = cos26cos()2f x x x π+-的最大值为( )A. 4B. 5C. 6D. 712. 已知函数()()f x x ∈R 满足()(2)f x f x =-,若函数223y x x =--与()y f x =图象的交点为11x y (,),22x y (,),…,m m x y (,),则1mi i x =∑=A. 0B. mC. 2mD. 4m姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第4页(共6页) 数学试卷 第5页(共6页) 数学试卷 第6页(共6页)第Ⅱ卷本卷包括必考题和选考题两部分.第13~12题为必考题,每个试题考生都必须作答.第22~24为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分. 13. 已知向量a ()4m =,,b ()32=-,,且a ∥b ,则m =________.14. 若x ,y 满足约束条件10,30,30,x y x y x -++--⎧⎪⎨⎪⎩≥≥≤则2z x y =-的最小值为________.15. ABC ∆的内角A B C ,,的对边分别为a b c ,,,若4cos 5A =,5cos 13C =,1a =,则b =________.16. 有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.三、解答题:解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分)等差数列{}n a 中,344a a +=,576a a +=.(Ⅰ)求{}n a 的通项公式;(Ⅱ)设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]0=,[2.6]2=.18. (本小题满分12分)某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(Ⅰ)记A 为事件:“一续保人本年度的保费不高于基本保费”。
2016年全国高考文科数学试题及答案-全国卷2

2016年普通高等学校招生全国统一考试文科数学一、选择题:本大题共12 小题。
每小题 5 分.(1)已知集合,则(A)(B)(C)(D)(2)设复数z 满足,则=(A)(B)(C)(D)(3)函数的部分图像如图所示,则(A)(B)(C)(D)(4)体积为8 的正方体的顶点都在同一球面上,则该球面的表面积为(A)(B)(C)(D)(5)设F为抛物线C: y2=4x的焦点,曲线y= (k>0)与C交于点P, PF丄x轴,则k=(A)(B)1(C)(D)2(6)圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1, 则a=(A)-(B)-(C)(D)2(7)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A) 20 n ( B) 24 n(C) 28 n ( D) 32 n(8)某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40 秒,若一名行人来到该路口遇到红灯,则至少需要等待15 秒才出现绿灯的概率为( A)( B)( C)( D)(9) xx 古代有计算多项式值得xx 算法,右图是实现该算法的程序框图.执行该程序框图,若x=2,n=2,输入的a为2, 2, 5,则输出的s=( A) 7( B) 12( C) 17( D) 34(10)下列函数中,其定义域和值域分别与函数y=10lgx 的定义域和值域相同的是( A)y=x(B)y=lgx (C)y=2x(D)(11)函数的最大值为(A)4(B)5(C)6(D)7(12)已知函数f(x) (x € R)满足f(x)二f(2-x),若函数y=|x2-2x-3|与y=f(x) 图像的交点为(x1,y1 ) , (x2,y2),…,(xm,ym),则(A)0(B)m(C) 2m(D) 4m二.填空题:共 4 小题,每小题5分.(13)已知向量a=(m,4) , b=(3,-2),且 a II b,则m= ___________(14)若x,y 满足约束条件,则z=x-2y 的最小值为__________(15) _______ A ABC的内角A, B, C的对边分别为a, b, c,若,,a=1, 则b= _ .( 16)有三张卡片,分别写有 1 和2, 1 和3, 2 和 3. 甲,乙, 丙三人各取走一张卡片, 甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是_________________ .三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分12分)等差数列{}中,(I )求{}的通项公式;(II)设=[],求数列{}的前10项和,其中[x]表示不超过x的最大整数,如[0.9]=0,[2.6]=2(18)(本小题满分12分)某险种的基本保费为a (单位:元),继续购买该险种的投保人称为xx人,xx人本年度的保费与其上年度出险次数的xx如下:随机调查了该险种的200名xx人在一年内的出险情况,得到如下统计表:(I )记A为事件:“一xx人本年度的保费不高于基本保费”求P(A)的估计值;(II)记B为事件:“一xx人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;(III )求xx 人本年度的平均保费估计值.(19)(本小题满分12 分)如图,菱形ABCD勺对角线AC与BD交于点Q点E、F分别在AD, CDxx AE=CF EF交BD于点H,将沿EF折到的位置.(I )证明:;(II)若,求五棱锥体积.(20)(本小题满分12 分)已知函数.(I )当时,求曲线在处的切线方程;(II)若当时,,求的取值范围.(21)(本小题满分12 分)已知A是椭圆E:的左顶点,斜率为的直线交E于A, M两点,点N 在Exx,.(I )当时,求的面积(II)当 2 时,证明: .请考生在第22~24题中任选一题作答,如果多做,则按所做的第一题计分.(22)(本小题满分10 分)选修4-1 :几何证明选讲如图,在正方形ABCDxx E, G分别在边DA DCxx (不与端点重合),且DE二DG过D点作DF1CE垂足为F.(I)证明:B, C, G, F四点共圆;(H)若AB=1 E为DA的中点,求四边形BCGF勺面积.23)(本小题满分10分)选修4-4 :坐标系与参数方程2016 年全国高考文科数学试题及答案-全国卷2 在直角坐标系xOyxx,圆C的方程为.(I)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求C 的极坐标方程;(H)直线I的参数方程是(t为参数),l与C交于A, B两点,,求l 的斜率.( 24)(本小题满分10 分)选修4-5 :不等式选讲已知函数,M为不等式的解集.(I)求M(H)证明:当a, b时,.2016 年普通高等学校招生全国统一考试文科数学答案(16)【答案】 1和 3 三、解答题(17) (本小题满分 12 分) 【答案】(i);(n )24. 【解析】试题分析: ( I ) 根据等差数列的性质求,,从而求得; 根据已知条件求,再求数列的前 10 项和.试题解析:(I )设数列的公差为d ,由题意有,解得,一 . 选择题 1)【答案】 D 【答案】A (5) 【答案】 D (8) 【答案】 B (9) 【答案】 C (12) 【答案】 B 二.填空题 (13) 【答案】2)【答案】 C (3) 答案】 A (4)(6) 【答案】 A (7) 【答案】 C(10) 【答案】 D (11) 【答案】 B(14) 【答案】 15)【答案】(n)所以的通项公式为.(H)由(I)知,当n=1,2,3 时,;当n=4,5 时,;当n=6,7,8 时,;当n=9,10 时,,所以数列的前10项和为.考点:等茶数列的性质,数列的求和.【结束】(18)(本小题满分12 分)【答案】(I)由求P(A)的估计值;(H)由求P(B)的估计值;III )根据平均值得计算公式求解.【解析】试题分析:试题解析:(I)事件A发生当且仅当一年内出险次数小于 2.由所给数据知,一年内险次数小于 2 的频率为,故P(A)的估计值为0.55.(H)事件B发生当且仅当一年内出险次数大于1且小于4.由是给数据知,一年内出险次数大于1且小于4的频率为,故P(B)的估计值为03(皿)由题所求分布列为:调查200名xx人的平均保费为因此,xx人本年度平均保费估计值为1.1925a.考点:样本的频率、平均值的计算.【结束】(19)(本小题满分12分)【答案】(I)详见解析;(H).【解析】试题分析:(I)证再证(H)证明再证平面最后呢五棱锥体积试题解析:(I)由已知得,又由得,故由此得,所以.(II )由得由得所以于是故由(I )知,又,所以平面于是又由,所以,平面又由得五边形的面积所以五棱锥体积考点:空间中的线面关系判断,几何体的体积【结束】(20)(本小题满分12 分)【答案】(I);(H)【解析】试题分析:(1)先求定义域,再求,,,由直线方程得点斜式可求曲线在处的切线方程为(H)构造新函数,对实数分类讨论,用导数法求解.试题解析:(I )的定义域为. 当时,,曲线在处的切线方程为(II )当时,等价于令,则(i )当,时,,故在上单调递增,因此;(ii )当时,令得由和得,故当时,,在单调递减,因此.综上,的取值范围是考点:导数的几何意义,函数的单调性.【结束】21)(本小题满分12 分)【答案】(I);(H).【解析】试题分析:(I)先求直线的方程,再求点的纵坐标,最后求的面积;(H)设,,将直线的方程与椭圆方程组成方程组,消去,用表示,从而表示,同理用表示,再由求.试题解析:(I)设,则由题意知.由已知及椭圆的对称性知,直线的倾斜角为,又,因此直线的方程为.将代入得,解得或,所以.因此的面积.(2)将直线的方程代入得由得,故.由题设,直线的方程为,故同理可得.由得,即.设,则是的零点,,所以在单调递增,又,因此在有唯一的零点,且零点在内,所以.考点:椭圆的性质,直线与椭圆的位置关系.【结束】请考生在22、23、24题中任选一题作答, 如果多做,则按所做的第一题计分, 做答时请写清题号(22)(本小题满分10分)选修4-1 :几何证明选讲【答案】(I)详见解析;(H).【解析】试题分析:(I)证再证四点共圆;(H)证明四边形的面积是面积的 2 倍.试题解析:(I)因为,所以则有所以由此可得由此所以四点共圆.(II )由四点共圆,知,连结,由为斜边的中点,知, 故因此四边形的面积是面积的2倍,即S = 2S GCB = 2 - - 1 =-彥 2 2 2考点:三角形相似、全等,四点共圆【结束】(23)(本小题满分10分)选修4—4:坐标系与参数方程【答案】(I);(H).【解析】试题分析:(I)利用,可得C的极坐标方程;(II )先将直线的参数方程化为普通方程,再利用弦长公式可得的斜率.试题解析:(I)由可得的极坐标方程(II )在(I )中建立的极坐标系中,直线的极坐标方程为由所对应的极径分别为将的极坐标方程代入的极坐标方程得‘2 12'cos:11 =0.于是| AB |=|「1 一「2 卜(「1 「2)2 -4「1『2 = 144cos2:-44,由得,所以的斜率为或.考点:圆的极坐标方程与普通方程互化,直线的参数方程,点到直线的距离公式.【结束】(24)(本小题满分10分)选修4—5:不等式选讲【答案】(I);(H)详见解析.【解析】试题分析:(I)先去掉绝对值,再分,和三种情况解不等式,即可得;(II )采用平方作差法,再进行因式分解,进而可证当,时,.试题解析:(I )当时,由得解得;当时,;当时,由得解得.所以的解集.(II )由(I )知,当时,,从而因此考点:绝对值不等式,不等式的证明【结束】。
2016年高考全国Ⅱ文科数学试题及答案(word解析版)

2016年普通高等学校招生全国统一考试(全国II )数学(文科)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)【2016年全国Ⅱ,文1,5分】已知集合{}1,2,3A =,{}2|9B x x =<,则A B = ( )(A ){}210123--,,,,, (B ){}21012--,,,, (C ){}1,2,3 (D ){}12,【答案】D【解析】由29x <得33x -<<,所以{|33}B x x =-<<,因为{}1,2,3A =,所以{}1,2A B = ,故选D .【点评】对于集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图处理.(2)【2016年全国Ⅱ,文2,5分】设复数z 满足i 3i z +=-,则z =( )(A )12i -+ (B )12i - (C )32i + (D )32i -【答案】C【解析】由i 3i z +=-得32i z =-,所以32i z =+,故选C .【点评】复数()i ,a b a b +∈R 的共轭复数是()i ,a b a b -∈R ,据此先化简再计算即可.(3)【2016年全国Ⅱ,文3,5分】函数()=sin y A x ωϕ+ 的部分图像如图所示,则( )(A )2sin 26y x π⎛⎫=- ⎪⎝⎭(B )2sin 23y x π⎛⎫=- ⎪⎝⎭(C )2sin +6y x π⎛⎫= ⎪⎝⎭(D )2sin +3y x π⎛⎫= ⎪⎝⎭【答案】A【解析】由题图知,2A =,最小正周期ππ2[()]π36T =--=,所以2π2πω==,所以2sin(2)y x ϕ=+. 因为图象过点π,23⎛⎫ ⎪⎝⎭,所以π22sin 23ϕ⎛⎫=⨯+ ⎪⎝⎭,所以2πsin 13ϕ⎛⎫+= ⎪⎝⎭,所以 ()2ππ2π32k k ϕ+=+∈Z ,令0k =,得π6ϕ=-,所以π2sin 26y x ⎛⎫=- ⎪⎝⎭,故选A . 【点评】根据图像求解析式问题的一般方法是:先根据函数=sin()y A x h ωϕ++图像的最高点、最低点确定A ,h的值,由函数的周期确定ω的值,再根据函数图像上的一个特殊点确定φ值.(4)【2016年全国Ⅱ,文4,5分】体积为8的正方体的顶点都在同一球面上,则该球的表面积为( )(A )12π (B )323π (C )8π (D )4π 【答案】A【解析】因为正方体的体积为8,所以棱长为2,所以正方体的体对角线长为,所以正方体的外接球的半径24π12π⋅=,故选A .【点评】与棱长为a 的正方体相关的球有三个:外接球、内切球和与各条棱都相切的球,、2a. (5)【2016年全国Ⅱ,文5,5分】设F 为抛物线2:4C y x =的焦点,曲线()0k y k x=>与C 交于点P ,PF x ⊥ 轴,则k =( )(A )12 (B )1 (C )32(D )2 【答案】D【解析】因为F 是抛物线24y x =的焦点,所以(1,0)F ,又因为曲线(0)k y k x=>与C 交于点P ,PF x ⊥轴,所以,A C ,所以2k =,故选D .【点评】抛物线方程有四种形式,注意焦点的位置. 对于函数()0k y k x=≠,当0k >时,在(),0-∞,()0,+∞上 是减函数,当0k <时,在(),0-∞,()0,+∞上是增函数.(6)【2016年全国Ⅱ,文6,5分】圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a =( )(A )43- (B )34- (C (D )2 【答案】A【解析】由2228130x y x y +--+=配方得()()22144x y -+-=,所以圆心为()1,4,因为圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为11=,解得43a =-,故选A . 【点评】直线与圆的位置关系有三种情况:相交、相切和相离.已知直线与圆的位置关系时,常用几何法将位置关系转化为圆心到直线的距离d 与半径r 的大小关系,以此来确定参数的值或取值范围.(7)【2016年全国Ⅱ,文7,5分】如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( ) (A )20π (B )24π (C )28π (D )32π【答案】C【解析】由题意可知,圆柱的侧面积为12π2416πS =⋅⋅=,圆锥的侧面积为212π248π2S =⋅⋅⋅=,圆柱 的底面面积为23π24πS =⋅=,故该几何体的表面积为12328πS S S S =++=,故选C .【点评】以三视图为载体考查几何体的体积,解题的关键是根据三视图想象原几何体的形状构成,并从三视图中发现几何体中各元素间的位置关系及数量关系,然后在直观图中求解.(8)【2016年全国Ⅱ,文8,5分】某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯 ,则至少需要等待15秒才出现绿灯的概率为( )(A )710 (B )58 (C )38(D )310 【答案】B【解析】因为红灯持续时间为40秒,所以这名行人至少需要等待15秒才出现绿灯的概率为40155408-=,故选B . 【点评】对于几何概型的概率公式中的“测度”要有正确的认识,它只与大小有关,而与形状和位置无关,在解题时,要掌握“测度”为长度、面积、体积、角度等常见的几何概型的求解方法.(9)【2016年全国Ⅱ,文9,5分】中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的2,2,x n == 依次输入的a 为2,2,5,则输出的s =( )(A )7 (B )12 (C )17 (D )34【答案】C【解析】由题意,2,2,0,0x n k s ====,输入2a =,则0222,1s k =⋅+==,循环;输入2a =,则2226,2s k =⋅+==,循环;输入5a =,62517,32s k =⋅+==>,结束循环.故输出的17s =,故选C .【点评】识别算法框图和完善算法框图是高考的重点和热点.解决这类问题:首先,要明确算法框图中的顺序结构、条件结构和循环结构;第二,要识别运行算法框图,理解框图解决的实际问题;第三,按照题目的要求完成解答.对框图的考查常与函数和数列等相结合,进一步强化框图问题的实际背景.(10)【2016年全国Ⅱ,文10,5分】下列函数中,其定义域和值域分别与函数lg 10x y =的定义域和值域相同的是( )(A )y x = (B )lg x = (C )2x y = (D )y=【答案】D【解析】lg 10x y x ==,定义域与值域均为()0,+∞,只有D 满足,故选D . 【点评】对于基本初等函数的定义域、值域问题,应熟记图象,运用数形结合思想求解.(11)【2016年全国Ⅱ,文11,5分】函数π()cos 26cos 2f x x x ⎛⎫=+- ⎪⎝⎭的最大值为( ) (A )4 (B )5 (C )6 (D )7【答案】B 【解析】因为22311()12sin 6sin 2sin 22f x x x x ⎛⎫=-+=--+ ⎪⎝⎭,而sin [1,1]x ∈-,所以当sin 1x =时,()f x 取得最大值5,故选B . 【点评】求解本题易出现的错误是认为当3sin 2x =时,函数23112sin 22y x ⎛⎫=--+ ⎪⎝⎭取得最大值. (12)【2016年全国Ⅱ,文12,5分】已知函数()()f x x ∈R 满足()()2f x f x =-,若函数223y x x =--与()y f x =图像的交点为()()()1122,,,,,,m m x y x y x y ,则1=mi i x =∑( )(A )0 (B )m (C )2m (D )4m【答案】B【解析】因为2(),|23|y f x y x x ==--的图像都关于1x =对称,所以它们图像的交点也关于1x =对称,当m 为偶数时,其和为22m m ⨯=;当m 为奇数时,其和为1212m m -⨯+=,故选B . 【点评】如果函数()f x ,x D ∀∈,满足x D ∀∈,恒有()()f a x f b x +=-,那么函数的图象有对称轴2a b x +=;如果函数()f x ,x D ∀∈,满足x D ∀∈,恒有()()f a x f b x -=-+,那么函数()f x 的图象有对称中心,02a b +⎛⎫ ⎪⎝⎭. 第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(24)题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上(13)【2016年全国Ⅱ,文13,5分】已知向量(),4a m =,()3,2b =-,且//a b ,则m = ______.【答案】6-【解析】因为//a b ,所以2430m --⨯=,解得6m =-.【点评】如果()11,a x y =,()()22,0b x y b ≠,则//a b 的充要条件是12210x y x y =-.(14)【2016年全国Ⅱ,文14,5分】若x ,y 满足约束条件10,30,30,x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩则2z x y =-的最小值为__ ____.【答案】5-【解析】由1030x y x y -+=⎧⎨+-=⎩得12x y =⎧⎨=⎩,记为点()1,2Α;由1030x y x -+=⎧⎨-=⎩得34x y =⎧⎨=⎩,记为点()3,4Β;由3030x x y -=⎧⎨+-=⎩得30x y =⎧⎨=⎩,记为点()3,0C .分别将A ,B ,C 的坐标代入2z x y =-,得1223Αz =-⨯=-,3245Βz =-⨯=-,3203C z =-⨯=,所以2z x y =-的最小值为5-.【点评】利用线性规划求最值,一般用图解法求解,其步骤是:(1)在平面直角坐标系内作出可行域;(2)考虑目标函数的几何意义,将目标函数进行变形;(3)确定最优解:在可行域内平行移动目标函数变形后的直线,从而确定最优解;(4)求最值:将最优解代入目标函数即可求出最大值或最小值.(15)【2016年全国Ⅱ,文15,5分】ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,若4c o s 5A =,5cos 13C =,1a =,则b =_______.【答案】2113【解析】因为45cos ,cos 513A C ==,且,A C 为三角形的内角,所以312sin ,sin 513A C ==,sin sin[π()]B AC =-+,63sin()sin cos cos sin 65A C A C A C =+=+=,又因为sin sin a b AB =,所以sin 21sin 13a B b A ==. 【点评】在解有关三角形的题目时,要有意识地考虑用哪个定理更合适,或是两个定理都要用,要抓住能够利用某个定理的信息.一般地,如果式子中含有角的余弦或边的二次式时,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.(16)【2016年全国Ⅱ,文16,5分】有三张卡片,分别写有1和2,1和3,2和3. 甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是_______.【答案】1和3【解析】由题意分析可知甲的卡片上的数字为1和3,乙的卡片上的数字为2和3,丙的卡片上的数字为1和2.【点评】演绎推理,就是从一般性的前提出发,通过推导即“演绎”,得出具体陈述或个别结论的过程.三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)【2016年全国Ⅱ,文17,12分】等差数列{}n a 中,34574,6a a a a +=+=.(1)求{}n a 的通项公式;(2)设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[]0.90=,[]2.62=. 解:(1)设数列{}n a 的公差为d ,有11254,53a d a d -=-=,解得121,5a d ==,所以{}n a 的通项公式为235n n a +=. (2)由(1)知235n n b +⎡⎤=⎢⎥⎣⎦,当1,2,3n =时,2312,15n n b +≤<=;当4,5n =时,2323,25n n b +≤<=; 当6,7,8n =时,2334,35n n b +≤<=;当9,10n =时,2345,45n n b +≤<=, 所以数列{}n b 的前10项和为1322334224⨯+⨯+⨯+⨯=.【点评】求解本题时常出现以下错误:对“[]x 表示不超过x 的最大整数”理解出错.(18)【2016年全国Ⅱ,文18,12分】某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保(1(2)记B 为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求()P B 的估计值;(3)求续保人本年度的平均保费估计值.解:(1)事件A 发生当且仅当一年内出险次数小于2.由所给数据知,一年内险次数小于2的频率为60500.55200+=, 故()P A 的估计值为0.55.(2)事件B 发生当且仅当一年内出险次数大于1且小于4.由是给数据知,一年内出险次数大于1且小于4的频率为30300.3200+=,故()P B 的估计值为0.3. (3a ,因此,续保人本年度平均保费估计值为1.1925a .【点评】样本的数字特征常见的命题角度有:(1)样本的数字特征与频率分布直方图交汇;(2)样本的数字特征与茎叶图交汇;(3)样本的数字特征与优化决策问题交汇.(19)【2016年全国Ⅱ,文19,12分】如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE CF =,EF 交BD 于点H ,将D E F △沿EF 折到D'EF △的位置. (1)证明:AC HD'⊥;(2)若55,6,,4AB AC AE OD'====D'ABCFE -的体积. 解:(1)由已知得,,AC BD AD CD ⊥=又由AE CF =得AE CF AD CD =,故//AC EF . 由此得,EF HD EF HD '⊥⊥,所以//AC HD '.(2)由//EF AC 得14OH AE DO AD ==,由5,6AB AC ==得4DO BO ===,所以1,3OH D H DH '===,于是2222219OD OH D H ''+=+==,故OD OH '⊥由(1)知AC HD '⊥,又,AC BD BD HD H '⊥= ,所以AC ⊥平面BHD ',于是AC OD '⊥,又由,OD OH AC OH O '⊥= ,所以,OD '⊥平面.ABC 又由EF DH AC DO =得9.2EF = 五边形ABCFE 的面积11969683.222S =⨯⨯-⨯⨯=所以五棱锥D ABCEF '-体积16934V =⨯⨯. 【点评】立体几何中的折叠问题,应注意折叠前后线段的长度、角哪些变了,哪些没变.(20)【2016年全国Ⅱ,文20,12分】已知函数()()()1ln 1f x x x a x =+--.(1)当4a =时,求曲线()y f x =在()()1,1f 处的切线方程;(2)若当()1,x ∈+∞时,()0f x >,求a 的取值范围.解:(1)()f x 的定义域为()0,+∞.当4a =时,1()(1)ln 4(1),()ln 3f x x x x f x x x'=+--=+-,()()12,10f f '=-=. 曲线()y f x =在(1,(1))f 处的切线方程为220x y +-=. (2)当()1,x ∈+∞时,()0f x >等价于()1ln 01a x x x -->+. 令(1)()ln 1-=-+a x g x x x ,则222122(1)1(),(1)0(1)(1)a x a x g x g x x x x +-+'=-==++, (i )当2a ≤,()1,x ∈+∞时,222(1)1210x a x x x +-+≥-+>,故()()0,g x g x '>在()1,x ∈+∞上单调递增,因此()0g x >;(ii )当2a >时,令()0g x '=得1211x a x a =-=-由21x >和121x x =得11x <,故当()21,x x ∈时,()0g x '<,()g x 在2(1,)x x ∈单调递减,因此()0g x <.综上,a 的取值范围是(],2-∞.【点评】求函数的单调区间的方法:(1)确定函数()y f x =的定义域;(2)求导数()y f x ''=;(3)解不等式()0f x '>,解集在定义域内的部分为单调递增区间;(4)解不等式()0f x '<,解集在定义域内部分为单调递减区间.(21)【2016年全国Ⅱ,文21,12分】已知A 是椭圆22:143x y E +=的左顶点,斜率为()0k k >的直线交E 于A ,M 两点,点N 在E 上,MA NA ⊥.(1)当AM AN =时,求AMN ∆的面积;(2)当2AM AN =2k <.解:(1)设11(,)M x y ,则由题意知10y >.由已知及椭圆的对称性知,直线AM 的倾斜角为4π, 又(2,0)A -,因此直线AM 的方程为2y x =+.将2x y =-代入22143x y +=得27120y y -=, 解得0y =或127y =,所以1127y =.因此AMN ∆的面积11212144227749AMN S ∆=⨯⨯⨯=. (2)将直线AM 的方程(2)(0)y k x k =+>代入22143x y +=得()2222341616120k x k x k +++-=.由()2121612234k x k-⋅-=+得()21223434k x k -=+,故1||2|AM x +=.由题设,直线AN 的方程为()12y x k =-+,故同理可得||AN =. 由2||||AM AN =得2223443k k k =++,即3246380k k k -+-=. 设()324638f t t t t =-+-,则k 是()f t 的零点,()()22'121233210f t t t t =-+=-≥,所以()f t 在()0,+∞单调递增,又260,(2)60f f =<=>,因此()f t 在()0,+∞有唯一的零点,且零点k 在)22k <. 【点评】对于直线与椭圆的位置关系问题,通常将直线方程与椭圆方程联立进行求解,注意计算的准确性. 请考生在(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,做答时请写清题号.(22)【2016年全国Ⅱ,文22,10分】(选修4-1:几何证明选讲)如图,在正方形ABCD 中,E ,G 分别在边DA ,DC 上(不与端点重合),且DE DG =,过D 点作DF CE ⊥,垂足为F .(1)证明:B ,C ,G ,F 四点共圆;(2)若1AB =,E 为DA 的中点,求四边形BCGF 的面积.解:(1)因为DF EC ⊥,所以,DEF CDF ∆~∆则有,,DF DE DG GDF DEF FCB CF CD CB∠=∠=∠== 所以,DGF CBF ∆~∆由此可得,DGF CBF ∠=∠由此0180,CGF CBF ∠+∠=所以,,,B C G F 四点共圆.(2)由,,,B C G F 四点共圆,CG CB ⊥知FG FB ⊥,连结GB ,由G 为Rt DFC ∆斜边CD 的中点,知GF GC =,故Rt Rt ,BCG BFG ∆~∆∴四边形BCGF 的面积S 是GCB ∆面积GCB S ∆的2倍, 即111221222GCB S S ∆==⨯⨯⨯=. 【点评】判定两个三角形相似要注意结合图形性质灵活选择判定定理,特别要注意对应角和对应边.通过相似三角形的性质可用来证明线段成比例、角相等,还可间接证明线段相等.(23)【2016年全国Ⅱ,文23,10分】(选修4-4:坐标系与参数方程)在直角坐标系xOy 中,圆C 的方程为22(+6)+=25x y .(1)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程;(2)直线l 的参数方程是cos sin x t α,y t α,=⎧⎨=⎩(t 为参数),l 与C 交于A ,B 两点,AB l 的斜率. 解:(1)由cos ,sin x y ρθρθ==可得C 的极坐标方程212cos 110ρρθ++=.(2)在(1)中建立的极坐标系中,直线l 的极坐标方程为()R θαρ=∈,由,A B 所对应的极径分别为12,,ρρ将l 的极坐标方程代入C 的极坐标方程得212cos 110ρρα++=.于是121212cos ,11ρραρρ+=-=,12AB ρρ=-AB =23cos ,tan 8αα==所以l或. 【点评】极坐标与直角坐标互化时要注意:将点的直角坐标化为极坐标时,一定要注意点所在的象限和极角的范围,否则点的极坐标将不唯一;将曲线方程进行互化时,一定要注意变量的范围.要注意转化的等价性.(24)【2016年全国Ⅱ,文24,10分】(选修4-5:不等式选讲)已知函数11()22f x x x =-++,M 为不等式()2f x <的解集.(1)求M ;(2)证明:当,a b M ∈时,1a b ab +<+.解:(1)12,,211()1,,2212,.2x x f x x x x ⎧-≤-⎪⎪⎪=-<<⎨⎪⎪≥⎪⎩当12x ≤-时,由()2f x <得22x -<,解得1x >-;当1122x -<<时,()2f x <; 当12x ≥时,由()2f x <得22,x <解得1x <.所以()2f x <的解集{}|11M x x =-<<. (2)由(1)知,当,a b M ∈时,11,11a b -<<-<<,从而22222222()(1)1(1)(1)0a b ab a b a b a b +-+=+--=--<,因此|||1|a b ab +<+.【点评】形如||||x a x b c -+-≥(或c ≤)型的不等式主要有两种解法:(1)分段讨论法:利用绝对值号内式子对应的方程的根,将数轴分为(,]a -∞,(,]a b ,(),b +∞ (此处设a b <)三个部分,在每个部分去掉绝对值号并分别列出对应的不等式进行求解,然后取各个不等式解集的并集.(2)图象法:作出函数1||||y x a x b =-+-和2y c =的图象,结合图象求解.。
2016年高考文科数学全国2卷试题及答案(Word版)

2016 年普通高等学校招生全国统一考试文科数学注意事项:一、选择题:本大题共12 小题。
每小题 5 分,在每个小题给出的四个选项中,只有一项是符合要求的。
2(1)已知集合 A {1,2,3},B { x | x 9} ,则 A B(A ){ 2,1,0,1,2,3} (B){ 2,1,0,1,2} (C){1 ,2,3} (D){1 ,2}(2)设复数z 满足z i 3 i ,则z =(A ) 1 2i (B)1 2i (C)3 2i (D)3 2i(3) 函数y =Asin( x ) 的部分图像如图所示,则(A )y 2sin(2 x ) (B)y 2sin(2 x)6 3(C)y 2sin(2 x+ ) (D)y 2sin(2 x+ )6 3(4) 体积为8 的正方体的顶点都在同一球面上,则该球面的表面积为(A )12 (B)323(C)(D)(5) 设F 为抛物线C:y2=4x 的焦点,曲线y=2=4x 的焦点,曲线y= kx(k>0)与C 交于点P,PF ⊥x 轴,则k=(A )12 (B)1 (C)32 (D)222- 2x- 8y+13=0 的圆心到直线ax+ y- 1=0 的距离为1,则a= (6) 圆x +y(A )-43 (B)-34(C) 3 (D)2(7) 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π(B)24π(C)28π(D)32π(8) 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40 秒.若一名行人来到该路口遇到红灯,则至少需要等待15 秒才出现绿灯的概率为(A )710 (B)58(C)38(D)310(9) 中国古代有计算多项式值得秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的 a 为2,2,5,则输出的s=(A )7 (B)12 (C)17 (D)34lgx 的定义域和值域相同的是(10) 下列函数中,其定义域和值域分别与函数y=10(A )y= x(B)y=lg x(C)y=2x(D)y 1x(11) 函数πf (x) cos2 x 6cos( x) 的最大值为2(A )4(B)5 (C)6 (D)7(12) 已知函数f(x )(x∈R)满足f(x)=f(2-x),若函数y=|x2-2x-3| 与y= f( x) 图像的交点为(x1,y1),(x2,y2),⋯,m(x m,y m),则xi=i 1(A)0 (B) m (C) 2m (D) 4m二.填空题:共4小题,每小题5分.(13) 已知向量a=(m,4),b=(3,-2) ,且a∥b,则m=___________.x y 1 0x y 3 0,则z= x-2y 的最小值为__________ (14) 若x,y 满足约束条件x 3 0(15)△ABC 的内角A,B,C 的对边分别为a,b,c,若cos4 5A ,cos C,a=1,则b=____________.5 13(16)有三张卡片,分别写有 1 和2,1 和3,2 和3. 甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________________.三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分12 分)等差数列{ a n } 中,a3 a 4 4, a5 a 7 6(I )求{ a n }的通项公式;(II)设b n =[ an ],求数列{bn} 的前10 项和,其中[x] 表示不超过x 的最大整数,如[0.9]=0,[2.6]=2(18)(本小题满分12 分)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200 名续保人在一年内的出险情况,得到如下统计表:(I )记 A 为事件:“一续保人本年度的保费不高于基本保费”。
2016全国2卷高考文科数学试卷及问题详解

2016年普通高等学校招生全统一考试文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共24题,共150分第Ⅰ卷一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 已知集合{}3,2,1=A ,{}92<=x x B ,则=B A (A ){}3,2,1,0,1,2-- (B ){}2,1,0,1- (C ){}3,2,1 (D ){}2,1(2) 设复数z 满足i i z -=+3,则=z(A )i 21+- (B )i 21- (C )i 23+ (D )i 23- (3) 函数)sin(ϕω+=x A y 的部分图像如图所示,则(A ))62sin(2π-=x y (B ))32sin(2π-=x y (C ))62sin(2π+=x y (D ))32sin(2π+=x y(4) 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为(A )π12 (B )π332(C )π8 (D )π4(5) 设F 为抛物线C :x y 42=的焦点,曲线)0(>=k xky 与C 交于点P ,x PF ⊥轴,则=k (A )21 (B )1 (C )23(D )2(6) 圆0138222=+--+y x y x 的圆心到直线01=-+y ax 的距离为1,则=a(A )3 (B )43-(C )3 (D )2 (7) 右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为 (A )20π(B )24π (C )28π (D )32π(8) 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为 (A )107 (B )85 (C )83 (D )103(9) 中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的2=x ,2=n ,依次输入的a 为2,2,5,则输出的=s (A )7 (B )12 (C )17 (D )34 (10)下列函数中,其定义域和值域分别与函数xy lg 10=的定义域和值域相同的是(A )x y = (B )x y lg = (C )xy 2= (D )xy 1=(11)函数)(x x x f -+=2cos6 2 cos )(π的最大值为 (A )4 (B )5 (C )6 (D )7(12)已知函数)( )(R x x f ∈满足)2()(x f x f -=,若函数322--=x x y 与)(x f y =图像的交点为),(,),,(),,(2211m m y x y x y x ⋯,则∑=mi ix1(A )0 (B )m (C )m 2 (D )m 4第Ⅱ卷本卷包括必考题和选考题两部分。
2016年高考新课标2文科数学真题及答案

2016年普通高等学校招生全国统一考试(新课标全国卷Ⅱ)文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分,考试时间120分钟。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)已知集合{1,2,3}A =,2{|9}B x x =<,则A B =A .{2,1,0,1,2,3}--B .{2,1,0,1,2}--C .{1,2,3}D .{1,2} (2)设复数z 满足i 3i z +=-,则z =A .12i -+B .12i -C .32i +D .32i -(3)函数sin()y A x ωϕ=+的部分图象如图所示,则A .2sin(2)6y x π=-B .2sin(2)3y x π=-C .2sin()6y x π=+D .2sin()3y x π=+(4)体积为8的正方体的顶点都在同一球面上,则该球的表面积为A .12πB .323πC .8πD .4π(5)设F 为抛物线2:4C y x =的焦点,曲线(0)k y k x=>与C 交于点P ,PF x ⊥轴,则k =A .12B .1C .32D .2(6)圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a =A .43-B .34-C.2(7)右图是由圆柱与圆锥组合而成的几何体 的三视图,则该几何体的表面积为A .20πB .24πC .28πD .32π(8间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为A .710B .58C .38D .310 (9)中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的2x =,2n =,依次输入的a 为2,2,5,则输出的s =A .7B .12C .17D .34(10)下列函数中,其定义域和值域分别与函数lg 10x y =的定义域和值域相同的是A .y x =B .lg y x =C .2x y =D.y =(11)函数()cos26cos()2f x x x π=+-的最大值为A .4B .5C .6D .7 (12)已知函数()()f x x ∈R 满足()(2)f x f x =-,若函数2|23|y x x =--与()y f x =图象的交点为11(,)x y ,22(,)x y ,…,(,)m m x y ,则1mi i x ==∑A .0B .mC .2mD .4m第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分. (13)已知向量(,4)m =a ,(3,2)=-b ,且a ∥b ,则m =.(14)若x ,y 满足约束条件10,30,30,x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩则2z x y =-的最小值为.(15)ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,若4c o s 5A =,5cos 13C =,1a =,则b =.(16)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是.三、解答题:解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分) 等差数列{}n a 中,344a a +=,576a a +=. (Ⅰ)求{}n a 的通项公式;(Ⅱ)设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]0=,[2.6]2=.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求()P A的估计值;(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求()P B的估计值;(Ⅲ)求续保人本年度的平均保费的估计值.如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD上,AE CF =,EF 交BD 于点H ,将DEF △沿EF 折到DEF'△的位置. (Ⅰ)证明:AC HD '⊥;(Ⅱ)若5AB =,6AC =,54AE =,OD '=求五棱锥D ABCFE '-的体积.(20)(本小题满分12分)D 'OECHFDBA已知函数()(1)ln(1)=+--.f x x x a x(Ⅰ)当4a=时,求曲线()f处的切线方程;y f x=在(1,(1))(Ⅱ)若当(1,)f x>,求a的取值范围.x∈+∞时,()0(21)(本小题满分12分)已知A 是椭圆22:143x y E +=的左顶点,斜率为(0)k k >的直线交E 于A ,M 两点,点N 在E 上,MA NA ⊥.(Ⅰ)当||||AM AN =时,求AMN △的面积; (Ⅱ)当2||||AM AN =2k <.请考生在第(22)、(23)、(24)题中任选一题做答,如果多做,按所做的第一题记分.(22)(本小题满分10分)选修4–1:几何证明选讲如图,在正方形ABCD 中,E ,G 分别在边DA ,DC 上(不与端点重合),且DE DG =,过D 点作DF CE ⊥,垂足为F . (Ⅰ)证明:B ,C ,G ,F 四点共圆;(Ⅱ)若1AB =,E 为DA 的中点,求四边形BCGF 的面积.(23)(本小题满分10分)选修4–4:坐标系与参数方程 在直角坐标系xOy 中,圆C 的方程为22(6)25x y ++=.(Ⅰ)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程;(Ⅱ)直线l 的参数方程是cos ,sin ,x t y t αα=⎧⎨=⎩(t 为参数),l 与C交于A ,B 两点,||AB =l 的斜率.(24)(本小题满分10分)选修4–5:不等式选讲 已知函数11()||||22f x x x =-++,M 为不等式()2f x <的解集.(Ⅰ)求M ;(Ⅱ)证明:当a ,b M ∈时,|||1|a b ab +<+.E GD CBA参考答案第Ⅰ卷一. 选择题:本大题共12小题。
2016年高考文科数学全国2卷试题与答案(Word版)

2016 年普通高等学校招生全国统一考试文科数学注意事项:一、选择题:本大题共12 小题。
每小题 5 分,在每个小题给出的四个选项中,只有一项是符合要求的。
2(1)已知集合 A {1,2,3},B { x | x 9} ,则 A B(A ){ 2,1,0,1,2,3} (B){ 2,1,0,1,2} (C){1 ,2,3} (D){1 ,2}(2)设复数z 满足z i 3 i ,则z =(A ) 1 2i (B)1 2i (C)3 2i (D)3 2i(3) 函数y =Asin( x ) 的部分图像如图所示,则(A )y 2sin(2 x ) (B)y 2sin(2 x)6 3(C)y 2sin(2 x+ ) (D)y 2sin(2 x+ )6 3(4) 体积为8 的正方体的顶点都在同一球面上,则该球面的表面积为(A )12 (B)323(C)(D)(5) 设F 为抛物线C:y2=4x 的焦点,曲线y=2=4x 的焦点,曲线y= kx(k>0)与C 交于点P,PF ⊥x 轴,则k=(A )12 (B)1 (C)32 (D)222- 2x- 8y+13=0 的圆心到直线ax+ y- 1=0 的距离为1,则a= (6) 圆x +y(A )-43 (B)-34(C) 3 (D)2(7) 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π(B)24π(C)28π(D)32π(8) 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40 秒.若一名行人来到该路口遇到红灯,则至少需要等待15 秒才出现绿灯的概率为(A )710 (B)58(C)38(D)310(9) 中国古代有计算多项式值得秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的 a 为2,2,5,则输出的s=(A )7 (B)12 (C)17 (D)34lgx 的定义域和值域相同的是(10) 下列函数中,其定义域和值域分别与函数y=10(A )y= x(B)y=lg x(C)y=2x(D)y 1x(11) 函数πf (x) cos2 x 6cos( x) 的最大值为2(A )4(B)5 (C)6 (D)7(12) 已知函数f(x )(x∈R)满足f(x)=f(2-x),若函数y=|x2-2x-3| 与y= f( x) 图像的交点为(x1,y1),(x2,y2),⋯,m(x m,y m),则xi=i 1(A)0 (B) m (C) 2m (D) 4m二.填空题:共4小题,每小题5分.(13) 已知向量a=(m,4),b=(3,-2) ,且a∥b,则m=___________.x y 1 0x y 3 0,则z= x-2y 的最小值为__________ (14) 若x,y 满足约束条件x 3 0(15)△ABC 的内角A,B,C 的对边分别为a,b,c,若cos4 5A ,cos C,a=1,则b=____________.5 13(16)有三张卡片,分别写有 1 和2,1 和3,2 和3. 甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________________.三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分12 分)等差数列{ a n } 中,a3 a 4 4, a5 a 7 6(I )求{ a n }的通项公式;(II)设b n =[ an ],求数列{bn} 的前10 项和,其中[x] 表示不超过x 的最大整数,如[0.9]=0,[2.6]=2(18)(本小题满分12 分)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:计表:随机调查了该险种的200 名续保人在一年内的出险情况,得到如下统(I )记 A 为事件:“一续保人本年度的保费不高于基本保费”。
2016年高考全国2卷文数试题与答案

2016年普通高等学校招生全国统一考试文科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的、号填写在本试卷和答题卡相应位置上。
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号框涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号框。
写在本试卷上无效。
3.答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷一、 选择题:本大题共12小题。
每小题5分,在每个小题给出的四个选项中,只有一项是符合要求的。
(1)已知集合{123}A =,,,2{|9}B x x =<,则A B =I (A ){210123}--,,,,, (B ){21012}--,,,, (C ){123},, (D ){12},(2)设复数z 满足i 3i z +=-,则z =(A )12i -+(B )12i -(C )32i +(D )32i - (3) 函数=sin()y A x ωϕ+的部分图像如图所示,则(A )2sin(2)6y x π=-(B )2sin(2)3y x π=-(C )2sin(2+)6y x π=(D )2sin(2+)3y x π=(4) 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为 (A )12π(B )323π(C )8π(D )4π (5) 设F 为抛物线C :y 2=4x 的焦点,曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,则k = (A )12(B )1 (C )32(D )2 (6) 圆x 2+y 2−2x −8y +13=0的圆心到直线ax +y −1=0的距离为1,则a = (A )−43(B )−34(C )3(D )2(7) 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π(B )24π(C )28π(D )32π(8) 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为 (A )710(B )58(C )38(D )310(9)中国古代有计算多项式值得九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的a 为2,2,5,则输出的s = (A )7 (B )12 (C )17 (D )34(10) 下列函数中,其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是 (A )y =x (B )y =lg x (C )y =2x (D )y x=(11) 函数π()cos 26cos()2f x x x =+-的最大值为 (A )4(B )5(C )6 (D )7(12) 已知函数f (x )(x ∈R )满足f (x )=f (2-x ),若函数y =|x 2-2x -3| 与y =f (x ) 图像的交点为(x 1,y 1),(x 2,y 2),…,(x m ,y m ),则1=mi i x =∑(A)0 (B)m (C) 2m (D) 4m 二.填空题:共4小题,每小题5分.(13) 已知向量a =(m ,4),b =(3,-2),且a ∥b ,则m =___________.(14) 若x ,y 满足约束条件103030x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩,则z =x -2y 的最小值为__________(15)△ABC 的角A ,B ,C 的对边分别为a ,b ,c ,若4cos 5A =,5cos 13C =,a =1,则b =____________.(16)有三卡片,分别写有1和2,1和3,2和3. 甲,乙,丙三人各取走一卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________________.三、解答题:解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分)等差数列{n a }中,34574,6a a a a +=+=(I )求{n a }的通项公式; (II)设nb =[na ],求数列{nb }的前10项和,其中[x]表示不超过x 的最大整数,如[0.9]=0,[2.6]=2(18)(本小题满分12分)某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年的出险情况,得到如下统计表:(I )记A 为事件:“一续保人本年度的保费不高于基本保费”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年普通高等学校招生全统一考试文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共24题,共150分第Ⅰ卷一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 已知集合{}3,2,1=A ,{}92<=x x B ,则=B A (A ){}3,2,1,0,1,2-- (B ){}2,1,0,1- (C ){}3,2,1 (D ){}2,1(2) 设复数z 满足i i z -=+3,则=z(A )i 21+- (B )i 21- (C )i 23+ (D )i 23- (3) 函数)sin(ϕω+=x A y 的部分图像如图所示,则(A ))62sin(2π-=x y (B ))32sin(2π-=x y (C ))62sin(2π+=x y (D ))32sin(2π+=x y (4) 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为(A )π12 (B )π332(C )π8 (D )π4 (5) 设F 为抛物线C :x y 42=的焦点,曲线)0(>=k xky 与C 交于点P ,x PF ⊥轴,则=k (A )21 (B )1 (C )23(D )2 (6) 圆0138222=+--+y x y x 的圆心到直线01=-+y ax 的距离为1,则=a(A )3 (B )43-(C )3 (D )2 (7) 右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π(B )24π (C )28π (D )32π(8) 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为(A )107 (B )85 (C )83 (D )103(9) 中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的2=x ,2=n ,依次输入的a 为2,2,5,则输出的=s(A )7 (B )12 (C )17 (D )34 (10)下列函数中,其定义域和值域分别与函数xy lg 10=的定义域和值域相同的是(A )x y = (B )x y lg = (C )xy 2= (D )xy 1=(11)函数)(x x x f -+=2cos6 2 cos )(π的最大值为 (A )4 (B )5 (C )6 (D )7(12)已知函数)( )(R x x f ∈满足)2()(x f x f -=,若函数322--=x x y 与)(x f y =图像的交点为),(,),,(),,(2211m m y x y x y x ⋯,则∑=mi ix1(A )0 (B )m (C )m 2 (D )m 4第Ⅱ卷本卷包括必考题和选考题两部分。
第(13)~(21)题为必考题,每个试题都必须作答。
第(22)~(24)题为选考题,考生根据要求作答。
二、填空题:本题共4小题,每小题5分。
(13)已知向量a )4,(m =,b )2,3(-=,且a ∥b ,则=m .(14)若y x ,满足约束条件⎪⎩⎪⎨⎧≤-≥-+≥+-,03,03,01x y x y x 则y x z 2-=的最小值为 .(15)ABC △的内角C B A ,,的对边分别为c b a ,,,若1,135cos ,54cos ===a C A ,则=b . (16)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 . 三、解答题:解答应写出文字说明、证明过程或演算步骤。
(17)(本小题满分12分)等差数列{}n a 中,且443=+a a ,675=+a a .(Ⅰ)求{}n a 的通项公式;(Ⅱ)记[]n n a b =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[]09.0=,[]26.2=.(18)(本小题满分12分)某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:随机调查了设该险种的200名续保人在一年内的出险情况,得到如下统计表:(Ⅰ)记A 为事件:“一续保人本年度的保费不高于基本保费”.求)(A P 的估计值;(Ⅱ)记B 为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求)(B P 的估计值;(Ⅲ)求续保人本年度平均保费的估计值.(19)(本小题满分12分)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点F E ,分别在CD AD ,上,CF AE =,EF 交BD 于点H .将DEF △沿EF 折到EF D '△的位置.(Ⅰ)证明:D H AC '⊥; (Ⅱ)若5=AB ,6=AC ,45=AE ,22='OD ,求五棱锥ABCFE D -'的体积.(20)(本小题满分12分)已知函数)1( ln )1()(--+=x a x x x f .(Ⅰ)当4=a 时,求曲线)(x f y =在))1(,1(f 处的切线方程;(Ⅱ)若当),1(+∞∈x 时,0)(>x f ,求a 的取值范围.(21)(本小题满分12分)已知A 是椭圆E :13422=+y x 的左顶点,斜率为)0(>k k 的直线交E 于M A ,两点,点N 在E 上,NA MA ⊥.(Ⅰ)当AN AM =时,求AMN △的面积;(Ⅱ)当AN AM =2时,证明:23<<k .请考生在第(22)~(24)题中任选一题作答,如果多做,则按所做的第一题计分。
(22)(本小题满分10分)选修4-1:几何证明选讲如图,在正方形ABCD 中,G E ,分别在边DC DA ,上(不与端点重合),且DG DE =,过D 点作CE DF ⊥,垂足为F .(Ⅰ)证明:F G C B ,,,四点共圆;(Ⅱ)若1=AB ,E 为DA 的中点,求四边形BCGF 的面积.(23)(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,圆C 的方程为25)6(22=++y x . (Ⅰ)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程;(Ⅱ)直线l 的参数方程是⎩⎨⎧==,sin ,cos ααt y t x (t 为参数),l 与C 交于B A ,两点,10=AB ,求l 的斜率.(24)(本小题满分10分)选修4-5:不等式选讲已知函数2121)(++-=x x x f ,M 为不等式2)(<x f 的解集. (Ⅰ)求M ;(Ⅱ)证明:当M b a ∈,时,ab b a +<+1.2016年全国卷Ⅱ高考数学(文科)答案一. 选择题(1)D (2)C (3) A (4)A (5) D (6)A(7)C (8)B (9) C (10)D (11) B (12)B 二.填空题(13)6-(14)5-(15)2113(16)1和3三、解答题(17)(本小题满分12分)(Ⅰ)设数列{}n a 的公差为d ,由题意有11254,53a d a d -=-=,解得121,5a d ==, 所以{}n a 的通项公式为235n n a +=. (Ⅱ)由(Ⅰ)知235n n b +⎡⎤=⎢⎥⎣⎦, 当n=1,2,3时,2312,15n n b +≤<=; 当n=4,5时,2323,25n n b +≤<=; 当n=6,7,8时,2334,35n n b +≤<=; 当n=9,10时,2345,45n n b +≤<=, 所以数列{}n b 的前10项和为1322334224⨯+⨯+⨯+⨯=. (18)(本小题满分12分)(Ⅰ)事件A 发生当且仅当一年内出险次数小于2.由所给数据知,一年内险次数小于2的频率为60500.55200+=, 故P(A)的估计值为0.55.(Ⅱ)事件B 发生当且仅当一年内出险次数大于1且小于4.由是给数据知,一年内出险次数大于1且小于4的频率为30300.3200+=, 故P(B)的估计值为0.3. (Ⅲ)由题所求分布列为:调查200名续保人的平均保费为0.850.300.25 1.250.15 1.50.15 1.750.3020.10 1.1925a a a a a a a ⨯+⨯+⨯+⨯+⨯+⨯=,因此,续保人本年度平均保费估计值为1.1925a. (19)(本小题满分12分)(I )由已知得,,.⊥=AC BD AD CD又由=AE CF 得=AE CFAD CD,故//.AC EF 由此得,'⊥⊥EF HD EF HD ,所以//.'AC HD .(II )由//EF AC 得1.4==OH AE DO AD 由5,6==AB AC得 4.===DO BO所以1, 3.'===OH D H DH于是2222219,''+=+==OD OH D H 故.'⊥OD OH由(I )知'⊥AC HD ,又,'⊥=AC BD BDHD H ,所以⊥AC 平面,'BHD 于是.'⊥AC OD 又由,'⊥=OD OH ACOH O ,所以,'⊥OD 平面.ABC又由=EF DH AC DO 得9.2=EF 五边形ABCFE 的面积11969683.2224=⨯⨯-⨯⨯=S 所以五棱锥体积169342=⨯⨯=V (20)(本小题满分12分)(I )()f x 的定义域为(0,)+∞.当4=a 时,'ABCEF D -1()(1)ln 4(1),()ln 3'=+--=+-f x x x x f x x x,(1)2,(1)0.'=-=f f 曲线()=y f x 在(1,(1))f 处的切线方程为220.x y +-=(II )当(1,)∈+∞x 时,()0>f x 等价于(1)ln 0.1-->+a x x x 令(1)()ln 1-=-+a x g x x x ,则 222122(1)1(),(1)0(1)(1)+-+'=-==++a x a x g x g x x x x ,(i )当2≤a ,(1,)∈+∞x 时,222(1)1210+-+≥-+>x a x x x ,故()0,()'>g x g x 在(1,)∈+∞x 上单调递增,因此()0>g x ;(ii )当2>a 时,令()0'=g x 得1211=-=-+x a x a由21>x 和121=x x 得11<x ,故当2(1,)∈x x 时,()0'<g x ,()g x 在2(1,)∈x x 单调递减,因此()0<g x .综上,a 的取值范围是(],2.-∞ (21)(本小题满分12分)(Ⅰ)设11(,)M x y ,则由题意知10y >.由已知及椭圆的对称性知,直线AM 的倾斜角为4π, 又(2,0)A -,因此直线AM 的方程为2y x =+.将2x y =-代入22143x y +=得27120y y -=, 解得0y =或127y =,所以1127y =.因此AMN ∆的面积11212144227749AMN S ∆=⨯⨯⨯=. (II )将直线AM 的方程(2)(0)y k x k =+>代入22143x y +=得 2222(34)1616120k x k x k +++-=.由2121612(2)34k x k -⋅-=+得2122(34)34k x k -=+,故2212121||1|2|34k AM k x k +=++=+. 由题设,直线AN 的方程为1(2)y x k=-+,故同理可得22121||43k k AN k +=+. 由2||||AM AN =得2223443k k k=++,即3246380k k k -+-=. 设32()4638f t t t t =-+-,则k 是()f t 的零点,22'()121233(21)0f t t t t =-+=-≥, 所以()f t 在(0,)+∞单调递增,又(3)153260,(2)60f f =-<=>,因此()f t 在(0,)+∞有唯一的零点,且零点k 在(3,2)内,所以32k <<.(22)(本小题满分10分)(I )因为DF EC ⊥,所以,DEF CDF ∆~∆则有,,DF DE DG GDF DEF FCB CF CD CB∠=∠=∠== 所以,DGF CBF ∆~∆由此可得,DGF CBF ∠=∠由此0180,CGF CBF ∠+∠=所以,,,B C G F 四点共圆. (II )由,,,B C G F 四点共圆,CG CB ⊥知FG FB ⊥,连结GB ,由G 为Rt DFC ∆斜边CD 的中点,知GF GC =,故,Rt BCG Rt BFG ∆~∆因此四边形BCGF 的面积S 是GCB ∆面积GCB S ∆的2倍,即111221.222GCB S S ∆==⨯⨯⨯= (23)(本小题满分10分)(I )由cos ,sin x y ρθρθ==可得C 的极坐标方程212cos 110.ρρθ++= (II )在(I )中建立的极坐标系中,直线l 的极坐标方程为()R θαρ=∈由,A B 所对应的极径分别为12,,ρρ将l 的极坐标方程代入C 的极坐标方程得212cos 110.ρρα++=于是121212cos ,11,ρραρρ+=-=12||||AB ρρ=-==由||AB =得23cos ,tan 8αα==,所以l 或 (24)(本小题满分10分)(I )先去掉绝对值,再分12x <-,1122x -≤≤和12x >三种情况解不等式,即可得M ;(II )采用平方作差法,再进行因式分解,进而可证当a ,b ∈M 时,1a b ab +<+.试题解析:(I )12,,211()1,,2212,.2x x f x x x x ⎧-≤-⎪⎪⎪=-<<⎨⎪⎪≥⎪⎩当12x ≤-时,由()2f x <得22,x -<解得1x >-; 当1122x -<<时,()2f x <; 当12x ≥时,由()2f x <得22,x <解得1x <. 所以()2f x <的解集{|11}M x x =-<<.(II )由(I )知,当,a b M ∈时,11,11a b -<<-<<,从而22222222()(1)1(1)(1)0a b ab a b a b a b +-+=+--=--<,因此|||1|.a b ab +<+成功就是先制定一个有价值的目标,然后逐步把它转化成现实的过程。
