初中一次函数典型应用题
一次函数经典例题20题
一次函数经典例题20题以下是一些关于一次函数的经典例题，共计20道。
每道题后面会给出解答和解析。
1.若函数y=2x+3，求当x等于5时的y值。
解答：将x=5代入函数，得到y=2(5)+3=13。
2.若函数y=-3x+2，求当y等于7时的x值。
解答：将y=7代入函数，得到-3x+2=7，解方程得到x=-1。
3.若函数y=4x-1，求函数在x轴上的截距。
解答：当y=0时，解方程4x-1=0，得到x=1/4。
所以函数在x轴上的截距为1/4。
4.若函数y=-2x+5，求函数的斜率。
解答：斜率即为函数中x的系数，所以斜率为-2。
5.若函数y=3x+2与函数y=-2x+1相交于点P，求点P的坐标。
解答：将两个函数相等，得到3x+2=-2x+1，解方程得到x=-1/5。
将x=-1/5代入其中一个函数，得到y=3(-1/5)+2=1/5。
所以点P的坐标为(-1/5,1/5)。
6.若函数y=kx+3与函数y=2x-1平行，求k的值。
解答：两个函数平行意味着它们的斜率相等。
所以k=2。
7.若函数y=5x+b与函数y=3x-2垂直，求b的值。
解答：两个函数垂直意味着它们的斜率之积为-1。
所以5*3=-1，解方程得到b=-17。
8.若函数y=ax+2与函数y=-bx+4平行且在点(1,3)相交，求a和b的关系。
解答：两个函数平行意味着它们的斜率相等。
所以a=-b。
将点(1,3)代入其中一个函数，得到a+2=3，解方程得到a=1。
所以b=-1。
9.若函数y=-2x+a与函数y=x-1垂直，求a的值。
解答：两个函数垂直意味着它们的斜率之积为-1。
所以-2*1=-1，解方程得到a=-1。
10.若函数y=4x+3与y轴平行，求函数在x轴上的截距。
解答：与y轴平行意味着函数的斜率为无穷大。
所以在x轴上的截距不存在。
11.若函数y=-3x+2与x轴平行，求函数在y轴上的截距。
解答：与x轴平行意味着函数的斜率为0。
所以在y轴上的截距为2。
一次函数习题(应用题及分段函数)
一次函数应用题及分段函数1、 如图，直线y=12x+2交x 轴于点Ａ，交y 轴于点Ｂ，点Ｐ（x , y ）是线段AB 上一动点（与Ａ，Ｂ不重合），△PAO 的面积为Ｓ，求Ｓ与x 的函数关系式。
2、如图，直线L ：221+-=x y 与x 轴、y 轴分别交于A 、B 两点，在y 轴上有一点C （0，4）,动点M 从A 点以每秒1个单位的速度沿x 轴向左移动。
（1）求A 、B 两点的坐标；（2）求△COM 的面积S 与M 的移动时间t 之间的函数关系式； （3）当t 何值时△COM ≌△AOB ，并求此时M 点的坐标。
3、和谐商场销售甲、乙两种商品，甲种商品每件进价15元，售价20元；乙种商品每件进价35元，售价45元.（1）若该商场同时购进甲、乙两种商品共100件，恰好用去2700元，求能购进甲、乙两种商品各多少件？（2）该商场为使甲、乙两种商品共100件的总利润（利润=售价-进价）不少于750元，且不超过760元，请你帮助该商场设计相应的进货方案.PB AOy4、上海世博园建设期间，计划在园内某处种植A、B两种花卉，共需购买这两种花卉1200棵. 种植A、B 两种花卉的相关信息如下表：设购买A种花卉x棵，种植A、B两种花卉的总费用为y元.（1）求y关于x的函数关系式；（2）由于景观效果的需要，B种花卉的棵数是A种花卉棵数的2倍，求此时种植A、B两种花卉的总费用.5.一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售．售出土豆千克数与他手中持有的钱数（含备用零钱）的关系如图所示，结合图象回答下列问题：（1）农民自带的零钱是多少？（2）降价前他每千克土豆出售的价格是多少？（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆？6、.辽南素以“苹果之乡”著称，某乡组织20辆汽车装满运三种苹果42吨到外地销售。
一次函数应用题精选
一次函数应用 姓名 班级1．某地长途汽车客运公司规定旅客可以随身携带一定重量的行李，如果超过规定，则需购买行李票，行李票费用y （元）是行李重量x （公斤）的一次函数，其图像如图所示． 求：（1）y 与x 之间的函数关系式；（2）旅客最多可免费携带行李多少公斤．2．在某地，人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。
下面是蟋蟀所叫次数与温度变化情况对照表：蟋蟀叫次数 … 84 98 119 … 温度（℃）…151720…（1）根据表中数据确定该一次函数的关系式；（2）如果蟋蟀1分钟叫了63次，那么该地当时的温度大约为多少摄氏度？3.如图，折线ABC 是在江门市乘出租车所付车费y （元）与行车里程x （km ）•之间的函数关系图象． ①求当x≥3时该图象的函数关系式；②某人乘坐2.5km ，应付多少钱？ ③某人乘坐13km ，应付多少钱？④若某人付车费30.8元，出租车行驶了多少千米？4.某医药研究所开发了一种新药，•在实验药效时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y(ug )随时间x(h)•的变化情况如图所示．(1) 当成人按规定剂量服药后_______h ，血液中含药量最高，达每毫升______ug ，接着逐步衰减． (2)当成人按规定剂量服药后5h ，血液中含药量为每毫升________ug ． (3)求当x ≤ 2时，y 与x 之间的函数关系式． (4)求当x ≥ 2时，y 与x 之间的函数关系式是．5．如图，1l 反映了甲离开A 的时间与离A 地的距离的关系，2l 反映了乙离开A 地的时间与离A 地的距离之间的关系，根据图象填空： （1）当时间 时，甲、乙两人离A 地距离相等。
（2）当时间 时，甲在乙的前面，当时间 时，乙超过了甲。
（3）求1l 对应的函数表达式和2l 对应的函数表达式6/已知一个正比例函数与一个一次函数的图象交于点A （3,4），且OA=OB （1） 求两个函数的解析式；（2）求△AOB 的面积；7．如图，一次函数y ＝kx ＋b 的图像 经过A 、B 两点，与x 轴相交于点C 。
一次函数应用题
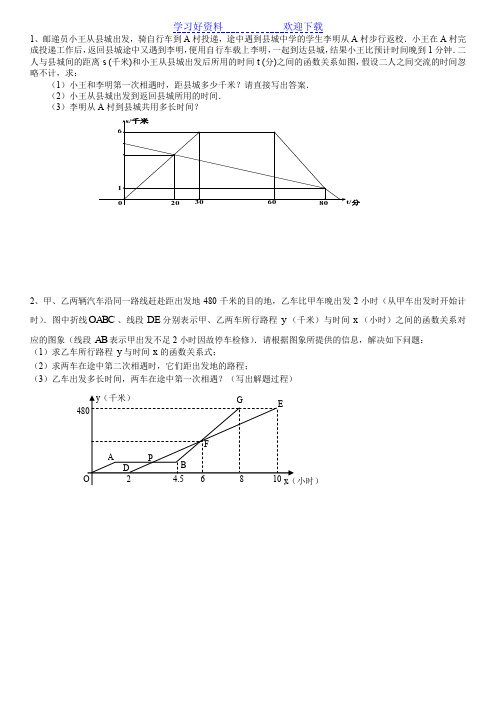
分1、邮递员小王从县城出发，骑自行车到A 村投递，途中遇到县城中学的学生李明从A 村步行返校．小王在A 村完成投递工作后，返回县城途中又遇到李明，便用自行车载上李明，一起到达县城，结果小王比预计时间晚到1分钟．二人与县城间的距离(千米)和小王从县城出发后所用的时间(分)之间的函数关系如图，假设二人之间交流的时间忽略不计，求：（1）小王和李明第一次相遇时，距县城多少千米？请直接写出答案．（2）小王从县城出发到返回县城所用的时间．（3）李明从A 村到县城共用多长时间？2、甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时（从甲车出发时开始计时）．图中折线、线段分别表示甲、乙两车所行路程（千米）与时间（小时）之间的函数关系对应的图象（线段表示甲出发不足2小时因故停车检修）．请根据图象所提供的信息，解决如下问题：（1）求乙车所行路程与时间的函数关系式；（2）求两车在途中第二次相遇时，它们距出发地的路程；（3）乙车出发多长时间，两车在途中第一次相遇？（写出解题过程）s t OABC DE y x AB y x3、春节期间，某客运站旅客流量不断增大，旅客往往需要长时间排队等候购票．经过调查发现，每天开始售票时，约有400人排队购票，同时又有新的旅客不断进入售票厅排队等候购票．售票时售票厅每分钟新增购票人数4人，每分钟每个售票窗口售票3张．某一天售票厅排队等候购票的人数y (人)与售票时间x (分钟)的关系如图所示，已知售票的前a 分钟只开放了两个售票窗口(规定每人只能购票一张)．(1)求a 的值．(2)求售票到第60分钟时，售票厅排队等候购票的旅客人数．(3)若要在开始售票后半小时内让所有的排队旅客都能够购到票，以便后来到站的旅客随到随购，至少需要同时开放几个售票窗口？4、有甲乙两个均装有进水管和出水管的容器，初始时，两容器同时开进水管，甲容器到8分钟时，关闭进水管打开出水管；到16分钟时，又打开了进水管，此时既进水又出水，到28分钟时，同时关闭两容器的进水管。
一次函数应用题(选择方案)(一)
一次函数应用题（选择方案）（一）1类型一: 利用函数值的大小选择方案例1 紧俏商品，经过市场调查发现，如果月初出售，可获得15%的利润，并可用本和利再投资其他商品，到月末又可获利10%；如果月末出售可获利30%，但要付存储费700元，请根据商场的资金情况，判断一下选择哪种销售方式获利较多，并说明商场投资25000元时，哪种销售方式获利较多。
2 类型二选择购买方案例2 甲乙两家体育器材商店出售同样地乒乓球拍和乒乓球，球拍每幅定价60元，乒乓求每盒定价10元。
今年世界乒乓球锦标赛期间，两家商店都搞促销活动：甲商店规定每买1副乒乓球拍赠2盒乒乓球；乙商店规定所有商品9折优惠。
某校乒乓球队需要2副乒乓球拍，乒乓球若干盒（不少于4盒）设该校要买乒乓求x盒，所需商品在甲商店购买需用y1元，在乙商店购买需要用y2元。
（1）请分别写出y1、y2与之间的函数解析式（不注明自变量x的取值范围）；（2）对x的取值情况进行分析，试说明在哪一家商店购买所需商品比较便宜；（3）若该校要买2副乒乓球拍和20盒乒乓球，在不考虑其他因素的情况下，请你设计一个最省钱的购买方案。
例3、商店出售茶壶和茶杯，茶壶每只定价为20元，茶杯每只定价为5元，该店制定了两种优惠办法：(1)买一只茶壶送一只茶杯；（2）按总价的92%付款。
某顾客需购茶壶4只，茶杯若干只（不少于4只），若设购买茶杯数为x（只），付款数为y(元)，试分别写出两种优惠办法中y(元)与x（只）之间的函数解析式，并讨论两种办法中哪种更省钱。
3类型三选择生产方案问题例4、某工厂生产某种产品，每件产品出厂价为1万元，其原材料成本价（含其他损耗）为0.55万元，同时在生产过程中平均每生产一件产品有1吨的废渣产出，为达到国家环保要求，需要对废渣进行处理，现有两种方案可供选择：方案一：由工厂对废渣直接处理，每处理1吨废渣所用的原料费为0.05万元，并且每月设备维护及损耗费为20万元。
方案二：工厂将废渣集中到废渣厂处理，每处理一吨需付0.1万元的处理费。
中考一次函数应用题
中考中的一次函数应用题1、“五一黄金周”的某一天，小明全家上午8时自驾小汽车从家里出发，到距离180千米的某著名旅游景点游玩。
该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示。
根据图象提供的有关信息，解答下列问题：（1）小明全家在旅游景点游玩了多少小时？（2）求出返程途中，s(千米)与时间t(时)的函数关系，并回答小明全家到家是什么时间？3）若出发时汽车油箱中存油15升，该汽车的油箱总容量为35升，汽车每行驶1千米耗油1/9升。
请你就“何时加油和加油量”给小明全家提出一个合理化建议。
(加油所用时间忽略不计)2、近几年来，由于经济和社会发展迅速，用电矛盾越来越突出。
为缓解用电紧张，某电力公司特制定了新的用电收费标准，每月用电量x（度）与应付电费y （元）的关系如图所示。
⑴请你根据图像所描述的信息，分别求出当0≤x≤50和x>50时，y与x的函数关系式。
⑵根据你的分析：当每月用电量不超过50度时，收费标准是_0.5元/度；当每月用电量超过50度时，收费标准是:3、甲乙两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查如图(所示)提供两方面的信息。
甲调查表明：每个甲鱼池个数由第一年1万只上升到第6年2万只。
乙调查表明：甲鱼池个数由第一年30个减少到第6年10个。
请你根据提供的信息说明：(1)第二年全县出产甲鱼的总数；(2)到第6年这个县的甲鱼养殖规模比第一年是扩大了还是缩小了？说明理由。
4、为了美化校园环境，争创绿色学校，某县教育局委托园林公司对A、B两校进行校园绿化。
已知A校有如图1的阴影部分空地需铺设草坪，B校有如图2的阴影部分空地需铺设草坪。
在甲、乙两地分别有同种草皮3500平方米和2500平方米出售，且售价一样。
若园林公司向甲、乙两地购买草皮，其路程和运费单价表如下：（注：运费单价表示每平方米草皮运送1千米所需的人民币。
）求(1)分别求出图1、图2的阴影部分面积；(2)请你给出一种草皮运送方案，并求出总运费；(3)请设计总运费最省的草皮运送方案，并说明理由。
九年级数学 专题25题一次函数应用典型例题
25题一次函数应用专题 一、近五年某某中考一次函数应用题 例1（09某某）某公司装修需用A 型板材240块、B 型板材180块，A 型板材规格是60 cm×30 cm ，B 型板材规格是40 cm×30 cm ．现只能购得规格是150 cm×30 cm 的标准板材．一X 标准板材尽可能多地裁出A 型、B 型板材，共有下列三种裁法：（图15是裁法一的裁剪示意图）裁法一 裁法二 裁法三 A 型板材块数1 2 0 B 型板材块数 2 m n设所购的标准板材全部裁完，其中按裁法一裁x X 、按裁法二裁yX 、按裁法三裁z X ，且所裁出的A 、B 两种型号的板材刚好够用．（1）上表中，m =，n =；（2）分别求出y 与x 和z 与x 的函数关系式；（3）若用Q 表示所购标准板材的X 数，求Q 与x 的函数关系式，并指出当x 取何值时Q 最小，此时按三种裁法各裁标准板材多少X ？解：（1）0 ，3．（2）由题意，得x+2y=240，∴y=120–12 x ．2x+3z=180，∴z=60–23x ．（3）由题意，得Q ＝x+y+z=x+120–12 x+60–23x .整理，得 ．Q=180–16x由题意，得⎩⎪⎨⎪⎧120–12x ≥060–23≥0 解得 x ≤90．【注：事实上，0≤x ≤90 且x 是6的整数倍】由一次函数的性质可知，当x =90时，Q 最小．此时按三种裁法分别裁90X 、75X 、0X ．例2（07某某）一手机经销商计划购进某品牌的A 型、B 型、C 型三款手机共60部，每款手机至少要购进8部，且恰好用完购机款61000元．设购进A 型手机x 部，B 型手机y 部．三款手机的进价和预售价如下表：手机型号 A型 B 型 C 型（1）用含x ，y （2）求出y 与x 之间的函数关系式；（3）假设所购进手机全部售出，综合考虑各种因素，该手机经销商在购销这批手机过程中需另外支出各种费用共1500元．①求出预估利润P （元）与x （部）的函数关系式；（注：预估利润P ＝预售总额-购机款-各种费用）②求出预估利润的最大值，并写出此时购进三款手机各多少部．25．解：（1）60-x-y ； …………………………………………………………………（2分）（2）由题意，得 900x+1200y+1100（60-x-y ）= 61000，整理得 y=2x-50． ………………………………………………………（5分）（3）①由题意，得 P= 1200x+1600y+1300（60-x-y ）- 61000-1500，整理得 P=500x+500． …………………………………………………（7分）②购进C 型手机部数为：60-x-y =110-3x ．根据题意列不等式组，得⎩⎪⎨⎪⎧x ≥82x-50≥8110–3x ≥8解得 29≤x ≤34．∴ xX 围为29≤x ≤34，且x 为整数．（注：不指出x 为整数不扣分） …（10分）∵P 是x 的一次函数，k=500＞0，∴P 随x 的增大而增大．∴当x 取最大值34时，P 有最大值，最大值为17500元． ………（11分）此时购进A 型手机34部，B 型手机18部，C 型手机8部． ………（12分）例3（06某某）有两段长度相等的河渠挖掘任务，分别交给甲、乙两个工程队同时进行挖掘．图11是反映所挖河渠长度y （米）与挖掘时间x （时）之间关系的部分图象．请解答下列问题： （1）乙队开挖到30米时，用了_____小时．开挖6小时时，甲队比乙队多挖了______米； （2）请你求出： ①甲队在0≤x ≤6的时段内，y 与x 之间的函数关系式；②乙队在2≤x ≤6的时段内，y 与x 之间的函数关系式；③开挖几小时后，甲队所挖掘河渠的长度开始超过乙队？（3）如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加到12米/时，结果两队同时完成了任务．问甲队从开挖到完工所挖河渠的长度为多少米？解：（1）2；10； ……………………………………………………………………（2分）（2）①设甲队在0≤x ≤6的时段内y 与x 之间的函数关系式为y =k 1x ，由图可知，函数图象过点（6，60），∴6 k 1=60，解得k 1=10，∴y =10x . …………………………………………………………………（4分）②设乙队在2≤x ≤6的时段内y 与x 之间的函数关系式为y =k 2x +b ，由图可知，函数图象过点（2，30）、（6，50），时)∴22230,650.k b k b +=⎧⎨+=⎩ 解得25,20.k b =⎧⎨=⎩ ∴y =5x ＋20． …………………………………………………………（7分）③由题意，得10x ＞5x ＋20，解得x ＞4.所以，4小时后，甲队挖掘河渠的长度开始超过乙队. ………………（9分）（说明：通过观察图象并用方程来解决问题，正确的也给分）（3）由图可知，甲队速度是：60÷6=10（米/时）．设甲队从开挖到完工所挖河渠的长度为z 米，依题意，得6050.1012z z --=…………………………………………………（11分） 解得 z =110．答：甲队从开挖到完工所挖河渠的长度为110米． ……………………（12分）例4（05某某）在一次蜡烛燃烧实验中，甲、乙两根蜡烛燃烧时剩余部分的高度y （厘米）与燃烧时间x（小时）之间的关系如图10所示. 请根据图象提供的信息解答下列问题：（1）甲、乙两根蜡烛燃烧前的高度分别是______________________，从点燃到燃烧尽所用的时间分别是_______________________.；（2）分别求甲、乙两根蜡烛燃烧时y 与x 之间的函数关系式；（3）燃烧多长时间时，甲、乙两根蜡烛的高度相等（不考虑都燃尽的情况）？在什么时间段内，甲蜡烛比乙蜡烛高？在什么时间段内，甲蜡烛比乙蜡烛低？二、一次函数应用——方案设计例5（某某市2009年）某公司为了开发新产品，用A 、B 两种原料各360千克、290千克，试制甲、乙两种新型产品共50件，下表是试验每件新产品所需原料的相关数据： x 的取值X 围；（2）若甲种产品每件成本为70元，乙种产品每件成本为90元，设两种产品的成本总额为y 元，写出成本总额y （元）与甲种产品件数x （件）之间的函数关系式；当甲、乙两种产品各生产多少件时，产品的成本总额最少？并求出最少的成本总额．1．解：（1）依题意列不等式组得94(50)360310(50)290x x x x +-⎧⎨+-⎩≤≤ ······································· 3分 由不等式①得32x ≤ ························································································· 4分由不等式②得30x ≥ ························································································· 5分 x ∴的取值X 围为3032x ≤≤ ············································································ 6分（2）7090(50)y x x =+- ·············································································· 8分 化简得204500y x =-+200y -<∴，随x 的增大而减小． ··································································· 9分 而3032x ≤≤∴当32x =，5018x -=时，203245003860y =-⨯+=最小值（元） ··················· 11分 答：当甲种产品生产32件，乙种18件时，甲、乙两种产品的成本总额最少，最少的成本总额为3860元． ····························································································· 12分 迁移点拨：本题是一道表格信息题，既考查不等式，又考查一次函数解析式及一次函数最值问题，通常一次函数的最值问题首先油不等式找到x 的取值X 围，进而利用一次函数的增减性在前面X 围的前提下求出最值。
一次函数应用题精编(附答案)
一次函数应用题专题训练1．一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶.设行驶的时间为x(时)，两车之间的距离为y(千米)，图中的折线表示从两车出发至快车到达乙地过程中y与x 之间的函数关系．（1）根据图中信息，求线段AB所在直线的函数解析式和甲乙两地之间的距离；（2）已知两车相遇时快车比慢车多行驶40千米，若快车从甲地到达乙地所需时间为t时，求t的值；（3）若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图像. (温馨提示：请画在答题卷相对应的图上)2．春节期间，某客运站旅客流量不断增大，旅客往往需要长时间排队等候购票．经调查发现，每天开始售票时，约有400人排队购票，同时又有新的旅客不断进入售票厅排队等候购票．售票时售票厅每分钟新增购票人数4人，每分钟每个售票窗口出售的票数3张．某一天售票厅排队等候购票的人数y（人）与售票时间x（分钟）的关系如图所示，已知售票的前a分钟只开放了两个售票窗口（规定每人只购一张票）．（1）求a的值．（2）求售票到第60分钟时，售票听排队等候购票的旅客人数．（3）若要在开始售票后半小时内让所有的排队的旅客都能购到票，以便后来到站的旅客随到随购，至少需要同时开放几个售票窗口？3.在一条直线上依次有A 、B 、C 三个港口，甲、乙两船同时分别从A 、B 港口出发，沿直线匀速驶向C 港，最终达到C 港．设甲、乙两船行驶x （h ）后，与．B ．港的距离．．．．分别为1y 、2y （km ），1y 、2y 与x 的函数关系如图所示．（1）填空：A 、C 两港口间的距离为 km ， a ；（2）求图中点P 的坐标，并解释该点坐标所表示的实际意义；（3）若两船的距离不超过10 km 时能够相互望见，求甲、乙两船可以相互望见时x 的取值范围．4.一家蔬菜公司收购到某种绿色蔬菜140吨，准备加工后进行销售，销售后获利的情况如下表所示：已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行.受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完.⑴如果要求12天刚好加工完140吨蔬菜，则公司应安排几天精加工，几天粗加工？⑵如果先进行精加工，然后进行粗加工.①试求出销售利润W 元与精加工的蔬菜吨数m 之间的函数关系式；②若要求在不超过10天的时间内，将140吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多可获得多少利润？此时如何分配加工时间？小时)5.某物流公司的甲、乙两辆货车分别从A 、B 两地同时相向而行，并以各自的速度匀速行驶，途径配货站C ，甲车先到达C 地，并在C 地用1小时配货，然后按原速度开往B 地，乙车从B 地直达A 地，图16是甲、乙两车间的距离y （千米）与乙车出发x （时）的函数的部分图像（1）A 、B 两地的距离是 千米，甲车出发 小时到达C 地；（2）求乙车出发2小时后直至到达A 地的过程中，y 与x 的函数关系式及x 的取值范围，并在图16中补全函数图像；（3）乙车出发多长时间，两车相距150千米6．张师傅驾车运送荔枝到某地出售，汽车出发前油箱有油50升，行驶若干小时后，途中在加油站加油若干升，油箱中剩余油量y (升)与行驶时间t (小时)之间的关系如图所示．请根据图象回答下列问题：（1）汽车行驶 小时后加油，中途加油 升；（2）求加油前油箱剩余油量y 与行驶时间t 的函数关系式；（3）已知加油前、后汽车都以70千米/小时匀速行驶，如果加油站距目的地210千米，要到达目的地，问油箱中的油是否够用？请说明理由．7.某学校组织340名师生进行长途考察活动，带有行李170件，计划租用甲、乙两种型号的汽车10辆．经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李．（1）请你帮助学校设计所有可行的租车方案；（2）如果甲车的租金为每辆2000元，乙车的租金为每辆1800元，问哪种可行方案使租车费用最省？8．自20XX年6月1日起我省开始实施家电以旧换新政策，消费者在购买政策限定的新家电时，每台新家电用一台同类的旧家电换取一定数额的补贴.为确保商家利润不受损失，补贴部分由政府提设购进的电视机和洗衣机数量均为x台，这100台家电政府需要补贴y元，商场所获利润w元（利润=售价-进价）（1）请分别求出y与x和w与x的函数表达式；（2）若商场决定购进每种家电不少于30台，则有几种进货方案？若商场想获得最大利润，应该怎样安排进货？若这100台家电全部售出，政府需要补贴多少元钱？。
一次函数应用题含答案
一次函数应用题含答案一次函数应用题含答案一、方案优化问题我市某乡A、B两村盛产柑桔，A村有柑桔200吨，B村有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库，已知C仓库可储存240吨，D仓库可储存260吨；从A村运往C、D两处的费用分别为每吨20元和25元，从B村运往C、D两处的费用分别为每吨15元和18元.设从A村运往C仓库的柑桔重量为x吨，A、B两村运往两仓库的柑桔运输费用分别为yA元和yB元.（1）请填写下表，并求出yA，yB与x之间的函数关系式；（2）试讨论A、B两村中，哪个村花的运费较少；（3）考虑到B村的经济承受能力，B村的柑桔运费不得超过4830元.在这种情况下，请问该怎样调运才能使两村运费之和最小？求出这个最小值.解：（1）yA=-5x+5000（0≤x≤200），yB=3x+4680（0≤x≤200）.（2）当yA=yB时，-5x+5000=3x+4680，x=40；当yA>yB时，-5x+5000>3x+4680，x<40；当yA<yb时，-5x+5000<3x+4680，x style="padding: 0px; margin: 0px; font-family: Arial, 宋体; font-size: 14px; white-space: normal; background-color: rgb(255, 255, 255);">40.当x=40时，yA=yB即两村运费相等；当0≤x<40时，ya>yB即B村运费较少；当40<x≤200时，ya<yb即a村费用较少.（3）由yB≤4830得3x+4680≤4830∴x≤50设两村的运费之和为y，∴y=yA+yB.即：y=-2x+9680.又∵0≤x≤50时，y随x增大而减小，∴当x=50时，y有最小值，y最小值=9580（元）.答：当由A村调往C仓库的柑桔重量为50吨、调往D仓库为150吨，由B村调往C仓库为190吨、调往D仓库110吨的时候，两村的运费之和最小，最小费用为9580元.要点提示：解答方案比较问题，求函数式时，对有图象的，多用待定系数法求；对没有给出图象的，直接依题意列式子；方案比较问题通常与不等式、方程相联系；比较方案，即比较同一自变量所对应的函数值，要将函数问题转化为方程、不等式问题；解答方案比较问题尤其要注意：不同的区间，对应的大小关系也多不同.二、利润最大化问题某个体小服装店主准备在夏季来临前，购进甲、乙两种T恤.两种T恤的相关信息如下表：根据上述信息，该店决定用不少于6195元，但不超过6299元的资金购进这两种T恤共100件.请解答下列问题：（1）该店有哪几种进货方案？（2）该店按哪种方案进货所获利润最大，最大利润是多少？（3）两种T恤在夏季很快销售一空，该店决定再拿出385元全部用于购进这两种T恤，在进价和售价不变的情况下，全部售出.请直接写出该店按哪种方案进货才能使所获利润最大.解：（1）设购进甲种T恤x件，则购进乙种T恤（100-x）件.可得，6195≤35x+70（100-x）≤6299.解得，20■≤x≤23.∵x为解集内的正整数，∴x=21，22，23.∴有三种进货方案：方案一：购进甲种T恤21件，购进乙种T恤79件；方案二：购进甲种T恤22件，购进乙种T恤78件；方案三：购进甲种T恤23件，购进乙种T恤77件.（2）设所获得利润为W元.W=30x+40（100-x）=-10x+4000.∵k=-10<0，∴W随x的增大而减小.∴当x=21时，W=3790.该店购进甲种T恤21件，购进乙种T恤79件时获利最大，最大利润为3790元.（3）购进甲种T恤9件、乙种T恤1件.要点提示：在一次函数y=kx+b中，x、y均可取一切实数.如果缩小x的取值范围，则其函数值就会出现最大值或最小值.求一次函数的最大值、最小值，一般都是采用“极端值法”，即用自变量的端点值，根据函数的增减性，对应求出函数的端点值（最值）.三、行程问题从甲地到乙地，先是一段平路，然后是一段上坡路.小明骑车从甲地出发，到达乙地后立即原路返回甲地，途中休息了一段时间.假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km.设小明出发x h后，到达离甲地y km的地方，图1中的折线OABCDE表示x与y之间的函数关系.（1）小明骑车在平路上的速度为 km/h；他途中休息了 h；（2）求线段AB、BC所表示的y与x之间的函数关系式；（3）如果小明两次经过途中某一地点的时间间隔为0.15h，那么该地点离甲地多远？解：（1）小明骑车在平路上的速度为：4.5÷0.3=15，∴小明骑车在上坡路的速度为：15-5=10，小明骑车在下坡路的速度为：15+5=20.∴小明返回的时间为：（6.5-4.5）÷20+0.3=0.4小时，∴小明骑车到达乙地的时间为：0.3+2÷10=0.5.∴小明途中休息的时间为：1-0.5-0.4=0.1小时.故答案为：15，0.1（2）小明骑车到达乙地的时间为0.5小时，∴B（0.5，6.5）.小明下坡行驶的时间为：2÷20=0.1，∴C（0.6，4.5）.设直线AB的解析式为y=k1x+b1，由题意得4.5=0.3k1+b16.5=0.5k1+b1，解得：k1=10b1=1.5，∴y=10x+1.5（0.3≤x≤0.5）；设直线BC的解析式为y=k2x+b2，由题意得6.5=0.5k2+b24.5=0.6k2+b2，解得：k2=-20b2=16.5，∴y=-20x+16.5（0.5<x≤0.6）（3）小明两次经过途中某一地点的时间间隔为0.15h，由题意可以得出这个地点只能在坡路上.设小明第一次经过该地点的时间为t，则第二次经过该地点的时间为（t+0.15）h，由题意得10t+1.5=-20（t+0.15）+16.5，解得：t= 0.4，∴y=10×0.4+1.5=5.5，∴该地点离甲地5.5km.要点提示：行程类一次函数试题以图象、点坐标相组合的形式呈现，灵活性强，对学生分析问题、解决问题的能力要求较高，重在考查学生的识图能力和创新意识.解决图象中的行程问题除了要掌握好路程、速度和时间三者之间的基本关系外，最重要的'是要学会从图象中获取信息，理清各变量之间的关系，然后根据题意选择适当的解题方法.四、分段计费问题已知某市2013年企业用水量x（吨）与该月应交的水费y（元）之间的函数关系.（1）当x≥50时，求y关于x的函数关系式；（2）若某企业2013年10月份的水费为620元，求该企业2013年10月份的用水量；（3）为实施省委“五水共治”发展战略，鼓励企业节约用水，该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费，规定若企业的月用水量x超过80吨，则除按2013年收费标准收取水费外，超过80吨部分每吨另加收■元.若某企业2014年3月份的水费和污水处理费共600元，求这个企业该月的用水量.解：（1）设y关于x的函数关系式y=kx+b，∵直线y=kx+b经过点（50，200），（60，260）∴50k+b=20060k+b=260解得k=6b=-100∴y关于x的函数关系式是y=6x-100（x≥50）；（2）由可知，当y=620时，x>50∴6x-100=620，解得x=120.答：该企业2013年10月份的用水量为120吨.（3）由题意得6x-100+■（x-80）=600，化简得x2+40x-14000=0解得：x1=100，x2=-140（不合题意，舍去）.答：这家企业2014年3月份的用水量是100吨.要点提示：分段函数的特征是不同的自变量区间所对应的函数式不同，其函数图象是一个折线.解决分段计费问题，关键是要与所在的区间相对应.分段函数中“折点”既是两段函数的分界点，同时又分别在两段函数上，在求解析式时要用好“折点”坐标，同时在分析图象时还要注意“折点”所表示的实际意义，“折点”的纵坐标通常是不同区间的最值.2015年第3期《锐角三角函数》参考答案1.D；2.A；3.B；4.■；5.9■；6.2■；7.120；8. 解：（1）■-3tan30°+（π-4）0-（■）-1=2■-3×■+1-2=■-1（2）■（2cos45°-sin60°）+■=■（2×■-■）+■=2-■+■=29. 解：过点A作直线BC的垂线，垂足为D.则∠CDA=90°，∠CAD=60°，∠BAD=30°，CD=240米，在Rt△ACD中，tan∠CAD=■，∴AD=■=■=80■，在Rt△ABD中，tan∠BAD=■，∴BD=ADtan30°=80■×■=80，∴BC=CD-BD=240-80=160. 答：这栋大楼的高为160米. 10.解：在Rt△CDB中，∠C=90°，BC=■=■=4，∴tan∠CBD=■.在Rt△ABC中，∠C=90°，AB=■=4■，∴sinA=■.。
一次函数常见应用题
S （千米） t （时） O 1022.5 7.50.5 3 1.5 l B l A 一次函数应用1、如图，l A l B 分别表示A 步行与B 骑车在同一路上行驶的路程S 与时间t 的关系。
（1）B 出发时与A 相距 千米。
（2）走了一段路后，自行车发生故障，进行修理，所用的时间是 小时。
（3）B 出发后 小时与A 相遇。
（4）若B 的自行车不发生故障，保持出发时 的速度前进， 小时与A 相遇，相遇点 离B 的出发点 千米。
在图中表示出这个相遇点C 。
（5）求出A 行走的路程S 与时间t 的函数关系式。
2．一农民带了若干自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出土豆千克数与他手中持有的钱数（含备用零钱）的关系如图所示，结合图象回答农民自带的零钱是 元；降价前他每千克土豆的出售的价格是 元；降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，那么他一共带了千克土豆。
3、某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用，那么服药后2小时时血液中含药量最高，达每毫升6微克，接着逐步衰减，10小时血液中含药量为每毫升3微克，每毫升血液中含药量y 微克随时间x 小时主变化如图所示,当成人按规定剂是服药后,(1)分别求出x<2和x>2时y 与x 的函数关系式,(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?(小时)(微克)210360xy4、某气象研究中心观测一场沙尘暴从发生到结束全过程，开始时风暴平均每小时增加2千米/时，4小时后，沙尘暴经过开阔荒漠地，风速变为平均每小时增加4千米/时，一段时间，风暴保持不变，当沙尘暴遇到绿色植被区时，其风速平均每小时减小1千米/时，最终停止. 结合风速与时间的图像，回答下列问题：（1）在y 轴（ ）内填入相应的数值；（2）沙尘暴从发生到结束，共经过多少小时？（3）求出当x ≥25时，风速y （千米/时）与时间x （小时）之间的函数关系式.（4）若风速达到或超过20千米/时，称为强沙尘暴，则强沙尘暴持续多长时间？5．一家小型放影厅的盈利额ｙ（元）同售票数ｘ之间的关系如下图所示，其中保险部门规定：超过150人时，要缴纳公安消防保险费50元，试根据图象回答：当售票数ｘ满足0＜ｘ≤150元时，盈利额ｙ（元）与ｘ之间的函数关系式是 ；：当售票数ｘ满足150＜ｘ≤200元时，盈利额ｙ（元）与ｘ之间的函数关系式是 ；当售票数ｘ为 时，不赔不赚，当ｘ满足 时，放影厅要赔本。
八年级数学：一次函数(应用题)练习(含解析)
C．10000,13200D．13200,15400
二.填空题
7.利民商店中有3种糖果,单价及重量如下表,若商店将以上糖果配成什锦糖,则这种什锦糖果的单价是每千克________元.
品种
水果糖
花生糖
软 糖
单价（元/千克）
10
12
16
重量（千克）
3
3
4
8.某公园门票价格如下表,有27名中学生游公园,则最少应付费______元.（游客只能在公园售票处购票）
购票张数
1～29张
30～60张
60张以上
每张票的价格
10元
8元
6元
9.有一个附有进水管和出水管的容器,在单位时间内的进水量和出水量分别一定．设从某时刻开始的5分钟内只进水不出水,在随后的15分钟内既进水又出水,得到容器内水量y（升）与时间 （分）之间的函数图象如图．若20分钟后只放水不进水,这时（ ≥20时） 与 之间的函数关系式是_________.
八年级数学：一次函数（应用题）练习（含解析）
一.选择题
1.明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率．该绿化组完成的绿化面积S（单位：m2）与工作时间t（单位：h）之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是（ ）
A．300m2B．150m2C．330m2D．450m2
12.【答案】2050；
【解析】解：设小明、小刚新的速得,y=x+1.5③,
由②得,4y﹣3=6x④,
③代入④得,4x+6﹣3=6x,
解得x=1.5,
故这次越野赛的赛跑全程=1600+300×1.5=1600+450=2050m．
初中一次函数典型应用题
中考一次函数应用题例1 已知雅美服装厂现有A 种布料70米，B 种布料52米，现计划用这两种布料生产M ，N 两种型号的时装共80套。
已知做一套M 型号的时装需要A 种布料0.6米，B 种布料0.9米，可获利润45元；做一套N 型号的时装需要A 种布料1.1米，B 种布料0.4米，可获利润50元。
若设生产N 种型号的时装套数为x ，用这批布料生产这两种型号的时装所获总利润为y 元。
（1）求y 与x 的函数关系式，并求出自变量的取值范围；（2）雅美服装厂在生产这批服装中，当N 型号的时装为多少套时，所获利润最大？最大利润是多少？解：①由题意得：x x y 50)80(45+-=＝36005+x⎩⎨⎧≤-+≤-+52)80(9.04.070)80(6.01.1x x x x 解得：40≤x ≤44∴y 与x 的函数关系式为：36005+=x y ，自变量的取值范围是：40≤x ≤44②∵在函数36005+=x y 中，y 随x 的增大而增大∴当x ＝44时，所获利润最大，最大利润是：3600445+⨯＝3820（元）例2 某市电话的月租费是20元，可打60次免费电话（每次3分钟），超过60次后，超过部分每次0.13元。
（1）写出每月电话费y （元）与通话次数x 之间的函数关系式；（2）分别求出月通话50次、100次的电话费；（3）如果某月的电话费是27.8元，求该月通话的次数。
解；（1）由题意得：y 与x 之间的函数关系式为：y ＝⎩⎨⎧>-+≤≤)60)(60(13.020)600(20x x x（2）当x ＝50时，由于x ＜60，所以y ＝20（元）当x ＝100时，由于x ＞60，所以y ＝)60100(13.020-+＝25.2（元）（3）∵y ＝27.8＞20∴x ＞60∴8.27)60(13.020=-+x解得：x ＝120（次）例3 荆门火车货运站现有甲种货物1530吨，乙种货物1150吨，安排用一列货车将这批货物运往广州，这列货车可挂A 、B 两种不同规格的货厢50节，已知用一节A 型货厢的运费是0.5万元，用一节B 型货厢的运费是0.8万元。
八年级数学：一次函数应用题最大利润问题20道(含答案及解析)
八年级数学：一次函数应用题最大利润问题20道（含答案及解析）1．如图，1l 表示某公司一种产品一天的销售收入与销售量的关系，2l 表示该公司这种产品一天的销售成本与销售量的关系．（1）1x 时，销售收入＝______万元，销售成本＝______万元，盈利（收入－成本）＝______万元； （2）一天销售______件时，销售收入等于销售成本； （3）1l 对应的函数表达式是______；（4）你能写出利润与销售量间的函数表达式吗？2．消费也扶贫，万源市某村需要销售当地的优质土特产：香米和土豆，这两种商品的相关信息如下表： （1）达州市第一中学工会第一季度采购了香米和土豆共计1000袋，为该村创造利润17000元，求达州市第一中学工会采购了香米多少袋？（2）为了加大扶贫力度，达州市第一中学工会在第二季度想为该村创造20000元以上利润的目标．该工会计划购进香米和土豆共计1200袋，且香米不低于800袋，不超过1000袋．设购进香米m 袋，香米和土豆共创造利润w 元，求出w 与m 之间的函数关系式，并通过计算说明达州市第一中学工会能否实现扶贫目标？3．某水产品商店销售1千克A 种水产品的利润为10元，销售1千克B 种水产品的利润为15元，该经销商决定一次购进A 、B 两种水产品共200千克用于销售，设购进A 种水产品x 千克，销售总利润为y 元． （1）求y 与x 之间的函数关系式；（2）若其中B 种水产品的进货量不超过A 种水产品的3倍，请你帮该经销商设计一种进货方案使销售总利润最大，并求出总利润的最大值．4．某乡镇农贸公司新开设了一家网店，销售当地农产品，其中一种当地特产在网上试销售，其成本为每千克2元．公司在试销售期间，调查发现，每天销售量y （kg ）与销售单价x （元）满足如图所示的函数关系（其中210x <≤）． （1）求y 与x 之间的函数关系式；（2）销售单价x 为多少元时，每天的销售利润最大？最大利润是多少元？5．面临毕业季，某电脑营销商瞄准时机，在五月底筹集到资金12.12万元，用于一次性购进A 、B 两种型号的电脑共30台．根据市场需求，这些电脑可以全部销售，全部销售后利润不少于1.6万元，其中电脑的进价和售价见下表：A 型电脑B 型电脑 进价(元/台) 4200 3600 售价(元/台)48004000设营销商计划购进A 型电脑x 台，电脑全部销售后获得的利润为y 万元． （1）试写出y 与x 的函数关系式；（2）该营销商有几种购进电脑的方案可供选择？（3）该营销商选择哪种购进电脑的方案获利最大？最大利润是多少？6．某运动鞋专卖店通过市场调研，准备销售A 、B 两种运动鞋，其中A 种运动鞋的进价比B 种运动鞋的进价高20元，已知鞋店用3200元购进A 种运动鞋的数量与用2560元购进B 种运动鞋的数量相同． （1）求两种运动鞋的进价．（2）设A 运动鞋的售价为250元/双，B 运动鞋的售价是180元/双，鞋店共进货两种运动鞋200双，设总利润为W 元，A 运动鞋进货m 双，且90≤m ≤105． ①写出总利润W 元关于m 的函数关系式． ②要使该专卖店获得最大利润，应如何进货7．某水果经销商需购进甲，乙两种水果进行销售．甲种水果每千克的价格为a元，如果一次购买超过40千克，超过部分的价格打八折，乙种水果的价格为25元/千克．设经销商购进甲种水果x千克，付款y元，y与x之间的函数关系如图所示．（1）求a的值，并写出当x＞40时，y与x之间的函数关系式；（2）若经销商计划一次性购进甲，乙两种水果共80千克，且甲种水果不少于30千克，但又不超过50千克．如何分配甲，乙两种水果的购进量，才能使经销商付款总金额w（元）最少？8．为落实国家精准扶贫政策，某地扶贫办决定帮助扶贫对象推销当地特色农产品，该农产品成本价为18元每千克，销售单价y（元）与每天销售量x（千克）（x为正整数）之间满足如图所示的函数关系，其中销售单价不得低于成本价．（1）求出y与x之间所满足的函数关系式，并写出自变量x的取值范围；（2）当销售量为多少时，获利最大？最大利润是多少？9．某超市经销甲、乙两种品牌的洗衣液，进货时发现，甲品牌洗衣液每瓶的进价比乙品牌高6元，用1800元购进甲品牌洗衣液的数量是用100元购进乙品牌洗衣液数量的45．销售时，甲品牌洗衣液的售价为36元/瓶，乙品牌洗衣液的售价为28元/瓶．（1）求两种品牌洗衣液的进价；（2）若超市需要购进甲、乙两种品牌的洗衣液共120瓶，且购进两种洗衣液的总成本不超过3120元，超市应购进甲、乙两种品牌洗衣液各多少瓶，才能在两种洗衣液完全售出后所获利润最大？最大利润是多少元？10．昆明斗南花卉市场是全国鲜花市场的心脏，也是亚洲最大的鲜花交易市场之一．斗南某兰花专卖店专门销售某种品牌的兰花，已知这种兰花的成本价为60元/盆．市场管理部门规定：每盆兰花的销售价格不低于成本价，又不高于成本价的2倍．经过市场调查发现，该店某天的销售数量y（盆）与销售单价x（元/盆）之间的函数关系如图所示：（1）求y与x之间的函数关系式，并写出自变量x的取值范围：（2）在销售过程中，该店每天还要支付其他费用200元，求这一天销售兰花获得的利润w（元）的最大值．11．九年级数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤70且x为整数）天的售价与销量的相关信息如下表：已知该商品的进价为每件30元，设销售该商品的每天利润为y元．（1）求出y与x的函数关系式；（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少?（3）该商品在销售过程中，共有几天每天销售利润不低于3250元?请直接写出结果．12．2021年3月20日，三星堆遗址考古新发现揭晓，出土文物500余件，三星堆考古发掘成果再次成为炙手可热的话题．某商家看准商机后，计划购进一批“考古盲盒”（三星堆文物模型盲盒）进行销售．已知该商家用1570元购进了10个甲种盲盒和15个乙种盲盒，甲种盲盒的进货单价比乙种盲盒的进货单价多2元． （1）甲种盲盒和乙种盲盒的进货单价分别是多少元；（2）由于“考古盲盒”畅销，商家决定再购进这两种盲盒共50个，其中甲种盲盒数量不多于乙种盲盒数量的2倍，且每种盲盒的进货单价保持不变．若甲种盲盒的销售单价为83元，乙种盲盒的销售单价为78元．①假设此次购进甲种盲盒的个数为a （个），售完这两批盲盒所获总利润为w （元），请写出w 与a 之间的函数关系式；①商家如何安排第二批进货方案，才能使售完这两批盲盒获得总利润最大？最大利润是多少元？13．为迎接“五一”小长假购物高潮，某品牌专卖店准备购进甲、乙两种衬衫，其中甲、乙两种衬衫的进价和售价如下表：若用3000元购进甲种衬衫的数量与用2700元购进乙种衬衫的数量相同． （1）求甲、乙两种衬衫每件的进价；（2）要使购进的甲、乙两种衬衫共300件的总利润不少于34000元，且不超过34700元，问该专卖店有几种进货方案；（3）在（2）的条件下，专卖店准备对甲种衬衫进行优惠促销活动，决定对甲种衬衫每件优惠a 元(6080)a <<出售，乙种衬衫售价不变，那么该专卖店要获得最大利润应如何进货？14．某大型水果超市销售水蜜桃，根据前段时间的销售经验，每天的售价x（元/箱）与销售量y（箱）有如下表关系：已知y与x之间的函数关系是一次函数．（1）求y与x的函数解析式；（2）水蜜桃的进价是40元/箱，若该超市每天销售水蜜桃盈利1600元，要使顾客获得实惠，每箱售价是多少元？15．迎接大运，美化深圳，园林部门决定利用现有的3490盆甲种花卉和2590盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧，已知搭配一个A种造型需甲种花卉80盆，乙种花卉40盆，搭配一个B种造型需甲种花卉50盆，乙种花卉90盆．（1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来．（2）若搭配一个A种造型的成本是800元，搭配一个B种造型的成本是960元，试说明（1）中哪种方案成本最低？最低成本是多少元？16．九(4)班数学兴趣小组经过市场调查，整理出童威的某种高端商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：已知该商品的进价为每件30元，设销售该商品的每天利润为y元．（1）求出y与x的函数关系式；（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？（3）该商品在前49天销售中，每销售一件商品就捐赠m元（0＜m＜10）给希望工程．若前49天销售获得的最17．玩具批发市场A、B玩具的批发价分别为每件30元和50元，张阿姨花1200元购进A、B两种玩具若干件，并分别以每件35元与60元价格出售．设购入A玩具为x件，B玩具为y件．（1）若张阿姨将玩具全部出售赚了220元，则张阿姨购进A、B型玩具各多少件？（2）若要求购进A玩具的数量不得少于B玩具的数量，问如何购进玩具A、B的数量并全部出售才能获得最大利润，此时最大利润为多少元？18．某桶装水经营部每天的房租、人员工资等固定成本为250元，每桶水的进价是5元，规定销售单价不得高于12元，也不得低于7元，调查发现日均销售量p(桶)与销售单价x(元)的函数图象如图所示．（1）求日均销售量p(桶)与销售单价x(元)的函数关系式；（2）若该经营部希望日均获利1350元，那么日均销售多少桶水？19．某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于40%．经试销发现，销售量y（件）与销售单价x（元）符合一次函数y＝kx+b，且当x＝80时，y＝40，当x＝70时，y＝50．（1）求一次函数y＝kx+b的表达式；（2）若该商场获得的利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润？最大利润是多少元？20．某销售商准备采购一批儿童玩具，有A，B两种品牌可供选择，其进价和售价如下：销售商购进A，B两种品牌的儿童玩具共30件.（1）若销售商购进A品牌的儿童玩具为x （件）, 求销售商售完这30件儿童玩具获得的总利润y（元）与x之间的函数关系式;（2）若想使得销售完这30件儿童玩具获得的总利润为1300元，求应购进A品牌的儿童玩具多少件?（3）若购进A品牌的儿童玩具不能少于20件，求所获总利润最多为多少元?参考答案1．（1）1，1.5，-0.5；（2）2；（3）y x =；（4）112p x =- 【分析】（1）由题意根据线段中点的求法列式计算即可求出x =1时的销售收入和销售成本，根据盈利的求法计算即可得解；（2）由题意直接根据图象找出两直线的交点的横坐标即可；（3）根据题意设l 1对应的函数表达式为y =kx （k ≠0），然后利用待定系数法求一次函数解析式即可；（4）由题意结合l 1和l 2的解析式，设利润为p 然后根据利润=销售收入-销售成本列式表示即可． 【详解】解：（1）x =1时，销售收入= 212=（万元）， 销售成本=121.52+=（万元）， 盈利（收入-成本）= 310.52-=-（万元）； 故答案为：1，1.5，-0.5；（2）由图像可知一天销售2件时，销售收入等于销售成本； 故答案为：2；（3）设l 1对应的函数表达式为：y =kx ，则2=2k ，解得：k =1， 故l 1对应的函数表达式为：y =x ， 故答案为：y =x ；（4）∵l 1的表达式为y =x ，设l 2的表达式为y =kx +b （k ≠0），代入（0①1），（2①2）可得1,12k b ==， ∴l 2的表达式为112y x =+， 设利润为p ，∴利润p =11(1)122x x x -+=-，所以利润与销售量间的函数表达式为：112p x =-. 【点睛】本题考查一次函数的应用，考查了识别函数图象的能力以及利用待定系数法求一次函数解析式，准确观察图象提供的信息是解题的关键．2．（1）达州市第一中学工会采购香米400袋．（2）w 518000m =+（800≤m ＜1000），达州市第一中学工会能实现扶贫目标． 【分析】（1）设达州市第一中学工会采购香米x 袋，利用总利润为等量关系构建方程即可； （2）根据香米每袋利润×袋数+土豆每袋利润×袋数构建一次函数，利用一次函数的性质即可解决问题； 【详解】解：（1）设达州市第一中学工会采购香米x 袋． 由题意列方程得()()()80606045100017000x x -+--=，解得400x =，答：达州市第一中学工会采购香米400袋． （2）由题意得：()20151200w m m =+-，518000m =+（800≤m ①1000），∵800m ≥，且w 随m 的增大而增大，∴800m =时，5800180002200020000w =⨯+=>， 当m =1000时，510001800023000w =⨯+=， 2200023000w ≤＜，∴达州市第一中学工会能实现扶贫目标． 【点睛】本题考查一次函数的应用、一元一次方程的应用等知识，解题的关键是理解题意，正确寻找等量关系解决问题．3．（1）y =-5x +3000；（2）购进A 水产品50kg 、B 种150kg 时，利润最大是2750元 【分析】（1）设购进A 种水产品x 千克，则购进B 种水产品（200-x ）千克，根据等量关系表示出函数解析式即可；（2）由题意得：2003x x -≤，解得：50x ≥，即50200x ≤<，根据53000y x =-+的性质得y 随x 的增大而减小，则当50x =时，销售利润最大，把50x =代入53000y x =-+即可得．【详解】解：（1）设购进A 种水产品x 千克，则购进B 种水产品（200-x ）千克，1015(200)y x x =+-10300015y x x =+-即53000y x =-+，则y 与x 之间的函数关系式为：53000y x =-+；（2）由题意得：2003x x -≤，4200x ≥解得：50x ≥，∴50200x ≤<，∵53000y x =-+，50-<，∴y 随x 的增大而减小，∴当50x =时，销售利润最大，55030002750y =-⨯+=，200-50=150（千克），故购进A 种水产品50千克，购进B 种水产品150千克，销售总利润最大，总利润的最大值为2750元．【点睛】本题考查了一次函数的应用，解题的关键是根据题意找出等量关系表示出函数解析式．4．（1）600(25)40800(510)x y x x <≤⎧=⎨-+<≤⎩；（2）当销售单价x 为10元时，每天的销售利润最大，最大利润是3200元．【分析】1）运用待定系数法计算即可；（2）列出二次函数解析式，计算最值即可．【详解】（1）当25x <≤时，600y =；当510x <≤时，设(0)y kx b k =+≠，把(5,600)，(10,400)代入得：560010400k b k b +=⎧⎨+=⎩，解得40800k b =-⎧⎨=⎩，40800y x ∴=-+，综上，y 与x 之间的函数关系式为：600(25)40800(510)x y x x <≤⎧=⎨-+<≤⎩（2）设每天的销售利润为w 元，当25x <≤时，600(2)6001200w x x =-=-，6000> w 随x 的增大而增大∴当5x =时，600512001800w =⨯-=最大（元）当510x <≤时，(40800)(2)w x x =-+-2240880160040(11)3240x x x =-+-=--+400-<抛物线开口向下对称轴为直线11x =，∴当11x <时，w 随x 的增大而增大510x <≤ ∴当10x =时，40132403200w =-⨯+=最大（元）32001800> 10x ∴=时，w 最大答：当销售单价x 为10元时，每天的销售利润最大，最大利润是3200元．【点睛】本题考查了二次函数的最值，一次函数的解析式，熟练掌握待定系数法，灵活运用二次函数的最值是解题的关键．5．（1）y =200x +12000；（2）该经销商有三种购进电脑的方案可供选择；（3）当进A 型电脑22台，B 型电脑8台时获利最大，利润为16400元【分析】（1）根据利润的计算公式，先求出A 型电脑每台的利润为：（4800-4200）元，B 型电脑每台的利润为（4000-3600)元，购进A 型电脑x 台，则购进B 型电脑为()30x -台，即可得出y 与x 的函数关系；（2）根据题意列出相应不等式组，求解，然后依据电脑台数为整数即可确定有几种方案；（3）根据（1）中一次函数性质，可得当x 取最大值22时，获利最大，代入即可求出最大利润．【详解】解（1）根据题意：购进A 型电脑x 台，则购进B 型电脑为()30x -台，A 型电脑每台的利润为：（4800-4200）元，B 型电脑每台的利润为（4000-3600)元，依据题意可得：y 与x 的函数关系式为：()()()480042004000360030?20012000y x x x =-+--=+， 即为：20012000y x =+；(2)由题意得：200120001600042003600(30)121200x x x +≥⎧⎨+-≤⎩解得2022x ≤≤，∵x 为整数 ，∴x 取20、21或22，即该经销商有三种购进电脑的方案可供选择；（3）由（1)知：20012000y x =+，∵2000>，∴y 随x 的增大而增大，即当x 取最大值22， 308x -=时，y 有最大值，y 最大=200×22+12000=16400（元）∴当进A 型电脑22台，B 型电脑8台时获利最大，利润为16400元．【点睛】题目主要考查一次函数的应用、不等式的应用，理解题意列出相应方程时解题关键． 6．（1）A 种运动鞋的进价为100元/双，B 种运动鞋的进价是80元/双；（2）①W =50m +20000；②要使该专卖店获得最大利润，此时应购进A 种运动鞋105双，购进B 种运动鞋95双【分析】（1）设B 种运动鞋的进价x 元，根据等量关系：用3200元购进A 种运动鞋的数量=用2560元购进B 种运动鞋的数量，列出分式方程并解分式方程即可；（2）①根据总利润=A 种运动鞋的利润+B 种运动鞋的利润，即可列出W 关于m 的函数关系式；②根据W 与m 的函数关系式及m 的取值范围，可确定W 的最大值．【详解】（1）设B 种运动鞋的进价x 元，则A 种运动鞋的进价(20)x +元，则3200256020x x=+ 解得：80x = 经检验80x =是原分式方程的解，且符合题意．①208020100x+=+=故A种运动鞋的进价为100元/双，B种运动鞋的进价是80元/双．（2）①W=（250-100）m+（180-80）（200-m）=50m+20000即总利润W元关于m的函数关系式为W=50m+20000②∵W=50m+20000①50＞0，W随m的增大而增大又①90≤m≤105①当m=105时，W取得最大值，200-m=95故要使该专卖店获得最大利润，此时应购进A种运动鞋105双，购进B种运动鞋95双．【点睛】本题考查了分式方程与一次函数的实际应用，对于分式方程的应用，关键是理解题意，找到相等关系并列出方程；对于一次函数的应用，关键是掌握它的性质．注意解分式方程要检验．7．（1）a=30，y=24x+240；（2）甲水果应购进30克，乙水果购进50克时，才能使经销商付款总金额w最少．【分析】（1）先根据图象求出a的值，再根据一次购买超过40千克，超过部分的价格打八折写出函数关系式；（2）先根据甲种水果不少于30千克，但又不超过50千克求出x的取值范围，在分30≤x≤40和40＜x≤50两种情况写出函数解析式，再根据函数的性质求最值．【详解】解：（1）由图象知：a=1200÷40=30（元），当x＞40时，y=30×40+（x-40）×30×80%=24x+240，∴当x＞40时，y与x之间的函数关系式为y=24x+240，a的值为30；（2）由题意，得：30≤x≤50，①当30≤x≤40时，w=30x+25（80-x）=5x+2000，∵5＞0，∴w随x的增大而增大，∴当x=30时，w最小，最小值=5×30+2000=2150（元）；②当40＜x≤50时，w=24x+240+25（80-x）=-x+2240，∵-1＜0，∴w 随x 的增大而减小，∴当x =50时，w 最小，最小值=-50+2240=2190（元），∵2150＜2190，∴x =30，∴甲水果应购进30克，乙水果购进50克时，才能使经销商付款总金额w 最少．【点睛】本题考查了一次函数的应用，关键是根据x 的取值确定函数解析式．8．（1）40(020)150(2064)2x x y x x x <≤⎧⎪=⎨-+<≤⎪⎩且为正整数且为正整数；（2）当32x ＝时，获利最大，最大利润是512元．【分析】（1）当0＜x ≤20且x 为整数时，y ＝40；当x ＞20时，设y ＝kx +b ，由待定系数法求得函数解析式；（2）设所获利润为w （元），分两种情况：①当0＜x ≤20且x 为整数时，②当20＜x ≤64且x 为整数时，分别得出w 的表达式，并分别得出w 的最大值，然后两者比较即可得出答案．【详解】解：（1）当020x <≤且x 为整数时，40y ＝；当20x >时，设y kx b +＝，代入(20,40)和(50,25)得：20405025k b k b +=⎧⎨+=⎩，解得1250k b ⎧=-⎪⎨⎪=⎩． ∴1502y x =-+． 当18y ＝时，代入1502y x =-+，得64x ＝． ∴2064x <≤且x 为整数，综上所述，y 与x 之间所满足的函数关系式为40(020)150(2064)2x x y x x x <≤⎧⎪=⎨-+<≤⎪⎩且为正整数且为正整数． （2）设所获利润为w （元），当020x <≤且x 为整数时，y ＝40，∴(4018)22w x x ==﹣．∵22＞0，∴w 随着x 的增大而增大，则当x ＝20时，w 有最大值，最大值为440；当2064x <≤且x 为整数时，1502y x =-+， ∴22111(5018)32(32)512222w x x x x x =-+-=-+=--+， ∵102-<， ∴当x ＝32时，w 最大，最大值为512元．∵512440>，∴当x ＝32时，获利最大，最大利润是512元．【点睛】本题主要考查了一次函数与二次函数实际应用问题中的销售问题，利用二次函数的性质求得最值以及数形结合思想是解题的关键．9．（1）甲品牌洗衣液进价为30元/瓶，乙品牌洗衣液进价为24元/瓶；（2）购进甲品牌洗衣液40瓶，乙品牌洗衣液80瓶时所获利润最大，最大利润是560元【分析】（1）设甲品牌洗衣液每瓶的进价是x 元，则乙品牌洗衣液每瓶的进价是（x -6）元，根据数量=总价÷单价，结合用1800元购进乙品牌洗衣液数量的45，即可得出关于x 的分式方程，解之经检验后即可得出结论；（2）设可以购买m 瓶乙品牌洗手液，则可以购买（100-m ）瓶甲品牌洗手液，根据总价=单价×数量，结合总费用不超过1645元，即可得出关于m 的一元一次不等式，解之即可得出m 的取值范围，再取其中的最大整数值即可得出结论．【详解】解：（1）设甲品牌洗衣液进价为x 元/瓶，则乙品牌洗衣液进价为()6x -元/瓶， 由题意可得，180********x x =⋅-， 解得30x =，经检验30x =是原方程的解.答：甲品牌洗衣液进价为30元/瓶，乙品牌洗衣液进价为24元/瓶.（2）设利润为y 元，购进甲品牌洗衣液m 瓶，则购进乙品牌洗衣液()120m -瓶，由题意可得，()30241203120m m +-≤，解得40m ≤，由题意可得，()()()363028*********y m m m =-+--=+，∵20k =>，∴y 随m 的增大而增大，∴当40m =时，y 取最大值，240480560y =⨯+=最大值.答：购进甲品牌洗衣液40瓶，乙品牌洗衣液80瓶时所获利润最大，最大利润是560元①【点睛】本题考查分式方程的应用，一次函数的应用，一元一次不等式的应用，解题的关键是灵活运用所学知识解决问题．10．（1）140y x =-+，自变量x 的取值范围是60120x ≤≤；（2）这一天销售兰花获得的利润的最大值为1400元．【分析】（1）根据函数图象和图象中的数据，可知该函数为一次函数，过点（80，60），（110，30），然后代入函数解析式，即可得到y 与x 之间的函数关系式，再根据每盆兰花的销售价格不低于成本价，又不高于成本价的2倍．即可得到x 的取值范围；（2）根据题意，可以得到w 与x 的函数关系式，将函数关系式化为顶点式，即可得到这一天销售兰花获得的利润w （元）的最大值．【详解】解：（1）设y 与x 之间的函数关系式为(0)y kx b k =+≠，把（80，60）和（110，30）代入，得806011030k b k b +=⎧⎨+=⎩， 解得1140k b =-⎧⎨=⎩； ∴y 与x 之间的函数关系式为140y x =-+，①每盆兰花的销售价格不低于成本价，又不高于成本价的2倍．①60≤x ≤120，由上可得，y 与x 之间的函数关系式为140y x =-+(60120)x ≤≤；（2）根据题意，得6010()(0)402w x x =--+-22008600x x =-+-21001400()x =--+；∵10-<∴当100x =时，w 有最大值，为1400．答：这一天销售兰花获得的利润的最大值为1400元．【点睛】本题考查二次函数的应用、待定系数法求一次函数解析式，解答本题的关键是明确题意，求出一次函数解析式，利用二次函数的性质求出w 的最大值．11．（1）221202250(140)1108250(4070)x x x y x x ⎧-++≤<=⎨-+≤≤⎩；（2）第30天时，当天销售利润最大，最大利润是4050元；（3）共有36天每天销售利润不低于3250元【分析】（1）根据总利润=(售价-进价)×数量，列式整理即可；（2）结合二次函数和一次函数的性质，分别求解在各自变量范围内的最值，从而对比即可得出结论；（3）分别利用两个范围内的函数解析式建立方程或不等式，并结合自变量的取值范围求解即可．【详解】解：（1）当140x ≤<时，()()45301502y x x =+--⎡⎤⎣⎦，整理得：221202250y x x =-++；当4070x ≤≤时，()()85301502y x =--，整理得：1108250y x =-+；∴221202250(140)1108250(4070)x x x y x x ⎧-++≤<=⎨-+≤≤⎩； （2）对于函数221202250y x x =-++，整理可得：()22304050y x =--+，∵20-<，∴当30x =时，y 取得最大值，最大值为4050；对于函数1108250y x =-+，∵1100-<，∴y 随x 的增大而减小，∵4070x ≤≤，∴当40x =时，y 取得最大值，最大值为3850，∵4050＞3850，∴第30天时，当天销售利润最大，最大利润是4050元；（3）当140x ≤<时，由题意，2212022503250x x -++=，解得：10x =或50x =，由（2）中，二次函数的性质可得：当1040x ≤<时，每天销售利润不低于3250元，共有30天；当4070x ≤≤时，由题意，11082503250x -+≥， 解得：54511x ≤， ∴当4045x ≤≤时，每天销售利润不低于3250元，共有6天；∴30+6=36(天)，∴共有36天每天销售利润不低于3250元．【点睛】本题考查二次函数与一次函数的综合实际应用，理解二次函数和一次函数的基本性质，准确建立不等式并分类讨论是解题关键．12．（1）甲种盲盒的进货单价为64元，则乙种盲盒的进货单价为62元；（2）①w =1230+3a ；①购进甲种盲盒33个，则购进乙种盲盒17个，最大利润是1329元．【分析】（1）设甲种盲盒的进货单价为x 元，则乙种盲盒的进货单价为（x -2）元，根据题意即可列出一元一次方程，即可求解；（2）①设购进甲种盲盒a 个，则购进乙种盲盒（50- a ）个，根据题意得到a 的取值，再列出w 关于a 的一次函数；①根据一次函数的性质即可求解．【详解】解：（1）设甲种盲盒的进货单价为x 元，则乙种盲盒的进货单价为（x -2）元，根据题意得10x +15(x -2)=1570解得x =64，∴甲种盲盒的进货单价为64元，则乙种盲盒的进货单价为62元．（2）①设购进甲种盲盒a 个，则购进乙种盲盒（50-a ）个，依题意可得()2500a a a ⎧≤-⎨≥⎩解得10003a ≤≤ ∴w =(83-64)(10+a )+（78-62）（50-a +15）=1230+3a①①w =1230+3a ，故w 随a 的增大而增大故当a =33时，50-a ＝17．w 最大=1230+3×33=1329（元）．∴第二批进货方案为：购进甲种盲盒33个，购进乙种盲盒17个．售完第二批盲盒最多获得总利润1329元．【点睛】此题主要考查一元一次方程、一次函数以及不等式组的应用，解题的关键是根据题意找到数量关系列方程或函数进行求解．13．（1）甲种衬衫每件进价100元，乙种衬衫每件进价90元；（2）共有11种进货方案；（3）当6070a <<时，应购进甲种衬衫110件，乙种衬衫190件；当70a =时，所有方案获利都一样；当7080a <<时，购进甲种衬衫100件，乙种衬衫200件．【分析】（1）依据用3000元购进甲种衬衫的数量与用2700元购进乙种衬衫的数量相同列方程解答； （2）根据题意列不等式组解答；（3）设总利润为w ，表示出w 与x 的函数解析式，再分三种情况：①当6070a <<时，②当70a =时，③当7080a <<时，分别求出利润的最大值即可得到答案．【详解】解：（1）依题意得：3000270010m m =-，整理，得：3000(10)2700m m -=，解得：100m =，经检验，100m =是原方程的根，答：甲种衬衫每件进价100元，乙种衬衫每件进价90元；（2）设购进甲种衬衫x 件，乙种衬衫(300)x -件，根据题意得：(260100)(18090)(300)34000(260100)(18090)(300)34700x x x x -+--⎧⎨-+--⎩， 解得：100110x ， x 为整数，110100111-+=，答：共有11种进货方案；（3）设总利润为w ，则(260100)(18090)(300)(70)27000(100110)w a x x a x x =--+--=-+，①当6070a <<时，700a ->，w 随x 的增大而增大，∴当110x =时，w 最大，此时应购进甲种衬衫110件，乙种衬衫190件；②当70a =时，700a -=，27000w =，（2）中所有方案获利都一样；③当7080a <<时，700a -<，w 随x 的增大而减小，∴当100x =时，w 最大，此时应购进甲种衬衫100件，乙种衬衫200件．综上：当6070a <<时，应购进甲种衬衫110件，乙种衬衫190件；当70a =时，（2）中所有方案获利都一样；当7080a <<时，购进甲种衬衫100件，乙种衬衫200件．【点睛】此题考查分式方程的实际应用，不等式组的实际应用，一次函数的性质，正确理解题意熟练应用各知识点解决问题是解题的关键．14．（1）y ＝﹣5x +380；（2）56元．【分析】（1）设y 与x 的函数解析式为y ＝kx +b （k ≠0），根据表格中的数据，利用待定系数法即可求出y 与x 的函数解析式；（2）利用该超市每天销售水蜜桃获得的利润＝每箱的利润×每天的销售量，即可得出关于。
一次函数应用题(习题及答案)
一次函数应用题(习题及答案)一次函数应用题(习题及答案)题一：某手机品牌每月销售量与售价之间存在一次函数关系，已知售价为3000元时销售量为4000台，售价为5000元时销售量为3000台，请问每增加一台售价，销售量减少多少台？解析：这是一个典型的一次函数应用题。
首先，我们可以设定售价为x元，销售量为y台。
根据题目已知条件，可以列出两个点的坐标：(3000, 4000)和(5000, 3000)。
根据一次函数的一般式y = kx + b，可以得到方程组：4000 = 3000k + b -------(1)3000 = 5000k + b -------(2)通过解方程组，可以求解出k和b的值，从而确定函数关系。
首先，我们用(1)式减去(2)式，消去b的项，得到：1000 = -2000k解得k = -1/2。
将k的值代入(1)式或(2)式，可解得b = 7000/2 = 3500。
因此，该函数的函数关系为：y = -1/2x + 3500。
根据函数关系，我们可以计算每增加一台售价，销售量减少的台数。
由于每增加一台售价，x的变化量为1，代入函数关系，得到y的变化量为-1/2。
因此，每增加一台售价，销售量减少的台数为1/2台。
答案：每增加一台售价，销售量减少0.5台。
题二：一家电商公司将某商品的售价从每件100元提高到120元后，销售量下降了25%。
求原来的每件商品的销售量。
解析：这同样是一个一次函数的应用题。
我们可以设定原售价为x 元，销售量为y件。
根据题目已知条件，可以得到两个点的坐标：(100, y)和(120, 0.75y)（销售量下降25%相当于销售量的0.75倍）。
根据一次函数的一般式y = kx + b，可以得到方程组：y = 100k + b -------(1)0.75y = 120k + b -------(2)通过解方程组，我们可以求解出k和b的值，从而确定函数关系。
将(1)式代入(2)式，得到：0.75(100k + b) = 120k + b化简可得：75k + 0.75b = 120k + b整理得：0.25b = 45k解得：k = 0.25b/45将k的值代入(1)式，解得b = 11y/12因此，该函数的函数关系为：y = (0.25b/45)x + (11y/12)由于题目求解的是原来的每件商品的销售量，即求解y的值。
一次函数应用题(含答案)
一次函数应用题初一( )班 姓名: 学号： ．１、一次时装表演会预算中票价定位每张100元，容纳观众人数不超过200０人,毛利润y(百元）关于观众人数ｘ（百人)之间的函数图象如图所示，当观众人数超过1０00人时,表演会组织者需向保险公司交纳定额平安保险费5０00元（不列入成本费用)请解答下列问题:⑴求当观众人数不超过1０00人时，毛利润ｙ（百元）关于观众人数x （百人)的函数解析式和成本费用s(百元）关于观众人数x （百人)的函数解析式;⑵若要使这次表演会获得３6００0元的毛利润,那么要售出多少张门票？需支付成本费用多少元?（注:当观众人数不超过１00０人时,表演会的毛利润＝门票收入—成本费用;当观众人数超过１０0０人时,表演会的毛利润=门票收入—成本费用—平安保险费）２、转炉炼钢产生的棕红色烟尘会污染大气,某装置可通过回收棕红色烟尘中的氧化铁从而降低污染，该装置的氧化铁回收率与其通过的电流有关，现经过试验得到下列数据:通过电流强度（单位：A ) 1 1.７ 1．９ 2.1 2.４ 氧化铁回收率（%)757988８778如图建立直角坐标系，用横坐标表示通过的电流强度,纵坐标表示氧化铁的回收率． (1） 将试验所得数据在如图所示的直角坐标系中用点表示;（注：该 图中坐标轴的交点代表点（１,70）)（２)ﻩ用线段将题（1)中所画的点从左到右顺次连接,若用此图象来模拟氧化铁回收率ｙ关于通过电流ｘ的函数关系,试写出该函数在1.7≤x ≤2.4时的表达式;(3) 利用（２）所得函数关系,求氧化铁回收率大于8５%时，该装置通过的电流应该控制的范围（精确到0.１A ）.O x （A ） y （%）（2，70） （1，70） 75 8085３、如图(1),在矩形ABCＤ中，AB = 10ｃm,ＢＣ＝ 8cm. 点P从A点出发,沿Ａ→Ｂ→C →D路线运动,到D停止；点Q从D出发，沿D→C→B→A路线运动,到A停止. 若点P、点Q 同时．．出发,点P的速度为每秒１cｍ,点Q的速度为每秒2ｃｍ,a秒时,点P、点Ｑ同时．．改变速度，点P的速度变为每秒b cｍ,点Q的速度变为每秒d cm. 图(2)是点P出发x秒后△APD的面积．．1S(ｃm2）与x（秒）的函数关系图象;图(３)是点Q出发x秒后△AQD的面积．．2S （cm2）与x(秒)的函数关系图象.（1）(１）参照图（2），求a、ｂ及图(2）中ｃ的值;(2)求d的值；(3）设点P离开点Ａ的路程为1y(cm）,点Q到点A还需要走的路程为2y（cm),请分别写出改变速度后1y、2y与出发后的运动时间x(秒)的函数关系式,并求出P、Q相遇时x的值；(4)当点Q出发＿_＿______秒时,点P、点Ｑ在运动路线上相距的路程为25cm.4、教室里放有一台饮水机，饮水机上有两个放水管。
一次函数应用题
一次函数应用题1.已知XXX现有A种布料70米，B种布料52米，现计划用这两种布料生产M、N两种型号的时装共80套。
已知做一套M型号的时装需要A种布料6米，B种布料0.9米，可获利润45元；做一套N型号的时装需要A种布料1.1米，B种布料0.4米，可获利润50元。
设生产N种型号的时装套数为$x$，用这批布料生产这两种型号的时装所获总利润为$y$元。
1) $y$与$x$的函数关系式为：$$y=45(80-x)\cdot\frac{70-6x}{6}+50x\cdot\frac{52-0.4x}{0.4}$$其中，第一项是生产M型号时装所获利润，第二项是生产N型号时装所获利润。
自变量$x$的取值范围为$0\leq x\leq 52/0.4=130$，因为B种布料的数量有限制。
2) 当生产N型号的时装为$20$套时，所获利润最大，最大利润为$y_{\max}=3850$元。
2.某市电话的月租费是$20$元，可打$60$次免费电话（每次$3$分钟），超过$60$次后，超过部分每次$0.13$元。
1) $y$与$x$的函数关系式为：$$y=\begin{cases}20.& x\leq 60 \\20+0.13(x-60)。
& x>60end{cases}$$2) 月通话$50$次的电话费为$20$元，月通话$100$次的电话费为$23$元。
3) 设该月通话次数为$t$，则$$y=\begin{cases}20.& t\leq 60 \\20+0.13(t-60)。
& t>60end{cases}$$解得$t=60+5(y-20)$，代入$y=27.8$得$t=98$次。
3.荆门火车货运站现有甲种货物$1530$吨，乙种货物$1150$吨，安排用一列货车将这批货物运往广州，这列货车可挂A、B两种不同规格的货厢$50$节，已知用一节A型货厢的运费是$0.5$万元，用一节B型货厢的运费是$0.8$万元。
(含答案解析)一次函数应用题“行程问题”典型例题20题
(2)求线段BC所表示的y与x之间的函数关系式；
（3）若在第一列快车与慢车相遇时，第二列快车从乙地出发驶往甲地，速度与第一列快车相同．求第二列快车出发多长时间，与慢车相距200km.
③该品牌汽车的油箱加满50L，若以100km/h的速度匀速行驶，该车最多能行驶多远．
7．快、慢两车分别从相距360km的佳市、哈市两地出发，匀速行驶，先相向而行，慢车在快车出发1h后出发，到达佳市后停止行驶，快车到达哈市后，立即按原路原速返回佳市（快车调头的时间忽略不计），快、慢两车距哈市的路程y1（单位：km），y2（单位：km）与快车出发时间x（单位：h）之间的函数图象如图所示，请结合图象信息解答下列问题：
3．在一条笔直的公 路上依次有A，C，B三地，甲、乙两人同时出发，甲从A地骑自行车去B地，途经C地休息1分钟，继续按原速骑行至B地，甲到达B地后，立即按原路原速返回A地；乙步行从B地前往A地．甲、乙两人距A地的路程y（米）与时间x（分）之间的函数关系如图所示，请结合图象解答下列问题：
（1）请写出甲的骑行速度为米/分，点M的坐标为；
(2)采用方程思想列出小东离家路程y与时间x之间的函数关系式；
(3)两人相遇实际上是函数图象求交点．
【详解】
解：(1)结合题意和图象可知，线段CD为小东路程与时间函数图象，折现O﹣A﹣B为小玲路程与时间图象
则家与图书馆之间路程为4000m，小玲步行速度为（4000-2000）÷（30-10）=100m/s
（1）乙车的速度为千米/时， ， ．
（2）求甲、乙两车相遇后 与 之间的函数关系式．
（3）当甲车到达距 地70千米处时，求甲、乙两车之间的路程．
一次函数应用题及答案
一次函数应用题及答案一次函数应用题及答案 1有一群猴子，分一堆桃子，第一只猴子分了4个桃子和剩下桃子的1/10，第二只猴子分了8个桃子和这时剩下桃子的1/10，第三只猴子分了12个桃子和这时剩下桃子的1/10........依次类推。
最后发现这堆桃子正好分完，且每只猴子分得的桃子同样多。
那么这群猴子有多少只？方法一：方程解法：设总的桃子个数是10a＋4个，那么第一只猴子分得a＋4个桃子剩下9a，假设9a＝10b＋8个，那么第二只猴子分得b＋8个桃子。
所以a＋4＝b＋8，即b＝a－4个。
那么就有9a＝10（a－4）＋8。
解得a＝32。
所以桃子有32×10＋4＝324个。
每只猴子分得32＋4＝36个，所以猴子有324÷36＝9只。
方法二：第一只猴子分得的那1/10比第二只猴子的那1/10多8－4＝4个第一只猴子分得的那1/10对应的单位1比第二只猴子分得的1/10对应的单位1多4÷1/10＝40个。
那么第一只猴子分得的那1/10是40－8＝32个。
所以桃子总数是32×10＋4＝324个。
每只猴子吃32＋4＝36个，那么有324÷36＝9只猴子。
一次函数应用题及答案 21、题目：某市出租车收费标准为：起步价10元，3千米后每千米的价格为2.4元，小明乘坐出租车走了x千米（x>3），则小明应付车费____元．小明乘坐出租车走了x千米（x>3），则前3千米的费用为10元，超过3千米的费用为：2.4（x3）元，则小明应付车费为：10+2.4（x3）=2.4x+2.8（元）．故答案为：2.4x+2.8．2、题目：某市居民用电的价格为每千瓦时0.62元．小明家上个月付电费40.3元，小明家用电多少千瓦时？小明家上个月用电的千瓦数为：40.3÷0.62=65（千瓦时）答：小明家用电65千瓦时．3、题目：某市居民用电的价格为每千瓦时0.62元．小明家上个月付电费40.3元，小明家用电多少千瓦时？小明家上个月用电的千瓦数为：40.3÷0.62=65（千瓦时）答：小明家用电65千瓦时．4、题目：某市居民用电的价格为每千瓦时0.62元．小明家上个月付电费46.5元，小明家用电多少千瓦时？小明家上个月用电的千瓦数为：46.5÷0.62=75（千瓦时）答：小明家用电75千瓦时．5、题目：某市居民用电的价格为每千瓦时0.52元．小明家上个月付电费44.2元，小明家用电多少千瓦时？小明家用电的千瓦数为：44.2÷0.52=85（千瓦时）答：小明家用电85千瓦时．。
初中数学一次函数应用(含答案)
17题一次函数应用1．A、B两地之间的路程为2380米，甲、乙两人分别从A、B两地出发，相向而行，已知甲先出发5分钟后，乙才出发，他们两人在A、B之间的C地相遇，相遇后，甲立即返回A地，乙继续向A地前行．甲到达A地时停止行走，乙到达A 地时也停止行走．在整个行走过程中，甲、乙两人均保持各自的速度匀速行走，甲、乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的关系如图所示，则乙到达A地时，甲与A地相距的路程是米．2．在一条笔直的公路上有A、B、C三地，C地位于A、B两地之间，甲车从A 地沿这条公路匀速驶向C地，乙车从B地沿这条公路匀速驶向A地．在甲车出发至甲车到达C地的过程中，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．下列结论：①甲车出发2h时，两车相遇；②乙车出发1.5h时，两车相距170km；③乙车出发2h时，两车相遇；④甲车到达C地时，两车相距40km．其中正确的是（填写所有正确结论的序号）．3．快、慢两车分别从相距480km的甲，乙两地同时出发，匀速行驶，相向而行，途中慢车因故停留了1小时，然后继续以原速驶向甲地，到达甲地后即停止行驶；快车到达乙地后，立即按原路原速返回甲地（调头时间忽略不计）．如图是快、慢两车距乙地路程y（km）与所用时间x（h）之间的函数图象，则当两车第一次相遇时，快车距离甲地的路程是千米．4．甲，乙两车分别从A，B两地同时相向匀速行驶，乙车到达A地后未作停留，继续保持原速向远离B地的方向行驶，而甲车到达B地后修整了1个小时，然后调头并保持原速与乙车同向行驶，经过一段时间后两车同时到达C地．设两车行驶的时间为x（小时），两车之间的距离为y（千米），y与x之间的函数图象如图所示，则A，C两地相距千米．5．小兵早上从家匀速步行去学校，走到途中发现数学书忘在家里了，随即打电话给爸爸，爸爸立即送书去，小兵掉头以原速往回走，几分钟后，路过一家书店，此时还未遇到爸爸，小兵便在书店挑选了几支笔，刚付完款，爸爸正好赶到，将书交给了小兵．然后，小兵以原速继续上学，爸爸也以原速返回家．爸爸到家后，过一会小兵才到达学校．两人之间的距离y（米）与小兵从家出发的时间x（分钟）的函数关系如图所示．则家与学校相距米．6．周末小明和爸爸从家里出发到野外郊游，小明骑自行车出发0.3小时后爸爸开始骑摩托车追赶，爸爸在追上小明前停留了0.1小时与碰到的朋友聊天，聊天完毕后以原来的速度继续追赶．在整个过程中，他们离家的路程y（千米）与爸爸出发的时间x（小时）之间的关系如图所示，则爸爸出发小时后与小明相遇．7．5月13日，周杰伦2017“地表最强”世界巡回演唱会在奥体中心盛大举行，1号巡逻员从舞台走往看台，2号巡逻号从看台走往舞台，两人同时出发，分别以各自的速度在舞台与看台间匀速走动，出发1分钟后，1号巡逻员发现对讲机遗忘在出发地，便立即返回出发地，拿到对讲机后（取对讲机时间不计）立即再从舞台走往看台，结果1号巡逻员先到达看台，2号巡逻员继续走到舞台，设2号巡逻员的行驶时间为x（min），两人之间的距离为y（m），y与x的函数图象如图所示，则当1号巡逻员到达看台时，2号巡逻员离舞台的距离是米．8．甲、乙两人相约从A地到B地，甲骑自行车先行，乙开汽车，两人均在同一路线上匀速行驶，乙到B地后即停车等甲，甲、乙两人之间的距离y（千米）与甲行驶的时间x（小时）之间的函数关系如图所示，则乙从A地到B地所用的时间为小时．9．小鹏早晨到校发现作业忘带，就打电话叫爸爸立即把作业送到学校，小鹏也同时往家赶，两人相遇后，小鹏以原速度返回学校，爸爸则以原速度的返回家．设爸爸行走的时间为x分钟，小鹏和爸爸两人之间的距离为y米，y与x的函数关系如图所示，则当小鹏回到学校时，爸爸还需要分钟才能到家．10．快车和慢车同时从甲地出发以不同的速度匀速前往乙地，当快车到达乙地后停留了一段时间，立即从原路以另一速度匀速返回，在途中与慢车相遇，相遇后两车朝各自的方向继续行驶，两车之间的距离y（千米）与慢车行驶的时间t（小时）之间的函数图象如图所示，则甲乙两地的距离是千米．11．甲、乙两车分别从A、B两地同时出发匀速相向而行，大楼C位于AB之间，甲与乙相遇在AC中点处，然后两车立即掉头，以原速原路返回，直到各自回到出发点．设甲、乙两车距大楼C的距离之和为y（千米），甲车离开A地的时间为t（小时），y与t的函数图象所示，则第21小时时，甲乙两车之间的距离为千米．12．某天早晨，小刚从家跑步去体育场锻炼，同时妈妈从体育场晨练结束回家，途中两人相遇，小刚跑到体育场后发现要下雨，立即以另一速度按原路返回，遇到妈妈后，妈妈立即以小刚返回的速度和小刚一起回家（妈妈与小刚行进的路线相同）．如图是两人离家的距离y（米）与小刚出发的时间x（分）之间的函数图象，则小刚第一次和妈妈相遇时，妈妈离家的距离为米．13．甲、乙两辆汽车从A地出发前往相距250千米的B地，乙车先出发匀速行驶，一段时间后，甲车出发匀速追赶，途中因油料不足，甲到服务区加油花了6分钟，为了尽快追上乙车，甲车提高速度仍保持匀速行驶，追上乙车后继续保持这一速度直到B地，如图是甲、乙两车之间的距离s（km2），乙车出发时间t（h）之间的函数关系图象，则甲车比乙车早到分钟．14．某周末，小明到彩云湖公园画画写生，小明家到彩云湖公园的路程为3.5千米，步行20分钟后，在家的小明妈妈发现小明画画的某工具没拿，立即通知小明等着自己把工具送过去，小明妈追上小明把工具给了小明后立即返回，同时小明以原来1.5倍的速度前往目的地，如图是小明与小明妈距家的路程（千米）与小明所用时间（分钟）之间的函数图象，则小明到达目的地比小明妈返回家晚分钟．15．甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地，乙车匀速前往A地，中途与甲车相遇后休息了一会儿，然后以原来的速度继续行驶直到A地．设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时）．y与x之间的函数图象如图所示，则乙车到达A地时甲车距B地的路程为千米．16．已知A市到B市的路程为260千米，甲车从A市前往B市运送物资，行驶2小时在M地汽车出现故障，立即通知技术人员乘乙车从A市赶来维修（通知时间忽略不计），乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市，同时甲车以原来1.5倍的速度前往B市，如图是两车距A市的路程y（千米）与甲车所用时间x（小时）之间的函数图象，则当甲车到达B市时乙车已返回A市的时间为小时．17．一段笔直的公路AC长20千米，途中有一处休息点B，AB长15千米，甲、乙两名长跑爱好者同时从点A出发，甲以v1的速度匀速跑至点B，原地休息半小时后，再以v2的速度匀速跑至终点C；乙以v3的速度匀速跑至终点C，甲、乙两人出发后2小时内运动路程y（千米）与时间x（小时）函数关系的图象如图所示，则AB长为千米，v1﹣v2=．18．一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设先发车辆行驶的时间为x小时，两车之间的距离为y千米，图中的折线表示y与x之间的函数关系．当两车之间的距离首次为300千米时，经过小时后，它们之间的距离再次为300千米．19．“欢乐跑中国•重庆站”比赛前夕，小刚和小强相约晨练跑步．小刚比小强早1分钟跑步出门，3分钟后他们相遇．两人寒暄2分钟后，决定进行跑步比赛．比赛时小刚的速度始终是180米/分，小强的速度是220米/分．比赛开始10分钟后，因雾霾严重，小强突感身体不适，于是他按原路以出门时的速度返回，直到他们再次相遇．如图所示是小刚、小强之间的距离y（千米）与小刚跑步所用时间x（分钟）之间的函数图象．问小刚从家出发到他们再次相遇时，一共用了分钟．20．在甲、乙两城市之间有一服务区，一辆客车从甲地驶往乙地，一辆货车从乙地驶往甲地．两车同时出发，匀速行驶，客车、货车离服务区的距离y1（千米），y2（千米）与行驶的时间x（小时）的函数关系图象如图所示．在客车和货车出发的同时，有一辆邮政车从服务区匀速去甲地取货后返回乙地（取货的时间忽略不计），邮政车离服务区的距离y3（千米）与行驶时间x（小时）之间的函数关系图线如图中的虚线所示，在行驶的过程中，经过小时时邮政车与客车和货车的距离相等．21．欢欢和乐乐骑自行车从滨江路上相距10600米的A、B两地同时出发，先相向而行，行驶一段时间后欢欢的自行车坏了，她立刻停车并马上打电话通知乐乐，乐乐接到电话后立刻提速至原来的倍，碰到欢欢后用了5分钟修好了欢欢的自行车，修好车后乐乐立刻骑车以提速后的速度继续向终点A地前行，欢欢则留在原地整理工具，2分钟以后欢欢再以原速返回A地，在整个行驶过程中，欢欢和乐乐均保持匀速行驶（乐乐停车和打电话的时间忽略不计），两人相距的路程s （米）与欢欢出发的时间t（分钟）之间的关系如图所示，则乐乐到达A地时，欢欢与A地的距离为米．22．甲、乙两人同时从各自家里出发，沿同一条笔直的公路向公园进行跑步训练．乙的家比甲的家离公园近100米，5分钟后甲追上乙，此时乙将速度提高到原来的2倍，又经过15分钟，乙先到达公园并立即返回，但因体力不支，乙返回时的速度又降低到原来的速度．甲跑到公园后也立即掉头回家，整个过程中，甲的速度始终保持不变，甲、乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的部分函数关系如图所示，则当乙回到自己家时，甲离自己的家还有米．23．如图，小明和小亮同时从学校放学，两人以各自速度匀速步行回家，小明的家在学校的正西方向，小亮的家在学校的正东方向，小明准备一回家就开始做作业，打开书包时发现错拿了小亮的练习册，于是立即跑步去追小亮，终于在途中追上了小亮并交还了练习册，然后再以先前的速度步行回家，（小明在家中耽搁和交还作业的时间忽略不计）结果小明比小亮晚回到家中．如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图．则小明的家和小亮的家相距米．24．如图所示的图象反映的过程是：甲乙两人同时从A地出发，以各自的速度匀速向B地行驶，甲先到B地停留半小时后，按原路以另一速度匀速返回，直至与乙相遇．乙的速度为60km/h，y（km）表示甲乙两人相距的距离，x（h）表示乙行驶的时间．现有以下4个结论：①A、B两地相距305km；②点D的坐标为（2.5，155）；③甲去时的速度为152.5km/h；④甲返回的速度是95km/h．以上4个结论中正确的是．25．甲、乙两车在依次连通A、B、C三地的公路上行驶，甲车从B地出发匀速向C地行驶，同时乙车人B地出发匀速向A地行驶，到达A地并在A地停留1小时后，调头按原速向C地行驶．在两车行驶的过程中，甲、乙两车与B地的距离y（千米）与行驶时间x（小时）之间的函数图象如图所示，当甲、乙两车相遇时，所用时间为小时．26．已知A，B两港航程为60km，甲船从A港出发顺流匀速驶向B港，同时乙船从B港出发逆流匀速驶向A港，行至某刻，甲船发现船上一救生圈不知何时落入水中，立刻原路返回，找到救生圈后，继续顺流驶向B港．这样甲乙两船同时到达各自目的地，若甲、乙两船在静水中的速度相同，两船之间的距离y（km）与行驶时间x（h）之间的函数图象如图所示，则水流速度为km/h．27．“渝黔高速铁路”即将在2017年底通车，通车后，重庆到贵阳、广州等地的时间将大大缩短．9月初，铁路局组织甲、乙两种列车在该铁路上进行试验运行，现两种列车同时从重庆出发，以各自速度匀速向A地行驶，乙列车到达A地后停止，甲列车到达A地停留20分钟后，再按原路以另一速度匀速返回重庆，已知两种列车分别距A地的路程y（km）与时间x（h）之间的函数图象如图所示．当乙列车到达A地时，则甲列车距离重庆km．28．甲、乙两名大学生去距学校36千米的某乡镇进行社会调查．他们从学校出发，骑电动车行驶20分钟时发现忘带相机，甲下车前往，乙骑电动车按原路返回．乙取相机后（在学校取相机所用时间忽略不计），骑电动车追甲．在距乡镇13.5千米处追上甲后同车前往乡镇．乙电动车的速度始终不变．设甲与学校相距y甲（千米），乙与学校相离y乙（千米），甲离开学校的时间为t（分钟）．y甲、y与x之间的函数图象如图所示，则乙返回到学校时，甲与学校相距千米．乙29．某客运公司的特快巴士与普通巴士同时从甲地出发，以各自的速度匀速向乙地行驶，普通巴士到达乙地后停止，特快巴士到达乙地停留45分钟后，按原路以另一速度匀速返回甲地，已知两辆巴士分别距乙地的路程y（千米）与行驶时间x（小时）之间的函数图象如图所示．求普通巴士到达乙地时，特快巴士与甲地之间的距离为千米．30．快车和慢车同时从甲地出发，以各自的速度匀速向乙地行驶，快车到达乙地后停留了45分钟，立即按原路以另一速度匀速返回，直至与慢车相遇．已知慢车的速度为60千米/时，两车之间的距离y（千米）与两车行驶时间x（小时）之间的函数图象如图所示，则快车从乙地返回时的速度为千米/时．31．不览夜景，未到重庆．山城夜景，早在清乾隆时期就已有名气，被时任巴县知县王尔鉴，列为巴渝十二景之一．在朝天门码头坐船游两江（即长江、嘉陵江），是游重庆赏夜景的一个经典项目．一艘轮船从朝天门码头出发匀速行驶，1小时后一艘快艇也从朝天门码头出发沿同一线路匀速行驶，当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇．设轮船行驶的时间为t（h），快艇和轮船之间的距离为y（km），y与t的函数关系式如图所示．问快艇与轮船第二次相遇时到朝天门码头的距离为千米．32．初三某班学生去中央公园踏青，班级信息员骑自行车先从学校出发，5分钟后其余同学以60米/分的速度从学校向公园行进，信息员先到达公园后用5分钟找到聚集地点，再立即按原路以另一速度返回到队伍汇报聚集地点，最后与同学们一起步行到公园，信息员离其余同学的距离y（米）与信息员出发的时间x（分）之间的关系如图所示，则信息员开始返回之后，再经过分钟与其余同学相距720米．33．甲、乙两组工人同时开始加工某种零件，乙组在工作中有一次停产更换设备，更换设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量y（件）与时间x（时）之间的函数图象如图所示．甲、乙两组加工出的零件合在一起装箱，每够300件装一箱，零件装箱的时间忽略不计，求经过小时恰好装满第1箱．34．国家“5A”级景区某日迎来客流高峰，从索道开始运行前3小时开始，每小时都有a名游客源源不断地涌入候客大厅排队．索道每小时运送b名游客上山，索道运行2小时后，景区调来若干辆汽车和索道一起送游客上山，其中每小时有b 名游客乘坐汽车上山．5小时后，在候客大厅排队的游客人数降至1000人，候客大厅排队的游客人数y（人）与游客开始排队后的时间x（小时）之间的关系如图所示．则a=．35．甲、乙两人骑车从学校出发，先上坡到距学校6千米的A地，再下坡到距学校16千米的B地，甲、乙两人行驶的路程y（千米）与时间x（小时）之间的函数关系如图所示，若甲、乙两人同时从B地按原路返回到学校，返回时，甲和乙上、下坡的速度仍保持不变，则在返回途中二人相遇时离A地的距离是千米．36．甲、乙二人同时从A地出发以相同速度匀速步行去B地，甲途中发现忘带物品匀速跑步回A地取，之后立刻返程以相同速度跑步追赶乙，期间乙继续步行去往B地，会合时乙发现仍然有物品没带，时间紧迫，故乘车返回A地取，期间甲继续以先前的速度步行至B地后等待乙，乙取到物品后乘车也到了终点B 地（假定来回车速匀速不变，且甲、乙二人取物品的时间忽略不计）．如图所示是甲乙二人之间的距离y（米）与他们从A地出发所用的时间x的（分钟）的函数图象，则当曱到达B地时，乙与A地相距米．37．在一次集训中，一支队伍出发10分钟后，通讯员骑自行车追上队尾传达命令，然后按原速到队首传达命令后继续按原速原路返回．在此过程中队伍一直保持匀速行进，如图所示是通讯员与队首的距离S（米）和通讯员所用时间t（分钟）之间的函数图象．若传达命令所花时间都为2分钟，则当通讯员再次回到队尾时，他一共走了米．38．在我校刚刚结束的缤纷体育节上，初三年级参加了60m迎面接力比赛．假设每名同学在跑步过程中是匀速的，且交接棒的时间忽略不计，如图是A、B两班的路程差y（米）与比赛开始至A班先结束第二棒的时间x（秒）之间的函数图象．则B班第二棒的速度为米/秒．39．已知重庆和成都相距340千米，甲车早上八点从重庆出发往成都运送物资，行驶1小时后，汽车突然出现故障，立即通知技术人员乘乙车从重庆赶来维修（通知时间不计），乙车达到后经30分钟修好甲车，然后以原速返回重庆，同时甲车以原来速度的1.5倍继续前往成都．两车分别距离成都的路程y（千米）与甲车所用时间x（小时）之间的函数图象如图所示，下列四个结论：①甲车提速后的速度是90千米/时；②乙车的速度是70千米/时；③甲车修好的时间为10点15分；④甲车达到成都的时间为13点15分，其中，正确的结论是（填序号）40．甲、乙两车在连通A、B、C三地的公路上行驶，B地在A地、C地之间，甲车从A地出发匀速向C地行驶，同时乙车从C地出发匀速向B地行驶，到达B 地并在B地停留1h后，按原路原速返回到C地．在两车行驶的过程中，甲、乙两车距B地的路程y（km）与行驶时间x（h）之间的函数图象如图所示．当甲车出发h后，甲、乙两车与B地距离相等．17题一次函数应用参考答案与试题解析一．填空题（共40小题）1．A、B两地之间的路程为2380米，甲、乙两人分别从A、B两地出发，相向而行，已知甲先出发5分钟后，乙才出发，他们两人在A、B之间的C地相遇，相遇后，甲立即返回A地，乙继续向A地前行．甲到达A地时停止行走，乙到达A 地时也停止行走．在整个行走过程中，甲、乙两人均保持各自的速度匀速行走，甲、乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的关系如图所示，则乙到达A地时，甲与A地相距的路程是180米．【分析】根据题意和函数图象中的数据可以求得甲乙的速度和各段用的时间，从而可以求得乙到达A地时，甲与A地相距的路程．【解答】解：由题意可得，甲的速度为：（2380﹣2080）÷5=60米/分，乙的速度为：（2080﹣910）÷（14﹣5）﹣60=70米/分，则乙从B到A地用的时间为：2380÷70=34分钟，他们相遇的时间为：2080÷（60+70）=16分钟，∴甲从开始到停止用的时间为：（16+5）×2=42分钟，∴乙到达A地时，甲与A地相距的路程是：60×（42﹣34﹣5）=60×3=180米，故答案为：180．【点评】本题考查一次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用一次函数的性质解答．2．在一条笔直的公路上有A、B、C三地，C地位于A、B两地之间，甲车从A 地沿这条公路匀速驶向C地，乙车从B地沿这条公路匀速驶向A地．在甲车出发至甲车到达C地的过程中，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．下列结论：①甲车出发2h时，两车相遇；②乙车出发1.5h时，两车相距170km；③乙车出发2h时，两车相遇；④甲车到达C地时，两车相距40km．其中正确的是②③④（填写所有正确结论的序号）．【分析】①观察函数图象可知，当t=2时，两函数图象相交，结合交点代表的意义，即可得出结论①错误；②根据速度=路程÷时间分别求出甲、乙两车的速度，再根据时间=路程÷速度和可求出乙车出发1.5h时，两车相距170km，结论②正确；③根据时间=路程÷速度和可求出乙车出发2h时，两车相遇，结论③正确；④结合函数图象可知当甲到C地时，乙车离开C地0.5小时，根据路程=速度×时间，即可得出结论④正确．综上即可得出结论．【解答】解：①观察函数图象可知，当t=2时，两函数图象相交，∵C地位于A、B两地之间，∴交点代表了两车离C地的距离相等，并不是两车相遇，结论①错误；②甲车的速度为240÷4=60（km/h），乙车的速度为200÷（3.5﹣1）=80（km/h），∵（240+200﹣60﹣170）÷（60+80）=1.5（h），∴乙车出发1.5h时，两车相距170km，结论②正确；③∵（240+200﹣60）÷（60+80）=2（h），∴乙车出发2h时，两车相遇，结论③正确；④∵80×（4﹣3.5）=40（km），∴甲车到达C地时，两车相距40km，结论④正确．综上所述，正确的结论有：②③④．故答案为：②③④．【点评】本题考查了一次函数的应用，根据函数图象逐一分析四条结论的正误是解题的关键．3．快、慢两车分别从相距480km的甲，乙两地同时出发，匀速行驶，相向而行，途中慢车因故停留了1小时，然后继续以原速驶向甲地，到达甲地后即停止行驶；快车到达乙地后，立即按原路原速返回甲地（调头时间忽略不计）．如图是快、慢两车距乙地路程y（km）与所用时间x（h）之间的函数图象，则当两车第一次相遇时，快车距离甲地的路程是320千米．【分析】根据行程问题的数量关系：速度=路程÷时间及路程=速度×时间就可以得出：乙的速度和a的值，所以可求出点D的坐标，再由题意可以求出快车的速度就可以求出点B的坐标，由待定系数法求出AB的解析式及OD的解析式就可以求出结论．【解答】解：由题意，得慢车的速度为：480÷（9﹣1）=60千米/时，∴a=60×（7﹣1）=360．则5×60=300，∴D（5，300），设y OD=k1x，由题意，得300=5k1，∴k1=60，∴y OD=60x．∵快车的速度为：（480+360）÷7=120千米/时．∴480÷120=4小时．∴B（4，0），C（8，480）．设y AB=k2x+b，由题意，得，解得：，∴y AB=﹣120x+480∴，解得：．∴480﹣160=320千米．答：快车与慢车第一次相遇时，距离甲地的路程是320千米；故答案为：320．【点评】本题考查了行程问题的数量关系路程=速度×时间的运用，待定系数法求一次函数的解析式的运用，一次函数与一元一次方程的关系的运用，解答时求出一次函数的解析式是关键．4．甲，乙两车分别从A，B两地同时相向匀速行驶，乙车到达A地后未作停留，继续保持原速向远离B地的方向行驶，而甲车到达B地后修整了1个小时，然后调头并保持原速与乙车同向行驶，经过一段时间后两车同时到达C地．设两车行驶的时间为x（小时），两车之间的距离为y（千米），y与x之间的函数图象如图所示，则A，C两地相距420千米．。
初二一次函数应用题
初二一次函数应用题（1）已知一次函数Y=-2X+M的图像与X轴，Y轴所围成的三角形的面积为1.求M的值。
（2）直线M经过点（2，3）和（-1，-3），直线N与M交于点（-2，A），与Y 轴交点的纵坐标为7.①直线M，N的关系式；②求M,N与X轴围成的三角形的面积；③X取何值时，M的函数值大于N的函数值。
（3）预防“非典”时期，某种消毒液广宁需要6吨，怀柔需要8吨，正好端州储备有10吨，四会储备有4吨。
市领导小组决定将这14吨消毒液调往广宁和怀柔。
消毒液的运费价格如下表广宁怀柔端州 60 100四会 35 70设从端州调运X吨到广宁①求调运14吨消毒液的总运费Y关于X的函数关系式；②求出总运费最低的调运方案，最低运费是多少？（3）一农民带了若干千克自产的土豆进程出售，为了方便，他带了些零钱备用，按市场价售出一些土豆后，又降价出售，售出土豆千克数与他手中持有的钱数（含备用零钱）的关系，如图农民自带的零钱是多少？降价前他每千克土豆售价的价格是多少？降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零用钱）是26元，问他一共带了多少千克土豆？1.二分之M的绝对值乘以M的绝对值除以2等于1,所以M等于2或者-22.①设M的解析式为y=kx+b,所以3=2k+b,-3=-k+b,所以k=2.b=-1,所以M的解析式为y=2x-1设N的解析式为y=kx+7,又因为"直线N与M交于点（-2，A）"，所以A=-2×2-1=-5 所以-5=-2k+7,所以k=6,N的解析式为y=6x+7②M与x轴交于1/2,N与x轴交于-7/6,M与N的交点的纵坐标为-5所以面积s=(1/2+7/6)×5÷2=25/6③依题得2x-1＞6x+7,x＜-23.①依题得y=60x+100(10-x)+35(6-x)+70(x-2)=1070-5x,(2≤x≤6)②当x=6时,y最小,为1040方案是端州到广宁6吨,到怀柔4吨;四会到怀柔4吨,总运费为1040元4.农民自带的零钱是5元降价前他每千克土豆售价的价格是(20-5)÷30=0.5元降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零用钱）是26元，他一共带了(26-20)÷0.4+30=45千克土豆。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中考一次函数应用题近几年来，各地的中考题中越来越多地出现了与函数有关的经济型考试题，这种类型的试题，由于条件多，题目长，很多考生无法下手，打不开思路，在考场上出现了僵局，在这里，我特举几例，也许对你有所帮助。
例1 已知雅美服装厂现有 A 种布料70 米，B 种布料52 米，现计划用这两种布料生产M，N两种型号的时装共80 套。
已知做一套M型号的时装需要 A 种布料0. 6 米，B种布料0.9 米，可获利润45 元；做一套N型号的时装需要A种布料 1.1 米，B 种布料0. 4 米，可获利润50 元。
若设生产N种型号的时装x，用这批布料生产这两种型号的时装所获总利润为y 元。
套数为（1）求y 与x的函数关系式，并求出自变量的取值范围；（2）雅美服装厂在生产这批服装中，当N型号的时装为多少套时，所获利润最大？最大利润是多少？例2 某市电话的月租费是20 元，可打60 次免费电话（每次 3 分钟），超过60 次后，超过部分每次0. 13 元。
（1）写出每月电话费y （元）与通话次数x之间的函数关系式；（2）分别求出月通话50 次、100 次的电话费；（3）如果某月的电话费是27. 8 元，求该月通话的次数。
例3 荆门火车货运站现有甲种货物1530 吨，乙种货物1150 吨，安排用一列货车将这批货物运往广州，这列货车可挂A、B两种不同规格的货厢50 节，已知用一节 A 型货厢的运费是0. 5 万元，用一节 B 型货厢的运费是0.8 万元。
（1）设运输这批货物的总运费为y （万元），用A 型货厢的节数为x（节），试写出y 与x之间的函数关系式；（2）已知甲种货物35 吨和乙种货物15 吨，可装满一节 A 型货厢，甲种货物25 吨和乙种货物35 吨可装满一节B型货厢，按此要求安排A、B两种货厢的节数，有哪几种运输方案？请你设计出来。
（3）利用函数的性质说明，在这些方案中，哪种方案总运费最少？最少运费是多少万元？例4 某工厂现有甲种原料360 千克，乙种原料290 千克，计划利用这两种原料生产A、B 两种产品，共50 件。
已知生产一件A种产品，需用甲种原料9 千克、乙种原料 3 千克，可获利润700 元；生产一件B 种产品，需用甲种原料 4 千克、乙种原料10 千克，可获利润1200 元。
（1）按要求安排A、B 两种产品的生产件数，有哪几种方案？请你设计出来；（2）设生产A、B 两种产品获总利润为y （元），生产 A 种产品x件，试写出y 与x之间的函数关系式，并利用函数的性质说明（1）中哪种生产方案获总利润最大？最大利润是多少？例5 某地上年度电价为0. 8 元，年用电量为 1 亿度。
本年计划将电价调至0.55~0. 75 元之间，经测算，x元，则本年度新增用电量y （亿度）与( x 0.4) （元）成反比例，又当x＝0. 65 时，y若电价调至＝0. 8。
（1）求y 与x之间的函数关系式；（2）若每度电的成本价为0. 3 元，则电价调至多少元时，本年度电力部门的收益将比上年度增加20%？[ 收益＝用电量×（实际电价－成本价）]例6 为加强公民的节水意识，某城市制定了以下用水收费标准：每户每月用水未超过7 立方米时，每立方米收费 1. 0 元并加收0. 2 元的城市污水处理费，超过7 立方米的部分每立方米收费 1.5 元并加收0. 4 元的城市污水处理费，设某户每月用水量为x（立方米），应交水费为y （元）（1）分别写出用水未超过7 立方米和多于7 立方米时，y 与x之间的函数关系式；（2）如果某单位共有用户50 户，某月共交水费514. 6 元，且每户的用水量均未超过10 立方米，求这个月用水未超过7 立方米的用户最多可能有多少户？例7 辽南素以“苹果之乡”著称，某乡组织20 辆汽车装运三种苹果42 吨到外地销售。
按规定每辆车只装同一种苹果，且必须装满，每种苹果不少于 2 车。
（1）设用x辆车装运A 种苹果，用y 辆车装运 B 种苹果，根据下表提供的信息求y 与x之间的函数关系式，并求x的取值范围；（2）设此次外销活动的利润为W（百元），求W与x的函数关系式以及最大利润，并安排相应的车辆分配方案。
苹果品种 A B C每辆汽车运载量（吨） 2. 2 2. 1 2每吨苹果获利（百元） 6 8 5解：（1）由题意得： 2.2 x 2. 1y 2( 20 x y) 42化简得：y 2x 20当y ＝0 时，x＝10∴1＜x＜10答：y 与x之间的函数关系式为：y 2x 20 ；自变量x的取值范围是：1＜x＜10 的整数。
（2）由题意得：W＝2.2 6x 2.1 8y 2 5 (20 x y)＝3.2 x 6.8y 200＝3.2 x 6. 8( 2x 20) 200＝10. 4x 336∵W与x之间的函数关系式为：y ＝10. 4x 336 ∴W随x的增大而减小∴当x＝2 时，W有最大值，最大值为：W最大值10.4 2 336＝315. 2（百元）当x＝2 时，y 2x 20 ＝16，20 x y ＝2答：为了获得最大利润，应安排 2 辆车运输 A 种苹果，16 辆车运输 B 种苹果，2 辆车运输C种苹果。
同学们，从以上几例的解答过程中，你学到了解决这类问题的基本思路和方法吗？小结：确定函数解析式，求函数值确定自变量取值范围实际问题――――――数学问题方案设计：利用不等式或不等式组及题意方案决策：最优方案：利用一次函数的性质及自变量取值范围确定最优方案解决问题――――――――――――――――――次函第 3 页共9 页数应用题例析一次函数是初中数学中的重点内容之一，设计一次函数模型解决实际问题，备受各地命题者的青睐.本文采撷几例中考试题加以评析，供参考.一、图象型例1 (2003 年广西) 在抗击“非典”中，某医药研究所开发了一种预防“非典”的药品. 经试验这种药品的效果得知：当成人按规定剂量服用该药后1小时时，血液中含药量最高，达到每毫升 5 微克，接着逐步衰减，至8小时时血液中含药量为每毫升 1.5 微克. 每毫升血液中含药量y( 微克) 随时间x( 小时) 的变化如图所示.在成人按规定剂量服药后：(1) 分别求出x≤1，x≥1时y 与x 之间的函数关系式；(2) 如果每毫升血液中含药量为 2 微克或 2 微克以上，对预防“非典”是有效的，那么这个有效时间为多少小时？解析本题涉及的背景材料专业性很强，但只要读懂题意，用我们学过的函数知识是不难解答的. 题目的主要信息是由函数图象给出的，图象是由两条线段组成的折线，可把它看成是两个一次函数图象的组合.(1) 当x≤1时，设y=k1x. 将(1 ，5) 代入，得k1=5.∴y=5x.当x＞1 时，设y=k2x+b. 以(1 ，5) ，(8 ，1.5) 代入，得，∴(2) 以y=2 代入y=5x，得；以y=2 代入，得x2=7..故这个有效时间为小时.注：题中图像是已知条件的重要组成部分，必须充分利用.二、预测型例2 (2002 年辽宁省) 随着我国人口增长速度的减慢，小学入学儿童数量有所减少，下表中的数据近似地呈现了某地区入学儿童人数的变化趋势，试用你所学的函数知识解决下列问题：(1) 求入学儿童人数y( 人) 与年份x( 年) 的函数关系式；(2) 利用所求函数关系式，预测该地区从哪一年起入学儿童的人数不超过1000 人？年份(x) 2000 2001 2002 ,入学儿童人数(y) 2520 2330 2140解析建立反比例函数，一次函数或二次函数模型，考察哪一种函数能较好地描述该地区入学儿童人数的变化趋势，这就要讨论. 若设(k ＞0) ，在三点(2000 ，2520) ，(2001 ，2330) ，(2002 ，2140) 中任选一点确定k 值后，易见另两点偏离曲线较远，故反比例函数不能较好地反映入学儿童人数的变化趋势，从而选用一次函数.(1) 设y=kx+b (k ≠0) ，将(2000 ，2520) 、(2001 ，2330) 代入，得故y=-190x+382520.又因为y=-190x+382520 过点(2002 ，2140) ，所以y=-190x+382520 能较好地描述这一变化趋势.所求函数关系式为y=-190x+382520.(2) 设x 年时，入学儿童人数为1000 人，由题意得-190x+382520=1000. 解得x=2008. 所以，从2008 年起入学儿童人数不超过1000 人.注：从数学的角度去分析，能使我们作出的预测更准确. 本题也可构造二次函数模型来描述这一变化趋势.三、决策型例3 (2003 年甘肃省) 某工厂生产某种产品，每件产品的出厂价为 1 万元，其原材料成本价( 含设备损耗等) 为0.55 万元，同时在生产过程中平均每生产一件产品有 1 吨的废渣产生. 为达到国家环保要求，需要对废渣进行脱硫、脱氮等处理. 现有两种方案可供选择.方案一：由工厂对废渣直接进行处理，每处理 1 吨废渣所用的原料费为0.05 万元，并且每月设备维护及损耗费为20 万元.方案二：工厂将废渣集中到废渣处理厂统一处理. 每处理 1 吨废渣需付0.1 万元的处理费.(1) 设工厂每月生产x 件产品，每月利润为y 万元，分别求出用方案一和方案二处理废渣时，y 与x 之间的函数关系式( 利润=总收入- 总支出) ；(2) 如果你作为工厂负责人，那么如何根据月生产量选择处理方案，既可达到环保要求又最合算.解析先建立两种方案中的函数关系式，然后根据月生产量的多少通过分类讨论求解.(1)y 1=x-0.55x-0.05x-20=0.4x-20 ；y 2=x-0.55x-0.1x=0.35x.(2) 若y1＞y2，则0.4x-20 ＞0.35x ，解得x＞400；若y1=y2，则0.4x-20=0.35x ，解得x=400；若y1＜y2，则0.4x-20 ＜0.35x ，解得x＜400.故当月生产量大于400 件时，选择方案一所获利润较大；当月生产量等于400 件时，两种方案利润一样；当月生产量小于400 件时，选择方案二所获利润较大.注：在处理生产实践和市场经济中的一些问题时，用数学的眼光来分辨，会使我们作出的决策更合理.四、最值型例4 (2003 年江苏省扬州市) 杨嫂在再就业中心的支持下，创办了“润扬”报刊零售点，对经营的某种晚报，杨嫂提供了如下信息.①买进每份0.2 元，卖出每份0.3 元；②一个月( 以30 天计) 内，有20 天每天可以卖出200 份，其余10 天每天只能卖出120 份.③一个月内，每天从报社买进的报纸份数必须相同，当天卖不掉的报纸，以每份0.1 元退回给报社.(1) 填表：一个月内每天买进该种晚报的份数100 150当月利润( 单位：元)(2) 设每天从报社买进这种晚报x 份(120≤x≤200)时，月利润为y元，试求y 与x 之间的函数关系式，并求月利润的最大值.解析(1) 由题意，当一个月每天买进100 份时，可以全部卖出，当月利润为300 元；当一个月内每天买进150 份时，有20 天可以全部卖完，其余10 天每天可卖出120 份，剩下30 份退回报社，计算得当月利润为390 元.(2) 由题意知，当120≤x≤200 时，全部卖出的20 天可获利润：20[(0.3-0.2)x]=2x( 元) ；其余10 天每天卖出120 份，剩下(x-120) 份退回报社，10 天可获利润：10[(0.3- 0.2) ×120 -0.1(x-120)]=-x+240( 元).∴月利润为y=2x-x+240=x+240(120≤x≤200).由一次函数的性质知，当x=200 时，y 有最大值，为y=200+240=440( 元).注：对于一次函数y=kx+b ，当自变量x在某个范围内取值时，函数值y 可取最大( 或最小) 值，这种最值问题往往用来解决“成本最省”、“利润最大”等方面的问题.五、学科结合型例5 (2002 年南京市) 声音在空气中传播的速度y(m/s)( 简称音速) 是气温x( ℃) 的一次函数.下表列出了一组不同气温时的音速：气温x( ℃) 0 5 10 15 20音速y(m/S) 331 334 337 340 343(1) 求y 与x 之间的函数关系式；(2) 气温x=22(℃) 时，某人看到烟花燃放5s 后才听到声响，那么此人与燃放的烟花所在地约相距多远？解析(1)设y=kx+b，任取表中的两对数，用待定系数法即可求得(2) 当x=22 时，334.2×5=1671(m).故此人与燃放的烟花所在地约相距1671m.注：本题考查了物理中声音的速度与温度的函数关系，是物理与数学结合的一道好题.。