高中数学 第3章3.3.1知能优化训练 新人教B版选修11
高中数学 第3章3.1.3知能优化训练 新人教B版选修11

1.设f ′(x 0)=0,则曲线y =f (x )在点(x 0,f (x 0))处的切线( )A .不存在B .与x 轴平行或重合C .与x 轴垂直D .与x 轴相交但不垂直解析:选B.函数在某点处的导数为零,说明相应曲线在该点处的切线的斜率为零.2.曲线y =-1x 在点(1,-1)处的切线方程为( ) A .y =x -2 B .y =xC .y =x +2D .y =-x -2解析:选A.f ′(1)=lim Δx →0 -11+Δx +11Δx=lim Δx →0 11+Δx =1,则在(1,-1)处的切线方程为y +1=x -1,即y =x -2.3.函数y =x 2+4x 在x =x 0处的切线斜率为2,则x 0=________.解析:2=lim Δx →0 x 0+Δx 2+4x 0+Δx -x 20-4x 0Δx=2x 0+4,∴x 0=-1.答案:-14.求证:函数y =x +1x图象上的各点处的切线斜率小于1. 证明:∵y ′=lim Δx →0 f x +Δx -f x Δx=lim Δx →0 x +Δx +1x +Δx -x +1x Δx=x 2-1x 2=1-1x 2<1, ∴y =x +1x图象上的各点处的切线斜率小于1.一、选择题1.函数y =f (x )在x =x 0处的导数f ′(x 0)的几何意义是( )A .在点x 0处的斜率B .在点(x 0,f (x 0))处的切线与x 轴所夹锐角的正切值C .曲线y =f (x )在点(x 0,f (x 0))处切线的斜率D .点(x 0,f (x 0))与点(0,0)连线的斜率答案:C2.已知曲线y =2x 2上一点A (2,8),则A 处的切线斜率为( )A .4B .16C .8D .2解析:选C.曲线在点A 处的切线的斜率就是函数y =2x 2在x =2处的导数.f ′(x )=lim Δx →0 Δy Δx =lim Δx →0 2x +Δx 2-2x 2Δx=lim Δx →0 4x ·Δx +2Δx 2Δx=4x .则f ′(2)=8.3.已知曲线y =f (x )在点P (x 0,f (x 0))处的切线方程为2x +y +1=0,那么( )A .f ′(x 0)=0B .f ′(x 0)<0C .f ′(x 0)>0D .f ′(x 0)不确定解析:选B.曲线在某点处的切线的斜率为负,说明函数在该点处的导数也为负.4.下列点中,在曲线y =x 2上,且在该点处的切线倾斜角为π4的是( ) A .(0,0) B .(2,4) C .(14,116) D .(12,14) 解析:选D.k =lim Δx →0 Δy Δx =lim Δx →0 x +Δx 2-x 2Δx=limΔx →0(2x +Δx )=2x . ∵倾斜角为π4,∴斜率为1. ∴2x =1,得x =12,故选D. 5.y =-1x +1在点⎝ ⎛⎭⎪⎫12,-2处的切线方程是( ) A .y =4x B .y =4x -4C .y =4x +4D .y =2x -4解析:选B.先求y =-1x +1的导数:Δy =-1x +Δx +1x =Δx x x +Δx ,Δy Δx =1x x +Δx,lim Δx →0 Δy Δx =lim Δx →0 1x x +Δx =1x 2,即y ′=1x 2.所以y =-1x +1在点⎝ ⎛⎭⎪⎫12,-2处的切线斜率k =y ′|x =12=4. 所以切线方程是y +2=4⎝ ⎛⎭⎪⎫x -12,即y =4x -4. 6.设f (x )为可导函数,且满足lim x →0 f 1-f 1-x x=-1,则曲线y =f (x )在点(1,f (1))处的切线的斜率是( )A .2B .-1 C.12D .-2 解析:选B.∵lim x →0f 1-f 1-x x=-1, ∴lim x →0 f 1-x -f 1-x=-1, ∴f ′(1)=-1. 二、填空题7.若曲线y =2x 2-4x +a 与直线y =1相切,则a =________.解析:设切点坐标为(x 0,1),则f ′(x 0)=4x 0-4=0,∴x 0=1.即切点坐标为(1,1).∴2-4+a =1,即a =3.答案:38.已知函数y =ax 2+b 在点(1,3)处的切线斜率为2,则ba=________. 解析: lim Δx →0 a 1+Δx 2-a Δx =lim Δx →0(a ·Δx +2a )=2a =2,∴a =1,又3=a ×12+b ,∴b =2,即b a =2. 答案:2 9.已知曲线y =3x 2,则在点A (1,3)处的曲线的切线方程为________.解析:∵Δy Δx =31+Δx 2-3×12Δx=6+3Δx , ∴y ′|x =1=lim Δx →0(6+3Δx )=6. ∴曲线在点A (1,3)处的切线斜率为6.∴所求的切线方程为y -3=6(x -1),即6x -y -3=0.答案:6x -y -3=0三、解答题10.曲线y =-x 2+4x 上有两点A (4,0),B (2,4).求:(1)割线AB 的斜率k AB ;(2)点A 处的切线的斜率;(3)点A 处的切线方程.解:(1)k AB =4-02-4=-2. (2)f ′(x )=lim Δx →0 -x +Δx 2+4x +Δx +x 2-4x Δx=lim Δx →0 -2x ·Δx -Δx 2+4Δx Δx=limΔx →0(-2x +4-Δx )=-2x +4, ∴点A (4,0)处的切线的斜率k =f ′(4)=-2×4+4=-4.(3)点A 处的切线方程为y =-4(x -4),即4x +y -16=0.11.求过点P (-1,2)且与曲线y =3x 2-4x +2在点M (1,1)处的切线平行的直线.解:先求曲线y =3x 2-4x +2在M (1,1)处的切线的斜率,k =y ′|x =1=lim Δx →0 31+Δx 2-41+Δx +2-3+4-2Δx=limΔx →0(3Δx +2)=2. 设过点P (-1,2)且斜率为2的直线为l ,则由点斜式y -2=2(x +1),化为一般式2x -y +4=0.所以所求直线方程为2x -y +4=0.12.已知抛物线y =x 2+4与直线y =x +10,求:(1)它们的交点;(2)抛物线在交点处的切线方程.解:(1)由⎩⎪⎨⎪⎧y =x 2+4,y =x +10,得x 2+4=10+x , 即x 2-x -6=0,∴x =-2或x =3.代入直线的方程得y =8或13.∴抛物线与直线的交点坐标为(-2,8)或(3,13).(2)∵y =x 2+4,∴y ′=lim Δx →0 x +Δx 2+4-x 2+4Δx=lim Δx →0 Δx 2+2x ·Δx Δx=lim Δx →0 (Δx +2x )=2x . ∴y ′|x =-2=-4,y ′|x =3=6,即在点(-2,8)处的切线斜率为-4,在点(3,13)处的切线斜率为6. ∴在点(-2,8)处的切线方程为4x+y=0;在点(3,13)处的切线方程为6x-y-5=0.。
2022高中数学 第3章3.3.1知能优化训练 新人教B版选修1-1

1.函数=3+的递增区间是A.0,+∞B.-∞,1C.-∞,+∞ D.1,+∞解析:选′=32+1>0对于任何实数都恒成立.2.命题甲:对任意∈a,b,有f′>0;命题乙:f在a,b内是单调递增的.则甲是乙的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选=3在-1,1内是单调递增的,但f′=32≥0-10,解得>1;再令1-错误!错误!0,∴>错误!即函数的单调递增区间为错误!,+∞.3.若在区间a,b内,f′>0,且fa≥0,则在a,b内有A.f>0 B.f0,所以f在a,b内是增函数,所以f>fa≥0 4.下列函数中,在区间-1,1上是减函数的是A.=2-32B.=nC.=错误!D.=in解析:=错误!,其导数′=错误!<0,且函数在区间-1,1上有意义,所以函数=错误!在区间-1,1上是减函数,其余选项都不符合要求,故选C5.函数=co-in在下面哪个区间内是增函数解析:选′=co-in-co=-in,若=f在某区间内是增函数,只需在此区间内′恒大于或等于0即可.∴只有选项B符合题意,当∈π,2π时,′≥0恒成立.6.函数=a3-在R上是减函数,则A.a≥错误!B.a=1C.a=2 D.a≤0解析:′=3a2-1,函数=a3-在-∞,+∞上是减函数,所以′=3a2-1≤0恒成立,即3a2≤1恒成立.当=0时,3a2≤1恒成立,此时a∈R;当≠0时,若a≤错误!恒成立,则a≤0综上可得a≤0二、填空题7.=2e的单调递增区间是________.解析:∵=2e,∴′=2e+2e=e2+>0⇒0∴递增区间为-∞,-2和0,+∞.答案:-∞,-2,0,+∞8.若函数f=3+b2+c+d的单调减区间为[-1,2],则b=________,c=________ 解析:∵′=32+2b+c,由题意知[-1,2]是不等式32+2b+c0,∴a>0答案:0,+∞三、解答题10.求下列函数的单调区间.1f=3+错误!;2f=+错误!b>0.解:1函数的定义域为-∞,0∪0,+∞,f′=32-错误!=32-错误!,由f′>0,解得1,由f′0,结合-4≤≤4,得-4≤0时,要使f′=a错误!-错误!2+a-错误!≥0恒成立,则a-错误!≥0,解得a≥1综上,a的取值范围为{a|a≥1或a=0}.。
【优化方案】2020高中数学 第3章3.1.3知能优化训练 新人教B版选修1-1.doc

1.设f ′(x 0)=0,则曲线y =f (x )在点(x 0,f (x 0))处的切线( )A .不存在B .与x 轴平行或重合C .与x 轴垂直D .与x 轴相交但不垂直解析:选B.函数在某点处的导数为零,说明相应曲线在该点处的切线的斜率为零.2.曲线y =-1x 在点(1,-1)处的切线方程为( ) A .y =x -2 B .y =xC .y =x +2D .y =-x -2解析:选A.f ′(1)=lim Δx →0 -11+Δx +11Δx=lim Δx →0 11+Δx =1,则在(1,-1)处的切线方程为y +1=x -1,即y =x -2.3.函数y =x 2+4x 在x =x 0处的切线斜率为2,则x 0=________.解析:2=lim Δx →0 x 0+Δx 2+4x 0+Δx -x 20-4x 0Δx=2x 0+4,∴x 0=-1.答案:-14.求证:函数y =x +1x图象上的各点处的切线斜率小于1. 证明:∵y ′=lim Δx →0 f x +Δx -f x Δx=lim Δx →0 x +Δx +1x +Δx -x +1x Δx=x 2-1x 2=1-1x 2<1, ∴y =x +1x图象上的各点处的切线斜率小于1.一、选择题1.函数y =f (x )在x =x 0处的导数f ′(x 0)的几何意义是( )A .在点x 0处的斜率B .在点(x 0,f (x 0))处的切线与x 轴所夹锐角的正切值C .曲线y =f (x )在点(x 0,f (x 0))处切线的斜率D .点(x 0,f (x 0))与点(0,0)连线的斜率答案:C2.已知曲线y =2x 2上一点A (2,8),则A 处的切线斜率为( )A .4B .16C .8D .2解析:选C.曲线在点A 处的切线的斜率就是函数y =2x 2在x =2处的导数.f ′(x )=lim Δx →0 Δy Δx =lim Δx →0 2x +Δx 2-2x 2Δx=lim Δx →0 4x ·Δx +2Δx 2Δx=4x .则f ′(2)=8. 3.已知曲线y =f (x )在点P (x 0,f (x 0))处的切线方程为2x +y +1=0,那么( )A .f ′(x 0)=0B .f ′(x 0)<0C .f ′(x 0)>0D .f ′(x 0)不确定解析:选B.曲线在某点处的切线的斜率为负,说明函数在该点处的导数也为负.4.下列点中,在曲线y =x 2上,且在该点处的切线倾斜角为π4的是( ) A .(0,0) B .(2,4) C .(14,116) D .(12,14) 解析:选D.k =lim Δx →0 Δy Δx =lim Δx →0 x +Δx 2-x 2Δx=limΔx →0(2x +Δx )=2x . ∵倾斜角为π4,∴斜率为1. ∴2x =1,得x =12,故选D. 5.y =-1x +1在点⎝ ⎛⎭⎪⎫12,-2处的切线方程是( ) A .y =4x B .y =4x -4C .y =4x +4D .y =2x -4解析:选B.先求y =-1x +1的导数:Δy =-1x +Δx +1x =Δx x x +Δx ,Δy Δx =1x x +Δx,lim Δx →0 Δy Δx =lim Δx →0 1x x +Δx =1x 2,即y ′=1x 2.所以y =-1x +1在点⎝ ⎛⎭⎪⎫12,-2处的切线斜率k =y ′|x =12=4. 所以切线方程是y +2=4⎝ ⎛⎭⎪⎫x -12,即y =4x -4. 6.设f (x )为可导函数,且满足lim x →0 f 1-f 1-x x=-1,则曲线y =f (x )在点(1,f (1))处的切线的斜率是( )A .2B .-1 C.12D .-2 解析:选B.∵lim x →0f 1-f 1-x x=-1, ∴lim x →0 f 1-x -f 1-x=-1, ∴f ′(1)=-1. 二、填空题7.若曲线y =2x 2-4x +a 与直线y =1相切,则a =________.解析:设切点坐标为(x 0,1),则f ′(x 0)=4x 0-4=0,∴x 0=1.即切点坐标为(1,1).∴2-4+a =1,即a =3.答案:38.已知函数y =ax 2+b 在点(1,3)处的切线斜率为2,则ba=________. 解析: lim Δx →0 a 1+Δx 2-a Δx =lim Δx →0(a ·Δx +2a )=2a =2,∴a =1,又3=a ×12+b ,∴b =2,即b a =2. 答案:2 9.已知曲线y =3x 2,则在点A (1,3)处的曲线的切线方程为________.解析:∵Δy Δx =31+Δx 2-3×12Δx=6+3Δx , ∴y ′|x =1=lim Δx →0(6+3Δx )=6. ∴曲线在点A (1,3)处的切线斜率为6.∴所求的切线方程为y -3=6(x -1),即6x -y -3=0.答案:6x -y -3=0三、解答题10.曲线y =-x 2+4x 上有两点A (4,0),B (2,4).求:(1)割线AB 的斜率k AB ;(2)点A 处的切线的斜率;(3)点A 处的切线方程.解:(1)k AB =4-02-4=-2. (2)f ′(x )=lim Δx →0 -x +Δx 2+4x +Δx +x 2-4x Δx=lim Δx →0 -2x ·Δx -Δx 2+4Δx Δx=limΔx →0(-2x +4-Δx )=-2x +4, ∴点A (4,0)处的切线的斜率k =f ′(4)=-2×4+4=-4.(3)点A 处的切线方程为y =-4(x -4),即4x +y -16=0.11.求过点P (-1,2)且与曲线y =3x 2-4x +2在点M (1,1)处的切线平行的直线.解:先求曲线y =3x 2-4x +2在M (1,1)处的切线的斜率,k =y ′|x =1=lim Δx →0 31+Δx 2-41+Δx +2-3+4-2Δx=limΔx →0(3Δx +2)=2. 设过点P (-1,2)且斜率为2的直线为l ,则由点斜式y -2=2(x +1),化为一般式2x -y +4=0.所以所求直线方程为2x -y +4=0.12.已知抛物线y =x 2+4与直线y =x +10,求:(1)它们的交点;(2)抛物线在交点处的切线方程.解:(1)由⎩⎪⎨⎪⎧y =x 2+4,y =x +10,得x 2+4=10+x , 即x 2-x -6=0,∴x =-2或x =3.代入直线的方程得y =8或13.∴抛物线与直线的交点坐标为(-2,8)或(3,13).(2)∵y =x 2+4,∴y ′=lim Δx →0 x +Δx 2+4-x 2+4Δx=lim Δx →0 Δx 2+2x ·Δx Δx=lim Δx →0 (Δx +2x )=2x . ∴y ′|x =-2=-4,y ′|x =3=6,即在点(-2,8)处的切线斜率为-4,在点(3,13)处的切线斜率为6. ∴在点(-2,8)处的切线方程为4x+y=0;在点(3,13)处的切线方程为6x-y-5=0.。
优化方案2020高中数学第3章3.3.3知能优化训练新人教A版选修11
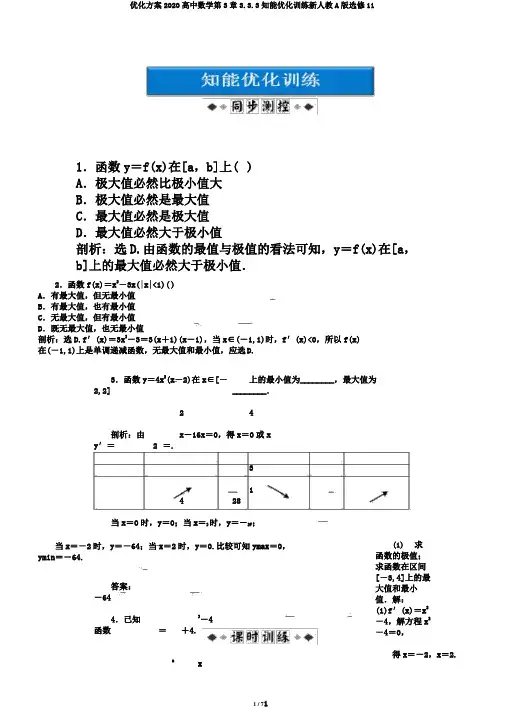
1.函数y=f(x)在[a,b]上( )A.极大值必然比极小值大B.极大值必然是最大值C.最大值必然是极大值D.最大值必然大于极小值剖析:选D.由函数的最值与极值的看法可知,y=f(x)在[a,b]上的最大值必然大于极小值.2.函数f(x)=x3-3x(|x|<1)( )A.有最大值,但无最小值B.有最大值,也有最小值C.无最大值,但有最小值D.既无最大值,也无最小值剖析:选D.f′(x)=3x2-3=3(x+1)(x-1),当x∈(-1,1)时,f′(x)<0,所以f(x)在(-1,1)上是单调递减函数,无最大值和最小值,应选D.3.函数y=4x2(x-2)在x∈[-2,2]上的最小值为________,最大值为________.剖析:由y′=1224x-16x=0,得x=0或x =.34128当x=0时,y=0;当x=3时,y=-27;当x=-2时,y=-64;当x=2时,y=0.比较可知ymax=0,ymin=-64.答案:-6404.已知函数()=13-4+4.x3x x(1)求函数的极值;求函数在区间[-3,4]上的最大值和最小值.解:(1)f′(x)=x2-4,解方程x2-4=0,得x=-2,x=2.12当x变化时,f′(x),f(x)的变化情况以下表:x(-∞,-2)-2(-2,2)′()+0-fx28f(x)3从上表可看出,当x=-2时,函数有极大值,且极大值为4小值,且极小值为-.3(2,+∞)0 +4328;而当x=2时,函数有极3f(-3)=1×(-3)3-4×(-3)+4=7,31 328f(4)=×4-4×4+4=,3 328 4与极值比较,得函数在区间[-3,4]上的最大值是3,最小值是-3.一、选择题1.函数f(x)=-x2+4x+7,在x∈[3,5]上的最大值和最小值分别是()A.f(2),f(3)B.f(3),f(5)C.f(2),f(5)D.f(5),f(3)剖析:选B.∵f′(x)=-2x+4,∴当x∈[3,5]时,f′(x)<0,故f(x)在[3,5]上单调递减,故f(x)的最大值和最小值分别是f(3),f(5).2.f(x)=x3-3x2+2在区间[-1,1]上的最大值是()A.-2B.0C.22D.4剖析:选C.′()=3x -6=3(x-2),令′()=0可得x=0或x=2(舍去),f x x x fx当-1≤x<0时,f′(x)>0,当0<x≤1时,f′(x)<0.所以当x=0时,f(x)获取最大值为2.lnx3.函数y=x的最大值为()A.e-1B.e210C.e D.3剖析:选A.令y′=lnx′x-lnx·x′x21-lnxx2=0.解得x=e.当x>e时,y′<0;当x<e时,y′>0.y=f(e)1极=e,在定义域内只有一个极大值值,1所以ymax=.e4.函数y=x-sinx,xπ,π的最大值是()∈2πA.π-1 B.2-1 C.πD.π+1剖析:选C.因为y′=1-cosx,当x∈π,π时,y′>0,则函数y在区间π,π22上为增函数,所以y的最大值为ymax=π-sinπ=π,应选C.5.函数f(x)=x3-3x2-9x+k在区间[-4,4]上的最大值为10,则其最小值为() A.-10B.-71C.-15D.-22剖析:选B.′()=3x 2-6-9=3(x-3)(x+1).fx x由f′(x)=0得x=3,-1.又f(-4)=k-76,f(3)=k-27,f(-1)=k+5,f(4)=k-20.由f(x)max=k+5=10,得k=5,∴f(x)min=k-76=-71.6.已知函数y=-x2-2x+3在区间[a,2]上的最大值为15,则a等于()431A.-2 B.21 13C .- 2 D.2或- 2剖析:选C.当a ≤-1 时,最大值为 4,不吻合题意,当-1<a<2时,f(x)在[a,2]上是2 151 3减函数,f(a)最大,-a -2a +3=4,解得a =-2或a =-2(舍去). 二、填空题7.函数y =xe x的最小值为________.x剖析:令y ′=(x +1)e =0,得x =-1.1ymin =f(-1)=-e . 1答案:-e2+8.已知 f ( x)=- x+1 在区间[-2,-1]上的最大值就是函数f ( x)的极大值,则mxm 的取值范围是________.m剖析: f′()=-2x,令 f′()=0,得=.xm xx2m1],故m ∈[-4,-2]. 由题设得2∈[-2,- 答案:[-4,-2]9.函数f ( x )= ax 4-4ax 2+( >0,1≤≤2)的最大值为 3,最小值为-5,则=________,b a xab =________.32剖析:f ′(x)=4ax -8ax =4ax(x -2)=0,又f(1)=a -4a +b =b -3a ,f(2)=16a -16a +b =b ,f(2)=b-4a,f(0)=b,f(-2)=b-4a.∴b-4a=-5,∴a=2.=3,b答案:2 3三、解答题10.已知函数f(x)=x3+ax2+2,x=2是f(x)的一个极值点,求:实数a的值;f(x)在区间[-1,3]上的最大值和最小值.解:(1)∵f(x)在x=2处有极值,∴f′(2)=0.f′(x)=3x2+2ax,∴3×4+4a=0,∴a=-3.由(1)知a=-3,∴f(x)=x3-3x2+2,f′(x)=3x2-6x.令f′(x)=0,得x1=0,x2=2.当x变化时f′(x),f(x)的变化情况以下表:x-1(-1,0)0(0,2)2(2,3)3f′(x)+0-0+f(x)-22-22从上表可知f ()在区间[-1,3]上的最大值是2,最小值是-2. x11.设f(x)=x3-12x2-2x+5.求函数f(x)的单调递加、单调递减区间;解:f′(x)=3x2-x-2=(3x+2)(x-1).令f′(x)>0,得x<-2或x>1.3令′()<0,得-2<x <1.fx 3∴函数f(x)的单调递加区间为(-∞,-23),(1,+∞);单调递减区间为12.已知函数f(x)=x3-ax2+3x.(1)若f(x)在x∈[1,+∞)上是增函数,求实数a的取值范围;若x=3是f(x)的极值点,求f(x)在x∈[1,a]上的最大值和最小值.解:(1)令f′(x)=3x2-2ax+3>0,3 1∴a<2x+x min=3(当x=1时取最小值).x≥1,∴a<3,a=3时亦吻合题意,∴a≤3.f′(3)=0,即27-6a+3=0,∴a=5,f(x)=x3-5x2+3x,f′(x)=3x2-10x+3.∴ 1令f′(x)=0,得x1=3,x2=(舍去).3当1<x<3时,f′(x)<0,当3<x<5时,f′(x)>0,即当x=3时,f(x)的极小值f(3)=-9.又f(1)=-1,f(5)=15,f(x)在[1,5]上的最小值是f(3)=-9,最大值是f(5)=15.2(-3,1).。
高中数学 第2章231知能优化训练 选修11 试题(共6页)

知能优化训练(x ùnli àn)[学生用书 P 33]1.动点P 到直线x +4=0的间隔 与它到M (2,0)的间隔 之差等于2,那么P 的轨迹是( ) A .直线 B .椭圆 C .双曲线D .抛物线解析:选D.依题意知,动点P 到定直线x =-2的间隔 与到定点M (2,0)的间隔 相等,故动点P 的轨迹是抛物线.2.抛物线y =14a x 2(a ≠0)的焦点坐标为( )A .当a >0时,(0,a ),当a <0时,(0,-a )B .当a >0时,⎝ ⎛⎭⎪⎫0,a 2,当a <0时,⎝ ⎛⎭⎪⎫0,-a 2C .(0,a )D.⎝ ⎛⎭⎪⎫1a,0 解析:选C.a >0时,x 2=4ay 的焦点为(0,a ),这时焦点在y 轴正半轴上;a <0时,x 2=4ay 的焦点为(0,a ),这时焦点在y 轴负半轴上.故不管a 为何值,x 2=4ay 的焦点总为(0,a ),所以选C.3.(2021年模拟)点P 是抛物线y 2=2x 上的动点,点P 到准线的间隔 为d ,点A (72,4),那么|PA |+d 的最小值是( ) A.72 B .4C.92D .5y 2=2x 的焦点为F ,那么F (12,0).又点A (72,4)在抛物线的外侧,且点P 到准线的间隔 为d ,所以d =|PF |,那么|PA |+d =|PA |+|PF |≥|AF |=5.应选D.4.抛物线y =ax 2的准线(zhǔn xiàn)方程是y =2,那么a 的值是______. 解析:由y =ax 2的准线方程为y =-14a =2,得a =-18.答案:-18一、选择题1.准线方程为x =1的抛物线的HY 方程是( ) A .y 2=-2x B .y 2=-4x C .y 2=2xD .y 2=4xx =1知,抛物线的HY 方程是y 2=-4x .应选B.2.抛物线y =mx 2的准线方程是y =1,那么实数m 的值是( ) A.14 B .-14C .4D .-4y =mx 2,得x 2=1m y ,14m =-1,a =-14.3.P (8,a )在抛物线y 2=4px 上,且P 到焦点的间隔 为10,那么焦点到准线的间隔 为( ) A .2 B .4 C .8D .16x =-p ,∴8+p =10,p =2.∴焦点到准线的间隔 为2p =4.4.(2021年高考卷)抛物线y 2=2px (p >0)的准线与圆x 2+y 2-6x -7=0相切,那么p 的值是( ) A.12 B .1 C .2D .4x =-p 2.由x 2+y 2-6x -7=0得(x -3)2+y 2=16.∵准线(zhǔn xiàn)与圆相切,∴3+p2=4,∴p =2.5.(2021年高考卷)设抛物线y 2=8x 上一点P 到y 轴的间隔 是4,那么点P 到该抛物线焦点的间隔 是( ) A .4 B .6 C .8 D .12解析:选 B.如下图,抛物线的焦点为F (2,0),准线方程为x =-2,由抛物线的定义知:|PF |=|PE |=4+2=6.6.假设点P 到定点F (4,0)的间隔 比它到直线x +5=0的间隔 小1,那么点P 的轨迹方程是( ) A .y 2=-16x B .y 2=-32xC .y 2=16xD .y 2=16x 或者y =0(x <0)解析:选C.∵点F (4,0)在直线x +5=0的右侧,且P 点到点F (4,0)的间隔 比它到直线x +5=0的间隔 小1,∴点P 到F (4,0)的间隔 与它到直线x +4=0的间隔 相等.故点P 的轨迹为抛物线,且顶点在原点,开口向右,p =8,故P 点的轨迹方程为y 2=16x . 二、填空题7.抛物线y 2=2px (p >0)过点M (2,2),那么点M 到抛物线准线的间隔 为________.解析:y 2=2px 过点M (2,2),于是p =1,所以点M 到抛物线准线的间隔 为2+p 2=52.答案(dá àn):528.抛物线y 2=4x 的弦AB ⊥x 轴,假设|AB |=43,那么焦点F 到直线AB 的间隔 为________.解析:由抛物线的方程可知F (1,0),由|AB |=43且AB ⊥x 轴得y 2A =(23)2=12,∴x A =y 2A4=3,∴所求间隔 为3-1=2. 答案:29.动点P 到点F (2,0)的间隔 与它到直线x +2=0的间隔 相等,那么点P 的轨迹方程为________.解析:由抛物线定义知,点P 的轨迹是以点F (2,0)为焦点,x =-2为准线的抛物线,那么其方程为y 2=8x . 答案:y 2=8x 三、解答题10.假设抛物线y 2=-2px (p >0)上有一点M ,其横坐标为-9.它到焦点的间隔 为10,求抛物线方程和M 点的坐标.解:由抛物线定义知焦点为F (-p 2,0),准线为x =p2,由题意设M 到准线的间隔 为|MN |, 那么|MN |=|MF |=10, 即p2-(-9)=10,∴p =2.故抛物线方程为y 2=-4x ,将M (-9,y )代入y 2=-4x ,解得y =±6, ∴M (-9,6)或者M (-9,-6).11.指出抛物线方程为x =ay 2(a ≠0)的顶点坐标、焦点坐标、准线方程. 解:∵原抛物线方程(fāngchéng)为y 2=1a x ,∴2p =1|a |.当a >0时,p 2=14a ,抛物线顶点坐标为(0,0),开口向右,焦点坐标为⎝ ⎛⎭⎪⎫14a ,0,准线方程为x =-14a;当a <0时,p 2=-14a ,抛物线顶点坐标为(0,0),开口向左,焦点坐标为⎝ ⎛⎭⎪⎫14a ,0,准线方程为x =-14a.综上,当a ≠0时,抛物线x =ay 2的顶点坐标为(0,0),焦点坐标为(14a ,0),准线方程为x=-14a.12.根据以下所给条件,写出抛物线的HY 方程及准线方程: (1)焦点是F (0,-2); (2)焦点是F (3,0); (3)准线方程为x =-14;(4)焦点到准线的间隔 是2.解:(1)∵焦点F (0,-2)在y 轴的负半轴上, ∴抛物线的HY 方程的形式为x 2=-2py (p >0). 由p2=2,得p =4, ∴抛物线的HY 方程的形式为:x 2=-8y , 其准线方程为y =2.(2)∵焦点F (3,0)在x 轴的正半轴上, ∴抛物线的HY 方程的形式为y 2=2px (p >0). 由p2=3,得p =6, ∴抛物线的HY 方程(fāngchéng)为:y 2=12x , 其准线方程为x =-3.(3)∵准线方程为x =-14,∴抛物线的HY 方程为:y 2=2px (p >0).由p 2=14,得p =12, 所以抛物线的HY 方程为:y 2=x . (4)由参数p 的几何意义,可知p =2.焦点在x 轴的正半轴上时,抛物线的HY 方程为:y 2=4x ,其准线方程为x =-1;焦点在x 轴的负半轴上时,抛物线的HY 方程为:y 2=-4x ,其准线方程为x =1;焦点在y 轴的正半轴上时,抛物线的HY 方程为:x 2=4y ,其准线方程为y =-1;焦点在y 轴的负半轴上时,抛物线的HY 方程为:x 2=-4y ,其准线方程为y =1.内容总结。
高中数学 第3章3知能优化训练 选修11 试题

卜人入州八九几市潮王学校1.曲线y =x n(n∈N+)在x=2处的导数为12,那么n 等于()A.1 B.2C.3 D.4解析:选C.∵y′=nx n-1,∴y′|x=2=n·2n-1=12,∴n=3.2.以下结论:①假设y=,那么y′|x=2=-;②假设y=cos x,那么y′|x==-1;③假设y=e x,那么y′=e x.其中正确的个数是()A.0 B.1C.2 D.3②③,一共有2个,应选C.3.函数f(x)=x3的切线的斜率等于3,那么这样的切线有()A.1条B.2条C.多于2条D.不确定解析:选B.f′(x)=3x2,令f′(x)=3,即3x2=3,∴x=±1,故应有2条.4.f(x)=x2,g(x)=x3,假设f′(x)-g′(x)=-2,那么x=________.解析:f′(x)=2x,g′(x)=3x2,于是有2x-3x2=-2,解得x=.答案:一、选择题1.(2021年检测)假设f(x)=cos x,那么f′(α)等于()A.sinαB.cosαC.2α+sinαD.-sinα解析:选D.∵f′(x)=(cos x)′=-sin x,∴f′(α)=-sinα.2.在曲线y=x2上切线倾斜角为的切点是()A.(0,0) B.(2,4)C. D.解析:选D.设切点为(x0,x),∵倾斜角为,∴y′=2x0=1,∴x0=,故切点为(,).3.函数f(x)=a x,且f′(e)=4,那么a=()A.4-B.4-eC.e-4D.4解析:选D.∵f′(x)=a x ln a,∴f′(e)=a e=4,∴a=4.4.曲线f(x)=x5上一点M处的切线与直线y=-x+3垂直,那么该切线方程为()A.5x+5y+4=0 B.5x-5y-4=0C.5x+5y±4=0 D.5x-5y±4=0y=-x+3垂直,所以切线的斜率为1.又f′(x)=x4,∴x4=1,∴x=±1.当x=1时,切点为,切线方程为5x-5y-4=0.当x=-1时,切点为,切线方程为5x-5y+4=0.5.假设函数f(x)的导数为f′(x)=-sin x,那么函数图像在点(4,f(4))处的切线的倾斜角为() A.90°B.0°C.锐角D.钝角f(x)在点(4,f(4))处的切线斜率为f′(4)=-sin4>0,∴此切线的倾斜角为锐角.6.(2021年高考大纲全国卷Ⅱ)假设曲线y=x-在点(a,a-)处的切线与两个坐标轴围成的三角形的面积为18,那么a=()A.64 B.32C.16 D.8y′=-x-(x>0),所以曲线y=x-在点(a,a-)处的切线l的斜率k=-a-,由点斜式得切线的方程为y-a-=-a-(x-a),易求得直线l与x轴,y轴的交点分别为(3a,0),,所以直线l与两个坐标轴围成的三角形面积S=×3a×a-=a=18,解得a=64.二、填空题7.(1)函数f(x)=,那么f′(0)=________;(2)函数f(x)=x n,且f′(1)=2,那么n=________.解析:(1)因为f′(x)=0,所以f′(0)=0.(2)由公式得f′(x)=nx n-1,所以f′(1)=n=2,即n=2.答案:028.0<x<,f(x)=x2,g(x)=,那么f′(x)与g′(x)之间的大小关系是________.解析:f′(x)=2x,g′(x)=,因为0<x<,所以f′(x)=2x∈,g′(x)=∈(1,+∞),所以f′(x)<g′(x).答案:f′(x)<g′(x)9.假设曲线y=x2-1的一条切线平行于直线y=4x-3.那么这条切线的方程为________.解析:f′(x)====(2x+Δx)=2x.设切点坐标为(x0,y0),那么由题意知,f′(x0)=4,即2x0=4,∴x0=2.代入曲线方程得y0=3.故该切线过点(2,3)且斜率为4.∴这条切线的方程为y-3=4(x-2),即4x-y-5=0.答案:4x-y-5=0三、解答题10.求以下函数的导数.(1)y=2;(2)y=;(3)y=10x;(4)y=log x;(5)y=2cos2-1.解:(1)∵y′=c′=0,∴y′=2′=0.(2)∵y′=(x n)′=n·x n-1,∴y′=()′=(x)′=x-1=x-=.(3)∵y′=(a x)′=a x·ln a,∴y′=(10x)′=10x·ln10.(4)∵y′=(log a x)′=,∴y′=(log x)′==-.(5)∵y=2cos2-1=cos x,∴y′=(cos x)′=-sin x.11.求曲线y=与y=x2在它们交点处的两条切线与x轴所围成的三角形的面积.解:由,解得交点为(1,1).而′=-;(x2)′=2x,∴斜率分别为-1和2,∴切线方程分别为y-1=-(x-1),及y-1=2(x-1);令y=0,得与x轴交点为(2,0)及,∴S△=·×1=.12.点P是曲线y=e x上任意一点,求点P到直线y=x的最小间隔.解:由设平行于直线y=x的直线与曲线y=e x相切于点(x0,y0),该切点即为与直线y=x间隔最近的点.∵y=e x,∴y′=e x.又∵在点(x0,y0)处的切线斜率为1,∴e x0=1,∴x0=0,代入y=e x,可得:y0=1,∴切点为(0,1),利用点到直线的间隔公式可以求出d=.。
高中数学 第3章3.2.2知能优化训练 湘教版选修11
高中数学 第3章3.2.2知能优化训练 湘教版选修11[学生用书 P 33]1.已知f (x )=x 2,则f ′(3)=( )A .0B .2xC .6D .9解析:选C.∵f ′(x )=2x ,∴f ′(3)=6.2.已知函数f (x )=1x ,则f ′(-3)=( )A .4 B.19C .-14 D .-19解析:选D.∵f ′(x )=-1x 2,∴f ′(-3)=-19.3.(2011年青州高二检测)若f (x )=cos x ,则f ′(α)等于( )A .sin αB .cos αC .2α+sin αD .-sin α解析:选D.f ′(x )=(cos x )′=-sin x ,∴f ′(α)=-sin α.4.曲线y =e x 在点(2,e 2)处的切线与坐标轴所围成三角形的面积为________. 解析:y ′=(e x )′=e x ,∴k =e 2,∴切线方程为:y -e 2=e 2(x -2).令x =0得y =-e 2;令y =0得x =1.∴S △=12e 2·1=12e 2.答案:12e 2一、选择题1.函数y =cot x 的导数是( )A.1sin 2x B .-1cos 2xC .-1sin 2x D.1cos 2x解析:选C.由导数公式表可知(cot x )′=-1sin 2x .2.下列结论中不正确的是( )A .若y =3,则y ′=0B .若y =1x ,y ′=-12xC .若y =-x ,则y ′=-12xD .若y =3x ,则y ′=3解析:选B.∵y ′=(1x )′=(x -12)′=-12x -12-1=-12x -32=-12x x ,∴B 错误.3.若f (x )=sin x ,则f ′(2π)等于( )A .1B .-1C .0D .cos x解析:选A.因为f (x )=sin x ,所以f ′(x )=cos x ,所以f ′(2π)=cos2π=1.4.(2011年高考江西卷)曲线y =e x 在点A (0,1)处的切线斜率为( )A .1B .2C .e D.1e解析:选A.y ′=(e x )′=e x ,∴当x =0时,y ′=e 0=1,故y =e x 在A (0,1)处的切线斜率为1,选A.5.若曲线y =x 4的一条切线l 与直线x +4y -8=0垂直,则l 的方程为( )A .4x -y -3=0B .x +4y -5=0C .4x -y +3=0D .x +4y +3=0解析:选A.y ′=(x 4)′=4x 3.设切点为(x 0,y 0),则4x 30×(-14)=-1, ∴x 0=1.∴切点为(1,1).∴l 的方程为y -1=4(x -1),即4x -y -3=0,故选A.6.设f 0(x )=sin x ,f 1(x )=f 0′(x ),f 2(x )=f 1′(x ),…,f n +1(x )=f n ′(x ),n ∈N ,则f 2010(x )等于( )A .sin xB .-sin xC .cos xD .-cos x解析:选B.利用正、余弦函数的求导公式及函数的周期性求解.f 0(x )=sin x ,f 1(x )=f 0′(x )=cos x ,f 2(x )=f 1′(x )=-sin x ,f 3(x )=f 2′(x )=-cos x ,f 4(x )=f 3′(x )=sin x ,…,∴周期为4,故f 2010(x )=f 2(x )=-sin x .故选B.二、填空题7.已知函数f (x )=3x ,则f ′(0)=________.解析:f ′(x )=3x ln3,则f ′(0)=ln3.答案:ln38.已知f (x )=ln x ,且f ′(x 0)=1x 20,则x 0=________. 解析:f ′(x )=1x ,所以f ′(x 0)=1x 0, 又f ′(x 0)=1x 20,所以1x 0=1x 20, 所以x 0=x 20.所以x 0=0(舍)或x 0=1.答案:19.y =1x的斜率为-1的切线方程为________. 解析:令y ′=-1x 2=-1,得x =±1. ∴切点为(1,1)或(-1,-1).∴切线方程为y -1=-(x -1)或y +1=-(x +1).即x +y -2=0或x +y +2=0.答案:x +y -2=0或x +y +2=0三、解答题10.求下列函数的导数.(1)y =2;(2)y =4x 3;(3)y =10x ;(4)y =log 12x ;(5)y =2cos 2x 2-1. 解:(1)∵y ′=c ′=0,∴y ′=2′=0.(2)∵y ′=(x n )′=n ·x n -1,∴y ′=(4x 3)′=(x 34)′=34x 34-1 =34x -14=344x. (3)∵y ′=(a x )′=a x ·ln a ,∴y ′=(10x )′=10x ·ln10.(4)∵y ′=(log a x )′=1x ·ln a, ∴y ′=(log 12x )′=1x ·l n 12=-1x ·ln2. (5)∵y =2cos 2x 2-1=cos x , ∴y ′=(cos x )′=-sin x .11.已知抛物线y =2x 2+1,求:(1)抛物线上哪一点处的切线的倾斜角为45°?(2)抛物线上哪一点处的切线平行于直线4x -y -2=0?解:设点的坐标为(x 0,y 0),则Δy =2(x 0+Δx )2+1-2x 20-1=4x 0·Δx +2(Δx )2.∴Δy Δx=4x 0+2Δx . 当Δx 无限趋近于零时,Δy Δx无限趋近于4x 0. 即f ′(x 0)=4x 0.(1)∵抛物线的切线的倾斜角为45°,∴斜率为tan45°=1.即f ′(x 0)=4x 0=1,得x 0=14,该点为(14,98). (2)∵抛物线的切线平行于直线4x -y -2=0,∴斜率为4.即f ′(x 0)=4x 0=4,得x 0=1,该点为(1,3).12.已知两条曲线y =sin x ,y =cos x ,是否存在这两条曲线的一个公共点,使在这一点处,两条曲线的切线互相垂直?并说明理由.解:设两条曲线的一个公共点为P (x 0,y 0).∴两条曲线在P (x 0,y 0)处的斜率分别为k 1=cos x 0,k 2=-sin x 0.若使两条切线互相垂直,必须cos x 0·(-sin x 0)=-1,即sin x 0·cos x 0=1,也就是sin2x 0=2,这是不可能的.∴两条曲线不存在公共点,使在这一点处的两条曲线的切线互相垂直.。
人教A版高中数学选修1-1全册同步测控知能训练题集含答案
人教A版高中数学选修1-1全册同步测控知能训练题集目录第1章1.1.1知能优化训练第1章1.1.3知能优化训练第1章1.2知能优化训练第1章1.3知能优化训练第1章1.4知能优化训练第2章2.1.1知能优化训练第2章2.1.2第一课时知能优化训练第2章2.1.2第二课时知能优化训练第2章2.2.1知能优化训练第2章2.2.2知能优化训练第2章2.3.1知能优化训练第2章2.3.2知能优化训练第3章3.1.2知能优化训练第3章3.1.3知能优化训练第3章3.2知能优化训练第3章3.3.1知能优化训练第3章3.3.2知能优化训练第3章3.3.3知能优化训练第3章3.4知能优化训练1.下列语句是命题的是( )A .梯形是四边形B .作直线ABC .x 是整数D .今天会下雪吗答案:A2.(2011年高考课标全国卷)已知a 与b 均为单位向量,其夹角为θ,有下列四个命题:p 1:|a +b |>1⇔θ∈[0,2π3) p 2:|a +b |>1⇔θ∈(2π3,π] p 3:|a -b |>1⇔θ∈[0,π3) p 4:|a -b |>1⇔θ∈(π3,π] 其中的真命题是( )A .p 1,p 4B .P 1,p 3C .P 2,p 3D .P 2,p 4解析:选A.|a +b |>1⇔1+1+2cos θ>1⇔θ∈[0,2π3). |a -b |>1⇔1+1-2cos θ>1⇔θ∈(π3,π]. 3.判断下列命题的真假:①3≥3:________;②100或50是10的倍数:________.答案:①真命题 ②真命题4.写出命题“如果一个函数的图象是一条直线,那么这个函数为一次函数”的条件p 和结论q .解:条件p :一个函数的图象是一条直线;结论q :这个函数为一次函数.一、选择题1.下列语句不是命题的有( )①2<1;②x <1;③若x <2,则x <1;④函数f (x )=x 2是R 上的偶函数.A .0个B .1个C .2个D .3个解析:选B.①③④可以判断真假,是命题;②不能判断真假,所以不是命题.2.下列命题是真命题的是( )A .{∅}是空集B.{}x ∈N||x -1|<3是无限集C .π是有理数D .x 2-5x =0的根是自然数解析:选D.x 2-5x =0的根为x 1=0,x 2=5,均为自然数.3.(2010年高考山东卷)在空间,下列命题正确的是( )A .平行直线的平行投影重合B .平行于同一直线的两个平面平行C .垂直于同一平面的两个平面平行D .垂直于同一平面的两条直线平行答案:D4.下列命题中真命题的个数为( )①面积相等的两个三角形是全等三角形;②若xy =0,则|x |+|y |=0;③若a >b ,则a +c >b +c ;④矩形的对角线互相垂直.A.1 B.2C.3 D.4解析:选A.①错;②错,若xy=0,则x,y至少有一个为0,而未必|x|+|y|=0;③对,不等式两边同时加上同一个常数,不等号开口方向不变;④错.5.已知A、B是两个集合,则下列命题中为真命题的是()A.如果A⊆B,那么A∩B=AB.如果A∩B=A,那么(∁U A)∩B=∅C.如果A⊆B,那么A∪B=AD.如果A∪B=A,那么A⊆B解析:选A.由集合的Venn图知选项A中的命题是真命题.6.下列命题中,是真命题的为()A.若一个四边形的对角线互相垂直且平分,则该四边形为正方形B.若集合M={x|x2+x<0},N={x|x>0},则M⊆NC.若a2+b2≠0,则a,b不全为零D.若x2+x+1<0,则x∈R⊆/解析:选C.A也可为菱形;B中的集合M={x|-1<x<0},M N;D中的不等式无解,x∈∅.二、填空题7.命题:一元二次方程x2+bx-1=0(b∈R)有两个不相等的实数根.则条件p:________,结论q:________,是________(填“真”或“假”)命题.答案:一元二次方程为x2+bx-1=0(b∈R)有两个不相等的实数根真8.下列语句中是命题的有________,其中是假命题的有________.(只填序号)①垂直于同一条直线的两条直线必平行吗?②一个数不是正数就是负数;③大角所对的边大于小角所对的边.解析:根据命题的概念,判断是否是命题;若是,再判断其真假.①是疑问句,没有对垂直于同一条直线的两条直线是否平行作出判断,不是命题;②是假命题,因为0既不是正数也不是负数;③是假命题,没有考虑到“在两个三角形中”的情况.答案:②③②③9.给出下列几个命题:①若x,y互为相反数,则x+y=0;②若a>b,则a2>b2;③若x>-3,则x2+x-6≤0;④若a,b是无理数,则a b也是无理数.其中的真命题有________个.解析:①是真命题.②设a=1>b=-2,但a2<b2,假命题.③设x=4>-3,但x2+x-6=41>0,假命题.④设a=(2)2,b=2,则a b=(2)2=2是有理数,假命题.答案:1三、解答题10.指出下列命题的条件p与结论q,并判断命题的真假:(1)若整数a是偶数,则a能被2整除;(2)对角线相等且互相平分的四边形是矩形;(3)相等的两个角的正切值相等.解:(1)条件p:整数a是偶数,结论q:a能被2整除,真命题.(2)命题“对角线相等且互相平分的四边形是矩形”,即“若一个四边形的对角线相等且互相平分,则该四边形是矩形”.条件p:一个四边形的对角线相等且互相平分,结论q:该四边形是矩形,真命题.(3)命题“相等的两个角的正切值相等”,即“若两个角相等,则这两个角的正切值相等”.条件p:两个角相等,结论q:这两个角的正切值相等,假命题.11.将下列命题改写成“若p,则q”的形式,并判断命题的真假:(1)6是12和18的公约数;(2)当a >-1时,方程ax 2+2x -1=0有两个不等实根;(3)已知x 、y 为非零自然数,当y -x =2时,y =4,x =2.解:(1)若一个数是6,则它是12和18的公约数,是真命题.(2)若a >-1,则方程ax 2+2x -1=0有两个不等实根,是假命题.因为当a =0时,方程变为2x -1=0,此时只有一个实根x =12. (3)已知x 、y 为非零自然数,若y -x =2,则y =4,x =2,是假命题.12.已知p :x 2+mx +1=0有两个不等的负根,q :方程4x 2+4(m -2)x +1=0(m ∈R)无实根,求使p 正确且q 正确的m 的取值范围.解:若p 为真,则⎩⎪⎨⎪⎧ Δ=m 2-4>0,m >0,解得m >2. 若q 为真,则Δ=16(m -2)2-16<0,解得1<m <3.p 真,q 真,即⎩⎪⎨⎪⎧m >2,1<m <3.故m 的取值范围是(2,3).1.(2011年高考山东卷)已知a ,b ,c ∈R ,命题“若a +b +c =3,则a 2+b 2+c 2≥3”的否命题是( )A .若a +b +c ≠3,则a 2+b 2+c 2<3B .若a +b +c =3,则a 2+b 2+c 2<3C .若a +b +c ≠3,则a 2+b 2+c 2≥3D .若a 2+b 2+c 2≥3,则a +b +c =3解析:选A.命题“若p ,则q ”的否命题是“若綈p ,则綈q ”.2.命题“若a >0,则3a 4a =34”的逆命题为( ) A .若a ≤0,则3a 4a ≠34 B .若3a 4a ≠34,则a >0 C .若3a 4a ≠34,则a ≤0 D .若3a 4a =34,则a >0 解析:选D.逆命题为把原命题的条件和结论对调.3.命题“若A ∪B =B ,则A ⊆B ”的否命题是________.答案:若A ∪B ≠B ,则A B 4.已知命题p :“若ac ≥0,则二次方程ax 2+bx +c =0没有实根”.(1)写出命题p 的否命题;(2)判断命题p 的否命题的真假.解:(1)命题p 的否命题为:“若ac <0,则二次方程ax 2+bx +c =0有实根”(2)命题p 的否命题是真命题.证明如下:∵ac <0,∴-ac >0⇒Δ=b 2-4ac >0⇒二次方程ax 2+bx +c =0有实根.∴该命题是真命题.一、选择题1.若“x >y ,则x 2>y 2”的逆否命题是( )A .若x ≤y ,则x 2≤y 2B .若x >y ,则x 2<y 2C .若x 2≤y 2,则x ≤yD .若x <y ,则x 2<y 2解析:选C.由互为逆否命题的定义可知,把原命题的条件的否定作为结论,原命题的结论的否定作为条件即可得逆否命题.2.命题“若△ABC 有一内角为π3,则△ABC 的三内角成等差数列”的逆命题( ) A .与原命题同为假命题B .与原命题的否命题同为假命题C .与原命题的逆否命题同为假命题D .与原命题同为真命题解析:选D.原命题显然为真,原命题的逆命题为“若△ABC 的三内角成等差数列,则△ABC有一内角为π3”,它是真命题.故选D. 3.已知原命题“菱形的对角线互相垂直”,则它的逆命题、否命题、逆否命题的真假判断正确的是( )A .逆命题、否命题、逆否命题都为真B .逆命题为真,否命题、逆否命题为假C .逆命题为假,否命题、逆否命题为真D .逆命题、否命题为假,逆否命题为真⊆/解析:选D.因为原命题“菱形的对角线互相垂直”是真命题,所以它的逆否命题为真;其逆命题:“对角线互相垂直的四边形是菱形”显然是假命题,所以原命题的否命题也是假命题.4.若命题p的逆命题是q,命题q的否命题是r,则p是r的()A.逆命题B.逆否命题C.否命题D.以上判断都不对解析:选B.命题p:若x,则y,其逆命题q:若y,则x,那么命题q的否命题r:若綈y,则綈x,所以p是r的逆否命题.所以选B.5.与命题“能被6整除的整数,一定能被3整除”等价的命题是()A.能被3整除的整数,一定能被6整除B.不能被3整除的整数,一定不能被6整除C.不能被6整除的整数,一定不能被3整除D.不能被6整除的整数,不一定能被3整除解析:选B.一个命题与它的逆否命题是等价命题,选项B中的命题恰为已知命题的逆否命题.6.存在下列三个命题:①“等边三角形的三个内角都是60°”的逆命题;②“若k>0,则一元二次方程x2+2x-k=0有实根”的逆否命题;③“全等三角形的面积相等”的否命题.其中真命题的个数是()A.0 B.1C.2 D.3解析:选C.①②正确.二、填空题7.命题“若a>1,则a>0”的逆命题是________,逆否命题是________.答案:若a>0,则a>1若a≤0,则a≤18.有下列几个命题:①“若a>b,则a2>b2”的否命题;②“若x+y=0,则x,y互为相反数”的逆命题;③“若x2<4,则-2<x<2”的逆否命题.其中真命题的序号是________.答案:②③9.在空间中,①若四点不共面,则这四点中任意三点都不共线;②若两条直线没有公共点,则这两条直线是异面直线.以上两个命题中,逆命题为真命题的是________.解析:①中的逆命题是:若四点中任何三点都不共线,则这四点不共面.我们用正方体AC1做模型来观察:上底面A1B1C1D1中任意三点都不共线,但A1,B1,C1,D1四点共面,所以①中的逆命题不是真命题.②中的逆命题是:若两条直线是异面直线,则两条直线没有公共点.由异面直线的定义可知,成异面直线的两条直线不会有公共点.所以②中的逆命题是真命题.答案:②三、解答题10.写出下列原命题的其他三种命题,并分别判断真假.(1)在△ABC中,若a>b,则∠A>∠B;(2)正偶数不是素数.解:(1)逆命题:在△ABC中,若∠A>∠B,则a>b,真命题;否命题:在△ABC中,若a≤b,则∠A≤∠B,真命题;逆否命题:在△ABC中,若∠A≤∠B,则a≤b,真命题.(2)逆命题:若一个数不是素数,则它一定是正偶数,假命题;否命题:若一个数不是正偶数,则它一定是素数,假命题;逆否命题:若一个数是素数,则它一定不是正偶数,假命题.11.判断下列命题的真假:(1)“若x∈A∪B,则x∈B”的逆命题与逆否命题;(2)“若自然数能被6整除,则自然数能被2整除”的逆命题.解:(1)逆命题:若x∈B,则x∈A∪B.根据集合“并”的定义,逆命题为真.逆否命题:若x∉B,则x∉A∪B.逆否命题为假.如2∉{1,5}=B,A={2,3},但2∈A∪B.(2)逆命题:若自然数能被2整除,则自然数能被6整除.逆命题为假.反例:2,4,14,22等都不能被6整除.12.判断命题“若m>0,则方程x2+2x-3m=0有实数根”的逆否命题的真假.解:∵m>0,∴12m>0,∴12m+4>0.∴方程x2+2x-3m=0的判别式Δ=12m+4>0.∴原命题“若m>0,则方程x2+2x-3m=0有实数根”为真命题.又因原命题与它的逆否命题等价,所以“若m>0,则方程x2+2x-3m=0有实数根”的逆否命题也为真命题.1.(2011年高考福建卷)若a ∈R ,则“a =2”是“(a -1)(a -2)=0”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分又不必要条件解析:选A.a =2⇒(a -1)(a -2)=0,但(a -1)(a -2)=0⇒a =1或2,故选A.2.“θ=0”是“sin θ=0”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:选A.由于“θ=0”时,一定有“sin θ=0”成立,反之不成立,所以“θ=0”是“sin θ=0”的充分不必要条件.3.用符号“⇒”或“ ”填空:(1)整数a 能被4整除________a 的个位数为偶数;(2)a >b ________ac 2>bc 2.答案:(1)⇒ (2)4.“a =2”是“直线ax +2y =0平行于直线x +y =1”的什么条件?解:当a =2时,直线ax +2y =0,即2x +2y =0与直线x +y =1平行,因为直线ax +2y =0平行于直线x +y =1,所以a 2=1,a =2, 综上,“a =2”是“直线ax +2y =0平行于直线x +y =1”的充要条件.一、选择题1.设集合M ={x |0<x ≤3},N ={x |0<x ≤2},那么“a ∈M ”是“a ∈N ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:选B.M ={x |0<x ≤3},N ={x |0<x ≤2},所以N M ,故a ∈M 是a ∈N 的必要不充分条件.2.(2010年高考福建卷)若向量a =(x,3)(x ∈R),则“x =4是|a |=5”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分又不必要条件解析:选A.由x =4知|a |=42+32=5;反之,由|a |=x 2+32=5,得x =4或x =-4.故“x =4”是“|a |=5”的充分而不必要条件,故选A.3.“b =c =0”是“二次函数y =ax 2+bx +c (a ≠0)经过原点”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:选A.b =c =0⇒y =ax 2,二次函数一定经过原点;二次函数y =ax 2+bx +c 经过原点⇒c =0,b 不一定等于0,故选A.4.已知p,q,r是三个命题,若p是r的充要条件且q是r的必要条件,那么q是p的() A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件解析:选B.p是r的充要条件且q是r的必要条件,故有p⇔r⇒q,即p⇒q,q p,所以q是p的必要条件.5.已知条件:p:y=lg(x2+2x-3)的定义域,条件q:5x-6>x2,则q是p的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选A.p:x2+2x-3>0,则x>1或x<-3;q:5x-6>x2,即x2-5x+6<0,由小集合⇒大集合,∴q⇒p,但p⇒/ q.故选A.6.下列所给的p、q中,p是q的充分条件的个数是()①p:x>1,q:-3x<-3;②p:x>1,q:2-2x<2;③p:x=3,q:sin x>cos x;④p:直线a,b不相交,q:a∥b.A.1B.2C.3 D.4解析:选C.①由于p:x>1⇒q:-3x<-3,所以p是q的充分条件;②由于p:x>1⇒q:2-2x<2(即x>0),所以p是q的充分条件;③由于p:x=3⇒q:sin x>cos x,所以p是q的充分条件;④由于p:直线a,b不相交q:a∥b,所以p不是q的充分条件.二、填空题7.不等式x2-3x+2<0成立的充要条件是________.解析:x2-3x+2<0⇔(x-1)(x-2)<0⇔1<x<2.答案:1<x<28.在△ABC中,“sin A=sin B”是“a=b”的________条件.解析:在△ABC中,由正弦定理及sin A=sin B可得2R sin A=2R sin B,即a=b;反之也成立.答案:充要9.下列不等式:①x<1;②0<x<1;③-1<x<0;④-1<x<1.其中,可以是x2<1的一个充分条件的所有序号为________.解析:由于x2<1即-1<x<1,①显然不能使-1<x<1一定成立,②③④满足题意.答案:②③④三、解答题10.下列命题中,判断条件p是条件q的什么条件:(1)p:|x|=|y|,q:x=y;(2)p:△ABC是直角三角形,q:△ABC是等腰三角形;(3)p:四边形的对角线互相平分,q:四边形是矩形.解:(1)∵|x|=|y|⇒/ x=y,但x=y⇒|x|=|y|,∴p是q的必要条件,但不是充分条件.(2)△ABC是直角三角形△ABC是等腰三角形.△ABC是等腰三角形△ABC是直角三角形.∴p既不是q的充分条件,也不是q的必要条件.(3)四边形的对角线互相平分四边形是矩形.四边形是矩形⇒四边形的对角线互相平分.∴p是q的必要条件,但不是充分条件.11.命题p :x >0,y <0,命题q :x >y ,1x >1y,则p 是q 的什么条件? 解:p :x >0,y <0,则q :x >y ,1x >1y成立; 反之,由x >y ,1x >1y ⇒y -x xy>0, 因y -x <0,得xy <0,即x 、y 异号,又x >y ,得x >0,y <0.所以“x >0,y <0”是“x >y ,1x >1y”的充要条件. 12.已知条件p :-1≤x ≤10,q :x 2-4x +4-m 2≤0(m >0)不变,若綈p 是綈q 的必要而不充分条件,如何求实数m 的取值范围?解:p :-1≤x ≤10.q :x 2-4x +4-m 2≤0⇔[x -(2-m )][x -(2+m )]≤0(m >0)⇔2-m ≤x ≤2+m (m >0).因为綈p 是綈q 的必要而不充分条件,所以p 是q 的充分不必要条件,即{x |-1≤x ≤10}{x |2-m ≤x ≤2+m },故有⎩⎪⎨⎪⎧ 2-m ≤-12+m >10或⎩⎪⎨⎪⎧2-m <-12+m ≥10, 解得m ≥8.所以实数m 的范围为{m |m ≥8}.1.若命题p∧q为假,且綈p为假,则()A.p∨q为假B.q为假C.q为真D.不能判断答案:B2.命题“平行四边形的对角线相等且互相平分”是()A.简单命题B.“p或q”形式的复合命题C.“p且q”形式的复合命题D.“非p”形式的复合命题答案:C3.判断下列命题的形式(从“p∨q”、“p∧q”中选填一种):(1)6≤8:________;(2)集合中的元素是确定的且是无序的:________.答案:p∨q p∧q4.已知命题p:6是12的约数,q:6是24的约数,试写出由它们构成的“p∧q”、“p∨q”、“綈p”形式的命题.解:“p∧q”:6既是12的约数又是24的约数.“p∨q”:6是12或24的约数.“綈p”:6不是12的约数.一、选择题1.如果命题“p∨q”与命题“綈p”都是真命题,那么()A.命题p不一定是假命题B.命题q一定为真命题C.命题q不一定是真命题D.命题p与命题q的真假相同解析:选B.“p∨q”为真,则p、q至少有一个为真.綈p为真,则p为假,∴q是真命题.2.若命题p:0是偶数,命题q:2是3的约数,则下列命题中为真的是()A.p∧q B.p∨qC.綈p D.(綈p)∧(綈q)解析:选B.∵p是真命题,q是假命题,∴“p∨q”是真命题.3.命题p:a2+b2<0(a,b∈R);命题q:a2+b2≥0(a,b∈R),则下列结论中正确的是() A.“p∨q”为真B.“p∧q”为真C.“綈p”为假D.“綈q”为真解析:选A.∵p为假命题,q为真命题,∴“p∨q”为真命题.4.若命题p:2m-1(m∈Z)是奇数,命题q:2n+1(n∈Z)是偶数,则下列说法正确的是() A.p∨q为真B.p∧q为真C.綈p为真D.綈q为假解析:选A.命题p:“2m-1(m∈Z)是奇数”是真命题,而命题q:“2n+1(n∈Z)是偶数”是假命题,所以p∨q为真.5.已知命题p:所有有理数都是实数,命题q:正数的对数都是负数,则下列命题为真命题的是()A.(綈p)∨q B.p∧qC.(綈p)∧(綈q) D.(綈p)∨(綈q)解析:选D.p为真,q为假,所以綈q为真,(綈p)∨(綈q)为真.6.给出两个命题:p :函数y =x 2-x -1有两个不同的零点;q :若1x<1,则x >1,那么在下列四个命题中,真命题是( ) A .(綈p )∨q B .p ∧q C .(綈p )∧(綈q ) D .(綈p )∨(綈q )解析:选D.对于p ,函数对应的方程x 2-x -1=0的判别式Δ=(-1)2-4×(-1)=5>0. 可知函数有两个不同的零点,故p 为真.当x <0时,不等式1x<1恒成立;当x >0时,不等式的解为x >1.故不等式1x<1的解为x <0或x >1.故命题q 为假命题.所以只有(綈p )∨(綈q )为真.故选D. 二、填空题7.用“或”、“且”、“非”填空,使命题成为真命题: (1)若x ∈A ∪B ,则x ∈A ________x ∈B ; (2)若x ∈A ∩B ,则x ∈A ________x ∈B ; (3)若ab =0,则a =0________b =0;(4)a ,b ∈R ,若a >0________b >0,则ab >0. 答案:(1)或 (2)且 (3)或 (4)且8.设命题p :2x +y =3;q :x -y =6.若p ∧q 为真命题,则x =________,y =________. 解析:若p ∧q 为真命题,则p ,q 均为真命题,所以有⎩⎪⎨⎪⎧ 2x +y =3,x -y =6.解得⎩⎪⎨⎪⎧x =3,y =-3. 答案:3 -39.命题“若a <b ,则2a <2b ”的否命题为________,命题的否定为________. 解析:命题“若a <b ,则2a <2b ”的否命题为“若a ≥b ,则 2a ≥2b ”,命题的否定为“若a <b ,则2a ≥2b ”. 答案:若a ≥b ,则2a ≥2b 若a <b ,则2a ≥2b 三、解答题10.指出下列命题的形式及构成它们的简单命题: (1)方程x 2-3=0没有有理根;(2)不等式x 2-x -2>0的解集是{x |x >2或x <-1}.解:(1)这个命题是“綈p ”的形式,其中p :方程x 2-3=0有有理根.(2)这个命题是“p 或q ”的形式,其中p :不等式x 2-x -2>0的解集是{x |x >2},q :不等式x 2-x -2>0的解集是{x |x <-1}.11.判断由下列命题构成的p ∨q ,p ∧q ,綈p 形式的命题的真假: (1)p :负数的平方是正数,q :有理数是实数; (2)p :2≤3,q :3<2;(3)p :35是5的倍数,q :41是7的倍数.解:(1)p 真,q 真,∴p ∨q 为真命题,p ∧q 为真命题,綈p 为假命题; (2)p 真,q 假,∴p ∨q 为真命题,p ∧q 为假命题,綈p 为假命题; (3)p 真,q 假,∴p ∨q 为真命题,p ∧q 为假命题,綈p 为假命题.12.设命题p :实数x 满足x 2-4ax +3a 2<0,其中a >0,命题q :实数x 满足⎩⎪⎨⎪⎧x 2-x -6≤0,x 2+2x -8>0. (1)若a =1,且p ∧q 为真,求实数x 的取值范围;(2)綈p 是綈q 的充分不必要条件,求实数a 的取值范围. 解:(1)由x 2-4ax +3a 2<0得 (x -3a )(x -a )<0.又a >0,所以a <x <3a ,当a =1时,1<x <3,即p 为真命题时, 实数x 的取值范围是1<x <3.由⎩⎪⎨⎪⎧x 2-x -6≤0,x 2+2x -8>0. 解得⎩⎪⎨⎪⎧-2≤x ≤3,x <-4或x >2.即2<x ≤3.所以q 为真时实数x 的取值范围是2<x ≤3.若p ∧q 为真,则⎩⎪⎨⎪⎧1<x <32<x ≤3⇔2<x <3,所以实数x 的取值范围是(2,3). (2)綈p 是綈q 的充分不必要条件, 即綈p ⇒綈p 且綈q 綈q .设A ={x |x ≤a 或x ≥3a },B ={x |x ≤2或x >3},则A B .所以0<a ≤2且3a >3,即1<a ≤2. 所以实数a 的取值范围是(1,2].1.下列是全称命题且是真命题的是( ) A .∀x ∈R ,x 2>0 B .∀x ∈Q ,x 2∈Q C .∃x 0∈Z ,x 20>1 D .∀x ,y ∈R ,x 2+y 2>0 答案:B2.命题“一次函数都是单调函数”的否定是( ) A .一次函数都不是单调函数 B .非一次函数都不是单调函数 C .有些一次函数是单调函数 D .有些一次函数不是单调函数解析:选D.命题的否定只对结论进行否定,“都是”的否定是“不都是”,即“有些”. 3.(2010年高考安徽卷)命题“对任何x ∈R ,|x -2|+|x -4|>3”的否定是________. 答案:存在x ∈R ,使得|x -2|+|x -4|≤34.(1)用符号“∀”表示命题“不论m 取什么实数,方程x 2+x -m =0必有实根”; (2)用符号“∃”表示命题“存在实数x ,使sin x >tan x ”. 解:(1)∀m ∈R ,x 2+x -m =0有实根. (2)∃x 0∈R ,sin x 0>tan x 0.一、选择题1.下列语句不是特称命题的是( ) A .有的无理数的平方是有理数 B .有的无理数的平方不是有理数 C .对于任意x ∈Z,2x +1是奇数 D .存在x 0∈R,2x 0+1是奇数 答案:C2.(2010年高考湖南卷)下列命题中的假命题是( ) A .∃x ∈R ,lg x =0 B .∃x ∈R ,tan x =1 C .∀x ∈R ,x 3>0 D .∀x ∈R,2x >0解析:选C.对于A ,当x =1时,lg x =0,正确;对于B ,当x =π4时,tan x =1,正确;对于C ,当x <0时,x 3<0,错误;对于D ,∀x ∈R,2x>0,正确. 3.下列命题中,是正确的全称命题的是( ) A .对任意的a ,b ∈R ,都有a 2+b 2-2a -2b +2<0 B .菱形的两条对角线相等 C .∃x 0∈R ,x 20=x 0D .对数函数在定义域上是单调函数解析:选D.A 中含有全称量词“任意”,a 2+b 2-2a -2b +2=(a -1)2+(b -1)2≥0,是假命题.B 、D 在叙述上没有全称量词,实际上是指“所有的”.菱形的对角线不一定相等;C 是特称命题.所以选D.4.将“x 2+y 2≥2xy ”改写成全称命题,下列说法正确的是( ) A .∀x ,y ∈R ,都有x 2+y 2≥2xyB .∃x 0,y 0∈R ,使x 20+y 20≥2x 0y 0C .∀x >0,y >0,都有x 2+y 2≥2xyD .∃x 0<0,y 0<0,使x 20+y 20≤2x 0y 0解析:选A.这是一个全称命题,且x ,y ∈R ,故选A. 5.下列命题的否定是假命题的是( )A .p :能被3整除的整数是奇数;綈p :存在一个能被3整除的整数不是奇数B.p:每一个四边形的四个顶点共圆;綈p:存在一个四边形的四个顶点不共圆C.p:有的三角形为正三角形;綈p:所有的三角形不都是正三角形D.p:∃x0∈R,x20+2x0+2≤0;綈p:∀x∈R,都有x2+2x+2>0解析:选C.p为真命题,则綈p为假命题.6.下列命题中,假命题的个数是()①∀x∈R,x2+1≥1;②∃x0∈R,2x0+1=3;③∃x0∈Z,x0能被2和3整除;④∃x0∈R,x20+2x0+3=0.A.0 B.1C.2 D.3解析:选B.①②③都是真命题,而④为假命题.二、填空题7.写出命题“每个函数都有奇偶性”的否定:________.解析:命题的量词是“每个”,即为全称命题,因此否定是特称命题,用量词“有些、有的、存在一个、至少有一个”等,再否定结论.答案:有些函数没有奇偶性8.命题“存在实数x,y,使得x+y>1”,用符号表示为________;此命题的否定是________(用符号表示),是________命题(填“真”或“假”).解析:原命题为真,所以它的否定为假.也可以用线性规划的知识判断.答案:∃x0,y0∈R,x0+y0>1∀x,y∈R,x+y≤1假9.下列命题:①存在x0<0,使|x0|>x0;②对于一切x<0,都有|x|>x;③已知a n=2n,b n=3n,对于任意n∈N+,都有a n≠b n;④已知A={a|a=2n},B={b|b=3n},对于任意n∈N+,都有A∩B=∅.其中,所有正确命题的序号为________.解析:命题①②显然为真命题;③由于a n-b n=2n-3n=-n<0,对于任意n∈N+,都有a n<b n,即a n≠b n,故为真命题;④已知A={a|a=2n},B={b|b=3n},例如n=1,2,3时,A∩B={6},故为假命题.答案:①②③三、解答题10.判断下列语句是不是命题?如果是,说明其是全称命题还是特称命题:(1)有一个向量a0,a0的方向不能确定;(2)存在一个函数f(x0),使f(x0)既是奇函数又是偶函数;(3)对任何实数a,b,c,方程ax2+bx+c=0都有解;(4)平面外的所有直线中,有一条直线和这个平面垂直吗?解:(1)(2)(3)都是命题,其中(1)(2)是特称命题,(3)是全称命题.由于(4)是一个问句,因此(4)不是命题.11.用“∀”“∃”写出下列命题的否定,并判断真假:(1)二次函数的图象是抛物线;(2)直角坐标系中,直线是一次函数的图象;(3)∀a,b∈R,方程ax+b=0恰有一解.解:(1)綈p:∃x0∈{二次函数},x0的图象不是抛物线.假命题.(2)綈p:在直角坐标系中,∃x0∈{直线},x0不是一次函数的图象.真命题.(3)綈p:∃a0,b0∈R,方程a0x+b0=0无解或至少有两解.真命题.12.判断下列命题的真假,并写出这些命题的否定:(1)三角形的内角和为180°;(2)每个二次函数的图象都开口向下;(3)存在一个四边形不是平行四边形.解:(1)是全称命题且为真命题.命题的否定:三角形的内角和不全为180°,即存在一个三角形的内角和不等于180°.(2)是全0称命题且为假命题.命题的否定:存在一个二次函数的图象开口不向下.(3)是特称命题且为真命题.命题的否定:所有的四边形都是平行四边形.1.设P 是椭圆x 225+y 216=1上的点,若F 1,F 2是椭圆的两个焦点,则|PF 1|+|PF 2|等于( )A .4B .5C .8D .10 答案:D2.椭圆x 216+y 225=1的焦点坐标是( )A .(±4,0)B .(0,±4)C .(±3,0)D .(0,±3) 答案:D3.已知椭圆的两个焦点为F 1(-1,0),F 2(1,0),且2a =6,则椭圆的标准方程为________.答案:x 29+y 28=14.已知B 、C 是两定点,|BC |=8,且△ABC 的周长等于18,求这个三角形顶点A 的轨迹方程.解:以过B 、C 两点的直线为x 轴,线段BC 的中点为原点,建立平面直角坐标系(图略). 由|BC |=8,可设B (-4,0),C (4,0). 由|AB |+|BC |+|AC |=18, 得|AB |+|AC |=10>|BC |=8.因此,点A 的轨迹是以B 、C 为焦点的椭圆,这个椭圆上的点与两焦点的距离之和为2a =10,即a =5,且点A 不能在x 轴上.由a =5,c =4,得b 2=9.所以A 点的轨迹方程为x 225+y 29=1(y ≠0).一、选择题1.已知椭圆的焦点为(-1,0)和(1,0),点P (2,0)在椭圆上,则椭圆的方程为( ) A.x 24+y 23=1 B.x 24+y 2=1 C.y 24+x 23=1 D.y 24+x 2=1 解析:选A.c =1,a =2,∴b 2=a 2-c 2=3.∴椭圆的方程为x 24+y 23=1.2.椭圆x 29+y225=1的焦点为F 1、F 2,AB 是椭圆过焦点F 1的弦,则△ABF 2的周长是( )A .20B .12C .10D .6 解析:选A.∵AB 过F 1,∴由椭圆定义知 ⎩⎪⎨⎪⎧|BF 1|+|BF 2|=2a ,|AF 1|+|AF 2|=2a , ∴|AB |+|AF 2|+|BF 2|=4a =20.3.椭圆x 225+y 2=1上一点P 到一个焦点的距离为2,则点P 到另一个焦点的距离为( )A .5B .6C .7D .8解析:选D.设到另一焦点的距离为x ,则x +2=10,x =8.4.已知椭圆x 2a 2+y 22=1的一个焦点为(2,0),则椭圆的方程是( )A.x 24+y 22=1B.x 23+y 22=1 C .x 2+y 22=1 D.x 26+y 22=1解析:选D.由题意知a 2-2=4,∴a 2=6.∴所求椭圆的方程为x 26+y 22=1.5.已知椭圆x 210-m +y 2m -2=1的长轴在y 轴上,若焦距为4,则m 等于( )A .4B .5C .7D .8解析:选D.焦距为4,则m -2-(10-m )=⎝⎛⎭⎫422,∴m =8.6.椭圆的两焦点为F 1(-4,0)、F 2(4,0),点P 在椭圆上,若△PF 1F 2的面积最大为12,则椭圆方程为( ) A.x 216+y 29=1 B.x 225+y 29=1 C.x 225+y 216=1 D.x 225+y 24=1 解析:选B.S △PF 1F 2=12×8b =12,∴b =3,又∵c =4,∴a 2=b 2+c 2=25,∴椭圆的标准方程为x 225+y 29=1.二、填空题7.椭圆的焦点在y 轴上,其上任意一点到两焦点的距离和为8,焦距为215,则此椭圆的标准方程为________. 解析:∵2a =8,∴a =4,∵2c =215,∴c =15,∴b 2=1.即椭圆的标准方程为y 216+x 2=1.答案:y216+x 2=18.在平面直角坐标系xOy 中,已知△ABC 顶点A (-4,0)和C (4,0),顶点B 在椭圆x 225+y 29=1上,则sin A +sin C sin B=________.解析:由题意知,|AC |=8,|AB |+|BC |=10.所以,sin A +sin C sin B =|BC |+|AB ||AC |=108=54.答案:549.若方程x 25-k +y 2k -3=1表示椭圆,则k 的取值范围是________.解析:由题意知⎩⎪⎨⎪⎧5-k >0,k -3>0,5-k ≠k -3,解得3<k <5且k ≠4.答案:3<k <5且k ≠4 三、解答题10.已知椭圆8x 281+y 236=1上一点M 的纵坐标为2.(1)求M 的横坐标;(2)求过M 且与x 29+y 24=1共焦点的椭圆的方程.解:(1)把M 的纵坐标代入8x 281+y 236=1,得8x 281+436=1,即x 2=9.∴x =±3.即M 的横坐标为3或-3.(2)对于椭圆x 29+y 24=1,焦点在x 轴上且c 2=9-4=5,故设所求椭圆的方程为x 2a 2+y 2a 2-5=1(a 2>5),把M 点坐标代入得9a 2+4a 2-5=1,解得a 2=15.故所求椭圆的方程为x 215+y 210=1.11.已知椭圆的中心在原点,两焦点F 1,F 2在x 轴上,且过点A (-4,3).若F 1A ⊥F 2A ,求椭圆的标准方程.解:设所求椭圆的标准方程为x 2a 2+y 2b2=1(a >b >0).设焦点F 1(-c,0),F 2(c,0).∵F 1A ⊥F 2A ,∴F 1A →·F 2A →=0, 而F 1A →=(-4+c,3), F 2A →=(-4-c,3), ∴(-4+c )·(-4-c )+32=0, ∴c 2=25,即c =5. ∴F 1(-5,0),F 2(5,0). ∴2a =|AF 1|+|AF 2|= (-4+5)2+32+ (-4-5)2+32 =10+90=410. ∴a =210,∴b 2=a 2-c 2=(210)2-52=15.∴所求椭圆的标准方程为x 240+y 215=1.12.已知椭圆的两焦点为F 1(-1,0)、F 2(1,0),P 为椭圆上一点,且2|F 1F 2|=|PF 1|+|PF 2|. (1)求此椭圆方程;(2)若点P 满足∠F 1PF 2=120°,求△PF 1F 2的面积. 解:(1)由已知得|F 1F 2|=2, ∴|PF 1|+|PF 2|=4=2a ,∴a =2.∴b 2=a 2-c 2=4-1=3,∴椭圆的标准方程为x 24+y 23=1.(2)在△PF 1F 2中,由余弦定理得|F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1||PF 2|cos 120°,即4=(|PF 1|+|PF 2|)2-|PF 1||PF 2|,∴4=(2a )2-|PF 1||PF 2|=16-|PF 1||PF 2|, ∴|PF 1||PF 2|=12,∴S △PF 1F 2=12|PF 1||PF 2|sin120°=12×12×32=3 3.1.已知点(2,3)在椭圆x 2m 2+y 2n2=1上,则下列说法正确的是( )A .点(-2,3)在椭圆外B .点(3,2)在椭圆上C .点(-2,-3)在椭圆内D .点(2,-3)在椭圆上 答案:D2.直线y =x +2与椭圆x 2m +y 23=1有两个公共点,则m 的取值范围是( )A .m >1B .m >1且m ≠3C .m >3D .m >0且m ≠3 答案:B3.直线y =a 与椭圆x 23+y 22=1恒有两个不同的交点,则a 的取值范围是________.答案:(-2,2)4.如图,已知斜率为1的直线l 过椭圆y 28+x24=1的下焦点,交椭圆于A 、B 两点,求弦AB之长.解:令A 、B 坐标分别为A (x 1,y 1)、B (x 2,y 2). 由椭圆方程知a 2=8,b 2=4, ∴c =a 2-b 2=2,∴椭圆的下焦点F 的坐标为F (0,-2), ∴直线l 的方程为y =x -2.将其代入y 28+x 24=1,化简整理得3x 2-4x -4=0,∴x 1+x 2=43,x 1·x 2=-43,∴|AB |=(x 2-x 1)2+(y 2-y 1)2=2(x 2-x 1)2= 2 (x 1+x 2)2-4x 1x 2= 2 ⎝⎛⎭⎫432-4×(-43) =823.一、选择题1.点A (a,1)在椭圆x 24+y 22=1的内部,则a 的取值范围是( )A .-2<a <2B .a <-2或a > 2C .-2<a <2D .-1<a <1答案:A2.椭圆x 24+y 23=1的右焦点到直线y =3x 的距离是( )A.12B.32 C .1 D. 3 解析:选B.椭圆的右焦点为F (1,0),∴d =33+1=32.3.过椭圆x 225+y 29=1的右焦点且倾斜角为45°的弦AB 的长为( )A .5B .6 C.9017D .7 解析:选C.椭圆的右焦点为(4,0),直线的斜率为k =1, ∴直线AB 的方程为y =x -4,由⎩⎪⎨⎪⎧y =x -4x 225+y 29=1得9x 2+25(x -4)2=225, 由弦长公式易求|AB |=9017.4.直线y =x +m 与椭圆x 2144+y 225=1有两个公共点,则m 的取值范围是( )A .(-5,5)B .(-12,12)C .(-13,13)D .(-15,15)解析:选C.联立直线与椭圆方程,由判别式Δ>0,可得-13<m <13.5.已知椭圆x 2a 2+y 2b2=1(a >b >0)的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF ⊥x 轴,直线AB 交y 轴于点P .若AP →=2PB →,则椭圆的离心率是( )A.32B.22C.13D.12解析:选D.如图,由于BF ⊥x 轴,故x B =-c ,y B =b 2a.设P (0,t ),∵AP →=2PB →,∴(-a ,t )=2⎝⎛⎭⎫-c ,b 2a -t .∴a =2c , ∴c a =12. 6.经过椭圆x 22+y 2=1的一个焦点作倾斜角为45°的直线l ,交椭圆于A 、B 两点.设O 为坐标原点,则OA →·OB →等于( )A .-3B .-13C .-13或-3D .±13解析:选B.不妨设l 过椭圆的右焦点(1,0), 则直线l 的方程为y =x -1.。
高中数学 第3章331知能优化训练 选修11 试题
知能优化训练[学生用书 P 33]1.命题甲:对任意x ∈(a ,b ),有f ′(x )>0;命题乙:f (x )在(a ,b )内是单调递增的.那么甲是乙的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件解析:选A.例如:f (x )=x 3在(-1,1)内是单调递增的,但f ′(x )=3x 2≥0(-1<x <1),故甲是乙的充分不必要条件,选A.2.函数y =x -ln(1+x )的单调增区间为( ) A .(-1,0) B .(-∞,-1)和(0,+∞) C .(0,+∞)D .(-∞,-1)解析:选C.y ′=1-11+x =x 1+x .令y ′>0,得x1+x >0,∴x >0或者xx +1>0,∴x >0.3.假设在区间(a ,b )内,f ′(x )>0,且f (a )≥0,那么在(a ,b )内有( ) A .f (x )>0 B .f (x )<0 C .f (x )=0D .不能确定f ′(x )>0,所以f (x )在(a ,b )上是增函数,所以f (x )>f (a )≥0.4.(2021年高考卷改编)函数f (x )=2log 5x +1的单调增区间是________. 解析:令f ′(x )=2x ln5>0,得x ∈(0,+∞).答案:(0,+∞)一、选择题1.函数f (x )=(x -3)e x 的单调递增区间是( ) A .(-∞,2) B .(0,3) C .(1,4)D .(2,+∞)解析:选D.f ′(x )=(x -3)′e x +(x -3)(e x )′=(x -2)e x , 令f ′(x )>0,解得x >2,应选D.2.函数y =12x 2-ln x 的单调递减区间为( )A .(0,1)B .(0,1)和(-∞,-1)C .(0,1)∪(1,+∞)D .(0,+∞)解析:选A.y =12x 2-ln x 的定义域为(0,+∞),由y ′=x -1x =x 2-1x<0,∴0<x <1.所以选A.3.设f (x )、g (x )是定义域为R 的恒大于零的可导函数,且f ′(x )g (x )-f (x )g ′(x )<0,那么当a <x <b 时,有( ) A .f (x )g (x )>f (b )g (b ) B .f (x )g (a )>f (a )g (x ) C .f (x )g (b )>f (b )g (x ) D .f (x )g (x )>f (a )g (a ) F (x )=f (x )g (x ),那么F ′(x )=f ′(x )·g (x )-f (x )g ′(x )g 2(x )<0.∵f (x )、g (x )是定义域为R 的恒大于零的可导函数, ∴F (x )在R 上为递减函数,当x ∈(a ,b )时,f (x )g (x )>f (b )g (b ).∴f (x )g (b )>f (b )g (x ).4.函数y =f (x )在定义域[-4,6]内可导,其图象如图,记y =f (x )的导函数为y =f ′(x ),那么不等式f ′(x )≤0的解集为( ) A .[-43,1]∪[113,6]B .[-3,0]∪[73,5]C .[-4,-43]∪[1,73]D .[-4,-3]∪[0,1]∪[5,6]f ′(x )≤0的解集即为原函数f (x )的单调递减区间所对应的x 的取值范围,知选A. 5.设f (x ),g (x )在(a ,b )上可导,且f ′(x )>g ′(x ),那么当a <x <b 时有( ) A .f (x )>g (x ) B .f (x )<g (x )C .f (x )+g (a )>g (x )+f (a )D .f (x )+g (b )>g (x )+f (b )解析:选C.利用函数的单调性判断.令φ(x )=f (x )-g (x ),那么φ′(x )=f ′(x )-g ′(x ),∵f ′(x )>g ′(x ),∴φ′(x )>0,即函数φ(x )为定义域上的增函数.又a <x <b ,∴φ(a )<φ(x ),即f (a )-g (a )<f (x )-g (x ),从而得f (x )+g (a )>g (x )+f (a ). 6.函数y =x cos x -sin x 在下面哪个区间内是增函数( ) A.⎝⎛⎭⎫π2,3π2 B.()π,2π C.⎝⎛⎭⎫3π3,5π2D.()2π,3π解析:选B.y ′=cos x -x sin x -cos x =-x sin x ,假设y =f (x )在某区间内是增函数,只需在此间内y ′恒大于或者等于0即可.∴只有选项B 符合题意,当x ∈(π,2π)时,y ′≥0恒成立. 二、填空题7.函数y =3x -x 3在(-1,1)内的单调性是________. 解析:y ′=3-3x 2,由y ′>0得-1<x <1, ∴y =3x -x 3在(-1,1)内单调递增. 答案:增函数8.y =x 2e x 的单调递增区间是________. 解析:∵y =x 2e x ,∴y ′=2x e x +x 2e x =e x x (2+x )>0⇒x <-2或者x >0. ∴递增区间为(-∞,-2)和(0,+∞). 答案:(-∞,-2),(0,+∞)9.函数f (x )=x 3+ax 在区间[0,+∞)上是增加的,那么a 的取值范围是________. 解析:f ′(x )=3x 2+a ,那么当x ≥0时,f ′(x )≥0恒成立,即3x 2+a ≥0,∴a ≥-3x 2.又当x ≥0时,-3x 2≤0,∴a ≥a 的取值范围是[0,+∞). 答案:[0,+∞) 三、解答题10.求以下函数的单调区间. (1)f (x )=x 3+3x;(2)f (x )=sin x (1+cos x )(0≤x ≤2π).解:(1)函数的定义域为(-∞,0)∪(0,+∞), f ′(x )=3x 2-3x 2=3(x 2-1x 2),由f ′(x )>0,解得x <-1或者x >1, 由f ′(x )<0,解得-1<x <1且x ≠0,∴递增区间为(-∞,-1),(1,+∞), 递减区间为(-1,0),(0,1).(2)f ′(x )=cos x (1+cos x )+sin x (-sin x ) =2cos 2x +cos x -1 =(2cos x -1)(cos x +1). ∵0≤x ≤2π,∴由f ′(x )=0得x 1=π3,x 2=π,x 3=53π,那么区间[0,2π]被分成三个子区间,如表所示:∴f (x )=sin x (1+cos x )(0≤x ≤2π)的单调递增区间为[0,π3],[53π,2π],单调递减区间为(π3,53π).11.函数f (x )=ax -ax -2ln x (a ≥0),假设函数f (x )在其定义域内为单调函数,求a 的取值范围.解:∵f ′(x )=a +a x 2-2x,要使函数f (x )在定义域(0,+∞)内为单调函数, 那么在(0,+∞)内f ′(x )恒大于等于0或者恒小于等于0. 当a =0时,f ′(x )=-2x <0在(0,+∞)内恒成立;当a >0时,要使f ′(x )=a (1x -1a )2+a -1a ≥0恒成立,那么a -1a≥0,解得a ≥1.综上,a 的取值范围为a ≥1或者a =0.12.设k ∈R ,函数f (x )=⎩⎪⎨⎪⎧11-x , x <1,-x -1,x ≥1,F (x )=f (x )-kx ,x ∈F (x )的单调性.解:F (x )=f (x )-kx =⎩⎨⎧11-x-kx , x <1,-x -1-kx ,x ≥1.F ′(x )=⎩⎪⎨⎪⎧1(1-x )2-k , x <1,-12x -1-k ,x ≥1.对于F (x )=11-x-kx (x <1),当k ≤0时,函数F (x )在(-∞,1)上是增函数; 当k >0时,函数F (x )在(-∞,1-1k )上是减函数,在(1-1k,1)上是增函数. 对于F (x )=-x -1-kx (x ≥1),当k ≥0时,函数F (x )在(1,+∞)上是减函数;当k <0时,函数F (x )在(1,1+14k 2)上是减函数,在(1+14k2,+∞)上是增函数.励志赠言经典语录精选句;挥动**,放飞梦想。
高中数学 第3章333知能优化训练 A选修11 试题(共6页)
1.函数(hánshù)y =f (x )在[a ,b ]上( ) A .极大值一定比极小值大 B .极大值一定是最大值 C .最大值一定是极大值 D .最大值一定大于极小值解析:选 D.由函数的最值与极值的概念可知,y =f (x )在[a ,b ]上的最大值一定大于极小值.2.函数f (x )=x 3-3x (|x |<1)( ) A .有最大值,但无最小值 B .有最大值,也有最小值 C .无最大值,但有最小值 D .既无最大值,也无最小值解析:选 D.f ′(x )=3x 2-3=3(x +1)(x -1),当x ∈(-1,1)时,f ′(x )<0,所以f (x )在(-1,1)上是单调递减函数,无最大值和最小值,应选D.3.函数y =4x 2(x -2)在x ∈[-2,2]上的最小值为________,最大值为________. 解析:由y ′=12x 2-16x =0,得x =0或者x =43.当x =0时,y =0;当x =43时,y =-12827;当x =-2时,y =-64;当x =2时,y =0. 比拟可知y max =0,y min =-64. 答案:-64 04.函数f (x )=13x 3-4x +4.(1)求函数的极值(jí zhí);(2)求函数在区间[-3,4]上的最大值和最小值. 解:(1)f ′(x )=x 2-4,解方程x 2-4=0, 得x 1=-2,x 2=2.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (-∞,-2)-2 (-2,2) 2 (2,+∞)f ′(x ) +0 -0 + f (x )283-43从上表可看出,当x =-2时,函数有极大值,且极大值为3;而当x =2时,函数有极小值,且极小值为-43.(2)f (-3)=13×(-3)3-4×(-3)+4=7,f (4)=13×43-4×4+4=283,与极值比拟,得函数在区间[-3,4]上的最大值是283,最小值是-43.一、选择题1.函数f (x )=-x 2+4x +7,在x ∈[3,5]上的最大值和最小值分别是( ) A .f (2),f (3) B .f (3),f (5) C .f (2),f (5)D .f (5),f (3)解析:选B.∵f ′(x )=-2x +4, ∴当x ∈[3,5]时,f ′(x )<0, 故f (x )在[3,5]上单调递减,故f (x )的最大值和最小值分别是f (3),f (5).2.f (x )=x 3-3x 2+2在区间[-1,1]上的最大值是( ) A .-2B .0C .2D .4解析(jiě xī):选C.f ′(x )=3x 2-6x =3x (x -2),令f ′(x )=0可得x =0或者x =2(舍去),当-1≤x <0时,f ′(x )>0,当0<x ≤1时,f ′(x )<0. 所以当x =0时,f (x )获得最大值为2. 3.函数y =ln xx的最大值为( )A .e -1B .eC .e 2D.103y ′=ln x ′x -ln x ·x ′x2=1-ln xx 2x =e.当x >e 时,y ′<0; 当x <e 时,y ′>0.y 极大值=f (e)=1e,在定义域内只有一个极值,所以y max =1e.4.函数y =x -sin x ,x ∈⎣⎢⎡⎦⎥⎤π2,π的最大值是( ) A .π-1 B.π2-1 C .πD .π+1y ′=1-cos x ,当x ∈⎣⎢⎡⎦⎥⎤π2,π时,y ′>0,那么函数y 在区间⎣⎢⎡⎦⎥⎤π2,π上为增函数,所以y 的最大值为y max =π-sinπ=π,应选C.5.函数(hánshù)f (x )=x 3-3x 2-9x +k 在区间[-4,4]上的最大值为10,那么其最小值为( )A .-10B .-71C .-15D .-22解析:选B.f ′(x )=3x 2-6x -9=3(x -3)(x +1). 由f ′(x )=0得x =3,-1. 又f (-4)=k -76,f (3)=k -27,f (-1)=k +5,f (4)=k -20.由f (x )max =k +5=10,得k =5, ∴f (x )min =k -76=-71.6.函数y =-x 2-2x +3在区间[a,2]上的最大值为154,那么a 等于( )A .-32B.12 C .-12D.12或者-32a ≤-1时,最大值为4,不符合题意,当-1<a <2时,f (x )在[a,2]上是减函数,f (a )最大,-a 2-2a +3=154,解得a =-12或者a =-32(舍去).二、填空题7.函数y =x e x的最小值为________. 解析:令y ′=(x +1)e x=0,得x =-1. 当x <-1时,y ′<0;当x >-1时,y ′>0. ∴y min =f (-1)=-1e .答案:-1e8.f (x )=-x 2+mx +1在区间[-2,-1]上的最大值就是函数f (x )的极大值,那么m 的取值范围是________.解析(jiě xī):f ′(x )=m -2x ,令f ′(x )=0,得x =m2.由题设得m2∈[-2,-1],故m ∈[-4,-2].答案:[-4,-2]9.函数f (x )=ax 4-4ax 2+b (a >0,1≤x ≤2)的最大值为3,最小值为-5,那么a =________,b =________.解析:f ′(x )=4ax 3-8ax =4ax (x 2-2)=0,x 1=0,x 2=2,x 3=-2,又f (1)=a -4a +b =b -3a ,f (2)=16a -16a +b =b ,f (2)=b -4a ,f (0)=b ,f (-2)=b -4a .∴⎩⎪⎨⎪⎧b -4a =-5,b =3,∴a =2.答案:2 3 三、解答题10.函数f (x )=x 3+ax 2+2,x =2是f (x )的一个极值点,求: (1)实数a 的值;(2)f (x )在区间[-1,3]上的最大值和最小值. 解:(1)∵f (x )在x =2处有极值,∴f ′(2)=0. ∵f ′(x )=3x 2+2ax , ∴3×4+4a =0,∴a =-3.(2)由(1)知a =-3,∴f (x )=x 3-3x 2+2,f ′(x )=3x 2-6x .令f ′(x )=0,得x 1=0,x 2=2.当x 变化时f ′(x ),f (x )的变化情况如下表:11.设f (x )=x 3-12x 2-2xf (x )的单调递增、单调递减区间;解:f ′(x )=3x 2-x -2=(3x +2)(x -1). 令f ′(x )>0,得x <-23或者x >1.令f ′(x )<0,得-23<x <1.∴函数f (x )的单调递增区间为(-∞,-23),(1,+∞);单调递减区间为(-23,1).12.函数f (x )=x 3-ax 2+3x .(1)假设f (x )在x ∈[1,+∞)上是增函数,务实数a 的取值范围;(2)假设x =3是f (x )的极值点,求f (x )在x ∈[1,a ]上的最大值和最小值. 解:(1)令f ′(x )=3x 2-2ax +3>0,∴a <⎣⎢⎡⎦⎥⎤32x +1x min =3(当x =1时取最小值).∵x ≥1,∴a <3,a =3时亦符合题意, ∴a ≤3.(2)f ′(3)=0,即27-6a +3=0, ∴a =5,f (x )=x 3-5x 2+3x ,f ′(x )=3x 2-10x +3.令f ′(x )=0,得x 1=3,x 2=13(舍去).当1<x <3时,f ′(x )<0,当3<x <5时,f ′(x )>0, 即当x =3时,f (x )的极小值f (3)=-9. 又f (1)=-1,f (5)=15,∴f (x )在[1,5]上的最小值是f (3)=-9, 最大值是f (5)=15.内容总结。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.函数y =x 3+x 的递增区间是( )
A .(0,+∞)
B .(-∞,1)
C .(-∞,+∞)
D .(1,+∞)
解析:选C.y ′=3x 2+1>0对于任何实数都恒成立.
2.命题甲:对任意x ∈(a ,b ),有f ′(x )>0;命题乙:f (x )在(a ,b )内是单调递增的.则甲是乙的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
解析:选A.f (x )=x 3在(-1,1)内是单调递增的,但f ′(x )=3x 2≥0(-1<x <1),故甲是
乙的充分不必要条件,选A.
3.函数y =x 3+x 2-5x -5的单调递增区间是________.
解析:令y ′=3x 2+2x -5>0得
x <-53
或x >1. 答案:(-∞,-53
),(1,+∞) 4.求下列函数的单调区间:
(1)y =x -ln x ;(2)y =12x
. 解:(1)函数的定义域为(0,+∞).
其导数为y ′=1-1x
. 令1-1x >0,解得x >1;再令1-1x
<0,解得0<x <1. 因此,函数的单调增区间为(1,+∞),
函数的单调减区间为(0,1).
(2)函数的定义域为(-∞,0)∪(0,+∞).
y ′=-12x 2,所以当x ≠0时,y ′=-12x 2<0, 而当x =0时,函数无意义,
所以y =12x
在(-∞,0),(0,+∞)内都是减函数, 即y =12x
的单调减区间是(-∞,0),(0,+∞).
一、选择题
1.函数f (x )=x -2ln x 的单调减区间为( )
A .(-∞,0)
B .(2,+∞)
C .(0,2)
D .(-∞,0),(2,+∞)
答案:C
2.函数y =4x 2+1x
的单调递增区间是( )
A .(0,+∞)
B .(-∞,1)
C .(12
,+∞) D .(1,+∞) 解析:选C.∵y ′=8x -1x 2=8x 3-1x 2>0,∴x >12
. 即函数的单调递增区间为(12
,+∞). 3.若在区间(a ,b )内,f ′(x )>0,且f (a )≥0,则在(a ,b )内有( )
A .f (x )>0
B .f (x )<0
C .f (x )=0
D .不能确定
解析:选A.因f ′(x )>0,所以f (x )在(a ,b )内是增函数,所以f (x )>f (a )≥0.
4.下列函数中,在区间(-1,1)上是减函数的是( )
A .y =2-3x 2
B .y =ln x
C .y =1x -2
D .y =sin x 解析:选C.对于函数y =1x -2,其导数y ′=-1x -2
<0,且函数在区间(-1,1)上有意义,所以函数y =1x -2
在区间(-1,1)上是减函数,其余选项都不符合要求,故选C. 5.函数y =x cos x -sin x 在下面哪个区间内是增函数( )
A.⎝ ⎛⎭⎪⎫π2
,3π2 B.()π,2π C.⎝ ⎛⎭⎪⎫π3
,5π2 D.()2π,3π 解析:选B.y ′=cos x -x sin x -cos x =-x sin x ,若y =f (x )在某区间内是增函数,只需在此区间内y ′恒大于或等于0即可.
∴只有选项B 符合题意,当x ∈(π,2π)时,y ′≥0恒成立.
6.函数y =ax 3-x 在R 上是减函数,则( )
A .a ≥13
B .a =1
C .a =2
D .a ≤0
解析:选D.因为y ′=3ax 2-1,函数y =ax 3-x 在(-∞,+∞)上是减函数,
所以y ′=3ax 2-1≤0恒成立,
即3ax 2≤1恒成立.
当x =0时,3ax 2≤1恒成立,此时a ∈R ;
当x ≠0时,若a ≤13x 2恒成立,则a ≤0. 综上可得a ≤0.
二、填空题
7.y =x 2e x 的单调递增区间是________.
解析:∵y =x 2e x ,
∴y ′=2x e x +x 2e x =e x x (2+x )>0⇒x <-2或x >0.
∴递增区间为(-∞,-2)和(0,+∞).
答案:(-∞,-2),(0,+∞)
8.若函数f (x )=x 3+bx 2+cx +d 的单调减区间为[-1,2],则b =________,c =________.
解析:∵y ′=3x 2+2bx +c ,由题意知[-1,2]是不等式3x 2+2bx +c <0的解集,∴-1,2
是方程3x 2+2bx +c =0的根,由根与系数的关系得b =-32
,c =-6. 答案:-32
-6
9.若函数y =-43
x 3+ax 有三个单调区间,则a 的取值范围是________. 解析:∵y ′=-4x 2+a ,且y 有三个单调区间,
∴方程y ′=-4x 2+a =0有两个不等的实根,
∴Δ=02-4×(-4)×a >0,∴a >0.
答案:(0,+∞)
三、解答题
10.求下列函数的单调区间.
(1)f (x )=x 3+3x
; (2)f (x )=x +b x
(b >0). 解:(1)函数的定义域为(-∞,0)∪(0,+∞),
f ′(x )=3x 2-3x 2=3(x 2-1x 2), 由f ′(x )>0,解得x <-1或x >1,
由f ′(x )<0,解得-1<x <1且x ≠0,
∴递增区间为(-∞,-1),(1,+∞),
递减区间为(-1,0),(0,1).
(2)函数的定义域为x ≠0.
f ′(x )=⎝ ⎛⎭⎪⎫x +b x ′=1-b x 2=1x 2(x +b )(x -b ). 令f ′(x )>0,则1x (x +b )(x -b )>0, ∴x >b 或x <-b .
∴函数的单调递增区间为(-∞,-b )和(b ,+∞).
令f ′(x )<0,则1x 2(x +b )(x -b )<0, ∴-b <x <b 且x ≠0.
∴函数的单调递减区间为(-b ,0)和(0,b ).
11.求函数f (x )=x 3-3x 2-9x +1在区间[-4,4]上的单调性.
解:∵f (x )=x 3-3x 2-9x +1,
∴f ′(x )=3x 2-6x -9.
令f ′(x )>0,结合-4≤x ≤4,
得-4≤x <-1或3<x ≤4.
令f ′(x )<0,结合-4≤x ≤4,
得-1<x <3.
∴函数f (x )在[-4,-1)和(3,4]上为增函数,在(-1,3)上为减函数.
12.已知函数f (x )=ax -a x
-2ln x (a ≥0),若函数f (x )在其定义域内为单调函数,求a 的取值范围. 解:∵f ′(x )=a +a x 2-2x
, 要使函数f (x )在定义域(0,+∞)内为单调函数,
则在(0,+∞)内f ′(x )恒大于等于0或恒小于等于0.
当a =0时,f ′(x )=-2x
<0在(0,+∞)内恒成立;
当a >0时,要使f ′(x )=a (1x -1a )2+a -1a ≥0恒成立,
则a -1a ≥0,解得a ≥1. 综上,a 的取值范围为{a |a ≥1或a =0}.。
