密立根实验电荷计算
密立根油滴法测定电子电荷

选十三 密立根油滴法测定电子电荷R ·A.密立根花了七年功夫(1909~1917)所做的测量微小油滴上所带电荷的工作,即著名的密立根油滴试验,是近代物理学发展史上最有重要意义的实验。
他证明了电荷的不连续性(即所有电荷都是基本电荷e 的整数倍),测得了基本电荷e ,即电子的电荷值。
e=v12(1.602+0.002)×10-10库仑。
一、目的要求应用密立根油滴法测定基本电荷。
具体要求:1. 验证电荷的不连续性原理。
2. 测定电子的电荷值e 。
3. 测出的电子电荷量e 与公认值比较,求出其正确度。
二、实验仪器密立根油滴仪、机时秒表、喷雾器、调焦针。
三、参考书目1.南京工学院等七所工科院校编《物理学》中册P.36—38。
2.F.W.SEARS 《大学物理学》第三册P.70—72。
3.保罗·A ·蒂普勒《近代物理基础及其应用》P.105—118。
4.哈尔滨工业大学主编《物理实验》(近代物理与综合部分)P.43—53。
四、实验原理用喷雾器将雾状油滴喷入相距为d 的水平放置的平行极板之间。
由于摩擦,油滴在喷射时一般都是带电的。
调解加在平行极板上电压V ,可使作用在某一油滴上的电场力与重力平衡,油滴静止在空中,如图1所示,此时有mg=q dV (1) 要从上式测出油滴带电量q ,还必须定出油滴质量m ;图1平行极板未加电压时,油滴在重力作用下加速下降,由于空气的粘滞阻力与油滴速度成正比,当到达某一速度v 时,阻力与重力平衡,油滴将均速下降,由斯托克斯定理可知: mg v a f r ==ηπ6 (2)其中η是空气粘滞系数,a 为油滴的半径。
设油滴密度为ρ则:ρπ334a m =(3) 由(2)、(3)两式得:gv a ρη29= (4) 对于半径小到10-6米的小球,油滴半径近于空气中孔隙的大小,空气介质不能再认为是均匀的,因而在应用对于均匀介质才适用的斯托克斯定律时,必须对空气粘滞系数作如下修正:a pb a ⋅+=ηη'b 为常数,p 为大气压强,用η代'η得到:a pb g v a ⋅+⋅=1129ρη (5)上式根号中的阿处于修正项中,不需十分精确,故它仍可用(4)式计算。
油滴实验

密立根油滴法测电子电荷一、实验介绍杰出的美国物理学家密立根在1909年至1917年所做的测量微小油滴上带的电荷的工作,即所谓油滴实验。
在全世界是享负盛名的,堪称物理实验的典范.Millikan在这一实验工作中花费里近10年的心血,而取得了有重大意义的结果,那就是:(1)证明电荷的不连续性(具有颗粒性),所有电荷都是基本电荷e的整数倍。
(2)测量并得到了基本电荷即为电子电荷,其值为e=1.60⨯10-19库仑。
现公认e是基本电荷,对其值的测量测量精度不断提高,目前给出的最好结果为:e=(1.60217731±0.00000049)⨯10-19库仑。
正是由于这一实验成就,他荣获了1932年诺贝尔物理奖金。
八十多年过去了,物理学发生了根本的变化,而这个实验又重新站到了实验物理的前列。
近年来,根据这一实验的设计思想改进的用磁漂浮的方法测量分数电荷的实验,使古老的实验又焕发青春,也就更说明,Millikan油滴实验是富有巨大生命力的实验。
二、实验原理按油滴作匀速直线运动或静止两种运动方式分类,油滴法测电子电荷分为动态测量法和平衡测量法。
动态测量法考虑重力场中一个足够小油滴的运动,设此油滴半径为r,质量为m1,空气是粘滞流体,故此运动油滴除重力和浮力外还受粘滞阻力的作用。
由斯托克斯定律,粘滞阻力与物体运动速度成正比。
设油滴以匀速v f下落,则有(1)此处m2为与油滴同体积空气的质量,K为比例常数,g为重力加速度。
油滴在空气及重力场中的受力情况如图示。
若此油滴带电荷为q,并处在场强为E的均匀电场中,设电场力qE方向与重力方向相反,如图8.1.1-2所示,如果油滴以匀速v r上升,则有(2)由式(1)和(2)消去K,可解出q为:(3)由(3)式可以看出来,要测量油滴上的电荷q,需要分别测出m1,m2,E,v r,v f 等物理量。
由喷雾器喷出的小油滴半径r是微米量级,直接测量其质量m1也是困难的,为此希望消去m1,而带之以容易测量的量。
密立根油滴实验电子电荷的测量

4.8 密立根油滴实验——电子电荷的测量实验简介密立根 (Robert Andrews Millikan ,1868~1953,美国物理学家) 于1907年开始,经历7年时间,用油滴法直接证实了“电”的不连续性,并用实验的方法直接测量了电子的电荷量,这就是著名的密立根油滴实验,它是近代物理学发展史中具有重要意义的实验。
因对基本电荷和光电效应的工作,密立根荣获1932年度诺贝尔物理学奖。
实验目的1.通过对带电油滴在重力场和静电场中运动的测量,验证电荷的不连续性,并测定电子的电荷e 。
2.了解、掌握密立根油滴实验的设计思想、实验方法和实验技巧。
实验原理用油滴法测量电子的电荷,需要测量油滴的带电量q ,可以用静态(平衡)测量法或动态(非平衡)测量法测q ,也可以通过改变油滴的带电量,用静态法或动态法测量油滴带电量的改变量。
测量方法分析如下:一.静态(平衡)测量法。
用喷雾器将油喷入两块相距为d 的水平放置的平行极板之间。
油在喷射撕裂成油滴时,一般都是带电的。
设油滴的质量为m ,所带的电荷为q ,两块极板间的电压为U ,则油滴在平行极板间将同时受到重力mg 和静电力qE 的作用。
如图(4.8-2)所示。
如果调节两极板间的电压U ,可使这两个力达到平衡,这时U mg qE q d== (4.8-1) 从式(4.8-1)可见,为了测出油滴所带电量q ,除了需测定平衡电压U 和极板间距离d 外,还需要测量油滴的质量m 。
因为m 很小,需要用如下特殊方法测定:平行极板不加电压时,油滴受重力作用而加速下降,由于空气粘滞阻力的作用,下降一定距离达到某一速度v g 后,阻力与重力mg 平衡,如图4.8-3所示(空气浮力忽略不计),油滴将匀速下降 。
根据斯托克斯定律,油滴匀速下降时6g f a v mg πη== (4.8-2)式中,η是空气的粘滞系数;a 是油滴的半径(由于表面张力的原因,油滴总是呈小球状)。
设油的密度为ρ,油滴的质量可以用下式表示f r mg v g343m a πρ= (4.8-3) 由式(4.8-2)和式(4.8-3)得到油滴的半径a =(4.8-4)对于半径小到610-m 的小球,空气的粘滞系数应作如下修正1b pa ηη'=+式中,b 为修正常数,p 为大气压强,单位用Pa 。
密立根油滴实验基本电荷测定

? 100 %
e0=1.602 ×10 -19C
已知参数值
钟油密度: ? ? 981kgm?3 (200 c) ? ? 986kgm?3(100 c) 空气粘滞系数: ? ? 1.83? 10?5 kg.m?1.s?1
重力加速度 : g ? 9.79m.s ?2
修正常数 : b ? 6.17 ? 10?6 m.cmHg
e = (1.6021892±0.0000046)×10-19C) 。
实验设计巧妙,将微观测量量转化为宏观量的测量 ,在近代 物理学的发展史上具有里程碑意义。密立根本人也因此荣获 1923 年诺贝尔物理学奖。
二、实验目的
1) 学习密立根油滴实验的设计思想。 2) 验证电荷的“量子化”,即电量是不连续的,而是
? '?
?
1?
b
pr
b为修正系数,p为空气压强, r油滴的半径 。
修正后的q公式
P229?? ?? q?18? (? )3 2 (2g? )1 2
?d U
?
tg
3
l2
1?
b pr0
3 2
1
r0 ?
? ? ?
9 ??
2g
?
0
? ? ?
2
测量tg 时,U=?
该式就是静态法测量油滴所带电荷的公式
2. 动态非平衡测量法
2、测量练习 (1)练习控制油滴。 (2)练习测量油滴运动的时间,即测量速度。 (3)练习选择油滴。 ①平衡电压约150~250V 左右。 ②油滴匀速下降时间约10 ~25s 左右。
操作步骤
?水平调节
?寻找合适的油滴: 预置电压~ 220 伏 大小合适,屏幕中央 粗测 tg~20s ,熟练控制
电子电荷的测量(密立根油滴实验)

实验57电子电荷的测量(密立根油滴实验)由美国物理学家密立根(Millikan,R.A.)完成的测量微小油滴上所带电荷的实验——油滴实验,是物理学发展史上具有重要意义的实验。
这一实验首次证明了电荷的不连续性,即任何带电体所带的电量都是基本电荷的整数倍,并精确测定了基本电荷e=1.60×10-19库仑。
电子电荷是物理学中基本常数之一,在理论和实际工作中都有重要意义,它的精确测定,为从实验上测定许多基本物理量提供了可能性。
密立根油滴实验设计精巧,设备简单,而实验结论却有不容置疑的说服力,因此这一实验历来被看做是物理实验的一个光辉典范。
密立根由于这一杰出工作和在光电效应方面的研究成果而荣获1923年诺贝尔物理奖。
【预习重点】(1)用油滴法测量电子电荷的原理。
(2)密立根油滴仪的结构原理和调节使用方法。
【仪器】密立根油滴仪(包括油滴盒、照明装置、显微镜、电源及油喷雾器)、电子停表。
MOD—4型油滴仪简介如下。
MOD—4型油滴仪结构如图57—1所示。
油滴盒由两块经过精磨的平行极板、中间垫以胶木圆环组成,两平行极板的间距为d。
胶木圆环上有进光孔(插导光棒)、观察孔(正对显微镜)和石英玻璃窗(旁边装有笔形汞灯)。
上电极板中央有一个直径为0.4mm的小孔,油滴从油雾室经此孔下落,进入油滴盒。
油滴盒可用调平螺丝调节水平并用水准器校验。
图57—1油滴实验仪照明装置包括照明灯室和导光棒。
灯室中装一2.2V聚光小灯泡,通过调节小灯泡方向,可使油滴更为清晰明亮。
显微镜通过胶木圆环上的观察孔观察平行极板间的油滴。
显微镜目镜中装有分划板,其垂直方向的总刻度相当于视物中的3.00mm,用以测量油滴运动的距离l。
电源共提供4种电压:2.2V照明小灯泡电压,500V直流平衡电压,250V直流升降电压和笔形汞灯工作电压。
500V直流平衡电压可连续调节,读数从电压表上读出,并由反向开关换向以改变上下电极板的极性。
开关置“+”位置时,能使带正电的油滴与重力平衡,置“-”位置时,能平衡带负电的油滴,反向开关置“0”位置时,上下电极短路,极板间电场为零。
密立根油滴实验电子电荷的测量

密立根油滴实验电子电荷的测量密立根(Robert Andrews Millikan , 1868〜1953,美国物理学家)于1907 年开始,经历7 年时间,用油滴法直接证实了“电”的不连续性,并用实验的方法直接测量了电子的电荷量,这就是著名的密立根油滴实验,它是近代物理学发展史中具有重要意义的实验。
因对基本电荷和光电效应的工作,密立根荣获1932 年度诺贝尔物理学奖。
1 .通过对带电油滴在重力场和静电场中运动的测量,验证电荷的不连续性,并测定电子的电荷e。
2.了解、掌握密立根油滴实验的设计思想、实验方法和实验技巧。
用油滴法测量电子的电荷,需要测量油滴的带电量q,可以用静态(平衡)测量法或动态(非平衡)测量法测q,也可以通过改变油滴的带电量,用静态法或动态法测量油滴带电量的改变量。
测量方法分析如下:一.静态(平衡)测量法。
用喷雾器将油喷入两块相距为d的水平放置的平行极qE板之间。
油在喷射撕裂成油滴时,一般都是带电的。
设油滴Vd的质量为m所带的电荷为q,两块极板间的电压为U,则mg油滴在平行极板间将同时受到重力mg和静电力qE的作用。
图4.8-2如图(4.8-2 )所示。
如果调节两极板间的电压U,可使这两个力达到平衡,这时UmgqEq,, (4.8-1 )d从式(4.8-1 )可见,为了测出油滴所带电量q,除了需测定平衡电压U和极板间距离d外,还需要测量油滴的质量m因为m很小,需要用如下特殊方法测定:平行极板不加电压时,油滴受重力作用而加速下降,由于空气粘滞阻力的作用,下降一定距离达到某一速度v后,阻力与重力mg平衡,如图4.8-3所示(空气浮力忽略不计),fgr 油滴将匀速下降。
根据斯托克斯定律,油滴匀速下降时favmg,,6,, (4.8-2) vgg 式中,a是空气的粘滞系数;是油滴的半径(由于表面张力的原因,油滴,mg总是呈小球状)。
设油的密度为,油滴的质量可以用下式表示,143 (4.8-3) ma 图4.8-3 ,,,3由式( 4.8-2 )和式( 4.8-3 )得到油滴的半径9,vga, (4.8-4 )2,g,6对于半径小到m的小球,空气的粘滞系数应作如下修正10,,,,b ,1pa式中,为修正常数,为大气压强,单位用Pa。
用密立根油滴实验测电子电荷

用密立根油滴实验测电子电荷实验背景杰出的美国物理学家密立根在1909年至1917年所做的测量微小油滴上带的电荷的工作,即所谓油滴实验。
在全世界是享负盛名的,堪称物理实验的典范.Millikan在这一实验工作中花费里近10年的心血,而取得了有重大意义的结果,那就是:(1)证明电荷的不连续性(具有颗粒性),所有电荷都是基本电荷e的整数倍。
(2)测量并得到了基本电荷即为电子电荷,其值为e=1.60⨯10-19库仑。
现公认e是基本电荷,对其值的测量测量精度不断提高,目前给出的最好结果为:e=(1.60217731±0.00000049)⨯10-19库仑。
正是由于这一实验成就,他荣获了1932年诺贝尔物理奖金。
八十多年过去了,物理学发生了根本的变化,而这个实验又重新站到了实验物理的前列。
近年来,根据这一实验的设计思想改进的用磁漂浮的方法测量分数电荷的实验,使古老的实验又焕发青春,也就更说明,Millikan油滴实验是富有巨大生命力的实验。
⏹实验目的本实验的目的,是学习测量元电荷的方法,并训练物理实验时应有的严谨态度和坚韧不拔的科学精神。
⏹实验原理按油滴作匀速直线运动或静止两种运动方式分类,油滴法测电子电荷分为动态测量法和平衡测量法。
●动态测量法考虑重力场中一个足够小油滴的运动,设此油滴半径为r,质量为m1,空气是粘滞流体,故此运动油滴除重力和浮力外还受粘滞阻力的作用。
由斯托克斯定律,粘滞阻力与物体运动速度成正比。
设油滴以匀速v f下落,则有(1)此处m2为与油滴同体积空气的质量,K为比例常数,g为重力加速度。
油滴在空气及重力场中的受力情况如图8.1.1-1所示。
若此油滴带电荷为q,并处在场强为E的均匀电场中,设电场力qE方向与重力方向相反,如图8.1.1-2所示,如果油滴以匀速v r上升,则有(2)由式(1)和(2)消去K,可解出q为:(3)由(3)式可以看出来,要测量油滴上的电荷q,需要分别测出m1,m2,E,v r,v f等物理量。
密立根油滴实验数据处理表格(包含静态法动态法电荷计算和误差计算)
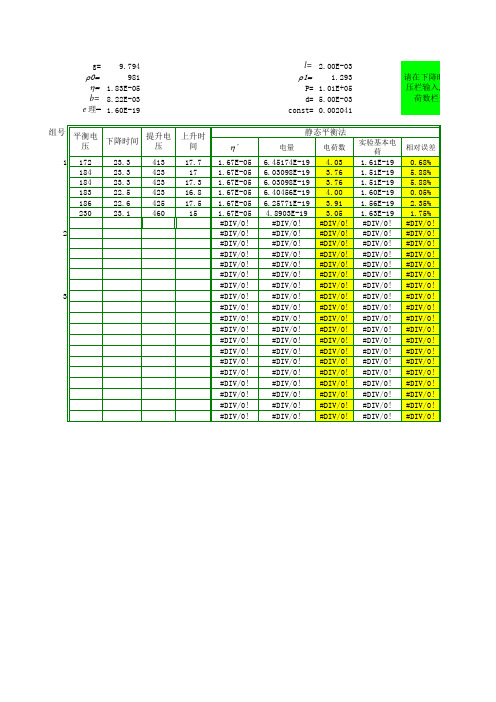
请在下降时间和平衡电 压栏输入,在电量和电 荷数栏查看结果.
动态平衡法
电量 电荷数 实验基本电荷 相对误差
8.18E-19 8.34E-19 8.18E-19 8.57E-19 8.15E-19 8.82E-19 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! ห้องสมุดไป่ตู้DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
1.61E-19 1.51E-19 1.51E-19 1.60E-19 1.56E-19 1.63E-19 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
2.08% 4.08% 2.14% 6.99% 1.75% 8.24% #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
静态平衡法平衡电压下降时间提升电压上升时间降时间和平衡电电量电荷数实验基本电荷相对误差818e19510164e19208834e19520167e19408818e19511164e19214857e19535171e19699815e19509163e19175882e19551147e19824div0
