苏科版八年级数学下册分式PPT教学课件
合集下载
苏科版八年级数学下册10.1 分式 (共18张PPT)

a 买练习本 本. b-1
10.1 分式
a-3 的值. 问题2 求当a=1时,分式 a+2
如果a=3呢?
请你选择一个喜欢的数a来计算这个分式的值.
2 a=- 呢? 5
当a=-2时呢? 分式的分母不能为0,如果分式中的字母所 取的值使分母为0,那么分式无意义。
10.1 分式
问题3
x-2 当x取什么值时,分式 有意义? 2 x-3
3、当x取何值时,下列分式的值为零?
2 x 1 x
x 2 4 3x
3x 2 3 5x 4
| x | 3 4 x3 归纳:对于分式,当 时分式有意义; 当 分式无意义; 当 时分式值为零。
x 2 64 5 x8
10.1 分式
做一做
2.填表: x -3 -2 -1
12 x
小时.
(2)班学生组成后队, 速度比(1)班每小时快 12 2千米,则(2)班到达目的地需要 x+2 小时.
10.1 分式
情境4 有两块棉田,一块面积为a ha,产棉花m kg; 另一块面积为b ha,产棉花n kg. 这两块棉田平均 每公顷产棉花
m+n a+b
kg.
a ha
b ha
10.1 分式
2
分式: 整式: __________________________(填写序号)
10.1 分式
问题1 小明a元钱去购买练习本,原价每本b
元,如果每本降价 1 元,那么现在可以购
a 分式 还可以表示什么? b-1
如果a表示长方形的面积, b表示长方形的宽, a 那么 b 1 表示宽减少1个单位长度后,面积仍 为a的长方形的长。
什么时候有意义?
3 解:由分母2x-3=0 ,得 x= , 2
苏科版八年级数学下册课件:10.1分式 (共12张PPT)
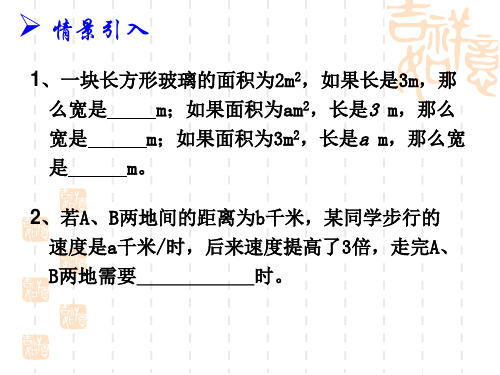
a3 例1:求分式 的值。 a2
(1) a = 1 ( 2) a = 3
(3) a= - 2
例题教学
x2 例2、当x取什么值时,分式 2x 3 (1)没有意义?(2)有意义?(3)值为零。
x2 4 拓展:当x是什么数时,分式 的值是0? x2
10.1 分式
1
x
1- x
-3
将其中2张卡片分别放在分子、分母上, 可以组成哪些代数式,其中哪些是分式?
A 字母 ,那么代数式 叫做分式,其中A是分式的分 B
子,B是分式的分母。
一般地,如果A、B表示两个整式,并且B中含有
分式
A B
B中含有字母
试一试
请同学们自己举出几个分式的例子。
试一试
请判断下列各式是否为分式?若不是, 请说明理由。
××√ × √ √
(1 )
5 , 3
b , 2
2 x 1 , , 2a+b, 4x b
情景引入
1、一块长方形玻璃的面积为2m2,如果长是3m,那
么宽是
宽是 是 m。
m;如果面积为am2,长是3 m,那么
m;如果面积为3m2,长是a m,那么宽
2、若A、B两地间的距离为b千米,某同学步行的 速度是a千米/时,后来速度提高了3倍,走完A、 B两地需要 时。
情景引入
3、小丽用b元钱买3袋同样的瓜子,后来又增 加了a袋,那么每袋瓜子的价格是 元。
(4) (5)
a b
(2) (3)
(6)
交流探讨
a a 试解释分式 b 、b 1 所表示的实际意义
例如: 如果a(元)表示购买笔记本的钱数,b(元) a 表示每本笔记本的售价,那么 表示买到笔 b a 记本的数量; 表示 每本笔记降价1元后, b 1 用a元可购得笔记本的本数;例题教学Βιβλιοθήκη 这些分式,它什么时候有意义?
苏科版八年级数学下册10.5分式方程(18)课件

设自行车的速度为xkm/h,则汽车速度为_3x _km/h
可得方程:
15= 15 + 40 . x 3x 60
10.5 分式方程(1)
20= 24 . x x+1
410+x =7. 10x+4 4
15= 15 + 40 . x 3x 60
上面方程与一元一次方程有没有区分?若有,
其本质区分是什么?
所列方程的分母中含有未知数.
练习巩固:见学案
10.5 分式方程(1)
谈谈本课的收获
谢谢
20(x+1)=24x
解之得: x=5
把x=5代入原方程:左边=4,右边=4,左边 =右边
∴x=5是原方程的解.
归纳:解分式方程步骤
解方程:1 2 x 1 x2 1
解:方程两边同乘(x+1)(x-1),得
x+1=2
解之得
x=1
把x=1代入原方程: 分母为0,无意义
∴x=1是增根,原方程无解.
注意:解分式方程有可能产生增根, 所以一定要检验.
像这样的方程叫做分式方程.
10.5 分式方程(1)
辨析
下列方程中,哪些是分式方程?
(1) 2x+ x-1=0
5
;
×
(2) 2 + x =5 ;
√
x2
(3) x+1 1=2 ;
√
(4) 2 y + y-1=1 . ×
32
10.5 分式方程(1)
解分式方程:
20= 24 . x x+1
解: 方程两边同乘x(x+1),得
位数字与十位数字对调,那么所得的两位数与原两 位数的比值是 7.求原二位数的十位数字
4
设这个两位数的十位数字是x,则原二位数为_10x_+4
可得方程:
15= 15 + 40 . x 3x 60
10.5 分式方程(1)
20= 24 . x x+1
410+x =7. 10x+4 4
15= 15 + 40 . x 3x 60
上面方程与一元一次方程有没有区分?若有,
其本质区分是什么?
所列方程的分母中含有未知数.
练习巩固:见学案
10.5 分式方程(1)
谈谈本课的收获
谢谢
20(x+1)=24x
解之得: x=5
把x=5代入原方程:左边=4,右边=4,左边 =右边
∴x=5是原方程的解.
归纳:解分式方程步骤
解方程:1 2 x 1 x2 1
解:方程两边同乘(x+1)(x-1),得
x+1=2
解之得
x=1
把x=1代入原方程: 分母为0,无意义
∴x=1是增根,原方程无解.
注意:解分式方程有可能产生增根, 所以一定要检验.
像这样的方程叫做分式方程.
10.5 分式方程(1)
辨析
下列方程中,哪些是分式方程?
(1) 2x+ x-1=0
5
;
×
(2) 2 + x =5 ;
√
x2
(3) x+1 1=2 ;
√
(4) 2 y + y-1=1 . ×
32
10.5 分式方程(1)
解分式方程:
20= 24 . x x+1
解: 方程两边同乘x(x+1),得
位数字与十位数字对调,那么所得的两位数与原两 位数的比值是 7.求原二位数的十位数字
4
设这个两位数的十位数字是x,则原二位数为_10x_+4
八下数学课件: 分式方程( 利用解分式方程解决实际问题)
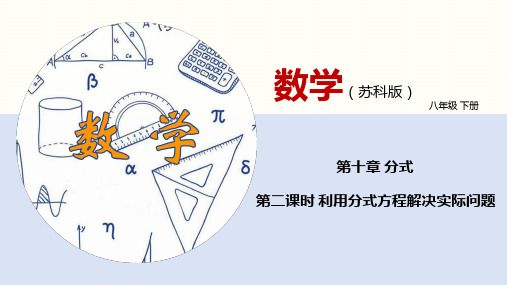
−
3
=2
解得: = 100
经检验: = 100是原方程的解,
∴高铁的平均速度是每小时3×100=300千米.
答:高铁的平均速度是每小时300千米.
情景引入(销售问题)
某商场经市场调查,预计一款夏季童装能获得市场青睐,便花费15000元购
进了一批此款童装,上市后很快售罄.该店决定继续进货,由于第二批进货数量是
解得a=
检验,由S、v都是正数,当a=
所以,原分式方程的解为a=
≠0
。答:略
练一练(距离问题)
小刚家(点A)、王老师家(点B)、学校(点C)在同一条路上,小刚家到王老师家的
路程为3千米,王老师家到学校的路程为1千米。为了使小刚能按时到校,王老师每天
骑自行车接小刚上学。已知王老师骑自行车的速度是步行的3倍,每天比平时步行上
1)本题等量关系为_______________________________________;
2)设提速前平均速度为a km/h。
S
3)提速前行驶距离___________,提速前时间表示为____________;
+
S+50
4)提速后行驶距离___________,提速后时间表示为____________;
解:设第一次该干果的进货价是每千克x元,
则第二次购进干果的进货价是每千克(x+5)元,
9000
5000
1.5
根据题意得: × = +5
,
解得:x=25,
经检验,x=25是所列方程的解.
答:该种干果的第一次进价是每千克25元.
课后回顾
3
=2
解得: = 100
经检验: = 100是原方程的解,
∴高铁的平均速度是每小时3×100=300千米.
答:高铁的平均速度是每小时300千米.
情景引入(销售问题)
某商场经市场调查,预计一款夏季童装能获得市场青睐,便花费15000元购
进了一批此款童装,上市后很快售罄.该店决定继续进货,由于第二批进货数量是
解得a=
检验,由S、v都是正数,当a=
所以,原分式方程的解为a=
≠0
。答:略
练一练(距离问题)
小刚家(点A)、王老师家(点B)、学校(点C)在同一条路上,小刚家到王老师家的
路程为3千米,王老师家到学校的路程为1千米。为了使小刚能按时到校,王老师每天
骑自行车接小刚上学。已知王老师骑自行车的速度是步行的3倍,每天比平时步行上
1)本题等量关系为_______________________________________;
2)设提速前平均速度为a km/h。
S
3)提速前行驶距离___________,提速前时间表示为____________;
+
S+50
4)提速后行驶距离___________,提速后时间表示为____________;
解:设第一次该干果的进货价是每千克x元,
则第二次购进干果的进货价是每千克(x+5)元,
9000
5000
1.5
根据题意得: × = +5
,
解得:x=25,
经检验,x=25是所列方程的解.
答:该种干果的第一次进价是每千克25元.
课后回顾
分式ppt课件初中数学苏科版八年级下册

问题2
求当a=1时,分式
a- a+
3 2
的值.
如果a=3呢? a = - 2 呢? 5
请你选择一个喜欢的数a来计算这个分式的值.
问题3
当x取什么值时,分式
x- 2 x-
2 3
有意义?
解:由分母2x-3=0 ,得 x = 3 , 2
所以当 x =
3 时,分式有意义. 2
做一做
1.列代数式,并说明列出的代数式是否为分式.
(1)某校八年级有学生m人,集合排成方队.
m
若恰好排成20排,那么每排有 2 0
m
名学生;
若恰好排成a排,那么每排有 a
名学生.
(2)帆船在静水中每小时行驶a千米,水流的速
度为每小时b千米.
s
若帆船逆流行驶s千米,需要
a- b
h;
s
若帆船顺流行驶s千米,需要
a+ b
h.
做一做
2.填表:
x -3 -2 -1 0 1
m+ n
每公顷产棉花
a+ b
kg.
a ha
b ha
试一试
(1)一个n边形,若每个内角都相等,
1 8 0(n- 2 )
则每个内角为
n
度.
(2)小明用a元钱去购买练么现在可以
购买练习本
b- 1
本.
议一议
2、 n、 1 2、 1 2、 m + n 、 1 8 0 (n - 2 )、 a amxx + 2a + b n b - 1
m袋
情境3
某校八年级学生步行到距学校12千米的郊外野
炊,(1)班学生组成的前队步行速度为x千米/时,
12
(1)班到达目的地需要
苏科版八年级数学下册10.1 分式 课件 (共23张PPT)

分 式
1.什么是分式,分式与分数有什么不同? 2.什么是分式的值,如何求分式的值? 3.分式的讨论,当字母取什么值时分式有 意义或无意义?
问题1
1÷2 -5÷4
a÷b
分母不能等于0!
1 2 -5 4 a b
如果用字母 a、b分别表示 分数的分子和 分母。如何?
⑴两个数相除可以把它们的商表示成分数的形式
5.x为何值时,分式 x 2 x 1 的值为负数?
2
x2
1 x 6.当x________时,分式 无意义,; 2x 5
当x________时,此分式的值为1;
7.当x________时,分式
x 2 x 1
2
的值为负
xb 8.已知:x=-2时,分式 无意义; xa
X=4时,此分式值为0,求
3 7
a 4 当a取什么数时,分式 a2
2
的值为0?
x5 当X =-5 时,分式 4 x
2x 6 呢? x3
的值为0。
的值为0。
x2 x 1
2
当X =2
时,分式
当X =-1 时,分式
x 5
x2 1 的值为0。 x1
当x取何值时, x 2 4x 5
分式的值为零?
1)当a=-1 时, 解: 3 a 3( - -1) =4 -12 a2 3 a 3 3 2)当a=3时, =0 3 2 a2
17 3) 8
练习三:对于分式
2 x 3 x 2
分母为0,则 分式无意义 分母不为0, 则分式有意义
⑴当x取什么值时,分式有意义? 解:由分母x-2≠0,得x≠2 ∴ 当x≠2时,分式有意义。 ⑵当x取什么值时,分式无意义?
讨论:字母a、b可以表示任何实数吗?
1.什么是分式,分式与分数有什么不同? 2.什么是分式的值,如何求分式的值? 3.分式的讨论,当字母取什么值时分式有 意义或无意义?
问题1
1÷2 -5÷4
a÷b
分母不能等于0!
1 2 -5 4 a b
如果用字母 a、b分别表示 分数的分子和 分母。如何?
⑴两个数相除可以把它们的商表示成分数的形式
5.x为何值时,分式 x 2 x 1 的值为负数?
2
x2
1 x 6.当x________时,分式 无意义,; 2x 5
当x________时,此分式的值为1;
7.当x________时,分式
x 2 x 1
2
的值为负
xb 8.已知:x=-2时,分式 无意义; xa
X=4时,此分式值为0,求
3 7
a 4 当a取什么数时,分式 a2
2
的值为0?
x5 当X =-5 时,分式 4 x
2x 6 呢? x3
的值为0。
的值为0。
x2 x 1
2
当X =2
时,分式
当X =-1 时,分式
x 5
x2 1 的值为0。 x1
当x取何值时, x 2 4x 5
分式的值为零?
1)当a=-1 时, 解: 3 a 3( - -1) =4 -12 a2 3 a 3 3 2)当a=3时, =0 3 2 a2
17 3) 8
练习三:对于分式
2 x 3 x 2
分母为0,则 分式无意义 分母不为0, 则分式有意义
⑴当x取什么值时,分式有意义? 解:由分母x-2≠0,得x≠2 ∴ 当x≠2时,分式有意义。 ⑵当x取什么值时,分式无意义?
讨论:字母a、b可以表示任何实数吗?
苏科版八年级下册数学课件:1分式的意义

例题分析:
例2、当x=-3、y=2时,分别计算下列分式 的值:
(1)3x 2 y ;(2)y 3。
x
x7
思考题2: 在下表空格中填写适当的数。
y
-1
0
1
y2 y
2y 1 y2 1 2y y 1
学生发现问题, 通过小组讨论 交流后得出: 如果分式中分 母的值等于零, 这个分式无意 义。
同学们在填表的过程中发现了什么问题?你 认为这个问题该怎么处理?
两个整式A、B相除,即A÷B时, 可以表示为 。A如果B中含有 字母且B≠0,那么B 叫做A分式, A叫做分式的分子,B叫做B分式 的分母。
教学过程: 三、指点运用,巩固概念
巩固练习:
1、判断下列各式中哪些是分式?哪些是整式?
4 、3x2 、x y 、 xy 、 x , 1 x 2x 3 x y c 2b 3c
(6)当x、y满足什么关系时,分式的值为0?
思考题3:
一个分子为x-5的分式,且知它在x≠1时 有意义。你能写出一个符合上面条件的 分式吗?试试看。
教学过程: 六、分层作业,发展深化
布置作业:
练习题:
(1)当x为何值时,分式(
x
x4 4)(x
有意义?
3)
(2)当x为何值时,分式(x 4)(x 3)的值为0?
y3
变式训练:
| y | 3
(1)当y是什么值时,分式 y 3 的值是0?
(2)当y是什么值时,分式 y 3 的值是正数?
y3
探究得出:分式的值为0需满足的条件是 分子的值为0且分母的值不为0。
应用拓展:
如图是一个半径为r的半圆和一个长 方形组成的一扇窗,根据设计要求整 扇窗的面积应为4平方米。 用r的代数式表示h.
苏教版八年级数学下册8.1《分式》课件

VS
详细描述
分式的值不变性是指当分子和分母同时乘 以或除以同一个非零数时,分式的值不变 。例如,(2/3) * (3/2) = 1。分式的约简 是指将分式化简为其最简形式的过程。例 如,将4/8约简为1/2。分式的运算包括 加法、减法、乘法和除法等基本运算。例 如,(2/3) + (1/2) = (4/6) + (3/6) = 7/6 。
02 分式的运算
分式的加减法
总结词
分式加减法的关键是通分,即找到分母的最小公倍数,使分式化为同分母,然后进行加减运算。
详细描述
在进行分式的加减法时,首先需要确定各分式的分母,然后找到这些分母的最小公倍数。接着,将每个分式的分 子和分母都乘以适当的倍数,使所有分式具有相同的分母。最后,根据同分母分式的加减法则,对分子进行相应 的加减运算。
分式的表示方法
总结词
分式可以用分数、小数或百分数等多种形式来表示。
详细描述
分式可以用分数形式来表示,如2/3。也可以用小数形式来表示,如0.666...。 此外,分式还可以用百分数形式来表示,如66.67%。这些不同的表示方法只是 表现形式上的差异,其本质都是分式。
分式的性质
总结词
分式具有一些基本的性质,包括分式的 值不变性、分式的约简和分式的运算等 。
化学问题
在化学反应速率、化学平 衡等问题的求解中,分式 方程也扮演着重要的角色。
工程问题
在机械、建筑、航空等领 域,分式方程常常用于解 决各种工程问题。
04 分式在实际生活中的应用
物理中的应用
速度计算
在物理学中,速度是距离与时间 的比值,可以用分式表示。例如 ,如果一辆车的速度是60公里/小 时,它可以在1小时内行驶60公 里。TANKS FOR WATCHING
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长 卧室 客 厅
3.书房面积是7平方米,宽是a米, 那么长是___7__米。
a
长 书房
4.书房面积是a平方米,宽是b米, 则长是___a__米。
b
宽
5、如果总房款是 55万元,室内总面积是 n平方
米,那么每平方米是______5__5___万元。
n
6、如果总房款是 a 万元,装修费用是5万元;
室内面积是 m平方米,露台面积是 3平方米,
那么总花费平均每平方米是___a___5_______
万元。
m3
观察
11,s , 7 , a , 55 , a 5 3 3 a b n m3
交流 (1)上面的这些代数式有什么相同点?
有什么不同点?
10.1 分 式
分式的定义:
A一、般B地,如果 表示两个整式,并且 B
A 中含有字母,那么代数式 叫做分式,(其 B
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
小结
1.形如 B A并且B中含有字母的式子叫做 分式。
2.分式
A B
中B≠0时,分式有意义;分式
A B
中B=0时,分式无中意,义;分式
A B
当A=0且B≠0时,分式的值为零。
苏科版八年级数学下册 课件-10.1 分式
x 当 =1 时,分式的值为0
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
5、 已知,当x=5时,分式 等于零,则k =-10。
的值
2x k
3x 2
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
谢谢
苏科版八年级数学下册 课件-10.1 分式
小结
分式
A B
中,当 A =0且B ≠0时,
分式的值为零。
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
谈一谈
宽
露台
b
a长 卧室 客厅
a
长 书房
例4、运用我们所学的知识,
如果 a的售价,那么每块砖
在降价 1 元后,用 元可购
苏科版八年级数学下册 课件-10.1 分式
10.1 分式
苏科版八年级数学下册 课件-10.1 分式
数你 学能 问帮 题小 吗明 ?回
答 其 中 的 一 些
用代数式表示
1.卧室面积是11平方米,宽是3米,
11
则长是 __3__ 米。
宽
2.卧室面积s 是s平方米,宽是3米,
露台 则长是 __3__ 米
(2) x (3) x
x2
4 3x
(4) x (5)3 x
x2 1
x2 2
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
a例3 当 取什么数时,分式 2a的a值14为0?
讨论分式的值为0的问题,必须在分式有意 义的前提下! 分式的值=0的需同时满足两个条件: (1)分子为0; (2)分母不为0。
B
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
例2:当x取什么值时,分式 x 2 2x 3
(1)无意义;(2)有意义?
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
练一练
当x取什么数时,下列分式有意义:
(1)2 x x
A
分式 B 中,当A =0且B ≠0时,分式的值为
零。
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
当x取何值时,下列分式的值为0?
(1)x 5 4x
(2)x 1 3+4x
(3)x 5 x5
(4)x2 1 x 1
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
A中 是分式的分子, 是分B式的分母)
练一练
1.下列各式中,哪些是分式?
1 x
,
x 2p
,
a a
+
3 2
,
a
3
b
,
是 不是 是
不是
2.你能写出一些分式吗?
苏科版八年级数学下册 课件-10.1 分式
例1:求分式 a 3的值.
1 a 3; a 1
2a 2.
5
3 选一个你喜欢的数,并求出
分式的值。
a
得的瓷砖数为_____a____块。
b1
我们每天都会接触许多不同的事和物,
a
想一想,你还能对分式
所表示
b 1
的实际意义作出解释吗?
苏科版八年级数学下册 课件-10.1 分式
宽
苏科版八年级数学下册 课件-10.1 分式
现实生活中的一些数量关系可 以用某个分式来表示,但同一 个分式可以表示不同的实际意 义,更可能代表的是一种类型
x2
有意义。
2
2x 1
⑵
当x =2 时,分式
x 2 的值为零。 2x 1
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
x 3、在分式 2x 1 中,当
6x 5
5 6
x 当 12时,分式的值为0
时,分式无意义;
x 4、在分式 1 x2 中,当 =-3时,分式的值 =4 x 1
苏科版八年级数学下册 课件-10.1 分式
苏科版八年级数学下册 课件-10.1 分式
分式的定义: A一、般B地,如果 表示两个整式,并且 B
A 中含有字母,那么代数式 叫做分式,(其 B
A中 是分式的分子, 是分B式的分母)
分式
A B
中 B≠0时,分式有意义;
分式 A 中 B =0时,分式无意义;
苏科版八年级数学下册 课件-10.1 分式
1、⑴ 在下面四个代数式中,分式为( )B
A、 2 x 5 B、 1
C、 x 8 D、- 1 + x
考 考
你 7
3x
8
45
⑵ 当 x=-1时,下列分式没有意义的是(
A、x 1 B、 x C、 2 x
D、 x 1
C)
x
x1
x1
x
2、⑴ 当x ≠ 1时,分式
