【导学案+习题】第1课时相似三角形的性质定理(一)九年级数学上册北师大版(20200921023748)
【最新】北师大版九年级数学上册《相似三角形的性质(2)》导学案

新北师大版九年级数学上册《相似三角形的性质(2)》导学案我的疑问【合作探究】(小组交流,全班点评展示)[来源:Z。
xx。
]【学习目标】1.掌握三角形相似,则周长的比与相似比,面积的比与相似比的平方之间存在的等量关系;2.能熟练运用此性质进行计算,并能解决一些实际问题。
【学习重难点】重点:探索相似三角形的性质。
难点:利用相似三角形的性质定理解决实际问题。
【使用说明与学法指导】用8分钟左右的时间阅读课本p106-p108,认真完成导学案的问题,并把自己的疑问写出来,最后小组交流并解决。
【自主学习】一、旧知链接:1.已知△ABC∽△ADE,12ADDB=,则△ABC的BC边上的高线与△ADE的DE边上高线的比为________;对应中线的比为________;对应顶角平分线的比为_________;相似比为____________。
2.如果5,(0)7a c eb d fb d f===++≠,那么a c eb d f++++=_________________[来源:]二、自主探究(仔细阅读课本p106-p107,并完成以下问题)如图,若△ABC∽△A1B1C1,且相似比为3:4,1.求△ABC的周长与△A1B1C1的周长之比?2.求△ABC与△A1B1C1的面积如何表示?它们的比是多少?3.观察1的结果,你能从中发现什么?[来源:学*科*网Z*X*X*K]观察2的结果,你能从中发现什么?4.你的结论是什么?[来源:][来源学科网Z,X,X,K]1.如图,在△ABC中,D,E分别是边AB,AC上的点,::2:3AD AB AE AC==,求:ADE BCEDS S∆四边形。
2.如图所示,在△ABC中,DE∥BC,且:1:2,3,ADE BECDS S BC∆==四边形则DE的长为多少?【课堂小结】通过本节课学习,你有哪些收获【课后记】家长签字:CBEDACA BC1A1B1D D1AB CD E。
北师大版九年级数学上册导学案三角形相似的条件(2)
年级
九
班级
学科
数学
课题
探索三角形相似的条件(2)
第课时
编制人
审核人
使用时间
第周
星期
使用者
课堂流程
具体内容
学习
目标
1、理解并掌握三角形相似的判定定理:“两边对应成比例且夹角相等的两个三角形相似”。
2、在进行探索的活动过程中,发展类比的数学思想,激发学生的探索发现归纳意识,增强合情推理的语言表达能力。
此题是“共角型”相似三角形的典型例题,旨在让学生观察认识图形,并充分体会从直观发现到自觉说理的过渡过程,渗透了简单逻辑推理的思想,为第五节的学习做好铺垫,从而达到承前启后的目的。
课
堂
检
测
1.如图,(1)若 ________,则△ABC∽△AEF;(2)若∠E=________,则△ABC∽△AEF。
2、如图,正方形ABCD中,E为AB中点ቤተ መጻሕፍቲ ባይዱBF= BC。
求证:△ADE∽△BEF
学生先独立完成,然后师生共同评价,第二题让学生上黑板展示。
教后
反思
学法指导
温故
知新
1、相似三角形的定义。
2、已学三角形相似的条件是什么?
学生回答,3分钟
操
作
探究一:三角形相似的条件
以小组为单位合作探究、交流展示:
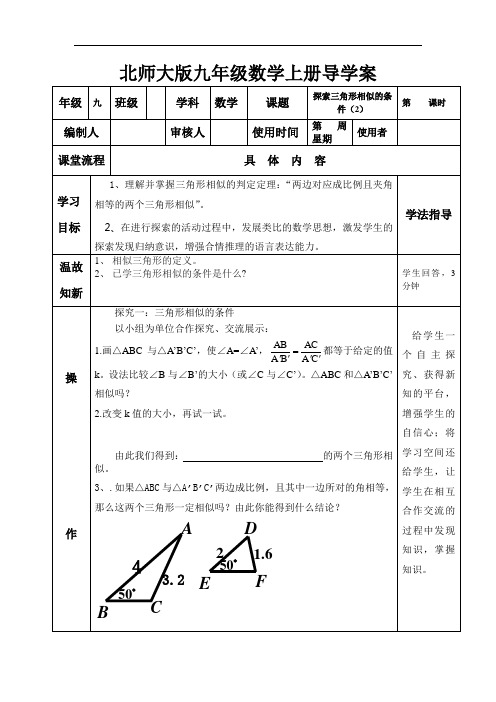
1.画△ABC与△A’B’C’,使∠A=∠A’, 都等于给定的值k。设法比较∠B与∠B’的大小(或∠C与∠C’)。△ABC和△A’B’C’相似吗?
2.改变k值的大小,再试一试。
由此我们得到:的两个三角形相似。
3、.如果△ABC与△A’B’C’两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?
北师大版九年级数学上册相似三角形的性质导学案

相似三角形的性质【学习目标】1、理解相似三角形的性质;2、利用相似三角形的性质解决一些实际问题.【重点】理解并初步掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方【难点】掌握相似三角形的周长比、面积比在实际中的应用.【教学过程】一、知识回顾:(1)相似三角形有哪些判定方法?(2)什么叫相似比?(3)相似三角形有什么性质?二、知识点突破活动1:相似三角形的周长比等于相似比,面积比等于相似比的平方【典型例题一】例题1:如图,△ABC∽△A'B'C' ,相似比为2.(1)请你写出图中所有成比例的线段;(2)△ABC与△A'B'C' 的周长比是多少?面积比呢?拓展:若△ABC∽△A'B'C',相似比为k,那么你能求△ABC与△A'B'C' 的周长之比吗?从这两个题中,你能发现什么规律?结论:相似三角形的周长比等于,面积比等于。
【变式练习一】例1判断正误:(1)如果把一个三角形三边的长同时扩大为原来的10倍,那么它的周长也扩大为原来的10倍;()(2)如果把一个三角形的面积扩大为原来的9倍,那么它的三边的长都扩大为原来的9倍。
2、填空1.若△ABC∽△A′B′C′,相似比为1∶2,则△ABC与△A′B′C′的面积的比为______.2.已知△ABC与△DEF相似且对应中线之比为3∶4,则△ABC与△DEF的相似比为______.3.已知两个相似三角形的相似比是,那么它们的对应高的比是___.活动2:相似多边形的周长比等于相似比,面积比等于相似比的平方例1、如图,四边形ABCD∽四边形A′B′C′D′,相似比为k。
(1)四边形ABCD与四边形A′B′C′D′的周长比是多少?(2)连接相应的对角线BD,B′D′,所得的△BCD与△B′C′D′相似吗?如果相似,它们周长的相似比各是多少?为什么?(3)△ABD,△A′B′D′,△BCD,△B′C′D′的面积分别是 S△ABD,S△A′B′D′,S△BCD,S△B′C′D′,那么S△ABD/S△A′B′D′,S△BCD/S△B′C′D′各是多少?(4)四边形ABCD与四边形A′B′C′D′的面积比是多少?拓展:如果把四边形换成五边形,那么结论又如何呢?两个相似的n边形呢?结论:相似多边形的周长比等于,面积比等于 .【典型例题二】例2:如图,将∆ABC沿BC方向平移得到∆DEF,∆ABC与∆DEF重叠部分(图中阴影部分)的面积是∆ABC的面积的一半。
北师大版九年级数学上册《图形的相似》导学案:相似三角形判定定理的证明

北师大版九年级数学上册《图形的相似》导学案相似三角形判定定理的证明【学习目标】1.了解相似三角形判定定理会证明相似三角形判定定理;2.掌握推理证明的方法,发展演绎推理能力.【知识梳理】1.两角 的两个三角形相似. 2.两边 且 的两个三角形相似.3.三边 的两个三角形相似.【典型例题】知识点一:两角分别相等的两个三角形相似.1.已知:如图,∠ABD=∠C ,AD=2, AC=8,求AB.知识点二:两边成比例且夹角相等的两个三角形相似.2.如图,△ABC,AB=12,AC=15,D 为AB 上一点,且AD=23AB,在AC 上取一点E,使以A. D. E 为顶点的三角形与ABC 相似,则AE 等于( )A. 6.4B. 10C. 6.4或10D. 以上答案都不对知识点三:定理 三边成比例的两个三角形相似.3.下列四个三角形,与左图中的三角形相似的是( )【巩固训练】1. 如图,在△ABC 中,D 、E 分别为AB 、AC 边上的点,DE ∥BC ,BE 与CD 相交于点F ,则下列结论一定正确的是( )A. =B.C.D.2如图,矩形ABCD 中,AD =4,AB =10,P 为CD 边上的动点,当DP = 时,△ADP 与△BCP 相似2题1题图3.如图,在等边三角形 ABC 中, D , E , F 分别是三边上的点, AE = BF = CD ,那么△ABC 与△DEF 相似吗? 请证明你的结论.4.已知:如图,ΔABC 中,AD=DB,∠1=∠2.求证:ΔABC ∽ΔEAD.【拓展延伸】5.如图,在△ABC 中,AB=AC ,点D 、E 、F 分别在AB 、BC 、AC 边上,DE=DF ,∠EDF=∠A .(1)找出图中一对相似的三角形,并证明(2)求证:BC AB CE BD .6.如图,AB ∥CD ,AC 与BD 交于点E ,且∠ACB =90°,AB =6,BC =6,CE =3. (1)求CD 的长;(2)求证:△CDE ∽△BDC .4题图 A D B E C F。
4.7第1课时相似三角形的性质定理1-北师大版九年级数学上册习题课件(共17张PPT)

思维训练
• 11.某中学为新生设计的板凳的正面视图如图所示,其中BA=CD,BC =20 cm,BC、EF平行于地面AD且到地面AD的距离分别为40 cm、8 cm. 为使板凳两腿底端A、D之间的距离为50 cm,那么横梁EF应为多长? (材质及其厚度等忽略不计)
解:如图,过点 B 作 BH⊥AD 于点 H,交 EF 于点 M,过点 C 作 CG⊥AD 于 点 G,交 EF 于点 N.由题意,得 MH=8 cm,BH=40 cm,则 BM=32 cm.∵四边形 ABCD 是等腰梯形,AD=50 cm,BC=20 cm,∴AH=12(AD-BC)=15 cm.由 EF∥ AD,易证△BEM∽△BAH,∴EAMH=BBMH,即E1M5 =3420,解得 EM=12,故 EF=EM +MN+NF=2EM+BC=44 cm.即横梁 EF 应为 44 cm.
(1)求矩形纸片较长边EH的长; (2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪 的:先沿着剩余料△AEH中与边EH平行的中位线剪一刀,再 沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计 算,判断小聪的剪法是否正确.
解:(1)设 EF=2x cm,则 EH=5x cm.∵矩形对边 EH∥BC,∴易证△AEH∽△ ABC,∴EBHC=AADR,即152x0=80-802x,解得 x=15.∴EH=15×5=75(cm).即矩形纸 片较长边 EH 的长为 75 cm.
第四章 图形的相似
7 相似三角形的性质
第一课时 相似三角形的性质定理1
以练助学 名师点睛 基础过关 能力提升 思维训练
以练助学
名师点睛
• 知识点 相似三角形的性质定理1 • 相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相
北师版九年级上册数学导学案 相似三角形判定定理的证明1

4.5 相似三角形判定定理的证明
二.探究新知
(一)自主学习
定理1 两角分别相等的两个三角形相似。
已知:如图,在△ABC和△A’B’C’中,∠A=∠A’,∠B=∠B’。
求证: △ABC∽△A’B’C’。
第三步:写出证明过程。
(分析现在能说明两个三角形相似的方法只有相似三角形的定义,我们可以利用这一线索进行探索,已知两角对应相等,根据三角形内角和定理可以推出第三个角也相等,从而可得三角对应相等,下一步,我们只要再证明三边对应成比例即可。
根据平行线分线段成比例的推论,我们可以在△ABC内部或外部构造平行线,从而构造出与△A′B′C′全等的三角形。
)
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,过点D作BC的平行线,交AC于点E,则∠ADE=∠B,∠AED=∠C,
________(平行于三角形一边的直线与其他两边相交,截得的对应线段成比例)。
过点D作AC的平行线,交BC于点F,则
__________(平行于三角形一边的直线与其他两边相交,
定理3三边成比例的两个三角形相似
小结:相似三角形的判定定理的选择:1.已知有一角相等,可选判定定理1和2;2.已知有两边对应成比例,可选判定定理2和3。
三.学以致用
1.已知:如图,∠ABD=∠C,AD=2, AC=8,求AB.
2.已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=
12
7 ,
求AD的长.。
北师大版九年级数学上册相似三角形的性质1导学案

神木县第五中学导学案年级九班级学科数学课题相似三角形的性质第 1 课时总课时编制人审核人使用时间第周星期使用者课堂流程具体内容学习目标1.理解并掌握相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.2.能利用相似三角形的性质解决一些实际问题.学法指导温故知新1.什么叫相似三角形?相似比指的是什么?2.全等三角形是相似三角形吗?全等三角形的相似比是多少?3.相似三角形的判定方法有哪些?4.根据相似三角形的概念可知相似三角形有哪些性质?5.相似三角形还有其他的性质吗?本节我们就来探索相似三角形的其他性质.教学一.新课导入:阅读教材P106页的内容二.本节课的学习目标是:(指定一名学生宣读)三.新旧知识链接:按要求完成“温故知新”栏中的问题四.探究新知:合作探究:(一)1.如图,△ABC和△A′B′C′是两个相似三角形,相似比为k,其中AD、A′D′分别为BC、B′C′边上的高,那么,AD和A′D′之间有什么关系?证明:∵△ABC∽△A′B′C′∴_______=_______=90°∴∠B=_______ ∴△ABD∽△A′B′D′又∵AD⊥BC,A′D′⊥B′C′∴AB∶A′B′=__________=k.归纳结论:____________________________________________。
.合作探究:(二)2.△ABC∽△A′B′C′,AD、A′D′分别是△ABC和△A′B′C′边上的中线,AE、A′E′分别是△ABC和△A′B′C′的角平分线,且AB∶A′B′=k,那么AD与A′D′、AE与A′E′之间有怎样的关系?归纳结论:____________________________________________将阅读教材时“生成的问题”和通过“合作探究”得出的“结论”展示在小黑板上.并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑流程典例讲解:1.自学自研教材P107页的例1.2,如右图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S 在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.(1)△ASR与△ABC相似吗?为什么?(2)求正方形PQRS的边长.解:(1)△ASR∽△ABC理由:∵四边形PQRS是正方形,∴SR∥BC.∴∠ASR=∠B,∠ARS=∠C.∴△ASR∽△ABC(两角分别相等的两个三角形相似);(2)由(1)可知△ASR∽△ABC.∴AEAD=SRBC(相似三角形对应高的比等于相似比).设正方形PQRS的边长为x cm,则AE=(40-x)cm.∴40-x40=x60,解得x =24.∴正方形PQRS的边长为24cm.(完善过程)课堂小结反思查漏补缺1.收获:___________________________________。
北师大版九年级数学上册导学案相似三角形的性质2

北师大版九年级数学上册导学案年级九班级学科数学课题相似三角形的性质第 2 课时总课时编制人审核人使用时间第周星期使用者课堂流程具体内容学习目标1.理解并初步掌握相似三角形的周长比,面积比与相似比的关系.2.会运用相似三角形的性质解决简单的实际问题.学习重难点:相似三角形的周长比及面积比与相似比的关系.相似三角形的面积比等于相似比的平方.学法指导温故知新1.顺次连接三角形三边的中点,所成的三角形与原三角形对应边上的中线的比是( ) A.1∶2 B.2∶1 C.1∶4 D.4∶12.如右图,DE∥BC,则△ADE∽△ABC.若AD=3,BD=2,AF⊥BC,交DE于G,则AG∶AF=3∶5,△AGE∽△AFC,且它们的相似比为_________3.已知△ABC与△DEF相似且对应角平分线之比为2∶3,若△ABC的最长边为6,则△DEF的最长边为________。
教学一.新课导入:阅读教材P109页的内容二.本节课的学习目标是:(指定一名学生宣读)三.新旧知识链接:按要求完成“温故知新”栏中的问题四.探究新知:(一)自主探究:先阅读教材P109页的内容,然后完成下面的填空:1.相似三角形的对应角__________________,对应边__________________;2.相似三角形的____________、______________与对__________都等于相似比。
(二)合作探究:1:如果△ABC∽△A′B′C′,相似比为2,那么△ABC与△A′B′C′的周长比多少?面积比呢?2:如果△ABC∽△A′B′C′,相似比为k,那么△ABC与△A′B′C′的周长比和面积比分别是多少?归纳结论:_____________________________________________________。
目的:使学生建立从特殊到一般的思想.流程(三)两个相似四边形的周长比等于相似比吗?面积比等于相似比的平方吗?两个相似五边形的周长比与面积比怎样呢?两个相似的n边形呢?结论:_______________________________________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.7 相似三角形的性质
第1课时相似三角形的性质定理(一)
出示H标
相似三角形对应高的比,对应角平分线的比和对应中线的比与相似比的关系
侦討甲学
阅读教材P106-107,自学“想一想”、“议一议”与“例1 ”,理解相似三角形对应的三条重要线段的比等于相似比•
自学反馈学生独立完成后集体订正
如图,△ AB3A A B' C'相似比为k, ADL BC于D, A D'丄B' C'于D'.
①你能发现图中还有其他的相似三角形吗?
②相似三角形对应中线的比、对应高的比、对应角平分线的比都等于
综介探究1
活动1小组讨论
血如润3-33-2見、庇的焉,自巴Q在SC边上■点人在月匚血匕点K在屈边上-J^ = 40cni,叫边形尸总皿是正方形.
(1 ) £1ASR与i.4SC相個吗?目fl么?
(2》求正方形陀超的边E 解:f 1 )△一
业WsATflC一理由息
v 四边陥电甩址正方羽.
・・.SRjVBC t
:、Z = Za.厶庄s = Zc
/. △磁“、站<7 (两角分训HI溶的関
个三角醪相假I .
{2 »
由{丄)可知
乩」ST? sAXHL
/■器=啓{和低二肃昭对应禺的比筛「相低比). AD DU
设正狞形吃疮的辿长为工cm,测.P/=(40-x) cm,
• M 二M — JT
…40 一丽
懈得耳=24.
1E丹形FQES的山任力21 cm
相似三角形的对应高的比、对应角平分线的比和对应中线的比都等于相似比
活动2跟踪训练(独立完成后展示学习成果
1.如果两个相似三角形对应中线的比为
7.若厶AB(S^ A B' C' .AD、A D'分别是△ ABG △ A B' C'的高,AD:A D'= 3 : 4, △ A B' C'的一条中线B' E'=
16cm,则△ ABC的中线BE= ________________ cm.
活动3课堂小结本节课主要根据相似三角形的性质和判定推导出了相似三角形的性质:相似三角形的对应高的比、对应角平分线的比和对应中线的比都等于相似比.
占第训练
教学至此,敬请使用《名校课堂》相应课时部分
禅案提示
【预习导学】
自学反馈
①厶ABD^A A B' D△AD(S^ A D' C'
②相似比相似比
【合作探究1】
活动 2 跟踪训练
1.A
2.A
3.C
4.ADE , ABC 3 , 5, 3 : 5
5.3 : 2
6.5
7.12
敎师点按
)
9,则它们的相似比为(
A. 8 : 9
B.9 : 8
C.64 :81
D. 2 2 : 3
2.已知△ AB(S^ DEF且相似比为
A.
3,则厶ABW A DEF的对应高之比为(
2:
.4: 9 D . 9: 4
3.如图, 电灯P在横杆AB的正上方,AB在灯光下的影子为CD, AB // CD ,AB 2m,CD 5m,点P 到CD 的
距离是3m则点P到AB的距离是(
A. 5 m
6
B. 6m
7
C . 6m
5
4.如图,DE// BC,则厶
△ AG SA AFC且它们的相似比为
.若AD- 3, BD= 2, AF丄BC,交DE于点G,贝U AG: AF=
5.若ABC s ABC,且AB 2cm, A B
6.已知ABC s ABC,对应角平分线的比为
1
1—cm,则对应角平分线的比为________ .
3
2: . 2,且BC 边上的中线是5.2,贝U B C边上的中线是。
