01热力学第一定律及其在等值过程中的应用
合集下载
01章-热力学第一定律及其应用1
T2 T1
Hale Waihona Puke CVdT= CV (T2 T1)
(设CV 与T 无关)
因为计算过程中未引入其它限制条件,所以该公式适 用于定组成封闭体系的一般绝热过程,不一定是可逆过 程。
上一内容 下一内容 回主目录第18页,共29页。
返回
2022/2//1188
节流过程的U和H
节流过程是在绝热筒中进行的,Q=0 ,所以:
绝热过程的功
在绝热过程中,体系与环境间无热的交换,但可以 有功的交换。根据热力学第一定律:
dU Q W
= W
(因为Q 0)
这时,若体系对外作功,热力学能下降,体系温度必然 降低,反之,则体系温度升高。因此绝热压缩,使体系温度 升高,而绝热膨胀,可获得低温。
上一内容 下一内容 回主目录第15页,共29页。
可逆过程的特点:
(1)状态变化时推动力与阻力相差无限小,体系与环 境始终无限接近于平衡态;
(2)过程中的任何一个中间态都可以从正、逆两个
方向到达;
(3)体系变化一个循环后,体系和环境均恢复原态,变 化过程中无任何耗散效应;
(4)等温可逆过程中,体系对环境作最大功,环境对体系作最 小功。
上一内容 下一内容 回主目录第9页,共29页。
返回
2022/22//1188
燃烧焓
指定产物通常规定为:
C CO2 (g) S SO2 (g) Cl HCl(aq)
H H2O(l)
N N2 (g)
金属 游离态
显然,规定的指定产物不同,焓变值也不同,查表时应注
意。298.15 K时的燃烧焓值有表可查。
上一内容 下一内容 回主目录第25页,共29页。
2022/22//1188
§7.2 热力学第一定律及其应用(打印稿)

§7. 2 热力学第一定律及其应用
2. 定压过程: 定压过程:p=Const.
W = ∫ pdV = p(V2 −V1 )
V1
V2
p
=ν R(T2 −T1 )=ν R∆T ∆
1
2
∆ E =ν ⋅CV ,m∆T
Qp = ∆ E + W =ν (CV ,m + R)∆T o
V1
W
V
V2
=ν ⋅ Cp,m∆T
二、摩尔热容量的计算
1. 定体摩尔热容量 CV,m
1 (dQ) 而 dQ = dE + dW = dE+ pdV = 0 CV ,m = ν dT V
定体过程:V=Const. 或 dV=0 : dV=
∴
dQ= dE
CV ,m = 1 (dE)V ν dT dE =ν ⋅ i RdT 2
}
6·
CV ,m = 1 ⋅ν ⋅ i R 2 ν
转化为系统对外作的机械功。
即:系统吸收的热量一部分转化为系统内能,一部分 系统吸收的热量一部分转化为系统内能,一部分
10 ·
Chapter 7. 热力学基础
§7. 2 热力学第一定律及其应用
3. 等温过程: 等温过程:T=Const.
p
pV =ν RT0= p1V1 = p2V2
1 2
W = ∫ pdV = ∫
1. 定体过程: 定体过程:V=Const.
p
{
W=0
∆ E =ν ⋅ i R∆T =ν ⋅CV ,m∆T 2 Q = ∆E + W=ν ⋅ CV ,m∆T V
p
2
1
o
1
V
V2
注意
大学物理《热一律在四个等值过程中的应用》课件

M
P2
§2.热一律在等值过程中的应用 / 三、等压过程
四、绝热过程
1.过程特点
dQ 0
系统与外界绝热。
无热量交换。
绝热材料
dQ 0
绝热过程摩尔热容为0。 Ca 0
系统对外作功全部靠内能提供。
V E T P
V E T P
§2.热一律在等值过程中的应用 / 四、绝热过程
2.内能增量
双原子分子气体 i 5 ,
§2.热一律在等值过程中的应用 / 一、等容过程
CV
3R 2
CV
5R 2
多原子分子气体 i 6 , CV 3R
内能增量又可写成
E
m M
CV
T
此公式不仅适用于等容过程,对任何 过程都适用。
CV
iR 2
§2.热一律在等值过程中的应用 / 一、等容过程
二、等压过程
1.过程特点
CPT
7.热力学第一定律应用
Q E W
§2.热一律在等值过程中的应用 / 二、等压过程
QP E PV
m
mi
m
M
CP T
M
RT 2
M
RT
CP
iR 2
R
i 2R 2
等压摩尔热容 CP CV R Mayer公式
单原子分子气体 i 3 , 双原子分子气体 i 5 ,
§2.热一律在等值过程中的应用 / 二、等压过程
M
RdT 2
M
CV dT
(1)
§2.热一律在等值过程中的应用 / 四、绝热过程
mi
m
PdV
M
RdT 2
M
CV dT
(1)
由理想气体状态方程
6热力学第一定律对理想气体在典型准静态过程中的应用

11
由 pV RT 分别消去P 和V,得
TV
γ 1
γ 1
γ
常数
常数
P p1 Q p2 O
V1 pdV V2 V
12
p T
3. 过程曲线
在P - V 图上,每 一个绝热过程对应一 条曲线,称为绝热线。
4. 热量 Q = 0 5. 内能变化 E CV T 6. 绝热功 由热力学第一定律 Q A E ( 1)
pdV Vdp RdT (2)
由 (1),(2) 两式,得
CV pdV CVVdp RpdV
(CV R) pdV CVVdp
10
由
R Cp CV ; Cp / CV
dV dp V p
得到
两边积分,得
ln V ln p C
γ
即 pV 常数 泊松公式
V2
pV RT
A R(T2 T1 )
5. 热量 等压摩尔热容 C p
V1
p p
A
O V1 V2 V
dQp
dT 若为mol 理想气体,温度由T1 T2
5
Q p Cp (T2 T1 )
6. 内能变化
E CV (T2 T1 )
由热力学第一定律 Q A E
§6 热力学第一定律对理想 气体各等值过程中的应用 一、等体过程 在等体过程中,理想气体的体积保持不变。
1. 特征 V = C,dV = 0
2.过程方程
p T
C (查理定律)
1
3. 过程曲线 平行于p 轴的等体线。 4. 功
p2 p1 O
p
A dA pdV 0
由 pV RT 分别消去P 和V,得
TV
γ 1
γ 1
γ
常数
常数
P p1 Q p2 O
V1 pdV V2 V
12
p T
3. 过程曲线
在P - V 图上,每 一个绝热过程对应一 条曲线,称为绝热线。
4. 热量 Q = 0 5. 内能变化 E CV T 6. 绝热功 由热力学第一定律 Q A E ( 1)
pdV Vdp RdT (2)
由 (1),(2) 两式,得
CV pdV CVVdp RpdV
(CV R) pdV CVVdp
10
由
R Cp CV ; Cp / CV
dV dp V p
得到
两边积分,得
ln V ln p C
γ
即 pV 常数 泊松公式
V2
pV RT
A R(T2 T1 )
5. 热量 等压摩尔热容 C p
V1
p p
A
O V1 V2 V
dQp
dT 若为mol 理想气体,温度由T1 T2
5
Q p Cp (T2 T1 )
6. 内能变化
E CV (T2 T1 )
由热力学第一定律 Q A E
§6 热力学第一定律对理想 气体各等值过程中的应用 一、等体过程 在等体过程中,理想气体的体积保持不变。
1. 特征 V = C,dV = 0
2.过程方程
p T
C (查理定律)
1
3. 过程曲线 平行于p 轴的等体线。 4. 功
p2 p1 O
p
A dA pdV 0
01章_热力学第一定律及其应用魏杰12.9.17 172页PPT

(2)内能是容量性质。 (3)内能具有能量的量纲,用J表示 (4)内能的微分是一个全微分
上一内容 下一内容 回主目录
返回
2019/8/30
4、第一定律的文字表述
热力学第一定律(The First Law of Thermodynamics) 是能量守恒与转化定律在热现象领域内所具有
的特殊形式,说明内能、热和功之间可以相互转化, 但总的能量不变。
历史上曾一度热衷于制造这种机器,均以失 败告终,也就证明了能量守恒定律的正确性。
上一内容 下一内容 回主目录
返回
2019/8/30
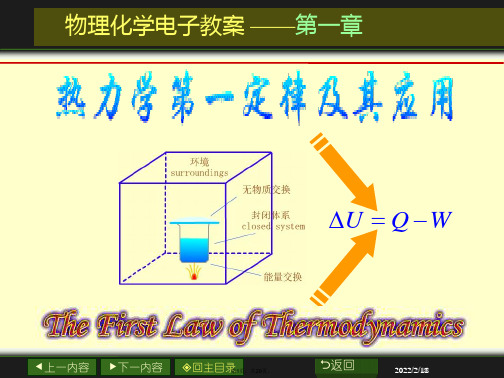
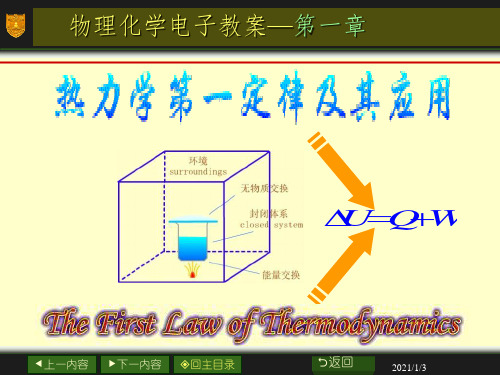
5、第一定律的数学表达式
设想系统由状态(1)变到状态(2),系
统与环境的热交换为Q,功交换为W,则系统
的热力学能的变化为:
U U 2 U 1 Q W
T1 T2 T环 p1 p2 p环 dV 0
(4)绝热过程
Q 0
(5)环状过程
dU 0
上一内容 下一内容 回主目录
返回
2019/8/30
过程和途径
途径:
实现过程的具体路线叫途径。 或者说系 统状态发生变化时,由一始态到另一 终态, 可以经由不同方式,这种由同一始态到同 一终态的不同方式可称为不同的途径 。
上一内容 下一内容 回主目录
返回
2019/8/30
3、热力学能(内能)
定义:它是指体系内部能量的总和。
包括分子运动的平动能、分子内的转动 能、振动能、电子能、核能以及各种粒子之 间的相互作用位能等。
上一内容 下一内容 回主目录
返回
2019/8/30
3、热力学能(内能)
特点: (1)内能是一个状态函数。
自然界的一切物质都具有能量,能量有各 种不同形式,能够从一种形式转化为另一种形 式,但在转化过程中,能量的总值不变。
上一内容 下一内容 回主目录
返回
2019/8/30
4、第一定律的文字表述
热力学第一定律(The First Law of Thermodynamics) 是能量守恒与转化定律在热现象领域内所具有
的特殊形式,说明内能、热和功之间可以相互转化, 但总的能量不变。
历史上曾一度热衷于制造这种机器,均以失 败告终,也就证明了能量守恒定律的正确性。
上一内容 下一内容 回主目录
返回
2019/8/30
5、第一定律的数学表达式
设想系统由状态(1)变到状态(2),系
统与环境的热交换为Q,功交换为W,则系统
的热力学能的变化为:
U U 2 U 1 Q W
T1 T2 T环 p1 p2 p环 dV 0
(4)绝热过程
Q 0
(5)环状过程
dU 0
上一内容 下一内容 回主目录
返回
2019/8/30
过程和途径
途径:
实现过程的具体路线叫途径。 或者说系 统状态发生变化时,由一始态到另一 终态, 可以经由不同方式,这种由同一始态到同 一终态的不同方式可称为不同的途径 。
上一内容 下一内容 回主目录
返回
2019/8/30
3、热力学能(内能)
定义:它是指体系内部能量的总和。
包括分子运动的平动能、分子内的转动 能、振动能、电子能、核能以及各种粒子之 间的相互作用位能等。
上一内容 下一内容 回主目录
返回
2019/8/30
3、热力学能(内能)
特点: (1)内能是一个状态函数。
自然界的一切物质都具有能量,能量有各 种不同形式,能够从一种形式转化为另一种形 式,但在转化过程中,能量的总值不变。
物理化学 01章_热力学第一定律及其应用
功可分为膨胀功和非膨胀功两大类。W的取号:
环境对体系作功,W>0;体系对环境作功,W<0 。
Q和W都不是状态函数,其数值与变化途径有关。
上一内容 下一内容 回主目录
返回
2021/1/3
1.2 热力学第一定律
•热功当量 •能量守恒定律 •热力学能 •第一定律的文字表述 •第一定律的数学表达式
上一内容 下一内容 回主目录
返回
2021/1/3
热功当量
焦耳(Joule)和迈耶(Mayer)自1840年起,历经 20多年,用各种实验求证热和功的转换关系, 得到的结果是一致的。
即: 1 cal = 4.1840 J
这就是著名的热功当量,为能量守恒原理 提供了科学的实验证明。
上一内容 下一内容 回主目录
返回
2021/1/3
热力学的方法和局限性
热力学方法 •研究对象是大数量分子的集合体,研究 宏观性质,所得结论具有统计意义。
•只考虑变化前后的净结果,不考虑物质 的微观结构和反应机理。
•能判断变化能否发生以及进行到什么程 度,但不考虑变化所需要的时间。
局限性 不知道反应的机理、速率和微观性
状态函数的特性可描述为:异途同归,值变 相等;周而复始,数值还原。
状态函数在数学上具有全微分的性质。
上一内容 下一内容 回主目录
返回
2021/1/3
状态方程
体系状态函数之间的定量关系式称为状态方 程(state equation )。
对于一定量的单组分均匀体系,状态函数 T,p,V 之间有一定量的联系。经验证明,只有两个 是独立的,它们的函数关系可表示为:
•体系与环境 •体系的分类 •体系的性质 •热力学平衡态 •状态函数 •状态方程 •热和功
