IB Math HL Syllabus
ib数学介绍

ib数学介绍
IB数学是国际文凭项目(International Baccalaureate,简称IB)中的一个科目,是一门高级数学课程。
IB数学主要有两个级别:标准水平(Standard Level,简称SL)和高级水平
(Higher Level,简称HL)。
IB数学的教学内容涵盖了数学
的各个领域,包括代数、几何、概率统计、微积分等。
IB数学的教学目标是培养学生的数学思维能力和解决问题的
能力。
在IB数学课程中,学生会学习数学的基本理论、技巧
和方法,并通过解决实际问题来应用这些数学知识。
同时,IB 数学还注重培养学生的数学推理和证明能力,鼓励学生通过逻辑推理和严密的论证来解决复杂的数学问题。
IB数学的教学方法也有所不同。
IB数学强调学生的主动学习
和合作学习,通过讨论、探究和研究来深化对数学概念的理解和应用。
此外,IB数学还鼓励学生进行数学建模和实际应用,以培养学生将数学知识应用到实际生活中的能力。
IB数学课程的评估主要有两个方面:内部评估和外部评估。
内部评估包括作业、考试和课堂表现等,由学校内部的教师进行评估。
而外部评估则由国际文凭组织进行,主要包括统一考试和数学研究报告。
IB数学作为一门高级的数学课程,注重培养学生的数学思维
和解决问题的能力,为学生提供了扎实的数学基础,为他们进入大学或者从事与数学相关的职业打下坚实的基础。
IB数学课程简介

谢谢!
张齐 mickalpha@
IBDP课程设置
Over the course of the two-year programme, students: • study six subjects chosen from the six subject groups • complete an extended essay (EE) • follow a theory of knowledge course (TOK) • participate in creativity, action, service (CAS).
IBDP课程介绍
• 我们所谓的IB课程其实是IBDP (International Baccalaureate Diploma Programme) 的简称,是 IBO (International Baccalaureate Organization) 于1968年创办的。 • 目前全球共有138个国家和地区,2771所学校, 超过763000位学生在接受IB课程学习。 • IBDP文凭也被包括英国、美国、加拿大、澳大利 亚等在内的全球很多大学所认可,成为通往世界 名校的通行证。
• • • • Statistics & probability Sets, relations & groups Series & differential equations Discrete mathematics
IBDP数学考题鉴赏
• Sample questions
双语数学教师,你准备好了吗?IB课程目标• The International Baccalaureate aims to develop inquiring, knowledgeable and caring young people who help to create a better and more peaceful world through intercultural understanding and respect. • To this end the organization works with schools, governments and international organizations to develop challenging programmes of international education and rigorous assessment. • These programmes encourage students across the world to become active, compassionate and lifelong learners who understand that other people, with their differences, can also be right.
解析IB数学的四层教学内容

解析IB数学的四层教学内容!IB数学在安排上,采用了分层教学,分为了SSL(studies),SL(standardlevel),HL(high level)和Further HL这四层,难度依次递增,学生可以根据自身能力和学校开设情况来选择自己合适的那一层进行学习。
我们将会给大家介绍IB学校必开设的两个层SL 和HL的大纲,以供参考。
其中SL课程只有必修课,总计140课时,其中论文占10课时;而HL课程具有必修课和选修课必修课,总计240课时,其中必修课182课时,选修课48课时,论文10课时。
SL教学内容和教学目标Topic 1 代数(algebra) 总课时:9课时1.1 等差数列,有限项等比数列,无限项等比数列,求和符号sigma,汇率和人口等应用问题1.2 指数和对数运算1.3 二项式定理,帕斯卡三角形,组合计算Topic 2 函数(function) 总课时:24课时2.1 定义域值域,复合函数,反函数2.2 图像平移,图像拉伸,复合图像(平移与拉伸结合)2.3 二次函数:顶点式,交点式,2.4 分式函数2.5 指数和对数图像2.6 计算器作图及求图像性质Topic 3 三角函数(trigonometry) 总课时:16课时3.1 弧度制计算,弧长和扇形面积计算3.2 单位圆,特殊角三角比(0至360)3.3 三角比关系,双倍角公式3.4 三角函数性质及实际运用3.5 三角方程3.6 正弦定理,余弦定理Topic 4 向量(vector) 总课时:16课时4.1 二维三维向量的加减和模的计算,单位向量4.2 点乘向量,向量夹角4.3 三维直线表达式,直线夹角4.4 两直线的位置关系(相交,平行,异面)Topic 5 概率统计(statistic and probability) 总课时:40课时5.1 离散和连续数据,box-and-whisker图5.2 平均数,中位数,众数,四分位数,方差,标准差5.3 频数,累计频数5.4 直线相关与回归5.5 概率定义,文氏图,树状图5.6 独立事件,条件概率5.7 概率分布,期望值5.8 二项分布5.9 正态分布Topic 6 微积分(calculus) 总课时:35课时6.1 第一定律6.2 求导运算,高次求导6.3 一阶及二阶求导应用6.4 积分运算6.5 积分运用:图像围成面积,旋转体体积6.6 求导及积分在运动学中的运用HL教学内容和教学目标Topic 1 代数(algebra) 总课时:30课时1.1 等差数列,有限项等比数列,无限项等比数列,求和符号sigma,汇率和人口等应用问题1.2 指数和对数运算,换底公式1.3 二项式定理,帕斯卡三角形,组合计算1.4 数学归纳法1.5 复数及其四则运算1.6 极坐标形式,复数平面1.7 棣莫弗定理及其运用1.8 共轭复数及在多项式中运用Topic 2 函数(function) 总课时:22课时2.1 定义域值域,复合函数,反函数,奇偶函数,一一对应及一对多函数2.2 图像平移,图像拉伸,复合图像(平移与拉伸结合),绝对值函数,倒数函数2.3 二次函数:顶点式,交点式,韦达定理2.4 高次函数:因数和余数定理,图像,韦达定理2.5 分式函数(含高次除以高次函数)2.6 指数和对数图像2.7 计算器作图及求图像性质(含不等式)Topic 3 三角函数(trigonometry) 总课时:22课时3.1 弧度制计算,弧长和扇形面积计算3.2 单位圆,特殊角三角比(0至360)3.3 三角比关系,双倍角公式,复合角公式3.4 反三角函数及图像3.5 三角函数性质及实际运用3.6 三角方程3.7 正弦定理,余弦定理Topic 4 向量(vector) 总课时:24课时4.1 二维三维向量的加减和模的计算,单位向量4.2 点乘向量,向量夹角4.3 差乘向量,三角形面积运用4.4 三维直线表达式,直线夹角4.5 两直线的位置关系(相交,平行,异面)4.6 三维平面表达式4.7 线与面,面与面之间的夹角及焦点4.8 三个平面间的位置关系Topic 5 概率统计(statistic and probability) 总课时:36课时5.1 平均数,中位数,众数,四分位数,方差,标准差5.2 概率定义,文氏图,树状图5.3 计数原理,排列组合5.4 独立事件,条件概率5.5 概率密度及在平均数和方差中的运用5.6 二项分布5.7 泊松分布5.8 正态分布Topic 6 微积分(calculus) 总课时:48课时6.1 第一定律,求导运算,高次求导6.2 变化速率,隐函数求导6.3 一阶及二阶求导应用6.4 积分运算(分部积分)6.5 积分运用:图像围成面积,旋转体体积6.6 求导及积分在运动学中的运用Topic 7 选修(option) 四选一总课时:48课时选修1:概率与统计(statistic andprobability)选修2:集合,关系与群论(set,relation andgroup)选修3:微积分(calculus)选修4:离散数学(discrete math)升学学习的瓶颈问题9年级升10年级(Pre-IB)学习的瓶颈问题语言:同学们要及早适应全英语教学的语境;语言问题的解决同时意味着思维方式的转换。
IB数学高分攻略

IB数学高分攻略IB数学目前按照水平和要求不同分为4个层次,包括数学学习(SL),标准水平(SL),较高水平(HL)和深度数学(SL),学生根据自己的实际情况自行选择课程进行修读,每门考试的满分都是7分。
IB课程被称为“国际课程之王”,难度较大,但是我们在课堂中能够学到的很少,想找到并解决疑难问题并从中得出经验完全依靠我们自身。
以下这些是具体的学习数学课程的指导建议,希望对大家有所帮助。
预习预习时应对要学的内容,认真研读,理解并应用预习提示、查阅工具书或有关资料进行学习,对有关问题加以认真思考,把不懂的问题做好标记,以便课上有重点地去听、去学、去练。
查漏补缺翻开你的数学课本,关注那些你不是特别有把握的课题。
选择完成15到20个开头或中间的题目,以确保自己基础仍在。
然后继续完成所有的课程难题,以确定你可以完成更难的题目。
在这个过程中如果出现无法解决的难题,就应该向老师寻求帮助。
当你克服了那些你不自信的课题并觉得有些把握时,就着手解决所有其他你觉得一般或者非常自信的课题。
逐步升级完成5到7个开头或中间的问题以验证你在这些科目上有非常坚实的基础。
接着再做一遍所有的“难题”,即使你觉得它们很简单。
因为这表明你对这些课题很有把握并能解决所有的难题。
不要自鸣得意,然后跳过那些课题,未来就有可能在这些地方丢掉易得的分数。
留心日常生活中的数学现象这样可以为你们的数学论文积累素材。
把过往不同时期的所有考卷连同它们的参考答案都打印出来,在限时条件内完成过去年份的所有考试试卷。
做完所有试卷后,回顾每一张试卷,复习做过的题目,确保记住它们并且明白自己当时为什么这样做。
劳逸结合学习和可有休息要相辅相成,和朋友们出去玩,健身锻炼,做点交易,找份工作,总之做一切让你觉得开心的事情。
最重要的是,保证充足的睡眠,因为没有比数学考试之前有一个清晰快速的头脑更好的准备工作。
上海新托福精讲班多少钱?一、整体情况培训对象:英语基础薄弱大学生或未接触过托福考试的高中生培训目的:通过对托福基础听说读写的巩固及强化训练,帮助学员提高托福基础和应试技巧,顺利通过考试。
IB数学课程详细内容介绍

IB数学课程详细内容介绍IB数学作为IB课程的必选学科之一,由易到难的划分总共四种不同的难度等级供学生选择,更利于学习与适应。
IB注重综合性发展,因此学好数学也有利于培养学生的全面发展。
接下来编辑来为大家具体介绍一番。
IB课程数学的4个难度等级及适合的群体同学们可以根据自身的实力、兴趣、专业倾向等来选择合适自己的难度等级,以便有针对性地学习,充分发挥自身的潜力。
Mathematical studies SL:本课程会带给学生丰富的生活背景和知识。
更具体地说,它的目的是培养学生学习数学的信心和鼓励学生理解数学。
学生学习本课程需要具备基本的运算、对图形的理解分析能力。
本课程适合在未来的学习中不需要运用大量数学知识,将来就读艺术、人文学科的学生。
Mathematics SL:本课程满足学生具备基本的数学知识和概念,并具备正确应用简单的数学技术所需要的技能。
大多数选择本课程的学生需要良好的数学背景。
本课程适合在未来选择化学、经济学、心理学和商业管理等学科的学生,对于那些希望在大学修读理工科类专业的学生来说,选择HL课程会更有帮助。
Mathematics HL:本课程需要学生具备优秀的数学背景,并且能胜任一系列数据的分析。
大部分选修这门课程的学生将会把数学或数学中的一个主题或其他课程如物理、工程和技术作为他们大学研究的重要组成部分。
Further mathematics HL:本课程是4个选项中最具有挑战性的一个,也是难度最大的一个,它给将来要在大学主修数学的学生提供了很好的辅助。
但是在全国,只有区区几所IB学校提供了本课程。
IB课程数学HL中4个不同的option的内容有何区别IB课程数学HL除了学习共同的核心课程之外,还有一个选修的部分(option)要学习。
IBO一共提供了四个不同的选项,分别为统计学(Statistics & probability)、微积分(calculus)、图论与数论(Number theory and graph theory)和群论(Group and set)。
IBDP地理课程简介
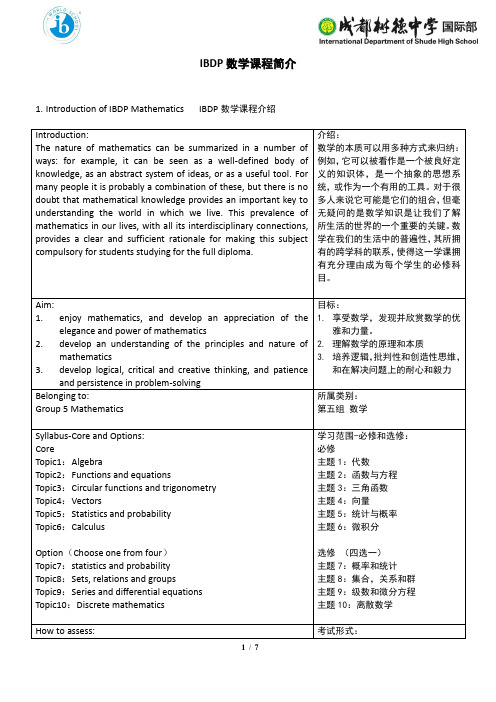
IBDP 数学课程简介1. Introduction of IBDP Mathematics IBDP 数学课程介绍Introduction:The nature of mathematics can be summarized in a number of ways: for example, it can be seen as a well-defined body of knowledge, as an abstract system of ideas, or as a useful tool. For many people it is probably a combination of these, but there is no doubt that mathematical knowledge provides an important key to understanding the world in which we live. This prevalence of mathematics in our lives, with all its interdisciplinary connections, provides a clear and sufficient rationale for making this subject compulsory for students studying for the full diploma.介绍: 数学的本质可以用多种方式来归纳:例如,它可以被看作是一个被良好定义的知识体,是一个抽象的思想系统,或作为一个有用的工具。
对于很多人来说它可能是它们的组合,但毫无疑问的是数学知识是让我们了解所生活的世界的一个重要的关键。
数学在我们的生活中的普遍性,其所拥有的跨学科的联系,使得这一学课拥有充分理由成为每个学生的必修科目。
Aim:1. enjoy mathematics, and develop an appreciation of the elegance and power of mathematics2. develop an understanding of the principles and nature of mathematics3. develop logical, critical and creative thinking, and patience and persistence in problem-solving目标: 1. 享受数学,发现并欣赏数学的优雅和力量。
IB数学和IB课程简介

吴老师
IB数学和IB课程简介
• • • • • • • IB课程总体介绍 IB课程特点 IB课程目标 IB课程设置 IBDP数学课程的特点 IB数学HL教学大纲 一些建议
IB课程介绍
• IB课程是International Baccalaureate Diploma Programme的简称。 • 目前全球共有138个国家和地区,2771所学 校,超过763000位学生在接受IB课程学习。 • IB文凭被包括英国、美国、加拿大、澳大利 亚等在内的全球很多大学所认可,成为通 往世界名校的通行证。
IB数学HL教学大纲(Core)
• • • • • • • Algebra Functions & equations Circular functions & trigonometry Matrices Vectors Statistics & probability Calculus
IBDP数学学科特点
• 涵盖广泛的知识领域(Syllabus) • 有不同难度的子课程可供选择(HL, SL, etc.) • 重视数学软件及图形计算器的应用 (Technology) • 侧重知识的形成过程(TOK) • 培养学生对数学知识的运用(IA) • 激发学生对数学本身的学科热情(EE)
IB课程特点
• 自成体系:不以世界上任何一个国家的课 程体系为基础而,广泛吸收了当代许多发 达国家主流课程体系的优点,涵盖了其主 要的核心内容。 • 富有挑战性 • 有较高承认度 • 具备国际性
IB课程目标
• The International Baccalaureate aims to develop inquiring, knowledgeable and caring young people who help to create a better and more peaceful world through intercultural understanding and respect. • To this end the organization works with schools, governments and international organizations to develop challenging programmes of international education and rigorous assessment. • These programmes encourage students across the world to become active, compassionate and lifelong learners who understand that other people, with their differences, can also be right.
IB选课:IB计算机科学学科学那些内容

作为国际课程中认可度最高,真正全球通用的课程,I B的课程内容含金量极高,同时也意味着难度很大。
对于申请大学是理工方向的学生来说,属于I B D P第四组的计算机科学是一门相对容易的课程。
一、计算机学啥?计算机科学也分为H L(H i g h l e v e l)和S L(S t a n d a r d l e v e l)。
H L在两年内一共学240小时,S L在两年内要学习150个小时的课程。
下面是计算机H L的学习内容。
其中,在H L e x t e n t i o n部分,学生需要在四个方向上选择一个,包括:数据库、建模、W e b S c i e n c e和面向对象编程。
二、计算机考啥?下表是H L的考试内容。
主要以问答题为主,包括一些计算机原理、设计的原理、运用计算机知识解决一些实际问题、算法、编程等。
三、难度多大?下面是计算机科学的两道样题,看着都不太难。
如果把学习内容都掌握了,应当都能做出来。
1.D r a w t h e r e p r e s e n t a t i o n o f t h e b i n a r y s e a r c ht r e e i f t h e f o l l o w i n g d a t a w e r e i n s e r t e d i n t h i s o r d e r:•F A L C O N,C A N A R Y,P I G E O N,T U R K E Y,O S P R E Y.2.D i s c u s s t h e m e t h o d s u s e d b y c r i m i n a l s t o h i d e o rd i s g u i se c e r t a i nf i l e s.F o r e a c h m e t h o d,i d e n t i f y t h ec o u n t e r m e a s u r e s t h a t c a n b e t a k e n b y a c o m p u t e rf o r e n s i c s c i e n t i s t.有的学校的计算机专业还会特意要求I B考生选择计算机科学作为考试项目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Mathematics HL First examinations 2008DIPLOMA PROGRAMMEMATHEMATICS HLFirst examinations 2008International Baccalaureate OrganizationBuenos Aires Cardiff Geneva New York SingaporeDiploma ProgrammeMathematics HLFirst published in September 2006International Baccalaureate OrganizationPeterson House, Malthouse Avenue, Cardiff GateCardiff, Wales GB CF23 8GLUnited KingdomPhone: + 44 29 2054 7777Fax: + 44 29 2054 7778Web site: © International Baccalaureate Organization 2006The International Baccalaureate Organization (IBO) was established in 1968 and is anon-profit, international educational foundation registered in Switzerland.The IBO is grateful for permission to reproduce and/or translate any copyrightmaterial used in this publication. Acknowledgments are included, where appropriate,and, if notified, the IBO will be pleased to rectify any errors or omissions at theearliest opportunity.IBO merchandise and publications in its official and working languages can be purchased through the IB store at . General ordering queriesshould be directed to the sales and marketing department in Cardiff.Phone: +44 29 2054 7746Fax: +44 29 2054 7779E-mail: sales@Printed in the United Kingdom by Antony Rowe Ltd, Chippenham, Wiltshire.5007CONTENTSINTRODUCTION 1 NATURE OF THE SUBJECT 3 AIMS 6 OBJECTIVES 7 SYLLABUS OUTLINE 8 SYLLABUS DETAILS 9 ASSESSMENT OUTLINE 53 ASSESSMENT DETAILS 55INTRODUCTIONThe International Baccalaureate Diploma Programme (DP) is a rigorous pre-university course of studies, leading to examinations, that meets the needs of highly motivated secondary school students between the ages of 16 and 19 years. Designed as a comprehensive two-year curriculum that allows its graduates to fulfill requirements of various national education systems, the DP model is based on the pattern of no single country but incorporates the best elements of many. The DP is available in English, French and Spanish.The programme model is displayed in the shape of a hexagon with six academic areas surrounding the core. Subjects are studied concurrently and students are exposed to the two great traditions of learning: the humanities and the sciences.INTRODUCTIONDP students are required to select one subject from each of the six subject groups. At least three and not more than four are taken at higher level (HL), the others at standard level (SL). HL courses represent 240 teaching hours; SL courses cover 150 hours. By arranging work in this fashion, students are able to explore some subjects in depth and some more broadly over the two-year period; this is a deliberate compromise between the early specialization preferred in some national systems and the breadth found in others.Distribution requirements ensure that the science-orientated student is challenged to learn a foreign language and that the natural linguist becomes familiar with science laboratory procedures. While overall balance is maintained, flexibility in choosing HL concentrations allows the student to pursue areas of personal interest and to meet special requirements for university entrance.Successful DP students meet three requirements in addition to the six subjects. The interdisciplinary theory of knowledge (TOK) course is designed to develop a coherent approach to learning that transcends and unifies the academic areas and encourages appreciation of other cultural perspectives. The extended essay of some 4,000 words offers the opportunity to investigate a topic of special interest and acquaints students with the independent research and writing skills expected at university. Participation in the creativity, action, service (CAS) requirement encourages students to be involved in creative pursuits, physical activities and service projects in the local, national and international contexts.First examinations 2008NATURE OF THE SUBJECTIntroductionThe nature of mathematics can be summarized in a number of ways: for example, it can be seen as a well-defined body of knowledge, as an abstract system of ideas, or as a useful tool. For many people it is probably a combination of these, but there is no doubt that mathematical knowledge provides an important key to understanding the world in which we live. Mathematics can enter our lives in a number of ways: we buy produce in the market, consult a timetable, read a newspaper, time a process or estimate a length. Mathematics, for most of us, also extends into our chosen profession: artists need to learn about perspective; musicians need to appreciate the mathematical relationships within and between different rhythms; economists need to recognize trends in financial dealings; and engineers need to take account of stress patterns in physical materials. Scientists view mathematics as a language that is central to our understanding of events that occur in the natural world. Some people enjoy the challenges offered by the logical methods of mathematics and the adventure in reason that mathematical proof has to offer. Others appreciate mathematics as an aesthetic experience or even as a cornerstone of philosophy. This prevalence of mathematics in our lives provides a clear and sufficient rationale for making the study of this subject compulsory within the DP.Summary of courses availableBecause individual students have different needs, interests and abilities, there are four different courses in mathematics. These courses are designed for different types of students: those who wish to study mathematics in depth, either as a subject in its own right or to pursue their interests in areas related to mathematics; those who wish to gain a degree of understanding and competence better to understand their approach to other subjects; and those who may not as yet be aware how mathematics may be relevant to their studies and in their daily lives. Each course is designed to meet the needs of a particular group of students. Therefore, great care should be taken to select the course that is most appropriate for an individual student.In making this selection, individual students should be advised to take account of the following types of factor.• Their own abilities in mathematics and the type of mathematics in which they can be successful • Their own interest in mathematics, and those particular areas of the subject that may hold the most interest for them• Their other choices of subjects within the framework of the DP• Their academic plans, in particular the subjects they wish to study in future• Their choice of careerTeachers are expected to assist with the selection process and to offer advice to students about how to choose the most appropriate course from the four mathematics courses available.NATURE OF THE SUBJECTMathematical studies SLThis course is available at SL only. It caters for students with varied backgrounds and abilities. More specifically, it is designed to build confidence and encourage an appreciation of mathematics in students who do not anticipate a need for mathematics in their future studies. Students taking this course need to be already equipped with fundamental skills and a rudimentary knowledge of basic processes. Mathematics SLThis course caters for students who already possess knowledge of basic mathematical concepts, and who are equipped with the skills needed to apply simple mathematical techniques correctly. The majority of these students will expect to need a sound mathematical background as they prepare for future studies in subjects such as chemistry, economics, psychology and business administration. Mathematics HLThis course caters for students with a good background in mathematics who are competent in a range of analytical and technical skills. The majority of these students will be expecting to include mathematics as a major component of their university studies, either as a subject in its own right or within courses such as physics, engineering and technology. Others may take this subject because they have a strong interest in mathematics and enjoy meeting its challenges and engaging with its problems. Further mathematics SLThis course is available at SL only. It caters for students with a good background in mathematics who have attained a high degree of competence in a range of analytical and technical skills, and who display considerable interest in the subject. Most of these students will intend to study mathematics at university, either as a subject in its own right or as a major component of a related subject. The course is designed specifically to allow students to learn about a variety of branches of mathematics in depth and also to appreciate practical applications.Mathematics HL—course detailsThis course caters for students with a good background in mathematics who are competent in a range of analytical and technical skills. The majority of these students will be expecting to include mathematics as a major component of their university studies, either as a subject in its own right or within courses such as physics, engineering and technology. Others may take this subject because they have a strong interest in mathematics and enjoy meeting its challenges and engaging with its problems. The nature of the subject is such that it focuses on developing important mathematical concepts in a comprehensible, coherent and rigorous way. This is achieved by means of a carefully balanced approach. Students are encouraged to apply their mathematical knowledge to solving problems set in a variety of meaningful contexts. Development of each topic should feature justification and proof of results. Students embarking on this course should expect to develop insight into mathematical form and structure, and should be intellectually equipped to appreciate the links between concepts in different topic areas. They should also be encouraged to develop the skills needed to continue their mathematical growth in other learning environments.The internally assessed component, the portfolio, offers students a framework for developing independence in their mathematical learning through engaging in mathematical investigation and mathematical modelling. Students will be provided with opportunities to take a considered approach to these activities, and to explore different ways of approaching a problem. The portfolio also allows students to work without the time constraints of a written examination and to develop skills in communicating mathematical ideas.NATURE OF THE SUBJECTThis course is a demanding one, requiring students to study a broad range of mathematical topics through a number of different approaches and to varying degrees of depth. Students wishing to study mathematics in a less rigorous environment should therefore opt for one of the standard level courses, mathematics SL or mathematical studies SL.© International Baccalaureate Organization 20065AIMSThe aims of all courses in group 5 are to enable students to: • appreciate the multicultural and historical perspectives of all group 5 courses • enjoy the courses and develop an appreciation of the elegance, power and usefulness of the subjects • develop logical, critical and creative thinking • develop an understanding of the principles and nature of the subject • employ and refine their powers of abstraction and generalization • develop patience and persistence in problem solving • appreciate the consequences arising from technological developments • transfer skills to alternative situations and to future developments • communicate clearly and confidently in a variety of contexts.InternationalismOne of the aims of this course is to enable students to appreciate the multiplicity of cultural and historical perspectives of mathematics. This includes the international dimension of mathematics. Teachers can exploit opportunities to achieve this aim by discussing relevant issues as they arise and making reference to appropriate background information. For example, it may be appropriate to encourage students to discuss: • differences in notation • the lives of mathematicians set in a historical and/or social context • the cultural context of mathematical discoveries • the ways in which specific mathematical discoveries were made and the techniques used to make them • how the attitudes of different societies towards specific areas of mathematics are demonstrated • the universality of mathematics as a means of communication.6© International Baccalaureate Organization 2006OBJECTIVESHaving followed any one of the mathematics courses in group 5, students are expected to know and use mathematical concepts and principles. In particular, students must be able to: • read, interpret and solve a given problem using appropriate mathematical terms • organize and present information and data in tabular, graphical and/or diagrammatic forms • know and use appropriate notation and terminology • formulate a mathematical argument and communicate it clearly • select and use appropriate mathematical strategies and techniques • demonstrate an understanding of both the significance and the reasonableness of results • recognize patterns and structures in a variety of situations, and make generalizations • recognize and demonstrate an understanding of the practical applications of mathematics • use appropriate technological devices as mathematical tools • demonstrate an understanding of and the appropriate use of mathematical modelling.© International Baccalaureate Organization 20067SYLLABUS OUTLINEMathematics HLThe course consists of the study of seven core topics and one option topic.Total 240 hrsCore syllabus contentRequirements190 hrsAll topics in the core are compulsory. Students must study all the sub-topics in each of the topics in the syllabus as listed in this guide. Students are also required to be familiar with the topics listed as presumed knowledge (PK). Topic 1—Algebra Topic 2—Functions and equations Topic 3—Circular functions and trigonometry Topic 4—Matrices Topic 5—Vectors Topic 6—Statistics and probability Topic 7—Calculus 20 hrs 26 hrs 22 hrs 12 hrs 22 hrs 40 hrs 48 hrsOption syllabus contentRequirements40 hrsStudents must study all the sub-topics in one of the following options as listed in the syllabus details. Topic 8—Statistics and probability Topic 9—Sets, relations and groups Topic 10—Series and differential equations Topic 11—Discrete mathematics 40 hrs 40 hrs 40 hrs 40 hrsPortfolio• mathematical investigation • mathematical modelling.10 hrsTwo pieces of work, based on different areas of the syllabus, representing the following two types of tasks:8© International Baccalaureate Organization 2006SYLLABUS DETAILSFormat of the syllabusThe syllabus to be taught is presented as three columns. • Content: the first column lists, under each topic, the sub-topics to be covered. • Amplifications/inclusions: the second column contains more explicit information on specific sub-topics listed in the first column. This helps to define what is required in terms of preparing for the examination. • Exclusions: the third column contains information about what is not required in terms of preparing for the examination. Although the mathematics HL course is similar in content to parts of the mathematics SL course, there are differences. In particular, students and teachers are expected to take a more sophisticated approach for mathematics HL, during the course and in the examinations. Where appropriate, guidelines are provided in the second and third columns of the syllabus details (as indicated by the phrase “See SL guide”). Teaching notes and calculator suggestions linked to the syllabus content are contained in a separate publication.Course of studyTeachers are required to teach all the sub-topics listed for the seven topics in the core, together with all the sub-topics in the chosen option. The topics in the syllabus do not need to be taught in the order in which they appear in this guide. Similarly, it is not necessary to teach all the topics in the core before starting to teach an option. Teachers should therefore construct a course of study that is tailored to the needs of their students and that integrates the areas covered by the syllabus, and, where necessary, the presumed knowledge (PK).Integration of portfolio assignmentsThe two pieces of work for the portfolio, based on the two types of tasks (mathematical investigation and mathematical modelling), should be incorporated into the course of study, and should relate directly to topics in the syllabus. Full details of how to do this are given in the section on internal assessment.Time allocationThe recommended teaching time for higher level courses is 240 hours. For mathematics HL, it is expected that 10 hours will be spent on work for the portfolio. The time allocations given in this guide are approximate, and are intended to suggest how the remaining 230 hours allowed for the teaching of the syllabus might be allocated. However, the exact time spent on each topic depends on a number of factors, including the background knowledge and level of preparedness of each student. Teachers should therefore adjust these timings to correspond to the needs of their students.© International Baccalaureate Organization 20069SYLLABUS DETAILSUse of calculatorsStudents are expected to have access to a graphic display calculator (GDC) at all times during the course. The minimum requirements are reviewed as technology advances, and updated information will be provided to schools. It is expected that teachers and schools monitor calculator use with reference to the calculator policy. Regulations covering the types of calculator allowed are provided in the Vade Mecum. Further information and advice is provided in the teacher support material. There are specific requirements for calculators used by students studying the statistics and probability option.Mathematics HL information bookletBecause each student is required to have access to a clean copy of this booklet during the examination, it is recommended that teachers ensure students are familiar with the contents of this document from the beginning of the course. The booklet is provided by the IBO and is published separately.Teacher support materialsA variety of teacher support materials will accompany this guide. These materials will include suggestions to help teachers integrate the use of GDCs into their teaching, guidance for teachers on the marking of portfolios, and specimen examination papers and markschemes. These will be distributed to all schools.External assessment guidelinesIt is recommended that teachers familiarize themselves with the section on external assessment guidelines, as this contains important information about the examination papers. In particular, students need to be familiar with notation the IBO uses and the command terms, as these will be used without explanation in the examination papers.Presumed knowledgeGeneralStudents are not required to be familiar with all the topics listed as PK before they start this course. However, they should be familiar with these topics before they take the examinations, because questions assume knowledge of them. Teachers must therefore ensure that any topics designated as PK that are unknown to their students at the start of the course are included at an early stage. They should also take into account the existing mathematical knowledge of their students to design an appropriate course of study for mathematics HL. This list of topics is not designed to represent the outline of a course that might lead to the mathematics HL course. Instead, it lists the knowledge, together with the syllabus content, that is essential to successful completion of the mathematics HL course Students must be familiar with SI (Système International) units of length, mass and time, and their derived units.10© International Baccalaureate Organization 2006SYLLABUS DETAILSTopicsNumber and algebraRoutine use of addition, subtraction, multiplication and division using integers, decimals and fractions, including order of operations. Example: 2 ( 3 + 4 × 7 ) = 62 . Simple positive exponents. Examples: 23 = 8 ; (−3)3 = −27 ; (−2) 4 = 16 .Simplification of expressions involving roots (surds or radicals).Examples:27 + 75 = 8 3 ;3 × 5 = 15 .Prime numbers and factors, including greatest common factors and least common multiples. Simple applications of ratio, percentage and proportion, linked to similarity. Definition and elementary treatment of absolute value (modulus), a . Rounding, decimal approximations and significant figures, including appreciation of errors. Expression of numbers in standard form (scientific notation), that is, a × 10k , 1 ≤ a < 10 , k ∈ .Concept and notation of sets, elements, universal (reference) set, empty (null) set, complement, subset, equality of sets, disjoint sets. Operations on sets: union and intersection. Commutative, associative and distributive properties. Venn diagrams. Number systems: natural numbers; integers, ; rationals, , and irrationals; real numbers, .Intervals on the real number line using set notation and using inequalities. Expressing the solution set of a linear inequality on the number line and in set notation. The concept of a relation between the elements of one set and between the elements of one set and those of another set. Mappings of the elements of one set onto or into another, or the same, set. Illustration by means of tables, diagrams and graphs. Basic manipulation of simple algebraic expressions involving factorization and expansion. Examples: ab + ac = a(b + c) ; (a ± b) 2 = a 2 + b 2 ± 2ab ; a 2 − b 2 = (a − b)(a + b) ; 3x 2 + 5 x + 2 = (3 x + 2)( x + 1) ; xa − 2a + xb − 2b = ( x − 2)(a + b) . Rearrangement, evaluation and combination of simple formulae. Examples from other subject areas, particularly the sciences, should be included. The linear function xax + b and its graph, gradient and y-intercept.Addition and subtraction of algebraic fractions with denominators of the form ax + b .Example:2x 3x + 1 + . 3x − 1 2 x + 4ac > bc ; a > b, c < 0 5 . 7 ac < bc .The properties of order relations: <, , >, . Examples: a > b, c > 0Solution of equations and inequalities in one variable, including cases with rational coefficients. Example: 3 2x 1 − = (1 − x ) 7 5 2 x=Solution of simultaneous equations in two variables.© International Baccalaureate Organization 200611SYLLABUS DETAILSGeometryElementary geometry of the plane including the concepts of dimension for point, line, plane and space. Parallel and perpendicular lines, including m1 = m2 , and m1m2 = −1 . Geometry of simple plane figures. The function x ax + b : its graph, gradient and y-intercept.Angle measurement in degrees. Compass directions and bearings. Right-angle trigonometry. Simple applications for solving triangles. Pythagoras’ theorem and its converse. The Cartesian plane: ordered pairs ( x, y ) , origin, axes. Mid-point of a line segment and distance between two points in the Cartesian plane. Simple geometric transformations: translation, reflection, rotation, enlargement. Congruence and similarity, including the concept of scale factor of an enlargement. The circle, its centre and radius, area and circumference. The terms “arc”, “sector”, “chord”, “tangent” and “segment”. Perimeter and area of plane figures. Triangles and quadrilaterals, including parallelograms, rhombuses, rectangles, squares, kites and trapeziums (trapezoids); compound shapes.StatisticsDescriptive statistics: collection of raw data, display of data in pictorial and diagrammatic forms (for example, pie charts, pictograms, stem and leaf diagrams, bar graphs and line graphs). Calculation of simple statistics from discrete data, including mean, median and mode.12© International Baccalaureate Organization 2006Core syllabus contentTopic 1—Core: AlgebraAimsThe aim of this section is to introduce students to some basic algebraic concepts and applications.20 hrsDetailsContent 1.1 Amplifications/inclusions ExclusionsArithmetic sequences and series; sum of finite arithmetic series; geometric sequences and series; sum of finite and infinite geometric series. Sigma notation.Examples of applications: compound interest and population growth.1.2Exponents and logarithms. Laws of exponents; laws of logarithms. Change of base.Elementary treatment only is required.log b a =log c a . log c b Formula for n Pr . Permutations where some objects are identical.1.3Counting principles, including permutations and Simple applications only. combinations. n The formula for also denoted by n Cr . r The binomial theorem: expansion of ( a + b) n , n ∈ .See SL guide© International Baccalaureate Organization 200613Topic 1—Core: Algebra (continued)Content 1.4 Amplifications/inclusions ExclusionsProof by mathematical induction. Forming conjectures to be proved by mathematical induction.Proof of binomial theorem.1.5Complex numbers: the number i = −1 ; the terms real part, imaginary part, conjugate, modulus and argument. Cartesian form z = a + ib . Modulus–argument form z = r ( cosθ + isin θ ) . Awareness that z = r ( cosθ + isin θ ) can be written as z = r eiθ and z = r cisθ . The complex plane. The complex plane is also known as the Argand diagram. Loci in the complex plane.1.6 1.7Sums, products and quotients of complex numbers. De Moivre’s theorem. Powers and roots of a complex number. Proof by mathematical induction for n ∈+.1.8Conjugate roots of polynomial equations with real coefficients.Equations with complex coefficients.© International Baccalaureate Organization 200614Topic 2—Core: Functions and equationsAims26 hrsThe aims of this section are to explore the notion of function as a unifying theme in mathematics, and to apply functional methods to a variety of mathematical situations. It is expected that extensive use will be made of a GDC in both the development and the application of this topic.DetailsContent 2.1 Amplifications/inclusions ExclusionsConcept of function f : x range; image (value).f ( x) : domain,On examination papers: if the domain is the set The term “codomain”. of real numbers then the statement “ x ∈ ” will be omitted. The composite function ( f g )( x) is defined as f ( g ( x)) . Distinction between one-to-one and many-to-one functions. Domain restriction.See SL guideComposite functions f g ; identity function.Inverse function f −1 .2.2The graph of a function; its equation y = f ( x) .On examination papers: questions may be set that require the graphing of functions that do not explicitly appear on the syllabus.Function graphing skills: use of a GDC to graph a variety of functions investigation of key features of graphs solutions of equations graphically. Identification of asymptotes. May be referred to as roots of equations, or zeros of functions.© International Baccalaureate Organization 200615Topic 2—Core: Functions and equations (continued)Content 2.3 Amplifications/inclusions ExclusionsTransformations of graphs: translations; stretches; reflections in the axes.Translations: y = f ( x) + b; y = f ( x − a ) . Stretches: y = pf ( x); y = f ( x q ) . Reflections (in both axes): y = − f ( x); y = f (− x) . Examples: y = x 2 used to obtain y = 3 x 2 + 2 by a stretch of scale factor 3 in the y-direction 0 . followed by a translation of 2y = sin x used to obtain y = 3sin 2 x by a stretch of scale factor 3 in the y-direction and a 1 stretch of scale factor in the x-direction. 2 The graph of y = f −1 ( x) as the reflection in the line y = x of the graph of y = f ( x) . The graph of y = 1 from y = f ( x) . f ( x)The graphs of the absolute value functions, y = f ( x) and y = f ( x ) .2.4The reciprocal function x graph; its self-inverse nature.1 , x ≠ 0 : its x© International Baccalaureate Organization 200616。
