平面解析几何抛物线.pdf
抛物线课件-2025届高三数学一轮复习

A. 2
B. 3
[解析]
2
C. 4
2
D. 8
由题意,知抛物线的焦点坐标为( ,0),椭圆的焦点坐标为(±
2
所以 = 2 ,解得 p =8,故选D.
D )
2 ,0),
5. 已知抛物线 y 2=2 px ( p >0)的焦点为 F ,点 M (2,2 2 )为抛物线上一点,则
|MF|=(
A. 2
2
即 p =2,所以A选项正确.
= − 3( − 1),
对于B,不妨设 M ( x 1, y 1), N ( x 2, y 2), x 1< x 2,联立方程得 2
= 4,
1
消去 y 并整理得3 x 2-10 x +3=0,解得 x 1= , x 2=3.由抛物线的定义得,| MN|=
x 1+ x 2+ p =
B )
B. 3
C. 4
D. 5
[解析] 因为点 M (2,2 2 )为抛物线上一点,所以将点 M 的坐标代入抛物线的方程
y 2=2 px ( p >0),可得 p =2,所以抛物线的方程为 y 2=4 x ,可得其准线方程为 x =
-1.根据抛物线的定义,得| MF |=2-(-1)=3.故选B.
三、知识点例题讲解及方法技巧总结
1
S △ AOB = ×| AB |× ×
2
2
由(2)的推导过程可得,
sin
1
||
2
+
= 2 ,
1−cos
1+cos
si
1
2
α= × 2 × ×
2
si
2
+
《解析几何》第17讲 抛物线的几何性质

例题3. 已知抛物线 y2 = 6x , 求以点M(4,1)为中点的
弦所在直线的方程.
嵊州市长乐中学
课后自己探究
例1.过抛物线y2=2px(p>0)的焦点的一条直线和 抛物线相交,两交点为A(x1,y1)、B(x2,y2),则
(1)|AB|=x1+x2+p
(2)通径长为2 p (3)x1x2=p2/4; (4) y1y2=-p2;
O B y A
θ F
x
1 1 2 (5) AF BF p
嵊州市长乐中学
课堂小结
1. 会利用定义解题. 2.注意过不过焦点的弦. 3. 数形结合、转化化归和分类讨论.
嵊州市长乐中学
Байду номын сангаас
此时P点的坐标为 (2,2)
.
M Q
P F
P1
A(3,2)
|PA| + |PF| = |PA| + |PQ|
≥ |AM|=3+0.5
嵊州市长乐中学
探究二. 抛物线的最值问题
变式1. 已知点P是以F为焦点的抛物线 y2=2x 的一动 点, 过P分别作直线x= -1/2和4x-3y+6=0的垂线,
垂足为A,B, 则|PA|+ |PB|的最小值是
抛物线的几何性质
第17讲
探究一. 方程中P 的几何意义
y
B
P 的几何意义是:
[ 焦点到准线的距离 ]
K
O
F A
x
[
P = |FK|
]
l
嵊州市长乐中学
例题1.作业选做题2
p=2 P/2=1 10 10 K F 8
y2=4x
p=18 P/2=9 10
平面解析几何 抛物线
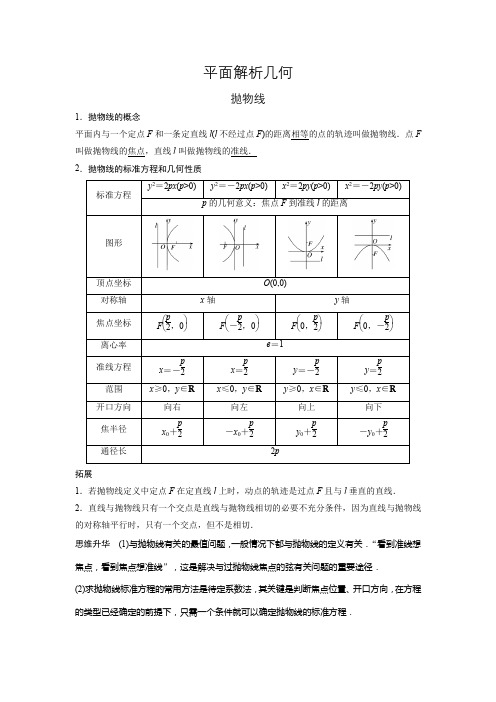
平面解析几何抛物线1.抛物线的概念平面内与一个定点F 和一条定直线l (l 不经过点F )的距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的准线. 2.抛物线的标准方程和几何性质标准方程y 2=2px (p >0)y 2=-2px (p >0)x 2=2py (p >0)x 2=-2py (p >0)p 的几何意义:焦点F 到准线l 的距离图形顶点坐标 O (0,0)对称轴 x 轴y 轴焦点坐标 F ⎝⎛⎭⎫p 2,0F ⎝⎛⎭⎫-p 2,0F ⎝⎛⎭⎫0,p 2F ⎝⎛⎭⎫0,-p 2离心率 e =1准线方程 x =-p 2 x =p 2 y =-p 2 y =p 2 范围 x ≥0,y ∈Rx ≤0,y ∈Ry ≥0,x ∈Ry ≤0,x ∈R开口方向 向右 向左 向上 向下 焦半径 x 0+p 2-x 0+p 2y 0+p 2-y 0+p 2通径长2p拓展1.若抛物线定义中定点F 在定直线l 上时,动点的轨迹是过点F 且与l 垂直的直线. 2.直线与抛物线只有一个交点是直线与抛物线相切的必要不充分条件,因为直线与抛物线的对称轴平行时,只有一个交点,但不是相切.思维升华 (1)与抛物线有关的最值问题,一般情况下都与抛物线的定义有关.“看到准线想焦点,看到焦点想准线”,这是解决与过抛物线焦点的弦有关问题的重要途径.(2)求抛物线标准方程的常用方法是待定系数法,其关键是判断焦点位置、开口方向,在方程的类型已经确定的前提下,只需一个条件就可以确定抛物线的标准方程.思维升华 在解决与抛物线的性质有关的问题时,要注意利用几何图形的形象、直观的特点来解题,特别是涉及焦点、顶点、准线的问题更是如此.思维升华 (1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点.若过抛物线的焦点(设焦点在x 轴的正半轴上),可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.提醒:涉及弦的中点、斜率时一般用“点差法”求解. (4)设AB 是过抛物线y 2=2px (p >0)焦点F 的弦, 若A (x 1,y 1),B (x 2,y 2),则 ①x 1x 2=p 24,y 1y 2=-p 2.②弦长|AB |=x 1+x 2+p =2psin 2α(α为弦AB 的倾斜角). ③以弦AB 为直径的圆与准线相切.④通径:过焦点垂直于对称轴的弦,长等于2p ,通径是过焦点最短的弦.题型一 抛物线的定义和标准方程 命题点1 定义及应用例1 设P 是抛物线y 2=4x 上的一个动点,F 是抛物线y 2=4x 的焦点,若B (3,2),则|PB |+|PF |的最小值为________. 答案 4解析 如图,过点B 作BQ 垂直准线于点Q ,交抛物线于点P 1, 则|P 1Q |=|P 1F |.则有|PB |+|PF |≥|P 1B |+|P 1Q |=|BQ |=4, 即|PB |+|PF |的最小值为4.本例中的B 点坐标改为(3,4),则|PB |+|PF |的最小值为________.答案 25解析 由题意可知点B (3,4)在抛物线的外部.∵|PB |+|PF |的最小值即为B ,F 两点间的距离,F (1,0), ∴|PB |+|PF |≥|BF |=22+42=25,即|PB |+|PF |的最小值为2 5.若将本例中的条件改为已知抛物线方程为y 2=4x ,直线l 的方程为x -y +5=0,在抛物线上有一动点P 到y 轴的距离为d 1,到直线l 的距离为d 2,则d 1+d 2的最小值为________. 答案 32-1解析 由题意知,抛物线的焦点为F (1,0).点P 到y 轴的距离d 1=|PF |-1,所以d 1+d 2=d 2+|PF |-1.易知d 2+|PF |的最小值为点F 到直线l 的距离,故d 2+|PF |的最小值为|1+5|12+(-1)2=32,所以d 1+d 2的最小值为32-1. 命题点2 求标准方程例2 (1)顶点在原点,对称轴为坐标轴,焦点为直线3x -4y -12=0与坐标轴的交点的抛物线的标准方程为( ) A .x 2=-12y 或y 2=16x B .x 2=12y 或y 2=-16x C .x 2=9y 或y 2=12x D .x 2=-9y 或y 2=-12x答案 A解析 对于直线方程3x -4y -12=0,令x =0,得y =-3;令y =0,得x =4,所以抛物线的焦点为(0,-3)或(4,0).当焦点为(0,-3)时,设抛物线方程为x 2=-2py (p >0),则p2=3,所以p =6,此时抛物线的标准方程为x 2=-12y ;当焦点为(4,0)时,设抛物线方程为y 2=2px (p >0),则p2=4,所以p =8,此时抛物线的标准方程为y 2=16x .故所求抛物线的标准方程为x 2=-12y 或y 2=16x .(2)设抛物线C :y 2=2px (p >0)的焦点为F ,点M 在C 上,|MF |=5,若以MF 为直径的圆过点(0,2),则C 的标准方程为( ) A .y 2=4x 或y 2=8x B .y 2=2x 或y 2=8x C .y 2=4x 或y 2=16x D .y 2=2x 或y 2=16x答案 C解析 由题意知,F ⎝⎛⎭⎫p 2,0,抛物线的准线方程为x =-p 2,则由抛物线的定义知,x M =5-p 2,设以MF 为直径的圆的圆心为⎝⎛⎭⎫52,y M 2,所以圆的方程为⎝⎛⎭⎫x -522+⎝⎛⎭⎫y -y M 22=254,又因为圆过点(0,2),所以y M =4,又因为点M 在C 上,所以16=2p ⎝⎛⎭⎫5-p 2,解得p =2或p =8,所以抛物线C 的标准方程为y 2=4x 或y 2=16x ,故选C.跟踪训练1 (1)若抛物线y 2=2px (p >0)上一点到焦点和到抛物线对称轴的距离分别为10和6,则抛物线的方程为( ) A .y 2=4x B .y 2=36xC .y 2=4x 或y 2=36xD .y 2=8x 或y 2=32x 答案 C解析 因为抛物线y 2=2px (p >0)上一点到抛物线的对称轴的距离为6,所以若设该点为P , 则P (x 0,±6).因为P 到抛物线的焦点F ⎝⎛⎭⎫p 2,0的距离为10,所以由抛物线的定义得x 0+p 2=10.① 因为P 在抛物线上,所以36=2px 0.②由①②解得p =2,x 0=9或p =18,x 0=1,则抛物线的方程为y 2=4x 或y 2=36x .(2)(2020·四川资阳、眉山、遂宁、广安四市联考)已知点A (-1,0)是抛物线y 2=2px 的准线与x 轴的交点,F 为抛物线的焦点,P 是抛物线上的动点,则|PF ||P A |的最小值为( ) A.13 B.22 C.45 D.32答案 B解析 由题设知p =2,设点P (x ,y ),点P 到直线x =-1的距离为d ,则d =x +1. 所以|PF ||P A |=d|P A |=x +1(x +1)2+4x =11+4x (x +1)2=11+4xx 2+2x +1=11+4x +1x +2≥22.故当且仅当x =1x ,即x =1时等号成立,即当x =1时,|PF ||P A |取得最小值22.题型二 抛物线的几何性质例3 (1)(2020·广西四校联考)已知抛物线y 2=2px (p >0)上横坐标为4的点到此抛物线焦点的距离为9,则该抛物线的焦点到准线的距离为( ) A .4 B .9 C .10 D .18 答案 C解析 抛物线y 2=2px 的焦点为⎝⎛⎭⎫p 2,0,准线方程为x =-p 2.由题意可得4+p 2=9,解得p =10,所以该抛物线的焦点到准线的距离为10.(2)设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,O 为坐标原点,则△OAB 的面积为( ) A.334 B.938 C.6332 D.94 答案 D解析 由已知得焦点坐标为F ⎝⎛⎭⎫34,0,因此直线AB 的方程为y =33⎝⎛⎭⎫x -34,即4x -43y -3=0. 方法一 联立直线方程与抛物线方程化简得4y 2-123y -9=0, 则y A +y B =33,y A y B =-94,故|y A -y B |=(y A +y B )2-4y A y B =6. 因此S △OAB =12|OF ||y A -y B |=12×34×6=94.方法二 联立直线方程与抛物线方程得x 2-212x +916=0,故x A +x B =212.根据抛物线的定义有|AB |=x A +x B +p =212+32=12,同时原点到直线AB 的距离为d =|-3|42+(-43)2=38,因此S △OAB =12|AB |·d =94.(3)已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →,则|QF |等于( ) A.72 B.52 C .3 D .2 答案 C解析 利用|FP →|=4|FQ →|转化长度关系,再利用抛物线定义求解. ∵FP →=4FQ →,∴|PQ ||PF |=34.如图,过Q 作QQ ′⊥l ,垂足为Q ′,设l 与x 轴的交点为A ,则|AF |=4, ∴|PQ ||PF |=|QQ ′||AF |=34.∴|QQ ′|=3,根据抛物线定义可知|QQ ′|=|QF |=3.跟踪训练2 (1)从抛物线y 2=4x 在第一象限内的一点P 引抛物线准线的垂线,垂足为M ,且|PM |=9,设抛物线的焦点为F ,则直线PF 的斜率为( ) A.627 B.1827 C.427 D.227 答案 C解析 设P (x 0,y 0),由抛物线y 2=4x ,可知其焦点F 的坐标为(1,0),故|PM |=x 0+1=9,解得x 0=8,故P 点坐标为(8,42),所以k PF =0-421-8=427.(2)以原点为顶点,y 轴为对称轴的抛物线Ω与正方形ABCD 有公共点,其中A (2,2),B (4,2),C (4,4),则抛物线Ω的焦点F 到准线l 的最大距离为( ) A.12 B .4 C .6 D .8 答案 B解析 由题意可得D (2,4),设抛物线Ω:x 2=2py ,p >0,要使得抛物线Ω与正方形ABCD 有公共点,其临界状态应该是过B 或过D ,把B ,D 的坐标分别代入抛物线方程,得42=2p ×2,或22=2p ×4,可得p =4或p =12,故抛物线的焦点F 到准线l 的最大距离为4.题型三 直线与抛物线例4 (2018·全国Ⅱ)设抛物线C :y 2=4x 的焦点为F ,过F 且斜率为k (k >0)的直线l 与C 交于A ,B 两点,|AB |=8. (1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程. 解 (1)由题意得F (1,0),l 的方程为y =k (x -1)(k >0). 设A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =k (x -1),y 2=4x 得k 2x 2-(2k 2+4)x +k 2=0. Δ=16k 2+16>0,故x 1+x 2=2k 2+4k 2.所以|AB |=|AF |+|BF |=(x 1+1)+(x 2+1)=4k 2+4k 2. 由题意知4k 2+4k 2=8,解得k =-1(舍去)或k =1. 因此l 的方程为x -y -1=0.(2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为y -2=-(x -3), 即y =-x +5.设所求圆的圆心坐标为(x 0,y 0),则⎩⎪⎨⎪⎧y 0=-x 0+5,(x 0+1)2=(x 0-y 0-1)22+16,解得⎩⎪⎨⎪⎧ x 0=3,y 0=2或⎩⎪⎨⎪⎧x 0=11,y 0=-6. 因此所求圆的方程为(x -3)2+(y -2)2=16或(x -11)2+(y +6)2=144.跟踪训练3 在平面直角坐标系xOy 中,抛物线C :y 2=2px (p >0)的焦点为F ,点A (1,a )(a >0)是抛物线C 上一点,且|AF |=2. (1)求p 的值;(2)若M ,N 为抛物线C 上异于A 的两点,且AM ⊥AN .记点M ,N 到直线y =-2的距离分别为d 1,d 2,求d 1d 2的值.解 (1)因为点A (1,a )(a >0)是抛物线C 上一点,且|AF |=2, 所以p2+1=2,所以p =2. (2)由(1)得抛物线方程为y 2=4x .因为点A (1,a )(a >0)是抛物线C 上一点,所以a =2.设直线AM 方程为x -1=m (y -2)(m ≠0),M (x 1,y 1),N (x 2,y 2).由⎩⎪⎨⎪⎧x -1=m (y -2),y 2=4x 消去x , 得y 2-4my +8m -4=0, 即(y -2)(y -4m +2)=0, 所以y 1=4m -2.因为AM ⊥AN ,所以用-1m 代替m , 得y 2=-4m -2,所以d 1d 2=|(y 1+2)(y 2+2)|=⎪⎪⎪⎪4m ×⎝⎛⎭⎫-4m =16.。
第七节 抛物线 课件(共48张PPT)

(4)|A1F|+|B1F|=2p. (5)以弦AB为直径的圆与准线相切.
题组一 小题自测 1.(人A选修2-1·习题改编)过点P(-2,3)的抛物线 的标准方程是( ) A.y2=-92x或x2=43y B.y2=92x或x2=43y C.y2=92x或x2=-43y D.y2=-92x或x2=-43y
考点2 抛物线的标准方程与几何性质
角度 求抛物线方程
[例2] (1)抛物线y2=2px(p>0)的焦点为F,O为坐标
原点,M为抛物线上一点,且|MF|=4|OF|,△MFO的面
积为4 3,则抛物线的方程为( )
A.y2=6x
B.y2=8x
C.y2=16x
D.y2=152π
(2)设抛物线C:y2=2px(p>0)的焦点为F,点M在C 上,|MF|=5.若以MF为直径的圆过点(0,2),则C的方 程为( )
1.(2020·全国卷Ⅰ)已知A为抛物线C:y2=2px(p>0)
上一点,点A到C的焦点的距离为12,到y轴的距离为9,
则p=( )
A.2
B.3
C.6 D.9
解析:法一 因为点A到y轴的距离为9,所以可设
点A(9,yA),
所以y2A=18p.又点A到焦点p2,0的距离为12,
所以 9-p22+y2A=12,所以9-p22+18p=122,
A.y2=4x或y2=8x B.y2=2x或y2=8x C.y2=4x或y2=16x D.y2=2x或y2=16x 解析:(1)设M(x,y),因为|OF|=p2,|MF|=4|OF|, 所以|MF|=2p, 由抛物线定义知x+p2=2p,所以x=32p, 所以y=± 3p.
又△MFO的面积为4 3,
高考总复习一轮数学精品课件 第九章 平面解析几何 第七节 抛物线

方程为
5
x=- =- ,所以点
2 4
A 到抛物线 C 的准线的距离为
5
1+
4
=
9
.
4
增素能 精准突破
考点一京海淀一模)已知抛物线y2=4x的焦点为F,点P在该抛物线上,
且P的横坐标为4,则|PF|=(
A.2
B.3
)
C.4
D.5
(2)设F为抛物线C:y2=4x的焦点,点A在C上,点B(3,0),若|AF|=|BF|,则
F
B.
1
0, 16
.
考点二
抛物线的标准方程与简单几何性质
典例突破
例2.已知抛物线C:y2=2px(p>0)的焦点为F,准线为l,点M是抛物线C上一点,
过点M作准线l的垂线,交l于点H,若|MH|=2,∠HFM=30°,则抛物线C的标准
方程为
.
答案 y2=6x
解析 因为抛物线上的点到焦点的距离等于其到准线的距离,
距离相等
,直线l叫做抛物线的
的点的轨
准线 .
设点M是抛物线上的任意一点,它到准线l的距离为d,则抛物线定义的表达
式为|MF|=d
微思考抛物线定义中,若直线l过点F,则点的轨迹会怎么样?
提示 若直线l过点F,则到点F与到直线l距离相等的点的轨迹是过点F且与l
垂直的直线.
2.抛物线的标准方程和简单几何性质
y=x+2,联立
=
+2,
2 = 2,
得x2-2px-p2=0.
设A(x1,y1),B(x2,y2),
则x1+x2=2p,x1x2=-p2,不妨设x1>0,x2<0,
解析几何《抛物线》

解析几何【7】抛物线1、抛物线的定义、图像与性质2、直线与抛物线的位置关系联立直线:l y kx m 和抛物线22y px (0p )消y ,整理得 22220k x km p x m .(1)当0k 时,①0 直线与抛物线相交,有两个不同公共交点;②0 直线与抛物线相切,只有一个公共交点;③0 直线与抛物线相离,没有公共交点.(2)当0k 时,则直线是抛物线的对称轴或是与对称轴平行的直线,此时直线与抛物线相交,只有一个公共交点,但不能称为相切.向右向左向上向下0x ,y R 0x ,y R 0y ,x R 0y ,x R图像关于x 轴对称图像关于y 轴对称原点0,0O ,02p F ,02p F 0,2p F 0,2p Fp xp x2p yp y【温馨点睛】1、抛物线的定义实质上给出了一个重要的内容:可将抛物线上的点到焦点的距离转化为到准线的距离,可以使运算化繁为简.2、求抛物线标准方程的两种方法(1)定义法:根据条件确定动点满足的几何特征,从而确定p 的值,得到抛物线的标准方程.(2)待定系数法:根据条件设出标准方程,再确定p 的值,这里要注意抛物线标准方程有四种形式.从简单化角度出发,焦点在x 轴的,设为2y ax (0a ),焦点在y 轴的,设为2x ay (0a ).3、设过抛物线22y px (0p )的焦点,02p F的直线与抛物线交于 11,A x y 、 22,B x y ,直线OA 与212AB x x p ;【例(1)(2)【同类变式】设直线l 的方程为210x By ,倾斜角为 .(1)试将 表示为B 的函数;(2)若263,求B 的取值范围:(3)若 ,21,B ,求 的取值范围.【例(1)(2)(3)【同类变式】求适合下列条件的直线方程.(1)经过点 0,2A ,它的倾斜角的正弦值是35;(2)经过点 5,2B ,且在x 轴上的截距等于在y 轴上截距的2倍;(3)经过点 5,4C ,与两坐标轴围成的三角形面积为5.【考点三】直线过定点问题【例3】已知直线 :2311l a y a x .(1)求证;无论a 为何值,直线l 总经过第一象限;(2)直线l 是否有可能不经过第二象限?若有可能,求出a 的范围;若不可能,说明理由.【同类变式】已知直线方程为 22140m x m y .(1)该直线是否经过定点?若经过,求出该点坐标;若不经过,说明你的理由;(2)当m 为何值时,点 3,4Q 到直线的距离最大,最大值为多少?(3)当m 在什么范围时,该直线与两坐标轴负半轴均相交?【考点四】求与最值有关的直线方程【例4】如图,已知直线l 过点 3,2P ,且与x 轴、y 轴的正半轴分别交于A 、B 两点,求ABO 的面积的最小值及此时直线l 的方程.【同类变式】(1)若本例条件不变,求OA OB 的最小值及此时直线l 的方程;(2)若本例条件不变,求PA PB的最大值及此时直线l 的方程.【真题自测】1.现有下列四个命题:①经过定点 000,P x y 的直线都可以用方程 00y y k x x ;②经过任意两个不同的点 111,P x y 、 222,P x y 的直线都可以用方程121121x x y y y y x x 表示;③不经过原点的直线都可以用方程1x ya b表示:④经过定点0,A b 的直线都可以用方程y kx b 表示..A 0;2..A .B .C .D 3.直线:tan105l x y的倾斜角.4.已知点 2,3A 、 1,4B ,则直线AB 的点法式方程为.5.已知点 3,4A 、 2,2B ,直线20mx y m 与线段AB 相交,则实数m 的取值范围是.6.1212x y y .k ,0k。
《抛物线复习》课件

开口方向与大小
总结词
开口方向与大小是描述抛物线形状的重要参数,对于理解抛物线的几何性质和解决相关问题具有重要意义。
详细描述
抛物线的开口方向由二次函数的二次项系数决定,如果二次项系数大于0,则抛物线开口向上,如果小于0,则抛 物线开口向下。开口大小则由一次项系数和常数项决定,一次项系数决定了抛物线的宽度,常数项决定了抛物线 的高度。
标准方程
总结词
标准方程是y^2=2px(p>0),它描述了抛物线的形状和大小。
详细描述
标准方程是描述抛物线最常用的方程之一,其中p表示焦距的一半,x表示横坐标 ,y表示纵坐标。标准方程可以用来确定抛物线的开口方向、顶点位置和焦点的 位置。通过标准方程,我们可以进一步研究抛物线的几何性质和变化规律。
REPORT
CATALOG
DATE
ANALYSIS
ห้องสมุดไป่ตู้
SUMMAR Y
02
抛物线的几何性质
焦点与准线
总结词
理解抛物线的几何性质是掌握抛物线的基础,而焦点和准线是抛物线几何性质 中的重要概念。
详细描述
抛物线的焦点是抛物线上任一点到焦点的距离等于该点到准线的距离,准线是 与焦点相对的一条直线。了解焦点和准线的性质有助于理解抛物线的几何特性 。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
04
抛物线的解题策略与技 巧
抛物线的标准方程的求解方法
直接法
根据题目给出的条件,直接代入 抛物线的标准方程求解。
待定系数法
根据题目给出的条件,设出抛物线 的标准方程,然后通过已知条件求 解待定系数。
交点法
将抛物线与x轴的交点设为 $(x_{1},0)$和$(x_{2},0)$,然后代 入抛物线的标准方程求解。
第八章第七节抛物线

综 合 训 练 · 能 力 提 升
考 点 突 破 · 规 律 总 结
1 5 定义,y--2= ,y=2,所以 2
以点 M 的坐标为(± 2,2). 答案
菜 单
(± 2,2)
高考总复习·数学(理科)
第八章 平面解析几何
要 点 梳 理 · 基 础 落 实
考点二 抛物线的标准方程及其性质
例2
x2 2 (1)以双曲线 -y =1 的右焦点为焦点, 顶点在 3
原点的抛物线的标准方程是________.
【解析】 抛物线的右焦点为(2,0),所以抛物线的焦
考 点 突 破 · 规 律 总 结
p 点为(2,0),即抛物线的方程为 y =2px,其中 =2,所以 p 2
解析 p 抛物线的准线方程为 x=- ,双曲线 x2-y2 2
综 合 训 练 · 能 力 提 升
考 点 突 破 · 规 律 总 结
p =1 的左顶点为(-1,0),故- =-1,即 p=2. 2 答案 2
菜
单
高考总复习·数学(理科)
第八章 平面解析几何
要 点 梳 理 · 基 础 落 实
菜
单
高考总复习·数学(理科)
第八章 平面解析几何
要 点 梳 理 · 基 础 落 实
[规律方法]
与抛物线有关的最值问题的解题策略
该类问题一般情况下都与抛物线的定义有关.实现
由点到点的距离与点到直线的距离的转化. (1)将抛物线上的点到准线的距离转化为该点到焦点 的距离,构造出 “ 两点之间线段最短 ” ,使问题得
p - ,0 2 ____________
