连续系统零极点分布与频响特性的关系
§4.8由系统函数零、极点分布决定频响特性
m
sin(ω 0 t )
⋅ H( s )
m
0 2 0
2
2 0
2
H(− jω) = H0 e− jϕ0 0
K − jω 0 = ( s + j ω 0 ) R ( s ) K
jω 0
=
K − jω 0 s + jω 0
+
K jω 0 s − jω 0
+
Kn K1 K2 + + ⋅⋅⋅+ s − p1 s − p2 s − pn
θ1
−
1
ψ1
O
1 RC
σ
0.5
π ϕ(ω) = −arctan CRω 2
0
2 1.5 1 0.5 0
π ω= 0 ϕ(ω) = 2 1 π ω= ϕ(ω) = RC 4 ω= ∞ ϕ(ω) = 0
0
2
4
6
8
10
0
2
4
6
8
10
返回
例4-8-2
研究下图所示RC低通滤波网络 研究下图所示RC低通滤波网络 + 的频响特性。 的频响特性。 v1(t ) V2(jω) H(jω) = − V (jω) 1 解: 写出网络转移函数表达式 V2(s) 1 1 H(s) = = ⋅ 1 V (s) RC 1 s+ RC
∏(s − P )
i =1 i
见 可 H(jω)的 性 零 点 位 有 。 特 与 极 的 置关
令分子中每一项 jω− z j = Nj e 分母中每一项
jψj
− ∏( jω p )
i =1 i
jω− P = Mi ejθi i
零极点分布对系统频率响应的影响
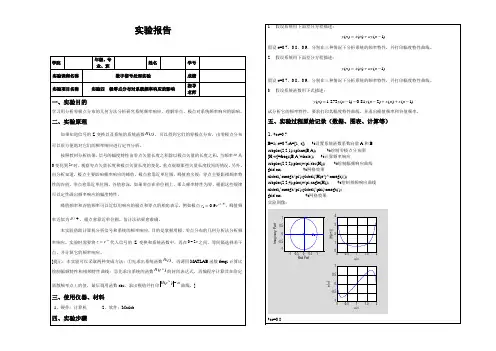
subplot(2,2,1);
zplane(B,A);%绘制零极点分布图
[H,w]=freqz(B,A,'whole');%计算频率响应
subplot(2,2,2);
plot(w/pi,abs(H));grid on;%绘制幅频响应曲线
实验图像：
%a=0.8
B=1;a=0.8;A=[1,-a];%设置系统函数系数向量A和B
subplot(2,2,1);
zplane(B,A);%绘制零极点分布图
[H,w]=freqz(B,A,'whole');%计算频率响应
subplot(2,2,2);
plot(w/pi,abs(H));grid on;%绘制幅频响应曲线
五、实验过程原始记录（数据、图表、计算等）
1.%a=0.7
B=1;a=0.7;A=[1,-a];%设置系统函数系数向量A和B
subplot(2,2,1);zplane(B,A);%绘制零极点分布图
[H,w]=freqz(B,A,'whole');%计算频率响应
subplot(2,2,2);plot(w/pi,abs(H));%绘制幅频响应曲线
grid on;%网格效果
xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|');
subplot(2,2,4);plot(w/pi,angle(H));%绘制相频响应曲线
xlabel('\omega/\pi');ylabel('\phi(\omega)');
零极点对系统的影响
增加零极点以及零极点分布对系统的影响一般说来，系统的极点决定系统的固有特性，而零点对于系统的暂态响应和频率响应会造成很大影响。
以下对于零极点的分布研究均是对于开环传递函数。
零点一般是使得稳定性增加，但是会使调节时间变长，极点会使调节时间变短，是系统反应更快，但是也会使系统的稳定性变差。
在波特图上反应为，增加一个零点会在幅频特性曲线上增加一个+20db/10倍频的曲线，幅频曲线上移，增加一个极点，会在幅频特性曲线上增加一个-20db/10倍频的曲线，幅频曲线下移。
在s左半平面增加零点时，会增加系统响应的超调量，带宽增大，能够减小系统的调节时间，增快反应速度，当零点离虚轴越近，对系统影响越大，当零点实部远大于原二阶系统阻尼系数ξ时，附加零点对系统的影响减小，所以当零点远离虚轴时，可以忽略零点对系统的影响。
从波特图上来看，增加一个零点相当于增加一个+20db/10倍频的斜率，可以使的系统的相角裕度变大，增强系统的稳定性。
在s右半平面增加零点，也就是非最小相位系统，非最小相位系统的相位变化范围较大，其过大的相位滞后使得输出响应变得缓慢。
因此，若控制对象是非最小相位系统，其控制效果特别是快速性一般比较差，而且校正也困难。
对于非最小相位系统而言，当频率从零变化到无穷大时，相位角的便变化范围总是大于最小相位系统的相角范围，当ω等于无穷大时，其相位角不等于-（n-m）×90º。
非最小相位系统存在着过大的相位滞后，影响系统的稳定性和响应的快速性。
在s左半平面增加极点时，系统超调量%pσ减小，调整时间st(s)增大，从波特图上看，s左半平面增加一个极点时，会在幅频特性曲线上增加一个-20db/10倍频的曲线，也就意味着幅频特性曲线会整体下移，导致相角域度减小，从而使得稳定性下降。
当极点离原点越近，就会增大系统的过渡时间，使得调节时间增加，稳定性下降，当系统影响越大当极点实部远大于原二阶系统阻尼系数ξ时，附加极点对系统的影响减小，所以当极点远离虚轴时可以忽略极点对系统的影响。
§4-6 系统函数与系统的频响特性
H (s)
k s1
(s 1)(s 2 )
H ( j)
k j1
( j 1)( j 2 )
系统函数的零极图如下：
《Signals & Systems》
《信号与系统》
大连海事大学信息科学技术学院
⑴ 当Ω=0，零点矢量的模等于0，相角
等于π/2，幅频响应|H( jΩ)|=0；极点 矢量的相角均等于零， φ(Ω)= (π/2)。 1
如上两例RC电路，试根据其零极图，粗略的画出其频响曲线。
先看以电容电压为输出的情况。其零极 图如下：
R
ui (t)
C
uo (t)
⑴ 当Ω=0，极点矢量指向原点，其模长 为α，相角等于0；于是 |H( jΩ)|=α/α=1,φ(Ω)=0。
⑵ 当Ω↑，极点矢量模↑，相角↑； |H( jΩ)|↓,φ(Ω)=-arctg(Ω/α)↓。
《信号与系统》
大连海事大学信息科学技术学院
§4-6 系统函数的零极点分布与系统的频率响应
一、H(s)与H(jΩ)
由前所讲，拉氏变换是傅氏变换由实频域Ω至复频域s的推广， 傅氏变换是拉氏变换在s平面虚轴上的特例。即
j
H ( j) H (s) |s j
二、H(s)的零极点分布与H(jΩ)
由于H(s)一般是有理分式，即它可表示为
s
C (s p1)(s p2)
上式中 1 ( 1 )2 4
p1,2 RC
RC 2
LC
1 ( 1 )2 1 2RC 2RC LC
《Signals & Systems》
《信号与系统》
大连海事大学信息科学技术学院
令 1
2RC
1 LC
由连续系统零极点分布分析系统的频率特性_MATLAB 2014从新手到高手_[共3页]
![由连续系统零极点分布分析系统的频率特性_MATLAB 2014从新手到高手_[共3页]](https://img.taocdn.com/s3/m/5e665dc9c5da50e2534d7f02.png)
由前面分析可知，连续系统的零极点分布完全决定了系统的系统函数 H (S )，显然，系统 的零极点分布也必然包含了系统的频率特性。
下面介绍如何通过系统的零极点分布来直接求出系统的频率响应 H (jω ) 的方法——几何 矢量法，以及如何用 MATLAB 来实现这一过程。
几何矢量法是通过系统函数零极点分布来分析连续系统频率响应 H (jω ) 的一种直观而又 简便的方法。该方法将系统函数的零极点视为 S 平面上的矢量，通过对这些矢量的模和幅角 的分析，即可快速确定出系统的幅频响应和相频响应。
h (t ) 的时域特性完全由系统函数 H (s ) 的极点位置决定，H (s ) 位于 S 平面左半平面的极点决定
了 h (t ) 随时间衰减的信号分量，位于 s 平面虚轴上的极点决定了冲激响应的稳态信号分量，
位于 s 平面右半平面的极点决定了冲激响应随时间增长的信号分量。
13.4.3 由连续系统零极点分布分析系统的频率特性
根据上述结论，若已知系统的零极点分布，即可直接由几何矢量法分析出系统的频率特性。 上述过程可用 MATLAB 快速实现。用 MATLAB 实现已知系统零极点分布，求系统频 率响应，并绘制其幅频特性和相频特性曲线的程序流程如下：首先定义包含系统014 从新手到高手
a=[1 -1 16.25]; b=[1]; impulse(b,a,5) 绘制的冲激响应 h (t ) 波形如下图（f）所示，此时 h (t ) 为按指数增长的正弦振荡信号。
（a）
（b）
（c）
（d）
（e）
（f）
从上述程序运行结果和绘制的系统冲激响应曲线，可以总结出以下规律：系统冲激响应
系统函数零极点分布对系统时域特性的影响
, 极点在实轴上，
h(t) tet u(t), 0, t , h(t) 0
H(s)
(s2
2s
2
)2
,在虚轴上，
h(t) t sintu(t), t , h(t) 增幅振荡
有实际物理意义的物理系统都是因果系统，即随 t ,
ht ，0 这H (表s)明的极点位于左半平面，由此可知，收敛 域包括虚轴， Fs均和存F在( j， )两者可通用，只需 将
（自由／强迫，瞬态／稳态）；
3．可以用来说明系统的正弦稳态特性。
1
二．H(s)零、极点与h(t)波形特征的对应
1．系统函数的零、极点
H (s) A(s) K (s z1 )(s z2 ) (s z j ) (s zm ) B(s) (s p1 )(s p2 ) (s pk ) (s pn )
零输入响应／零状态响应
s2 3s 2Rs s 3Es sr0 r0 3r0
则
Rzi s
sr0 r0 3r0
s2 3s 2
零输入响应为:
Rzs
s
s 3Es
s2 3s 2
rzi (t) 4et 3e2t t 0
即零状态响应为:
rzs (t) 0.5e 2t 2e t 1.5 (t 0)
即可s 。 j 6
三．H(s) 、E(s)的极点分布与自由响应、强迫响应特性的对应
激励： e(t) E(s) u
系统函数：h(t) Hm(s)
(s zl )
(s zj )
E(s) l1 v
H (s) j1 n
(s Pk )
(s Pi )
k 1
响应： r(t) R(s)
u
m
(s zl ) (s zj )
§5.8 系统函数的零极点与时域特性和频域特性的关系
有实际物理意义的物理系统都是因果系统，即随 t , h t 0 ，这表明H ( s ) 的极点位于左半平面。
X
1.2 由H(s) 的零、极点确定系统的时域响应
激励： e( t ) u E ( s )
E (s)
l 1 v
( s zl )
H ( s) 系统函数： h( t ) m H (s)
X
第 15 页
2.1 H(s)和频响特性的关系
设系统函数为 H s ，激励源 e t Em sinω0 t 系统的稳态响应 rss t E m H 0 sin ω0 t 0 其中H s s j ω0 H j ω0 H 0 e j0
平面内。
j ω pi M i e j θi
将 j ω z j、 j ω pi 都看作两矢量之差，将矢量图画于复
X
第 18 页
画零极点图
零点 ： jω N j e
jψ j
zj
极点 ： j ω M i e jθi pi
θi
jω
Mi pi
Nj
ψj
jω
Nj
zj
j
zj
O
σ
jω 是滑动矢量， jω 矢量变 , 则 N j、 ψ j 和 M i、 θ i 都 发生变化。
当α 0 ，极点在左半平面，衰减振荡 当 α 0 ，极点在右半平面，增幅振荡
X
第 7页
二阶极点
1 H ( s ) 2 , 极点在原点, h( t ) tu( t ), t , h( t ) s 1 H ( s) , 极点在实轴上， 2 (s a) h( t ) t e t u( t ),α 0, t , h( t ) 0 2s H (s) 2 , 在虚轴上， 2 2 (s ω ) h( t ) t sin tu( t ), t , h( t ) 增幅振荡
由系统函数零极点分布决定频响特性
i 1
X
第 8
页
m
j
ω
z
j
H jω
Hs s
jω
K
j1 n
j ω pi
i 1
令分子中每一项 jω z j N j ejψ j
分母中每一项 jω Pi Mi ejθi
将 jω z j、jω - pi都看作两矢量之差，将矢量图画于复 平面内。
s j0
K j0
s j0
Em H 2j
0
(
e j 0
s j0
s
e
j 0
j0
)
X
上式的逆变换为
第 4
页
LБайду номын сангаас1
K s
j 0
j0
K s
j 0
j
0
Em H0 2j
e
j 0
e
j 0 t
e
j 0
e
j0t
X
第
画零极点图
9
页
零点 ： jω N j ejψj z j 极点 ： jω Mi ejθi pi
jω
jω
θi
Mi
Nj
zj
j
pi Nj
zj
ψj
σ O
σ O
jω是滑动矢量，jω 矢量变动,则N j、ψ j和 Mi、θi都
发生变化。
X
由矢量图确定频率响应特性
第 10
页
H
jω
K
3 页
信号与系统实验六 连续系统的零极点及频率响应特性
实验名称：连续系统的零极点及频率响应特性报告人：姓名班级学号一、实验目的1、掌握系统函数零极点的定义；2、用MA TLAB实现部分分式展开；3、掌握零极点与频率响应的关系；4、掌握极点与系统稳定性的关系。
二、实验内容及运行结果1、已知下列系统函数H（s）或状态方程，求及其零极点，并且画出零极点图，试判断系统是否稳定，根据零极点位置推导单位冲激响应的形式，求解系统的冲激响应h(t)和频率响应H（w）。
(1)num=[1 0 1]; %分子系数，按降幂顺序排列den=[1 2 5]; %分母系数，按降幂顺序排列[z,p]=tf2zp(num,den); %求零点z和极点pfigure(1)zplane(z,p) %作出零极点图sys=tf(num,den);poles=roots(den)figure(2);pzmap(sys)t=0:0.02:10;h=impulse(num,den,t); %绘制冲激响应曲线figure(3);plot(t,h)title('Impulse Respone')[H,w]=freqs(num,den); %绘制频率响应曲线figure(4);plot(w,abs(H))xlabel('\omega')title('Magnitude Respone')poles =-1.0000 + 2.0000i-1.0000 - 2.0000i系统的稳定性和频响特点：由于系统函数的极点位于s虚轴，故系统稳定；并且单位冲激响应是等幅振荡（单位阶跃）信号。
(2)num=[3 -9 6]; %分子系数，按降幂顺序排列den=[1 2 2]; %分母系数，按降幂顺序排列[z,p]=tf2zp(num,den); %求零点z和极点pfigure(1)zplane(z,p) %作出零极点图sys=tf(num,den);poles=roots(den)figure(2);pzmap(sys)t=0:0.02:10;h=impulse(num,den,t); %绘制冲激响应曲线figure(3);plot(t,h)title('Impulse Respone')[H,w]=freqs(num,den); %绘制频率响应曲线figure(4);plot(w,abs(H))xlabel('\omega')title('Magnitude Respone')poles =-1.0000 + 1.0000i-1.0000 - 1.0000i系统的稳定性：由于系统函数的极点位于s右半平面，故系统不稳定；单位冲激响应是随时间增长的信号。
由系统函数零、极点分布决定频响特性
j 1 n
M1
H ( j ) k
( j z )
j
p1
N1
( j p )
i i 1
j 1 n
z1
j 1
j z1 N1e
j p1 M1e
j1
5
H ( j ) k
( j z j ) ( j p )
i i 1 j 1 n
28
对第四章的基本要求
理解拉普拉斯变换的定义；熟练掌握拉普拉斯 变换的性质、卷积定理的意义及它们的运用。 能利用拉普拉斯变换求解线性系统的冲激响应、 零输入响应、零状态响应和全响应。能根据系 统函数的零、极点分布情况分析、判断系统的 时域与频域特性，掌握频响特性曲线的几何作 图法。理解全通网络、最小相移网络的概念。 会判定系统的稳定性。
17
极点相同，零点以jw轴成镜 像，则它们的幅频特性相同
18
对应零点在左半面的图
对应零点在右半面的图
“最小相移网络” ：零点仅位于左半平面或 虚轴上的网络函数称为“最小相移网络”。 前提条件：极点都位于左半平面即为稳定系统。
19
非最小相移网络
非最小相移网络 可以看成最小相 移网络和全通网 络的级联
s j 0 t
0
单边拉氏变换
傅氏变换
s j t
LT [ f ( t )] FT [ f ( t )u( t )e t ] ( s j )
26
由已知的单边拉氏变换求取傅里叶变换 前提条件：函数f(t)为有始信号， 即当t<0时，f(t)=0。
29
最小相移网络
全通网络 不是最小相移网络
22
4.11 线性系统的稳定性 稳定系统对于有界激励信号产生有 界的响应函数（有界输入有界输出 BIBO系统）。 稳定性是系统自身的性质之一，系 统是否稳定与激励信号的情况无关 系统的冲激响应h(t)和系统函数 H(s)也表征了系统的稳定性
4-8由系统函数零、极点分布决定频响特性
j0
Em H ( j0 ) Em H 0e j0 2j 2j
0
其中 H ( j0 ) H0e j
H ( j0 ) H0e j0
Em H 0 j (0t 0 ) j ( 0t 0 ) RS ( s) e e 2j
rs (t ) Em H0 sin(0t 0 )
N
U 2 ( s) R s H ( s) 1 U1 ( s) R 1 s sc RC
—
H ( j ) | H ( j ) | e
j ( )
N j ( ) e M
j
0, N 0, M 1 RC N M 0 90 0 90
( jω p )
i i 1
j 1 n
ψ i θl ) N1 N 2 N m j ( k e i1 l 1 M 1M 2 M n
m
n
三 .一阶二阶系统的S平面分析
已知某系统的H(s)的零极点在S平面的分 布，根据几何法确定该系统的幅频特性 和相频特性的趋势和渐近线
e(t ) Em sin 0t
稳态响应
e(t)与e(t)通过系统后产生的稳态响应有什么异同？
系统频率响应特性
H (s) |s jω0 H ( jω0 ) H 0e | H ( jω0 ) | e
jφ0
jφ ( ω0 )
当正弦信号频率 ω改变时，则： H ( s ) |s jω H ( jω) H ( jω) e
M1
N N H ( j ) M M
( ) ( ) ( ` )
推广：
j p1 M1e
完整word版,信号与系统matlab实验 习题4 连续系统的零极点分布与频响特性的关系
连续系统零极点分布与频响特性的关系（答案在下方）1. 连续系统零极点图的画法pzplot()函数可用来绘制连续系统的零极点图，具体用法如下：pzplot(SYS) 计算LTI 模型SYS 的零点和极点并绘制零、极点图。
其中SYS 的产生可以采用传递函数法：SYS=tf(b,a)，b 和a 分别为系统函数的分子多项式和分母多项式系数矩阵。
例1：系统函数为()232251241420s s H s s s s ++=+++，完成一幅适当标注的零极点图。
解：MATLAB 代码如下：b=[2 5 12]; a=([1 4 14 20]); SYS=tf(b,a); pzplot(SYS);系统的零极点图如图1所示。
图1 例1系统的零极点图P ole-Zero MapReal AxisI m a g i n a r y A x i s2. 由系统的零极点分布决定系统的频率响应特性稳定的连续时间系统的频率响应特性可以由系统函数得到()()()()()()11j j 11j j j mmjjj j s ωs ωnniii i s z ωz H ωH s KKs p ωp ======--===--∏∏∏∏ (1)令分子中每一项j j ejψj j ωz N -=,分母中每一项j j e iθi i ωp M -=，则 ()1212j j j 12j j j 12e e e j e e e mnψψψm θθθn N N N H ωKM M M =L L (2) ()1212j mnN N N H ωKM M M =L L (3)()()()1212m n ωψψψθθθφ=++-++L L (4)分析频率响应特性的方法： 1.()()j j s ωH ωH s ==，带入数值，得到()j H ωω～的分布；2.根据零极点图中零极点的分布，用几何的方法定性判断系统的频率响应特性；3.对模拟系统，MATLAB 信号处理工具箱提供了freqs()函数是用来求取模拟滤波器的频率响应。
4-4系统函数零极点∽频响特性,拉氏变换VS傅里叶变换
m
( j p )
i i 1
j 1 n
频率特性取决于零、极点 z j , pi的分布
j z j N j e j j 令 ji j pi M i e
矢量：模、辐角
j
Mi
pi
i
Nj
j
zj
O
N1e j1 N 2e j 2 N me j m H ( j ) K M 1e j1 M 2e j2 M n e jn N1 N 2 N m j[(1 2 m ) (1 2 n )] K e M 1M 2 M n H ( j ) e
R
L
1 解： 令 Z1 sL, Z 2 ，则 Z1Z 2 R 2 sC 从 v2 端向左应用戴维南定理，
2Z1Z 2 Z Z1 V1 ( s) 2 内阻为 ，等效电源为 Z 2 Z1 Z1 Z 2
V2 ( s ) Z 2 Z1 ( Z 2 Z1 ) R R H (s) V1 ( s ) Z 2 Z1 R 2 Z 2 Z1 ( Z 2 Z1 ) R 2Z 2 Z1 Z 2 Z1 Z 2 Z1 Z 2 Z1 2 Z 2 Z1 R Z 2 Z1 R Z1 L R Z 2 Z1 R Z1 s L s
j ( )
j
Mi
pi
i
Nj
j
zj
N1 N 2 N m H ( j ) K M 1M 2 M n 其中 ( ) ( ) ( ) 1 2 m 1 2 n
0
[例2] 研究图示的 RC 高通滤波网络的频响特性
1 1 z1 0, p1 , p2 R1C1 R2C2
第四章零极点分布与频响特性
1绝对值减小， 2增大， 1 90 减小；
3)当 0时，电路谐振 1 N1 1 1 1 M 1 M 2 2 N1 , C M 1 M 2 C 2 G
为最大值；
1 2 90 , 1 90 , 1 1 2 0
当较高时， M 2 N1,1 1, 也可认为 它们不随 而变，极点 p1的作用与一阶 RC 低通系统一致，构成 高端的低通特性；
M 2 N1 j , 2 1 90 , 那么H j 可近似写作 k j H j 1 k 1 R1C1 1 j R2C2 R1C1 R1C1 这时的频响特性近似于常数
1 当位于中间频率范围时， 同时满足 M 1 ,1 0， R1C1
注：1)在低频端，主要是R2C2的高通滤波起作用； 2)在高频端，是R1C1的低通滤波起主要作用； 3)在中频端，C1相当于开路，C2相当于短路，电路为电阻网 络，幅频特性为常数； 4)该系统是带通滤波系统。 4－9 二阶谐振系统的s平面分析 含有L、C两类储能元件的二阶系统可具有谐振特性，利用 这一性质也可构成带通、带阻滤波网络。 一、GLC谐振电路的阻抗特性
V2 s 1 Z s V1 s G sC 1 sL 1 s C s p1 s p2
G 1 G 其中， p1, 2 2C 2C LC G 1 2 令 , 0 , d 0 2 2C LC p1, 2 jd 讨论： 1)0为谐振频率； 0 G 2) 为衰减因子， 越大，表示电路的损耗 越大；
2C 2Q C 3)Q 0 称为品质因数， Q愈高，电路的损耗越小 ； G
2
二、随电路损耗α 的改变Z(s)的极点位置分布（ω 0不变）
连续系统零极点分布与频响特性的关系连续系统的表示
连续系统零极点分布与频响特性的关系1. 连续系统的表示()()()()()()()12121212b b a a n n b n n a b s b s b n H s a s a s a n ----+++=+++通过下面例子，说明B, A 矩阵的写法：(a) ()20.532s H s s s +=++ [1,0.5];B = [1,3,2];A = (b) ()2132H s s s =++ [1];B = [1,3,2];A =(c) ()232sH s s s =++ [1 ];0B = [1,3,2];A =注意：(c)的B 矩阵由于缺少常数项，故补了一个0。
2.连续系统零极点图的画法pzplot()函数可用来绘制连续系统的零极点图，具体用法如下：pzplot(SYS) 计算LTI 模型SYS 的零点和极点并绘制零、极点图。
其中SYS 的产生可以采用传递函数法：SYS=tf(b,a)，b 和a 分别为系统函数的分子多项式和分母多项式系数矩阵。
例1：系统函数为()232251241420s s H s s s s ++=+++，完成一幅适当标注的零极点图。
解：MATLAB 代码如下：b=[2 5 12]; a=([1 4 14 20]); % 创建系统模型 SYS=tf(b,a); % 绘制零极点图 pzplot(SYS);系统的零极点图如图1所示。
图1 例1系统的零极点图3. 由系统的零极点分布决定系统的频率响应特性MATLAB 信号处理工具箱提供了freqs()函数是用来求取连续系统的频率响应。
具体函数的用法是：H=freqs(B, A, W) 返回模拟滤波器的频率响应()j H ω，即复数频率响应矩阵H ，其中的B 、A 是已知系统的传递函数模型，W 为已选定的频率点。
如果直接使用freqs(B, A, W)，则直接绘制幅度响应和相位响应曲线，不返回任何值。
如果缺省频率范围W ，函数将自动选用一组200个频率点范围。
信号与系统4.7.8系统零极点分布决定时域和频域特性
H(s)
s2
ω ω2
,
p1 jω, 在虚轴上
h(t) sinωtu(t)，等幅振荡
H(s)
(s
ω α )2
ω2
,
p1 α jω, p2 α j, 共轭根
α 0
α 0
第4章 拉普拉斯变换、连续时间系统的S域分析
若 H(s)具有多重极点，那么， 部分分式展开 式各项所对应的时间函数可能具有t,t2,t3,…与指 数函数相乘的形式，t的幂次由极点阶次决定。
第4章 拉普拉斯变换、连续时间系统的S域分析
几种典型情况的极点分布 与原函数波形的对应关系
(1)若极点位于s平面坐标原点，Hi (s)
1 s
，那么，冲
激响应就为阶跃函数，hi (t) u(t) 。
j
t
第4章 拉普拉斯变换、连续时间系统的S域分析
(2)若极点位于平面的实轴上，则冲激响应具有指数
函数形式。
17 2 16
]
10 et 10 cos(4t) 40 sin(4t)
17 17
17
10 et 10 cos(4t 760 )
17
17
强迫 响应
第4章 拉普拉斯变换、连续时间系统的S域分析
瞬态响应是指激励信号接入以后，完全响应中瞬时出现 的有关部分，随着时间增大，它将消失。
稳态响应 等于完全响应中减去瞬态响应。
如
L1[
(s
2
2s 2
)2
]
t
sin(t
)
这是幅度按线性增长的正弦振荡。
j
t sin(t)
t
j
第4章 拉普拉斯变换、连续时间系统的S域分析
几种典型情况
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
-1 100
-2
0
Phase (degrees)
-3
-100
-4
-4
-3
-2
-1
0
1
2
3
4
Real Axis (seconds-1)-200ຫໍສະໝຸດ 10-210-1100
101
Frequency (rad/s)
零极点图
频率特性曲线图
形
Magnitude
0
10
-1
10
-2
10
-3
10
-2
-1
0
1
10
10
10
10
Frequency (rad/s)
100
50
0
-50
-100
-2
-1
0
1
10
10
10
10
Frequency (rad/s)
频率特性曲线图 形
(5) H5(s)
;
程序如下：
close all b=[1 0 0]; a=([1 3 2]); SYS=tf(b,a); pzplot(SYS); axis([-4,4 -2,2]); figure; freqs(b,a);
MATLAB 绘制的零、极点图和频率响应特性曲线如图所示。 可知该系统具有全通滤波特性。
Imaginary Axis (seconds-1)
Pole-Zero Map 4
4.00196e-14
10
Magnitude
3
100
2
-4.00196e-14
10
1
-2
-1
0
1
10
10
10
10
Frequency (rad/s) 0
Magnitude
0
10 10-1 10-2
-3
10 10-2
100 50 0 -50
-100 10-2
10-1
100
101
Frequency (rad/s)
10-1
100
101
Frequency (rad/s)
频率特性曲线图 形
(6) H6(s)
;
程序如下：
close all b=[1 0]; a=([1 2 10]); SYS=tf(b,a); pzplot(SYS); axis([-4,4 -4,4]); figure; freqs(b,a);
100
50
0
Phase (degrees)
-3
-50
-4
-4
-3
-2
-1
0
1
2
3
4
-100 10-2
10-1
100
101
Real Axis (seconds-1)
Frequency (rad/s)
频率特性曲线图
形
零极点图
(7) H7(s)
;
程序如下：
close all b=[1 -3 2]; a=([1 3 2]); SYS=tf(b,a); pzplot(SYS); axis([-4,4 -4,4]); figure; freqs(b,a);
Magnitude
100
10-1
-2
10
-3
10
10-2
10-1
100
101
Frequency (rad/s)
0
-50
-100
-150
-200
-2
-1
0
1
10
10
10
10
Frequency (rad/s)
频率特性曲线图
形
零极点图
(4) H4(s)
;
程序如下：
close all b=[1 0]; a=([1 3 2]); SYS=tf(b,a); pzplot(SYS); axis([-4,4 -2,2]); figure; freqs(b,a);
MATLAB 绘制的零、极点图和频率响应特性曲线如图所示。 可知该系统具有带通滤波特性。
Imaginary Axis (seconds-1)
Pole-Zero Map 2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-4
-3
-2
-1
0
1
2
3
4
Real Axis (seconds-1)
零极点图
Phase (degrees)
;
Magnitude
Phase (degrees)
10-0.1
10-0.4
-0.7
10
-1
10 0 -20 -40 -60 -80
-1
10
0
1
10
10
Frequency (rad/s)
0
1
10
10
Frequency (rad/s)
频率特性曲线图 形
程序如下：
close all b=[1 0]; a=([1 2]); SYS=tf(b,a); pzplot(SYS); axis([-4,4 -2,2]); figure; freqs(b,a);
Magnitude
0
10
10-1
10-2
-3
10
10-2
10-1
100
101
Frequency (rad/s)
100
50
0
10-2
10-1
100
101
Frequency (rad/s)
频率特性曲线图 形
(3) H3(s)
;
程序如下：
close all b=[1]; a=([1 3 2]); SYS=tf(b,a); pzplot(SYS); axis([-4,4 -2,2]); figure; freqs(b,a);
MATLAB 绘制的零、极点图和频率响应特性曲线如图所示。 可知该系统具有高通滤波特性。
Imaginary Axis (seconds-1)
Pole-Zero Map 2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-4
-3
-2
-1
0
1
2
3
4
Real Axis (seconds-1)
零极点图
Phase (degrees)
MATLAB 绘制的零、极点图和频率响应特性曲线如图所示。
可知该系统具有高通滤波特性。
Imaginary Axis (seconds-1)
Pole-Zero Map 2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-4
-3
-2
-1
0
1
2
3
4
Real Axis (seconds-1)
零极点图
Phase (degrees)
MATLAB 绘制的零、极点图和频率响应特性曲线如图所示。
可知该系统具有低通滤波特性。
Imaginary Axis (seconds-1)
Pole-Zero Map 2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-4
-3
-2
-1
0
1
2
3
4
Real Axis (seconds-1)
零极点图
(2) H2(s)
连续系统零极点分布与频响特性的关系
班级：02 学号：2014210
请利用 MATLAB 软件绘制下列因果系统的零极点图和频率响应特性曲 线，并分析系统的滤波特性。
(1) H1(s)
;
程序如下：
close all b=[2]; a=([1 2]); SYS=tf(b,a); pzplot(SYS); axis([-4,4 -2,2]); figure; freqs(b,a);
MATLAB 绘制的零、极点图和频率响应特性曲线如图所示。 可知该系统具有带通滤波特性。
Imaginary Axis (seconds-1)
Pole-Zero Map 4 3 2 1 0 -1 -2
Magnitude
0
10
-1
10
-2
10
-3
10
10-2
10-1
100
101
Frequency (rad/s)
MATLAB 绘制的零、极点图和频率响应特性曲线如图所示。
可知该系统具有低通滤波特性。
Imaginary Axis (seconds-1)
Pole-Zero Map 2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-4
-3
-2
-1
0
1
2
3
4
Real Axis (seconds-1)
Phase (degrees)